Формула нахождения куба: Объем куба — формула, калькулятор онлайн и примеры расчета

3=a*a*a — то есть сторона куба, возведенная в третью степень.

1. В чем измеряется объем куба
2. Чему равен объем куба если ребро 5 см
3. Чему равен объем
4. Чему равен объем куба со стороной 1 м
5. Как рассчитать объем в кубах
6. Какая формула объема
7. Чему равен объем куба с ребром 12 см
8. Чему равен объем куба с ребром 11 см
9. Как найти площадь и объем куба
10. Как измеряется объем
11. Что измеряет объем
12. Как найти объем в математике
13. Чему равен объем в куба со стороной а
14. Как найти объем куба со стороной 10 см
15. Как найти сторону куба по его объему
16. Почему 3 в кубе 27
17. Что такое измерения куба
18. Что измеряется в кубе
19. Чему равен объем куба с ребром 9 см
20. Чему равен объем куба с ребром 8
21. Чему равен объем куба с ребром 3 см
22. Как найти объем воды
23. В чем измеряется объем воды
24. Как найти объем по массе
25. Что измеряется в кубах
26. Как правильно считать куб

В чем измеряется объем куба

Куби́ческий метр (от куб и метр) (кубометр) (м3) — единица объёма, производная в Международной системе единиц (СИ), а также в системах единиц МКГСС и МТС. Одному кубическому метру равен объём куба с длиной ребра 1 метр.

Чему равен объем куба если ребро 5 см

Объем куба считается перемножением длины, высоты и ширины. Они у куба равны. V = 5 * 5 * 5 = 125 куб.

Чему равен объем

Объём тела определяется его формой и линейными размерами. Основное свойство объёма — аддитивность, то есть объём любого тела равен сумме объёмов его (непересекающихся) частей.

Объём
Размерность	L3
Единицы измерения
СИ	м3
СГС	см3

Чему равен объем куба со стороной 1 м

1 000 000 / 1 = 1 000 000 кубов. Ответ: 1 000 000.

Как рассчитать объем в кубах

Объем кубической или прямоугольной тары можно рассчитать самостоятельно, используя школьные знания по геометрии. Для этого используется простая формула: умножаем длину, ширину и высоту.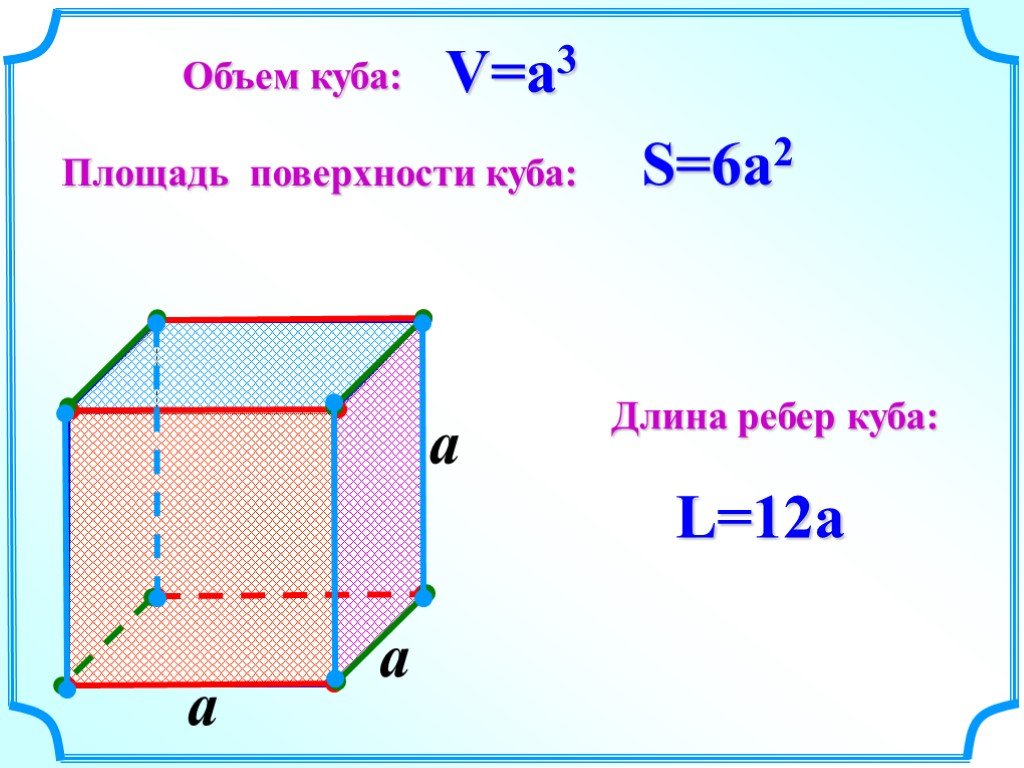

Какая формула объема

Объем рассчитывается по формуле V=πr2h. То есть умножаем число π (3,14159) на радиус в квадрате и на высоту h цилиндра. Пример: есть вертикальный цилиндрический резервуар диаметром 3 метра и высотой 5 метров. Рассчитываем объем: Радиус — 1,5 метра, в квадрате будет 2,25.

Чему равен объем куба с ребром 12 см

V = a 3 = 12 3 = 12 * 12 * 12 = 144 * 12 = 1728 (см 3). Ответ: таким образом, объем искомого куба составляет 1728 см 3. Как добавить хороший ответ?

Чему равен объем куба с ребром 11 см

То есть если длина куба ровна 11 см надо: Vк. =11•11•11=1331(см3)-объём куба (это писать не обязательно если в начале твита написал Vк.=).

Как найти площадь и объем куба

Объём куба равен произведению его ширины, на длину и на высоту. У куба все ребра равны. V = 4 * 4 * 4 = 4³ = 64 дм³; Площадь поверхности куба равна сумме площадей его граней.

Как измеряется объем

В международной системе единиц (СИ) единицей объёма является метр кубический м 3. 3, где V куба — объем куба, а — длина ребра куба (все они у куба равны между собой). Исходя из приведенной формулы, чтобы определить ребро куба, необходимо извлечь корень третьей степени из его объема.

Почему 3 в кубе 27

Число 27 можно представить в виде числа 3 в кубе. Тогда выражение (х³ + 27), можно представить в виде выражения (х³ + 3³). Теперь, применяя формулы сокращенного умножения, а именно, формулу суммы кубов, мы можем разложить данное выражение на множители: х³ + 27 = х³ + 3³ = (х + 3) * (х² — 3х + 3²).

Что такое измерения куба

Измерение куба представляет собой экземпляр измерения базы данных в пределах куба. Измерение базы данных может быть использовано в нескольких кубах, а измерения нескольких кубов могут быть основаны на одном измерении базы данных. В следующей таблице описаны свойства измерения куба.

Что измеряется в кубе

Кубическими метрами измеряется объем какого-либо вещества. Объем куба, все стороны которого равны одному метру, равен одному кубическому метру.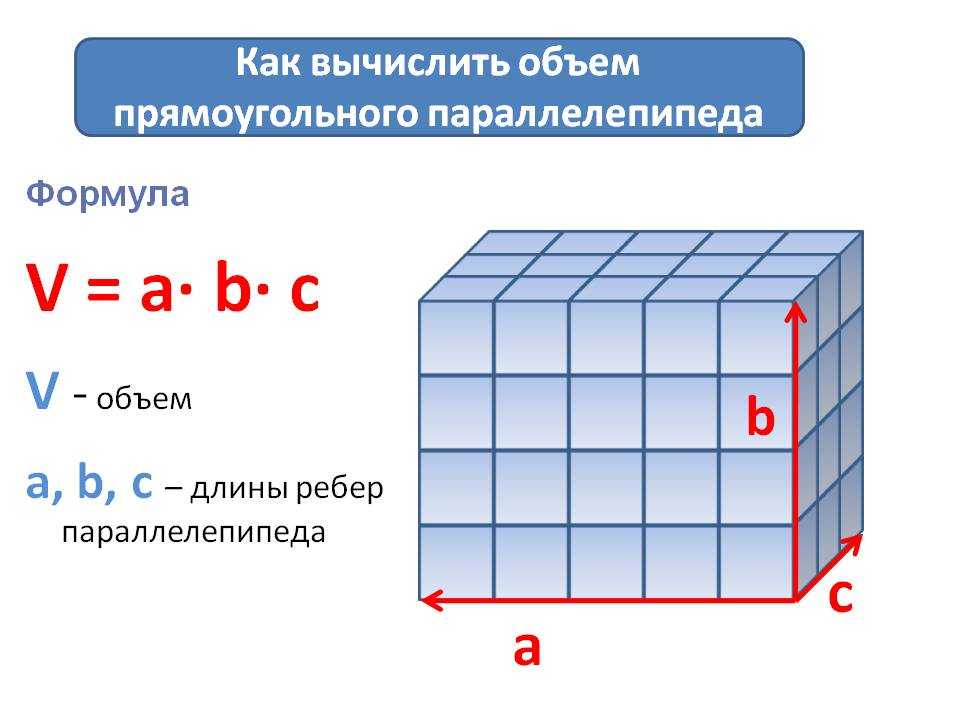 Этой величиной пользуются для измерения количества жидкостей, для вычисления нужного количества бетона, либо древесины.

Чему равен объем куба с ребром 9 см

4) Вычислим объем куба при а = 9 / 3 = 3 дм: V2 = а3 = 33 = 27 дм3.

Чему равен объем куба с ребром 8

Так как у куба ширина, длина и высота равные, то обозначим длину, ширину и высоту как 8 см. Чтобы найти объем такого куба, нужно умножить длину на ширину и на высоту: 8 * 8 * 8 = 512 см3. По этому запишем получившийся ответ: объем куба равен 512 см3.

Чему равен объем куба с ребром 3 см

Ответ: V = 27 см кубических, S поверхности куба = 54 см квадратных.

Как найти объем воды

V — обьем воды, S — скорость наполнения, t — время:

• Чтобы найти обьем воды V, перемножим скорость наполнения (л/ч) — d на время t. V = d * t.
• Для нахождения времени t, необходимо разделить обьем воды на скорость наполнения p.
• Чтобы вычислить скорость наполнения S, разделим обьем V на скорость наполнения t.

В чем измеряется объем воды

Литр (фр. litre, от лат. litra — мера ёмкости; русское обозначение — л; международное — L или l) — внесистемная метрическая единица измерения объёма и вместимости, равная 1 кубическому дециметру (дм³).

Как найти объем по массе

Если известна масса материала, то объем можно узнать по формуле: V = m/ p. При этом необходимо учитывать, что низкая плотность означает большую пустотность материала.

Что измеряется в кубах

Что такое кубатура

Пиломатериал измеряется в кубических метрах — кубометрах — кубах — общепринятых единицах меры. Куб — это единица объема, равная произведению 3 величин: высоты, ширины и длины. Все величины равны 1 метру.

Как правильно считать куб

При помощи формулы нахождения объема прямоугольного параллелепипеда, мы можем рассчитать ее объем: V = a * b * h, где V — это объем в метрах кубических, a — длина в метрах, b — ширина в метрах, h — высота в метрах.

Формулы куба и параллелепипеда.

Как найти объем в кубических метрах

Видеокурс «Получи пятерку» включает все темы, необходимые для успешной сдачи ЕГЭ по математике на 60-65 баллов. Полностью все задачи 1-13 Профильного ЕГЭ по математике. Подходит также для сдачи Базового ЕГЭ по математике. Если вы хотите сдать ЕГЭ на 90-100 баллов, вам надо решать часть 1 за 30 минут и без ошибок!

Курс подготовки к ЕГЭ для 10-11 класса, а также для преподавателей. Все необходимое, чтобы решить часть 1 ЕГЭ по математике (первые 12 задач) и задачу 13 (тригонометрия). А это более 70 баллов на ЕГЭ, и без них не обойтись ни стобалльнику, ни гуманитарию.

Вся необходимая теория. Быстрые способы решения, ловушки и секреты ЕГЭ. Разобраны все актуальные задания части 1 из Банка заданий ФИПИ. Курс полностью соответствует требованиям ЕГЭ-2018.

Курс содержит 5 больших тем, по 2,5 часа каждая. Каждая тема дается с нуля, просто и понятно.

Сотни заданий ЕГЭ. Текстовые задачи и теория вероятностей. Простые и легко запоминаемые алгоритмы решения задач. Геометрия. Теория, справочный материал, разбор всех типов заданий ЕГЭ. Стереометрия. Хитрые приемы решения, полезные шпаргалки, развитие пространственного воображения. Тригонометрия с нуля — до задачи 13. Понимание вместо зубрежки. Наглядное объяснение сложных понятий. Алгебра. Корни, степени и логарифмы, функция и производная. База для решения сложных задач 2 части ЕГЭ.

Измерьте все необходимые расстояния в метрах. Объем многих трехмерных фигур легко вычислить по соответствующим формулам. Однако все значения, подставляемые в формулы, должны измеряться в метрах. Таким образом, перед подстановкой значений в формулу убедитесь, что все они измеряются в метрах, или что вы конвертировали другие единицы измерения в метры.

• 1 мм = 0,001 м
• 1 см = 0,01 м
• 1 км = 1000 м

Для вычисления объема прямоугольных фигур (прямоугольный параллелепипед, куб) используйте формулу: объем = L × W × H (длину умножить на ширину умножить на высоту).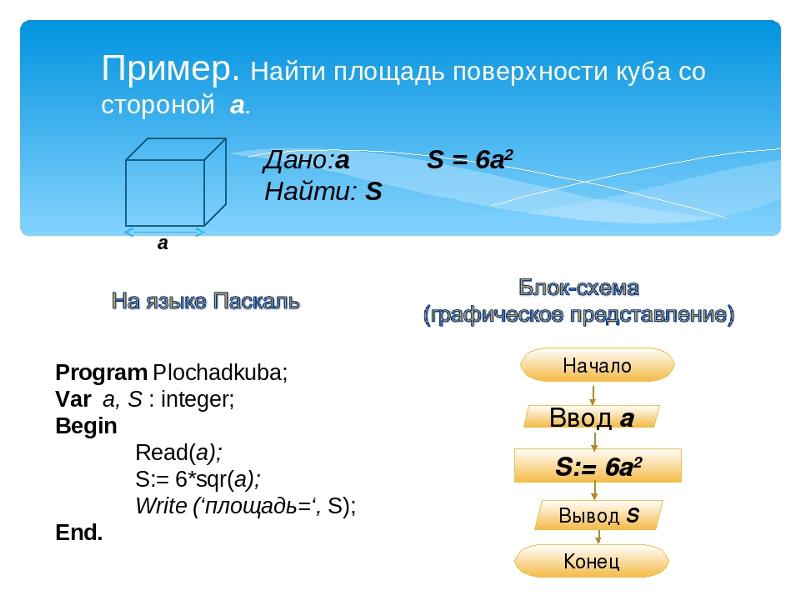 Эту формулу можно рассматривать как произведение площади поверхности одной из граней фигуры на ребро, перпендикулярное этой грани.

• Например, вычислим объем комнаты длиной 4 м, шириной 3 м и высотой 2,5 м. Для этого просто умножим длину на ширину и на высоту:
  • 4 × 3 × 2,5
  • = 12 × 2,5
  • = 30. Объем этой комнаты равен 30 м 3 .
• Куб – объемная фигура, у котрой все стороны равны. Таким образом, формулу для вычисления объема куба можно записать в виде: объем = L 3 (или W 3 , или H 3).

Для вычисления объема фигур в виде цилиндра используйте формулу:

пи × R 2 × H. Вычисление объема цилиндра сводится к умножению площади круглого основания на высоту (или длину) цилиндра. Найдите площадь круглого основания, умножив число пи (3,14) на квадрат радиуса круга (R) (радиус — расстояние от центра окружности до любой точки, лежащей на этой окружности). Затем полученный результат умножьте на высоту цилиндра (H), и вы найдете объем цилиндра. Все значения измеряются в метрах.

• Например, вычислим объем колодца диаметром 1,5 м и глубиной 10 м. Разделите диаметр на 2, чтобы получить радиус: 1,5/2=0,75 м.
  • (3,14) × 0,75 2 × 10
  • = (3,14) × 0,5625 × 10
  • = 17,66. Объем колодца равен 17,66 м 3 .

Для вычисления объема шара используйте формулу: 4/3 х пи × R 3 . То есть вам нужно знать только радиус (R) шара.

• Например, вычислим объем воздушного шара диаметром 10 м. Разделите диаметр на 2, чтобы получить радиус: 10/2=5 м.
  • 4/3 х пи × (5) 3
  • = 4/3 х (3,14) × 125
  • = 4,189 × 125
  • = 523,6. Объем воздушного шара равен 523,6 м 3 .

Для вычисления объема фигур в виде конуса используйте формулу: 1/3 х пи × R 2 × H. Объем конуса равен 1/3 объема цилиндра, который имеет такую же высоту и радиус.

• Например, вычислим объем конуса мороженного радиусом 3 см и высотой 15 см. Конвертируя в метры, получим: 0,03 м и 0,15 м соответственно.
  • 1/3 х (3,14) × 0,03 2 × 0,15
  • = 1/3 х (3,14) × 0.0009 × 0,15
  • = 1/3 × 0.0004239
  • = 0,000141. Объем конуса мороженного равен 0,000141 м 3 .

Для вычисления объема фигур неправильной формы используйте несколько формул.

Для этого попробуйте разбить фигуру на несколько фигур правильной формы. Затем найдите объем каждой такой фигуры и сложите полученные результаты.

• Например, вычислим объем небольшого зернохранилища. Хранилище имеет цилиндрический корпус высотой 12 м и радиус 1,5 м. Хранилище также имеет коническую крышу высотой 1 м. Вычислив отдельно объем крыши и отдельно объем корпуса, мы можем найти общий объем зернохранилища:
  • пи × R 2 × H + 1/3 х пи × R 2 × H
  • (3,14) × 1,5 2 × 12 + 1/3 х (3,14) × 1,5 2 × 1
  • = (3,14) × 2,25 × 12 + 1/3 х (3,14) × 2,25 × 1
  • = (3,14) × 27 + 1/3 х (3,14) × 2,25
  • = 84,822 + 2,356
  • = 87,178. Объем зернохранилища равен 87,178 м 3 .

Любое геометрическое тело можно охарактеризовать площадью (S) поверхности и объемом (V). Площадь и объем совсем не одно и то же. Объект может иметь сравнительно небольшой V и большую S, например, так устроен мозг человека. Вычислить данные показатели для простых геометрических фигур гораздо проще.

Параллелепипед: определение, виды и свойства

Параллелепипед – это четырехугольная призма, в основании которой находится параллелограмм. Для чего же может потребоваться формула нахождения объема фигуры? Подобную форму имеют книги, упаковочные коробки и еще множество вещей из повседневной жизни. Комнаты в жилых и офисных домах, как правило, являются прямоугольными параллелепипедами. Для установки вентиляции, кондиционеров и определение количества обогревательных элементов в комнате необходимо рассчитать объем помещения.

У фигуры 6 граней – параллелограммов и 12 ребер, две произвольно выбранные грани называют основаниями.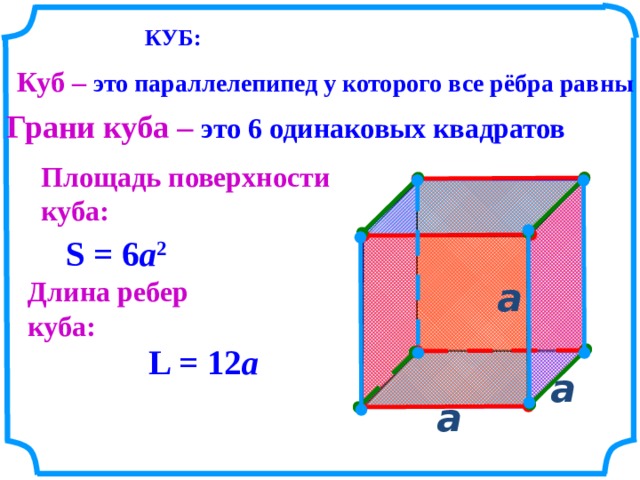 Параллелепипед может быть нескольких видов. Различия обусловлены углами между смежными ребрами. Формулы для нахождения V-ов различных многоугольников немного отличаются.

Если 6 граней геометрической фигуры представляют собой прямоугольники, то ее тоже называют прямоугольной. Куб – это частный случай параллелепипеда, в котором все 6 граней представляют собой равные квадраты. В этом случае, чтобы найти V, нужно узнать длину только одной стороны и возвести ее в третью степень.

Для решения задач понадобятся знания не только готовых формул, но свойств фигуры. Перечень основных свойств прямоугольной призмы невелик и очень прост для понимания:

1. Противолежащие грани фигуры равны и параллельны. Это значит, что ребра расположенные напротив одинаковы по длине и углу наклона.
2. Все боковые грани прямого параллелепипеда – прямоугольники.
3. Четыре главные диагонали геометрической фигуры пересекаются в одной точкой, и делятся ею пополам.
4. Квадрат диагонали параллелепипеда равен суме квадратов измерений фигуры (следует из теоремы Пифагора).

Теорема Пифагора гласит, что сумма площадей квадратов, построенных на катетах прямоугольного треугольника, равна площади треугольника, построенного на гипотенузе того же треугольника.

Доказательство последнего свойства можно разобрать на изображении представленном ниже. Ход решения поставленной задачи прост и не требует подробных объяснений.

Формула объема прямоугольного параллелепипеда

Формула нахождения для всех видов геометрической фигуры одна: V=S*h, где V- искомый объем, S – площадь основания параллелепипеда, h – высота, опущенная из противоположной вершины и перпендикулярная основанию. В прямоугольнике h совпадает с одной из сторон фигуры, поэтому чтобы найти объем прямоугольной призмы необходимо перемножить три измерения.

Объем принято выражать в см3. Зная все три значения a, b и c найти объем фигуры совсем не сложно. Наиболее часто встречающийся тип задач в ЕГЭ – это поиск объема или диагонали параллелепипеда. Решить многие типовые задания ЕГЭ без формулы объема прямоугольника – невозможно.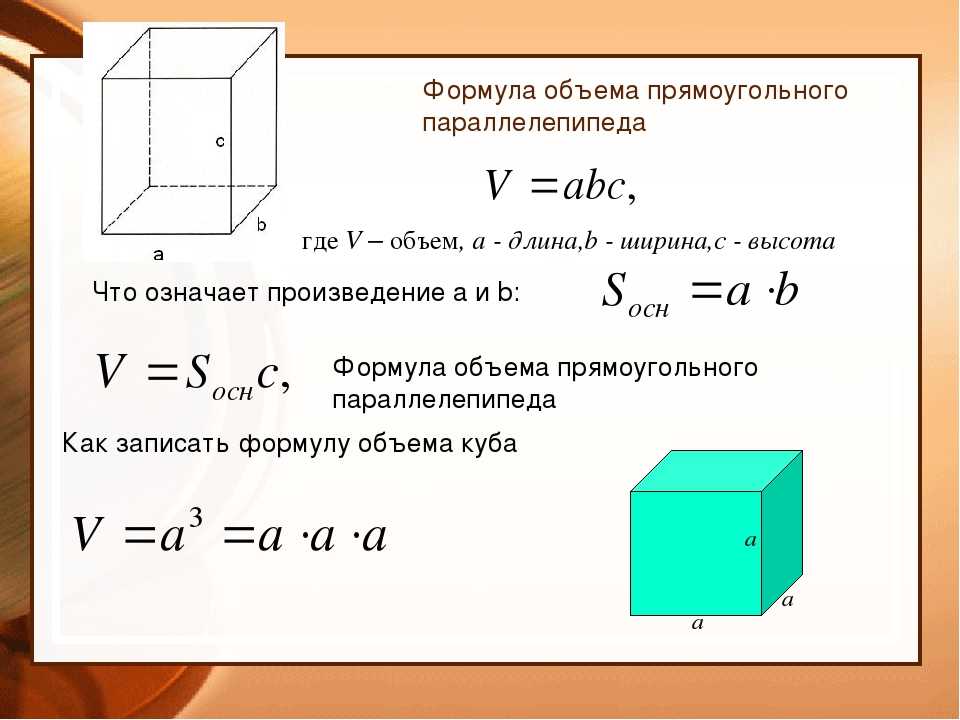

Пример задания и оформления его решения приведен на рисунке ниже.

Примечание 1 . Площадь поверхности прямоугольной призмы можно найти, если умножить на 2 сумму площадей трех граней фигуры: основания (ab) и двух смежных боковых граней (bc + ac).

Примечание 2 . Площадь поверхности боковых граней легко узнать умножив периметр основания на высоту параллелепипеда.

Исходя из первого свойства параллелепипедов AB = A1B1, а грань B1D1 = BD. Согласно следствиям из теоремы Пифагора сумма всех углов в прямоугольном треугольнике равна 180°, а катет, лежащий против угла в 30°, равен гипотенузы. Применив данные знания для треугольника, легко находим длину сторон AB и AD. Затем перемножаем полученные значения и вычисляем объем параллелепипеда.

Формула для нахождения объема наклонного параллелепипеда

Чтобы найти объем наклонного параллелепипеда необходимо площадь основания фигуры умножить на высоту, опущенную на данное основание из противоположного угла.

Таким образом, искомый V можно представить в виде h — количества листов с площадью S основания, так объем колоды складывается из V-ов всех карт.

Примеры решения задач

Задания единого экзамена должны быть выполнены за определенное время. Типовые задачи, как правило, не содержать большого количества вычислений и сложных дробей. Часто школьнику предлагают как найти объем неправильной геометрической фигуры. В таких случаях следует помнить простое правило, что общий объем равен сумме V-ов составных частей.

Как видно из примера на изображении выше, ничего сложного в решении подобных задач нет. Задания из более сложных разделов предполагают знания теоремы Пифагора и ее следствий, а так же формулу длины диагонали фигуры. Для успешного решения заданий тестов достаточно заранее ознакомится с образцами типовых задач.

Общий обзор. Формулы стереометрии!

Здравствуйте, Дорогие друзья! В этой статье решил сделать общий обзор задач по стереометрии, которые будут на ЕГЭ по математик е.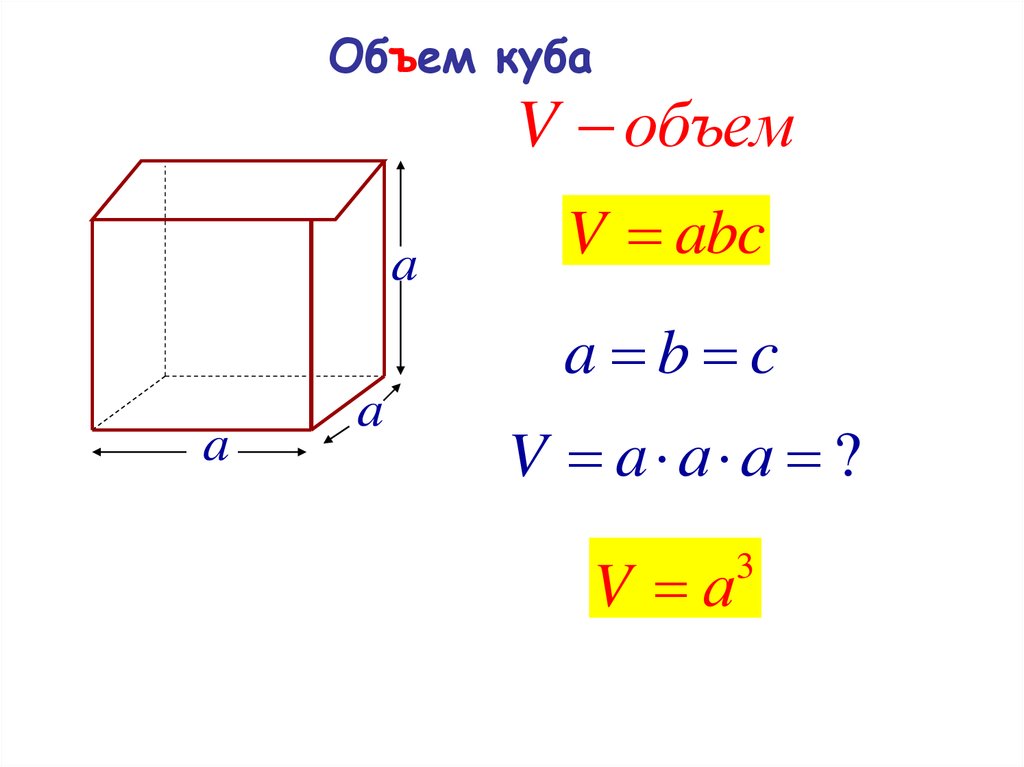 Нужно сказать, что задачи из этой группы довольно разнообразны, но не сложны. Это задачи на нахождение геометрических величин: длин, углов, площадей, объёмов.

Рассматриваются: куб, прямоугольный параллелепипед, призма, пирамида, составной многогранник, цилиндр, конус, шар. Печалит тот факт, что некоторые выпускники на самом экзамене за такие задачи даже не берутся., хотя более 50% из них решаются элементарно, практически устно.

Остальные требуют небольших усилий, знаний и специальных приёмов. В будущих статьях мы с вами будем рассмотривать эти задачи, не пропустите, подпишитесь на обновление блога.

Для решения необходимо знать формулы площадей поверхности и объёмов параллелепипеда, пирамиды, призмы, цилиндра, конуса и шара. Сложных задач нет, все они решаются в 2-3 действия, важно «увидеть» какую формулу необходимо применить.

Все нужные формулы представлены ниже:

Шар или сфера. Шаровой, или сферической поверхностью (иногда просто сферой) называется геометрическое место точек пространства, равноудаленных от одной точки — центра шара.

Объем шара равен объему пирамиды, основание которой имеет ту же площадь, что и поверхность шара, а высота есть радиус шара

Объем шара в полтора раза меньше, чем объем описанного вокруг него цилиндра.

Круглый конус может быть получен вращениемпрямоугольного треугольника вокруг одного из его катетов, поэтому круглый конус называт также конусом вращения. См. также Площадь поверхности круглого конуса

Объем круглого конуса равен трети произведения площади основания S на высоту H:

(H — высота ребра куба)

Параллелепипедом называется призма, основание которой параллелограмм. Параллелепипедимеет шесть граней, и все они — параллелограммы. Параллелепипед, четыре боковые грани которого — прямоугольники, называется прямым. Прямой параллелепипед у которого все шесть граней прямоугольники, называется прямоугольным.

Объем прямоугольного параллелепипеда равен произведению площади основания на высоту:

(S — площадь основания пирамиды, h — высота пирамиды)

Пирамида — это многогранник, у которого одна грань — основание пирамиды — произвольный многоугольник, а остальные — боковые грани — треугольники с общей вершиной, называемой вершиной пирамиды.

Сечение параллельное основанию пирамиды делит пирамиду на две части. Часть пирамиды между ее основанием и этим сечением — это усеченная пирамида.

Объем усеченной пирамиды равен одной трети произведения высоты h (OS) на сумму площадей верхнего основания S1 (abcde) , нижнего основания усеченной пирамиды S2 (ABCDE) и средней пропорциональной между ними.

1.

V =

n — число сторон правильного многоугольника — основания правильной пирамиды
a — сторона правильного многоугольника — основания правильной пирамиды
h — высота правильной пирамиды

Правильная треугольная пирамида — этомногогранник, у которого одна грань — основание пирамиды — правильныйтреугольник, а остальные — боковые грани — равные треугольники с общей вершиной. Высота опускается в центр основания из вершины.

Объем правильной треугольной пирамиды равен одной трети произведения площади правильного треугольника, являющегося основанием S (ABC) на высоту h (OS)

a — сторона правильного треугольника — основания правильной треугольной пирамиды
h — высота правильной треугольной пирамиды

Вывод формулы объема тетраэдра

Объем тетраэдра расчитывается по классической формуле объема пирамиды. В нее необходимо подставитьвысоту тетраэдра и площадь правильного (равностороннего) треугольника.

Объем тетраэдра — равен дроби в числителе которой корень квадратный из двух в знаменателе двенадцать, помноженной на куб длины ребра тетраэдра

(h — длина стороны ромба)

Длина окружности p составляет примерно три целых и одну седьмую длины диаметра круга. Точное отношение длины окружности к ее диаметру обозначается греческой буквой π

В итоге периметр круга или длина окружности вычисляется по формуле

(r — радиус дуги, n — центральный угол дуги в градусах.)

Функция КУБЗНАЧЕНИЕ — служба поддержки Майкрософт

Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel для iPad Excel Web App Excel для iPhone Excel для планшетов с Android Excel 2010 Excel 2007 Excel для Mac 2011 Excel для телефонов Android Excel Starter 2010 Дополнительно. .. Меньше

В этой статье описывается синтаксис формулы и использование КУБЗНАЧЕНИЕ  функция в Microsoft Excel.

Описание

Возвращает агрегированное значение из куба.

Синтаксис

КУБЗНАЧЕНИЕ(соединение, [выражение_члена1], [выражение_члена2], …)

Синтаксис функции КУБЗНАЧ имеет следующие аргументы:

• Соединение     Обязательно. Текстовая строка имени подключения к кубу.

• Member_expression     Необязательно. Текстовая строка многомерного выражения (MDX), результатом которой является элемент или кортеж в кубе. Кроме того, выражение_члена может быть набором, определенным с помощью функции КУБМНОЖ. Используйте member_expression в качестве среза, чтобы определить часть куба, для которой возвращается агрегированное значение. Если в member_expression не указана мера, используется мера по умолчанию для этого куба.

Примечания

• Когда функция КУБЗНАЧЕНИЕ вычисляет, она временно отображает сообщение «#GETTING_DATA…» в ячейке, прежде чем все данные будут извлечены.

• Если для member_expression используется ссылка на ячейку, и эта ссылка на ячейку содержит функцию CUBE, то member_expression использует выражение MDX для элемента в ячейке, на которую указывает ссылка, а не значение, отображаемое в этой ячейке, на которую указывает ссылка.

• org/ListItem»>

  Если имя соединения не является действительным соединением с рабочей книгой, хранящимся в рабочей книге, КУБЗНАЧЕНИЕ возвращает #ИМЯ? значение ошибки. Если сервер оперативной аналитической обработки (OLAP) не работает, недоступен или возвращает сообщение об ошибке, КУБЗНАЧЕНИЕ возвращает #ИМЯ? значение ошибки.

• Если хотя бы один элемент в кортеже является недопустимым, КУБЗНАЧЕНИЕ возвращает ошибку #ЗНАЧ! значение ошибки.

• КУБЗНАЧЕНИЕ возвращает значение ошибки #Н/Д, когда:

  • Синтаксис member_expression неверен.

  • org/ListItem»>

    Элемент, указанный выражением member_expression, не существует в кубе.

  • Кортеж недействителен, так как для указанных значений нет пересечения. (Это может произойти с несколькими элементами из одной иерархии.)

  • Набор содержит по крайней мере один элемент с размерностью, отличной от других элементов.

  • КУБЗНАЧЕНИЕ может возвращать значение ошибки #Н/Д, если вы ссылаетесь на объект на основе сеанса, такой как вычисляемый элемент или именованный набор, в сводной таблице при совместном использовании соединения, и эта сводная таблица удаляется или вы преобразуете сводную таблицу в формулы. (на Вкладка Параметры в группе Инструменты щелкните Инструменты OLAP , а затем щелкните Преобразовать в формулы .)

Проблема: нулевые значения преобразуются в строки нулевой длины

В Excel, если в ячейке нет данных, потому что вы никогда не изменяли ее или удалили содержимое, ячейка содержит пустое значение. Во многих системах баз данных пустое значение называется значением Null. Пустое значение или значение Null буквально означает «Нет значения». Однако формула никогда не может возвращать пустую строку или значение Null. Формула всегда возвращает одно из трех значений: числовое значение; текстовое значение, которое может быть строкой нулевой длины или значением ошибки, например #ЧИСЛО! или #ЗНАЧ.

Если формула содержит функцию КУБЗНАЧЕНИЕ, подключенную к базе данных оперативной аналитической обработки (OLAP), и запрос к этой базе данных дает значение Null, Excel преобразует это значение Null в строку нулевой длины, даже если в противном случае формула вернула бы числовое значение. Это может привести к ситуации, когда диапазон ячеек содержит комбинацию числовых и строковых значений нулевой длины, и эта ситуация может повлиять на результаты других формул, которые ссылаются на этот диапазон ячеек. Например, если A1 и A3 содержат числа, а A2 содержит формулу с функцией КУБЗНАЧЕНИЕ, которая возвращает строку нулевой длины, следующая формула вернет ошибку #ЗНАЧ! ошибка:

=А1+А2+А3

Чтобы предотвратить это, вы можете проверить строку нулевой длины с помощью функции ISTEXT и с помощью функции ЕСЛИ заменить нулевую длину на 0 (ноль), как показано в следующем примере:

= ЕСЛИ (ИСТЕКСТ (A1), 0, A1) + ЕСЛИ (ИСТЕКСТ (A2), 0, A2) + ЕСЛИ (ИСТЕКСТ (A3), 0, A3)

Кроме того, вы можете вложить функцию КУБЗНАЧЕНИЕ в условие ЕСЛИ, которое возвращает значение 0, если функция КУБЗНАЧЕНИЕ возвращает строку нулевой длины, как показано в следующем примере:

=ЕСЛИ (КУБЗНАЧЕНИЕ(«Продажи»,»[Показатели]. [Прибыль]»,»[Время].[2004]»,»[Все продукты].[Напитки]»)=»», 0, КУБЗНАЧЕНИЕ(» Продажи»,»[Показатели].[Прибыль]»,»[Время].[2004]»,»[Все продукты].[Напитки]»))

Обратите внимание, что функция СУММ не требует этого теста для строки нулевой длины, поскольку она автоматически игнорирует строки нулевой длины при вычислении возвращаемого значения.

Примеры

=КУБЗНАЧЕНИЕ(«Продажи»,»[Показатели].[Прибыль]»,»[Время].[2004]»,»[Все продукты].[Напитки]»)

=КУБЗНАЧЕНИЕ($A$1,»[Показатели].[Прибыль]»,D$12,$A23)

=КУБЗНАЧЕНИЕ(«Продажи»,$B$7,D$12,$A23)

Функции Excel CUBE • My Online Training Hub

Кто-то может сказать, что функции Excel CUBE — это новые сводные таблицы, поскольку они позволяют создавать отчеты на основе моделей Power Pivot в более свободной форме. В то время как сводные таблицы довольно ограничены в своем макете, и их ячейки нельзя редактировать. Как и сводные таблицы, мы можем использовать слайсеры для фильтрации функций CUBE для создания полностью интерактивных отчетов и информационных панелей.

Посмотреть видео

Загрузить рабочую тетрадь

Введите адрес электронной почты ниже, чтобы загрузить образец рабочей тетради.

Отправляя свой адрес электронной почты, вы соглашаетесь с тем, что мы можем отправить вам наш информационный бюллетень Excel по электронной почте.

Написание функций Excel CUBE

Когда вы начинаете работать с функциями CUBE, вам будет проще автоматически генерировать формулы CUBE путем преобразования существующей сводной таблицы, подобной приведенной ниже, содержащей данные о продажах по категориям и подкатегориям за каждый месяц.

Рекомендуется установить макет в табличной форме, чтобы у вас не было лишних заголовков после преобразования.

Чтобы преобразовать сводную таблицу, выберите любую ячейку в сводной таблице > затем перейдите на вкладку Инструменты сводной таблицы: Анализ > Инструменты OLAP > Преобразовать в формулы.

Примечание: Если у вас есть поля в области «Фильтры», вам будет предложено либо преобразовать их, либо сохранить, чтобы вы могли фильтровать данные. Я предпочитаю использовать слайсер для фильтрации, поэтому у меня нет фильтров в этой сводной таблице.

Это преобразование навсегда заменяет сводную таблицу формулами CUBE.

В строке формул вы можете видеть, что значения были заменены формулами КУБЭЛЕМЕНТ:

И метки строк и столбцов были заменены формулами КУБЭЛЕМЕНТ:

0 Формулы КУБЗНАЧЕНИЕ более внимательно вы можете видеть, что первый аргумент — это соединение, это ваша модель данных для книги, которая всегда будет называться «ThisWorkbookDataModel», а затем у нас есть ряд аргументов member_expression, которые по существу фильтруют данные.

Выражения-члены могут быть другими функциями куба, которые оцениваются как набор элементов или один элемент в вашей модели, или они могут ссылаться на другие ячейки, содержащие эти формулы куба или значения элементов, как мы можем видеть в формуле выше.

Для ясности; Членами могут быть поля, элементы, меры или срезы в вашей модели.

В приведенной выше формуле выражения-члены являются мерой; Сумма суммы, подкатегория в метке строки, месяц в метке столбца и срез для года.

Имя слайсера вводится при создании формул CUBE. Однако, если вам нужно найти имя слайсера, вы можете щелкнуть правой кнопкой мыши и просмотреть его в настройках слайсера. Это «Имя для использования в формулах».

Совет: Вы можете изменить имя слайсера через менеджер имен, если хотите.

КУБЭЛЕМЕНТ Функция

Ячейки меток строк и столбцов содержат формулы КУБЭЛЕМЕНТ:

Обратите внимание, что КУБЭЛЕМЕНТ также требует подключения для первого аргумента, а затем он ссылается на таблицу категорий, чтобы получить категорию, благотворительность. Эти элементы жестко закодированы, что не идеально, и мы рассмотрим, как мы можем автоматизировать это через мгновение, но сначала я хочу указать на приведенную ниже формулу общего итога КУБЭЛЕМЕНТ:

Здесь вместо жестко закодированного имени категории у нас есть [Все], что, по сути, говорит о включении всех категорий в этот КУБЭЛЕМЕНТ. Поскольку эта формула возвращает все имена категорий, мы можем использовать последний аргумент для заголовка, чтобы указать формуле отображать «общий итог» в ячейке. Вы можете изменить его, чтобы отображать что-то еще, если хотите.

Теперь, когда мы преобразовали нашу сводную таблицу в формулы куба, мы можем вырезать и вставлять их в другие места нашей книги, помня о ячейках, на которые они ссылаются. И, как и с любой другой формулой, с ними можно выполнять дальнейшие математические вычисления.

Обеспечение переносимости функций КУБ

Другим вариантом является вложение значений КУБЭЛЕМЕНТ в формулы КУБЗНАЧЕНИЕ, чтобы сделать их более переносимыми.

Например, вы можете просто скопировать аргументы формулы КУБЭЛЕМЕНТ после «ThisWorkbookDataModel» из ячеек, на которые ссылается формула КУБЗНАЧЕНИЕ, создав одну большую формулу следующим образом:

 =КУБЗНАЧ («ThisWorkbookDataModel»,
"[Меры].[Сумма суммы]",
"[Категории].[Категория].&[Благотворительность]",
"[Данные].[Подкатегория].&[Пожертвование]",
"[Данные].[Дата (Месяц)].&[Янв]",
Slicer_Date__Year) 

Теперь, когда эта формула куба напрямую ссылается на модель, я могу свободно перемещать ее в любое место в этой книге, поскольку она больше не зависит ни от каких других ячеек. Другое преимущество заключается в том, что эту формулу легко читать, поскольку все элементы перечислены в явном виде.

Создание динамических формул CUBE

Если вы пишете формулы с нуля, создание каждой формулы с указанием категории, подкатегории и месяца требует много работы.

Вместо этого мы можем сделать формулы динамическими, ссылаясь на ячейки, содержащие текстовые значения для меток строк и столбцов и даже меры.

No related posts.