Натуральные числа | Объемы. Объем прямоугольного параллелепипеда
Чтобы сравнить объемы двух сосудов, можно наполнить один из них водой и перелить ее во второй сосуд. Если второй сосуд окажется заполненным, в воды в первом сосуде не останется, то объемы сосудов равны. Если в первом сосуде вода останется, то его объем больше объема второго сосуда. А если заполнить водой второй сосуд не удастся, то объем первого сосуда меньше объема второго.
Если наполнить формочку влажным песком, а потом перевернуть и снять ее, получится фигура, имеющая тог же объем, что и формочка (рис. 67).
Рис. 67. Формочка и фигура из песка
Для измерения объемов применяют следующие единицы: кубический миллиметр (мм3), кубический сантиметр (см3), кубический дециметр (дм3), кубический метр (м3), кубический километр (км3).
Например: кубический сантиметр – это объем куба с ребром 1 см (рис. 68).
Рис. 68. Кубический сантиметр
Кубический дециметр называют также литром.
Фигура на рис. 69 состоит из 4 кубиков с ребром 1 см. Значит, ее объем равен 4 см3.
Рис. 69. Фигура из 4 кубиков с ребром 1 см
Выведем правило для вычисления объема прямоугольного параллелепипеда. Пусть прямоугольный параллелепипед имеет длину 4 см, ширину 3 см и высоту 2 см (рис. 70, а). Разобьем его на два слоя толщиной 1 см (рис. 70, б). Каждый из этих слоев состоит из 3 столбиков длиной 4 см (рис. 70, в), а каждый столбик – из 4 кубиков с ребром 1 см. Значит, объем каждого столбика равен 4 см3, каждого слоя – 4•3 (см3), а всего прямоугольного параллелепипеда – (4 • 3) • 2, то есть 24 см3.
Рис. 70. Прямоугольный параллелепипед, состоящий из кубиков
Чтобы найти объем прямоугольного параллелепипеде, надо его длину умножить на ширину и на высоту.
Формула объема прямоугольного параллелепипеда имеет вид:
V = abc,
где V – объем;
а, b, c – измерения.
Если ребро куба равно 4 см, то объем куба равен 4 • 4 • 4 = 43 (см3), то есть 64 см3.
Если ребро куба равно a, то объем V куба равен а • а • а = а3.
Значит, формула объема куба имеет вид:
V = а3.
Именно поэтому запись а3 называют кубом числа а.
Объем куба с ребром 1 м равен 1 м3.
А так как 1 м = 10 дм, то 1 м3 = 103 дм3, то есть 1 м3=1000 дм3 = 1000 л.
Таким же образом находим, что1 л = 1 дм3 = 1000 см3; 1 см3 = 1000 мм3; 1 км3 = 1 000 000 000 м3.
На рис. 71 изображен кубический сантиметр, состоящий из тысячи кубических миллиметров.
Рис. 71. Кубический сантиметр, состоящий из тысячи кубических миллиметров
Формулу V = аbс можно читать разными способами.
1. Если нужно напомнить правило, то говорят так: «Объем вэ прямоугольного параллелепипеда равен произведению а, бэ и цэ (трех его измерений)».
2. Если нужно только прочитать запись формулы, то говорят:
«Вэ равно произведению а, бэ и цэ» или «вэ равно а бэ цэ».
Названия единиц объема читают полностью.
Например:
15 см3 – пятнадцать кубических сантиметров, 1 м3 = 1000 дм3 – один кубический метр равен одной тысяче кубических дециметров.
200 лет назад в разных странах, в том числе и в России, применялись различные системы единиц для измерения длины, массы и других величин. Соотношения между мерами были сложны, существовали разные определения для единиц измерения. Например, и до сих пор в Великобритании существуют две различные «тонны» (в 2000 и в 2940 фунтов), более 50 различных «бушелей» и т.п. Это затрудняло развитие науки, торговли между странами. Поэтому назрела необходимость введения единой системы мер, удобной для всех стран, с простыми соотношениями между единицами.
Такая система – ее назвали метрической системой мер – была разработана во Франции. Основную единицу длины, 1 метр (от греческого слова «метрон» – мера), определили как сорокамиллионную долю окружности Земли, основную единицу массы, 1 кг – как массу 1 дм3 чистой воды. Остальные единицы определялись через эти две, соотношения между единицами одной величины равнялись 10, 100, 1000 и т.
д.
Метрическая система мер принята большинством стран мира. В России ее введение началось с 1899 года. Большие заслуги во введении и распространении метрической, системы, мер в нашей стране принадлежат Дмитрию Ивановичу Менделееву, великому русскому химику (рис. 72).
Рис. 72. Дмитрий Иванович Менделеев (1834-1907)
Однако по традиции и в настоящее время иногда пользуются старыми единицами. Моряки измеряют расстояния милями (1852 м) и кабельтовыми (десятая часть мили, то есть около 185 м), скорость – узлами (1 миля в час). Массу алмазов измеряют в каратах (200 мг, то есть пятая часть грамма – масса пшеничного зерна). Объем нефти измеряют в баррелях (159 л) и т.д.
Сообщающиеся сосуды — законы, принципы, формулы
Жидкое агрегатное состояние
Давайте для начало разберемся, как ведет себя жидкость в различных сосудах.
В мире есть три агрегатных состояния: твердое, жидкое и газообразное.
Их характеристики — в таблице:
Агрегатные состояния | Свойства | Расположение молекул | Расстояние между молекулами | Движение молекулы |
|---|---|---|---|---|
Твердое | сохраняет форму и объем | в кристаллической решетке | соотносится с размером молекул | колеблется около своего положения равновесия в кристаллической решетке |
Жидкое | сохраняет объем и текучесть | хаотично | близко друг к другу | малоподвижны, при нагревании скорость движения молекул увеличивается |
Газы | занимают весь предоставленный объем | хаотично | больше размеров молекул | хаотичное и непрерывное |
В этом состоянии сохраняется объем, но не сохраняется форма.
Например, если перелить молоко из кувшина в стакан — молоко, имевшее форму кувшина, примет форму стакана. Кстати, в корове у молока тоже была другая форма.
Расстояние между молекулами в жидком состоянии чуть больше, чем в твердом, но все равно невелико. При этом частицы не собраны в кристаллическую решетку, а расположены хаотично. Молекулы почти не двигаются, но при нагревании жидкости делают это более охотно.
Вспомните, что происходит, если залить чайный пакетик холодной водой — он почти не заваривается. А вот если налить кипяточку — чай точно будет готов.
Агрегатных состояния точно три? На самом деле, есть еще четвертое — плазма. Звучит, как что-то из научной фантастики, но это просто ионизированный газ — газ, в котором помимо нейтральных частиц, есть еще и заряженные. |
Ионизаторы воздуха как раз строятся на принципе перехода из газообразного вещества в плазму.Практикующий детский психолог Екатерина Мурашова
Бесплатный курс для современных мам и пап от Екатерины Мурашовой. Запишитесь и участвуйте в розыгрыше 8 уроков
Сообщающиеся сосуды
Поскольку жидкость принимает форму сосуда, в который ее поместили, имеет место быть такое явление, как сообщающиеся сосуды.
- Сообщающиеся сосуды — это сосуды, соединенные между собой ниже уровня жидкости (в каждом сосуде). Так жидкость может перемещаться из одного сосуда в другой.
Какую бы форму не имели такие сосуды, на поверхности однородных жидкостей в состоянии покоя на одном уровне действует одинаковое давление.
Если в колена сообщающихся сосудов налить жидкости, плотности которых будут различны, то меньший объём более плотной жидкости в одном колене уравновесит больший объём менее плотной жидкости в другом колене сосуда.
Другими словами, высота столба жидкости с меньшей плотностью больше, чем высота столба жидкости с большей плотностью. Давайте рассчитаем, во сколько высота столба жидкости с меньшей плотностью больше высоты столба жидкости с большей плотностью, если эти две несмешивающиеся жидкости находятся в сообщающихся сосудах.
p = ρgh, p1 = p2, ρ1 gh1= ρ2 gh2,
Отсюда:
Курсы подготовки к ОГЭ по физике помогут снять стресс перед экзаменом и получить высокий балл.
Применение сообщающихся сосудов
На принципе сообщающихся сосудов основано устройство очень простого прибора для определения плотности жидкости — ареометра. Этот прибор состоит из двух сообщающихся сосудов: двух вертикальных стеклянных трубок, соединенных между собой третьей изогнутой трубкой.
Одна из вертикальных трубок заполняется жидкостью, плотность которой нужно определить, а другая — жидкостью известной плотности (например, водой, плотность которой равна 1000 кг/м 3).
Жидкости должны заполнить трубки настолько, чтобы их уровень в изогнутой трубке посередине был на отметке прибора 0. Высоты жидкостей в трубках над этой отметкой измеряют и находят плотность исследуемой жидкости, зная, что высоты обратно пропорциональны плотностям (об этом мы говорили выше).
Также на законе сообщающихся сосудах основаны устройства, которые определяют уровень жидкости в закрытых сосудах: резервуарах, паровых котлах.
Чтобы судно могло переплыть из одной водного бассейна в другой, если уровни воды в них разные, необходимо использовать шлюз. Устройство шлюза также основано на принципе сообщающихся сосудов. В первых воротах шлюза открывается клапан, камера соединяется с водоёмом, они становятся сообщающимися сосудами, уровни воды в них выравниваются. После этого ворота открываются, и судно проходит в первую камеру. Открывается следующий клапан, после выравнивания уровней воды открываются ворота, и так повторяется столько раз, сколько камер имеет шлюз.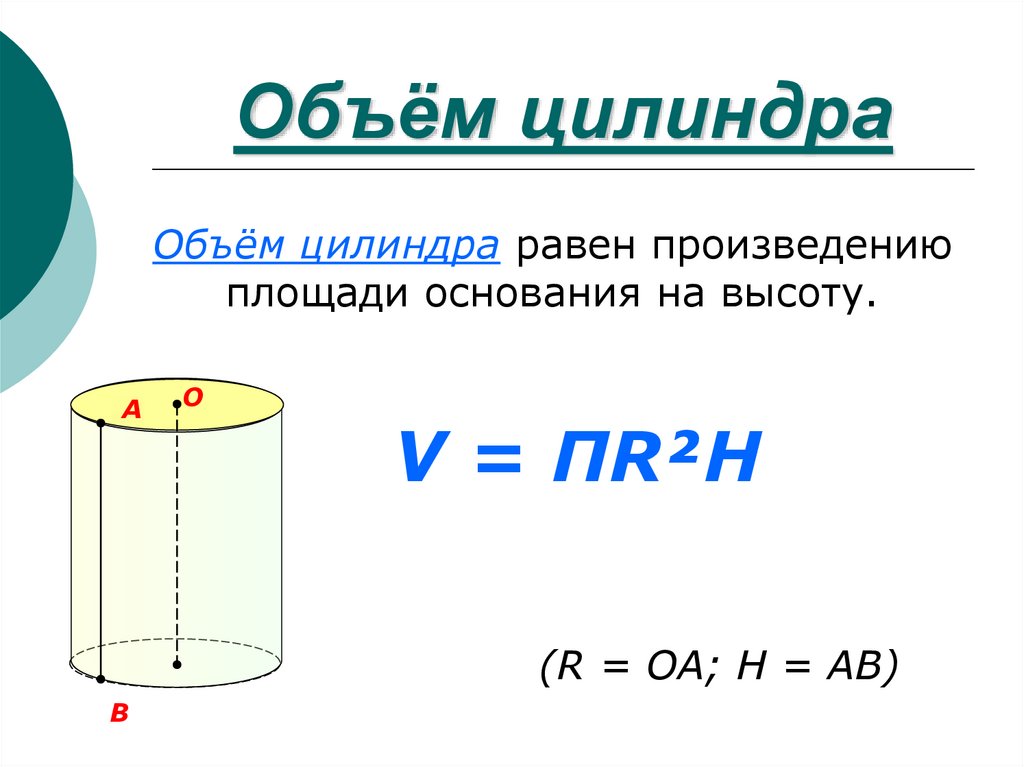
Бесплатные занятия по английскому с носителем
Занимайтесь по 15 минут в день. Осваивайте английскую грамматику и лексику. Сделайте язык частью жизни.
Давление столба жидкости
Выведем формулу давления столба жидкости через основную формулу давления.
Давление p = F/S p — давление [Па] F — сила [Н]S — площадь [м2] |
В случае давления жидкости на дно сосуда мы можем заменить силу в формуле на силу тяжести.
Также мы можем представить массу жидкости как произведение плотности на объем:
Из геометрии мы знаем, что объем тела вращения (например, цилиндра) — это произведение площади основания на высоту: V = Sh.
Следовательно, высота будет равна h = V/S. Подставляем в формулу высоту вместо отношения объема к площади.
В сообщающихся сосудах давление жидкости на одном уровне (на одной и той же высоте) будет одинаковым.
С помощью перегородки можно сделать так, чтобы уровень жидкости, а следовательно, и давления в сообщающихся сосудах отличались. Перегородка, установленная между сосудами перекроет сообщение. Далее доливая жидкость в один из сосудов мы создаем дополнительное давление. Если затем убрать перегородку, то жидкость начнет перетекать в тот сосуд, где её уровень ниже — до тех пор, пока высота жидкости в обоих сосудах не станет одинаковой. Этот принцип используют в водонапорной башне. |
Чтобы создать высокое давление, башню наполняют водой. Затем открывают трубы на нижнем этаже, и вода устремляется в дома в наши краны и батареи.Задачка
Какой площади необходимо сделать малый поршень в гидравлическом прессе, для того, чтобы выигрыш в силе получился равным 2? Площадь большого поршня равна 10 см2.
Решение:
Гидравлический пресс — это два цилиндрических сообщающихся сосуда. Площадь большого поршня, с приложенной силой F1, равна 10 см2.
Площадь малого поршня обозначим Sмал, к нему приложена сила F2.
Давления в сообщающихся сосудах на одинаковой высоте равны: p1 = p2
Подставим формулу давления:
F1 / Sбол = F2 / Sмал.
Выразим S
Sмал = (F2 / F1) · Sбол
Так как по условию выигрыш в силе F2 / F1 равен 2, то:
Sмал = 2 · Sбол = 2 · 10 = 20 см2
Ответ: малый поршень необходимо сделать с площадью равной 20 см2
Расчет объема головок сосудов под давлением
LZRFIT — Калькулятор объемаКалькулятор объема головки | |
Галлоны США для цилиндрических головок | |
Размеры: | |
| Головка Внутренний диаметр: | дюймы |
| Длина прямого фланца: | дюймы |
| Головка Тип: | Выберите тип головки ASME Фланцевая и выпуклая Стандартная Фланцевая и выпуклая 80:10 Фланцевая и выпуклаяПолусферическаяЭллиптическая |
| АСМЭ
Фланцевые и вогнутые: | Блюдо
Радиус = диаметр головки |
| Стандарт
Фланцевые и вогнутые: | Блюдо
Радиус = диаметр головки |
| 80:10
Фланцевые и вогнутые: | Блюдо
Радиус = 80% диаметра головки |
| Полусферический: | Блюдо
Радиус = 1/2 внутреннего диаметра головки |
| Эллиптический: | Блюдо
Радиус ≡ 90% диаметра головки |
| ASME: | 10% Блюдо
Радиус = диаметр головки |
Расчет Результаты: | |
| Объем
прямого фланца | Галлоны Литры |
| Объем
Головы (Делает не включает объем прямого фланца) | Галлоны Литры |
| Всего объем головы | Галлоны Литры |
| Затопленный том | Галлоны Литры |
Онлайн Калькулятор | Объем сосуда высокого давления
{CalQlata © 01.
01.20}
Это онлайн-версия загружаемого калькулятора; Сосуды под давлением.
Применяется та же страница технической помощи.
| Вертикальный | ||||
|---|---|---|---|---|
| Вход | Выход | Вместимость сосуда | Жидкость (заполнение) | |
| Ø: | В₁: | |||
| р: | В₂: | |||
| ч: | В₃: | |||
| Р: | В₄: | |||
| Г: | V₅: | |||
| д₁: | ||||
| д₂: | ||||
| д₃: | ||||
| д₄: | ||||
| д₅: | ||||
| В: | ||||
| Øₕ: | ||||
Помощь (вертикальный сосуд)
Приведенный выше калькулятор определяет внутренний объем(ы) вертикального сосуда под давлением со сферическими торцевыми крышками.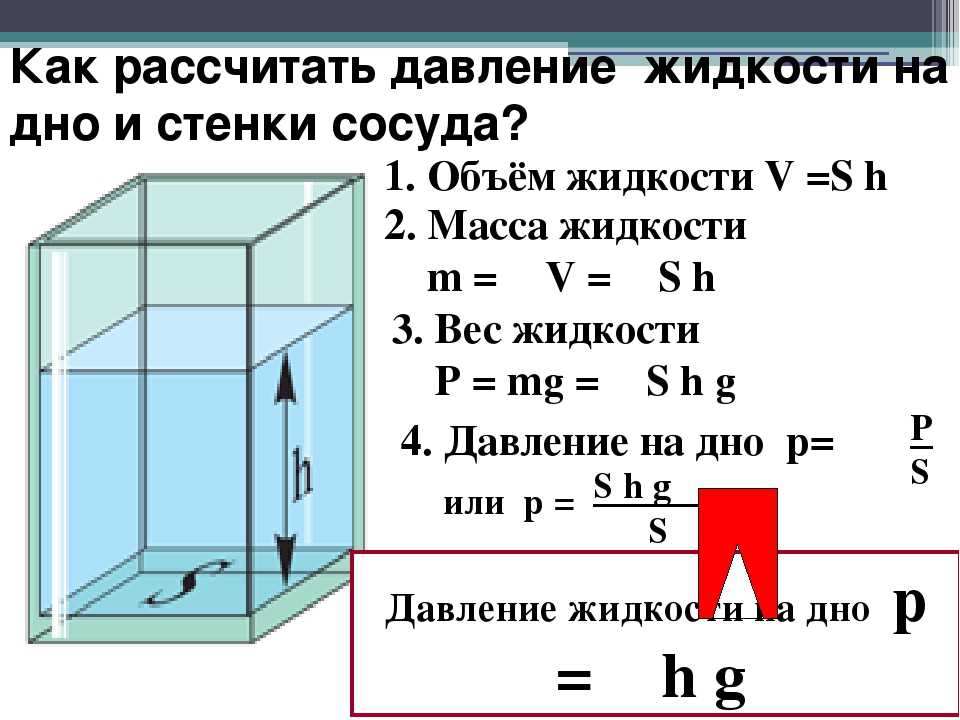
Судно состоит из пяти отдельных секций; нижняя головка (V₁,d₁), нижняя фаланга (V₂,d₂), центральный цилиндр (V₃,d₃), верхняя фаланга (V₄,d₄) и верхняя головка (V₅,d₅).
Верхняя и нижняя головки идентичны, как и верхний и нижний суставы пальцев.
Выходные данные (результаты расчета) отображаются в двух столбцах; сосуд слева и жидкость (заполнение) справа. Если определенный раздел (например, V₂,d₂) заполнен, в обоих столбцах будет отображаться один и тот же результат.
Из-за особенностей математики javascript вы можете иногда получать результат «NAN» в столбце жидкости для одного или нескольких результатов для полного сосуда. Когда это произойдет, вам нужно будет немного уменьшить высоту заполнения (h); например для высоты сосуда ‘5’ (H=5) может потребоваться установить высоту заполнения (h) равной ‘h=4,9999’
0), задайте головкам тот же радиус, что и у цилиндра (R = ½,Ø), и введите высоту, равную удвоенному радиусу (H = Ø).
Для простых (плоских) головок просто введите, например, очень большой радиус головки; R = 1000.
Если вы ввели недопустимое значение, т.е. h>H вы активируете оповещение.
Øₕ Жидкость (нижняя часть правой колонки): показывает диаметр поверхности жидкости в головке. Если высота жидкости (h) меньше, чем d₁, это значение будет показывать диаметр поверхности жидкости в нижнем напоре. Если высота жидкости (h) находится между d₄ и d₅, это значение будет показывать диаметр поверхности жидкости в верхнем напоре.
| Горизонтальный | ||||
|---|---|---|---|---|
| Вход | Выход | Вместимость сосуда | Жидкость (заполнение) | |
| Ø: | В₁: | |||
| р: | В₂: | |||
| ч: | В₃: | |||
| Р: | д₁: | |||
| Г: | д₂: | |||
| д₃: | ||||
| В: | ||||
| Øₕ: | ||||
Справка (горизонтальный сосуд)
Приведенный выше калькулятор определяет внутренний объем горизонтального сосуда высокого давления со сферическими торцевыми крышками.
Судно состоит из пяти отдельных секций; левая головка (V₁,d₁), левосторонний сустав (V₂,d₂), центральный цилиндр (V₃,d₃), правый сустав (V₂,d₂) и правая головка (V₁, д₁).
Левая и правая головки идентичны, как и правый и левый суставы пальцев.
Выходные данные (результаты расчета) отображаются в двух столбцах; сосуд слева и жидкость (заполнение) справа. Выходные результаты для объемов заполнения (от V₁ до V₃) и размеров (от d₁ до d₃) в этом калькуляторе немного отличаются от варианта вертикального сосуда.
В левой колонке [результаты]:
d₁ — глубина, а V₁ — объемный объем одной сферической головки, поэтому эти результаты применимы к каждому концу.
d₂ — глубина, а V₂ — вместимость одного сустава, поэтому эти результаты применимы к каждому концу.
d₃ — глубина, а V₃ — вместимость центрального цилиндра.
Таким образом, общий объем равен; 2.(В₁+В₂)+В₃
В правой колонке [результаты]:
d₁ — глубина жидкости до дна сферических головок.
V₁ — объем жидкости внутри одной сферической головки. Следовательно, эти результаты применимы к каждому концу.
d₂ — глубина жидкости до основания суставов. V₂ — объем жидкости внутри одного сустава. Следовательно, эти результаты применимы к каждому концу.
d₃ — глубина, а V₃ — вместимость центрального цилиндра.
Таким образом, общий объем равен; 2.(V₁+V₂)+V₃
Из-за особенностей математики javascript иногда вы можете получить результат «NAN» в столбце жидкости для одного или нескольких результатов для полного сосуда. Когда это произойдет, вам нужно будет немного уменьшить высоту заполнения (h); например для высоты сосуда «5» (H = 5) вам может потребоваться установить высоту заполнения (h) на «h = 4,9».999′
Для сферического сосуда просто установите радиус изгиба равным нулю (r=0), задайте головкам тот же радиус, что и у цилиндра (R = ½.Ø), и введите высоту, вдвое превышающую тот же радиус (H = Ø).
Для простых (плоских) головок просто введите, например, очень большой радиус головки; R = 1000.