Формула периметра пятиугольника 4 класс: 1,найди периметр пятиугольника К О А Е М, 2,Найди удобным способом периметр пятиугольника.каждая сторона которого…

Урок математики на тему «Периметр многоугольника » | План-конспект урока по математике (4 класс) на тему:

Учитель: Володина Людмила Николаевна Класс: 4 УМК  „Планета знаний”

Предмет: Математика Дата проведения: 19  октября 2015 г.

Тема урока: Периметр многоугольника

Форма: урок — путешествие.

Цель урока:

Образовательная:

— показать, как вычислить периметр многоугольника;

— учить выражать ответы в более крупных единицах длины;

— совершенствовать умения составлять выражения для вычисления периметра прямоугольника и квадрата разными способами.

Развивающая:

 развитие восприятия, наблюдательности внимания, пространственных представлений, умения выделять главный признак, классифицировать обобщать, развитие логики, навыков вычисления периметра многоугольника, развитие математической речи, критического и практического мышления.

Воспитательная:

 воспитание интереса к математике, познанию, творчеству, воспитание самостоятельности, организованности, трудолюбия, аккуратности, чувства дружбы и товарищества.

Задачи:

Личностные:

развитие познавательных интересов, учебных мотивов.

Регулятивные: принимать и сохранять учебную задачу и планировать своё действие в соответствии с поставленной задачей и условиями её реализации.

Познавательные:

 формировать умение находить периметр многоугольника.

Коммуникативные: умение работать в парах, контролировать действия партнера.

Тип урока: урок усвоения новых знаний.

Методы урока: объяснительный, иллюстративный, проблемный.

Оборудование:

— компьютер, мультимедийный проектор, экран;

— презентация;

— учебник «Математика. 4 класс»/ М.И. Башмаков, Н.Г. Нефедова. -М.:Астрель,2014г.

раздаточный материал для учащихся, карточки для самостоятельной работы;

задания для выполнения на уроке;

Формы организации учебной деятельности:

фронтальная             групповая                      индивидуальная

 СЦЕНАРИЙ УРОКА

Ход урока:

I.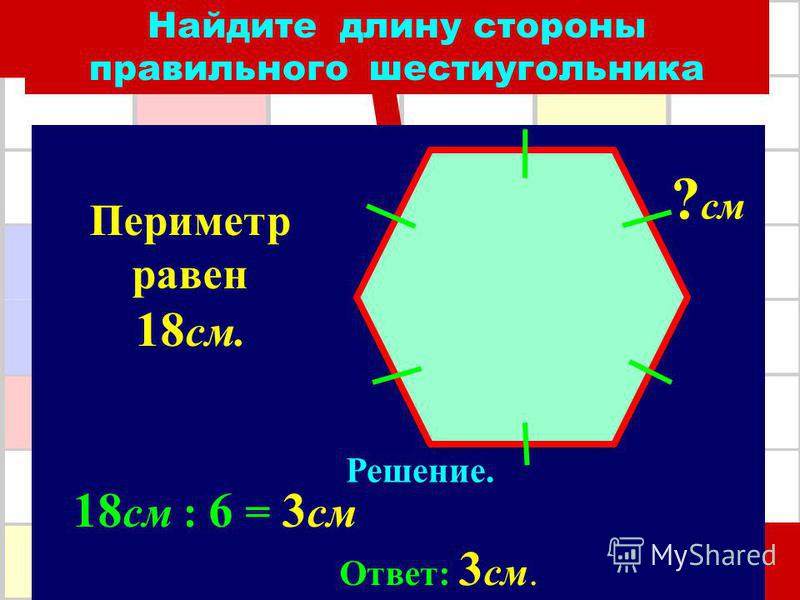 Организационный момент:

 – С хорошим настроением начинаем наш урок. Посмотрите друг другу в глаза, улыбнитесь, мысленно пожелайте друг другу добра, удачи, успехов.

— Ну а теперь:

— Руки? — На месте!
— Ноги? — На месте!
— Локти? — У края!
— Спинка? – Прямая!

– Кто из вас любит путешествовать? Поднимите руку.
– А для чего люди путешествуют? (Чтобы узнать что-то новое.)

Прозвенел уже звонок,

Начинается урок.

В путешествие пойдем,

В страну сказок попадем.

Слушай, думай, наблюдай,

Сказку радостно встречай!

Слайд 1

– Но прежде чем открыть что– то  новое , что нужно сделать? (Повторить старое.)

-Начинаем нашу работу с устного счета, который и поможет определить, в какую страну мы попадем.

Слайд 2

II. Устный счет:

— Расположите  величины в порядке их возрастания

Находят табличку с полученным ответом, на обратной стороне написана буква. Составляют слово

С    Т    Р    А    Н    А
165см	3м5дм	40 дм8см	7м30 см	975 дм
Ч	У	Д	Е	С

Слайд 3

— Умнички, мы с Вами действительно попали сегодня в удивительную Страну Чудес! А гости нашего урока — девочка Алиса и её друзья.

— Давайте откроем тетради и запишем число, классная работа.

 

Слайд 4

III  Актуализация имеющихся знаний:

— Какая геометрическая фигура лишняя и почему? (1 фигура – лишняя ,незамкнутая ломаная, остальные – замкнутые ломаные, многоугольники)

-У каждого из вас на парте лежит геометрическая фигура. (Квадрат, четырехугольник,  прямоугольник, многоугольник).

-Как она называется? Как вы это определили? (квадрат, четырехугольник,  прямоугольник, многоугольник).

Создание проблемной ситуации

Перед вами не простые фигуры, а основа для открытки. Скоро праздник и Алиса решила сделать открытку для мамы и хочет украсить её лентой. Но у неё  возникла проблема, и она попросила вас  помочь ее решить. Она не знает, хватит ли ей ленты. Сможем ли мы помочь в решении этой проблемы?

— Как мы поступим в такой ситуации? С чего начнем? (Измерим длину стороны)

— Что сделаем потом? (Сложим полученные результаты)

Практическая работа (Измерение длин сторон квадрата)

— Сколько сторон у нашей фигуры? (4)

— А сколько измерений нам нужно выполнить?

— Чему равны  длины  сторон?  (ответы)

— Сможем ли теперь узнать, сколько нужно ленты?

— Что для этого сделаем?  (Сложим результаты измерений)

— Какое действие мы использовали для решения задачи? (Сложение)

— Как называется результат сложения? (Сумма)

— Что мы складывали?  (Длины сторон).

—  Чтобы помочь Алисе, что же мы нашли?  (Сумму длин сторон)

— Давайте проверим, хватит ли ленты.

— А кто знает, как называют по – другому, сумму длин сторон? Назовите.

— Правильно, в  математике эта величина имеет особое название – периметр.

— Так чем же мы сегодня на уроке будем заниматься?  (Ответы детей)

— Мы узнаем, как найти периметр многоугольника. Это и будет темой нашего урока.

Слайд 5

Ребята, а кто из Вас помнит, что обозначает слово “ Периметр”?

Слайд 6

Это интересно! 

Ребята, я Вам напомню. В Древнем Египте границы земельных участков измерялись ходьбой, т.е. египтяне шли по границе своего участка и измеряли его. Здесь и появилось слово «периметр» (на доску вывешивается табличка со словами «пире» и «метрос»).

«Пире» – означает «ходить».
«Метрос» – измерять, т.е. измерять ходьбой.

— А  кто из Вас помнит, как мы обозначаем  периметр? (Обозначаем буквой P).

— А зачем нам нужно знать, что такое периметр?

— Где в нашей жизни нам могут пригодиться эти знания? (Классная доска, платье сшить, парту измерить можно. )

— Молодцы! Давайте отдохнем! 

Гимнастика для глаз

ІV  Актуализация новых знаний.

Слайд 7

— Алиса нашла  сундук с кладом, но он закрыт на замок. Давайте вместе подберем ключ.  Но без секретного кода нам сундук не открыть. Необходимо посчитать периметр фигур.

— Рассмотрите данные фигуры (учащиеся открывают с. 58 учебника №1).

— Как их можно назвать  одним словом? (многоугольники)

— Что необходимо знать для вычисления периметра многоугольника? (длину каждой из сторон)

— Что заметили?  (По условию стороны равные, значит длины сторон одинаковые)

— Итак, осталось выяснить,  как его вычислять. Это вам придется сделать самим в парах.

Самостоятельная работа (в парах).

1 группа вычисляет Р треугольника.
2 группа вычисляет Р четырёхугольника.
3 группа вычисляет Р пятиугольника.

4 группа вычисляет Р шестиугольника.

Периметр — это……..

Делается вывод. На доске появляются записи.

Р — сумма длин 3-х сторон

Р- сумма длин 4-х сторон

Р- сумма длин 5-ти сторон  и т. д.

— Какой великолепный клад мы нашли! Что мы сейчас делали? (учились вычислять периметр многоугольника)

Слайд 8

— Ребята, а вот и Чеширский кот, он предлагает нам составить выражения для вычисления периметра прямоугольника и квадрата  разными способами. Проверьте друг друга. (№2 с.58  Работа в парах)

— Как же правильно выполнить записи?

Р      = 8 дм + 8 дм + 8 дм + 8 дм = 32 дм — 1 ученик выходит к доске

— А можно ли вычислить более  удобным способом? (8дм*4, так как все стороны квадрата равны) 

Р =  7 дм + 9 дм + 7 дм + 9 дм =32 дм

— Как можно  вычислить более  удобным способом?

Р =  7 дм*2 + 9 дм *2 =32 дм   или Р =  (7 дм + 9 дм) *2 =32 дм  

-Как пришли к такому выводу?   (Противоположные стороны прямоугольника равны)

— Обозначим длины сторон квадрата и прямоугольника буквами. Задание: Подумайте, какие выражения подходят для вычисления периметра квадрата, а какие для вычисления периметра прямоугольника. (Работа в парах. Взаимопроверка.)

— Почему выбрали именно эти формулы? (Представители каждой группы доказывают правильность своего решения.)

-Давайте проверим, внимание на Слайд 9.   

Р  квадрата

a+а+a+а

a*4

Р прямоугольника

a+b+a+b

a*2+b*2

(a+b)*2

---

— Молодцы, мы хорошо поработали, давайте поапплодируем себе.

Физминутка (упражнения на расслабление мышц опорно – двигательного аппарата)

V   Закрепление нового материала.

 — Итак, продолжите мою мысль: чтобы найти периметр многоугольника, нужно точно знать…….  (сколько сторон у многоугольника, их длину и правило нахождения периметра).

Слайд 10

— Ой, а кто это? Да это же  Труляля и Траляля, а что они тут делают?

— Дело в том, что уважаемые наши гости решили задачу, но кто из них решил правильно, определить не могут. Ребята, давайте поможем им.

1. Решение задачи № 4 (а) с.58 (один ученик у доски)

— Можем ли сразу ответить на вопрос задачи? (нет)

— Почему? (Неизвестна длина одной из сторон прямоугольника)

— Можем ли её найти? Каким действием? (Можем, сложением). Решение.

— Зная длину и ширину прямоугольника, можем ли мы найти периметр? (Да)

— Что для этого нужно знать? (правило нахождения периметра прямоугольника). Решение. Ответ.

2. Решение №5 с.59

— Ребята, Алиса со своими друзьями очень любит спорт, особенно прыгать и бегать.  Давайте вместе с ними  решим задачу № 5 с.59.
На плане изображён стадион, размеры которого указаны в условии задачи. Вокруг стадиона проложена беговая дорожка.

— Что нужно найти? ( Нужно найти её длину, а ответ выразить в более крупных единицах)

— Как по-другому сформулировать вопрос задачи? (Найти периметр)

— В каких единицах измерения можно вычислить Р? (м, км)

— Поможем Алисе?  

Один решает у доски с комментированием.

 ( 600 м -345 м=255 м – длина, (600 м +255 м)*2= 1710 м =1 км 710 м)

VI   Повторение пройденного материала

Самостоятельная работа с  последующей  проверкой. 

 

— Ребята и снова  Алисе понадобилась наша помощь, дело в том, что рост Алисы 1м20 см. В Стране Чудес её рост постоянно менялся. Алиса выпила напиток, напоминающий вишнёвый пирог, ананас, жареную индейку и сливочную помадку, и стала в 6 раз меньше. Затем Алиса съела пирожок, и её рост увеличился в 24 раза. Нужно узнать, на сколько  больше своего нормального роста стала Алиса?

(Один человек  решает у доски, за шторкой. Есть дети, которые справятся с этим заданием быстрее остальных, им дополнительно решить  задания №6)

VII. Подведение итогов (Слайд 11)

— Молодцы, мы подошли к финалу нашего урока.

— Наше путешествие закончилось.

— Пора оценить свою работу на уроке.

— Что мы делали сегодня на уроке?

-Что нового узнали?

— Что называют периметром многоугольника?
— Как найти периметр треугольника? прямоугольника? квадрата? многоугольника?

— Где применяется знание о периметре в жизни?

VII Домашнее задание.

— Измерить  в своей квартире периметр входной двери в дециметрах.

—  Начертите в тетради фигуры, имеющие одинаковый периметр, но разную форму.  

VIII  Рефлексия. 

Обратная связь: 

— Отметьте мнение о своей работе на уроке:

Зеленый цвет — «На уроке мне всё было понятно.  Я со всеми заданиями справился самостоятельно».

Желтый цвет – «На уроке мне почти всё было понятно. Не всё получалось сразу, но я всё равно справился с заданиями».

Красный цвет – «Помогите! Мне многое не понятно! Мне требуется помощь!»

Выставление оценок.

— Молодцы!

— Спасибо всем за работу! 

Мерзляк 5 класс — § 13. Многоугольники. Равные фигуры

• Ответы к учебнику для 5 класса. А. Г. Мерзляк
• Переход на главную страницу сайта

Вопросы к параграфу

1. Какая фигура ограничивает многоугольник? — Замкнутая ломаная, звенья которой не пересекаются.

2. Могут ли звенья ломаной, ограничивающей многоугольник, пересекаться? — Нет, не могут.

3. Какие элементы многоугольника вы знаете? — Вершина, сторона, углы многоугольника.

4. Как называют и обозначают многоугольник? — Многоугольники называют и обозначают по его вершинам. Чтобы записать название многоугольника, надо последовательно записать все его вершины.

5. Что называют периметром многоугольника? — Периметр многоугольника — это сумма длин все его сторон.

6. Какие многоугольники называют равными? — Многоугольники называют равными, если они совпадают при наложении.

7. Какие фигуры называют равными? — Фигуры называют равными, если они совпадают при наложении.

Решаем устно

1. Сумму чисел 24 и 18 уменьшите на 33.

(24 + 18) — 33 = 42 — 33 = 9

2. Разность чисел 30 и 14 увеличьте в 3 раза.

(30 — 14) • 3 = 16 • 48

3. Произведение чисел 12 и 5 увеличьте на 19.

(12 • 5) + 19 = 60 + 19 = 79

4. Частное чисел 189 и 9 уменьшите в 7 раз.

(189 : 9) : 7 = 21 : 7 = 3

5. Укажите среди данных отрезков равные, если:

• АВ = 5 см 3 мм = 53 мм = TQ
• CD = 4 м 5 см = 405 см
• РК = 45 см
• EF = 2 дм 8 мм = 20 см 8 мм = 208 мм = MN
• TQ = 53 мм = 5 см 3 мм = АВ
• MN= 208 мм = 20 см 8 мм = 2 дм 8 мм = EF

Ответ: АВ = TQ и EF = MN.

Упражнения

321. Назовите вершины и стороны пятиугольника, изображённого на рисунке 109.

• Вершины пятиугольника: N, K, P, E, M
• Стороны пятиугольника: NK, KP, PE, EM, EN.

322. Начертите: 1) четырёхугольник; 2) пятиугольник; 3) шестиугольник; 4) семиугольник .

1. Четырехугольник ABCD
2. Пятиугольник EFGHJ
3. Шестиугольник SRQWXZ
4. семиугольник TKLMNOP

323. Вычислите периметр пятиугольника, стороны которого равны 2 см, 4 см, 5 см 5 мм, 6 см, 7 см.

Периметр многоугольника равен сумме длин его сторон.

2 см + 4 см + 5 см 5 мм + 6 см + 7 см = 24 см 5 мм — периметр данного пятиугольника.

Ответ: 24 см 5 мм.

324. Вычислите периметр шестиугольника, три стороны которого равны по 8 см, а три другие — по 10 см.

Периметр многоугольника равен сумме длин его сторон.

8 • 3 + 10 • 3 = 24 + 30 = 54 (см) — периметр данного шестиугольника.

Ответ: 54 см.

325. Нарисуйте в тетради фигуру, равную той, которая изображена на рисунке 110.

326. Нарисуйте в тетради фигуру, равную той, которая изображена на рисунке 111.

327. Одна из сторон четырёхугольника равна 8 см, вторая сторона в 3 раза больше первой, а третья — на 7 см меньше второй и на 9 см больше четвёртой. Вычислите периметр четырёхугольника.

1) 8 • 3 = 24 (см) — длина второй стороны четырёхугольника.

2) 24 — 7 = 17 (см) — длина третьей стороны четырёхугольника.

3) 17 — 9 = 8 (см) — длина четвёртой стороны четырёхугольника.

4) 8 + 24 + 17 + 8 = 57 (см) — периметр четырёхугольника.

Ответ: 57 см.

328. Стороны пятиугольника пронумеровали. Первая сторона равна 4 см, а каждая следующая сторона на 2 см длиннее предыдущей. Вычислите периметр пятиугольника.

1) 4 + 2 = 6 (см) — длина второй стороны пятиугольника.

2) 6 + 2 = 8 (см) — длина третьей стороны пятиугольника.

3) 8 + 2 = 10 (см) — длина четвёртой стороны пятиугольника.

4) 10 + 2 = 12 (см) — длина пятой стороны пятиугольника.

5) 4 + 6 + 8 + 10 + 12 = 40 (см) — периметр пятиугольника.

Ответ: 40 см.

329. 1) Сколько диагоналей можно провести из одной вершины: а) пятиугольника; б) девятиугольника; в) и-угольника, где п > 3?

а) Из одной вершины пятиугольника можно провести 2 диагонали.

б) Из одной вершины девятиугольника можно провести 6 диагоналей.

в) Из одной вершины n-угольника можно провести (n-3) диагоналей, так как:

• первая вершина является исходной;
• диагональ ко второй вершине совпадает со одной из сторон, прилегающей к исходной вершине;
• диагональ к последней вершине совпадает с другой из сторон, прилегающей к исходной вершине.

Ответ: 2, 6, n-3.

2) Сколько всего диагоналей можно провести: а) в пятиугольнике; б) в девятиугольнике; в) в и-угольнике, где п > 3?

а) Мы знаем, что из одной вершины пятиугольника можно провести 2 диагонали (n-3), Значит из 5 вершин можно провести 5 • 2 = 10 диагоналей (n • (n-3)). Но если провести все 10 диагоналей, то каждая пара из них будет совпадать, так как одна диагональ всегда соединяет две вершины. Значит всего в пятиугольнике можно провести 10 : 2 = 5 диагоналей ((n •(n-3) : 2). Рисунок подтверждает наш вывод.

б) Мы знаем, что из одной вершины девятиугольника можно провести 6 диагоналей (n-3 = 9 — 3 = 6), Значит из 9 вершин можно провести 9 • 6 = 54 диагонали (n • (n-3) = 9 • (9 — 3) = 9 • 6 = 54). Но если провести все 54 диагонали, то каждая пара из них будет совпадать, так как одна диагональ всегда соединяет две вершины. Значит всего в девятиугольнике можно провести 54 : 2 = 27 диагоналей ((n • (n-3) : 2 = 9 • (9 — 3) : 2 = 9 • 6 : 2 = 54 : 2 = 27).

Рисунок подтверждает наш вывод.

в) Исследуя предыдущие два задания мы вывели формулу, по которой можно посчитать количество возможных диагоналей в n-угольнике, при n > 3: n • (n-3) : 2. Это значит, у количество диагоналей:

• у четырёхугольника — n • (n-3) : 2 = 4 • (4 — 3) : 2 = 4 • 1 : 2 = 4 : 2 = 2 — верно
• у шестиугольника — n • (n-3) : 2 = 6 • (6 — 3) : 2 = 6 • 3 : 2 = 18 : 2 = 9 — верно
• у семиугольника — n • (n-3) : 2 = 7 • (7 — 3) : 2 = 7 • 4 : 2 = 1=28 : 2 = 14 — верно
• и т.д.

Ответ: 5, 27, n • (n-3) : 2.

330. Как, используя шаблон угла, градусная мера которого 13°, построить угол, градусная мера которого равна 2°?

Для того, чтобы используя шаблон угла, градусная мера которого 13°, построить угол, градусная мера которого равна 2° надо:

1. прочертить прямую линию и отметить на ней точку вершины развёрнутого угла;
2. начиная от одного из лучей развёрнутого угла последовательно 14 раз отложить по шаблону угол в 13°;
3. так как 13° • 14 = 182°, то последний из отложенных по шаблону углов будет на 2° выходить за границы развёрнутого угла;
4. угол, выходящий за границы развёрнутого угла, как раз и будет искомым углом с градусной мерой 2°.

331. Как построить угол, градусная мера которого 1°, используя шаблон угла, градусная мера которого равна:

а) 19°

Для того, чтобы используя шаблон угла, градусная мера которого 19°, построить угол, градусная мера которого равна 1° надо:

1. прочертить прямую линию и отметить на ней точку вершины развёрнутого угла;
2. начиная от одного из лучей развёрнутого угла последовательно 19 раз отложить по шаблону угол в 19°;
3. так как 19° • 19 = 361°, то последний из отложенных по шаблону углов будет на 1° выходить за границы двух развёрнутых углов;
4. угол, выходящий за границы развёрнутых углов, как раз и будет искомым углом с градусной мерой 1°.

б) 7°

Для того, чтобы используя шаблон угла, градусная мера которого 7°, построить угол, градусная мера которого равна 1° надо:

1. прочертить прямую линию и отметить на ней точку вершины развёрнутого угла.
2. провести из этой точки перпендикуляр к прямой;
3. начиная от одного из лучей развёрнутого угла последовательно 13 раз отложить по шаблону угол в 7°;
4. так как 7° • 13 = 91°, то последний из отложенных по шаблону углов будет на 1° выходить за границы прямого угла образованного перпендикуляром к прямой;
5. угол, выходящий за границы прямого угла, как раз и будет искомым углом с градусной мерой 1°.

332. Существует ли многоугольник с периметром, равным 1 000 000 см, который можно целиком расположить в квадрате со стороной 1 см?

Да, теоретически такой многоугольник существует. Для этого надо из квадрата со стороной 1 см вырезать множество полосок либо треугольников, либо ещё каких-нибудь фигур вдоль нескольких сторон исходного квадрата. Точное количество таких вырезанных фигур будет зависеть от длины вырезаемых из квадрата сторон фигуры, а также от длины оставшихся от исходного квадрата сторон.

В реальности такую операцию способны выполнить только суперточные приборы, например лазерный принтер. Кроме того, необходимо провести очень точный расчёт вырезаемых фигур.

Упражнения для повторения

333. Сравните:

1) 3 986 г и 4 кг: 4 кг = 4000 г ⇒ 3 986 г < 4 000 г ⇒ 3 986 г < 4 кг

2) 6 м и 712 см: 6 м = 600 см ⇒ 600 см < 712 см ⇒ 6 м < 712 см

3) 60 см и 602 мм: 60 см = 600 мм ⇒ 600 мм < 602 мм ⇒ 60 см < 602 мм

4) 999 кг и 10 ц: 10 ц = 1000 кг ⇒ 999 кг < 1000 кг ⇒ 999 кг < 10 ц

334. Выполните сложение, выбирая удобный порядок вычислений:

1) (636 + 927) + 364 = (636 + 364) + 927 = 1 000 + 927 = 1 927

2) (425 + 798) + 675 = (425 + 675) + 798 = 1 100 + 798 = 1 898

3) 212 + 493 + 788 + 807 = (212 + 788) + (493 + 807) = 1 000 + 1 300 = 2 300

4) 161 + 455 + 839 + 945 = (161 + 839) + (455 + 945) = 1 000 + 1 400 = 2 400

335. Известно, что ∠ABC = 74°, а луч BD — его биссектриса. Вычислите величину угла DBC.

Мы знаем, что биссектриса угла всегда делит угол пополам. Значит:

∠DBC = ∠ABC : 2 = 74° : 2 = 37°

Ответ: ∠DBC = 37°.

336. Высота самой высокой горы Западной Европы Монблан равна 4 809 м. Она на 2 151 м ниже самой высокой горы Южной Америки Аконкагуа, которая на 770 м выше самой высокой горы Северной Америки Денали. Какова высота самой высокой горы Африки Килиманджаро, если она на 295 м ниже горы Денали? Какова высота самой высокой горы мира Джомолунгмы (Эверест) (рис. 112), если она на 2 953 м выше горы Килиманджаро?

1) 4 809 + 2 151 = 6 960 (м) — высота горы Аконкагуа.

2) 6 960 — 770 = 6 190 (м) — высота горы Денали.

3) 6 190 — 295 = 5 895 (м) — высота горы Килиманджаро.

4) 5 895 + 2 953 = 8 848 (м) — высота горы Джомолунгма.

Ответ: 8 848 метров.

Задача от мудрой совы

337. Лимоны одинаковой массы продают поштучно. Масса каждого лимона составляет целое количество граммов. Купили больше двух, но меньше семи лимонов. Масса всей покупки составляет 850 г. Какова масса одного лимона?

Так как купили больше двух, но меньше семи лимонов, то количество купленных лимонов может быть либо 3, либо 4, либо 5, либо 6.

Масса каждого лимона — целое число, причём все лимоны одинаковые. Проверим, на какое из возможных чисел (3, 4, 5 или 6) общая масса покупки 850 г делится без остатка. Для этого применим метод подбора.

Под заданные условия подходит только число 5.

850 : 5 = 170 (г) — масса одного лимона.  

Ответ: 170 г.

• Ответы к учебнику для 5 класса. А. Г. Мерзляк
• Переход на главную страницу сайта

How To Find the Perimeter of a Pentagon (Formula & Example)

Written by

Malcolm McKinsey

January 16, 2023

Fact-checked by

Paul Mazzola

Perimeter of a pentagon

The perimeter ,  P , пятиугольника — это расстояние вокруг его пяти прямых сторон. Чтобы найти периметр пятиугольника, нужно сложить длины всех 5 сторон. Для правильных пятиугольников формула P = 5 x s , где s равно длине стороны.

Способ нахождения периметра пятиугольника зависит от того, какой у вас тип пятиугольника и что о нем известно.

Периметр пятиугольника

Правильные и неправильные пятиугольники

Правильные пятиугольники имеют пять конгруэнтных сторон, пять конгруэнтных внутренних углов и пять конгруэнтных внешних углов. Как и у всех правильных многоугольников, все стороны должны быть одинаковой длины и все углы должны быть одинаковой величины.

Неправильные пятиугольники имеют пять сторон и пять углов, но ни стороны, ни углы не равны. Неправильный многоугольник может иметь стороны пяти разных длин и углы пяти разных размеров.

Периметр правильного пятиугольника найти проще, так как у нас есть формула. Чтобы найти периметр неправильного пятиугольника, необходимо измерить и сложить пять сторон.

Периметр формулы пятиугольника

Используя формулу периметра пятиугольника, вы можете относительно легко найти периметр правильного пятиугольника. Чтобы найти периметр правильного пятиугольника со сторонами длиной s , используйте следующую формулу:

В нашей формуле 5   – это количество сторон, а0035 s  это известная нам длина стороны. Как и в случае с периметром квадрата или периметром многоугольника в целом, периметр пятиугольника находится путем сложения всех сторон.

Если вы находите периметр правильного пятиугольника, то вы знаете, что все пять сторон имеют одинаковую длину, поэтому вы можете упростить формулу, используя умножение вместо сложения.

Если вы предпочитаете использовать метод сложения, ваш периметр правильного пятиугольника будет выглядеть так:

У вас есть  s  для каждой стороны пятиугольника.

Формулы периметра пятиугольника

Периметр правильного пятиугольника пример

Предположим, что у нас есть правильный пятиугольник и что мы знаем длину одной стороны 3 см3 см. Чему равен периметр пятиугольника?

Если мы знаем одну сторону правильного пятиугольника, то мы знаем длину каждой стороны, потому что правильный пятиугольник имеет равные стороны. Мы можем просто подставить нашу известную сторону в нашу формулу:

Зная, что длина стороны равна 3 см , воспользовавшись формулой периметра пятиугольника, мы нашли, что периметр этого правильного пятиугольника равен 15 см .

Пример периметра правильного пятиугольника

Другой важной частью пятиугольника является апофема и площадь. Узнайте, как найти площадь пятиугольника, используя формулу площади. Вы можете найти площадь правильного пятиугольника или неправильного пятиугольника.

Периметр пятиугольника — формула, свойства, примеры

Периметр пятиугольника равен сумме всех его сторон. Пятиугольник — это многоугольник с пятью сторонами, пятью вершинами и пятью внутренними углами, сумма которых составляет 540°. Пятиугольники могут быть правильными или неправильными в зависимости от длины сторон. Давайте узнаем больше о периметре пятиугольника в этой статье.

1.	Что такое периметр пятиугольника?
2.	Периметр Пентагона Формулы
3.	Периметр пятиугольника с радиусом
4.	Часто задаваемые вопросы о периметре Пентагона

Что такое периметр пятиугольника?

Периметр пятиугольника — это общая мера его границы, и он рассчитывается путем сложения длин всех его сторон.

Поскольку пятиугольник является пятиугольником, можно сложить все пять сторон, чтобы найти его периметр. Периметр пятиугольника выражается в линейных единицах, таких как дюймы, ярды, сантиметры и так далее.

Правильный и неправильный пятиугольник

Правильный пятиугольник — это пятиугольник, у которого все пять сторон имеют одинаковую длину и все внутренние углы имеют одинаковую величину. Неправильный пятиугольник – это тот, у которого стороны не равны и углы не равны.

Свойства правильного пятиугольника

Слово «пятиугольник» происходит от греческого слова «пента», что означает «пять», и «гон», что означает «угол». Есть несколько основных свойств, которые помогают нам идентифицировать пятиугольник. Обратите внимание на следующий правильный пятиугольник, чтобы понять его свойства, указанные ниже.

Мы можем идентифицировать и отличить правильный пятиугольник с помощью следующих свойств:

• Пятиугольник — это многоугольник с 5 сторонами.
• Имеет 5 диагоналей.
• Сумма всех внутренних углов пятиугольника равна 540°
• Каждый внутренний угол правильного пятиугольника равен 108°
• Каждый внешний угол правильного пятиугольника равен 72°

Теперь давайте прочитаем о формулах, которые используются для нахождения периметра пятиугольника. Формулы отличаются известными размерностями.

Периметр Пентагона Формула

Мы знаем, что периметр пятиугольника равен сумме длин всех его сторон. Теперь, если это правильный пятиугольник, это означает, что все пять сторон имеют одинаковую длину. Рассмотрим правильный пятиугольник со стороной а. В этом случае периметр можно рассчитать по формуле Периметр = а + а + а + а + а, что равно 5а. Поэтому основная формула для периметра правильного пятиугольника приведена ниже.

Периметр пятиугольника = сумма всех его сторон

Пример 1: Найдите периметр правильного пятиугольника, длина стороны которого равна 7 единицам.

Решение:

Длина стороны (а) данного пятиугольника = 7 единиц.

Используя периметр формулы пятиугольника, Периметр = 5a = 5 × 7 = 35 единиц.

Пример 2: Найдите периметр пятиугольника, длина сторон которого равна 5 единицам, 4 единицам, 7 единицам, 3 единицам и 6 единицам.

Решение:

Чтобы найти периметр неправильного пятиугольника, мы сложим все пять сторон, периметр = 5 + 4 + 7 + 3 + 6 = 25 единиц.

Следовательно, периметр пятиугольника равен 25 единицам.

Периметр пятиугольника с радиусом

Периметр пятиугольника можно рассчитать, если известен радиус пятиугольника. Это тот случай, когда пятиугольник вписан в окружность, как показано ниже. В таких случаях радиус — это линия, проведенная от центра многоугольника к одной из его вершин. Его также называют радиусом окружности. Периметр этого пятиугольника можно рассчитать, если известна длина стороны по формуле: Длина стороны = 2r × Sin(180/n), где r — радиус, а n — количество сторон. Получив длину стороны, периметр можно легко рассчитать по формуле Периметр = 5а.

Пример: Найдите периметр правильного пятиугольника, вписанного в окружность радиусом 5 единиц.

Решение: Дано, радиус = 5 единиц, количество сторон = 5

Сначала вычислим длину стороны пятиугольника по формуле: Длина стороны = 2r × Sin(180/n)

Подставляя данные значения в формулу, получаем Длина стороны = 2r × Sin(180/n) = Длина стороны = 2 × 5 × Sin(180/5) = 10 × Sin(180/5) = 10 × Sin 36 = 10 × 0,58779= 5,8 ед. После этого периметр правильного пятиугольника можно рассчитать по формуле Периметр = 5а = 5 × 5,8 = 29 единиц.

☛ Похожие статьи

• Формулы периметра
• Периметр многоугольника
• Разница между площадью и периметром
• Периметр прямоугольника
• Периметр квадрата
• Периметр треугольника

 

Периметр формулы Пентагона Примеры

1. Пример 1: Найдите периметр правильного пятиугольника, если длина стороны пятиугольника равна 10 единицам.

   Решение: Длина данной стороны (a) = 10 единиц

   Используя формулу для периметра пятиугольника, P = 5a ⇒ 5 × 10 = 50 единиц
   Ответ: Периметр пятиугольника равен 50 единицам.

2. Пример 2: Найдите периметр пятиугольника со следующими длинами сторон: 3 единицы, 7 единиц, 8 единиц, 9 единиц.единиц и 6 единиц.

   Решение: Поскольку длины сторон пятиугольника различны, это неправильный пятиугольник. Длины сторон даны как 3 единицы, 7 единиц, 8 единиц, 9 единиц и 6 единиц.

   Используя формулу периметра пятиугольника, P = сумма всех его сторон = 3 + 7 + 8 + 9 + 6 = 33 единицы.

   Ответ: Следовательно, периметр пятиугольника равен 33 единицам.

3. Пример 3: Укажите истинное или ложное значение относительно периметра пятиугольника:

   а.) Периметр пятиугольника равен сумме длин всех его сторон.

   б. ) Если сторона правильного пятиугольника равна 7 единицам, то периметр пятиугольника будет равен 28 единицам.

   Решение:

   а.) Верно, что периметр пятиугольника равен сумме длин всех его сторон.

   б.) Неверно, если сторона правильного пятиугольника равна 7 единицам, то периметр пятиугольника будет равен 35 единицам.

перейти к слайдуперейти к слайдуперейти к слайду

Есть вопросы по основным математическим понятиям?

Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, почему математика стоит за нашими сертифицированными экспертами.

Часто задаваемые вопросы о периметре Пентагона

Что такое периметр пятиугольника?

Периметр пятиугольника представляет собой общую меру его границы и рассчитывается путем сложения длин всех его сторон. Если это правильный пятиугольник, формула для нахождения его периметра будет следующей: P = 5a, где a — длина стороны. В случае неправильного пятиугольника, у которого все стороны разной длины, формула такова: P = сумма всех его сторон. Периметр пятиугольника выражается в линейных единицах, таких как дюймы, ярды, сантиметры и так далее.

Как найти периметр пятиугольника?

Периметр пятиугольника можно рассчитать с помощью основной формулы Периметр пятиугольника = сумма его сторон. Иногда длина стороны правильного пятиугольника неизвестна, а указаны другие размеры, например радиус. В таких случаях длина стороны рассчитывается по формуле Длина стороны = 2r × Sin(180/n), где r — радиус, а n — количество сторон. Получив длину стороны, периметр можно рассчитать по формуле Периметр = 5а.

Какая формула периметра пятиугольника?

Основная формула, используемая для нахождения периметра пятиугольника: P = сумма его сторон. Если это правильный пятиугольник, формула может быть записана как P = 5a, где «a» — длина его стороны. Если это неправильный пятиугольник, можно сложить все его стороны, чтобы получить периметр.

Как найти периметр пятиугольника с радиусом?

Периметр пятиугольника можно рассчитать, если известен радиус пятиугольника. Это тот случай, когда пятиугольник вписан в окружность. В таких случаях радиус — это линия, проведенная от центра многоугольника к одной из его вершин. Его также называют радиусом окружности. Периметр этого пятиугольника можно рассчитать после нахождения длины стороны по формуле: Длина стороны = 2r × Sin(180/n), где r — радиус, а n — количество сторон. Получив длину стороны, периметр можно рассчитать по формуле Периметр = 5а.

Как найти периметр пятиугольника с помощью апофемы?

Периметр пятиугольника можно рассчитать, если известна апофема пятиугольника. Апофема — это перпендикулярный отрезок, проведенный из центра пятиугольника к стороне пятиугольника. Если дана апофема пятиугольника, длину стороны можно рассчитать по формуле Длина стороны = 2 × длина апофемы × тангенс (180/n), где «n» представляет количество сторон. Получив длину стороны, периметр пятиугольника можно рассчитать по формуле P = 5a.