Формула первообразной: Первообразная и интеграл | Формулы с примерами

Содержание

что это такое, основные свойства, как найти

Первообразная, основные понятия и определения

Рассмотрим некую функцию f(x)=x3. Попробуем вычислить производную от данной функции. Для этого следует вспомнить формулу:

(xn),=n?xn-1

Тогда получим:

f,(x)=(x3),=3×2

Из этого следует, что:

x2=(x3),3=(x33),

С помощью данной записи можно объяснить, что такое первообразная:

x2>x33

Аналогичным образом можно составить выражение:

x4>x55

Если обобщить рассматриваемые соотношения, то получится вывести формулу:

xn>xn+1n+1

Здесь n отлично от (-1)

Заметим, что в том случае, когда n = -1, первообразная функции будет вычисляться следующим образом:

x-1>1x

(lnx),=1x

1x=x-1=lnx

В результате, первообразная функция определяется, как функция, производная которой равна начальной функции.

Определение 1

Функцию y = F(x) называют первообразной функции y = f(x) на интервале Х в случае, когда для какого-либо х?Х справедливо следующее соотношение:

F(x) = f(x).

Определение 2

Ключевое свойство первообразных: какая-либо первообразная для функции f на интервале I может быть представлена в виде:

F(x) + C, где:

F(x) является одной из первообразных для функции f(х) на промежутке I;
С является произвольной постоянной.

Из основного свойства первообразной легко вывести несколько полезных свойств, которые можно применять как в средних классах школы, так и будучи студентом.

Любое число допустимо записать, как С. Независимо от его значения, получится первообразная для f на интервале I.
Если взять любую первообразную Ф для f на интервале I, то при этом получится найти такое С, при котором для каждого х из интервала I будет справедливо равенство Ф(х) = F(x) + C.

Первообразная и интеграл

Формула Ньютона-Лейбница определяет связь между первообразной функции и интегралом. Соотношение вытекает из соответствующей теоремы.

Определение 3

Теорема Ньютона-Лейбница: при непрерывности функции f(x) на интервале [a, b] и ?(x) в виде какой-либо первообразной данной функции на рассматриваемом отрезке справедливо следующее равенство:

Докажем теорему. Представим, что на интервале [a, b] имеется некая интегрируемая функция f. Запишем какую-то переменную х с произвольным значением:

x?[a,b]

Далее определим новую функцию:

F(x)=?axf(t)?dt.

Данная функция определена для любых значений:

x?[a,b]

Это возможно при условии существования интеграла от f на интервале [a, b]. При этом имеется также интеграл от f на интервале [a, x] при a?x?b. Заметим, что из определения вытекает следующее:

F(a)=?aaf(t)?dt=0(1)

В этом случае:

F(b)=?abf(t)?dt

Нужно подтвердить беспрерывность функции F на интервале [a, b]. Предположим, что:

x,x+h?[a,b].

В таком случае:

F(x+h)-F(x)=?a(x+h)f(t)?dt-?axf(t)?dt=?x(x+h)f(t)?dt

При условии: K=sup|f(t)|,a?t?b получим, что:

В результате F не прерывается на интервале [a, b]. При этом не имеет значение наличие разрывов у f. Важным условием является тот факт, что f интегрируется на [a, b].

График f имеет вид:

Источник: ru. wikipedia.org

Рассмотрим переменную фигуру aABx. Ее площадь можно определить, как F(x). Приращение при этом составит:

F(x+h)-F(x)

Выражение равно площади фигуры xBC(x+h), которая по причине ограниченности f стремится к нулю, когда h>0. При этом не имеет значение, будет ли x точкой непрерывности или разрыва f, к примеру, точкой x-d.

Далее допустим, что функция f, кроме того, что интегрируема на интервале [a, x], также не прерывается в точке x?[a,x]. Попробуем доказать, что в таком случае имеется производная функции F в данной точке, которая равна:

F'(x)=f(x)

В действительности, для рассматриваемой точки х справедливо, что:

F(x+h)-F(x)h=1h?xx+hf(t)?dt= 1h?xx+h(f(x)+?(t))?dt =1h?xx+hf(x)?dt+1h?xx+h?(t)?dt=f(x)+0,h>0

По предположению:

f(t)=f(x)+?(t)

В связи с тем, что f(x) является постоянной по отношению к t, получим:

?xx+hf(x)?dt=f(x)h

Так как функция f не прерывается в точке x для любого ?>0 допустимо такое значение ?, что |?(t)|<? в случае |x-t|<?. По этой причине:

1h?xx+h?(t)?dt? 1|h||h|?=?,|h|<?

Согласно записанному соотношению, было доказано, что левая часть рассматриваемого неравенства есть 0, когда h>0. Рассмотрим повторно выражение:

F(x+h)-F(x)h= 1h?xx+hf(t)?dt= 1h?xx+h(f(x)+?(t))?dt =1h?xx+hf(x)?dt+1h?xx+h?(t)?dt=f(x)+0,h>0

Если h>0, то существует производная от F в точке х. Кроме того, справедливым является равенство:

F'(x)=f(x)

Если x=a, b, здесь речь идет соответственно о правой и левой производной. В том случае, когда f не прерывается на интервале [a, b], по представленным ранее доказательствам, ей соответствует такая функция:

F(x)=?axf(t)?dt

Данная функция обладает производной:

F'(x)=f(x)

При этом:

a?x?b

В таком случае функция F(x) является первообразной для f на интервале [a, b]. Данное утверждение носит название теоремы об интеграле с переменным верхним пределом, либо теоремы Барроу.

В ходе вычислений получилось доказать, что в пределах отрезка [a, b] у произвольной функции f, которая не прерывается на рассматриваемом интервале, имеется первообразная. Уравнение первообразной имеет вид:

F(x)=?axf(t)?dt

Предположим существование произвольной первообразной функции f(x) в виде ? на интервале [a, b]. Известно, что:

?(x)=F(x)+C

В этом случае, С играет роль некой постоянной. Запишем предположительные условия:

x=a

F(a)=0

Тогда получим, что:

?(a)=C.

В результате:

F(x)=Φ(x)-Φ(a)

С другой стороны:

∫abf(x) dx=F(b)

В связи с этим:

Важно запомнить, что запрещено применять записанную формулу в том случае, когда в примере имеется разрывная функция, либо функция, не ограниченная в пределах рассматриваемого интервала интегрирования. Подобные вычисления будут некорректными, как в примере:

Заметим, что в записанном соотношении отсутствует смысл, так как интеграл от положительной функции не может быть меньше, чем ноль. Причина подобной ошибки заключается в разрывности и неограниченности функции под знаком интеграла в нуле. В таком случае, для решения этого примера нельзя использовать формулу Ньютона-Лейбница.

Таблица первообразных и правила их нахождения

Представим таблицу первообразных функций. Заметим, что любое из выражений справа требуется дополнить константой.

Источник: krasavtsev.blogspot.com

Решать задания на поиск первообразной функции удобно с использованием нескольких правил. Рассмотрим их подробнее.

Правило 1

Первообразная функции суммы или разности представляет собой сумму или разность соответственно первообразных функций:

F(x + у) = F(x) + F(у)

F(x – у) = F(x) – F(у).

Попробуем применить данное правило, чтобы найти первообразную для следующей функции:

у=4х3+cosx

В случае каждой из записанных функций определим первообразную, согласно правилу:

f(x)=4×3,F(x)=x4.

f(x) = cos x, F(x) = sin x.

В результате первообразная начальной функции равна:

у=х4+sinx

или любая функция вида

у=х4+sinx+C.

Правило 2

В том случае, когда F(x) является первообразной для f(x), получим, что k*F(x)представляет собой первообразную для функции k*f(x). При этом допускается вынесение коэффициента за функцию.

Представим, что имеется некая функция, первообразную которой нужно определить:

у = 8 sin x

Зная, что для sin x однозначная первообразная равна — cos x. В таком случае, первообразная начальной функции имеет следующий вид:

у = –8 cos x

Попробуем решить еще один типичный пример на нахождение первообразной функции:

у=3×2+4х+5

Запишем первообразную для x2:

x33

Запишем первообразную для х:

x22

Первообразная для 1 равна х. В таком случае, первообразная начальной функции будет записана в следующем виде:

у=x3+2×2+5x.

Правило 3

В том случае, когда y = F(x) является первообразной функции y = f(x), первообразная для функции y = f(kx + m) является y = 1/k F(kx + m).

В некоторых случаях по условию задачи требуется найти первообразные с определенной точкой. Следует отметить, что отличия между первообразными некой функции заключаются в сдвиге по вертикали на какое-либо число.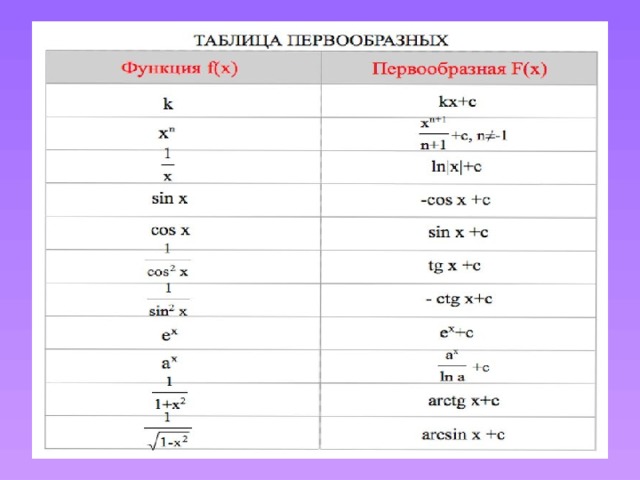 Из этого можно сделать вывод, что при рассмотрении любой точки на координатной плоскости в любом случае через нее проходит лишь одна первообразная.

Разберем типичную задачу. Дана функция:

f(x)=5×4+6×3–2x+6

Попробуем найти первообразную в точке:

М (–1; 4).

Выполним вычисления, относительно каждого из слагаемых:

x4→x55

x3→x44

x→x22

6→6х

Вычислим первообразную:

F(x)=5×55+6×44-2×22+6x+C=x5+3×42-x2+6x+C

Исходя из полного условия задачи, данная функция пересекает точку М (–1; 4). По этой причине при подстановке на место х числа -1 и на место F(x) числа 4 в итоге получается верное числовое равенство:

4=(-1)5+3(-1)42-(-1)2+6(-1)+C

Заметим, что данное соотношение записано, относительно константы С. Вычислим С:

4=-1+32–1–6+С

С=4+6+2-32=10,5

Путем подстановки значения С в общее уравнение получим первообразную:

F(x)=x5+3×42-x2+6x+10,5

Примеры решения задач

Задача 1

Дана функция, для которой нужно определить первообразную:

у = cos (7x)

Решение

у=17sin(7x)=sin(7x)7

Ответ: у=sin(7x)7

Задача 2

Найти интеграл, используя формулу Ньютона-Лейбница:

∫12x3dx

Решение

Сначала требуется определить непрерывность подынтегральной функции f(x)=x3 на интервале x∈[a;b]. Затем можно перейти к определению первообразной путем устранения пределов интегрирования и решения любым из методов. Здесь целесообразно воспользоваться способом непосредственного интегрирования. Согласно табличному значению:

∫xpdx=xp+1p+1

Тогда:

F(x)=∫x3dx=x3+13+1dx=x44+C

Если С имеет нулевое значение, то одна из первообразных равна:

F(x)=x44

Воспользуемся формулой Ньютона-Лейбница:

F(a)=F(1)=14

F(b)=F(2)=164=4

F(b)-F(a)=F(2)-F(1)=4-14=154

Таким образом:

∫12x3dx=F(2)-F(1)=4-14=154

Ответ: ∫12x3dx=154

Задача 3

Найти определенный интеграл:

∫0πxsinxdx

Решение

Вычислим определенный интеграл путем интегрирования по частям:

Здесь применена формула Ньютона-Лейбница. С ее помощью также можно найти второй интеграл:

Ответ: ∫0πxsinxdx=π

Задача 4

Дана одна из первообразных функции f(x):

F(x)=x3-2x+7

Требуется определить f(0).

Решение

Согласно определению первообразной:

f(x) = F'(x)

В результате:

f(x)=3×2–2

Тогда:

f(0) = -2

Ответ: -2

Задача 5

Дана первообразная функции f(x):

F(x)=2×4-x3+7x-π

Необходимо определить f(1).

Решение

Вспомним определение первообразной:

f(x) = F'(x)

В таком случае:

f(x)=8×3-3×2+7

В результате:

f(1) = 12

Ответ: 12

Связь между интегралом и первообразной. Формула ньютона-лейбница.

Если известна хотя бы одна первообразная подынтегральной функции, то определенный интеграл можно вычислить без интегральных сумм и предельного перехода с помощью формулы Ньютона-Лейбница.

где	а и b	—	нижний и верхний пределы интегрирования;
	F(x)	—	первообразная функции;
	F(b)-F(a)	—	приращение первообразной.

Правило вычисления интеграла по формуле Ньютона-Лейбница

Найти неопределенный интеграл от данной функции и из результата подстановки верхнего предела в первообразную функцию ВЫЧЕСТЬ результат подстановки нижнего предела.

ОСНОВНЫЕ СВОЙСТВА ОПРЕДЕЛЕННОГО ИНТЕГРАЛА

1		Интеграл от суммы функции равен сумме интегралов от всех слагаемых
2		Постоянный множитель можно выносить за знак интеграла
3		При перестановке пределов изменяется знак интеграла
4		Интеграл с одинаковыми пределами равен нулю
5	где a < c < b	Отрезок интегрирования можно разбивать на части

МЕТОДЫ ИНТЕГРИРОВАНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА

непосредственное интегрирование
метод введения новой переменной
интегрирование по частям

Непосредственное интегрирование определенного интеграла состоит в том, что путем тождественных преобразований и применения свойств определенного интеграла приводится к одному или нескольким табличным интегралам, которые вычисляются по формуле Ньютона-Лейбница.

Интегрирование методом введения новой переменной состоит в следующем:

часть подынтегральной функции заменить новой переменной так, чтобы затем получить табличный интеграл;
найти дифференциал от обеих частей замены;
найти новые пределы интегрирования определенного интеграла;
всё подынтегральное выражение выразить через новую переменную, после чего получится табличный интеграл;
вычислить полученный определенный интеграл, используя новые пределы интегрирования.

Интегрирование по частям осуществляется по формуле:

где u и — функции, зависящие от х, имеющие непрерывные производные

Свойства, химическая структура и применение

Первообразная — это все, что является обратной функцией и дифференцировано в тригонометрических терминах.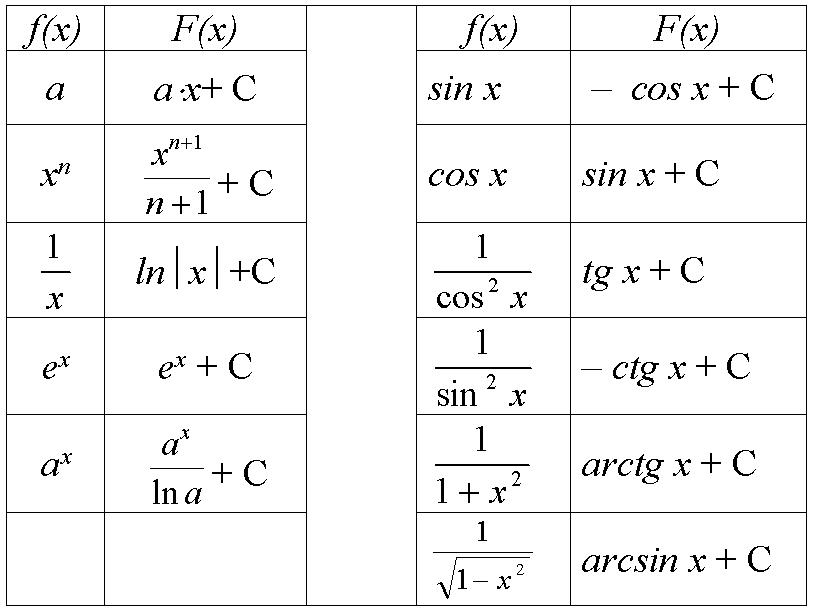 Первообразная формула и дифференцированные функции непрерывны на заданном интервале. Дифференцируемая функция F, производная которой идентична исходной функции f, называется первообразной, примитивной функцией, примитивным интегралом или неопределенным интегралом функции f в исчислении.

Формула первообразных Правила в математике являются фундаментальными принципами для определения первообразных различных комбинаций функций. Антидифференциация, как следует из названия, противоположна дифференциации. Эти первообразные формулы помогают нам определить первообразную суммы или разности функций, произведения и частного, скалярного множителя функции и постоянной функции, а также композиции функций. Антипроизводная формула 9Правила 0004 помогают нам упростить процесс нахождения первообразных производных.

Ниже приводится список наиболее часто используемых правил формулы первообразной для произведения, частного, суммы, разности и композиции функций: Правило отношения

Правило первообразной для скалярного кратного функции

Правило первообразных для суммы и разности функций

Основные первообразные
В этой части будут рассмотрены формулы для различных законов первообразных, подробно рассмотренные ранее. Они рассмотрят принципы антидифференцирования алгебраических функций со степенью, а также другие комбинации функций. Законы первообразной формулы часто используются для таких функций, как тригонометрические, экспоненциальные, логарифмические и алгебраические функции.
Правила первообразных
Правила формулы первообразных являются одними из наиболее важных принципов для определения первообразных различных комбинаций функций. Эти первообразные правила можно использовать для нахождения первообразных функций, таких как произведение, частное, сумма, разность, скалярное кратное и композиция функций. Эти законы применимы к алгебраическим функциям, экспоненциальным функциям, тригонометрическим функциям, гиперболическим функциям, логарифмическим функциям и постоянным функциям.
Важные правила первообразных Примечания
Принципы первообразных используются для вычисления первообразных различных комбинаций алгебраических, тригонометрических, логарифмических, экспоненциальных, обратных тригонометрических и гиперболических функций.
Большинство правил дифференциации имеют соответствующие первообразные правила для антидифференцировки.
Правило Первообразной Формулы для постоянной функции f(x) = k равно ∫k dx = kx + C
Тригонометрические Функции Первообразной Правила
Тригонометрические функции делятся на шесть категорий: синус, косинус, тангенс, котангенс, секанс и косеканс. Теперь они исследуют формулу первообразных этих тригонометрических функций следующим образом: | + C
∫cot x dx = ln |sin x| + C
∫sec x dx = ln |sec x + tan x| + C
∫csc x dx = ln |cosec x – cot x| + С
9b f(t)\, dt \), мы можем найти любую первообразную \(F(t)\) от \(f(t)\) и вычислить \(F(b) — F(a)\). Задача нахождения точного значения определенного интеграла сводится к нахождению некоторой (любой) первообразной \(F\) подынтегральной функции и последующему вычислению \(F(b) — F(a)\). Даже найти одну первообразную может быть сложно, и мы будем придерживаться функций, которые имеют простые первообразные.
Антидифференцировка идет в обратном направлении через производный процесс. Таким образом, самые простые антипроизводные правила — это просто обратные версии простейших производных правил. Напомним из главы 2: 9х\) перед.
Далее следуют соответствующие правила для первообразных — каждое из первообразных правил просто переписывает производное правило. Все эти первообразные можно проверить дифференцированием.
Есть один сюрприз – первообразная от \(\frac{1}{x}\) на самом деле не просто \(\ln(x)\), это \(\ln|x|\). Это хорошо — первообразная имеет область определения, совпадающую с областью определения \(\frac{1}{x}\), которая больше, чем область определения \(\ln(x)\), поэтому мы не Нам не нужно беспокоиться о том, являются ли наши \(x\) положительными или отрицательными. Но мы
должен быть осторожным, чтобы включить эти абсолютные значения, иначе мы можем столкнуться с проблемами домена.
Для просмотра этого видео включите JavaScript и рассмотрите возможность обновления до веб-браузера, поддерживающего видео HTML5
Первообразные правила: строительные блоки
В дальнейшем \(f\) и \(g\) являются дифференцируемыми функциями \(x\), а \(k\), \(n\) и \(C \) являются константами.
No related posts.