Квадрат. Формулы и свойства квадрата
Навигация по странице: Определение квадрата Основные свойства квадрата Диагональ квадрата Периметр квадрата Площадь квадрата Окружность описанная вокруг квадрата Окружность вписанная в квадрат
Определение.
Квадрат — это четырехугольник у которого все четыре стороны и углы одинаковы. Квадраты отличаются между собой только длиной стороны, но все четыре угла у них прямые, то есть по 90°.| Рис.1 | Рис.2 |
Основные свойства квадрата
Квадратом также могут быть параллелограмм, ромб или прямоугольник если они имеют одинаковые длины диагоналей, сторон и одинаковые углы.
1. Все четыре стороны квадрата имеют одинаковую длину, то есть они равны:AB = BC = CD = AD
2. Противоположные стороны квадрата параллельны:AB||CD, BC||AD
3. Все четыре угла квадрата прямые:∠ABC = ∠BCD = ∠CDA = ∠DAB = 90°
4.
Сумма углов квадрата равна 360 градусов:∠ABC + ∠BCD + ∠CDA + ∠DAB = 360°
5. Диагонали квадрата имеют одинаковой длины:AC = BD
6. Каждая диагональ квадрата делит квадрат на две одинаковые симметричные фигуры
7. Диагонали квадрата пересекаются под прямым углом, и разделяют друг друга пополам:| AC┴BD | AO = BO = CO = DO = | d | |
| 2 |
8. Точка пересечения диагоналей называется центром квадрата и также является центром вписанной и описанной окружности
9. Каждая диагональ делит угол квадрата пополам, то есть они являются биссектрисами углов квадрата:ΔABC = ΔADC = ΔBAD = ΔBCD
∠ACB = ∠ACD = ∠BDC = ∠BDA = ∠CAB = ∠CAD = ∠DBC = ∠DBA = 45°
ΔAOB = ΔBOC = ΔCOD = ΔDOA
Диагональ квадрата
Определение.
Диагональ любого квадрата всегда больше его стороны в√2 раз.
Формулы определения длины диагонали квадрата
1. Формула диагонали квадрата через сторону квадрата:d = a·√2
2. Формула диагонали квадрата через площадь квадрата:d = √2S
3. Формула диагонали квадрата через периметр квадрата:
| d = | P |
| 2√2 |
d = 2R
5. Формула диагонали квадрата через диаметр описанной окружности:d = Dо
6. Формула диагонали квадрата через радиус вписанной окружности:d = 2r√2
7. Формула диагонали квадрата через диаметр вписанной окружности:d = Dв√2
8. Формула диагонали квадрата через длину отрезка l:
| d = l | 2√10 |
| 5 |
Периметр квадрата
Определение.
Формулы определения длины периметра квадрата
1. Формула периметра квадрата через сторону квадрата:P = 4a
2. Формула периметра квадрата через площадь квадрата:P = 4√S
3. Формула периметра квадрата через диагональ квадрата:P = 2d√2
4. Формула периметра квадрата через радиус описанной окружности:P = 4R√2
5. Формула периметра квадрата через диаметр описанной окружности:P = 2Dо√2
6. Формула периметра квадрата через радиус вписанной окружности:P = 8r
7. Формула периметра квадрата через диаметр вписанной окружности:P = 4Dв
8. Формула периметра квадрата через длину отрезка l:
| P = l | 8 |
| √5 |
Площадь квадрата
Определение.
Площадью квадрата называется пространство, ограниченное сторонами квадрата, то есть в пределах периметра квадрата.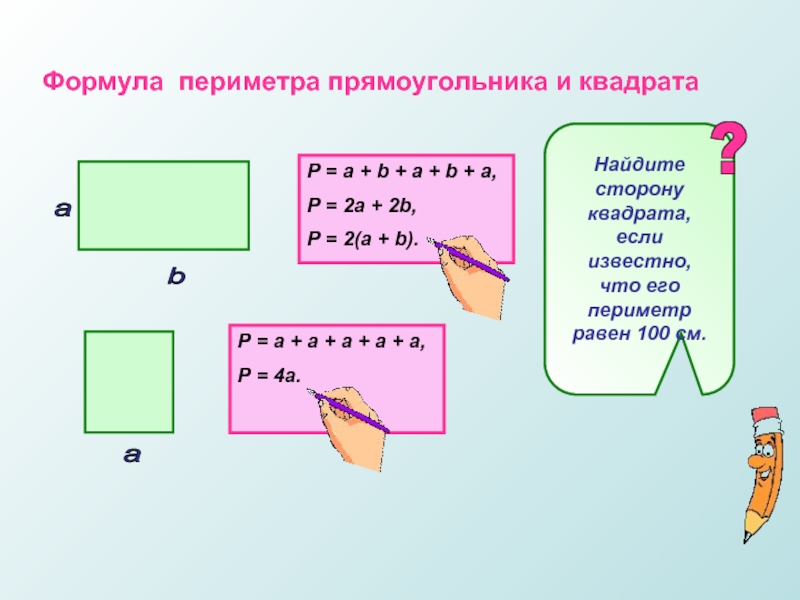
Площадь квадрата больше площади любого четырехугольника с таким же периметром.
Формулы определения площади квадрата
1. Формула площади квадрата через сторону квадрата:S = a2
2. Формула площади квадрата через периметр квадрата:
| S = | P2 |
| 16 |
3. Формула площади квадрата через диагональ квадрата:
| S = | d2 |
| 2 |
S = 2R2
5. Формула площади квадрата через диаметр описанной окружности:
| S = | Do2 |
| 2 |
S = 4r2
7. Формула площади квадрата через диаметр вписанной окружности:S = Dв2
8.
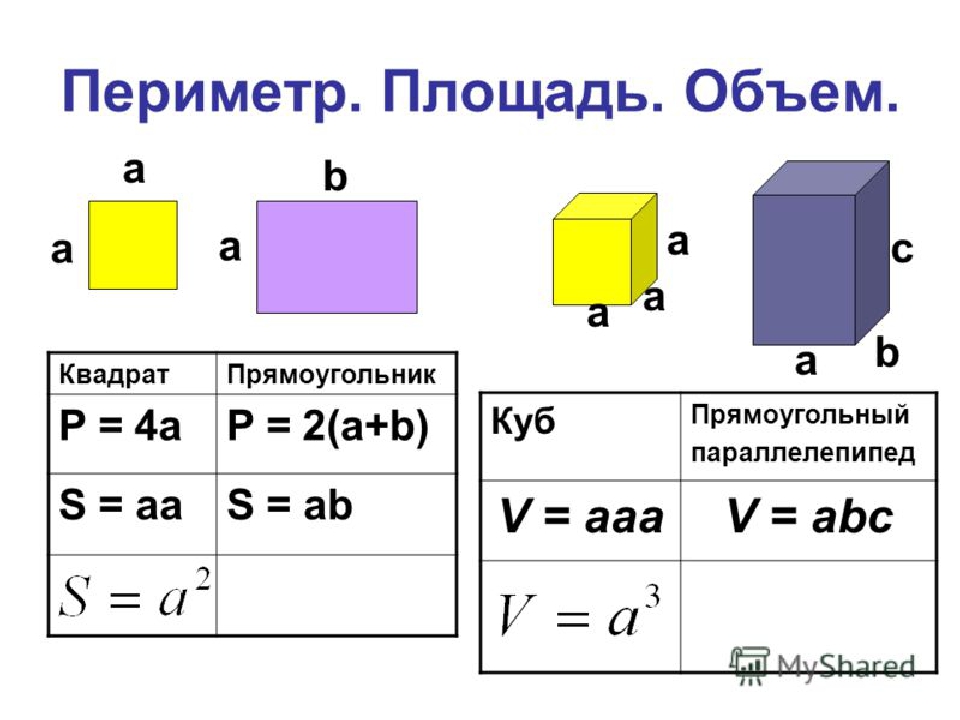Формула площади квадрата через длину отрезка l:
| S = l 2 | 16 |
| √5 |
Окружность описанная вокруг квадрата
Определение.
Кругом описанным вокруг квадрата называется круг проходящий через четыре вершины квадрата и имеющий центр на пересечении диагоналей квадрата.Радиус окружности описанной вокруг квадрата всегда больше радиуса вписанной окружности в√2 раз.
Радиус окружности описанной вокруг квадрата равен половине диагонали.
Площадь круга описанного вокруг квадрата большая площадь того же квадрата в π/2 раз.
Формулы определения радиуса окружности описанной вокруг квадрата
1. Формула радиуса окружности описанной вокруг квадрата через сторону квадрата:
| R = a | √2 |
| 2 |
2. Формула радиуса окружности описанной вокруг квадрата через периметр квадрата:
| R = | P |
| 4√2 |
3.
Формула радиуса окружности описанной вокруг квадрата через площадь квадрата:
| R = | √2S |
| 2 |
4. Формула радиуса круга описанного вокруг квадрата через диагональ квадрата:
| R = | d |
| 2 |
5. Формула радиуса круга описанного вокруг квадрата через диаметр описанной окружности:
| R = | Dо |
| 2 |
R = r √2
7. Формула радиуса круга описанного вокруг квадрата через диаметр вписанной окружности:
| R = Dв | √2 |
| 2 |
8. формула радиуса круга описанного вокруг квадрата через длину отрезка l:
| R = l | √10 |
| 5 |
Окружность вписанная в квадрата
Определение.
Радиус вписанной окружности равен половине стороны квадрата.
Площадь круга вписанного в квадрат меньше площади квадрата в π/4 раза.
Формулы определения радиуса круга вписанного в квадрат
1. Формула радиуса круга вписанного в квадрат через сторону квадрата:
| r = | a |
| 2 |
2. Формула радиуса круга вписанного в квадрат через диагональ квадрата:
| r = | d |
| 2√2 |
3. Формула радиуса круга вписанного в квадрат через периметр квадрата:
| r = | P |
| 8 |
4. Формула радиуса круга вписанного в квадрат через площадь квадрата:
| r = | √S |
| 2 |
5.
Формула радиуса круга вписанного в квадрат через радиус описанной окружности:
| r = | R |
| √2 |
6. Формула радиуса круга вписанного в квадрат через диаметр, описанной окружности:
| r = | Dо |
| 2√2 |
7 Формула радиуса круга вписанного в квадрат через диаметр вписанной окружности:
| r = | Dв |
| 2 |
8. Формула радиуса круга вписанного в квадрат через длину отрезка l:
| r = | l |
| √5 |
Формулы по геометрии
Квадрат. Формулы и свойства квадрата
Прямоугольник. Формулы и свойства прямоугольника
Параллелограмм. Формулы и свойства параллелограмма
Ромб. Формулы и свойства ромба
Трапеция. Формулы и свойства трапеции
— Равнобедренная трапеция. Формулы и свойства равнобедренной трапеции
— Прямоугольная трапеция.
Формулы и свойства прямоугольной трапеции
Формулы площади геометрических фигур
Формулы периметра геометрических фигур
Формулы объема геометрических фигур
Формулы площади поверхности геометрических фигур
Все таблицы и формулы
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Формулы / Натуральные числа и действия над ними / Справочник по математике 5-9 класс
- Главная
- Справочники
- Справочник по математике 5-9 класс
- Натуральные числа и действия над ними
- Формулы
Буквенные выражения, о которых мы говорили в статье «Числовые и буквенные выражения«, лежат в основе математических формул.
Буквенное выражение — математическое выражение, в котором используются цифры, знаки действий и буквы, также могут быть и скобки.
Математическая формула — совокупность величин, выраженных числами и буквами и соединенных посредством математических знаков.
Примеры математических формул
1) Формула периметра и площади прямоугольника.
Пусть мы имеем прямоугольник, ширина которого равна , а длина равна .
Если — периметр прямоугольника, тогда формула для вычисления периметра прямоугольника: или . Полученную формулу можно использовать для вычисления периметра
Если — площадь прямоугольника, тогда формула для вычисления площади прямоугольника: . Полученную формулу можно использовать для вычисления площади любого прямоугольника.
2) Формула периметра и площади квадрата.
Пусть мы имеем квадрат, сторона которого равна .
Если — периметр квадрата, тогда формула для вычисления периметра квадрата: . Полученную формулу можно использовать для вычисления периметра любого квадрата.
Если — площадь квадрата, тогда формула для вычисления площади квадрата: .
Полученную формулу можно использовать для вычисления площади любого квадрата.
3) Формула пути.
Если — пройденный путь (расстояние), — скорость движения, — время, за которое пройден путь , тогда формула пути: . Из данной формулы также можно получить формулы:
- скорости движения: ;
- времени: .
Обратите внимание:
При записи математических формул знак умножения «·» не пишут, что позволяет упростить запись выражения. Так, например, в формуле площади прямоугольника , между буквами и подразумевают знак «·» , но не пишут его.
Советуем посмотреть:
Понятие о натуральном числе
Сложение натуральных чисел
Вычитание натуральных чисел
Умножение натуральных чисел
Деление натуральных чисел
Порядок выполнения действий
Степень числа. Квадрат и куб числа
Меньше или больше
Меньше или больше на сколько? во сколько раз?
Уравнения
Натуральные числа и действия над ними
Правило встречается в следующих упражнениях:
5 класс
Задание 681, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 683, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 726, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 812, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Номер 249, Мерзляк, Полонский, Якир, Учебник
Номер 262, Мерзляк, Полонский, Якир, Учебник
Номер 612, Мерзляк, Полонский, Якир, Учебник
Номер 840, Мерзляк, Полонский, Якир, Учебник
Номер 3, Мерзляк, Полонский, Якир, Учебник
6 класс
Номер 659, Мерзляк, Полонский, Якир, Учебник
Номер 670, Мерзляк, Полонский, Якир, Учебник
Номер 671, Мерзляк, Полонский, Якир, Учебник
Номер 672, Мерзляк, Полонский, Якир, Учебник
Номер 673, Мерзляк, Полонский, Якир, Учебник
Номер 729, Мерзляк, Полонский, Якир, Учебник
Задание 598, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1168, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1169, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
7 класс
Номер 746, Мерзляк, Полонский, Якир, Учебник
Номер 754, Мерзляк, Полонский, Якир, Учебник
Номер 757, Мерзляк, Полонский, Якир, Учебник
Номер 758, Мерзляк, Полонский, Якир, Учебник
Номер 759, Мерзляк, Полонский, Якир, Учебник
Номер 778, Мерзляк, Полонский, Якир, Учебник
Номер 781, Мерзляк, Полонский, Якир, Учебник
Номер 782, Мерзляк, Полонский, Якир, Учебник
Номер 853, Мерзляк, Полонский, Якир, Учебник
Номер 860, Мерзляк, Полонский, Якир, Учебник
Периметр квадрата — вывод, примеры решений и часто задаваемые вопросы
Периметр квадрата определяется как общая длина границ этого квадрата.
Периметр любой фигуры можно получить по тому же шаблону, то есть найдя общую длину границы фигуры. Квадрат – это замкнутый правильный многоугольник, у которого все стороны равны, а все углы равны 90° каждый. Квадрат — это особый тип четырехугольника, так как все четыре стороны, углы и диагонали равны, а диагонали делят друг друга пополам под прямым углом. Поскольку все стороны квадрата равны, периметр квадрата можно получить, сложив все стороны или умножив одну сторону на 4.
Что такое периметр квадрата?
Периметр любой замкнутой геометрической формы получается путем нахождения общей длины границ ее формы. Периметр — это длина, очерчивающая форму двумерных фигур. Двухмерные фигуры включают квадраты, прямоугольники, треугольники, круги и другие многоугольники. Для двумерных форм периметр и площадь считаются общими расчетами, а для трехмерных форм площадь поверхности и объем считаются общими расчетами. Периметр можно найти и для неправильных форм. Вот некоторые из часто используемых терминов по отношению к двумерным формам:
- Вершины: Это конечные точки формы.
- Ребро/Сторона: Отрезок, соединяющий две соседние вершины.
- Диагонали: Отрезок, соединяющий две несмежные вершины.
- Площадь: Площадь — это пространство, занимаемое фигурой.
- Периметр: Периметр — это общая длина границы фигуры.
- Углы: Точка, где сходятся две стороны, — это угол, часто измеряемый в градусах или радианах.
Формула периметра квадрата
Периметр квадрата можно рассчитать, используя длину стороны квадрата. Если сторона квадрата представлена как «а», формула для периметра квадрата может быть выражена как
Как показано выше, периметр квадрата в 4 раза больше длины его сторон, так как все стороны равны. в квадрате. Единицей измерения периметра квадрата является единица измерения длины. Измеряется в метрах (м), сантиметрах (см), дюймах (дюймах) и т. д.
Пример: Вычислите периметр квадрата со стороной 8 см.
Решение:
Периметр квадрата = 4 × сторона
⇒ P = 4 × 8
⇒ P = 32 см.
Вывод периметра квадрата
Чтобы найти периметр замкнутой геометрической формы, необходимо сложить длины всех границ. Точно так же, чтобы получить периметр квадрата, нам нужно сложить все стороны квадрата, предположим, что длина сторон обозначается как «а»,
Периметр = а + а + а + а
⇒ Периметр квадрата = 4а
Где а — сторона квадрата.
Как найти периметр квадрата?
Периметр — это длина границы. Его часто называют расстоянием вокруг замкнутой 2D-фигуры. Периметры могут быть разными в зависимости от заданных форм. Периметр квадрата можно вычислить по длине стороны, а бывают случаи, когда длина стороны не указана, тогда периметр квадрата можно получить по диагонали и площади. Следовательно, периметр квадрата можно вычислить тремя способами:
- Используя длину стороны
- Используя диагональ
- Используя площадь
Периметр квадрата, используя длину стороны
Приведенные ниже шаги можно использовать для нахождения периметра квадрата, используя длину стороны,
- 900 11 Измерьте сторону квадрат.
- Умножьте длину стороны на 4.
- Выразите полученный периметр в соответствующих единицах.
Периметр квадрата с использованием диагонали
Однако, если сторона квадрата не дана, но дана диагональ, тогда формула принимает вид
Таким образом, периметр квадрата равен,
Приведенные ниже шаги можно использовать для нахождения площади периметра квадрата с помощью диагоналей,
- Измерьте диагональ квадрата.
- Вычислите периметр квадрата по формуле P = 4 × (Диагональ/√2).
Пример: Найдите периметр диагонали 4√2 м.
Решение:
Периметр квадрата,
P = 4 × (Диагональ/√2)
⇒ P = 4 × (4√2/√2)
⇒ P = 16 м
Периметр квадрата с использованием площади
Когда площадь квадрата дано, допустим, площадь квадрата равна а. Как мы все знаем, площадь = (сторона) 2
Следовательно, периметр квадрата равен
Следующие шаги можно использовать для нахождения площади периметра квадрата, используя площадь
- .
- Измерьте площадь квадрата.
- Рассчитайте площадь квадрата по формуле Периметр = 4 × √Площадь.
Пример: Найдите периметр, если площадь квадрата равна 49 квадратных единиц.
Решение:
Периметр квадрата равен
P = 4 × √Площадь
⇒ P = 4 × √49
⇒ P = 28 единиц
Решенные примеры по периметру квадрата
Пример 1: Найдите периметр квадрата, если длина заданной стороны равна 4 единицам.
Решение:
Периметр квадрата равен,
P = 4 × сторона
⇒ P = 4 × 4
⇒ P = 16 единиц
Пример 2. Найдите сторону и периметр квадрата, если данная диагональ равна 2√2 см.
Решение:
Сторона = Диагональ/√2
⇒ Сторона = 2√2/√2
⇒ Сторона = 2 см
900 02 Периметр квадрата = 4×сторона⇒ Периметр = 8 см
Пример 3.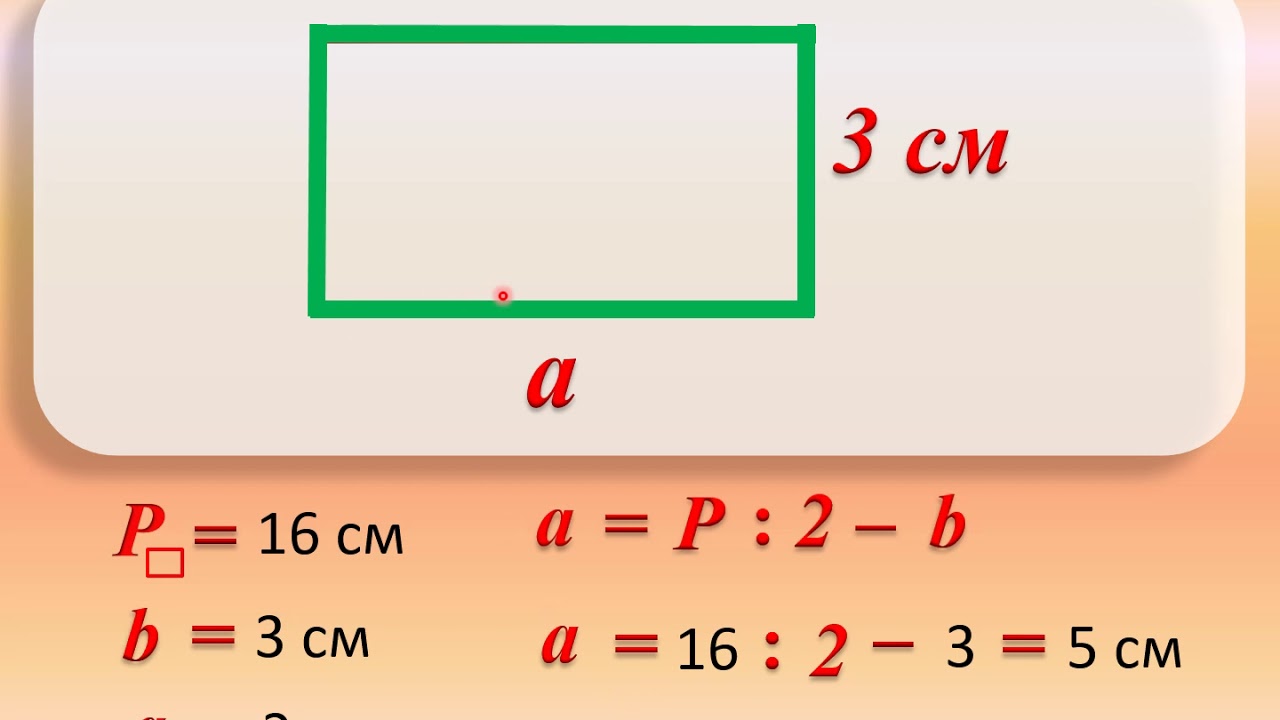
Найдите сторону периметра данного квадрата, равную √2.
Решение:
Периметр = сторона × 4
⇒ √2 = сторона × 4
Следовательно, сторона = √2/4 90 004
Пример 4. Найдите диагональ, если периметр квадрат равен 3√2 см.
Решение:
Периметр = 4 × (диагональ/√2)
⇒ (3√2 × √2)/4 = диагональ
⇒ Диагональ = 1,5 см
Пример 5. Найдите периметр, если заданная площадь равна 25 кв.
Решение:
Периметр = 4√Площадь
⇒ Периметр = 4√25
⇒ Периметр = 20 единиц 9 0004
Пример 6. Найдите площадь и периметр квадрата, если его сторона составляет 3 единицы.
Решение:
Периметр = 4 × сторона
⇒ Периметр = 4 × 3
⇒ Периметр = 12 единиц
Площадь = (Сторона)²
⇒ Площадь = (3)²
⇒ Площадь = 9 квадратных единиц
900 61Часто задаваемые вопросы по периметру площади
Вопрос 1: Чему равен периметр формулы квадрата?Ответ:
Вопрос 2: Какова единица измерения периметра квадрата?Периметр квадрата определяется как сумма длин его границ.
P = 4 × Сторона.
Ответ:
Вопрос 3: Что такое площадь и периметр квадрата?Единицы, используемые для периметра квадрата, — это единицы, используемые для длины. Используемые единицы измерения: метр (м), сантиметр (см), дюйм (дюйм) и т. д.
Ответ:
Вопрос 4: Как найти длину стороны квадрата, если известен периметр?Периметр квадрата определяется как общая длина его границ. Формула периметра квадрата равна 9.0005
P = 4 × сторона.
Пространство, занимаемое квадратом в двумерном пространстве, называется площадью квадрата. Формула, используемая для площади квадрата:
A = Сторона 2
Ответ:
Чтобы найти длину стороны квадрата, сначала запишите формулу периметра квадрата.
P = 4 × сторона
Сторона = P/4
Следовательно, чтобы найти длину стороны квадрата, зная периметр, разделите периметр на 4.
Подробнее
- Периметр прямоугольника
- Периметр треугольника
90 011 Окружность кругаПериметр площади. Калькулятор | Формула
Автор: Ханна Памула, доктор философии
Рецензию сделали Богна Шик и Адена Бенн
Последнее обновление: 20 ноября 2022 г.
Содержание:
- Каков периметр квадрата — формула
- Каков периметр квадрата 4?
- Как использовать калькулятор периметра квадрата?
- Другой аналогичный калькулятор
Калькулятор периметра квадрата поможет вам в основных вычислениях. Введите длину стороны, чтобы получить периметр, или используйте наш инструмент наоборот: введите периметр, чтобы получить длину стороны. Если вы не знаете, что такое периметр квадрата, или просто забыли формулу для периметра квадрата, продолжайте прокручивать! Вас также может заинтересовать наш квадратный калькулятор, который также находит площадь квадрата и диагональ.
Чему равен периметр квадрата — формула
Периметр квадрата равен сумме всех сторон квадрата. Поскольку у квадрата все четыре стороны равны по длине, периметр равен:
периметр = a + a + a + a = 4 × a
Квадрат – это четырехугольник наименьший периметр, охватывающий заданную площадь:
16 × площадь = периметр² (поскольку площадь = a ² и периметр² = (4 × a )² = 16 × a ²
Для любого четырехугольника кроме квадрата выполняется неравенство:
16 × площадь < периметра²
Это означает, что квадрат имеет большую площадь, чем любой другой четырехугольник с таким же периметром.
Каков периметр квадрата размером 4 дюйма?
Периметр такого квадрата вычисляется путем сложения всех сторон или умножения длины стороны на 4:
периметр = 4 дюйма + 4 дюйма + 4 дюйма + 4 дюйма = 4 × 4 дюйма = 16 дюймов
Как использовать калькулятор периметра квадрата?
Давайте посмотрим на пример.
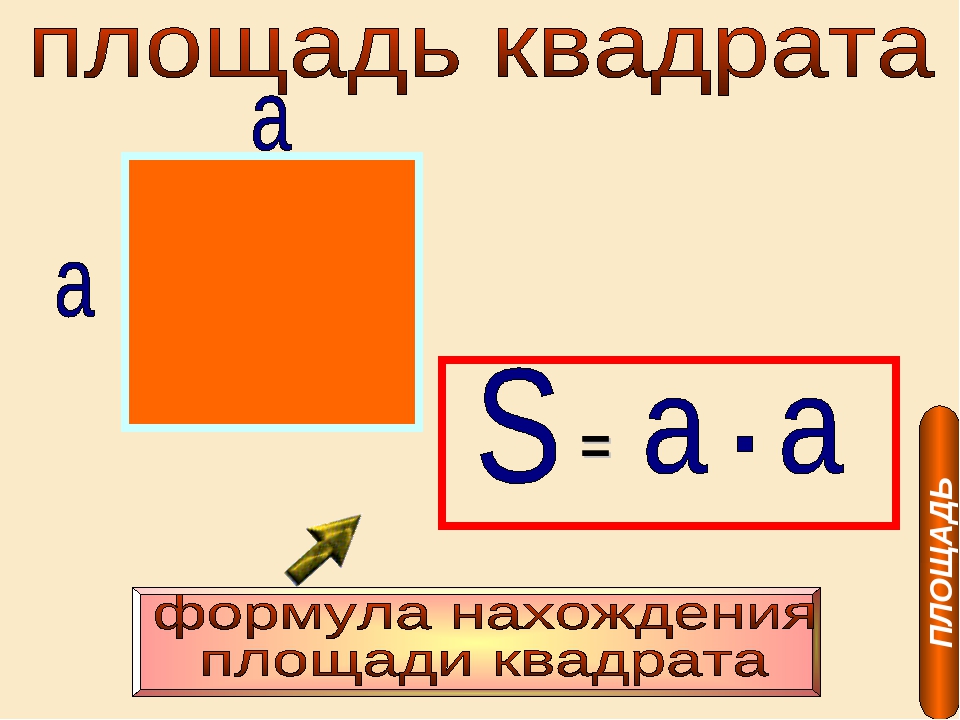Формула периметра квадрата:
