Формула площади овала: Площадь эллипса

Площадь эллипса. Формула площади эллипса. Вычислить площадь эллипса.

• Альфашкола
• Статьи
• Формула площади эллипса

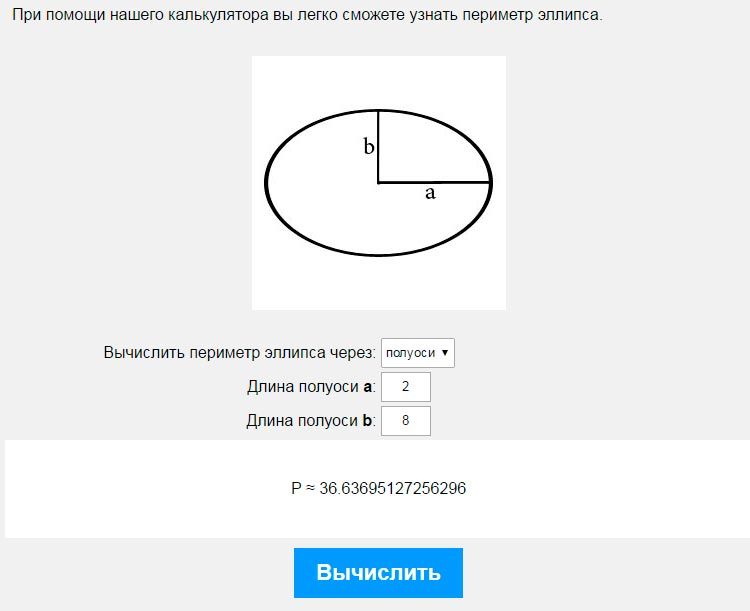
Для того чтобы вычислить площадь эллипса, надо знать длину его полуосей. Одна из них всегда больше другой:

\(S = π · a · b\)

 

Первая полуось a:

 

Вторая полуось b:

 

где a и b одной меры измерения.

 

Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!

Запишитесь на бесплатное тестирование знаний!

Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности

Наши преподаватели

Далер Евгеньевич Мануилов

Репетитор по математике

Стаж (лет)

Образование:

Самаркандский Государственный Университет

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Анна Александровна Ваструхина

Репетитор по математике

Стаж (лет)

Образование:

Краснодарский государственный университет культуры и искусств

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Алла Алексеевна Кандыба

Репетитор по математике

Стаж (лет)

Образование:

Полтавский государственный педагогический университет

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Предметы

• Математика
• Репетитор по физике
• Репетитор по химии
• Репетитор по русскому языку
• Репетитор по английскому языку
• Репетитор по обществознанию
• Репетитор по истории России
• Репетитор по биологии
• Репетитор по географии
• Репетитор по информатике

Специализации

• Репетитор по геометрии
• Репетитор по алгебре
• Репетитор по химии для подготовки к ЕГЭ
• Репетитор по химии для подготовки к ОГЭ
• Подготовка к олимпиадам по физике
• Репетитор по грамматике русского языка
• Репетитор для подготовки к ВПР по английскому языку
• Подготовка к ЕГЭ по биологии
• Подготовка к ОГЭ по биологии
• Программирование Pascal

Похожие статьи

• Функция
• Периметр ромба
• Центральный угол окружности
• Задачи на оптимальный выбор
• ЕГЭ по математике, профильный уровень. Уравнение смешанного типа
• ОГЭ по математике, базовый уровень. Квадратные уравнения
• Комплексы из-за внешности: учимся любить себя на примере звезд
• Как правильно общаться с ребенком об успеваемости?

Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности

Текст с ошибкой:

Расскажите, что не так

Площадь эллипса и окружности — презентация онлайн

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

1. Площадь эллипса и окружности

ПЛОЩАДЬ ЭЛЛИПСА И
ОКРУЖНОСТИ
АВТОР: ВСЕВОЛОД СЕЛЮНИН

2. История

ИСТОРИЯ
• Евдокс Книдский в пятом веке до нашей эры обнаружил, что площадь
диска пропорциональна квадрату его радиуса. Архимед показал, что
площадь внутри круга равна площади прямоугольного треугольника ,
основание которого имеет длину окружности круга, а высота равна
радиусу круга в его книге « Измерение круга» . До Архимеда Гиппократ
Хиосский был первым, кто показал, что площадь диска пропорциональна
квадрату его диаметра.

3. Формула

ФОРМУЛА
• Площадь окружности и эллипса имеют схожие формулы. Они
различаются лишь одной буквой:
• Площадь окружности:
• S=πR²
• Площадь эллипса:
• S=πRr (R-больший радиус, r-меньший радиус)
• Где π это отношение длинны окружности к радиусу R что равно
3,141592654

4.

ДоказательствоДОКАЗАТЕЛЬСТВО
• Следуя аргументу Архимеда в «Измерении круга» , сравните область, заключенную в круг, с
прямоугольным треугольником, основание которого имеет длину окружности круга, а высота
равна радиусу круга. Если площадь круга не равна площади треугольника, то она должна быть
больше или меньше. Мы исключаем каждое из них посредством противоречия, оставляя
равенство как единственную возможность. Мы используем правильные многоугольники таким
же образом.
• Правильный многоугольник — это выпуклый многоугольник, у которого все стороны между
собой равны и все углы между смежными сторонами равны.

5. Для понимания

ДЛЯ ПОНИМАНИЯ
• Площадь окружности считается как произведение половины длинны
окружности(πR) как одной стороны прямоугольника и радиуса(R) как
другой меньшей стороны она считается именно так потому что площадь
круга это сумма площадей равнобедренных треугольников состоящих из
прямоугольных треугольников чья площадь равна половине
прямоугольника поэтому радиус умножается именно на половину
длинны окружности. Что бы получить полную длину окружности нужно
умножить π на диаметр.

6. Эксперимент

ЭКСПЕРИМЕНТ
• Для лучшего понимания механики я решил провести эксперимент я решил сам
посчитать число π заново.
• Для этого я вписал правильный восьмиугольник в круг и круг такого же размера вписал
в больший правильный восьмиугольник, измерил длину одной стороны малого и
большого восьмиугольника, нашёл у них среднее арифметическое, умножил на 4 т.к. это
половина длинны окружности равняющейся 8 сторонам, измерил расстояние до точек
от центра у обоих восьмиугольников, вычислил среднее арифметическое расстояния до
любой точки у обоих восьмиугольников и поделил длину половины окружности на
среднее арифметическое расстояние до точки.
• Результат-число π
• Тоже самое можно провернуть с почти любыми правильными многоугольниками
желательно с чётным количеством углов например квадрат.

7. Вывод

ВЫВОД
• Понимая принципы вычисления площади окружности и эллипса можно
считать площадь любых правильных многоугольников и не только
правильных коими в какой-то степени соответственно и являются
окружность и эллипс.

8. Спасибо за внимание

СПАСИБО ЗА ВНИМАНИЕ
• Вопрос к учителю:
• Можно я сделаю ещё одну презентацию только по алгебре про теорию
вероятностей?

English     Русский Правила

Площадь эллипса – формула, определение, решенные примеры

Площадь эллипса определяется как количество области внутри эллипса. В качестве альтернативы, площадь эллипса  – это общее количество единичных квадратов, которые могут быть в нем размещены. Вы могли наблюдать много эллипсообразных форм в нашей повседневной жизни, например, площадка для крикета, ракетка для бадминтона, орбиты планет и т. д. 

Площадь эллипса равна произведению π, длины большая ось и длина малой полуоси. Давайте узнаем немного больше об этой фигуре, обсуждая ее площадь и формулу площади эллипса с решенными примерами и часто задаваемыми вопросами.

Площадь эллипса — это площадь или область, охватываемая эллипсом в двух измерениях.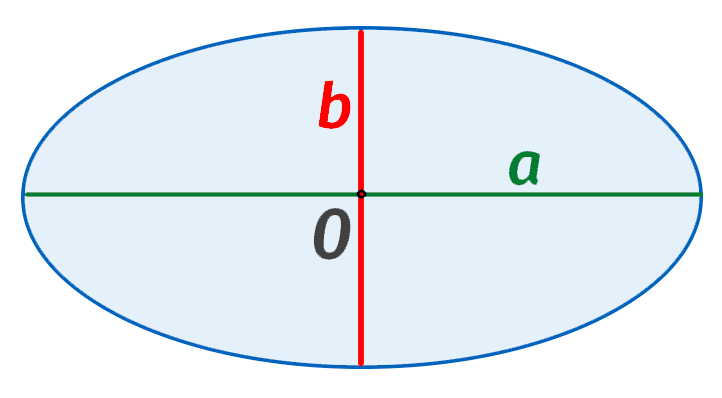

Площадь эллипса выражается в квадратных единицах, таких как ² , см ² , м ² , ярды ² , футы ² и т. д. Эллипс представляет собой двумерную форму, полученную путем соединения всех точки, находящиеся на постоянном расстоянии от двух фиксированных точек на плоскости. Неподвижные точки называются фокусами эллипса. F ₁ и F ₂  – два фокуса. Поскольку эллипс не является идеальной окружностью, расстояние от центра эллипса до точек на окружности не является постоянным. Итак, эллипс имеет два радиуса. Самая длинная хорда эллипса называется большой осью эллипса. Малая ось — это хорда, которая является биссектрисой, перпендикулярной к большой оси.

Эллипс — это геометрическое место всех точек, сумма расстояний которых от двух фиксированных точек на плоскости постоянна. Например, на приведенных ниже изображениях точки P

1 , P ₂ расположены так, что сумма расстояний точки P ₁ от неподвижных точек F ₁ и F ₂ равен сумме расстояний точки P ₂  от неподвижных точек F ₁  и F ₂ . Это означает, что если мы соединим все такие точки P ₁ , P _2, P ₃ и т. д.; мы получим фигуру, называемую эллипсом.

\(\begin{equation} \mathbf{P}_{1} \mathbf{F}_{1}+\mathbf{P}_{1} \mathbf{F}_{2}=\mathbf{ P}_{2} \mathbf{F}_{1}+\mathbf{P}_{2} \mathbf{F}_{2}=\mathbf{P}_{3} \mathbf{F}_ {1}+\mathbf{P}_{3} \mathbf{F}_{2}=…=\text{константа} \end{уравнение}\)
где,

Формула площади эллипса

Формула площади эллипса может быть рассчитана с использованием общей формулы, учитывая длины большой и малой осей. Формула для нахождения площади эллипса: 9{\pi/2}\)

⇒ A = 4ab (π/4)

⇒ A = πab
где

• а = длина большой полуоси
• b = длина малой полуоси

Как найти площадь эллипса?

Площадь эллипса можно рассчитать, используя следующие четыре шага и используя длину большой и малой осей.

Калькулятор площади эллипса | Выучить формулу площади эллипса

Создано Maria Kluziak

Отзыв от Bogna Szyk и Jack Bowater

Последнее обновление: 14 октября 2022 г.

Содержание:

• Что такое эллипс? Определение эллипса
• Каковы фокусы эллипса?
• Как пользоваться калькулятором площади эллипса?
• Как вычислить площадь эллипса?
• Другие геометрические калькуляторы, которые могут вам пригодиться

Калькулятор площади эллипса поможет вам определить площадь эллипса . В статье ниже вы найдете больше информации об инструменте и некоторую дополнительную информацию о площади овала, включая формула площади эллипса . Читайте дальше, если вы хотите узнать об определении эллипса, фокусах эллипса и узнать, что такое уравнение эллипса. А если вы уже знаете все основы и ищете что-то более сложное, чем этот калькулятор площади овала, ознакомьтесь с нашим продвинутым калькулятором эллипса.

Что такое эллипс? Определение эллипса Это обобщенный случай замкнутого конического сечения, что означает, что вы получаете его, разрезая конус наклонной плоскостью. Если угол наклона равен нулю, получится круг.

На самом деле круги — это часть эллипса! 92}=1a2(x−c1​)2​+b2(y−c2​)2​=1

где:

• (x,y)(x, y)(x,y) – Координаты произвольная точка на эллипсе;
• (c1,c2)(c_1,c_2)(c1​,c2​) – Координаты центра эллипса;
• aaa – Расстояние между центром и вершиной эллипса, лежащей на горизонтальной оси; и
• bbb – Расстояние между центром и вершиной эллипса, лежащей на вертикальной оси.

🙋 Если вас интересуют другие цифры, которые можно получить, разрезая конус, посетите наш калькулятор конических сечений!

Каковы фокусы эллипса?

фокуса эллипса — это две точки, лежащие на его самой длинной оси, равноудаленные от центра эллипса с каждой стороны. Их нужно определить, если вы хотите нарисовать овал. Фокусы в определении эллипса — это множество всех точек, для которых сумма расстояний до первого и второго фокусов равна постоянной величине.

На изображении выше фокусами являются точки F1F_1F1​ и F2F_2F2​.

Как пользоваться калькулятором площади эллипса?

Чтобы вычислить площадь овала с помощью нашего калькулятора, вам нужно сделать всего две вещи:

1. Введите значение YYY.
2. Введите значение XXX.
3. Найдите результат в самом нижнем поле калькулятора площади эллипса.

Как вычислить площадь эллипса?

Но как это работает? Формула площади эллипса намного короче, чем общее уравнение эллипса:

площадьэллипса=π×X×Y\mathrm{площадь_{эллипс}} = \pi\times X\times Yareaellipse​=π×X×Y

где:

• XXX – расстояние между центром эллипса и вершиной; и
• YYY – Расстояние между центром эллипса и ковершиной.

На иллюстрации над калькулятором площади овала можно увидеть, какие это расстояния.

Другие геометрические калькуляторы, которые могут вам пригодиться

Если вам нужно рассчитать площади, периметры или другие параметры фигур, отличных от эллипса, вам могут пригодиться некоторые из наших геометрических калькуляторов.