Нахождение площади трапеции по координатам — «Шпаргалка ЕГЭ»
Найдите площадь трапеции, вершины которой имеют координаты (3;2), (5;2), (9;6), (6;6).
Решение задачи
В данном уроке представлен пример решения задачи В5 на вычисление площади трапеции, которым с успехом можно воспользоваться в качестве подготовки к ЕГЭ по математике.
Для успешного решения задачи необходимо знать, что площадь трапеции определяется как произведение полусуммы оснований на высоту: S=(a+b)*h/2, где и – основания трапеции, а — высота. Согласно определению, трапеция — это четырехугольник, у которого две стороны параллельны, а две другие — нет. Параллельные стороны называются основаниями, они отмечается для наглядности красным цветом. По рисунку определяются значения оснований заданной трапеции и . В ходе решения также утверждается, что высота трапеции — это отрезок, перпендикулярный ее основаниям.
На рисунке выполняется построение высоты зеленым цветом, а затем вычисляется ее длина как разность между крайними отмеченными точками на оси . В результате, подставив все найденные значения в формулу определения площади трапеции, определяется искомый ответ.
Следует напомнить, что Трапеция (от древнегреческого τραπέζιον — «столик» от τράπεζα — «стол») — это четырехугольник, у которого две стороны параллельны. Две параллельные противоположные стороны называются основаниями трапеции, а две другие — боковыми сторонами. Средняя линия — отрезок, соединяющий середины боковых сторон. Средняя линия трапеции параллельна основаниям и равна их полусумме. Диагонали трапеции делят ее на 4 треугольника. Два из них, прилежащие к основаниям, подобны. Два других, прилежащие к боковым сторонам, имеют одинаковую площадь. Интересно, что в русском языке от слова трапеция происходит слово «трапеза».
Если при решении задач ЕГЭ данного типа у вас возникли сложности с пониманием темы, то всегда можно скачать презентацию или урок с сайта http://uchitelya.
Рекомендуем
Отзывы учеников
- Светлана Иванова
К ЕГЭ по математике я готовилась сама, без репетитора. Ничего сверхъестественного я не делала: зубрила формулы и решала задачи на сайте ШпаргалкаЕГЭ.
Вообще к части В я готовилась в основном в конце 10-го класса, в 11-ом я занималась только частью С. Мой результат — 75 баллов.
- Влад Долгорукий
К ЕГЭ готовился с репетитором. На занятиях использовали сайт для закрепления навыков решения различных типов задач, особенно части С. Всем рекомендую Генератор Вариантов. - Александр Шпик
Hello People. Я продвигаю свою идеологию «Втопку книжки». Зайди в ВК или на сайт ShpargalkaEGE смотри ролики по задачам. Все, что не знаешь, включая самые мелочи конспектируй и учи. Не ленись закреплять результат. Мои баллы ЕГЭ — 82.
К ЕГЭ готовился с репетитором. На занятиях использовали сайт для закрепления навыков решения различных типов задач, особенно части С. Всем рекомендую Генератор Вариантов.Площадь трапеции
Не откладывайте! ЗАГОВОРИТЕ на Английском!
ЗАМУЧИЛИ БОЛИ В СПИНЕ?
Александр | 2015-09-29
Площадь трапеции. Приветствую вас! В этой публикации мы рассмотрим указанную формулу. Почему она именно такая и как её понять. Если будет понимание, то и учить её вам нет необходимости. Если же вы просто хотите посмотреть эту формулу и при чём срочно, то сразу можете прокрутить страницу вниз ))
Теперь подробно и по порядку.
Трапеция это четырёхугольник, две стороны этого четырёхугольника параллельны, две другие нет. Те, что не параллельны – это основания трапеции. Две другие называются боковыми сторонами.
Если боковые стороны равны, то трапеция называется равнобедренной. Если одна из боковых сторон перпендикулярна основаниям, то такая трапеция называется прямоугольной.
В классическом виде трапецию изображают следующим образом – большее основание находится внизу, соответственно меньшее вверху. Но никто не запрещает изображать её и наоборот. Вот эскизы:
Следующее важное понятие.
Средняя линия трапеции это отрезок, который соединяет середины боковых сторон. Средняя линия параллельна основаниям трапеции и равна их полусумме.
Теперь давайте вникнем глубже. Почему именно так?
Рассмотрим трапецию с основаниями a и b и со средней линией l, и выполним некоторые дополнительные построения: через основания проведём прямые, а через концы средней линии перпендикуляры до пересечения с основаниями:
*Буквенные обозначения вершин и других точек не введены умышленно, чтобы избежать лишних обозначений.
Посмотрите, треугольники 1 и 2 равны по второму признаку равенства треугольников, треугольники 3 и 4 тоже самое. Из равенства треугольников следует равенство элементов, а именно катетов (они обозначены соответственно синим и красным цветом).
Теперь внимание! Если мы мысленно «отрежем» от нижнего основания синий и красный отрезок, то у нас останется отрезок (это сторона прямоугольника) равный средней линии. Далее, если мы «приклеим» отрезанные синий и красный отрезок к верхнему основанию трапеции, то у нас получится также отрезок (это тоже сторона прямоугольника) равный средней линии трапеции.
Уловили? Получается, что сумма оснований будет равна двум средним линиям трапеции:
Посмотреть ещё одно объяснение
Сделаем следующее – построим прямую проходящую через нижнее основание трапеции и прямую, которая пройдёт через точки А и В:
Получим треугольники 1 и 2, они равны по стороне и прилегающим к ней углам (второй признак равенства треугольников).
Это означает что полученный отрезок (на эскизе он обозначен синим) равен верхнему основанию трапеции.
Теперь рассмотрим треугольник:
*Средняя линия данной трапеции и средняя линия треугольника совпадают.
Известно, что средняя линия треугольника равна половине параллельного ей основания, то есть:
Всё!
Хорошо, разобрались. Теперь о площади трапеции.
Говорят: площадь трапеции равна произведению полусуммы её оснований и высоты.
То есть, получается, что она равна произведению средней линии и высоты:
Вы, наверное, уже заметили, что это очевидно. Геометрически это можно выразить так: если мы мысленно отрежем от трапеции треугольники 2 и 4 и положим их соответственно на треугольники 1 и 3:
То у нас получится прямоугольник по площади равный площади нашей трапеции. Площадь этого прямоугольника будет равна произведению средней линии и высоты, то есть можем записать:
Но дело тут не в записи, конечно, а в понимании.
Скачать (посмотреть) материал статьи в формате *pdf
На этом всё. Успеха вам!
С уважением, Александр.
Делитесь информацией в социальных сетях.
Категория: Формулы Теория | Формулы
НЕ ОТКЛАДЫВАЙ! Заговори на английском!
ДОЛОЙ обидные ошибки на ЕГЭ!!
Подготовка к ЕГЭ, онлайн-обучение с Фоксворд!
Замучили боль и скованность в мышцах спины?
*Нажимая на кнопку, я даю согласие на рассылку, обработку персональных данных и принимаю политику конфиденциальности.
Как найти площадь трапеции (формула и видео)
Трапеция это четырехугольник с одной парой параллельных сторон. Итак, этот четырехугольник представляет собой плоскую фигуру и замкнутую форму. Он имеет четыре отрезка и четыре внутренних угла. Параллельные стороны — это две 9 трапеции.0017 оснований ; две другие стороны — его ноги.
Обычно трапецию изображают с более длинной параллельной стороной — основанием — горизонтальной.
Перпендикулярная линия от основания к другой параллельной стороне даст вам высоту трапеции или высоту .
Что такое трапеция?Что такое средний балл по математике?
В математике среднее – это сумма группы чисел, деленная на количество элементов в группе.
Итак, если у вас есть три человека, держащие книги, вы можете найти среднее количество книг, которые они держат, следующим образом:
Мартин держит 5 книг, Мак держит 3 книги, а Мария держит 4 книги. Вместе 12 книг держат 3 человека .
Итак, 12 книг ÷ 3 человека = в среднем по 4 книги у каждого .
Чтобы найти площадь трапеции, нужно найти среднюю длину двух оснований.
Как найти площадь трапеции
Чтобы найти площадь любой трапеции, начните с обозначения ее оснований и высоты. В нашей трапеции обозначьте более длинное основание aa и более короткое основание b . Отметьте линию, перпендикулярную двум основаниям h для высоты или высоты трапеции.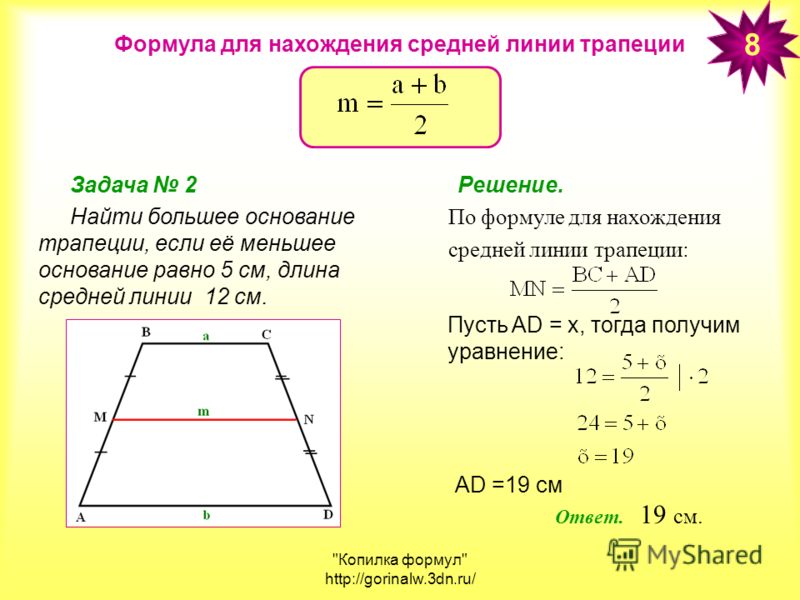
Обратите внимание, что мы не обозначили ноги. Нам не нужно ничего знать о длине катетов или углах вершин, чтобы найти площадь.
Площадь трапеции формула
Формула площади трапеции представляет собой произведение среднего основания на высоту. В формуле длинное и короткое основания равны a и b , а высота равна h :
. как деление на 222. Мы берем половину суммы длин двух оснований (их среднее значение), а затем умножаем ее на высоту или высоту, чтобы найти площадь в квадратных единицах.
Используя уравнение площади трапеции
Трапеция LMNO имеет параллельные основания LM и NO . Отрезок LM имеет длину 7 см , а отрезок NO имеет длину 13 см . Мы обозначим более длинную сторону NO как a , а более короткую сторону LM как b . Высота h , 5 см .
Сначала подставим эти числа в нашу формулу:
Затем складываем 13 плюс 7 и получаем:
Затем делим на два и получаем:
Наконец, умножаем и получаем ответ:
Площадь этой трапеции 50 квадратных сантиметров .
Площадь трапеции примеры
А теперь попробуй! Другая трапеция имеет длинное основание a , 11 метров и более короткое основание б , 7 метров . Его высота ч равна 9 метров . Какая площадь в квадратных метрах?
Вы получили 81 квадратный метр ? Ваш ответ для площади всегда в квадратных единицах линейного измерения.
Таким образом, трапеция, измеренная в футах, дает площадь в квадратных футах, сантиметры дают квадратные сантиметры и так далее.
Помните, что умножение на ½ равносильно делению на 9.0017 2 , поэтому вы можете сложить длины оснований, а затем разделить их сумму на два, если вам так проще.
Из-за коммутативного свойства умножения вы можете переставить эти три числа: 12\frac{1}{2}21, высоту h и длину основания a b в любом порядке для облегчения расчета.
Таким образом, с трапецией LMNO вы также могли бы написать формулу следующим образом:
Пример #2
Вот вам еще один пример. Новая трапеция перевернута, не так, как вы ее обычно видите, но пусть это вас не останавливает! Короткая база b имеет длину 21 дюйм . Длинное основание a (на этот раз вверху рисунка) имеет длину 31 дюйм . Высота h (независимо от того, как вы смотрите на трапецию) составляет 5 дюймов .
Пример трапеции — Найдите площадь 9{2}area=130in2Краткое содержание урока
В этом уроке и видео мы рассмотрели, что такое трапеция, рассмотрели роль средних значений в геометрии, узнали, как маркировать и использовать части трапеции для вычисления площади, а также Выучил формулу вычисления площади трапеции в квадратных единицах.
Видео-урок: Площадь трапеции
Стенограмма видео
В этом видео мы увидим, как мы можем найти площадь трапеции, используя две альтернативные формулы. Мы также увидим пример того, как мы можем применить эти формулы в контексте реальной жизни. Но сначала давайте подумаем о том, что именно мы подразумеваем под трапецией и о различных существующих типах трапеций.
Трапеция определяется как четырехугольник с одной парой параллельных сторон. Но предупреждаю: в некоторых частях мира вы можете знать это как трапецию, но здесь мы будем использовать термин трапеция. Когда мы думаем о трапеции, мы очень часто думаем о трапеции, которая выглядит как эта первая фигура или даже перевернутая, как вторая фигура. Фактически, обе они будут называться равнобедренными трапециями, и они являются трапециями, в которых непараллельные стороны имеют одинаковую длину. Но, конечно, по определению даже не обязательно, чтобы эти непараллельные стороны были конгруэнтными; у него просто должна быть одна пара параллельных сторон.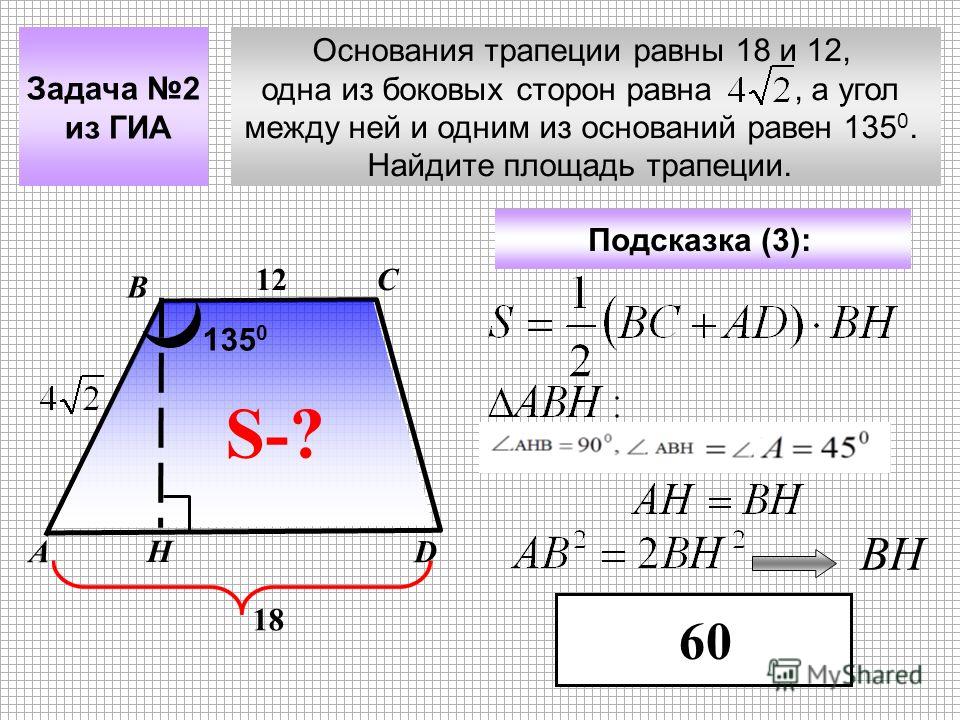
И если трапеция имеет прямой угол, то мы можем назвать ее прямоугольной трапецией.
Прежде чем мы увидим формулу для нахождения площади трапеции, давайте посмотрим, как мы можем определить разные стороны трапеции. Когда у нас есть трапеция, две параллельные стороны обычно называют основаниями, и часто они обозначаются буквами 𝑎 и 𝑏. Две непараллельные стороны называются катетами трапеции. Так, например, если бы мы определяли равнобедренную трапецию, мы могли бы сказать, что стороны конгруэнтны. Наконец, перпендикулярное расстояние между двумя основаниями является высотой трапеции, и мы обычно обозначаем это буквой ℎ.
Теперь мы рассмотрим, как можно найти площадь трапеции, используя эти буквы 𝑎 и 𝑏 для основания трапеции и ℎ для перпендикулярной высоты. Мы могли бы подумать о разделении трапеции на два треугольника, потому что, надеюсь, мы помним, как найти площадь треугольника. Площадь треугольника рассчитывается как половина произведения основания на высоту перпендикуляра.
Это означает, что если мы рассмотрим этот верхний треугольник, длина основания этого треугольника равна 𝑎. Итак, мы работаем в полтора раза 𝑎 раз ℎ, что является его перпендикулярной высотой. Это упрощается до 𝑎ℎ больше двух. Для нижнего треугольника его площадь будет рассчитана как половина, умноженная на 𝑏, умноженная на ℎ, то есть на 𝑏ℎ больше двух.
Теперь мы знаем, что площадь трапеции будет состоять из площади верхнего треугольника и площади нижнего треугольника. Это 𝑎ℎ больше двух плюс 𝑏ℎ больше двух. Затем мы можем сложить эти две дроби и вычесть общий делитель каждой из них, который равен 𝑎 плюс 𝑏 умножить на ℎ больше двух. Обратите внимание, что 𝑎 плюс 𝑏 — это сумма длин параллельных оснований трапеции. Таким образом, мы можем думать о площади трапеции как о половине суммы параллельных оснований, умноженной на высоту. Но когда дело доходит до нахождения площади трапеции, не волнуйтесь, нам не нужно всегда разбивать ее на треугольники, потому что мы фактически вывели общую формулу.
Формально можно сказать, что для трапеции с перпендикулярной высотой ℎ и основаниями 𝑎 и 𝑏 площадь трапеции равна половине умноженной на 𝑎 плюс 𝑏 умноженной на ℎ. Обратите внимание, что эта правая часть эквивалентна вычислению 𝑎 плюс 𝑏, умноженному на ℎ, и делению на два. На самом деле мы говорим, что площадь равна половине суммы длин параллельных оснований, умноженных на высоту. Теперь мы увидим, как мы можем применить эту формулу, чтобы найти площадь трапеции, зная ее высоту и длины ее оснований.
Длины параллельных сторон трапеции равны 82 и 70. Если высота равна 100, какова площадь трапеции?
Мы могли бы начать подобный вопрос с наброска трапеции, вспомнив, что трапеция — это просто четырехугольник с одной парой параллельных сторон. Нам дана информация о том, что параллельные стороны или основания этой трапеции имеют длины 82 и 70. И хотя у них нет единиц, они будут единицами длины. Высота, которая будет перпендикулярной высотой, дается как 100 единиц длины.
Для заданной трапеции мы можем заменить 𝑎 и 𝑏 на 82 и 70 соответственно, хотя если бы эти два значения поменялись местами, это не имело бы значения. Перпендикулярная высота ℎ равна 100. Следовательно, мы будем вычислять половину, умноженную на 82, плюс 70, умноженную на 100. Затем мы можем упростить 82 плюс 70, получив 152, и половина 152 будет 76. Умножив 76 на 100, мы получим 7600. В вопросе нам не дали никаких единиц измерения, но поскольку это площадь, то мы можем сказать, что это будут квадратные единицы или единицы площади. Значит, площадь этой трапеции равна 7600 квадратных единиц.
В следующем примере мы продолжим использовать ту же формулу. Но на этот раз нам будет дана площадь трапеции, и нам нужно будет определить длину одной из параллельных сторон.
Площадь трапеции 1760, а расстояние между параллельными сторонами равно 40.
Если одна параллельная сторона равна 39, чему равна другая сторона?
Давайте начнем этот вопрос с визуализации трапеции, а затем заполним полученную информацию. Во-первых, нам дана площадь трапеции. Это 1760, и это будет в квадратных единицах. Далее нам сообщают, что расстояние между параллельными сторонами равно 40 или 40 единицам длины. Заметьте, что в качестве альтернативы мы могли бы думать об этом как о высоте или перпендикулярной высоте трапеции. Наконец, нам говорят, что длина одной из параллельных сторон равна 39. И если мы нарисовали диаграмму и записываем ее, в данный момент не имеет значения, какую параллельную сторону мы можем обозначить числом 39.
Мы можем вспомнить, что мы можем связать две параллельные стороны 𝑎 и 𝑏 трапецию и ее перпендикулярную высоту по формуле, согласно которой площадь трапеции равна половине умноженной на 𝑎 плюс 𝑏 умноженной на ℎ. Часто мы используем эту формулу для фактического вычисления площади трапеции. Но здесь нам дана площадь трапеции, поэтому мы можем подставить ее в формулу.
Затем мы можем принять значение 𝑎 равным 39., неизвестная длина стороны как 𝑏 и высота ℎ как 40. Тогда мы получим, что 1760 равно половине, умноженной на 39, плюс 𝑏, умноженной на 40.
Мы можем начать упрощать правую часть, вычислив один- половина умножить на 40, что равно 20. Затем, разделив на 20 с обеих сторон, заметим, что 1760 разделить на 20 будет 88. Итак, у нас 88 равно 39 плюс 𝑏. Вычитая 39 из обеих частей уравнения, мы получаем, что 49 равно 𝑏. Следовательно, мы можем дать ответ, что длина другой параллельной стороны равна 49единицы длины.
Теперь рассмотрим другой способ задания формулы площади трапеции. Начнем с введения нового термина, который является средним основанием трапеции. Средним основанием трапеции называется отрезок, концы которого являются серединами катетов трапеции. Среднее основание трапеции параллельно двум основаниям трапеции. Итак, давайте рассмотрим, как это относится к нахождению площади трапеции. Если мы продолжим терминологию использования 𝑎 и 𝑏 для длин оснований, то длина среднего основания 𝑚 трапеции на самом деле является средним арифметическим длин оснований 𝑎 и 𝑏.
Это означает, что мы могли бы написать, что 𝑚 равно 𝑎 плюс 𝑏 больше двух.
Возможно, вы помните, что в этом видео мы уже видели 𝑎 плюс 𝑏 более двух. Концепция сложения двух параллельных сторон и деления пополам появляется в формуле площади. Поэтому мы можем заменить половину 𝑎 плюс 𝑏 на букву 𝑚 в формуле площади. Площадь трапеции может быть выражена как длина среднего основания, умноженная на высоту. Следовательно, теперь у нас есть две немного разные, но эквивалентные формулы. Помните, что они эквивалентны, потому что половина произведения 𝑎 плюс 𝑏 равно 𝑚, то есть длине среднего основания.
Это просто означает, что в зависимости от информации, которую нам дали в конкретном вопросе, даны ли нам длины двух параллельных сторон или длина среднего основания, мы можем выбрать наиболее подходящую формулу для использования. Теперь мы увидим, как мы можем применить эту вторую формулу в следующем примере.
Найдите среднюю длину основания трапеции площадью 28 квадратных сантиметров и высотой четыре сантиметра.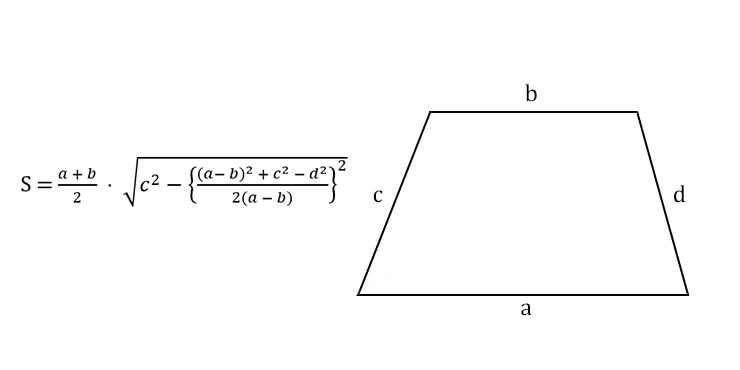
Рассмотрим в этой задаче трапецию. Нам дана информация, что эта трапеция имеет площадь 28 квадратных сантиметров и высоту четыре сантиметра. Нам нужно вычислить длину среднего основания этой трапеции. Напомним, что существует формула, связывающая площадь трапеции и длину ее среднего основания. И это дано, поскольку площадь трапеции равна 𝑚, умноженной на ℎ, где 𝑚 — среднее основание, а ℎ — перпендикулярная высота. Таким образом, мы можем подставить в значение, что 28 — это площадь, а четыре — высота, чтобы получить, что 28 равно 𝑚, умноженному на четыре. Затем, разделив обе части этого уравнения на четыре, мы получим, что 𝑚 равно семи. Таким образом, длина среднего основания этой трапеции равна семи сантиметрам.
Теперь мы рассмотрим последний пример, в котором мы находим площадь трапеции в реальной задаче.
Фермер владеет двумя полями равной площади: одно в форме ромба и одно в форме трапеции, как показано на рисунке. Вычислите длину среднего основания трапециевидного поля.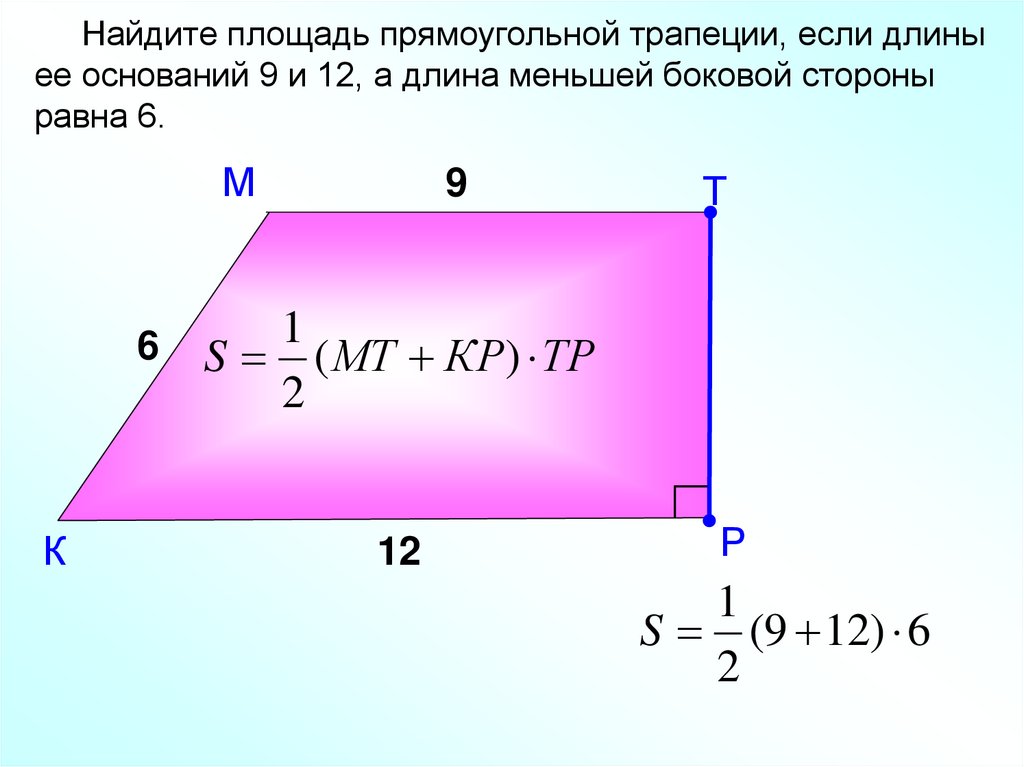
Начнем с рассмотрения поля слева на рисунке. Это поле имеет форму ромба, потому что мы видим, что длины его четырех сторон равны. Заметим, что нам даны длины двух диагоналей этого ромба. их 90 метров и 100 метров. Мы можем вспомнить, что площадь ромба определяется как 𝑑 меньше единицы, умноженной на 𝑑 меньше двух на два, где 𝑑 меньше единицы и 𝑑 меньше двух — длины его диагоналей. Чтобы найти площадь этого ромба, мы можем взять две диагонали 90 и 100 метров, умножить их вместе и разделить на два. А 9000 разделить на два это 4500 квадратных метров. Итак, мы нашли площадь этого поля в форме ромба.
Итак, учитывая, что эти два поля имеют одинаковую площадь, значит, теперь мы знаем, что площадь трапеции также равна 4500 квадратных метров. Но нас не просто попросили вычислить эту площадь. Нам нужно найти длину среднего основания этого трапециевидного поля. Среднее основание трапеции — это отрезок, концы которого являются серединами катетов. И мы должны помнить, что есть формула, которая связывает среднее основание трапеции с ее площадью.
Чтобы найти площадь трапеции, нужно длину среднего основания умножить на высоту перпендикуляра. Тогда мы можем подставить площадь 4500, и высота трапеции будет показана на диаграмме как 25 метров.
Слово предупреждения здесь только для того, чтобы распознать разницу между m в 25 метрах и 𝑚 среднего основания. Наше уравнение будет таким: 4500 равно 𝑚, среднему основанию, умноженному на 25. Затем мы можем разделить обе стороны на 25. И без калькулятора, чтобы вычислить 4500, разделенное на 25, одним из способов может быть деление на 100 и умножение. ответ на четыре. Это дало бы нам, что 𝑚 равно 180. Следовательно, мы можем дать ответ, что длина среднего основания этого трапециевидного поля составляет 180 метров.
Теперь мы можем закончить это видео, повторив ключевые моменты. Мы видели, что площадь трапеции с высотой ℎ и параллельными основаниями длин 𝑎 и 𝑏 определяется площадью трапеции, равной половине 𝑎 плюс 𝑏 умноженной на ℎ. Мы можем представить это неформально, как площадь трапеции равна половине суммы параллельных оснований, умноженных на высоту.