Формула радиус сферы: Найти радиус сферы, если его площадь равна 169Пи см (решение.)

Как найти радиус описанной около правильной пирамиды сферы (шара): формулы

Sign in

Password recovery

Восстановите свой пароль

Ваш адрес электронной почты

MicroExcel.ru Математика Геометрия Нахождение радиуса сферы (шара), описанной около правильной пирамиды

В данной публикации представлены формулы, с помощью которых можно найти радиус сферы (шара), описанной около правильной пирамиды: треугольной, четырехугольной, шестиугольной и тетраэдра.

• Формулы расчета радиуса сферы (шара)
  • Правильная треугольная пирамида
  • Правильная четырехугольная пирамида
  • Правильная шестиугольная пирамида

Приведенная ниже информация применима только к правильным пирамидам. Формула для нахождения радиуса зависит от вида фигуры, рассмотрим самые распространенные варианты.

Правильная треугольная пирамида

На этом рисунке и чертежах далее:

• a – ребро основания пирамиды;
• h – высота фигуры.

Если эти величины даны, вычислить радиус (R) описанной вокруг пирамиды сферы/шара можно по формуле ниже:

Правильный тетраэдр является разновидностью правильной треугольной пирамиды. Формула для него:

Правильная четырехугольная пирамида

Радиус (R) описанной сферы/шара вычисляется следующим образом:

Правильная шестиугольная пирамида

Формула для нахождения радиус (R) сферы/шара выглядит так:

ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ

Таблица знаков зодиака

Нахождение площади трапеции: формула и примеры

Нахождение длины окружности: формула и задачи

Римские цифры: таблицы

Таблица синусов

Тригонометрическая функция: Тангенс угла (tg)

Нахождение площади ромба: формула и примеры

Нахождение объема цилиндра: формула и задачи

Тригонометрическая функция: Синус угла (sin)

Геометрическая фигура: треугольник

Нахождение объема шара: формула и задачи

Тригонометрическая функция: Косинус угла (cos)

Нахождение объема конуса: формула и задачи

Таблица сложения чисел

Нахождение площади квадрата: формула и примеры

Что такое тетраэдр: определение, виды, формулы площади и объема

Нахождение объема пирамиды: формула и задачи

Признаки подобия треугольников

Нахождение периметра прямоугольника: формула и задачи

Формула Герона для треугольника

Что такое средняя линия треугольника

Нахождение площади треугольника: формула и примеры

Нахождение площади поверхности конуса: формула и задачи

Что такое прямоугольник: определение, свойства, признаки, формулы

Разность кубов: формула и примеры

Степени натуральных чисел

Нахождение площади правильного шестиугольника: формула и примеры

Тригонометрические значения углов: sin, cos, tg, ctg

Нахождение периметра квадрата: формула и задачи

Теорема Фалеса: формулировка и пример решения задачи

Сумма кубов: формула и примеры

Нахождение объема куба: формула и задачи

Куб разности: формула и примеры

Нахождение площади шарового сегмента

Что такое окружность: определение, свойства, формулы

Подготовка школьников к ЕГЭ (Справочник по математике — Стереометрия

Справочник по математике

Геометрия (Стереометрия)

Вписанные и описанные фигуры

Биссекторная плоскость. Основное свойство биссекторной плоскости

Сфера, вписанная в пирамиду. Свойства пирамиды, описанной около сферы

Радиус сферы, вписанной в правильную n — угольную пирамиду

Сфера, вписанная в треугольную пирамиду. Формула для радиуса вписанной сферы

Биссекторная плоскость. Основное свойство биссекторной плоскости

      Определение 1. Биссекторной плоскостью двугранного угла называют такую плоскость, которая проходит через ребро двугранного угла и делит этот угол на два равных двугранных угла (рис. 1).

Рис.1

      Утверждение 1. Точка, расположенная внутри двугранного угла, находится на одном и том же расстоянии от граней этого угла тогда и только тогда, когда она лежит на биссекторной плоскости.

      Доказательство. Рассмотрим произвольную точку   O,  расположенную внутри двугранного угла, и проведем через эту точку плоскость   δ,  перпендикулярную к ребру   AB  двугранного угла (рис. 2).

Рис.2

      Плоскость   δ   пересекает ребро   AB   двугранного угла в точке   C,   а грани двугранного угла   α   и   β   по лучам   CD   и   CE   соответственно. Угол   DCE  является линейным углом двугранного угла. Биссекторная плоскость   γ  пересекает плоскость   δ  по биссектрисе   CF   линейного угла   DCE .

      Поскольку плоскости   α   и   β   проходят через перпендикуляр   AB   к плоскости   δ,   то плоскости   α  и β  перпендикулярны к плоскости   δ. Поскольку плоскости   α   и   β   проходят через перпендикуляр   AB   к плоскости   δ,   то плоскости   α  и β  перпендикулярны к плоскости   δ.   Из свойств прямой, перпендикулярной к плоскости, свойств прямой, перпендикулярной к плоскости, следует, что и перпендикуляры, опущенные из точки   O  на грани двугранного угла   α  и β,  лежат в плоскости   δ.

      Таким образом, справедливость утверждения вытекает из соответствующих теорем о свойствах биссектрисы угла. Доказано.

      Следствие 1. Если сфера, расположенная внутри двугранного угла, касается каждой из плоскостей граней этого угла, то центр сферы находится на биссекторной плоскости двугранного угла (рис. 3).

Рис.3

Сфера, вписанная в пирамиду. Свойства пирамиды, описанной около сферы

      Определение 2. Сферой, вписанной в пирамиду, называют такую сферу, которая касается плоскостей всех граней пирамиды, причем точки касания лежат на гранях пирамиды (рис. 4).

Рис.4

      Определение 3. Если сфера вписана в пирамиду, то пирамиду называют описанной около сферы.

      Если сфера вписана в пирамиду, то она касается граней каждого внутреннего двугранного угла, образованного соседними гранями пирамиды. В соответствии со следствием 1 центр вписанной в пирамиду сферы должен находиться в точке пересечения биссекторных плоскостей всех внутренних двугранных углов, образованных соседними гранями пирамиды.

      Если у пирамиды нет точки, в которой пересекаются биссекторные плоскости всех внутренних двугранных углов, образованных соседними гранями пирамиды, то в такую пирамиду нельзя вписать сферу.

      Замечание 1. Для того, чтобы проверить, можно ли в пирамиду вписать сферу, достаточно проверить, существует ли точка пересения биссекторных плоскостей всех внутренних двугранных углов при основании пирамиды. Если такая точка существует, то она будет равноудалена как от основания пирамиды, так и от каждой из боковых граней.

      Рассмотрим несколько типов пирамид, в которые можно вписать сферу.

      Утверждение 2. Если у пирамиды   SA₁A₂ … A_n   основание   O  перпендикуляра, опущенного из вершины   S   на плоскость основания пирамиды, лежит внутри многоугольника   A₁A₂ .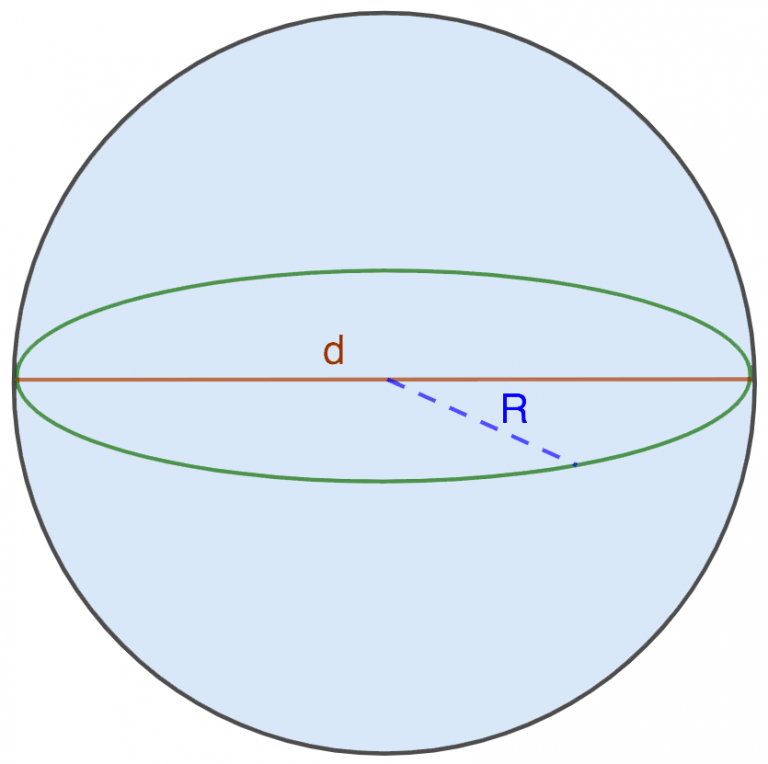 .. A_n ,   а все боковые грани пирамиды наклонены под одним и тем же углом к плоскости основания пирамиды, то в такую пирамиду можно вписать сферу.

     Доказательство. Пусть все боковые грани пирамиды наклонены к плоскости основания под углом   φ ,  а высота пирамиды равна   h.   Рассмотрим, например, боковую грань   SA₁A₂   и проведем в ней высоту   SB   (рис. 5).

Рис.5

      По теореме о трех перпендикулярах отрезок   OB   перпендикулярен ребру   A₁A₂.   Следовательно, угол   SBO   является линейным углом двугранного угла между боковой гранью   SA₁A₂   и плоскостью основания пирамиды и равен   φ.   Биссекторная плоскость этого двугранного угла пересекает высоту пирамиды в точке   O’   (рис. 6).

Рис.6

      Катет   OB   прямоугольного треугольника   SOB   выражается через высоту пирамиды   h   и угол   φ   по формуле

OB = h ctg φ .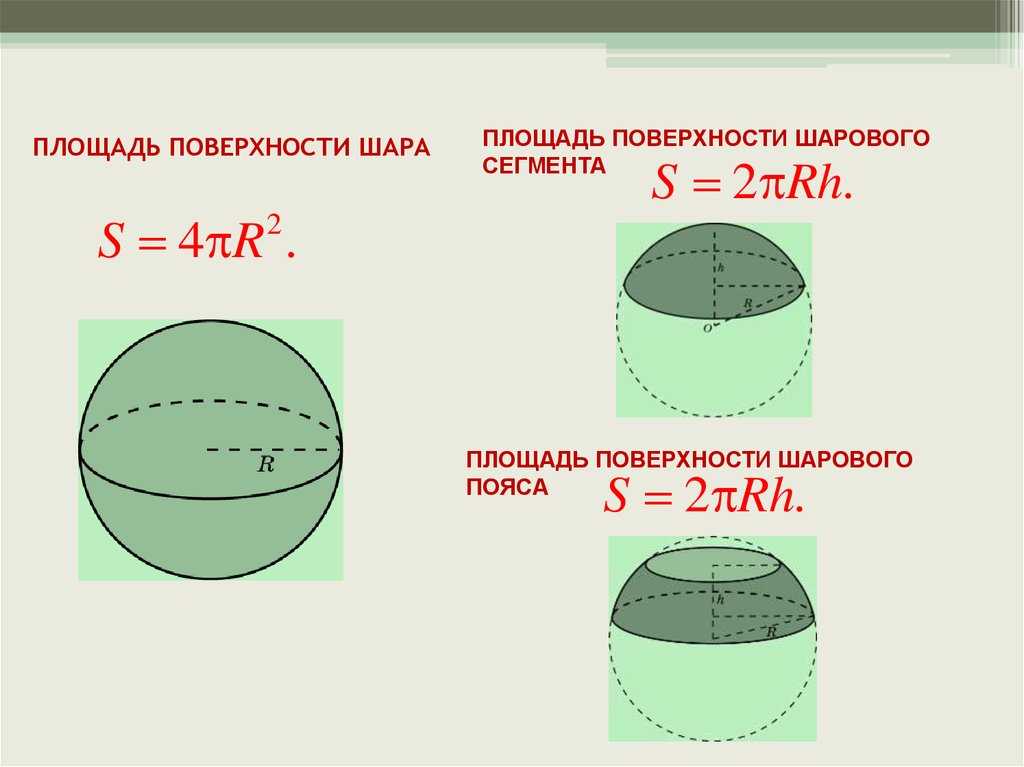

      Катет   OO’   прямоугольного треугольника   OO’B   выражается через высоту пирамиды   h   и угол   φ   по формуле

      Поскольку длина отрезка   OO’   не зависит от выбора боковой грани пирамиды, то биссекторные плоскости всех внутренних двугранных углов при основании пирамиды пересекаются в точке   O’,   которая и является центром вписанной в пирамиду сферы.

      Доказательство утверждения 2 завершено.

      Поскольку у любой правильной пирамиды все внутренние двугранные углы при основании равны, то справедливо

      Следствие 2. В любую правильную пирамиду можно вписать сферу, причем ее радиус   R  выражается через высоту пирамиды   h   и внутренний двугранный угол при основании пирамиды   φ   по формуле

(1)

Радиус сферы, вписанной в правильную n — угольную пирамиду

      Задача. Высота правильной n — угольной пирамиды равна   h ,   а длина ребра основания равна   a .   Найти радиус сферы, вписанной в пирамиду.

      Решение. Рассмотрим правильную n — угольную пирамиду   SA₁A₂ … A_n   и обозначим символом   O’   центр вписанной в пирамиду сферы, а буквой   O  – центр основания пирамиды. Проведем плоскость через высоту пирамиды   SO   и апофему   SB   какой-либо боковой грани (рис. 7).

Рис.7

      Буквой   R   на рисунке 7 обозначен радиус вписанной в пирамиду сферы, буквой   r   – радиус вписанной в основание пирамиды окружности, а буквой   φ   – внутренний двугранный угол при основании пирамиды. Из прямоугольного треугольника   OSB   получаем

(2)

      В силу следствия 2 из формул (1) и (2) получаем

(3)

      Поскольку радиус вписанной в правильный n — угольник окружности выражается через сторону этого многоугольника по формуле радиус вписанной в правильный n — угольник окружности выражается через сторону этого многоугольника по формуле

из формулы (3) получаем соотношение

      Ответ.

      Следствие 3. Радиус сферы, вписанной в правильную треугольную пирамиду с высотой   h   и ребром основания  a,   равен

      Следствие 4. Радиус сферы, вписанной в правильный тетраэдр с ребром  a,   равен

      Следствие 5. Радиус сферы, вписанной в правильную четырехугольную пирамиду с высотой   h   и ребром основания   a,   равен

      Следствие 6. Радиус сферы, вписанной в правильную шестиугольную пирамиду с высотой   h   и ребром основания  a,   равен

Сфера, вписанная в треугольную пирамиду.

Формула для радиуса вписанной сферы

      Утверждение 3. В любую треугольную пирамиду можно вписать сферу.

      Доказательство. Доказательство этого утверждения напоминает планиметрическое доказательство возможности вписать окружность в произвольный треугольник.

      Действительно, пусть   SABC   – произвольный тетраэдр. Биссекторная плоскость внутреннего двугранного угла с ребром   AC   и биссекторная плоскость внутреннего двугранного угла с ребром   AB   пересекаются по некоторой прямой, проходящей через вершину   A.   Биссекторная плоскость внутреннего двугранного угла в ребром   BC   пересекает эту прямую в единственной точке   O  , которая и является центром вписанной сферы (рис. 8).

Рис.8

        Получим формулу, позволяющую вычислить радиус вписанной в тетраэдр   SABC   сферы. Для этого заметим, что объем пирамиды   SABC   равен сумме объемов пирамид   OABC, OSCA, OSAB, OSCB,   причем высота каждой из пирамид   OABC, OSCA, OSAB, OSCB   равна радиусу   R   вписанной в пирамиду   SABC   сферы. Если обозначить площади граней тетраэдра   SABC   символами

S_ABC , S_ASC , S_ASB , S_BSC ,

а объемы пирамид   SABC, OABC, OSCA, OSAB, OSCB   – символами

V_ABC , V _ASC , V _ASB , V _BSC ,

то справедливы следующие равенства:

где символом   S_полн   обозначена площадь полной поверхности пирамиды   SABC.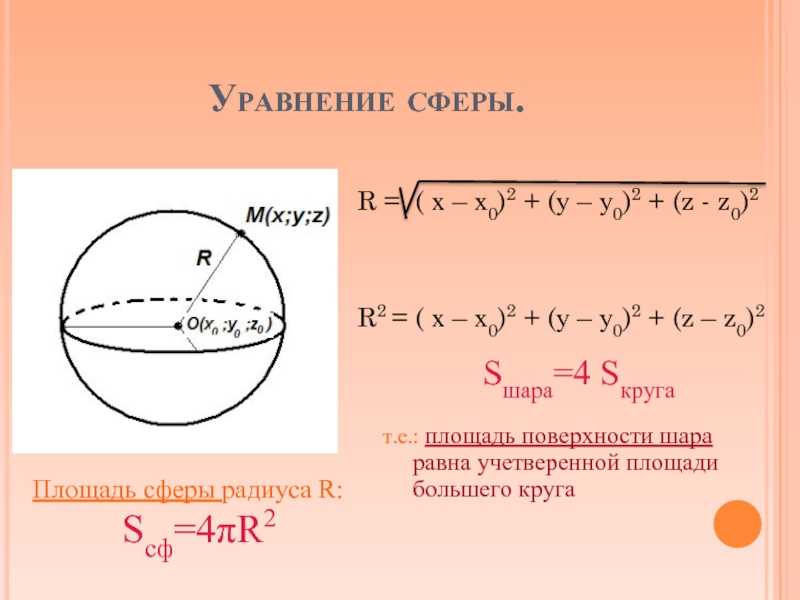

      Следовательно,

      Замечание 2. Если в пирамиду (необязательно треугольную) можно вписать сферу, то, рассуждая аналогично, можно получить следующую формулу для радиуса вписанной в пирамиду сферы

где символами   V_пир   и   S_полн   обозначены объем и площадь полной поверхности пирамиды соответственно.

      На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ по математике.

Какова площадь поверхности шара? Определение, формула, примеры

Что такое площадь поверхности сферы?

Площадь поверхности сферы — это область или область, покрытая внешней изогнутой поверхностью сферы.

Сфера представляет собой трехмерное твердое тело, все точки поверхности которого находятся на равном расстоянии от центра. Проще говоря, любой твердый круглый объект в форме шара является сферой.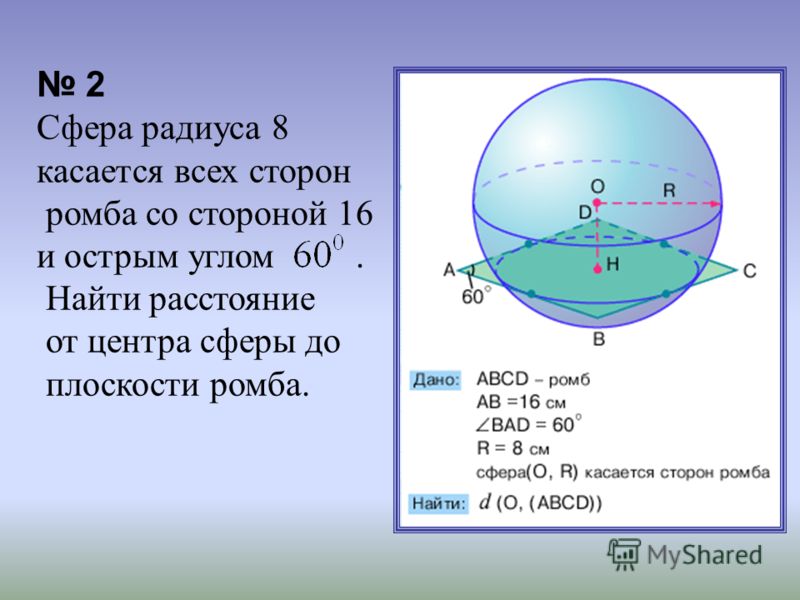 {2}$ квадратных единиц

Связанные рабочие листы

Вывод площади поверхности сферы

Теперь, когда вы поняли площадь поверхности сферы, пришло время вывести формулу.

Греческий математик Архимед открыл, что площадь поверхности сферы равна площади боковой поверхности цилиндра, так что радиус сферы равен радиусу цилиндра, а высота цилиндра равна как диаметр сферы. Согласно Архимеду, сфера может вписаться в цилиндр так, что высота цилиндра станет диаметром сферы.

Итак, если радиус сферы и цилиндра равен «r», то

Площадь поверхности сферы $=$ Площадь боковой поверхности цилиндра

Мы знаем, что площадь боковой поверхности цилиндра $= 2\pi r h $, 

, где «r» — радиус, а «h» — высота цилиндра.

Теперь высота цилиндра = диаметру сферы.

Итак, $h = 2r$

Подставив значение «h» вместо «2r», получим уравнение площади поверхности сферы 9{2}$

Существует три типа площади поверхности твердых тел: площадь боковой поверхности (LSA), площадь криволинейной поверхности (CSA) и общая площадь поверхности (TSA).

Площадь криволинейной поверхности сферы

Площадь криволинейной поверхности представляет собой сумму площадей всех криволинейных областей твердого тела.

Площадь изогнутой поверхности сферы равна общей площади поверхности сферы, поскольку сфера имеет полностью изогнутую форму. Таким образом, формула площади криволинейной поверхности сферы равна 9{2}$ квадратных единиц

Как найти площадь поверхности сферы

Давайте разберемся, как рассчитать площадь поверхности сферы на примере. Если радиус шара 8 см. Какова будет площадь его поверхности?

Шаги для определения площади поверхности сферы приведены ниже:

• Шаг 1:

Обратите внимание на радиус сферы. В приведенном выше примере радиус сферы равен 8 см. Если указан диаметр, разделите диаметр на 2, чтобы получить радиус. 9{2}_{2}}$

$\Rightarrow \frac{A_{1}}{A_{2}} = \frac{16}{9}$

Таким образом, отношение между суммой двух сфер площадь поверхности 16:9.

{2}$ $\примерно 804,57$ штук 9{2} = \frac{(616 \times 7)}{(4 \times 22)} = 49$
$\Rightarrow r = 7$ дюймов
Мы знаем, диаметр $= 2 \times$ радиус $= 2 \ умножить на 7 = 14$ дюймов
Следовательно, диаметр сферы равен 14 дюймам.

3

Твердый шар имеет диаметр 28 футов. Какова площадь криволинейной поверхности шара?

2444 кв. фута

2664 кв. фута

Правильный ответ: 2464 кв. фута к 9{2} = 441$
$r = 21$ см
Диаметр $= 2 х 21 = 42$ см

5

Площадь поверхности шара равна площади боковой поверхности ___ с таким же радиусом и высотой как диаметр сферы.

Конус

Куб

Пирамида

Цилиндр

Правильный ответ: Цилиндр
Площадь поверхности сферы равна площади боковой поверхности цилиндра, так что радиус сферы равен радиусу цилиндра, а высота цилиндра соответствует диаметру сферы. 9{2}$.

Сколько поверхностей у сферы?

Сфера имеет только одну грань, которая представляет собой изогнутую поверхность. У него нет плоских граней.

Калькулятор радиуса сферы с шагами

К

Мария Кондич

Высоко мотивированная студентка факультета машиностроения, желающая расширить свои знания и применить свои навыки в динамичной рабочей среде. Коммуникабельный, амбициозный и быстро обучаемый, с исключительным знанием английского языка и глубоким пониманием математических расчетов.

Последнее обновление: 1 марта 2023 г.

5/5 — (1 голос)

Калькулятор радиуса сферы — это инструмент, который обеспечивает точный результат не только для радиуса сферы, но также для окружности, площади и объема, только зная один из перечисленные параметры. Поэтому эти значения будут полностью описаны в следующем тексте.

Кроме того, предположим, что эта тема привлекает ваше внимание. В этом случае мы рекомендуем проверить другие связанные калькуляторы, такие как Калькулятор площади для расчета площади различных геометрических фигур, Калькулятор объема для определения объема геометрических фигур, Калькулятор сферических координат, Калькулятор окружности и другие, которые предлагает наш сайт.

Эта статья содержит информацию о геометрии сферы и всех формулах, необходимых для основных вычислений сферы, включая радиус, площадь, объем и т. д. Тема будет обработана сначала путем объяснения радиуса сферы, а затем его вычисления , прилагаемый к примеру и руководству по использованию нашего калькулятора. В целом, это впитается, просматривая текст. Не стесняйтесь оставлять отзывы и обращаться к нам, если есть определенные темы, на которые вы хотите, чтобы мы написали.

Что такое радиус сферы?

Сфера — трехмерный объект, аналог двухмерного круга. Это набор точек, расстояние от центра которых всегда одинаково. Расстояние от центра до любой точки на окружности равно радиусу , обозначенному буквой r. Имея это в виду, диаметр создается путем расширения радиуса до противоположной стороны сферы (d).

Однако диаметр должен проходить через центр, а точек, соединенных диаметром, противоположных точек друг друга. Напротив, линия, соединяющая две точки, лежащие на окружности сферы, не входящей в центр, называется хордой .

3D-сфера

Другие значения, важные для расчета радиуса сферы:

• Объем сферы (V) — это пространство, заключенное со всеми краевыми точками сферы. Архимед вывел формулу объема сферы, указав, что объем внутри сферы в два раза больше объема между сферой и описанным цилиндром.
• Площадь поверхности сферы (A) — это площадь, занимаемая поверхностью трехмерной сферы.
• Окружность сферы (C) – Эта же формула дает длину окружности сферы как одну для окружности.

Важным фактом является то, что сфера имеет наименьшее отношение поверхности к объему. Аналогично этому, круг охватывает наибольшую площадь с заданным периметром.

Радиус сферы – формулы

В этом разделе обсуждаются различные способы расчета радиуса сферы в зависимости от имеющихся данных. Formulas for the radius of a sphere are:

Data available	Formula
Volume	r=\sqrt[3]{3 \cdot \frac{V}{4 \cdot \pi}}
Площадь поверхности	r=\sqrt{\frac{A}{4 \cdot \pi}}
Диаметр	r=\frac{d}{2}
Отношение поверхности к объему	r=\frac{3}{\frac{A}{V}}
Окружность	r=\frac {C}{2 \cdot \pi}

Как найти радиус сферы?

Радиус сферы легко найти, если известен любой из перечисленных выше параметров. Например, если мы знаем диаметр сферы, радиус равен половине этого значения, как показывает формула. Но если мы не знаем, где находится центр нашей сферы, может быть немного сложнее найти ее радиус. Тем не менее, это не является неразрешимым, и вот два способа найти центральную точку:

• Поместите две параллельные плоскости, одну сверху сферы, а другую снизу, расстояние между ними равно диаметру. Теперь разделите эту длину на два, и вот где будет центр.

• Другой способ — найти объем сферы. Мы считаем это решение скорее экспериментальным, чем математическим. Во-первых, найдите цилиндрический предмет и налейте в него воду. Затем поместите сферу в этот цилиндр и измерьте количество воды, вытолкнутой из цилиндра, что является объемом сферы. После этого примените формулу для нахождения радиуса, чтобы можно было найти и другие параметры.

Калькулятор радиуса сферы – как пользоваться?

При разработке этого инструмента команда калькулятора CalCon приложила много усилий, чтобы сделать его простым в использовании и функциональным для любого случая, который может возникнуть при вычислении радиуса сферы. Этот калькулятор выдаст вам результат, введя только один из перечисленных параметров.

При нажатии на единицу измерения рядом с мерой указанного параметра появится раскрывающееся меню, позволяющее выбрать единицу измерения. Также эта функция позволяет конвертировать единицы измерения по вашему желанию.