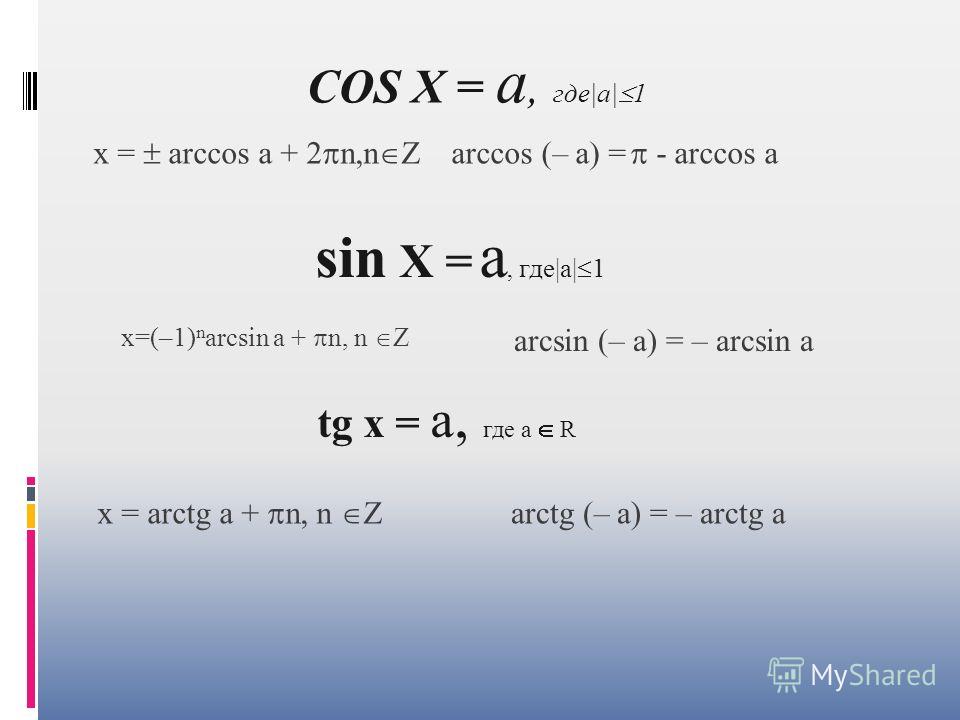2cos x/2 (sin x/2 – cos x/2 )=0
• Cos x/2 = 0
• x/2 = П/2 + Пn, n принад.Z
• X = П + 2Пn, n принад.Z
• Ответ: x = П/2 + 2Пn, n принад.Z
x = П + 2Пn, n принад.Z
• Sin x/2 – cos x/2 =0 l : cos x/2не=0
• Tg x/2 -1 = 0
• Tg x/2 = 1
• x/2 = П/4 + Пn, n принад.Z
• X = П/2 + 2Пn, n принад.Z
9. Использование формулы приведения и формулы суммы:
• Sinx — cosx = 1• Sinx – sin(П/2-x)=1
• 2sin ((x-П/2-x )/2) cos ((x+П/2-x)/2) =1
• 2sin(x-П/4) cos П/4=1
• 2sin(x-П/4) * √2/2 = 1
• Sin(x-П/4)= √2/2
• X-П/4 = П/4 + 2Пn, n принад.Z
• X-П/4=3П/4+2Пn, n принад.Z
• Ответ: x = П/2 + 2Пn, n принад.Z
• X=П/2 + 2Пn, n принад.Z
x = П + 2Пn, n принад.Z
• X=П+2Пn, n принад.Z
10. СПАСИБО ЗА ВНИМАНИЕ
English Русский Правила
Метод разложения на множители тригонометрических уравнений. Тригонометрические уравнения — формулы, решения, примеры
Вы можете заказать подробное решение вашей задачи !!!
Равенство, содержащее неизвестную под знаком тригонометрической функции (`sin x, cos x, tg x` или `ctg x`), называется тригонометрическим уравнением, именно их формулы мы и рассмотрим дальше.
n arcsin a + \pi n, n \in Z`
2. Уравнение `cos x=a`
При `|a|>1` — как и в случае с синусом, решений среди действительных чисел не имеет.
При `|a| \leq 1` имеет бесконечное множество решений.
Формула корней: `x=\pm arccos a + 2\pi n, n \in Z`
Частные случаи для синуса и косинуса в графиках.
3. Уравнение `tg x=a`
Имеет бесконечное множество решений при любых значениях `a`.
Формула корней: `x=arctg a + \pi n, n \in Z`
4. Уравнение `ctg x=a`
Также имеет бесконечное множество решений при любых значениях `a`.
Формула корней: `x=arcctg a + \pi n, n \in Z`
Формулы корней тригонометрических уравнений в таблице
Для синуса:
Для косинуса:
Для тангенса и котангенса:
Формулы решения уравнений, содержащих обратные тригонометрические функции:
Методы решения тригонометрических уравнений
Решение любого тригонометрического уравнения состоит из двух этапов:
- с помощью преобразовать его до простейшего;
- решить полученное простейшее уравнение, используя выше написанные формулы корней и таблицы.
2 x=0`, `sin x(1-sin x)=0`. Тогда `sin x=0` или `1-sin x=0`. - `sin x=0`, `x=\pi n`, `n \in Z`
- `1-sin x=0`, `sin x=-1`, `x=\pi /2+2\pi n, n \in Z`.
Учитывая, что ` x \ne \pi+2\pi n, n \in Z`, решениями будут `x=2\pi n, n \in Z` и `x=\pi /2+2\pi n`, `n \in Z`.
Ответ. `x=2\pi n`, `n \in Z`, `x=\pi /2+2\pi n`, `n \in Z`.
Тригонометрия, и тригонометрические уравнения в частности, применяются почти во всех сферах геометрии, физики, инженерии. Начинается изучение в 10 классе, обязательно присутствуют задания на ЕГЭ, поэтому постарайтесь запомнить все формулы тригонометрических уравнений — они вам точно пригодятся!
Впрочем, даже запоминать их не нужно, главное понять суть, и уметь вывести. Это не так и сложно, как кажется. Убедитесь сами, просмотрев видео.
Методы решения тригонометрических уравнений Содержание
- Метод замены переменной
- Метод разложения на множители
- Однородные тригонометрические уравнения
- С помощью тригонометрических формул:
- Формул сложения
- Формул приведения
- Формул двойного аргумента
Метод замены переменной
С помощью замены t = sinx или t = cosx, где t ∈ [−1;1] решение исходного уравнения сводится к решению квадратного или другого алгебраического уравнения.
См. примеры 1 – 3
Иногда используют универсальную тригонометрическую подстановку: t = tg
Пример 1 Пример 2 Пример 3 Метод разложения на множители
Суть этого метода заключается в том, что произведение нескольких множителей равно нулю, если хотя бы один из них равен нулю, а другие при этом не теряют смысл:
f(x) · g(x) · h(x) · … = 0 ⟺ f(x) = 0 или g(x) = 0 или h(x) = 0
и т.д. при условии существования каждого из сомножителей
См. примеры 4 – 5
Пример 4 Пример 5 Однородные тригонометрические уравнения Уравнение вида a sin x + b cos x = 0 называют однородным тригонометрическим уравнением первой степени.
a sin x + b cos x = 0
Замечание.
Деление на cos x допустимо, поскольку решения уравнения cos x = 0 не являются решениями уравнения a sin x + b cos x = 0.
a sin x b cos x 0
a tg x + b = 0
tg x = –
Однородные тригонометрические уравнения
a sin2x + b sin x cos x + c cos2x = 0
Уравнение вида a sin2x + b sin x cos x + c cos2x = 0 называют однородным тригонометрическим уравнением второй степени.
a tg2x + b tg x + c = 0
a sin2x b sin x cos x c cos2x 0
Замечание. Если в данном уравнении а = 0 или с = 0 то, уравнение решается методом разложения
на множители.
Пример 6
Пример 8 Пример 9 Пример 10 Пример 11 1. Формулы сложения:
sin (x + y) = sinx cosy + cosx siny
cos (x + y) = cosx cosy − sinx siny
tgx + tgy
tg (x + y) =
1 − tgx tgy
sin (x − y) = sinx cosy + cosx siny
cos (x − y) = cosx cosy + sinx siny
tgx − tgy
tg (x − y) =
1 + tgx tgy
сtgx сtgy − 1
сtg (x + y) =
сtgу + с tgх
сtgx сtgy + 1
сtg (x − y) =
сtgу − с tgх
Пример 12 Пример 13 С помощью тригонометрических формул 2. Формулы приведения:
Лошадиное правило
В старые добрые времена жил рассеянный математик, который при поиске ответа менять или не менять название функции (синус на косинус ), смотрел на свою умную лошадь, а она кивала головой вдоль той оси координат, которой принадлежала точка, соответствующая первому слагаемому аргумента π/ 2 + α или π + α .
Если лошадь кивала головой вдоль оси ОУ , то математик считал, что получен ответ «да, менять» , если вдоль оси ОХ , то «нет, не менять» .
С помощью тригонометрических формул 3. Формулы двойного аргумента:
sin 2x = 2sinx cosx
cos 2x = cos2x – sin2x
cos 2x = 2cos2x – 1
cos 2x = 1 – 2sin2x
1 – tg2x
ctg 2x =
ctg2x – 1
Пример 14 С помощью тригонометрических формул 4. Формулы понижения степени:
5. Формулы половинного угла:
С помощью тригонометрических формул 6. Формулы суммы и разности:
С помощью тригонометрических формул 7. Формулы произведения: Мнемоническое правило “Тригонометрия на ладони”Очень часто требуется знать наизусть значения cos , sin , tg , ctg для углов 0°, 30°, 45°, 60°, 90°.
Но если вдруг какое-либо значение забудется, то можно воспользоваться правилом руки.
Правило: Если провести линии через мизинец и большой палец,
то они пересекутся в точке, называемой “лунный бугор”.
Образуется угол 90°. Линия мизинца образует угол 0°.
Проведя лучи из “лунного бугра” через безымянный, средний, указательный пальцы, получаем углы соответственно 30°, 45°, 60°.
Подставляя вместо n : 0, 1, 2, 3, 4, получаем значения sin , для углов 0°, 30°, 45°, 60°, 90°.
Для cos отсчет происходит в обратном порядке.
Методы решения тригонометрических уравнений.
Решение тригонометрического уравнения состоит из двух этапов: преобразование уравнения для получения его простейшего вида (см. выше ) и решение полученного простейшего тригонометрического уравнения. Существует семь основных методов решения тригонометрических уравнений.
1.
Алгебраический метод.(метод замены переменной и подстановки).
2. Разложение на множители.
П р и м е р 1. Решить уравнение: sin x + cos x = 1 .
Р е ш е н и е. Перенесём все члены уравнения влево:
Sin x + cos x – 1 = 0 ,
Преобразуем и разложим на множители выражение в
Левой части уравнения:
П р и м е р 2. Решить уравнение: cos 2
Р е ш е н и е. cos 2 x + sin x · cos x – sin 2 x – cos 2 x = 0 ,
Sin x · cos x – sin 2 x = 0 ,
Sin x · (cos x – sin x ) = 0 ,
П р и м е р 3. Решить уравнение: cos 2 x – cos 8 x + cos 6 x = 1.
Р е ш е н и е. cos 2 x + cos 6 x = 1 + cos 8 x ,
2 cos 4x cos 2x = 2 cos ² 4x ,
Cos 4x · (cos 2x – cos 4x ) = 0 ,
Cos 4x · 2 sin 3x · sin x = 0 ,
1).
cos 4x = 0 , 2). sin 3x = 0 , 3). sin x = 0 ,3. Приведение к однородному уравнению.
Уравнение называется однородным от носительно sin и cos , если все его члены одной и той же степени относительно sin и cos одного и того же угла . Чтобы решить однородное уравнение, надо:а ) перенести все его члены в левую часть;
б ) вынести все общие множители за скобки;
в ) приравнять все множители и скобки нулю;
г ) скобки, приравненные нулю, дают однородное уравнение меньшей степени, которое следует разделить на
cos (или sin ) в старшей степени;
д ) решить полученное алгебраическое уравнение относительно tan .
sin 2 x + 4 sin x · cos x + 5 cos 2 x = 2.
Р е ш е н и е. 3sin 2 x + 4 sin x · cos
Sin 2 x + 4 sin x · cos x + 3 cos 2 x = 0 ,
Tan 2 x + 4 tan x + 3 = 0 , отсюда y 2 + 4y +3 = 0 ,
Корни этого уравнения: y 1 = — 1, y 2 = — 3, отсюда
1) tan x = –1, 2) tan x = –3,
4. Переход к половинному углу.
Рассмотрим этот метод на примере:
П р и м е р. Решить уравнение: 3 sin x – 5 cos x = 7.
Р е ш е н и е. 6 sin (x / 2) · cos (x / 2) – 5 cos ² (x / 2) + 5 sin ² (x / 2) =
7 sin ² (x / 2) + 7 cos ² (x / 2) ,
2 sin ² (x / 2) – 6 sin (x / 2) · cos (x / 2) + 12 cos ² (x / 2) = 0 ,
tan ² (x / 2) – 3 tan (x / 2) + 6 = 0 ,
.
. . . . . . . . .5. Введение вспомогательного угла.
Рассмотрим уравнение вида :
a sin x + b cos x = c ,
Где a , b , c – коэффициенты; x – неизвестное.
Теперь коэффициенты уравнения обладают свойствами синуса и косинуса , а именно : модуль ( абсолютное значение ) каждого из них не больше 1, а сумма их квадратов равна 1 . Тогда можно обозначить их соответственно как cos и sin (здесь — так называемый вспомогательный угол ), и наше уравнение прини
Тема: «Методы решения тригонометрических уравнений».
Цели урока:
образовательные:
Сформировать навыки различать виды тригонометрических уравнений;
Углубление понимания методов решения тригонометрических уравнений;
воспитательные:
Воспитание познавательного интереса к учебному процессу;
Формирование умения анализировать поставленную задачу;
развивающие:
Формировать навык проводить анализ ситуации с последующим выбором наиболее рационального выхода из нее.
Оборудование: плакат с основными тригонометрическими формулами, компьютер, проектор, экран.
Начнем урок с повторения основного приема решения любого уравнения: сведение его к стандартному виду. Путем преобразований линейные уравнения сводят к виду ах = в, квадратные – к виду ax 2 + bx + c =0. В случае тригонометрических уравнений необходимо свести их к простейшим, вида: sinx = a , cosx = a , tgx = a , которые легко можно решить.
В первую очередь, конечно, для этого необходимо использовать основные тригонометрические формулы, которые представлены на плакате: формулы сложения, формулы двойного угла, понижения кратности уравнения. Мы уже умеем решать такие уравнения. Повторим некоторые из них:
Вместе с тем существуют уравнения, решение которых требует знаний некоторых специальных приемов.
Темой нашего урока является рассмотрение этих приемов и систематизация методов решения тригонометрических уравнений.
Методы решения тригонометрических уравнений.
1. Преобразование к квадратному уравнению относительно какой-либо тригонометрической функции с последующей заменой переменной.
Рассмотрим каждый из перечисленных методов на примерах, но более подробно остановимся на двух последних, так как два первых мы уже использовали при решении уравнений.
1. Преобразование к квадратному уравнению относительно какой-либо тригонометрической функции.
2. Решение уравнений методом разложения на множители.
3. Решение однородных уравнений.
Однородными уравнениями первой и второй степени называются уравнения вида:
соответственно (а ≠ 0, b ≠ 0, с ≠ 0).
При решении однородных уравнений почленно делят обе части уравнения на cosx для (1) уравнения и на cos 2 x для (2). Такое деление возможно, так как sinx и cosx не равны нулю одновременно – они обращаются в нуль в разных точках. Рассмотрим примеры решения однородных уравнений первой и второй степени.
Запомним это уравнение: при рассмотрении следующего метода – введение вспомогательного аргумента, решим его другим способом.
4. Введение вспомогательного аргумента.
Рассмотрим уже решенное предыдущим методом уравнение:
Как видим, получается тот же результат.
Рассмотрим еще один пример:
В рассмотренных примерах было, в общем, понятно, на что требуется разделить исходное уравнение, чтобы ввести вспомогательный аргумент. Но может случиться, что не очевидно, какой делитель выбрать. Для этого существует специальная методика, которую мы сейчас и рассмотрим в общем виде. Пусть дано уравнение.
2}x = (\sin x + \cos x)(\sin x — \cos x)$
Теперь мы можем сделать с остальными то же самое, что и в решении.Недавно обновленные страницы
Если ab и c единичные векторы, то left ab2 right+bc2+ca2 математика класса 12 JEE_Main
Стержень AB длиной 4 единицы перемещается горизонтально, когда математика класса 11 JEE_Main
Вычислить значение intlimits0 cos 3xdx A 0 B 1 class 12 maths JEE_Main
Что из следующего верно 1 nleft S cup T right class 10 maths JEE_Main
Какова площадь треугольника с вершинами Aleft 11-й класс математики JEE_Main
Координаты точек A и B равны a0 и a0 11-му классу математики JEE_Main
Если ab и c единичные векторы, то left ab2 right+bc2+ ca2 class 12 maths JEE_Main
Стержень AB длиной 4 единицы перемещается горизонтально, когда class 11 maths JEE_Main
Оценить значение intlimits0pi cos 3xdx A 0 B 1 class 12 maths JEE_Main
Что из следующего верно 1 nleft S cup T правый класс 10 математика JEE_Main
Какова площадь треугольника с вершинами Aleft 11 класс JEE_Main
Координаты точек A и B равны a0 и a0 11 класс математики JEE_Main
Тенденции сомнения Что равно sinx CO
? – руль-онлайн. comДругое
Райли Брайан
Чему равен sinx COSX?
Тангенс x определяется как его синус, деленный на его косинус: tan x = sin x cos x .
Что происходит при синх COSX?
Из единичного круга видно, что sin x и cos x могут иметь одно и то же значение только в двух местах, в x = /4 и x = 5/4 (45° и 225°). Уравнение sin x = cos x также можно решить путем деления на cos x. Если положить k = 0 и k = 1, получим решения /4 (45°) и /4 + = 5/4 (45°+ 180°= 225°).
Каково минимальное значение sinx COSX?
-1
Минимальное значение sinx равно -1, а минимальное значение y равно -√2.Каков основной период sinx COSX?
Период sinx равен π, а cosx равен π. Данная функция четная, а sinx, cosx дополнительные.
Что такое COSX?
Арккосинус x определяется как функция арккосинуса x, когда -1≤x≤1.
Когда косинус y равен x: cos y = x. Тогда арккосинус x равен функции арккосинуса x, которая равна y: arccos x = cos-1 x = y.Как решить sin a cos a?
Синус угла равен отношению противолежащего катета к гипотенузе, тогда как косинус угла равен отношению прилежащего катета к гипотенузе.
- Sin θ = противоположная сторона гипотенузы.
- Cos θ = AdjacentSideHypotenuse.
Что такое sinx Сини?
sinx – siny = 2 cos. (x + y. 2. ) sin.
Каково минимальное значение sinA?
Ywhat минимальное значение sinA.
Каково минимальное и максимальное значение sin тета?
Свойства синусоиды Максимальное значение sin θ равно 1, когда θ = 90 ˚. Минимальное значение sin θ равно –1 при θ = 270 ˚. Итак, диапазон значений sin θ равен –1 ≤ sin θ ≤ 1.
Каков период для sinx?
2π
Период sinx равен 2π, тогда как период sinx/2 равен 4π.Каков период cos2x?
Период будет равен 2π2 или π .
2 x=0`, `sin x(1-sin x)=0`. Тогда `sin x=0` или `1-sin x=0`. 
Алгебраический метод.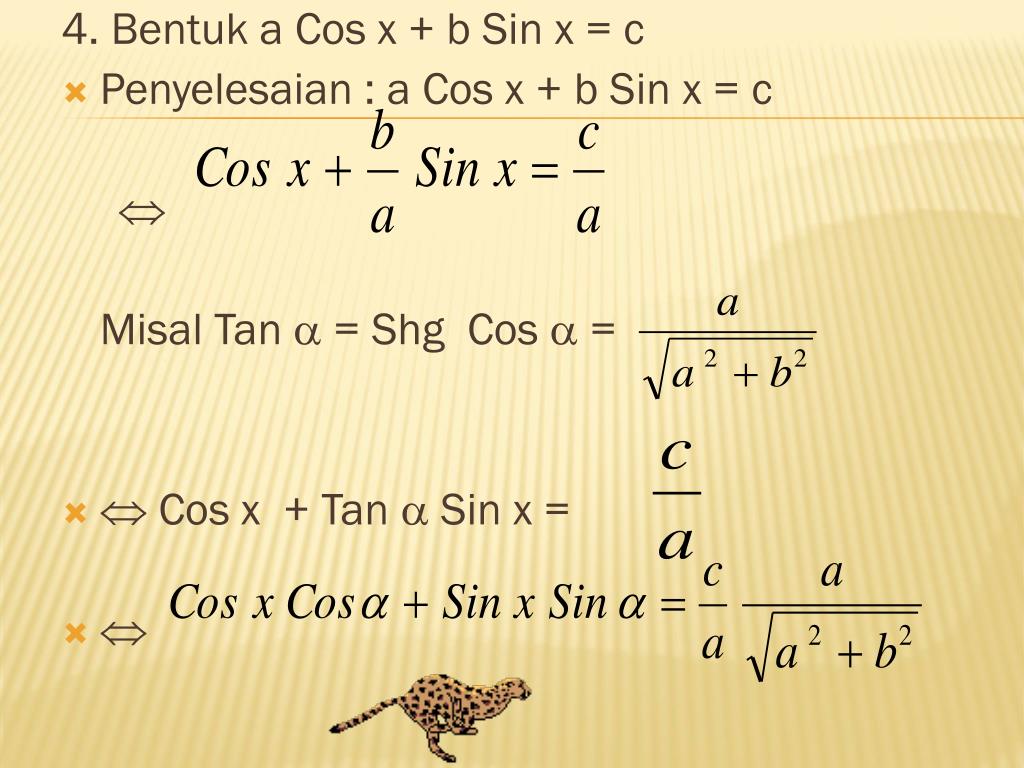
cos 4x = 0 , 2). sin 3x = 0 , 3). sin x = 0 ,
. . . . . . . . .
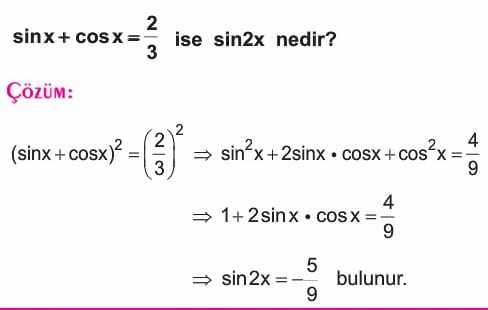com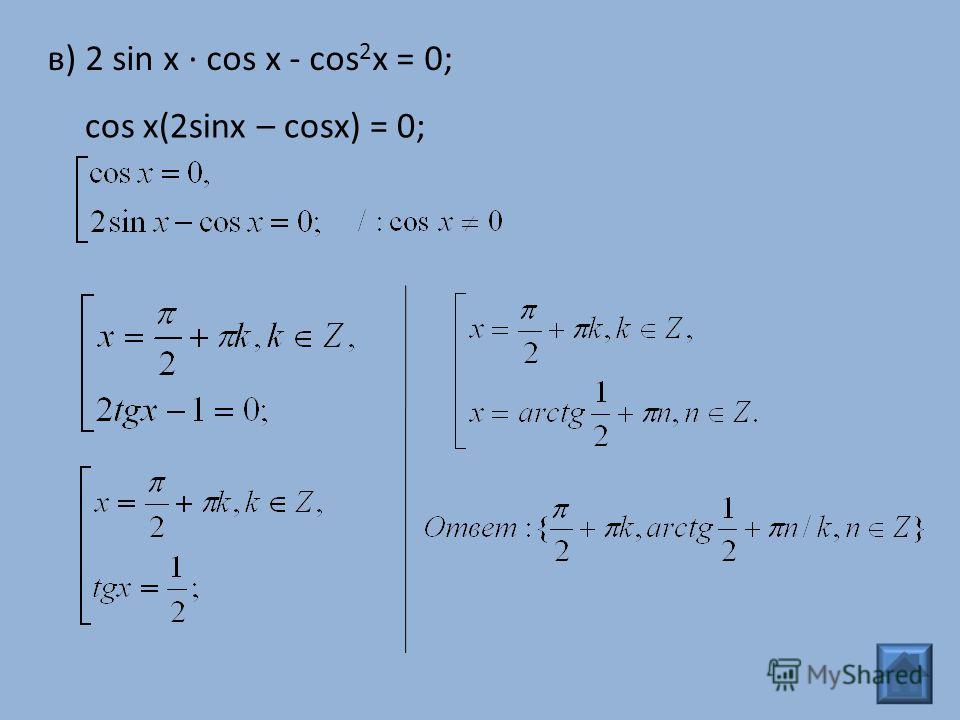
Когда косинус y равен x: cos y = x. Тогда арккосинус x равен функции арккосинуса x, которая равна y: arccos x = cos-1 x = y.