Сумма степеней положительных целых чисел
Автор(ы):
Джанет Бири (Университет Редлендса)
Томас Хэрриот был английским математиком и ученым, который жил в Лондоне и работал под покровительством сэра Уолтера Рэли и Генри Перси, Граф Нортумберленд. Рэли отправил Харриота в путешествие в колонию Вирджиния в 1585–1586 годах, что позволило Харриоту применить на практике свою навигационную теорию, а также собрать обширные заметки для своей книги . Краткий и правдивый отчет о новой земле Вирджинии 9.0008 , впервые опубликовано в 1588 году.
Харриот никогда не публиковал ни одной своей математической или научной работы, но он оставил более 5000 рукописных листов заметок на различные темы. В своих заметках по математике он гораздо больше использовал символические обозначения, чем его современники и многие из его последователей, включая Ферма и Паскаля (см. Ниже). Он также часто использовал таблицы разностей, применяя их для изучения пифагорейских троек и, как мы увидим, сумм степеней натуральных чисел.
Харриот написал формулы для сумм квадратов, кубов и четвертых степеней на листе рукописи, озаглавленном «Ad aggregata Z.C.ZZ. так далее.» («Для сумм квадратов, кубов, квадратов-квадратов и т. д.») (Харриот, лист 240). В этом заголовке мы заменили Z, C и ZZ на символы квадратов, кубов и четвертых степеней (квадрат-квадраты), которые Харриот, вероятно, позаимствовал из знаменитой книги по алгебре Роберта Рекорда, Whetstone of Witte (1557), и мы заменили «и т. д.» для символа Harriot, используемого для «et cetera».
Рис. 8. Коссистское обозначение степеней Роберта Рекорда можно увидеть в списке, начинающемся слева внизу и заканчивающемся в середине правой страницы, наряду с упрощенными версиями, записанными читателем. Символы R для «корень» (первая степень), Z для «квадрат», C для «кубайк» (куб) и ZZ для «квадрат квадратов» (четвертая степень). ) находятся слева. Дополнительные изображения из книги Рекорда по алгебре, Точильный камень Витте, см. Роберт Рекорд Точильный камень Витте в «Математических сокровищах». (Воспроизведено с разрешения библиотеки Колумбийского университета). ф. 239), как показано на рисунке 9.
Роберт Рекорд Точильный камень Витте в «Математических сокровищах». (Воспроизведено с разрешения библиотеки Колумбийского университета). ф. 239), как показано на рисунке 9.
Рисунок 9. Таблицы разностей для сумм квадратов, кубов и квадратов-квадратов
Эти таблицы называются таблицами «разностей», потому что, например, в треугольнике чисел
$$\matrix{ 14 & {}\cr 30 & 16\cr}$$
в верхней левой таблице на рисунке 9 разница между 30 и 14 составляет 16 (30 – 14 = 16). Это отношение разности сохраняется для каждого такого треугольника чисел в таблицах на рисунке 9 и характеризует эти таблицы как таблицы разностей. Если мы применим это свойство разности повторно, то увидим, что элементы любого столбца можно суммировать, чтобы получить элементы столбца слева. Например, в двух крайних левых столбцах верхней левой таблицы на рисунке 9, мы видим, что 14 + 16 + 25 = 55, 5 + 9 + 16 + 25 = 55, 1 + 4 + 9 + 16 + 25 = 55 и 1 + 4 + 9 + 16 = 30. Последние две суммы равны , соответственно, сумма первых пяти квадратов положительных целых чисел и сумма первых четырех квадратов положительных целых чисел, и это следует непосредственно из определения таблицы разностей и выбора Харриотом 1 в качестве первой записи столбца, помеченного p 3 и последовательные положительные целые квадраты в качестве записей столбца с пометкой 9.0007 p 2 , что n -е число в столбце с меткой p 3 является суммой первых n положительных целых квадратов. (Обратите внимание, что 2 и 3 здесь являются надстрочными индексами, а не показателями степени.) Точно так же в оставшихся двух таблицах разностей Харриота, поскольку вторые столбцы таблиц содержат кубы и четвертые степени последовательных положительных целых чисел, то первый или крайний левый столбец содержит, соответственно суммы кубов и суммы четвертых степеней последовательных натуральных чисел.
Последние две суммы равны , соответственно, сумма первых пяти квадратов положительных целых чисел и сумма первых четырех квадратов положительных целых чисел, и это следует непосредственно из определения таблицы разностей и выбора Харриотом 1 в качестве первой записи столбца, помеченного p 3 и последовательные положительные целые квадраты в качестве записей столбца с пометкой 9.0007 p 2 , что n -е число в столбце с меткой p 3 является суммой первых n положительных целых квадратов. (Обратите внимание, что 2 и 3 здесь являются надстрочными индексами, а не показателями степени.) Точно так же в оставшихся двух таблицах разностей Харриота, поскольку вторые столбцы таблиц содержат кубы и четвертые степени последовательных положительных целых чисел, то первый или крайний левый столбец содержит, соответственно суммы кубов и суммы четвертых степеней последовательных натуральных чисел.
Эти таблицы различий на самом деле называются «постоянными» таблицами различий, потому что различия становятся постоянными в столбце с надписью « e ».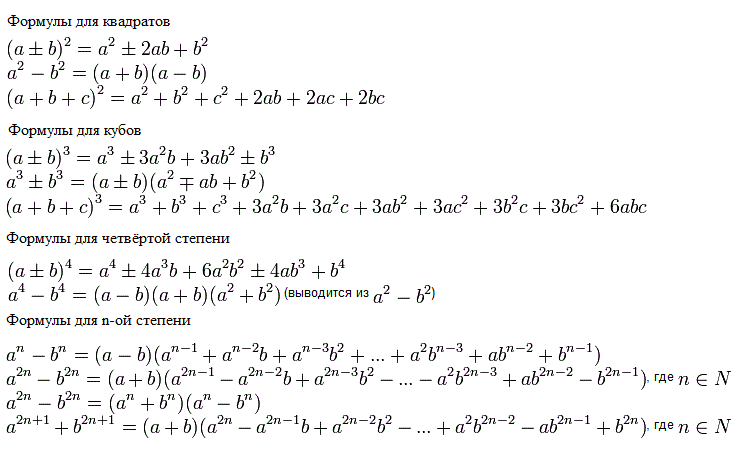 У Харриота были общие формулы для записей в таблицах постоянных разностей, и он мог применить эти формулы к крайним левым столбцам своих таблиц на рис. 9, чтобы получить общие формулы для сумм квадратов, кубов и четвертых степеней последовательных положительных целых чисел. Формулы Харриота, данные в терминах первой строки записей в таблице постоянных разностей, были следующими (Harriot, ff. 234, 246). 95 \ CR} $$
У Харриота были общие формулы для записей в таблицах постоянных разностей, и он мог применить эти формулы к крайним левым столбцам своих таблиц на рис. 9, чтобы получить общие формулы для сумм квадратов, кубов и четвертых степеней последовательных положительных целых чисел. Формулы Харриота, данные в терминах первой строки записей в таблице постоянных разностей, были следующими (Harriot, ff. 234, 246). 95 \ CR} $$
Здесь, V 1 Приведена N -й вход колонны с надписью P , V 2 2 , V 3 N -й вход колонны с надписью P 3 , V 4 N . и против 5 95 = 24nnnnn + 120nnnn + 120nnn — 120nn — 144n \cr & \quad \quad \quad \quad \quad \quad \quad — 60nnnn — 120nnn + 60nn + 120n \cr & \quad \quad \quad \quad \quad \ quad \quad \quad \quad \quad \quad + 40nnn — 0 — 40n \cr & \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad + 60nn — 60n \cr & \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \;\;\; + 120n — 120 \cr & \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \;\quad \;\quad \quad + 120 \кр} $$ 93 } \over 3} — {n \over {30}}. $$
$$
(Во всех этих вычислениях показатели степени n являются современными. Харриот всегда писал, например, nnn , где мы бы написали n 3 .)
Когда Хэрриот перечислил свои полученные формулы для сумм единиц, натуральных чисел, квадратов, кубов и квадратов-квадратов, он заменил v 0 , 7 v 4 0, v 2 , v 3 и v 4 с « s » (для суммы), за которыми следуют, соответственно, точка, отрезок, маленький квадрат, маленький куб и его символ квадрат-квадрат из Recorde. Он записал свою формулу для суммы квадратов, например, как s (квадрат): 6 = 2 nnn + 3 nn + 1 n . Несмотря на то, что вычисления долгие, они простые, и Харриот не показал столько работы, сколько мы. Он уже проделал тяжелую работу по выводу формул для записей в таблицах постоянных разностей. Для суммы кубов, например, на листе 239Харриот написал только
$$\eqalign{ & 6nnnn + 12nnn — 6nn — 12n \cr & \quad \quad \quad \quad \quad \quad + 12nn — 12n \cr & \quad \quad \quad \quad \quad \quad \quad \quad \quad + 24n \cr} $$
_______________________________________________
$$6nnnn + 12nnn + 6nn + 0n$$
а также проверил, что его формула для v 4 с 8 = 6, р = 0, р 2 = 1, р 3 = 1, p 4 = 1 и n = 5 дадут правильное значение 225 в пятой строке, прежде чем записать его окончательный результат на листе 240.
На листе 239 рукописный лист на которых появляются таблицы различий на рис. 9, Харриот процитировал три страницы из Maurolico Arithmeticorum Libri Duo, , страницы 52, 63 и 67. Что общего у этих трех страниц, так это список первых пяти различий четвертых степеней, 1 (= 1 4 – 0 4 ), 15 (= 2 4 – 1 4 ), 65, 175 и 369 = (5 4 – 4 4 ), которые Хэрриот сам отметил на листе 239. на листе 154 того же тома рукописи, что разности квадратов, кубов, четвертой и более высоких степеней в конечном счете постоянны, и иллюстрирует это свойство на рис. кубов или четвертых степеней можно расширить до таблицы постоянных разностей, изучая 9-е число Мауролико.0007 Арифметика.
Английский математик Генри Бриггс (1561-1631), прославившийся своим изобретением логарифмов совместно с Джоном Нэпьером, жил в Лондоне в то же время, что и Хэрриот. Бриггс отметил в своем 1624 Arithmetica Logarithmica , что разности квадратов, кубов, четвертых и более высоких степеней в конечном счете постоянны (Briggs, стр.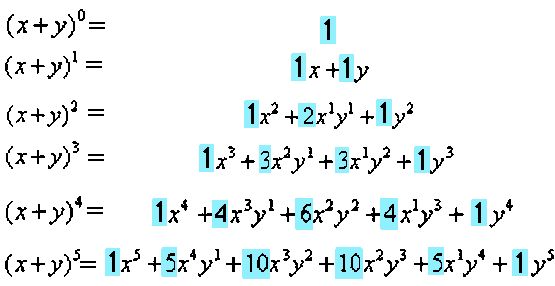 29-30, или Hutton, стр. 386-387), но не распространил свое наблюдение на формулы сумм этих степеней. Мы так и не нашли никаких доказательств контакта между Бриггсом и Хэрриотом. После смерти Харриота Бриггс уведомил Иоганна Кеплера в 1625 г. о готовящейся публикации некоторых работ Харриота (Фриш, стр. 661-662), а позже, в 1630 г. или чуть раньше, похвалил работу Харриота по «телесным углам» или сферической тригонометрии (Хейквилл , стр. 263-264), но ни разу не ссылался ни на какую другую работу Харриота.
29-30, или Hutton, стр. 386-387), но не распространил свое наблюдение на формулы сумм этих степеней. Мы так и не нашли никаких доказательств контакта между Бриггсом и Хэрриотом. После смерти Харриота Бриггс уведомил Иоганна Кеплера в 1625 г. о готовящейся публикации некоторых работ Харриота (Фриш, стр. 661-662), а позже, в 1630 г. или чуть раньше, похвалил работу Харриота по «телесным углам» или сферической тригонометрии (Хейквилл , стр. 263-264), но ни разу не ссылался ни на какую другую работу Харриота.
Упражнение 13. Напишите таблицу постоянных разностей, в которой второй столбец слева содержит пятые степени, а крайний левый столбец содержит суммы пятых степеней, начиная с 1. Включите не менее четырех строк. (Вам потребуется как минимум семь записей во втором столбце, чтобы получить по крайней мере две копии постоянной разности, 120, в крайнем правом столбце только путем взятия разностей.) Используйте формулу Харриота для v 6 , 96 \cr}$$
Упражнение 14: Чтобы использовать метод Харриота для получения формулы для суммы первых n шестых степеней, нам потребуется как таблица постоянных разностей, так и крайний левый столбец, содержащий первые несколько сумм шестых степеней и формула для v 7 , n -я запись крайнего левого столбца восьмистолбцовой таблицы разностей констант, с точки зрения записей, p 7 , стр. 6 , P 5 , P 4 , P 3 , P 2 , P, и E, из первой строки из контейнера, P, и E, из первой строки из контейнера. стол. Напишите формулы для V 5 , V 6 и V 7 , отметив шаблон в следующих формулах для V 1 , V 2 ,
6 , P 5 , P 4 , P 3 , P 2 , P, и E, из первой строки из контейнера, P, и E, из первой строки из контейнера. стол. Напишите формулы для V 5 , V 6 и V 7 , отметив шаблон в следующих формулах для V 1 , V 2 ,
Решения для этих упражнений доступны, нажав здесь.
Суммы и разности Дискретные функции |
|
Одним из многих способов выражения суммы степеней первых n целых чисел является
с точки зрения биномиальных коэффициентов и чисел Эйлера или чисел Стирлинга. |
|
|
|
Теперь предположим, что мы пишем строку под этой последовательностью состоящий из различий между последовательными членами этой последовательности, и затем еще одна строка, состоящая из различий между последовательными терминами |
|
|
|
Элементы каждой строки могут быть выражены в виде линейного
сочетание элементов ряда под ним. |
|
|
|
Каждое из чисел второго ряда также может быть выражается как кумулятивная сумма чисел в третьей строке следующим образом: |
|
|
|
Таким образом, собирая вхождения отдельных терминов, у нас есть |
|
|
|
Повторяя этот процесс, выражая каждое число в скобки как кумулятивная сумма чисел из четвертой строки исходная таблица, получаем |
|
|
|
Объединение коэффициентов, это становится |
|
|
|
Таким образом, коэффициенты каждой строки равны
совокупные суммы справа налево предыдущих коэффициентов, и, следовательно,
это биномиальные коэффициенты. |
|
|
|
Перечислены первые несколько строк чисел Эйлера ниже. |
|
|
|
Отсюда следует, что мы можем выразить любой термин в любой из строк
выше этой строки просто как сумма биномиальных коэффициентов, умноженных на эти
Эйлеровы числа. |
|
|
|
Таким образом, сумма m-х степеней первых n целых чисел равна . |
|
|
|
Мы также сразу получаем более общий результат, дающий суммы сумм m-х степеней и суммы сумм сумм m-х степеней и так далее. Обозначим через s количество кумулятивных уровней суммирования, у нас |
|
|
|
Естественно, эти формулы с s = 0 просто дают
сами последовательности m-х степеней, а при s = 1 они дают знакомые
многочлены от сумм степеней. |
|
|
|
Исходный массив различий, который позволяет нам
выразить степени целых чисел через числа Эйлера в этом
образом, также позволяет нам выразить числа Эйлера через степени
первые целые числа. Как видно из осмотра, первое число Эйлера
в m-й строке 1, а во второй 2 |
|
|
|
и т. д., используя ту же сумму сумм шаблон, как мы делали ранее. Таким образом, первые три элемента m-й строки можно записать как |
|
|
|
Легко проверить, что этот шаблон продолжается, и в вообще числа Эйлера могут быть выражены в закрытой форме как |
|
|
|
В некотором смысле числа Эйлера играют роль, аналогичную
импульсная функция Дирака, поскольку они обеспечивают конечную импульсную последовательность
что при достаточном интегрировании дает последовательности
чистые силы, а также все накопительные суммы. |
|
Альтернативным способом выражения сумм мощностей может быть собрал, снова взглянув на массив 5-х степеней и различия. Обратите внимание на диагональную последовательность чисел, выделенную синим цветом на рисунке. ниже. |
|
|
|
Эти диагональные числа представляют собой дискретные производные кумулятивной суммы 5-х степеней (т. е. первой строки) при n = 0, и мы можем выразить эту функцию, используя дискретный аналог функции Тейлора расширение серии, которое составляет |
|
|
|
, где f (j) обозначает j-ю дискретную производную
выключенный. |
|
|
|
Следовательно, пусть f m (n) обозначает сумму m-я степень первых n натуральных чисел, мы можем записать f м (н) в форма |
|
|
|
В дополнение к рекуррентному соотношению |
|
|
|
эти числа Стирлинга также могут быть выражены в виде суммы
биномиальные коэффициенты, аналогичные приведенному выше выражению для эйлеровой
числа. |
|
|
|
Подставляя это в выражение для f m (n), получаем выражение в замкнутой форме для суммы m-х степеней первые n положительных целых чисел: |
|
|
|
Стоит отметить, что описанные выше техники
не ограничивается только последовательностями целых степеней. Можем сразу подать заявку
этот подход для определения выражения для общих сумм сумм
произвольный многочлен или степенной ряд, или даже любая произвольная функция,
хотя конечные многочлены однозначно приводят к конечным выражениям. |
|
|
|
, где c j — константы. Начиная с бесконечная строка нулей слева, значения f(0), f(1), f(3) и т. д., перечисляются в первой строке таблицы ниже, за которыми следуют строки, содержащие различия между терминами каждой последующей строки. |
|
|
|
Используя три ненулевых члена последней строки, мы можем напишите сумму |
|
|
|
Как и в случае с чистыми силами, мы можем выразить сумму этих сумм,
и так далее, используя по существу то же уравнение, но просто сдвигая
биномиальные коэффициенты. |

 Происхождение этих
формулы лучше всего описать на примере. Рассмотрим последовательность 5-го
степени целых чисел 0, 1, 2, 3, как показано ниже.
Происхождение этих
формулы лучше всего описать на примере. Рассмотрим последовательность 5-го
степени целых чисел 0, 1, 2, 3, как показано ниже. Например, следующий
значение в самой верхней строке будет 12201, что является кумулятивной суммой
числа в следующей строке, т. е. имеем
Например, следующий
значение в самой верхней строке будет 12201, что является кумулятивной суммой
числа в следующей строке, т. е. имеем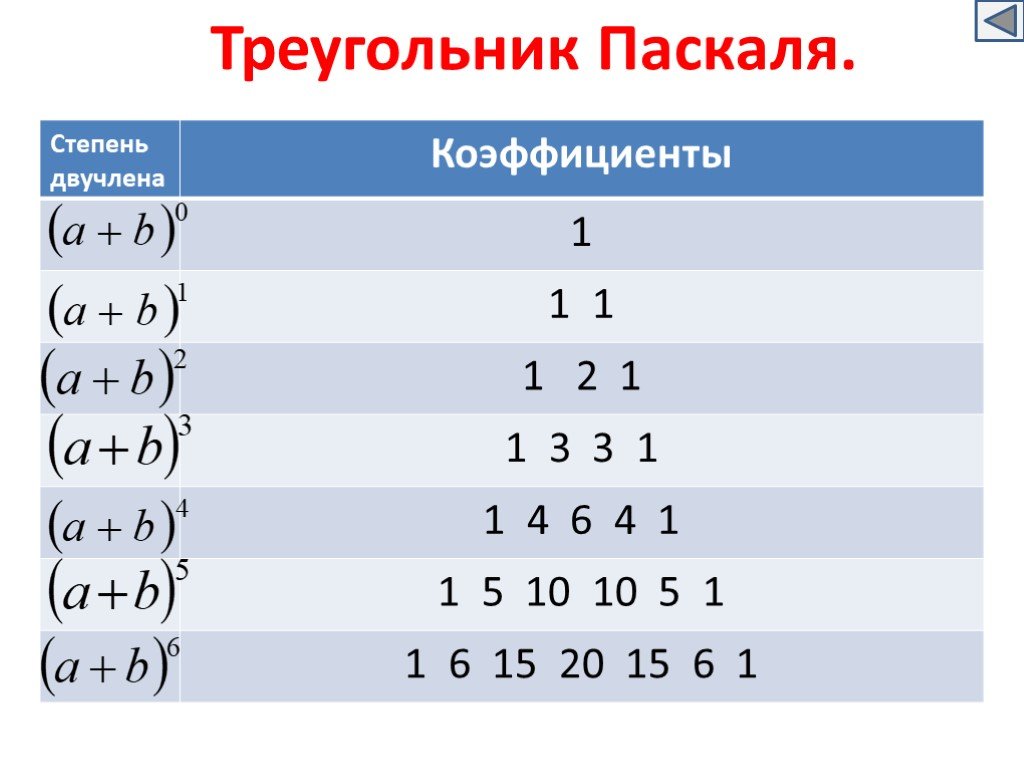 Поскольку члены каждой строки задаются формулой
полиномов в индексе, мы уверены, что в конце концов мы придем к
ряд постоянных различий за пределами некоторой точки. Например, в массиве
выше постоянная разница равна 120. Следующий ряд будет полностью состоять из
нули, за исключением некоторых ведущих ненулевых членов. В массиве выше этих
ведущими элементами являются 1, 26, 66, 26, 1, которые, конечно, являются 5-й строкой
Эйлеровы числа E m,k , который можно определить как E 1,1 = 1
и повторение
Поскольку члены каждой строки задаются формулой
полиномов в индексе, мы уверены, что в конце концов мы придем к
ряд постоянных различий за пределами некоторой точки. Например, в массиве
выше постоянная разница равна 120. Следующий ряд будет полностью состоять из
нули, за исключением некоторых ведущих ненулевых членов. В массиве выше этих
ведущими элементами являются 1, 26, 66, 26, 1, которые, конечно, являются 5-й строкой
Эйлеровы числа E m,k , который можно определить как E 1,1 = 1
и повторение
 Например, сумма пятых степеней
целые числа от 1 до n равны
Например, сумма пятых степеней
целые числа от 1 до n равны
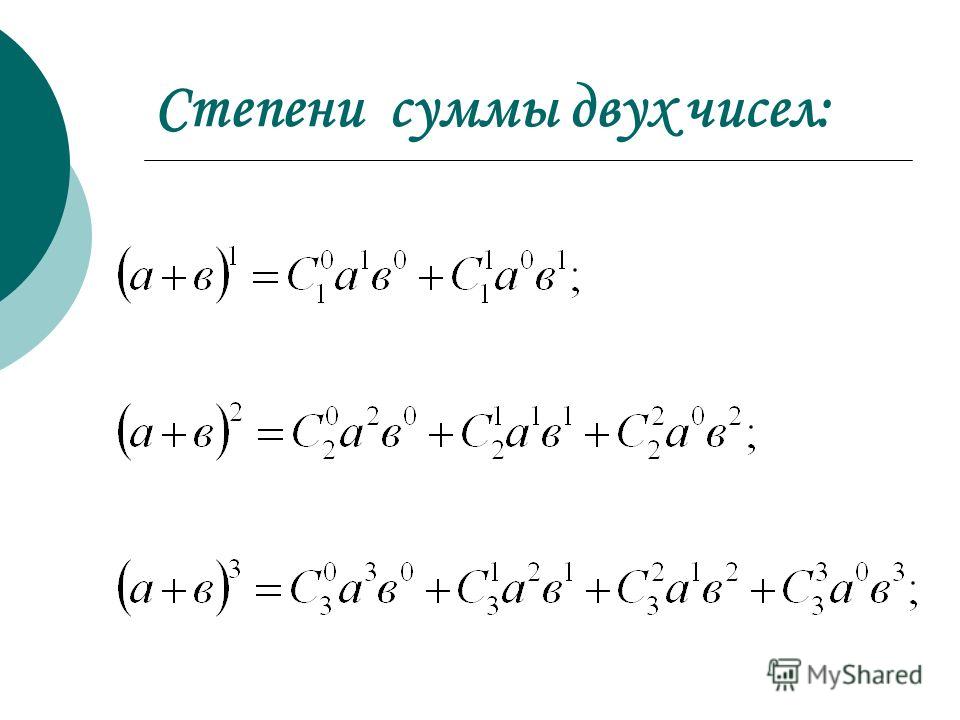 Выражения f (к) (0)/(к-1)!
известны как числа Стирлинга второго рода, которые мы будем обозначать через
S m,k , и первые несколько строк из них приведены в таблице ниже.
Выражения f (к) (0)/(к-1)!
известны как числа Стирлинга второго рода, которые мы будем обозначать через
S m,k , и первые несколько строк из них приведены в таблице ниже.
 Как простой
например, рассмотрим функцию
Как простой
например, рассмотрим функцию