РЯД.СУММ (функция РЯД.СУММ) — Служба поддержки Office
В этой статье описаны синтаксис формулы и использование функции РЯД.СУММ в Microsoft Excel.
Описание
Многие функции могут быть аппроксимированы разложениями в степенные ряды.
Возвращает сумму степенного ряда, вычисленную по формуле:
Синтаксис
Аргументы функции РЯД.СУММ описаны ниже.
-
x Обязательный. Значение переменной степенного ряда.
-
n Обязательный. Показатель степени x для первого члена степенного ряда.
-
m Обязательный. Шаг, на который увеличивается показатель степени n для каждого следующего члена степенного ряда.
-
Коэффициенты Обязательный. Набор коэффициентов при соответствующих степенях x. Количеством значений в аргументе «коэффициенты» определяется количество членов степенного ряда. Например, если в аргументе «коэффициенты» три значения, то степенной ряд содержит три слагаемых.
Замечание
Если какой-либо из аргументов не является числом, функция РЯД.СУММ возвращает значение ошибки #ЗНАЧ!.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
Данные | ||
|---|---|---|
|
Коэффициенты в виде чисел |
Коэффициенты в виде формулы |
|
|
0,785398163 |
=ПИ()/4 |
|
|
1 |
1 |
|
|
-0,5 |
=-1/ФАКТР(2) |
|
|
0,041666667 |
=1/ФАКТР(4) |
|
|
-0,001388889 |
=-1/ФАКТР(6) |
|
|
Формула |
Описание (результат) |
Результат |
|
=РЯД.СУММ(A3;0,2;A4:A7) |
Аппроксимация косинуса ПИ/4 радиан или 45 градусов (0,707103) |
0,707103 |
§4. Приближенное вычисление суммы числового ряда.
Поскольку точное значение суммы ряда удается вычислить далеко не всегда (такие задачи были нами рассмотрены), возникает проблема приближенного вычисления суммы ряда с заданной точностью.
Напомним, что 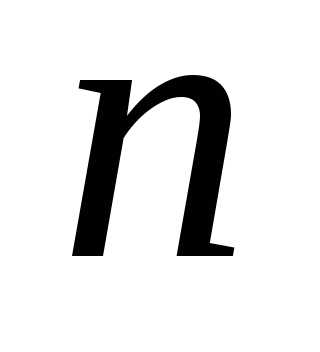 -ый
остаток ряда
-ый
остаток ряда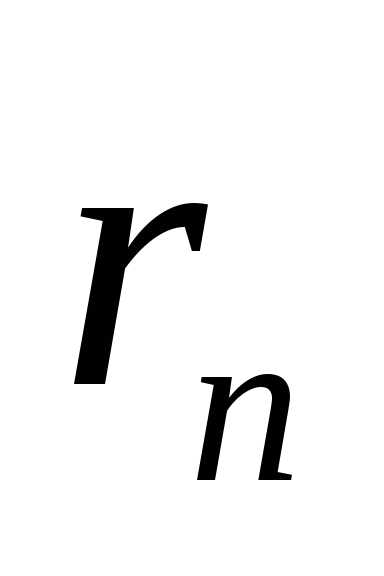 получается из исходного ряда
получается из исходного ряда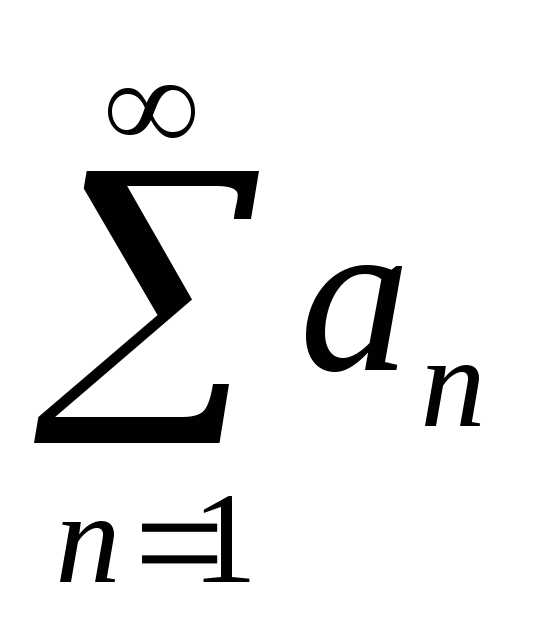 отбрасыванием первых
отбрасыванием первых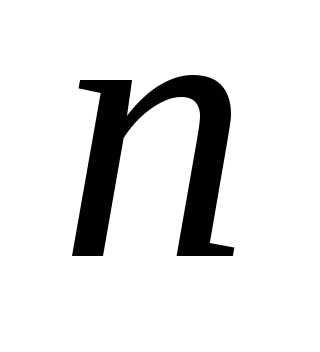 слагаемых:
слагаемых:
.
Тогда, поскольку для сходящегося ряда 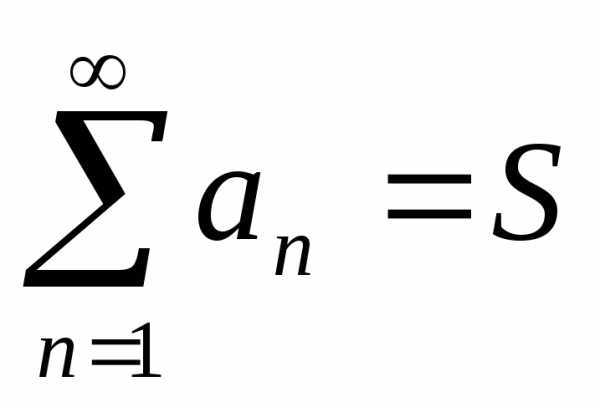
остаток сходящегося ряда равен разности
между суммой ряда и 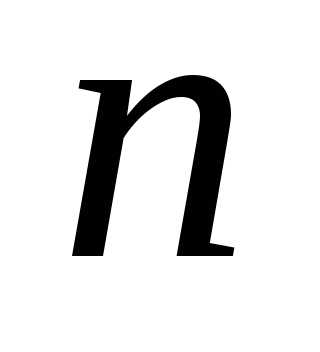 -ой
частичной суммой:
-ой
частичной суммой:
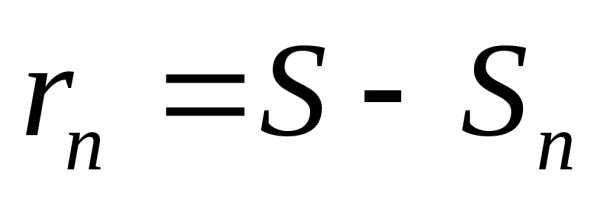 ,
,
и для достаточно больших 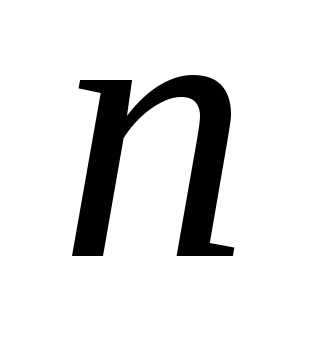 имеем
приближенное равенство
имеем
приближенное равенство
 .
.
Из определения остатка ряда следует,
что абсолютная погрешность при замене
точного неизвестного значения суммы  его частичной суммой
его частичной суммой равна модулю остатка ряда:
равна модулю остатка ряда:
.
Таким образом, если требуется вычислить
сумму ряда с заданной точностью  ,
то нужно оставить сумму такого числа
,
то нужно оставить сумму такого числа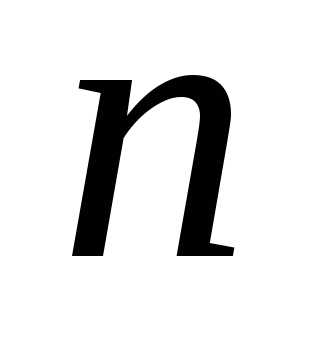
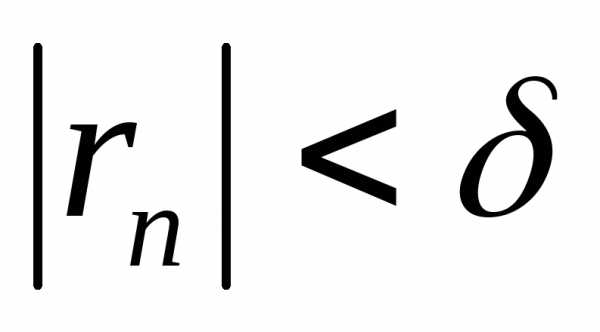 .
.
Метод приближенного вычисления суммы выбирается в зависимости от вида ряда:
если ряд положительный и может быть исследован на сходимость по интегральному признаку (удовлетворяет условиям соответствующей теоремы), то для оценки суммы используем формулу
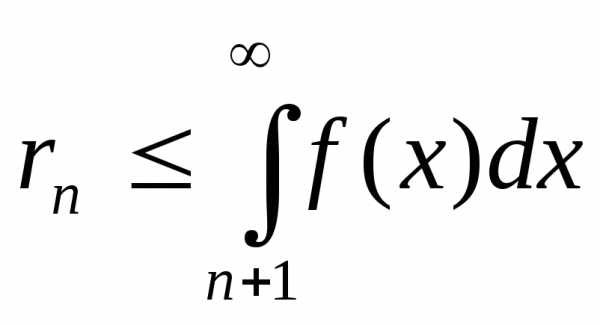 ;
;
если это ряд Лейбница, то применяем оценку:
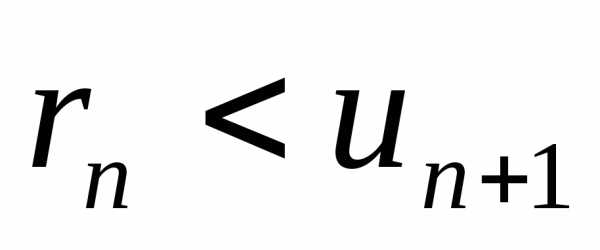 .
.
В других задачах можно использовать формулу суммы бесконечно убывающей геометрической прогрессии.
Задача №1. Сколько нужно взять
слагаемых ряда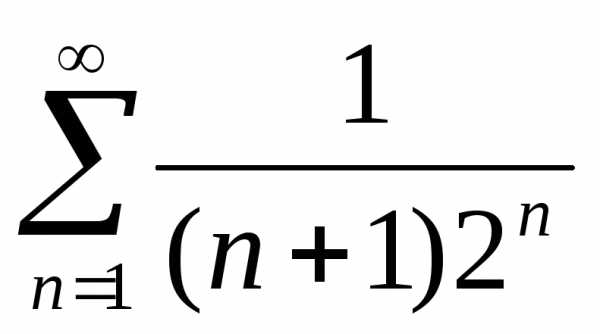 ,
чтобы получить его сумму с точностью
0,01.
,
чтобы получить его сумму с точностью
0,01.
Решение.Прежде всего отметим, что
данный ряд сходится. Рассмотрим
.
Оценим этот ряд с помощью бесконечно
убывающей геометрической прогрессии.
Для этого заменим в каждом слагаемом
множитель  на
на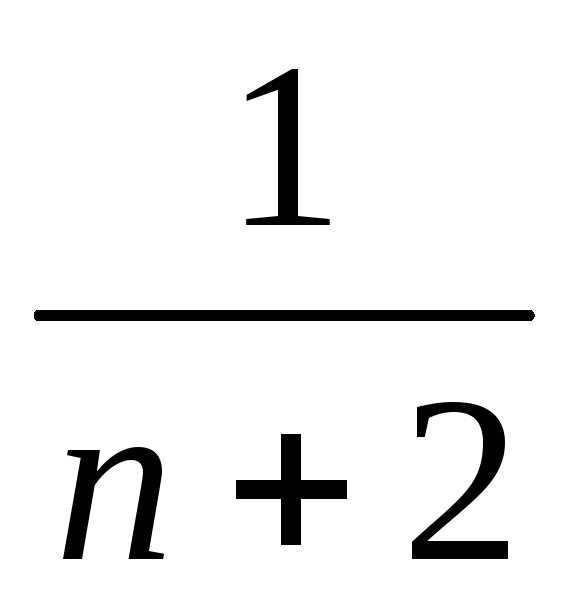 ,
при этом каждое слагаемое увеличится:
,
при этом каждое слагаемое увеличится:
После вынесения общего множителя за скобку, в скобке остался ряд, составленный из членов бесконечно убывающей геометрической прогрессии, сумму которого мы и вычислили по формуле
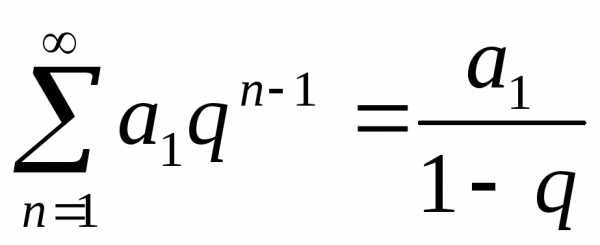 .
.
Заданная точность будет достигнута,
если 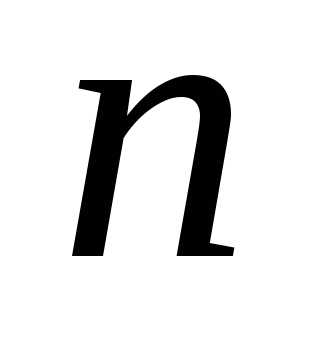 будет удовлетворять условию
будет удовлетворять условию
.
Решим неравенство, учитывая, что 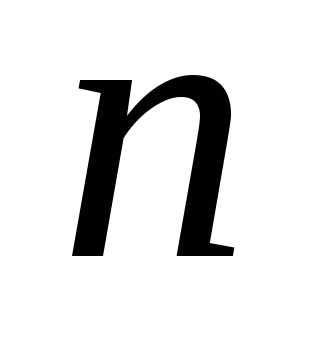
При 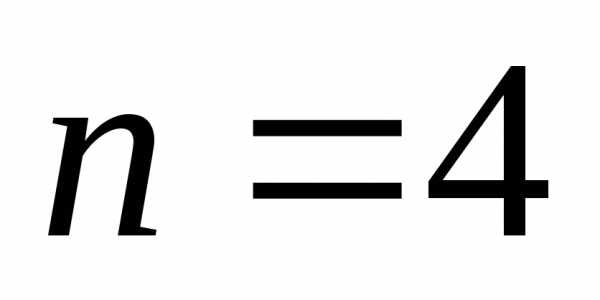 имеем
имеем
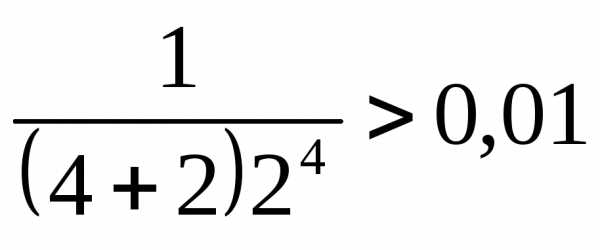 .
.
При 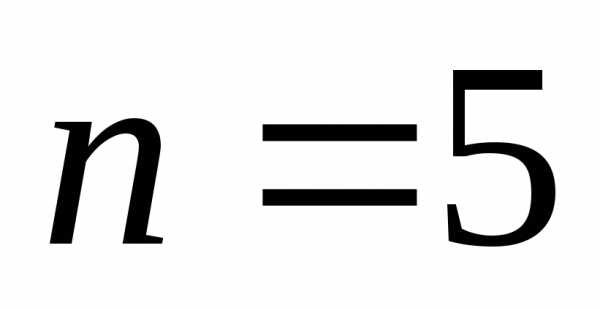 имеем
имеем
.
В силу монотонности функции 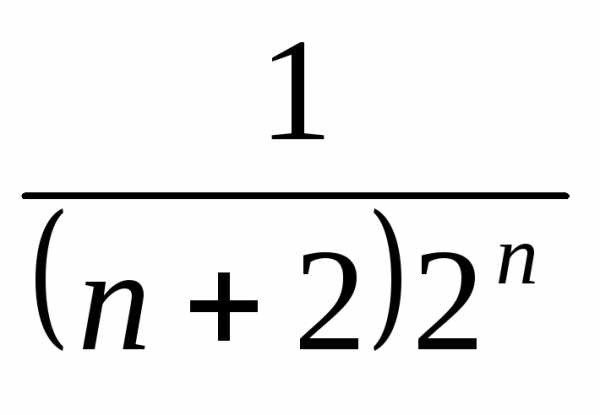 ,
неравенство
,
неравенство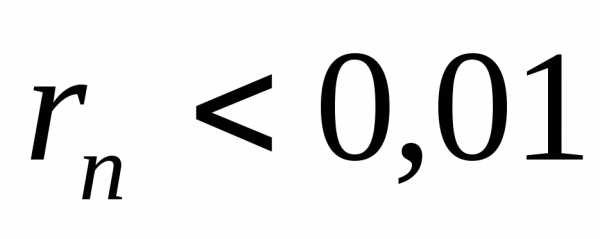 будет выполняться для всех
будет выполняться для всех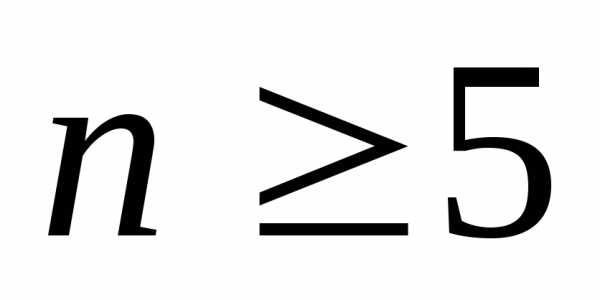 .
.
Следовательно, если вместо точного значения суммы мы возьмем первые пять (или более) слагаемых, то погрешность вычислений не превысит 0,01.
Ответ: 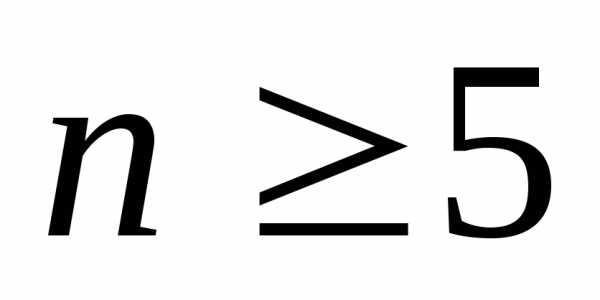 .
.
Задача №2. Оценить ошибку, получаемую
при замене суммы ряда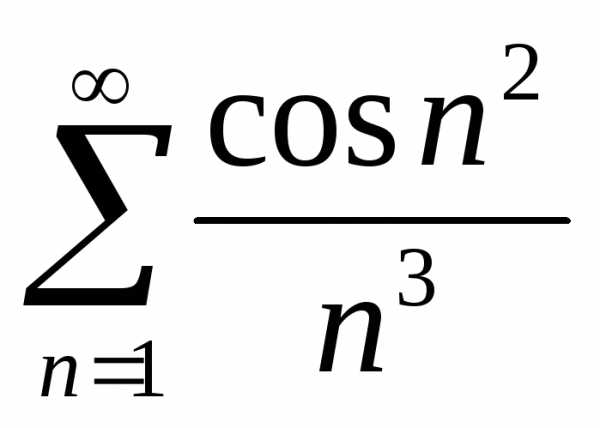 суммой
первых 100 слагаемых.
суммой
первых 100 слагаемых.
Решение.Заметим, что данный ряд
является сходящимся и знакопеременным.
Оценивать будем ряд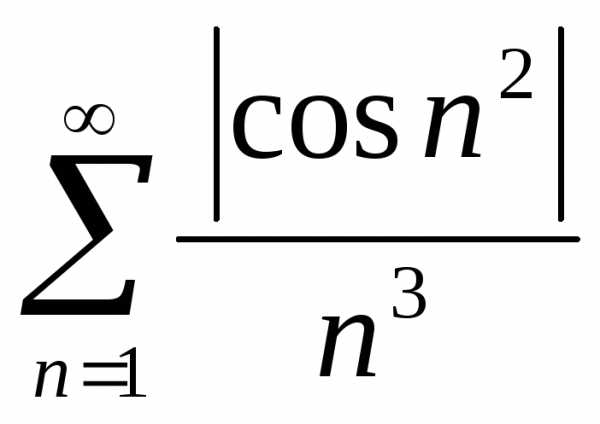
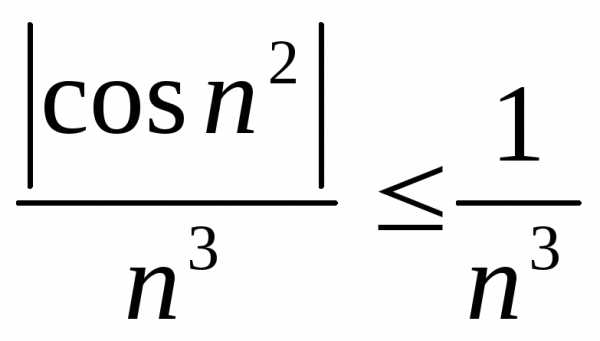 .
.
Рассмотрим ряд 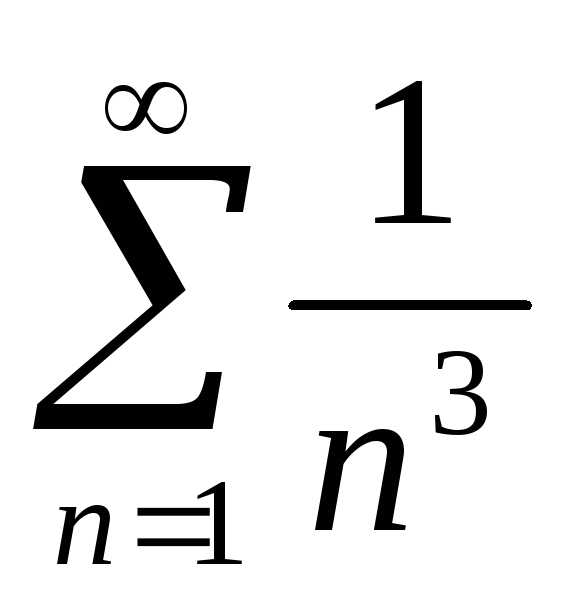 .
Поскольку этот ряд удовлетворяет
условиям теоремы – интегрального
признака сходимости, то для оценки
погрешности вычисления суммы используем
соответствующую формулу:
.
Поскольку этот ряд удовлетворяет
условиям теоремы – интегрального
признака сходимости, то для оценки
погрешности вычисления суммы используем
соответствующую формулу:
.
Вычислим несобственный интеграл:
,
погрешность вычислений можно оценить по формуле
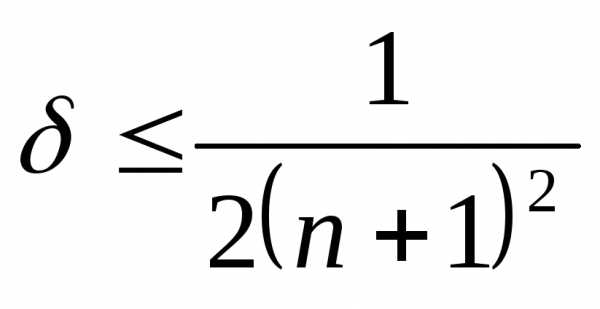 ,
,
по условию 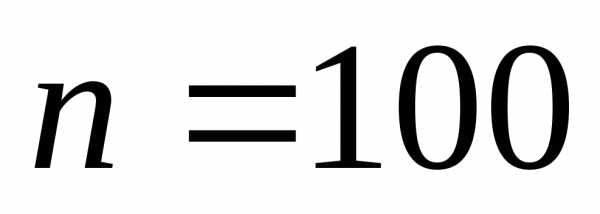 ,
тогда.
,
тогда.
Ответ: 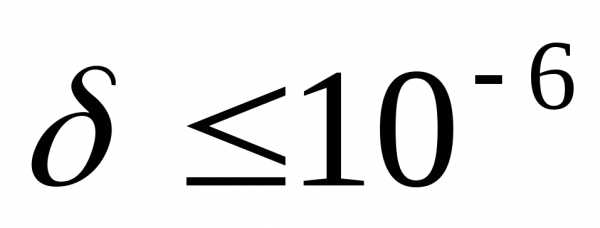
Задача №3. Оценить ошибку,
получаемую при замене суммы ряда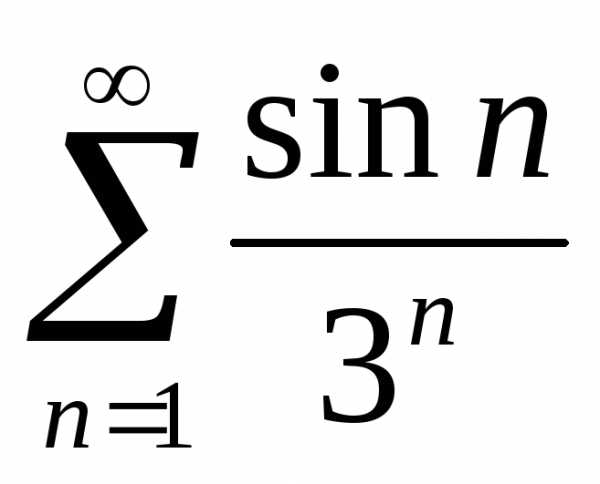 суммой
первых 10 слагаемых.
суммой
первых 10 слагаемых.
Решение.Подчеркнем еще раз, что задача о приближенном вычислении суммы имеет смысл только для сходящегося ряда, поэтому, прежде всего отметим, что данный ряд сходится. Поскольку исследуемый ряд является знакопеременным со сложным правилом изменения знака, то оценивать придется, как и в предыдущем примере, ряд из модулей данного ряда:
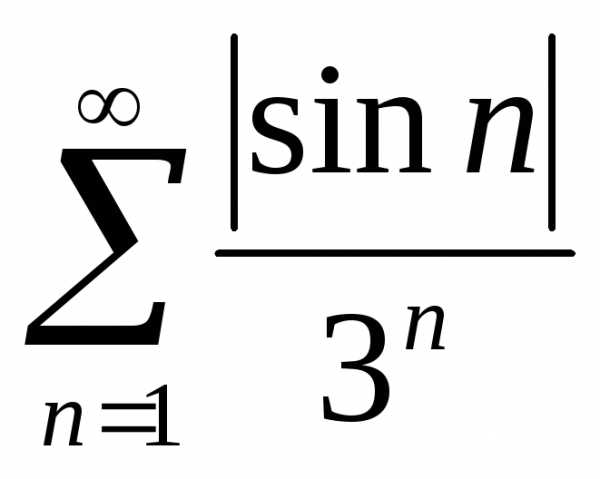 .
.
Используя тот факт, что при любом значении аргумента, имеем:
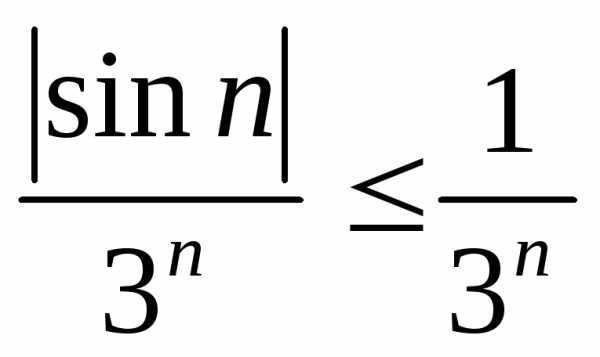 .
.
Оценим остаток ряда:
.
Мы получили ряд, составленный из членов бесконечно убывающей геометрической прогрессии, в которой
 ,
,
его сумма равна:
,
.
Ответ:  .
.
Задача №4. Вычислить сумму ряда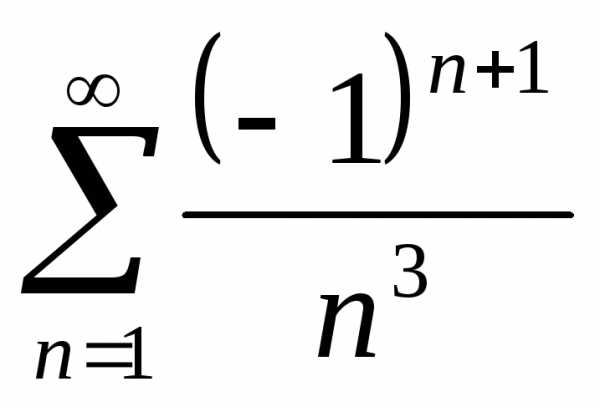 с
точностью 0,01.
с
точностью 0,01.
Решение.Данный ряд является рядом Лейбница. Для оценки погрешности верна формула:
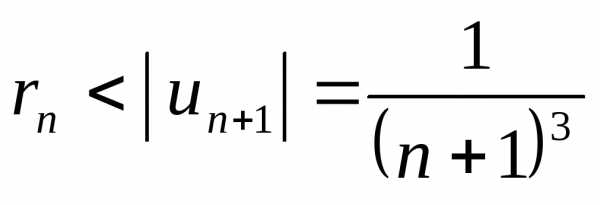 ,
,
другими словами, погрешность вычислений
меньше модуля первого отброшенного
слагаемого. Подберем номер 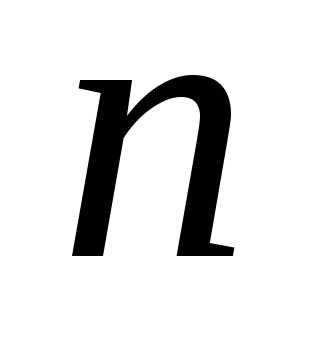 так, чтобы
так, чтобы
.
При 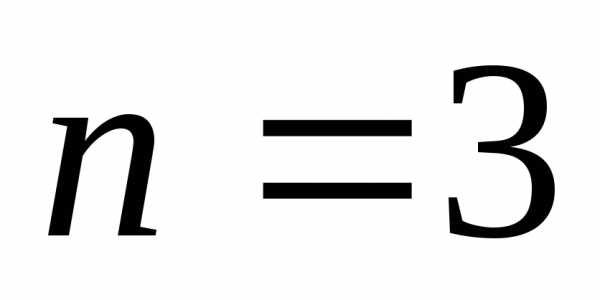 имеем
имеем
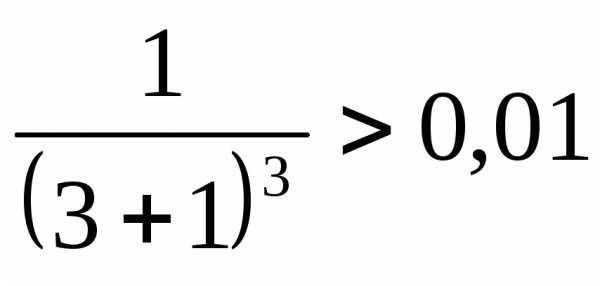 .
.
При 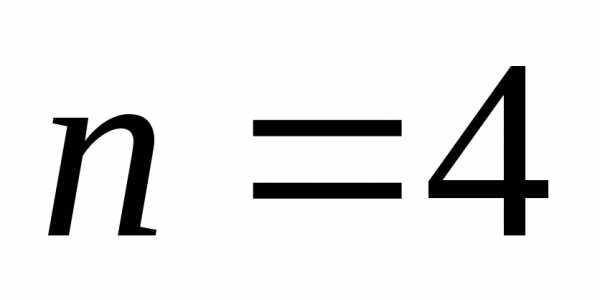 имеем
имеем
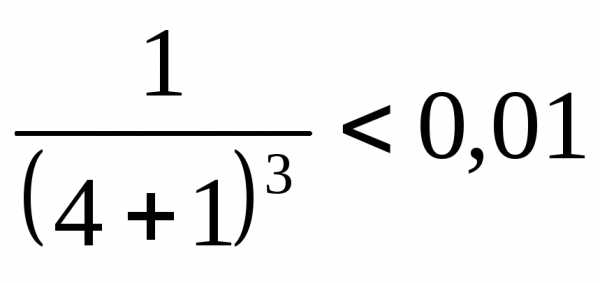 .
.
Погрешность 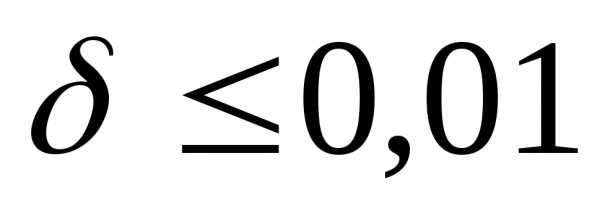 ,
если в качестве значения суммы возьмем
сумму первых четырех слагаемых:
,
если в качестве значения суммы возьмем
сумму первых четырех слагаемых:
.
Ответ:.
studfiles.net
Примеры числовых рядов. Вычисление суммы ряда — МегаЛекции
Основные понятия и определения
Пусть задана бесконечная числовая последовательность :
, … (1.1)
В прошлом году мы определяли числовую последовательность как функцию натурального аргумента. Это означает, что каждый член последовательности является функцией своего номера п: . В дальнейшем иногда будем рассматривать и п, равное нулю, поэтому числовую последовательность будем определять как функцию целочисленного аргумента (от слов «целое число»).
Определение 1. Выражение
(1.2)
называется бесконечным числовым рядом, или, короче, рядом. Члены последовательности ,… называются членами ряда; выражение с индексом п— общим членом ряда.
Отличить последовательность от ряда просто: члены последовательности пишутся через запятую, члены ряда соединены знаками плюс.
Таким образом, понятие ряда является обобщением суммирования на случай бесконечного числа слагаемых.
Ряд считается заданным, если известна (задана) формула его общего члена. Общий член ряда (1.2) совпадает с общим членом последовательности (1.1) и также является функцией целочисленного аргумента n, т.е. . Например, если задан общий член в виде
, (1.3)
то, полагая в этой формуле n = 1, 2, 3,…, можно найти любой член ряда, а тем самым и весь ряд:
— члены последовательности или члены ряда,
(1.4)
-числовой ряд.
Определение. Сумма n первых членов ряда называется n-ой частичной суммой ряда и обозначается символом :
. (1.5)
Можно записать так: .
В частности,
,
. (1.6)
Составим из всех частичных сумм ряда (1.2) числовую последовательность :
(1.7)
Она называется последовательностью частичных сумм. Как всякая числовая последовательность, она может иметь предел, т.е. сходиться, или не иметь предела, т.е. расходиться. Предел последовательности частичных сумм, если он существует, будем обозначать буквой S.
Определение. Ряд называется сходящимся (ряд сходится), если сходится последовательность частичных сумм этого ряда. При этом предел S последовательности частичных сумм называется суммой данного ряда, т.е.
. (1.8)
Для сходящегося ряда, имеющего сумму S, можно формально записать равенство:
. (1.9)
Ряд, не имеющий суммы (1.8), называют расходящимся. В частности, если , то говорят, что ряд расходится к , и в этом случае используют символическое равенство
.
Замечание.Из равенства (1.6) следует, что любой член ряда можно представить как разность частичных сумм и :
. (1.10)
Изобразим геометрически последовательность частичных сумм. На рис.1.1,а и б ряд сходится, на рис.1.1,в — расходится.
|
|
в)
|
Рис.1.1
Замечание 3. Иногда номер члена ряда начинается с нуля: .
Примеры числовых рядов. Вычисление суммы ряда
Пример 1º.
1 + 1 + 1 + . . . + 1 + . . .
Здесь , .
Данный ряд расходится Þ 1 + 1 + 1 + . . . + 1 + . . .=+¥.
Пример 2º.
Как обычно, чередование знаков + и — задается с помощью степени (-1). Здесь последовательность частичных сумм имеет вид:
т.е. значение частичной суммы зависит от чётности номера п:
Таким образом, чётные и нечётные частичные суммы стремятся к двум различным пределам:
чётные к нулю, нечётные — к единице:
|
Рис.1.2
Следовательно, последовательность не имеет предела, и данный ряд расходится.
Пример 3º.
1 + 2 + 3 + … + n + …
Это арифметическая прогрессия с разностью . Напомним, что название «арифметическая» происходит оттого, что каждый член этой прогрессии, начиная со второго, равен среднему арифметическому соседних с ним членов:
.
В данной прогрессии , а последовательность частичных сумм имеет вид:
Найдем предел .
Следовательно, данный ряд расходится Þ 1 + 2 + 3 + … + n + …=+¥.
Пример 4º.
Здесь общий член ряда можно преобразовать, разложив на простейшие дроби:
.
Тогда ряд примет вид:
Вычислим частичную сумму, раскрыв скобки:
Предел последовательности частичных сумм
Þ сумма ряда конечна, т. е. ряд сходится Þ
=1.
Пример 5º.
.
Вывод будет дан ниже. Этот ряд называется рядом Лейбница.
Пример 6º.
.
Вывод будет дан ниже. Здесь в знаменателе только нечётные числа.
Пример 7º.
. Вывод будет дан ниже.
Пример 8º.
Вывод будет дан ниже. Сумма ряда равна числу е — основанию натурального логарифма.
Сумму ряда вычислить не всегда легко и даже не всегда возможно. Поэтому в теории рядов чаще решается более простая задача — выяснение, сходится ряд или расходится. Это называется исследованием сходимости ряда.
Рекомендуемые страницы:
Воспользуйтесь поиском по сайту:
megalektsii.ru
Метод суммирования расходящихся рядов путем сведения к повторному ряду
В статье представлены формулы и методы нахождения обобщенных сумм знакопеременных рядов, в основном расходящихся, путем преобразования к повторным рядам вложенного типа.
Общий вид повторных рядов вложенного типа:
Расходящиеся знакопеременные ряды можно классифицировать по таким трем классам:
1. Ряды с постоянным радиусом обвертывания:
Сумма такого ряда равна , этот результат достигается многими методами, которые, в силу их известности, демонстрировать в данной статье нет смысла.
2. Ряды с ограниченным радиусом обвертывания: , где
На пример ряд: , его обобщенной суммой будет
3. Ряды с бесконечным радиусом обвертывания: , где
Самым известным таким рядом является:
Формула 1:
Доказательство:
Пусть — абсолютно сходящийся ряд. Тогда по известной теореме, если некоторый ряд сходится абсолютно, то и любой повторный ряд, составленный из его членов в произвольном порядке, сходится, и притом к той же сумме. И наоборот; абсолютная сходимость повторного ряда ведет за собою абсолютную сходимость одинарного, составленного из его членов и при том к той же сумме.
Далее, пусть ряд сходится не абсолютно, либо и вовсе расходится. По равенству в доказательстве, любой член ряда будет полностью просуммирован после начала суммирования -го ряда в двойном ряде , т. е. ряда .
Тогда каждому возрастанию номера будет отвечать факт следующего полностью просуммированного члена ряда
Исходя из этого, ряд, у которого сумма преобразится в ряд с аналогичной суммой: , а знакопеременный ряд с некоторой обобщенной суммой будет преобразован в ряд с такой же суммой. Этим доказательство завершается.
Следствие 1.1:
Следствие 1.2:
Следствие 1.3:
Наглядно, формула 1 представляет собою преобразование ряда в сумму бесконечного количества рядов , каждый последующий из которых лишен первого члена в сравнении с предыдущим:
Пусть рядсходится к сумме (сумма может быть и обобщенной). Тогда нетрудно заметить, что , ,…, .
Самым простым применением формулы 1 может быть суммирование ряда ;
Следующим применением формулы 1 есть суммирование ряда:
Так как , то
Исходя из этого,
Следует заметить, что хоть формула 1 с ее следствиями, знакопеременный ряд с некоторой обобщенной суммой преобразует в ряд с такой же суммой, но радиус обвертывания при этом может и не совпадать. Первым примером того будет суммирование по формуле 1, ряда:
В данном случае для отыскания суммы, ряд с бесконечным радиусом обвертывания был преобразован в ряд, у которого радиус обвертывания есть число постоянное.
Вторым примером может быть ряд . Применение к нему следствия 1.1, которое является частным случаем формулы 1, дает равенство:
Ряд имеет постоянный радиус обвертывания, следственно имеет лишь обобщенную сумму, в то время как ряд в последнем равенстве справа сходится, и соответственно имеет радиус обвертывания равный нулю.
Формула 2: ,
где — разностный оператор: , рядсходится, либо является знакопеременным и имеет обобщенную сумму.
Доказательство:
В силу того, что:
,
и учитывая, что сумма не зависит от обозначения переменной суммирования:
,
изначальную сумму можно представить в виде:
, (1*)
где — антиразностный оператор от :
Равенство (1*) может быть представлено в виде:
(2*)
Равенство (2*) является полностью аналогичным требуемой формуле:
В силу того, что абсолютная сходимость ряда влечет за собой и абсолютную сходимость любого повторного ряда, составленного из его членов в произвольном порядке, и притом к той же сумме; формула 2, в случае абсолютно сходящегося ряда, является оправданной. В противном случае рассуждения аналогичны с доказательством формулы 1, которая является частным случаем формулы 2 при . Этим доказательство и завершается.
Обобщением формулы 2 является
Формула 3:
Доказывается аналогично формуле 2.
Формулы: 2 и 3, как и формула 1, действительны и в случае, когда — знакопеременный сходящийся, либо знакопеременный расходящийся ряд с некоторой обобщенной суммой , что будет более детально показано ниже. Если в формулах 2 и 3 за последовательность принять последовательность знакопеременного расходящегося ряда первого типа по классификации, а за принять оставшуюся часть ряда, то при преобразованиях 2 и 3, знакопеременный расходящийся ряд переходит в знакопеременный расходящийся ряд, а обобщенная сумма не нарушится. Далее будут показаны такие случаи.
Формула 4:
Доказательство: по формуле 3, полагая , выходит равенство
(3*)
Так как ,
то две суммы справа в равенстве (3*) будут соответственно иметь вид:
и аналогично:
Если подставить оба результата в равенство (3*), то и выйдет требуемая формула
Общая формула 4:
Формула 4, вместе с ее общим вариантом, действительна и в случае сходящегося знакопеременного ряда , так как он представляет частный случай знакопеременного ряда, а именно ряда, у которого радиус обвертывания приближается к нулю.
В формуле 4 был использован тот факт, что сумма ряда , поэтому она дает нахождение суммы знакопеременного ряда только в ее обобщенном смысле и, не дает никаких сведений о его сходимости или расходимости. Но последнее определяется легко, путем дополнительного анализа.
При этом ряд, преобразованный по формуле 4 или ее общим вариантом, может оказаться как суммируемым обобщенно, так и сходящимся.
Формула 4 позволяет находить обобщенные суммы некоторых видов:
4.1 Нахождение суммы вида:
(В этом пункте и далее будет произвольным вещественным числом, большим нуля)
По формуле 4:
Если положить: , то выйдет легко разрешимое уравнение
, его решением будет:
Возвращение к подстановке приводит к окончательному результату:
Формула 4.1:
Следствие 4.1.1:
Данное следствие примечательно тем, что служит доказательством равенства .
Выводится достаточно просто:
Отсюда, в частности, выходит обобщенная сумма хорошо известного расходящегося ряда
Дальнейшие два следствия формулы 4.1 выводятся заменой на
Следствие 4.1.2:
Следствие 4.1.3:
Оба последних следствия при представляют собой формулы нахождения сумм абсолютно сходящихся знакопеременных рядов.
4.2 Нахождение обобщенной суммы:
Действия аналогичны; по формуле 4 для данного ряда будет справедливо равенство:
Полагая , и учитывая что , выходит уравнение:
, из чего следует
Формула 4.2:
Следствие 4.2.1:
4.3 Нахождение обобщенной суммы:
Очевидно, что , т. е. отсчет суммирования может быть начат с единицы.
Применив формулу 4, переводя для удобства отсчет суммы с единицы, выходит
Второе слагаемое справа равно нулю, а первая сумма справа выводится из известной формулы:
При логарифмировании обеих частей последнего равенства выходит результат:
,
или
;
тогда искомая сумма будет представлена следующей формулой:
Формула 4.3:
Данный результат может быть также представлен в виде:
4.4 Нахождение обобщенной суммы:
Применяя формулу 4,
Как известно, , из чего следует:
4.5 Общая рекуррентная формула нахождения сумм вида: ,
где — натуральное число.
Формула 4.5:
Эта формула может быть представлена в таких видах:
—
—
—
Последний вариант наиболее пригоден к вычислению.
Доказательство формулы 4.5: По формуле 4, будет справедливым равенство:
,
из чего следует:
При раскрытии скобок во всем равенстве и переносе из левой части равенства все слагаемые в правую, кроме , выходит:
Исходя из того, что , последнее равенство может быть окончательно представлено в виде требуемой формулы:
Этим доказательство и завершается.
С помощью рекуррентной формулы 4.5 легко вычислить обобщенные суммы следующих известных расходящихся рядов:
4.5.1:
4.5.2:
4.5.3:
4.5.4:
4.6 Рекуррентная формула для обобщенной суммы вида:
Формула 4.6:
Доказательство:
Если положить:
,
то выйдет уравнение: , решение которого:
Возвращая и их ранее подставленные значения, легко прийти к окончательной формуле.
Ранее было показано, что
С помощью последней выведенной рекуррентной формулы можно получить уже ранее выведенный результат:
Формула 5:
Доказательство: Сначала следует доказать, что ряд:
, имеет обобщенной суммой число .
Методом средних арифметических легко выводиться известная формула:
Тогда:
Аналогично, тем же методом выводится известная формула:
Пусть , тогда
Стало быть,
(4*)
Тогда по формуле 2:
(5*)
Так как , то
,
и тогда все с непарными номерами , в первой из сумм справа в равенстве (5*) будут произведены на , следовательно равняться нулю.
Второе слагаемое справа, в равенстве (5*), ввиду равенства (4*), будет равно
Исходя из этого, равенство (5*) примет вид:
, что и требовалось доказать.
Формула 5 так же имеет множество применений:
Формула 5.1:
Выводится просто; по формуле 5:
(6*)
Ранее уже была выведена формула: , для всех вещественных .
Если в ней положить , то правильность данной формулы при этом не изменится.
И тогда сумма будет равна ,
Это дает возможность равенство (9*) представить в виде
,
а затем, путем элементарных преобразований получить окончательный результат.
Формула 5.1 может быть представлена более наглядно в виде:
5.2 Нахождение обобщенной суммы вида:
Формула 5.2:
Выводится аналогично; по формуле 5:
После элементарных преобразований легко получить требуемую формулу.
5.3 Нахождение обобщенной суммы ряда:
По формуле 5:
Обобщенная формула 5:
Ее доказательство аналогично формуле 5, отличие лишь в том, что за основу берется формула 3.
5.4 Частный вид обобщенной формулы 5
Данная формула выводится подобно предыдущим:
Разложение аналогичным образом по степеням множителя в последнем равенстве, в выражении слева, дает возможность сократить обе части равенства на слагаемое:
Тогда, после перегруппировки, последнее равенство будет иметь вид:
Из этой формулы, в частности, при , и выходит ранее полученный результат:
При :
Формула 5.5:
Выводится аналогично предыдущим случаям из обобщения формулы 5:
В силу равенства:, легко прийти к требуемой формуле.
К примеру,
Формула 6 (общая рекуррентная формула суммирования расходящихся рядов):
,
где — уже вычисленная разность от : ,
— такой множитель, что при суммировании некоторого ряда , его суммирование происходит следующим образом: первая частичная сумма положительна, вторая частичная сумма:отрицательна, третья: положительна и т. д.
Выводится эта формула подобно формулам 4 и 5 на основе тех же соображений.
Так как обобщенная сумма ряда: , что может быть легко доказано методом средних арифметических, то формула 2 может быть применена и на этот более общий случай.
Более краткая интерпретация формулы 6 имеет вид:
Очевидно, при и из этой формулы следуют формула 4 и формула 5 соответственно.
К примеру, пусть требуется просуммировать ряд:
В данном случае, в операторе , будет , так как первые три члена положительны, далее идут три члена с отрицательным знаком, далее три с положительным и т. д.
Разность вычисляется легко: , тогда по общей формуле:
Более общий вариант формулы 6:
Его частные случаи будут иметь вид:
1.
2.
3.
Из первой формулы, в частности, при выходит результат ,
а именно:
Первые две формулы можно представить в более удобным для вычисления виде:
1.
2.
Этими тремя формулами вопрос о суммировании расходящихся рядов трех видов:
,, исчерпывается полностью.
moluch.ru
сумма ряда | C++ для приматов
Условие задачи:
Найти сумму сходящегося ряда:
[latex]\frac{1}{1 \cdot 2} + \frac{1}{2 \cdot 3} + \frac{1}{3 \cdot 4} + … + \frac{1}{n(n + 1)} + …[/latex]
Входные данные:
Целое число [latex]n[/latex] — номер искомой частичной суммы.
Выходные данные:
Искомая частичная сумма.
Тесты:
| № | Вход | Выход |
|---|---|---|
| 1 | 1 | 0.5 |
| 2 | 500 | 0.998004 |
| 3 | 100000 | 0.999965 |
Код на языке C++ (первый вариант):
#include <iostream> using namespace std; int main() { int n; double S = 0; cin >> n; for (int i = 1; i <= n; i++){ S += 1.0/(i*(i + 1)); } cout << S; return 0; } |
Код на языке Java (первый вариант):
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
import java.util.*; import java.lang.*; import java.io.*;
class Main { public static void main (String[] args) throws java.lang.Exception{ Scanner in = new Scanner(System.in); PrintWriter out = new PrintWriter(System.out); int n; n=in.nextInt(); double S = 0; for (int i = 1; i <= n; i++){ S += 1.0/(i*(i + 1)); } System.out.println(S); } } |
Код на языке C++ (второй вариант):
#include <iostream> using namespace std; int main() { int n; double S = 0; cin >> n; S = 1-(1/n); cout << S; return 0; } |
Код на языке Java (второй вариант):
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
import java.util.*; import java.lang.*; import java.io.*;
class Main { public static void main (String[] args) throws java.lang.Exception { Scanner in = new Scanner(System.in); PrintWriter out = new PrintWriter(System.out); int n; n=in.nextInt(); double S = 0; S=1-(1/n); System.out.println(S); } } |
Решения:
Вариант первый (решение с циклом): Зададим цикл с счетчиком [latex]i[/latex] от 1 до заданного пользователем числа [latex]n.[/latex] Именно такое количество необходимых слагаемых [latex]\frac{1}{n(n + 1)}[/latex] будет найдено на каждом шаге цикла для последующего суммирования и нахождения искомой частичной суммы.
Вариант второй (решение без цикла): Ряд сводится к ряду: [latex](1 — \frac{1}{2}) + (\frac{1}{2} — \frac{1}{3}) + … + (\frac{1}{n} — \frac{1}{n + 1})[/latex]. От сюда имеем: [latex]1 — \frac{1}{n + 1}.[/latex]
Ссылки:
Условие задачи (стр.248).
Первый вариант C++ .
Первый вариант Java .
Второй вариант C++ .
Второй вариант Java .
Задача
Исследовать сходимость ряда [latex]\sum_{n=1}^{\infty}\frac{ln(n!)}{n^{a}}[/latex] и вычислить его сумму при заданной точности.
Входные данные
Натуральное число [latex]a[/latex]
Выходные данные
Сумма ряда если она существует.
Тесты
| входящие данные | выходящие данные |
| 2 | -nan |
| 3 | 0.578615 |
| 6 | 0.0146958 |
| 12 | 0.000172786 |
| 22 | 1.65259e-07 |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
#include <cmath> #include <iostream> using namespace std; int poww(int a,int n) { return (!n)?1:a*poww(a,n-1); } int main() { int a; cin>>a; //ряд будет сходящимся только при a>2 double s=0; long double f=1; double e=10; for(int n=2;e>0.000001;n++){ f*=n; s+=log(f)/poww(n,a); e=log(f)/poww(n,a); } cout<<s; return 0;
} |
Решение задачи
Исследуем ряд на сходимость при различных значениях переменных [latex]a[/latex]. При [latex]a\leq 1[/latex] случай тривиальный — ряд будет расходиться.
Рассчит
cpp.mazurok.com
Примеры числовых рядов. Вычисление суммы ряда
Поиск ЛекцийОсновные понятия и определения
Пусть задана бесконечная числовая последовательность :
, … (1.1)
В прошлом году мы определяли числовую последовательность как функцию натурального аргумента. Это означает, что каждый член последовательности является функцией своего номера п: . В дальнейшем иногда будем рассматривать и п, равное нулю, поэтому числовую последовательность будем определять как функцию целочисленного аргумента (от слов «целое число»).
Определение 1. Выражение
(1.2)
называется бесконечным числовым рядом, или, короче, рядом. Члены последовательности ,… называются членами ряда; выражение с индексом п— общим членом ряда.
Отличить последовательность от ряда просто: члены последовательности пишутся через запятую, члены ряда соединены знаками плюс.
Таким образом, понятие ряда является обобщением суммирования на случай бесконечного числа слагаемых.
Ряд считается заданным, если известна (задана) формула его общего члена. Общий член ряда (1.2) совпадает с общим членом последовательности (1.1) и также является функцией целочисленного аргумента n, т.е. . Например, если задан общий член в виде
, (1.3)
то, полагая в этой формуле n = 1, 2, 3,…, можно найти любой член ряда, а тем самым и весь ряд:
— члены последовательности или члены ряда,
(1.4)
-числовой ряд.
Определение. Сумма n первых членов ряда называется n-ой частичной суммой ряда и обозначается символом :
. (1.5)
Можно записать так: .
В частности,
,
. (1.6)
Составим из всех частичных сумм ряда (1.2) числовую последовательность :
(1.7)
Она называется последовательностью частичных сумм. Как всякая числовая последовательность, она может иметь предел, т.е. сходиться, или не иметь предела, т.е. расходиться. Предел последовательности частичных сумм, если он существует, будем обозначать буквой S.
Определение. Ряд называется сходящимся (ряд сходится), если сходится последовательность частичных сумм этого ряда. При этом предел S последовательности частичных сумм называется суммой данного ряда, т.е.
. (1.8)
Для сходящегося ряда, имеющего сумму S, можно формально записать равенство:
. (1.9)
Ряд, не имеющий суммы (1.8), называют расходящимся. В частности, если , то говорят, что ряд расходится к , и в этом случае используют символическое равенство
.
Замечание.Из равенства (1.6) следует, что любой член ряда можно представить как разность частичных сумм и :
. (1.10)
Изобразим геометрически последовательность частичных сумм. На рис.1.1,а и б ряд сходится, на рис.1.1,в — расходится.
|
|
в)
|
Рис.1.1
Замечание 3. Иногда номер члена ряда начинается с нуля: .
Примеры числовых рядов. Вычисление суммы ряда
Пример 1º.
1 + 1 + 1 + . . . + 1 + . . .
Здесь , .
Данный ряд расходится Þ 1 + 1 + 1 + . . . + 1 + . . .=+¥.
Пример 2º.
Как обычно, чередование знаков + и — задается с помощью степени (-1). Здесь последовательность частичных сумм имеет вид:
т.е. значение частичной суммы зависит от чётности номера п:
Таким образом, чётные и нечётные частичные суммы стремятся к двум различным пределам:
чётные к нулю, нечётные — к единице:
|
Рис.1.2
Следовательно, последовательность не имеет предела, и данный ряд расходится.
Пример 3º.
1 + 2 + 3 + … + n + …
Это арифметическая прогрессия с разностью . Напомним, что название «арифметическая» происходит оттого, что каждый член этой прогрессии, начиная со второго, равен среднему арифметическому соседних с ним членов:
.
В данной прогрессии , а последовательность частичных сумм имеет вид:
Найдем предел .
Следовательно, данный ряд расходится Þ 1 + 2 + 3 + … + n + …=+¥.
Пример 4º.
Здесь общий член ряда можно преобразовать, разложив на простейшие дроби:
.
Тогда ряд примет вид:
Вычислим частичную сумму, раскрыв скобки:
Предел последовательности частичных сумм
Þ сумма ряда конечна, т. е. ряд сходится Þ
=1.
Пример 5º.
.
Вывод будет дан ниже. Этот ряд называется рядом Лейбница.
Пример 6º.
.
Вывод будет дан ниже. Здесь в знаменателе только нечётные числа.
Пример 7º.
. Вывод будет дан ниже.
Пример 8º.
Вывод будет дан ниже. Сумма ряда равна числу е — основанию натурального логарифма.
Сумму ряда вычислить не всегда легко и даже не всегда возможно. Поэтому в теории рядов чаще решается более простая задача — выяснение, сходится ряд или расходится. Это называется исследованием сходимости ряда.
Рекомендуемые страницы:
Поиск по сайту
poisk-ru.ru
6.2.3. Вычисление суммы ряда по общей формуле
Одной из основных областей применения циклов с условием являются приближенные математические вычисления, например, вычисление суммы ряда и решение нелинейных уравнений. Изучим особенности программной реализации некоторых из этих задач и начнем с задачи вычисления суммы бесконечного сходящегося ряда.
Рассмотрим ряд
,
где n= 1, 2, 3,… Требуется найти сумму ряда в некоторой заранее заданной точкеxс определенной точностью ε.
Исходными данными для этой задачи являются значение xи необходимая точность вычислений ε. Параметр «точность вычислений» означает, что слагаемые, которые по модулю меньше точности, считаются несущественными и в общую сумму не включаются. Для ввода исходных данных будем использовать функциюInputBox. Результатом программы является значение накопленной суммы. Но для проверки правильности вычислений мы будем еще выводить значение левой части выражения, номер и значение последнего слагаемого, вошедшего в сумму. Для вывода результатов будем использовать окно списка с именемlstA.
Для решения этой задачи нам потребуется организовать цикл с условием. На каждом шаге цикла мы будем по общей формуле вычислять значение очередного слагаемого и прибавлять его к общей сумме. Как только очередное слагаемое станет меньше заданной точности, мы закончим выполнение цикла.
Рассмотрим особенности программной реализации этого алгоритма. Для решения задачи нам потребуются следующие переменные: x– точка, в которой вычисляется сумма ряда,eps– требуемая точность вычислений,summa– искомая сумма ряда,slag– очередное слагаемое. Все эти переменные имеют рациональный тип данных. Для повышения точности наших вычислений будем использовать типDouble.
Dim x, summa, slag, eps As Double
Для вычисления факториала, стоящего в знаменателе дроби, заведем переменную f, которая будет иметь целый тип с максимально возможной емкостью –ULong.
Dim f As ULong
Так как для вычисления факториала необходимо организовать цикл, то нам потребуется специальная переменная – счетчик i. Заметим, что формула общего члена ряда зависит от номера слагаемого –n. Поэтому при решении задачи нам потребуется переменная для хранения номера очередного слагаемого. Назовем ееn. Она будем иметь целый тип данных.
Dim n, i As Integer
Работа программы начинается с очистки окна списка от ее предыдущих результатов.
lstA.Items.Clear()
Вводим исходные данные.
x = Val(InputBox(«Введите точку»))
eps = Val(InputBox(«Введите точность»))
Задаем начальные значения. Начальное значение суммы равно нулю. Номер текущего слагаемого тоже равен нулю, так как никакого слагаемого на данный момент времени мы не вычислили.
summa = 0
n = 0
Организуем основной цикл.
Do
На каждом шаге цикла будем вычислять очередного слагаемое. При этом его номер будет на единицу больше, чем на предыдущем шаге.
n += 1
Начинаем вычислять значение очередного слагаемого. Первым шагом будет вычисление факториала, стоящего в знаменателе дроби.
f = 1
For i = 2 To 2 * n — 1
f *= i
Next
Затем по общей формуле вычисляем само слагаемое, заменяя факториал на уже найденное значение.
slag = (-1) ^ (n + 1) * x ^ (2 * n — 1) / f
Полученное слагаемое добавляем к общей сумме.
summa += slag
Проверяем, если модуль слагаемого меньше заданной точности, то дальнейшие вычисления не приведут к заметным изменениям результата, и выполнение цикла можно завершить.
Loop Until Math.Abs(slag) <= eps
Выводим в окно списка полученную сумму, значение выражения, стоящего в левой части равенства, номер и значение последнего слагаемого.
lstA.Items.Add(«summa=» + Str(summa))
lstA.Items.Add(«sin(x)=» + Str(Math.Sin(x)))
lstA.Items.Add(«n=» + Str(n))
lstA.Items.Add(«Последнее слагаемое =» + Str(slag))
Полный текст программы представлен в приложении 17. Пример работы программы приведен на рис. 31. Исходные данные для этого случая: x = 1,eps = 1e-4 = 10-4.
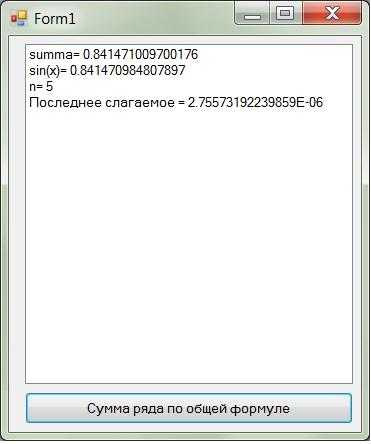
Рис. 31.Пример работы программы вычисления суммы ряда по общей формуле
studfiles.net








