Формула трапеция площадь: Формулы площади трапеции

Содержание

Вопрос № 2 Формула площади трапеции. Запись, вывод

Высотой трапеции называется перпендикуляр, проведённый из любой точки одного из оснований к прямой, содержащей другое основание.

‘1

Теорема. Площадь трапеции равна произведению полусуммы её оснований на высоту.

Дано: ABCD — трапеция,

ВС и AD — основания, BH — высота. Доказать: S_ABCD = 1 (AD BC )• BH.

A H

Диагональ BD разделяет трапецию ABCD на D ABD и D BCD, поэтому по свойству площадей S_ABCD = S_ABD + S_BCD.

Таким образом, S

ABCD

В D ABD AD — основание, ВН — высота, поэтому S_ABD = 1 AD • BH. В D BCD ВС — основание, DHi — высота, поэтому S_BCD = 2 BC • DH₁. Так как BH = DHj, то S_BCD

2 BC • BH. 2 AD • BH + 2 BC • BH, Sabcd = 2 (AD + BC )• BH.

Итак, площадь трапеции равна произведению полусуммы её оснований на высоту.

соту:

Ч.т.д.

Площадь трапеции равна произведению полусуммы её оснований на вы-

S = 2 (a + b) • h, a и b — основания трапеции, h — её высота.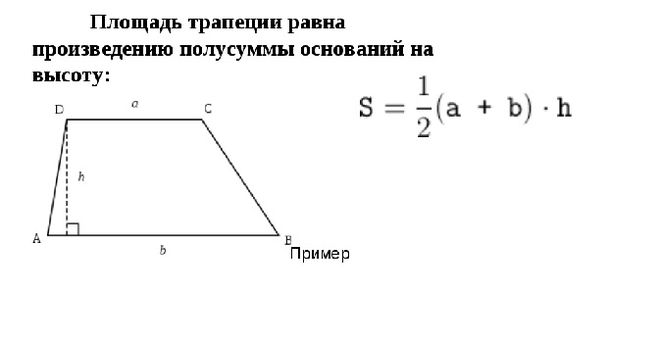

Площадь трапеции равна половине произведения её диагоналей на синус угла между ними: S = 2 d₁d₂ sin а, di и d₂ — диагонали трапеции, a — угол между ними.

Теорема об угле, вписанном в окружность.
Формула площади параллелограмма. Запись, вывод.

Вопрос № 1

Теорема об угле, вписанном в окружность. Следствия

Угол, вершина которого лежит на окружности, а стороны пересекают окружность, называется

вписанным углом.

На рисунке 1 Z АВС вписанный, и АС расположена внутри этого угла. В таком случае говорят, что вписанный Z АВС опирается на и АС.

Теорема.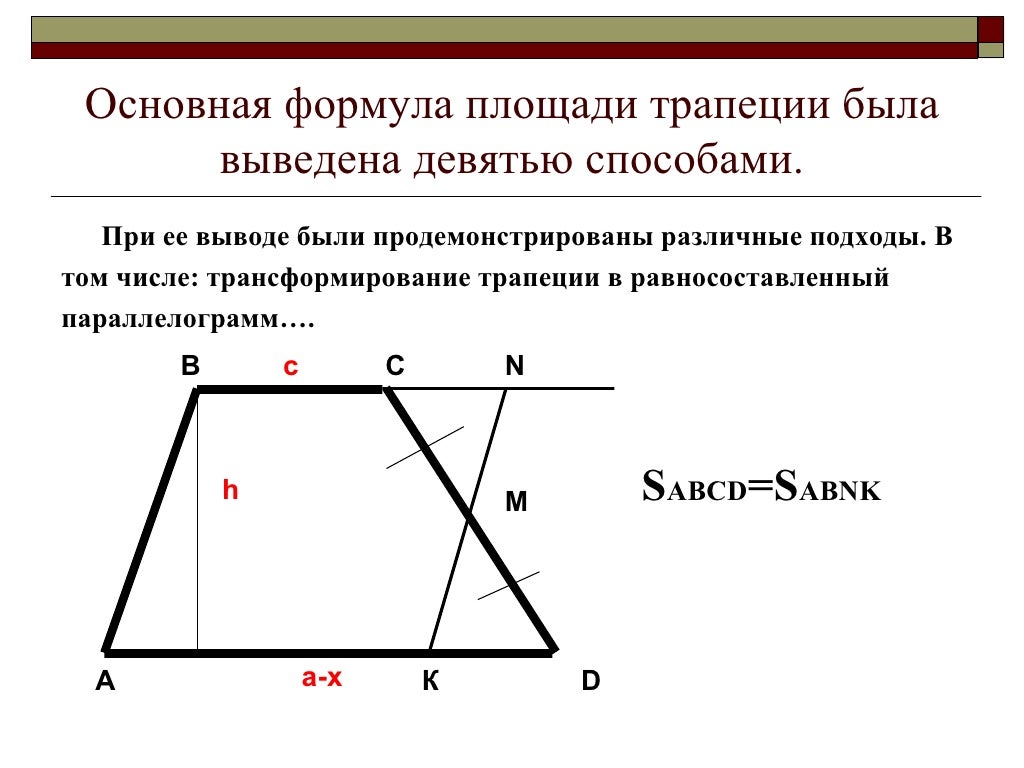 АВС

Рис.1

=¹ ZАОС. А т.к. ZАОС = и АС, то Z АВС =¹ иАС. 2 ‘ 2

II случай

Луч ВО делит Z АВС на два угла (рис. 2). В этом случае луч ВО, пересекает и АС в некоторой точке D, которая разделяет и АС на две дуги: и AD и и DС, а Z АВС на два угла: Z

ABD и Z DВС. По доказанному
B
выше, ZАВD =¹ и АD, Z DВС =¹ и СD.
и АВ + 1 и DG = 2
D Рис.2
22
Значит, ZАВС = ZMD + Z DВС
¹ (и АD + и DQ = ¹ и АС, т.е. Z АВС = ¹ и АС.
III случай
Луч ВО не делит Z АВС на два угла и не совпадает со сторонами этого угла (рис. 3). В этом случае и АС = и AD — и CD.
Z АВС = Z ABD — Z CBD = 1 и AD — 1 и CD =
B
2 2
¹
( и AD — и CD) = 1 и АС, т.е. Z АВС = ¹ и АС.
2
Рис.3
Итак, вписанный угол измеряется половиной дуги, на которую опирается.
Рис.4
Ч.т.д.
Следствие 1
Вписанные углы, опирающиеся на одну и ту же дугу, равны.
Z АКС = Z АМС = Z АВС = …, так как они опираются на одну и ту же и АС (рис. 4).
Следствие 2
Вписанный угол, опирающийся на полуокружность, — прямой.
M
C
ZАКС = ZАМС = ZАВС = … 90°, так как они опираются на диаметр АВ (рис. 5).
Рис.5
Замечание. Так как градусная мера дуги равна градусной мере соответствующего центрального угла, то теорему о вписанном угле можно сформулировать следующим образом: угол, вписанный в окружность, равен половине соответствующего центрального угла, т.е.
ZАВС = ¹Z АОС.
Вопрос № 2
Формула площади параллелограмма. Запись, вывод
Теорема. Площадь параллелограмма равна произведению двух его смежных сторон на синус угла между ними.
BC
Дано: ABCD — параллелограмм.
Доказать: S_A_ABCD = АВ • AD sin А.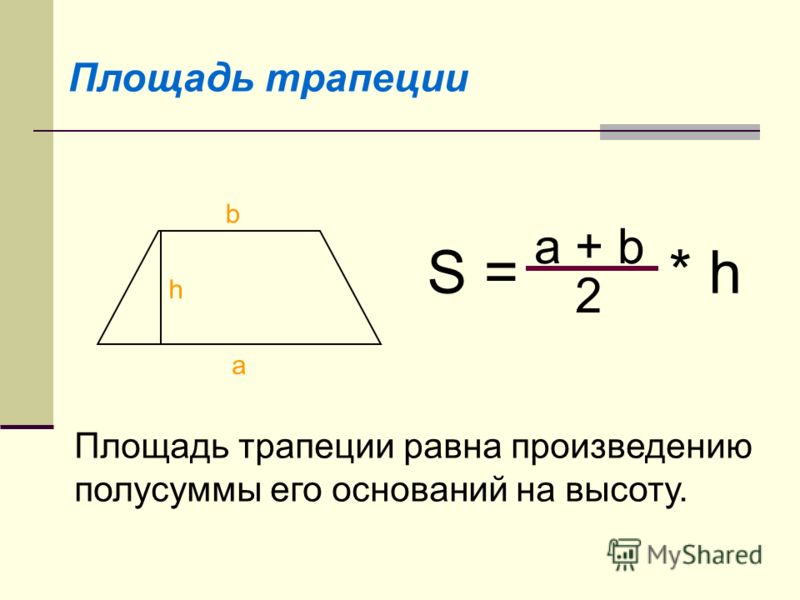
Доказательство
В параллелограмме

ABCD проведем диагональ BD, и рассмотрим получившиеся треугольники ABD и CDB.
АВ = CD, ВС = AD, т.к. в параллелограмме противолежащие стороны равны; BD — общая сторона. Следовательно, A ABD = A CDB по III признаку равенства треугольников (по трем сторонам).
Равные фигуры имеют равные площади, поэтому S_A
ABD = S_A
CDB.
По свойству площадей площадь параллелограмма равна сумме площадей треугольников, из которых он составлен, поэтому S_ABCD = S_AABD + S_A
CDB = 2 S_AABD.
Так как площадь треугольника равна половине произведения двух его сторон на синус угла между ними, то

S_ABCD = 2• 2АВ • AD sin А = АВ • AD sin А.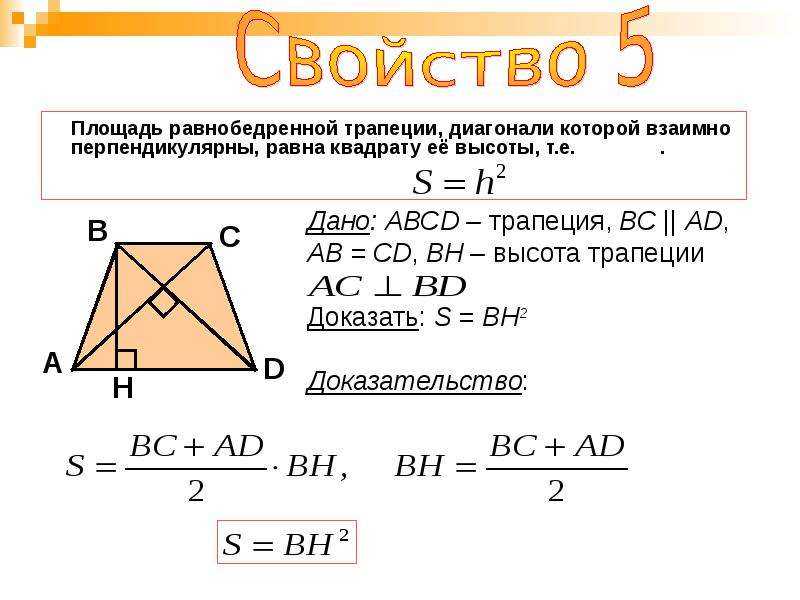
Итак, площадь параллелограмма равна произведению двух его смежных сторон на синус угла между ними.
Ч.т.д.
Площадь трапеции / Площадь / Справочник по геометрии 7-9 класс
Главная

Справочники

Справочник по геометрии 7-9 класс

Площадь

Площадь трапеции

Для вычисления площади произвольного многоугольника его разбивают на треугольники и находят площадь каждого из них. Площадь данного многоугольника равна сумме площадей этих треугольников.
Условимся называть высотой трапеции перпендикуляр, который проведен из любой точки одного из оснований к прямой, содержащей
другое основание.
Теорема
Площадь трапеции равна произведению полусуммы ее оснований на высоту
Доказательство
Дано: ABCD — трапеция, BH и DH₁ — высоты, S — площадь
Доказать: S = (AD + BC) ВН
Доказательство:
Диагональ BD разделяет трапецию на два треугольника ABD и BCD, поэтому S = S_ABD + S_BCD.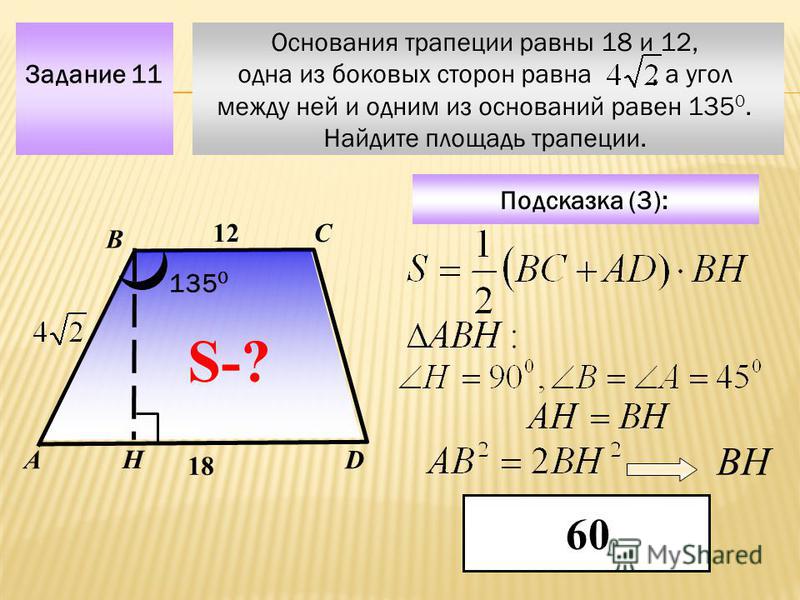 Примем отрезки AD и ВН за основание и высоту треугольника ABD, а отрезки BC и DH₁ за основание и высоту треугольника BCD. Тогда
S_ABD = AD BH, S_BCD = BC DH₁.
Так как DH₁ = BH, то S_BCD = BC BH.
Таким образом,
S = AD BH + BC BH = (AD + BC) BH.
Теорема доказана.
Советуем посмотреть:
Понятие площади многоугольника
Площадь квадрата
Площадь прямоугольника
Площадь параллелограмма
Площадь треугольника
Теорема Пифагора
Теорема, обратная теореме Пифагора
Формула Герона
Площадь
Правило встречается в следующих упражнениях:
7 класс
Задание 480, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 8, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 512*, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 518, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 527, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 625, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 725, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 735, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 892, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1070, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Доказательство площади трапеции
Первый хороший способ начать с доказательства площади трапеции — нарисовать трапецию и превратить трапецию в прямоугольник.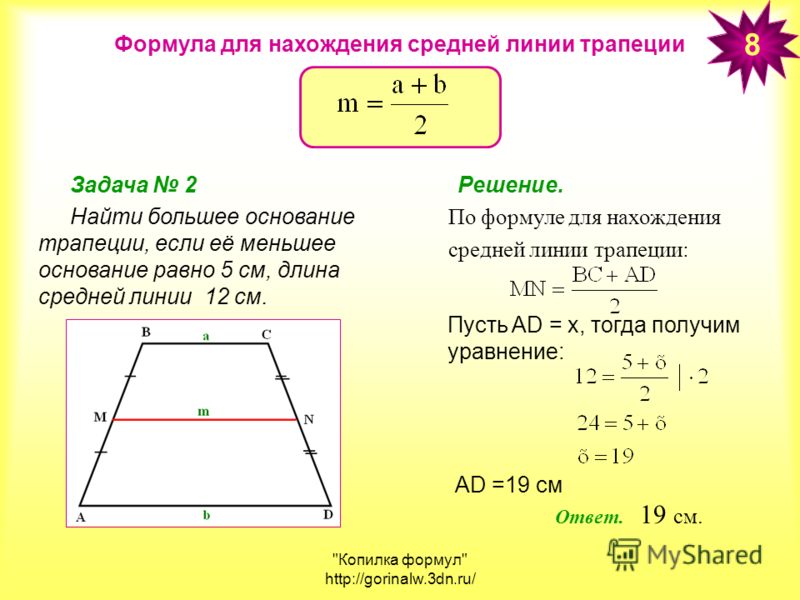

Посмотрите на трапецию ABCD выше. Как бы вы превратили это в прямоугольник?
Нарисуйте среднее основание (показано красным), которое соединяет середины двух непараллельных сторон.
Затем сделайте 4 треугольника, как показано ниже:
Обозначим две параллельные стороны синим цветом (основания) b ₁ и b ₂
Треугольники EDI и CFI конгруэнтны или равны, а треугольники KAJ и RBJ конгруэнтны или равны. Следовательно, вы можете сделать прямоугольник, повернув треугольники EDI вокруг точки I на 180 градусов против часовой стрелки и повернув треугольник KAJ по часовой стрелке, но все же на 180 градусов вокруг точки J.
Поскольку из трапеции можно сделать прямоугольник, обе фигуры имеют одинаковые область.
Причина, по которой треугольник EDI равен треугольнику IFC, связана с ASA. Мы можем найти два угла внутри треугольников, которые одинаковы, и сторона между углами одинакова для обоих треугольников.
Одинаковые углы показаны ниже. Они красного и зеленого цвета. Углы, выделенные зеленым цветом, прямые. Углы, выделенные красным цветом, являются вертикальными углами.

Это важно, потому что, если эти два треугольника не конгруэнтны или одинаковы, мы не можем составить прямоугольник из трапеции, вращая треугольник EDI. Он не подходит должным образом
Опять же, тот же аргумент применим к двум треугольникам слева
Следовательно, если мы сможем найти площадь прямоугольника, то площадь трапеции будет такой же.
Найдем площадь прямоугольника. Нам снова понадобится следующая цифра:
С. КЭ = б ₂ — АК — ЭД
AK = BR и ED = CF
Обратите внимание, что длину линии, выделенной красным (среднее основание), можно найти, взяв среднее значение длины BF и длины KE
Поскольку длина линии красного цвета равна основанию прямоугольника, мы можем просто умножить это на высоту, чтобы получить площадь трапеции.
Наконец, мы получаем:
Альтернативное доказательство площади трапеции можно сделать таким образом.

Начните с той же трапеции. Проведите высоты от вершин B и C. Это разобьет трапецию на 3 формы: 2 треугольника и прямоугольник.
Обозначьте основание маленького треугольника x и основание большего треугольника y
Обозначьте малое основание трапеции b ₁ и b ₂
b ₁ = b ₂ − ( x + y), поэтому x + y = b ₂ − b ₁
Площадь прямоугольника равна b ₁ × h, а площади треугольников с основаниями x и y равны:
Чтобы получить общую площадь, просто сложите эти площади вместе:
Доказательство площади трапеции завершено. Любые вопросы, свяжитесь со мной.
Квадратичная формула: простые шаги
26, 23 января 11:44
Узнайте о квадратичной формуле, дискриминанте, важных определениях, связанных с формулой, и приложениях.
Подробнее
Формула площади — список важных формул
25, 23 января 05:54
Что такое формула площади для двумерной фигуры? Вот список тех, которые вы должны знать!
Подробнее
Видео с вопросами: Нахождение площади трапеции
𝐴𝐵𝐶𝐷 — трапеция, где отрезок 𝐴𝐷 ⫽ отрезок 𝐵𝐶, 𝐴𝐷 = 22 см, а 𝐵𝐶 = 13 см. Если площадь △𝐴𝐵𝐶 равна 65 см², какова площадь трапеции?
Стенограмма видео
𝐴𝐵𝐶𝐷 — трапеция, где линия отрезок 𝐴𝐷 параллелен отрезку 𝐵𝐶, 𝐴𝐷 равен 22 сантиметрам, а 𝐵𝐶 равняется 13 сантиметрам.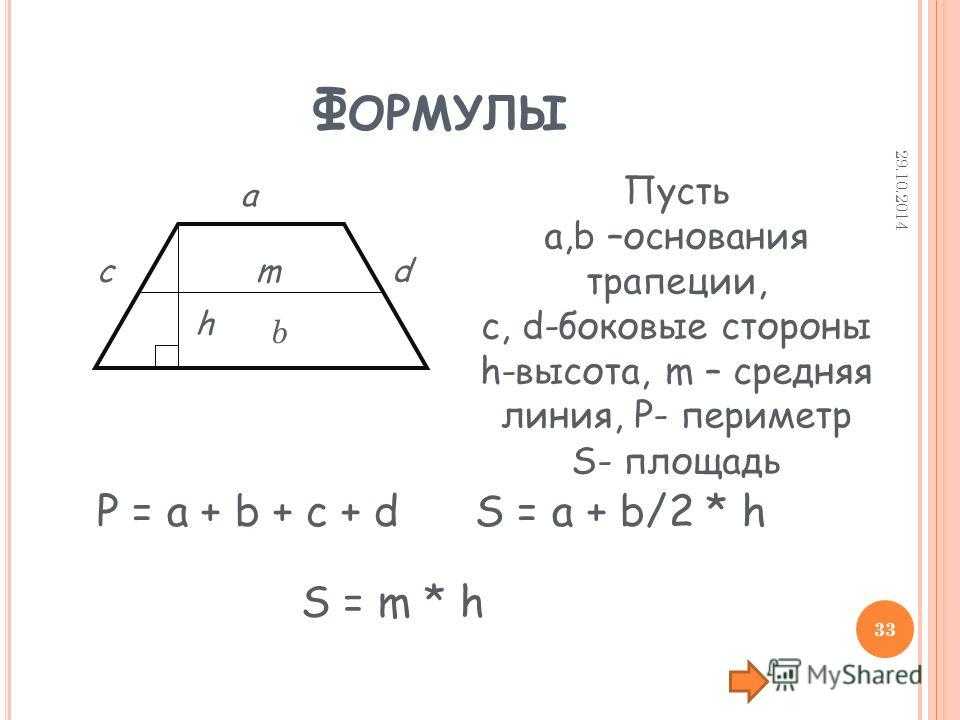 Если площадь треугольника 𝐴𝐵𝐶 равна 65 квадратных сантиметров, какова площадь трапеции?
Нам дали разные информацию об этой трапеции и попросили вычислить ее площадь. Площадь трапеции равна половина суммы длин его параллельных сторон, обычно обозначаемых 𝑎 и 𝑏, умножается на высоту, обозначаемую ℎ.
Нам известны длины параллельные стороны, отрезки 𝐴𝐷 и 𝐵𝐶, равные 22 и 13 сантиметрам, соответственно. Но нам не дали высота трапеции. Нам нужно использовать другой информация в вопросе, чтобы вычислить это, прежде чем мы сможем найти трапецию область.
Другая предоставленная информация заключается в том, что площадь треугольника 𝐴𝐵𝐶 равна 65 квадратных сантиметров. Вот этот треугольник. Теперь площадь треугольника находится по формуле: половина умножается на его основание, умноженное на его перпендикулярная высота. Основание треугольника 𝐴𝐵𝐶 равно общая со стороной трапеции, стороной 𝐵𝐶, которая имеет длину 13 сантиметры. Высота треугольника 𝐴𝐵𝐶 равна равно высоте трапеции. И так мы можем составить уравнение. 65 равно половине, умноженной на 13ℎ.
Мы можем решить это уравнение, чтобы найти высота треугольника и, следовательно, высота трапеции. Умножение обеих сторон уравнение на два дает 130 равно 13ℎ. А затем разделив обе стороны уравнение на 13 дает ℎ равно 10.
Теперь мы обнаружили, что высота трапеция равна 10 см. Итак, мы готовы вычислить его область. Подставляем 13 и 22 вместо длины параллельных сторон и 10 высоты в формулу площади трапеции дает, что площадь трапеции 𝐴𝐵𝐶𝐷 равна половине умножить на 13 плюс 22 умножить на 10. 13 плюс 22 будет 35 с половиной умножить на 10 будет пять.
No related posts.