Площадь треугольника – прямоугольного или равнобедренного, формула
Содержание
- Треугольник: определение и виды фигуры
- Как вычислить площадь треугольника?
- Прямоугольный треугольник
- Равнобедренный треугольник
- Равносторонний треугольник
- Определение площади треугольника с неизвестными данными
- Известны основание и высота
- Известны величины трех сторон
- Известны две стороны и угол между ними
- Известны одна сторона и прилежащие к ней углы
- Известны радиус вписанной окружности и полупериметр
- Известны радиус описанной окружности и периметр
Необходимость вычисления площади различных фигур, в том числе и треугольных, возникла за несколько веков до нашей эры. Над этим задумывались ученые и астрономы Древнем Египте.
В жизни иногда встречаются ситуации, когда требуется искать в закромах памяти знания из далеких школьных лет: подошла очередь ремонта в доме и нужно рассчитать количество необходимого материала, или потребовалось узнать площадь земельного участка в виде треугольника.
Человеческая память не может сразу воспроизвести убранные за ненадобностью школьные знания, что вполне естественно. Поэтому здесь собраны основные методы для расчета площади большинства видов треугольника.
Вычислить площадь треугольника можно различными вариантами, применяя определенные формулы. Методы расчета зависят от типов треугольных фигур и от того, какие вычислительные данные известны.
Треугольник: определение и виды фигуры
Из курса геометрии известно, что треугольник представляет собой многоугольную фигуру, которая имеет три лежащие на разных линиях точки, соединенные между собой отрезками. Размер площади треугольника выражается количеством заключенных в ней квадратных единиц и представляет собой положительное число, которое показывает размер фигуры, в части поверхности, ограниченной тремя отрезками в замкнутый контур.
ТреугольникВ зависимости от длины сторон и величины угла выделяется несколько разновидностей треугольников:
- прямоугольный, имеющий один прямой угол;
- остроугольный, все углы которого острые, то есть меньше 90 градусов;
- тупоугольный, содержащий один тупой угол в диапазоне от 90 до 180 градусов;
- равнобедренный, имеющий две равные по длине боковые стороны;
- равносторонний, у которого все три стороны имеют одинаковое значение.

Для расчета площади каждого типа треугольной фигуры используется специальная формула.
Как вычислить площадь треугольника?
Классические формулы расчета площади треугольных фигур соотносятся с видами треугольников. Приведенные ниже формулы определения площади произвольного треугольника подойдут для установления площади, вне зависимости от его характеристик, углов или размеров.
Прямоугольный треугольник
Прямоугольный треугольник характеризуется наличием прямого угла. Две его стороны, образующие этот угол носят название катетов. Противоположная прямому углу сторона треугольника именуется гипотенузой.
Прямоугольный треугольникОсновная формула расчета площади прямоугольного треугольника основывается на значениях катетов фигуры.
Формула:
где a, b – катеты треугольника.
Расчет:
- Перемножаются величины двух катетов.
- Полученное значение делится на два.
Вычислить площадь прямоугольного треугольника можно по другой формуле, где за основу берется величина гипотенузы и высота, проведенная к ней.
Формула:
где c – гипотенуза, hc – высота, проведенная к гипотенузе.
Расчет:
- Умножается длина гипотенуза на величину высоты, идущей от противоположной вершины.
- Полученное значение уменьшается вдвое.
Равнобедренный треугольник
В равнобедренном треугольнике две боковые стороны равны по значению, отличающаяся размерами сторона называется основанием.
Равнобедренный треугольникПлощадь равнобедренного треугольника рассчитывается по формуле:
где а – равные стороны треугольника, b – основание.
Расчет:
- Определяется разница из четырехкратного квадратного корня равных сторон и квадратного корня основания.
- Из полученного значения извлекается квадратный корень.
- Результат умножается на величину основания, уменьшенную в 4 раза.
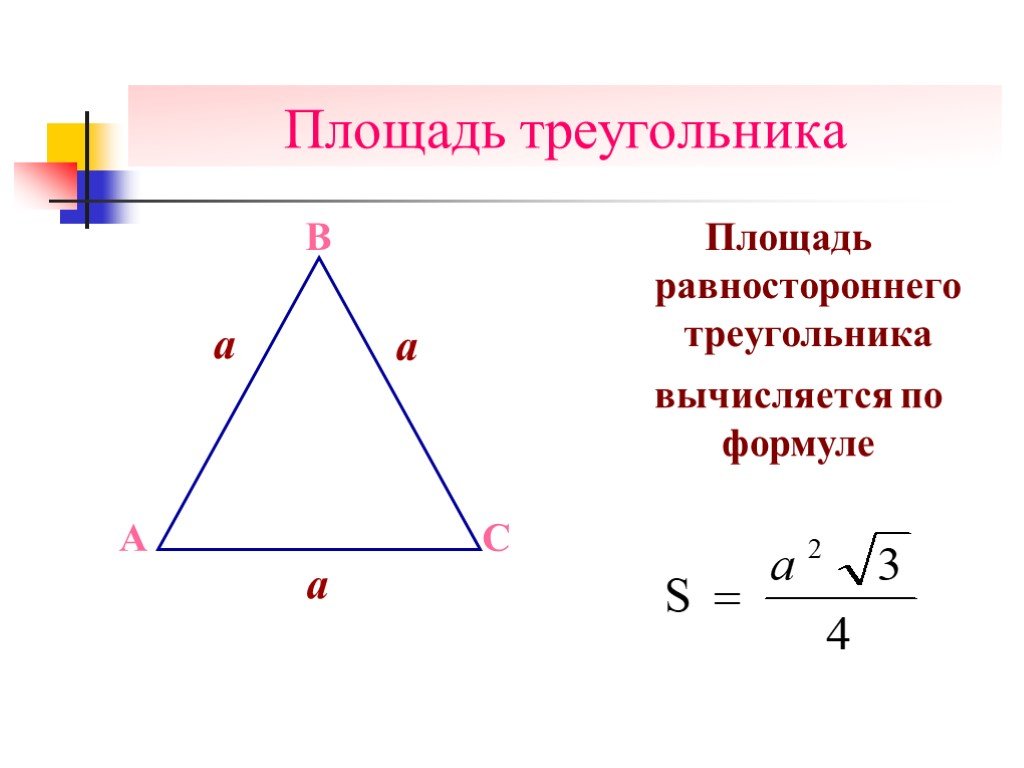
Равносторонний треугольник
Частным случаем равнобедренного треугольника является равносторонний, отличающийся тем, что все стороны и углы фигуры равны по значению.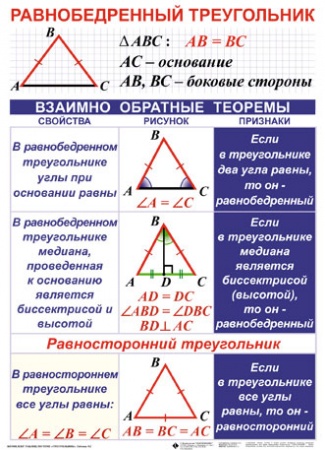
Площадь равностороннего треугольника определяется по формуле:
где a – сторона равностороннего треугольника.
Определение площади треугольника с неизвестными данными
Классические формулы расчета площади треугольника могут выручить не всегда. Существует ряд ситуаций, когда неизвестны необходимые для подстановки в формулу величины. При этом используют другие методы для расчета площади треугольника, напрямую зависящие от того, какие данные известны. Все варианты предусматривают конкретную формулу и определенный порядок проведения расчетов.
Известны основание и высота
Площадь треугольника определяется как половина произведения высоты фигуры и длины основания, то есть той стороны треугольника, к которой проведена высота.
Формула:
где b – длина основания; h – высота.
Расчет:
- Умножается высота на длину основания, получается площадь многоугольника.
- Для получения площади треугольника полученный результат делится на 2.

Известны величины трех сторон
Площадь треугольника рассчитывается по формуле Герона. Для облегчения формулы метод предусматривает предварительный расчет величины полупериметра.
Формула Герона:
где p – величина полупериметра; a, b, c – значения длины сторон треугольника.
Расчет:
- Вычисление полупериметра по формуле
- Расчет площади фигуры по формуле Герона.
Известны две стороны и угол между ними
Площадь треугольника рассчитывается как произведение двух сторон, умноженное на синус угла, расположенного между этими сторонами. Угол – геометрическая фигура, полученная из двух лучей, исходящих из одной точки (вершины угла).
ПирамидаФормула:
где a, b – стороны треугольника, C – угол между сторонами.
Расчет:
- Перемножение двух сторон.
- Определение синуса угла – тригонометрической функции, в прямоугольном треугольнике равной отношению противолежащего катета к гипотенузе.

- Умножение произведения двух сторон на синус угла.
- Полученный результат делится пополам.
Известны одна сторона и прилежащие к ней углы
Площадь подобного треугольника равна половине квадрата известной стороны, умноженной на дробь, с числителем, выражающим произведение синусов прилежащих углов, и знаменателем, указывающим синус противолежащего угла.
Формула:
Расчет:
- Рассчитывается квадрат известной стороны и делится на 2.
- Перемножаются синусы прилежащих углов и делятся на синус противолежащего. Вычисляется противолежащий угол по формуле:
γ= 180°−(α+ β)
β= 180°−(α+ γ)
α= 180°−(β+ γ)
- Перемножаются полученные значения.
Известны радиус вписанной окружности и полупериметр
Площадь треугольника определяется как произведение радиуса вписанной окружности на его полупериметр. Окружность называется вписанной, если имеет одну общую с многоугольником точку с каждой стороны фигуры. Центральная точка вписанной в треугольник окружности всегда располагается в точке, где пересекаются биссектрисы его внутренних углов.
Центральная точка вписанной в треугольник окружности всегда располагается в точке, где пересекаются биссектрисы его внутренних углов.
Формула:
S = p * r, где p – полупериметр треугольника, r – радиус вписанной окружности.
Расчет:
1. Полупериметр определяется как половина суммы всех сторон треугольника по формуле:
где a, b, c – стороны треугольника.
2. Перемножаются полупериметр треугольника и радиус вписанной окружности.
Известны радиус описанной окружности и периметр
Треугольник называется описанным вокруг окружности, если его стороны соприкасаются с кругом, а сам он находится снаружи. Площадь треугольника определяется как половина произведения периметра треугольника и радиуса описанной окружности.
Треугольник, вписанный в окружностьФормула:
где r – радиус описанной окружности, a, b, c – стороны треугольника.
Расчет:
- Определяется периметр треугольника как сумма всех его сторон.

- Умножается величина радиуса описанной окружности на величину периметра треугольника.
- Полученный результат делится пополам.
Знание формул вычисления площади треугольника поможет при определении площади объемных фигур, в основе граней которых лежат треугольные фигуры, таких, как например, пирамида.
Ебучий зачет. 1. Формулы площади для треугольника… | by Kochan
1. Формулы площади для треугольника (без вывода)
1/2*h*c
1/2*sin(a) * a * b
sqrt(p*(p-a)*(p-b)*(p-c)) (формула герона)
2.Медиана, высота в прямоугольном треугольнике (формулы с выво-
дом). Формулы радиусов вписанной и описанной окружности около
прямоугольного треугольника (с выводом)
Медиана равна половине гипотенузы. Достроить до прямоугольника и приравнять диагонали.
Высота равна sqrt(AH*HD). Из подобия треугольников ACH и CHD
r=(a+b-c)/2. Доказательство через периметр и равные кусочки, не забывая что вписанная окр. отсекает квадрат
R=1/2*c
3.
 Медиана в треугольнике:
Медиана в треугольнике:— свойства (с выводом)
- Медиана разбивает треугольник на два треугольника одинаковой площади. Через площадь и равные высоты
- Медианы треугольника пересекаются в одной точке, которая делит каждую из них в отношении 2:1, считая от вершины. Эта точка называется центром тяжести треугольника. Через подобие
- Весь треугольник разделяется своими медианами на шесть равновеликих треугольников. Через равновеликость треугольников по п.1 и вычитание
— формула нахождения медианы через стороны (с выводом)
характеристическое св-во параллелограма4. Свойства высот в треугольнике:
— отношение двух высот в треугольнике (с выводом)
Через площадь
— отсечение подобного треугольника двумя высотами (с выводом)
5. Биссектриса в треугольнике:
— свойство отношений и площадей с выводом
— формула биссектрисы с выводом
6) Теорема Чевы (прямая и обратная) (без вывода)
7) Теорема Менелая (прямая и обратная) (вывод прямой теоремы)
вывод через подобие
8) Вписанная и описанная окружность в треугольник (положение цен-
тра, формулы радиусов (с выводом)
9) Вневписанная окружность (формула радиуса с выводом)
выразить площадь треугольника через радиус10) Теорема синусов и косинусов (с выводом)
https://www. resolventa.ru/uslugi/ege/egebase2price.htm
resolventa.ru/uslugi/ege/egebase2price.htm
11) Отношение площадей подобных треугольников (с выводом)
k**2 удобно через площадь по синусам
12) Доказать, что радиус вписанной окружности в треугольник через
высоты выражается формулой
выразить площадь через высоты, выразить половинки сторон, выразить полупериметр через площадь и половинки сторон
13) Свойство вписанного четырехугольника в окружность (с доказа-
тельством)
14) Свойство описанного четырехугольника в окружность (с доказа-
тельством)
15) Свойство хорд и касательных к окружности. Вывод соотношений
для хорд и касательных.
- Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания.
- Отрезки касательных к окружности, проведенных из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.
- Диаметр (радиус), перпендикулярный к хорде, делит эту хорду и обе стягиваемые ею дуги пополам.
 Верна и обратная теорема: если диаметр (радиус) делит пополам хорду, то он перпендикулярен этой хорде.
Верна и обратная теорема: если диаметр (радиус) делит пополам хорду, то он перпендикулярен этой хорде. - Дуги, заключенные между параллельными хордами, равны.
- Угол между хордами равен полусумме высекаемых ими дуг
- Если две хорды окружности, AB и CD пересекаются в точке M, то произведение отрезков одной хорды равно произведению отрезков другой хорды: AM•MB = CM•MD. По подобию треугольников
16) Теорема об угле между касательной и секущей в окружности.
формул треугольника — Что такое формулы треугольника? Примеры
Формула треугольника используется для вычисления периметра и площади трехстороннего многоугольника, также известного как треугольник. Давайте подробно изучим формулы треугольника.
Что такое формулы треугольников?
Две важные формулы треугольника – формула площади треугольника и формула периметра треугольника. Кроме того, формулы треугольника применимы к различным типам треугольников.
Площадь треугольника Формула
Площадь треугольника равна половине произведения основания и высоты треугольника, она определяется как
Площадь треугольника, A = [(½) основание × высота] квадратных единиц.
Существуют две важные формулы треугольника, связанные с площадью треугольника, а именно формула Герона и теорема Пифагора.
Площадь треугольника по формуле Герона определяется как Периметр/2 = (а + b + с)/2 ·
Теорема Пифагора используется для нахождения стороны прямоугольного треугольника, которая математически выражается как h 2 = p 2 + b 2 . Здесь «h» — это гипотенуза (самая длинная сторона прямоугольного треугольника), p — перпендикулярная сторона, а b — основание.
В случае равностороннего треугольника формула для площади равностороннего треугольника: A = (√3/4)a 2 квадратных единиц, где a – сторона треугольника.
В случае равнобедренного треугольника формула для площади равнобедренного треугольника выглядит следующим образом: A = 1/2 × основание × высота в квадратных единицах, где высота = \(\sqrt{\text{a}^2 — \dfrac{ б^2}{4}}\). (Здесь «а» — равная сторона, а «b» — основание равнобедренного треугольника.)
(Здесь «а» — равная сторона, а «b» — основание равнобедренного треугольника.)
Формула периметра треугольника
Периметр треугольника равен сумме всех сторон треугольника, он задается как
Общая формула периметра треугольника, P = (a + b + c) единиц .
Формула равностороннего треугольника для периметра (а + а + а) = 3 а единиц. Здесь а — сторона равностороннего треугольника. (Примечание: в равнобедренном треугольнике все три стороны равны)
Формула для определения периметра равнобедренного треугольника: (s + s + b) = (2s + b) единиц, где s – это измерение двух равных сторон, а b – основание равнобедренного треугольника.
Хотите найти сложные математические решения за считанные секунды?
Воспользуйтесь нашим бесплатным онлайн-калькулятором, чтобы решить сложные вопросы. С Cuemath находите решения простыми и легкими шагами.
Записаться на бесплатный пробный урок
Примеры формул треугольника
Пример 1: Найдите площадь треугольника, основание которого равно 40 единицам, а высота — 25 единицам.
Решение:
Найти: Площадь треугольника
Основание треугольника = 40 единицам (дано)
Высота треугольника = 25 единицам (дано)
Используя формулы треугольника,
Площадь треугольника, A = [(½) основания × высота] квадратных единиц
= [(½) 40 × 25] квадратных единиц
= 500 квадратных единиц
Ответ: Площадь треугольника равна 500 квадратных единиц.
Пример 2: Стороны треугольника равны 5 единицам, b = 10 единицам и c = 6 единицам. Каков периметр этого треугольника?
Решение:
Чтобы найти: Периметр треугольника
Три стороны треугольника = 5, 10, 6. (Дано)
Используя формулы треугольника,
Периметр треугольника b, p = (a + +в) единицы.
= ( 5+10+6) единиц.
= 21 единица
Ответ: Периметр треугольника равен 21 единице.
Пример 3: Если длины сторон треугольника равны 4 дюймам, 7 дюймам и 9 дюймам, рассчитайте его площадь по формуле Герона.
Решение:
Найти: Площадь треугольника
Учитывая, что сторона a = 4 дюйма, сторона b = 7 дюймов, сторона c = 9 дюймов
Используя формулу треугольника (формула Герона),
A = √(s(s-a)(s-b)(s-c))
As, s = (a+b+c)/2
с = (4+7+9)/2
s = 20/2 = 10 дюймов
Подставляя значения в формулу Герона,
А = √(10(10-4)(10-7)(10-9))
⇒ А =√(10(6)(3)(1))
⇒ A = √(180) = 13,416 в 2
∴ Площадь треугольника равна 13,416 в 2 .
Часто задаваемые вопросы о формулах треугольников
Что такое формулы равностороннего треугольника?
Формула площади равностороннего треугольника: A = (√3/4)a 2 , где a — сторона треугольника
Формула равностороннего треугольника для периметра: (а + а + а) = 3 а. Здесь а обозначает сторону равностороннего треугольника одинакового размера.
Что такое формулы равнобедренного треугольника?
Формула площади равнобедренного треугольника: Площадь = 1/2 × Основание × Высота (единицы измерения 2 ).
Формула равнобедренного треугольника для периметра: (2s + b), где 2s – это измерение двух равных сторон, а b обозначает основание равнобедренного треугольника.
Каковы две основные формулы треугольника?
Две основные формулы треугольника — это площадь треугольника и формула периметра треугольника. Эти формулы треугольника могут быть математически выражены как;
- 90 160 Площадь треугольника, A = [(½) основания × высота] квадратных единиц.
- Периметр треугольника, P = (a + b + c) единиц
Что такое формулы разностороннего треугольника?
Формула площади разностороннего треугольника: Площадь = 1/2 × Основание × Высота (единицы измерения 2 ).
Формула разностороннего треугольника для периметра: (a + b + c), где a, b и c обозначают неравные стороны разностороннего треугольника.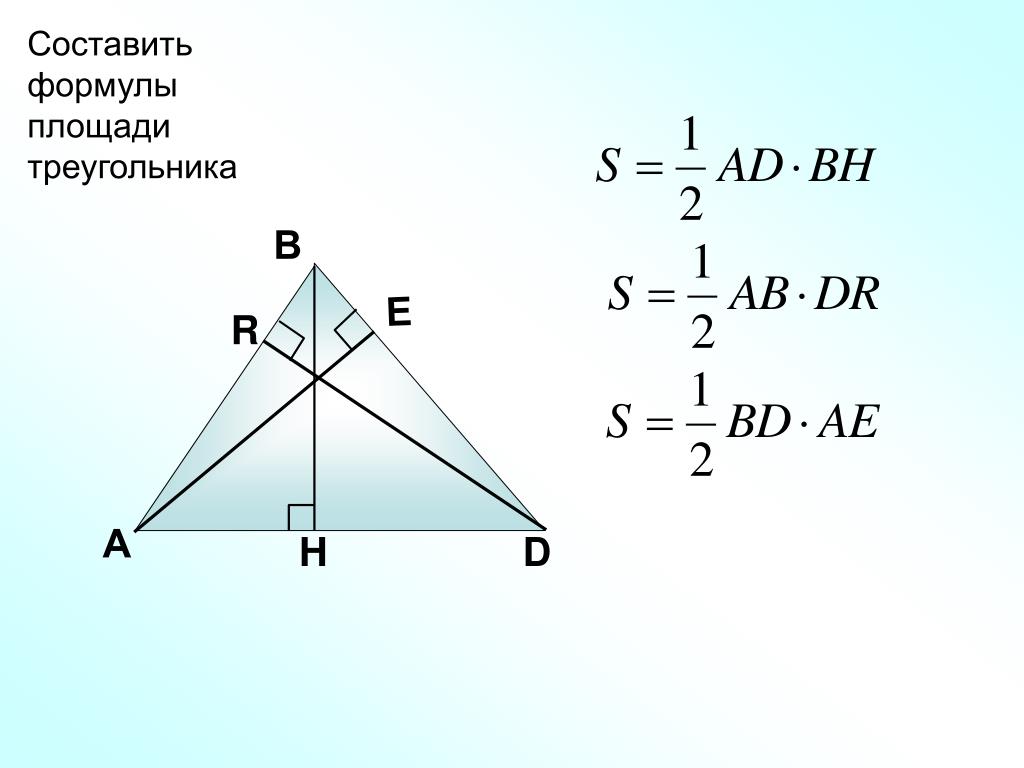
30-60-90 Треугольник — теорема, отношение и формула
Автор:
Малкольм МакКинси
Факт проверен
Пол Маццола
Что такое треугольник 30-60-90?
Треугольник 30-60-90 – это прямоугольный треугольник, три внутренних угла которого равны 30° , 60° и 90° . Прямоугольные треугольники с внутренними углами 30-60-90 известны как специальные прямоугольные треугольники .
Особые треугольники в геометрии из-за сильных взаимосвязей, которые раскрываются при изучении их углов и сторон.
Что такое треугольник 30-60-90Во всех треугольниках легко понять отношения между углами и их противоположными сторонами. Чем больше угол, тем длиннее противоположная сторона.
Соотношение треугольников между углами и противоположными сторонами Это означает, что из трех внутренних углов наибольший внутренний угол лежит напротив самой длинной из трех сторон, а наименьший угол будет находиться напротив самой короткой стороны.
В прямоугольном треугольнике напомним, что сторона, противолежащая прямому углу (наибольшему углу), называется гипотенузой (самая длинная сторона, а две другие стороны называются катетами.
Соотношение треугольников 30-60-90
Треугольник 30-60-90 градусов является особым прямоугольным треугольником, поэтому длины его сторон всегда соответствуют друг другу. Соотношение сторон соответствует соотношению треугольника 30-60-90:
Короткая сторона (против угла 30 градусов) = x
Гипотенуза (против угла 90 градусов) = 2 x
Длинная сторона (напротив угла 60 градусов) = x √3
30-60-90 теорема треугольника
Эти три специальных свойства можно рассматривать как теорему треугольника 30-60-90 и они являются уникальными для эти специальные прямоугольные треугольники:
Гипотенуза (самая длинная сторона треугольника) всегда в два раза больше длины короткого катета
Длина более длинного катета равна длине короткой катеты, умноженной на √3
Если известна длина любой стороны треугольника 30-60-90, можно найти недостающие длины сторон
Другие интересные свойства треугольников 30-60-90:
Другие интересные свойства специальных прямоугольные треугольникиКак решить треугольник 30-60-90
Образование — это знание того, что треугольники 30-60-90 обладают тремя свойствами, изложенными в теореме. Мудрость заключается в том, чтобы знать, что делать с этим знанием. Предположим, у вас есть треугольник 30-60-90:
Мудрость заключается в том, чтобы знать, что делать с этим знанием. Предположим, у вас есть треугольник 30-60-90:
Мы знаем, что гипотенуза этого треугольника в два раза больше длины короткой стороны:
Мы также знаем, что длинная сторона — это короткая сторона, умноженная на квадратный корень из 3:
Мы устанавливаем нашу специальную 30- 60-90, чтобы продемонстрировать простоту нахождения длины трех сторон. Попробуйте решить это:
30-60-90 Пример задачи треугольникаДлинная сторона равна короткой стороне, умноженной на √3 , поэтому можете ли вы вычислить длину короткой стороны? Вы сказали 5?
Длина гипотенузы всегда в два раза больше длины короткого катета. Вы получили 10 ?
Вы можете создать свою собственную формулу треугольника 30-60-90, используя известную информацию в вашей задаче и следующие правила. Эта таблица правил треугольника 30-60-90 поможет вам найти недостающие длины сторон.
30-60-90 правила треугольника
| Если вы знаете… | Тогда… | Чтобы получить… |
|---|---|---|
| Гипотенуза | Разделить на 2 | Короткая ножка |
| Короткая ножка | Умножить на 2 | Гипотенуза |
| Короткая ножка | Умножить на √3 | Длинная ножка |
| Длинная ножка | Разделить на √3 | Короткая ножка |
При работе с треугольниками 30-60-90 у вас может возникнуть соблазн установить соотношение между гипотенузой и длинным катетом. Это соотношение сложно из-за квадратного корня из 3,9.0003
Работайте осторожно, концентрируясь на соотношении гипотенузы и короткого катета, а затем короткого катета и длинного катета.
Вы заметите, что наши примеры до сих пор предоставляли только информацию, которую можно было бы легко «подключить», используя наши три свойства.
Что, если длинная сторона помечена простым целым числом?
Вы вскакиваете в проблему, так как для получения короткого катета нужно просто разделить длинный катет на квадратный корень из 3, а затем удвоить полученное значение, чтобы получить гипотенузу.
Но вы не можете оставить задачу так:
Правила математики не допускают радикала в знаменателе, поэтому вы должны рационализировать дробь. Умножьте числитель и знаменатель на √3 :
Это упрощает до:
Если вы не указали десятичный ответ, это может быть вашим окончательным ответом для длины короткой стороны. Удвоение дает 18 √3 для гипотенузы.
Еще один предупреждающий флаг с 30-60-90 треугольников заключается в том, что вы можете настолько увлечься тремя свойствами, что потеряете из виду сам треугольник. Это по-прежнему треугольник, поэтому сумма его внутренних углов должна составлять
Теорему Пифагора можно использовать для проверки своей работы или для ускорения решения.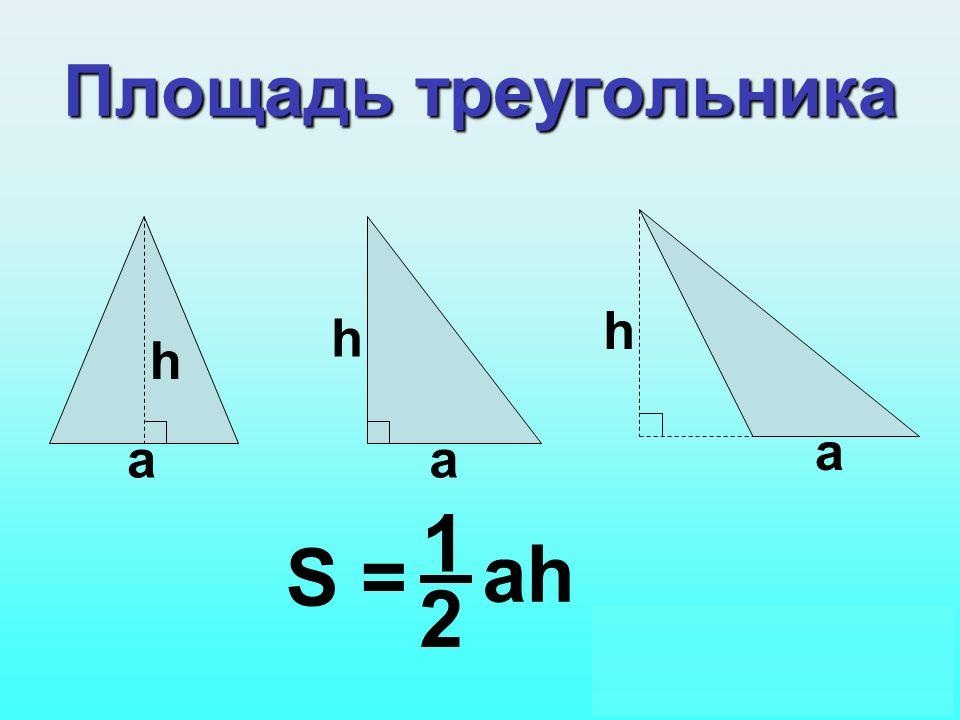
Примеры треугольника 30-60-90
У прямоугольного треугольника короткая сторона имеет длину 14 метров с измерением противоположного угла 30° . Каковы две другие длины?
Треугольник 30-60-90 — нахождение недостающих длинМы сразу знаем, что треугольник равен 30-60-90, так как сумма двух идентифицированных углов составляет 120° :
Недостающий угол измеряется 60° . Отсюда следует, что гипотенуза равна 28 м , а длинный катет равен 14 м * √3 .
What is you have a triangle with the hypotenuse labeled 2,020 mm , the short leg labeled 1,010 mm , and the long leg labeled 1,010√3 .
Ваше знание треугольника 30-60-90 поможет вам сразу это распознать. Вы можете уверенно обозначить три внутренних угла, потому что видите отношения между гипотенузой и коротким катетом, а также между коротким катетом и длинным катетом.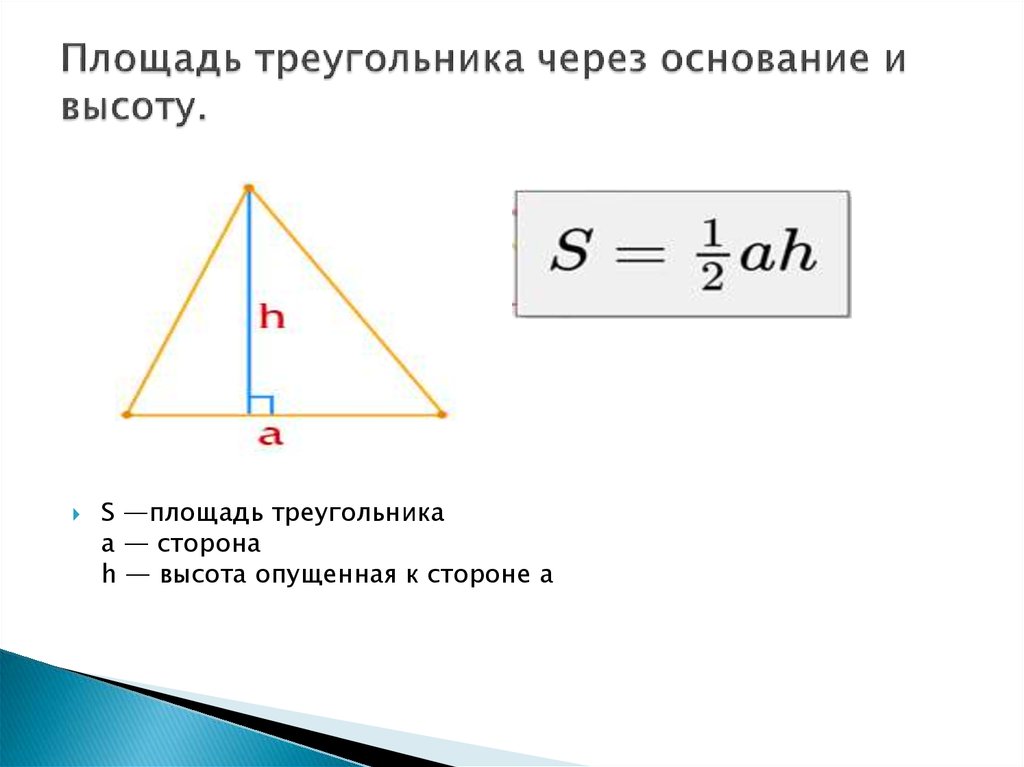




 Верна и обратная теорема: если диаметр (радиус) делит пополам хорду, то он перпендикулярен этой хорде.
Верна и обратная теорема: если диаметр (радиус) делит пополам хорду, то он перпендикулярен этой хорде.