Подготовка школьников к ЕГЭ в учебном центре «Резольвента» (Справочник по математике — Элементы математического анализа
Секущая графика функции. Уравнение секущей графика функции
Рассмотрим график некоторой функции y = f (x), точки A= (x0; f (x0)) и B = (x1; f (x1)) на графике, прямую, проходящую через точки A и B, и произвольную точку C = (x; y) на этой прямой (рис. 1).
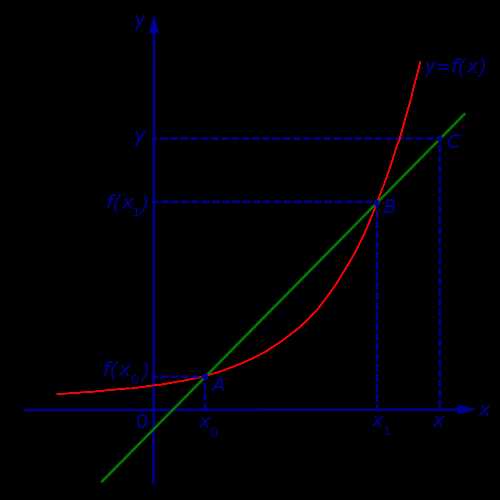
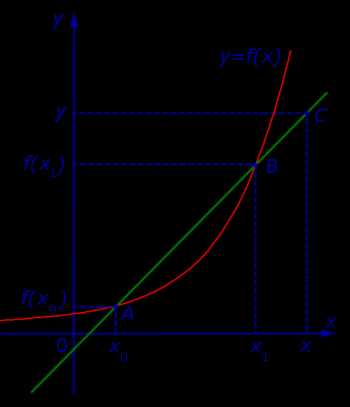
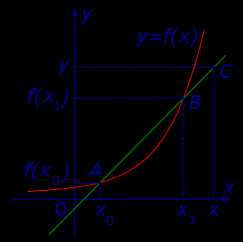
Рис.1
Определение 1. Прямую, проходящую через две произвольные точки графика функции, называют секущей графика функции.
В соответствии с определением 1 прямая, проходящая через точки A и B графика функции y = f (x), является секущей этого графика.
Выведем уравнение секущей графика функции.
Для этого рассмотрим векторы и , координаты которых имеют вид:
Поскольку векторы и лежат на одной прямой, то справедливо равенство
| (1) |
где k – некоторое число.
Переписывая равенство (1) в координатах, получим систему (2):
| (2) |
Исключая из системы (2) переменную k , получим систему (3):
| (3) |
второе уравнение которой можно записать в следующем виде
| (4) |
Уравнение (4) и является уравнением секущей графика функции y = f (x), проходящей через точки A = (x0; f (x0)) и B = (x1; f (x1)) этого графика.
Касательная к графику функции
Проведем секущую графика функции y = f (x), проходящую через точки A и B этого графика, и рассмотрим случай, когда точка A неподвижна, а точка B неограниченно приближается к точке A по графику функции y = f (x) (рис. 2).
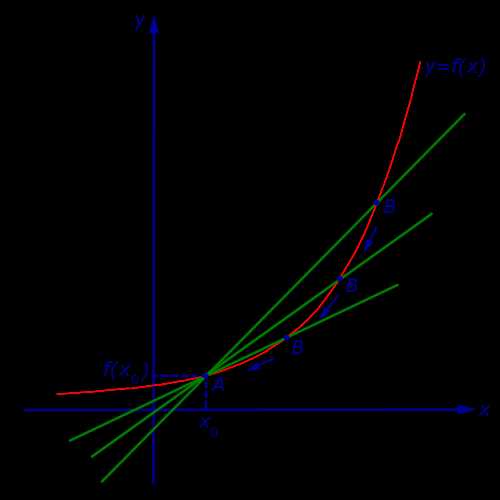

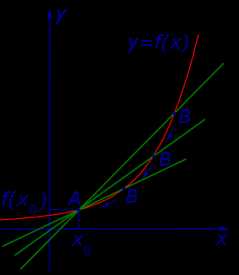
Рис.2
Неограниченное приближение точки B к точке A принято обозначать
B → A
и произносить «B стремится к A».
Заметим, что, если B → A для точек A = (x0; f (x0)) и B = (x1; f (x1)) графика функции y = f (x), то это означает, что x1 → x0 .
Определение 2. Если при x1 → x0 существует предельное положение секущей графика фукнкции y = f (x), то это предельное положение секущей называют касательной к графику функции y = f (x) в точке A = (x0; f (x0)) (рис. 3) .

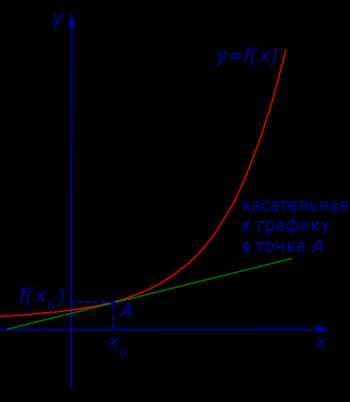
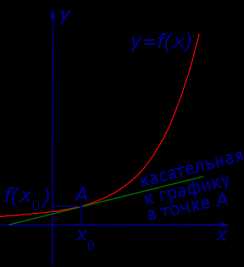
Рис.3
Производная функции
Определение 3. Если при x1 → x0 отношение
| (5) |
входящее в формулу (4), стремится к некоторому числу, то это число называют производной функции y = f (x) в точке x0 , обозначают f ′(x0) или и записывают так:
| (6) |
Уравнение касательной к графику функции
Из формул (4) и (6) вытекает следующее
Утверждение. Если у функции y = f (x) существует производная в точке x0 , то к графику функции y = f (x) в точке с координатами (x0; f (x0)) можно провести касательную, а уравнение этой касательной имеет вид:
| y = f′(x0) (x – x0) + f (x0) | (7) |
Геометрический смысл производной
Рассмотрим сначала возрастающую функцию y = f (x) и проведем секущую графика этой функции, проходящую через точки A = (x0; f (x0)) и B = (x1; f (x1)) (рис. 4).

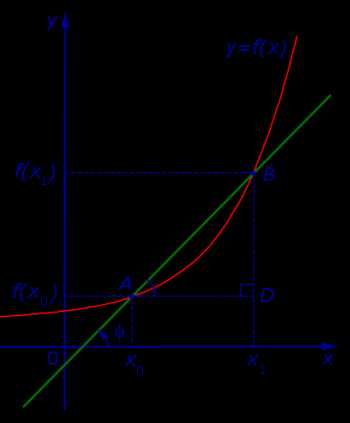
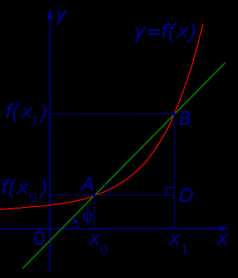
Рис.4
Обозначим буквой φ угол, образованный секущей и положительным направлением оси Ox, отсчитываемый против часовой стрелки. Тогда угол BAD в треугольнике ABD на рисунке 4 равен φ , и по определению тангенса угла получаем равенство
| (8) |
причем по определению углового коэффициента прямой tg φ является угловым коэффициентом секущей графика функции y = f (x), проходящей через точки A = (x0; f (x0)) и B = (x1; f (x1)) этого графика.
Случай, когда функция y = f (x) убывает, изображен на рисунке 5
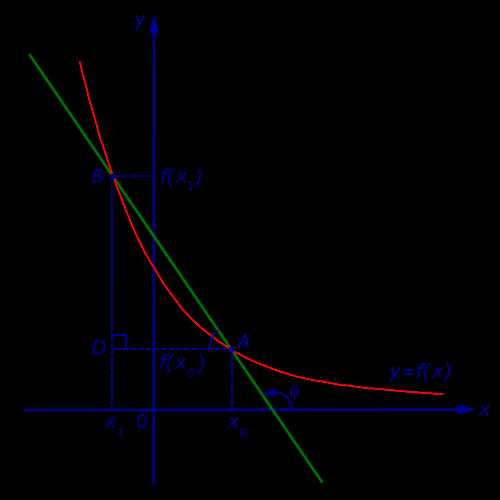

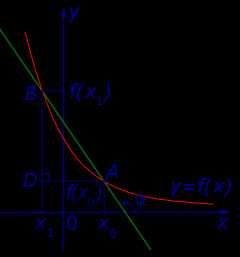
Рис.5
В этом случае угол φ является тупым, причем
то есть формула (8) справедлива и для случая, когда функция y = f (x) убывает.
Отсюда в соответствии с определением производной функции вытекает соотношение:
где буквой α обозначен угол, образованный касательной к графику функции y = f (x) в точке A = (x0; f (x0)) с положительным направлением оси Ox (рис. 6).
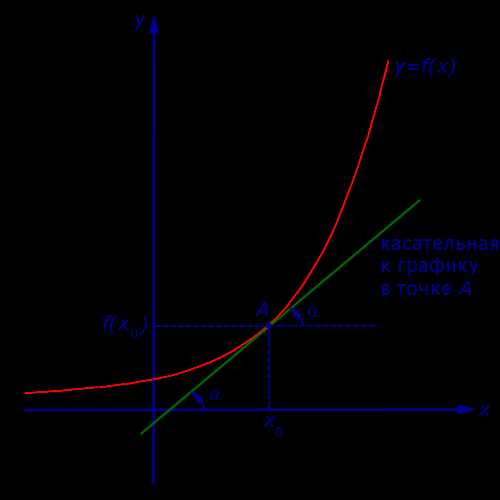
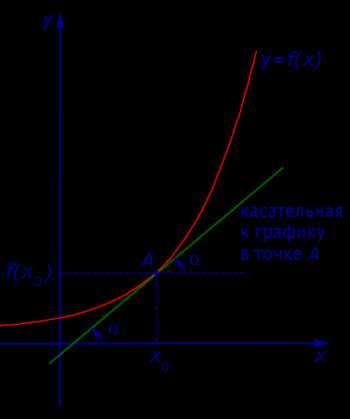

Рис.6
Таким образом, если у функции y = f (x) в точке x0 существует производная, то эта производная равна тангенсу угла наклона касательной к графику функции y = f (x) в точке (x0; f (x0)) :
f′(x0) = tg α ,
где угол наклона α образован касательной и положительным направлением оси Ox и отсчитывается в положительном направлении (то есть против часовой стрелки).
На нашем сайте можно также ознакомиться с разработанными преподавателями учебного центра «Резольвента» учебными материалами для подготовки к ЕГЭ по математике.
Приглашаем школьников (можно вместе с родителями) на бесплатное тестирование по математике, позволяющее выяснить, какие разделы математики и навыки в решении задач являются для ученика «проблемными». Запись по телефону (495) 509-28-10 |
Для школьников, желающих хорошо подготовиться и сдать ЕГЭ по математике или русскому языку на высокий балл, учебный центр «Резольвента» проводит
У нас также для школьников организованы
МОСКВА, СВАО, Учебный центр «РЕЗОЛЬВЕНТА»
www.resolventa.ru
Определение формулы касательной к окружности
| Общая формула окружности |
| Уравнение касательной в указанной точке |
Касательная к окружности
Если не использовать понятие производной, и взять объяснение из учебников середины прошлого века, то «Касательная к окружности — это прямая пересекающая окружность в двух совпадающих точках»
Окружность на плоскости может быть представлена в виде нескольких исходных данных
1. В виде координат центра окружности (x0,y0) и её радиуса R.
2. В виде общего уравнения
В виде параметрического вида и в полярных координатах мы рассматривать не будем, так как там формулы тоже на базируются на координатах центра окружности и радиусе.
Наша задача, зная параметры окружности и точку принадлежащую этой окружности вычислить параметры касательной к этой окружности.
Эта задача, является частным решением более общего калькулятор касательная к кривой второго порядка
Итак, если окружность выражена формулой
Уравнение касательной к окружности если нам известны параметры общего уравнения таково:
Таким образом, зная все коэффициенты, мы очень легко найдем уравнение касательной в заданной точке.
ВАЖНО: При указании точки, она должна быть обязательно(!!) принадлежать окружности,
и не быть точкой в какой либо стороне. В противном случае, уравнение касательной будет неверным.
Примеры
Вычислить уравнение касательной в точке (13.8, 0) к окружности выраженной формулой
Запишем коэффиценты этой кривой, взглянув на общую формулу
| Общая формула окружности |
| Уравнение касательной в указанной точке |
Второй пример:
Через окружность с центром (8.71, -4) и радиусом 7 проходит касательная и касается в точке (4,-4)
Найти уравнение этой прямой.
Раз у нас заданы радиус и коордианты центтра то уравнение имеет вид
раскроем скобки, получим
| Общая формула окружности |
| Уравнение касательной в указанной точке |
Отрисовав, полученные линии в GeoGebra мы убедимся что расчет произведен верно.
Формально, используя вышеупомянутую программу, касательную можно провести там проще и быстрее. Смотрите где и как проще.
Удачных расчетов!
- Определить формулу окружности по трем точкам >>
abakbot.ru
Уравнение касательной к графику функции в заданной точке
Пусть у нас имеется график некоторой непрерывной и дифференцируемой на некотором отрезке функции y = f(x) и задана некоторая точка x0 из этого отрезка.
Мы хотим написать уравнение касательной к графику функции в этой точке.
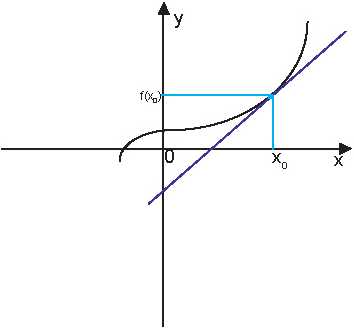
Касательная – это прямая, а уравнение прямой, как известно, выражается формулой y = kx+c, коэффициент k равен тангенсу угла между этой прямой и положительным направлением оси ОХ.
Как, известно, геометрический смысл производной f'(x) – тангенс угла наклона касательной к графику функции f(x) в точке x. Значит в нашем случае k = f'(x0).
Уравнение прямой примет вид y = f'(x0)×x+c (*).
Неизвестным остается только один коэффициент – с. Найдем его следующим образом, раз это касательная в точке x0, то она проходит через принадлежащую графику точку (x0; f(x0)). А раз прямая проходит через эту точку, значит, ее координаты удовлетворяют уравнению прямой.
Получаем уравнение:
f(x0) = f'(x0)×x0+c;
c = f(x0)-f'(x0)×x0.
Подставляя выражение для с в уравнение (*), получаем уравнение касательной к графику функции в точке x0:
y = f'(x0)×x+f(x0)-f'(x0)×x0 = f'(x0)(x-x0
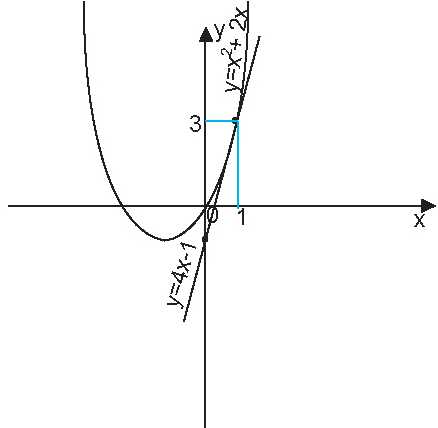
Пример.
Найти уравнение касательной к графику функции y = x2+2x в точке x0 = 1.
Уравнение касательной имеет вид:
y = f'(x0)(x-x0)+f(x0).
В нашем случае:
f'(x) = (x2+2x)’ = 2x+2;
f'(x0) = 2×1+2 = 4;
f(x0) = 12+2×1 = 3.
Уравнение касательной запишется в виде:
y = 4×(x-1)+3 = 4x-4+3 = 4x-1;
y = 4x-1.
studyport.ru
11.3. Уравнение касательной
и нормали. Физический смысл производной
Производная функции  в точке
в точке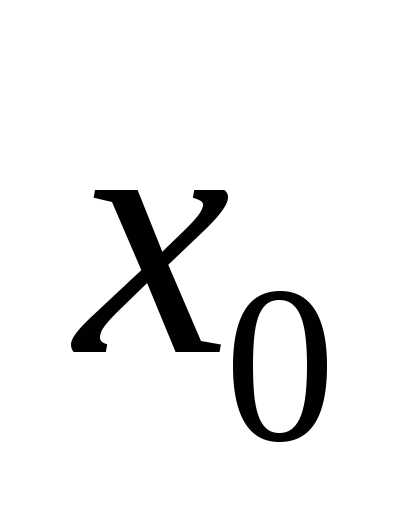 представляет собой угловой коэффициент
касательной, проведенной к графику
функции в точке
представляет собой угловой коэффициент
касательной, проведенной к графику
функции в точке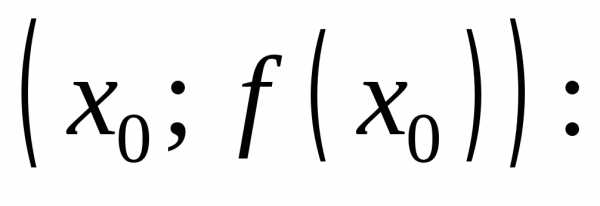
где  – угол наклона касательной к осиOx.
В этом состоит геометрический смысл производной.
– угол наклона касательной к осиOx.
В этом состоит геометрический смысл производной.
Уравнение касательной, проведенной к графику функции в точке гдеимеет вид:
(11.9)
Прямая, проходящая
через точку
графика функции перпендикулярно касательной, проведенной
в этой точке, называетсянормалью к графику функции
перпендикулярно касательной, проведенной
в этой точке, называетсянормалью к графику функции 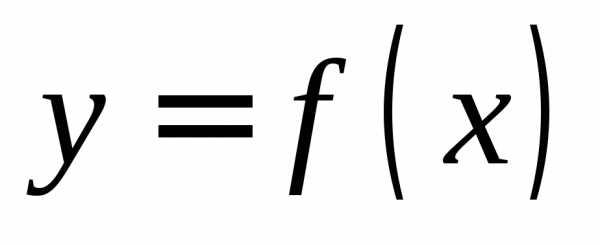
(11.10)
где 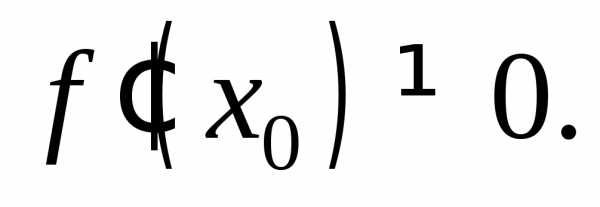
Рис. 11.1
Физические приложения производной
1. Если материальная
точка M движется неравномерно по пути, заданному
функцией 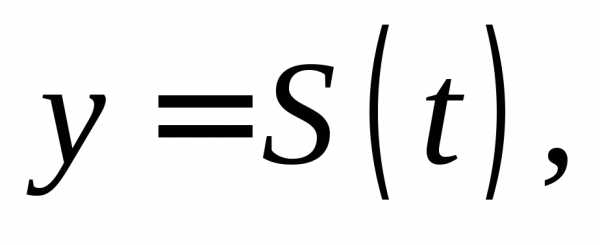 томгновенная
скорость движения в момент времени
томгновенная
скорость движения в момент времени 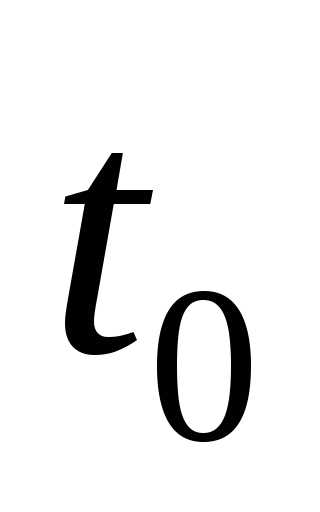 есть производная от путиS по времени t:
есть производная от путиS по времени t:
(11.11)
2. Если функцией 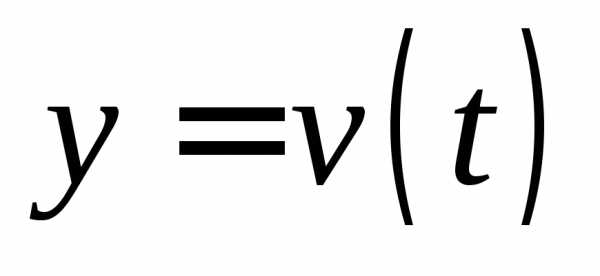 описывается процесс изменения скорости
неравномерного движения в зависимости
от времени, то мгновенное ускорение материальной точки в момент времени
описывается процесс изменения скорости
неравномерного движения в зависимости
от времени, то мгновенное ускорение материальной точки в момент времени 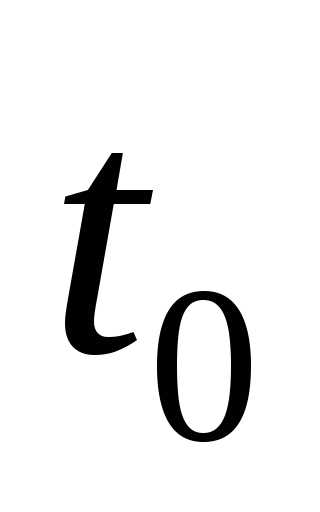
(11.12)
3. Если 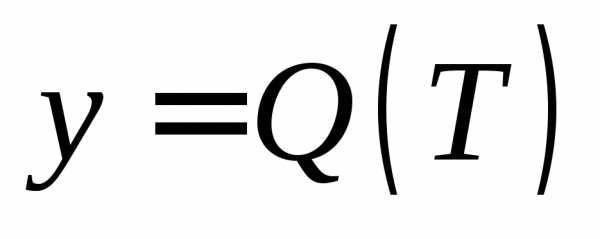 – функция, описывающая процесс изменения
количества теплоты, сообщаемой телу
при нагревании его до температурыT,
то теплоемкость
тела есть
производная от количества теплоты Q по температуре T:
– функция, описывающая процесс изменения
количества теплоты, сообщаемой телу
при нагревании его до температурыT,
то теплоемкость
тела есть
производная от количества теплоты Q по температуре T:
4. Линейная
плотность неоднородного тонкого стержня в точке 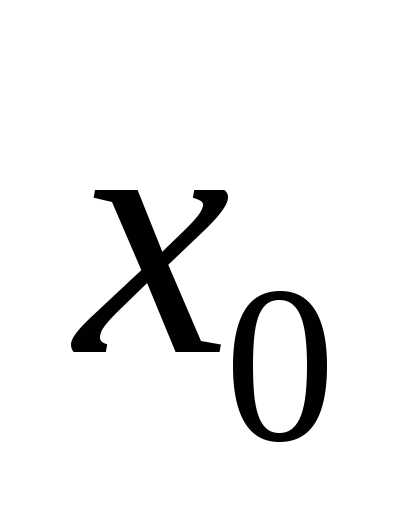 есть производная от массыm по длине l:
есть производная от массыm по длине l:
5. Мгновенное значение электродвижущей силы индукции равно скорости изменения магнитного потока, т. е. производной от магнитного потока по времени t:
6.
Пример 1. Написать уравнение касательной и
нормали, проведенной к графику функции 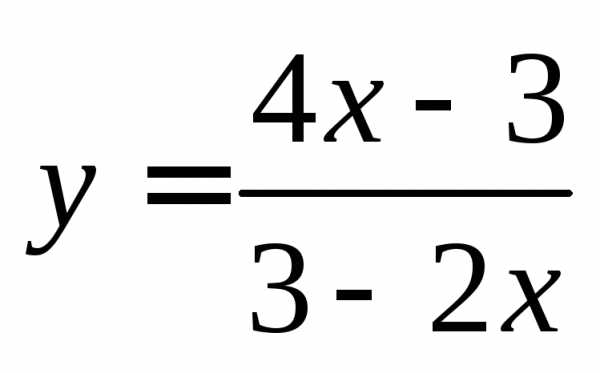 в точке с абсциссойx = 2.
в точке с абсциссойx = 2.
Решение. Для нахождения уравнения касательной
воспользуемся формулой (11.9). Сначала
найдем ординату точки касания 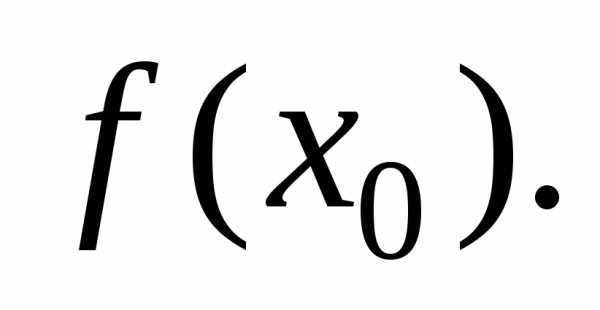 Для этого значение
Для этого значение подставим в уравнение функции:
подставим в уравнение функции:
Для нахождения
углового коэффициента найдем производную 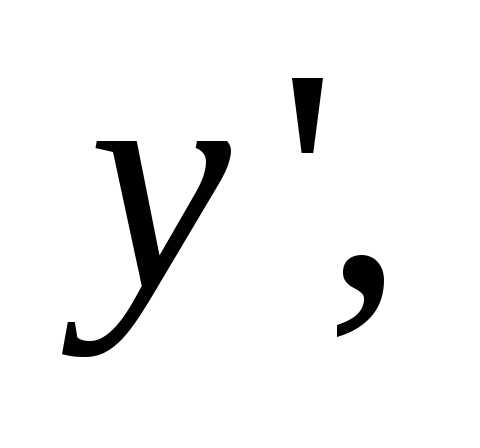 используя формулу дифференцирования
дроби:
используя формулу дифференцирования
дроби:
Найдем значение
производной при 
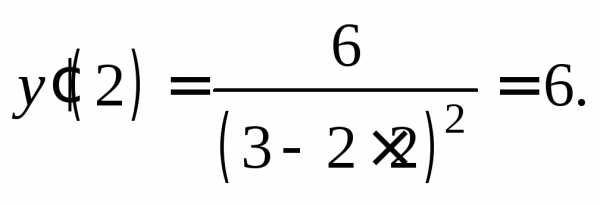
Подставив найденные значения в формулу (11.9), получаем уравнение касательной:
т. е.
Чтобы написать уравнение нормали, воспользуемся формулой (11.10):
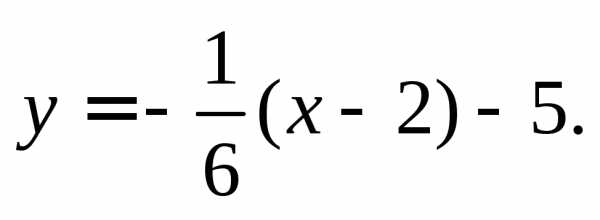
Получим, что
уравнение нормали, проведенной к заданной
кривой в заданной точке, имеет вид 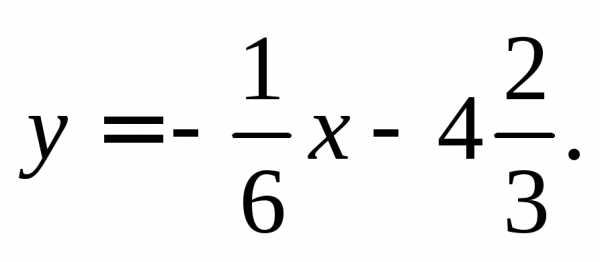
Пример 2. Определить, в какой точке кривой касательная наклонена к оси абсцисс под углом 45.
Решение. Так как тангенс угла наклона касательной к оси абсцисс равен значению производной в точке касания, найдем производную функции:
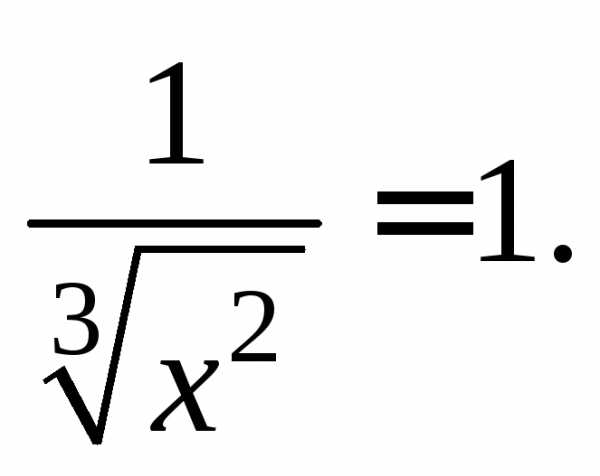
Отсюда:
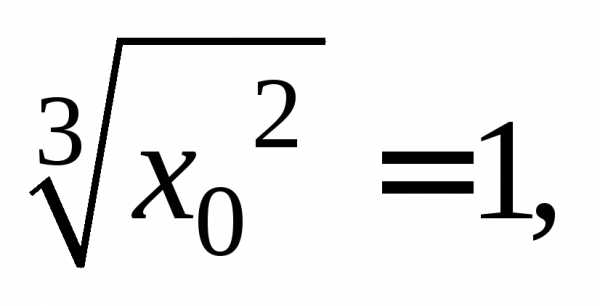


Получили два значения абсциссы точки касания:
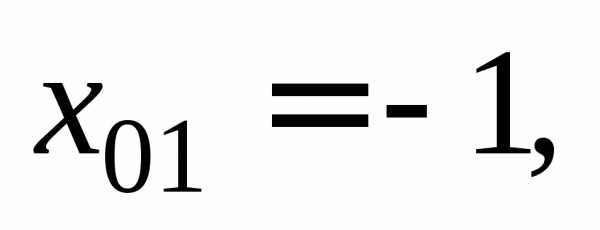
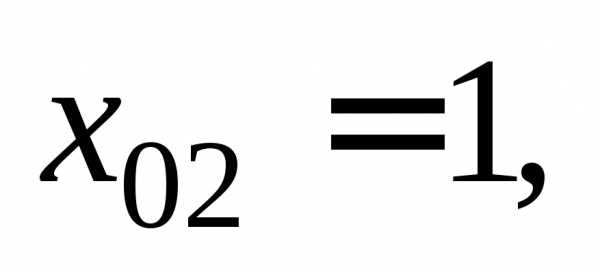
т. е. существуют две точки касания, в которых касательная образует угол 45 с осью Ох.
Найдем соответствующие
ординаты точек касания, подставляя
значения  в формулу функции:
в формулу функции:
Приходим к ответу: в точках икасательная к заданной кривой образует с осьюОх угол 45.
Пример 3. Найти острый угол между параболами 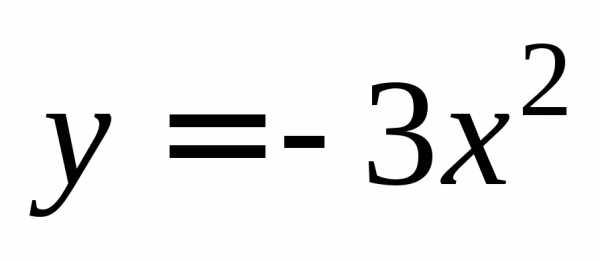 и
и в точке их пересечения, имеющей
отрицательную абсциссу.
в точке их пересечения, имеющей
отрицательную абсциссу.
Решение. Угол между двумя кривыми в точке их пересечения – это угол между касательными к этим кривым, проведенными в точке их пересечения. Тангенс этого угла вычислим по формуле
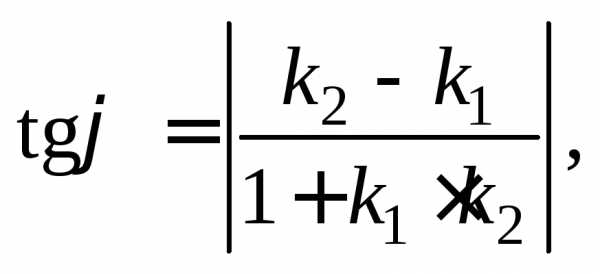 (11.13)
(11.13)
где k1 и k2 – угловые коэффициенты касательных, проведенных к параболам в заданной точке.
Найдем точку пересечения этих парабол. Для этого решим систему:
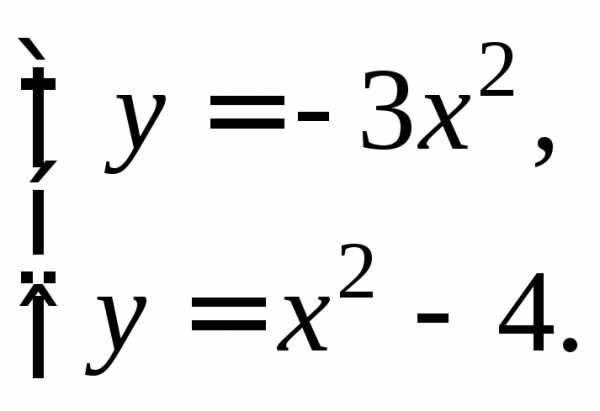
Отсюда 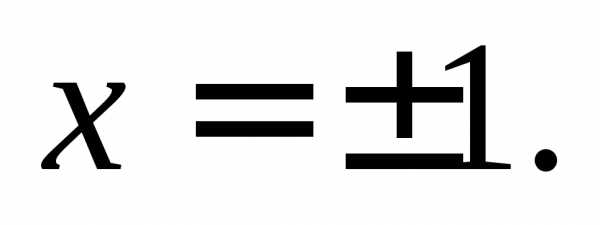 Условию задачи удовлетворяет точка
Условию задачи удовлетворяет точка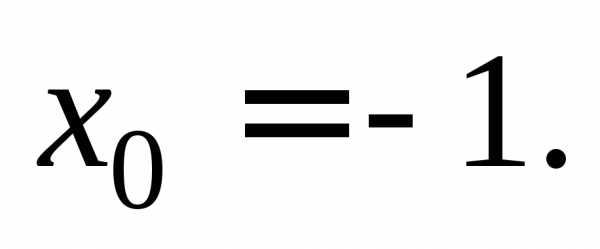 Найдем коэффициентk1:
Найдем коэффициентk1:
Аналогично найдем k2:
Воспользуемся формулой (11.13) и получим:
откуда 
Пример 4. Тело движется прямолинейно по закону
Найти скорость движения тела в тот момент, когда ускорение равно нулю.
Решение. Согласно формуле (11.11), скорость есть производная функции S(t), а, согласно формуле (11.12), ускорение а(t) есть производная скорости v(t).
Последовательно вычислим производные:
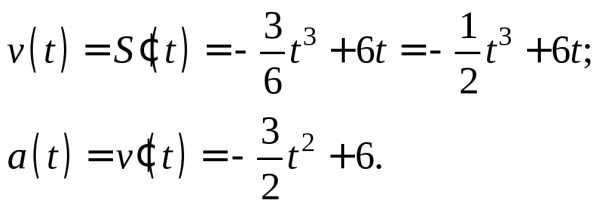
Найдем момент времени, когда ускорение равно нулю:
Вычислим скорость
движения тела в момент времени 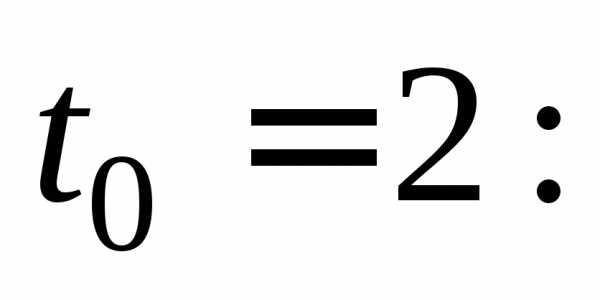
Задания
studfiles.net
Уравнение касательной к графику функции
Лекция
Тема: Уравнение касательной к графику функции
Цель: Рассмотреть уравнений касательной к графику функции
1. Уравнение касательной к графику функции
На предыдущих занятиях были рассмотрены задачи на технику дифференцирования. Это очень важные задачи, и нахождение производных необходимо в разных задачах, в том числе и в составлении уравнения касательной.
Построим кривую (см. рис.1).
Рис. 1. График функции .
Зафиксируем точку . Если , то значение функции равно . Значит, имеем точку с координатами (.
Задача: составить уравнение касательной. Более строгая формулировка – написать уравнение касательной к функции в точке с абсциссой , в которой — существует.
Уравнение касательной – это прямая, которая задается формулой
Любая прямая, в том числе и касательная, определяется двумя числами: и . Исходя из геометрического смысла производной (тангенс угла наклона касательной) – это есть угловой коэффициент .
Параметр найдем из условия, что касательная проходит через точку (, то есть .
.
Стало быть .
Запишем уравнение касательной
.
Или, .
Получили уравнение касательной к кривой в точке с абсциссой .
2. Смысл элементов уравнения касательной
Смысл каждого элемента, который входит в уравнение касательной.
1) ( – точка касания касательной и графика функции.
2) — угловой коэффициент касательной к графику функции.
3) – произвольная точка на касательной.
Очень много задач, когда задана точка, которая не лежит на графике функции, и через нее надо провести касательную к данной функции. Надо четко понимать, что – это произвольная точка на касательной.
Итак, получили уравнение касательной, проанализировали смысл каждого элемента этой касательной, и теперь приведем пример, и на нем изложим методику построения касательной.
3. Алгоритм составления уравнения касательной к графику функции
Задача.
К кривой в точке с абсциссой провести касательную. Проиллюстрируем поиск касательной на рисунке (см. рис.2).
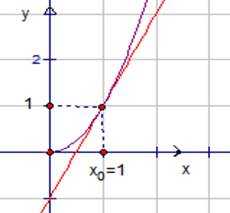
Рис. 2. Касательная к графику функции .
Зафиксируем точку . Значение функции в этой точке равно 1.
Алгоритм составления уравнения касательной к графику функции:
1) Найти и точку касания.
— дано.Точка касания: (;.
2) Найти производную в любой точке .
.
3) Найти значение производной в точке с абсциссой .
.
4) Выписать и проанализировать уравнение касательной.
.
Упрощаем и получаем: .
Ответ: .
4. Сопутствующие задачи
Задача 1.
Пусть дано уравнение касательной .
Найдите точки пересечения касательной с осями координат.
Если , то . – это первая точка.
Если , то . — вторая точка.
Итак, первая точка – это точка с координатами . Вторая точка – точка пересечения с осью , точка с координатами (см. рис.3).
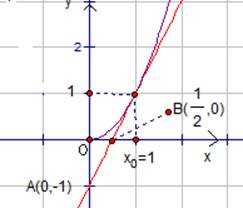
Рис.3. Точки пересечения касательной к графику функции с осями координат. Задача 2.
Найти длину отрезка касательной, которая отсекается осями координат, то есть надо найти длину отрезка .
Рассмотрим прямоугольный треугольник (Рис. 3). Длина катета равна 1. Длина катета . Длину отрезка из прямоугольного треугольника найдем по теореме Пифагора:
Задача 3.
Найти площадь треугольника, образованного касательной и осями координат. Ясно, что это площадь треугольника (Рис. 3) — площадь треугольника, образованного касательной и осями координат.
Следующая задача для самостоятельного решения.
Найдите радиус окружности, вписанной в треугольник . Радиус окружности, описанной около треугольника .
5. Касательная к графику тригонометрической функции
Рассмотрим пример.
Дана функция . Написать уравнение касательной к данной кривой в точке с данной абсциссой.
Рассмотрим графическую иллюстрацию (см. рис.4).
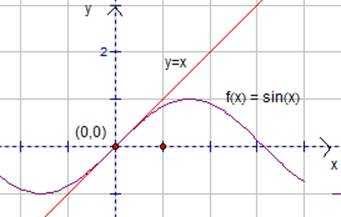
Рис. 4. Касательная к графику функции .
Нахождение точки касания.
1. Точка касания имеет координаты .
2. Найти .
3. Найти
И, последнее действие, – написать уравнение касательной.
4. .
Упростим и получим .
Заметим в точке синусоида и касательная соприкасаются. В районе точки синусоида и прямая почти не различаются.
Задачи для самостоятельного выполнения.
Написать уравнение касательной к графику функции в точке .
Написать уравнение касательной к графику функции в точке .
Найти абсциссы точек, в которых касательные к графику функции параллельны оси абсцисс.
Дано уравнение касательной у=3х-1. Найдите точки пересечения касательной с осями координат. Если , то . – это первая точка. Если , то . — вторая точка.
infourok.ru
Уравнение касательной и нормали к графику функции
Поиск ЛекцийИзвестно из школьного курса математики, что уравнение прямой линии, проходящей через точку с координатами и имеющей угловой коэффициент , имеет вид:
(7.1)
Подставляя в эту формулу вместо значениепроизводная функции в точке , получим уравнение касательной к графикуфункции в точке с координатами : или .
Определение 7.7. Нормальюк графику функции в точке с координатами называется прямая, перпендикулярная касательной и проходящая через те же точку .
Уравнение нормали к графику функции в точке с координатами получается из уравнения (7.1) прямой линии, имеющей угловой коэффициент , путем замены углового коэффициента
при условии, что .
Поэтому уравнение нормали имеет вид или .
Правила дифференцирования
Теорема 7.2.Постоянная функция имеет в любой точке производную, равную нулю.

Рисунок 7.2 Изображение функции
Рассмотрим функцию , её графиком будет прямая линия (см. рис.7.2). Возьмем произвольную точку , лежащую на графике функции. Дадим приращение . Получим точку , тоже лежащую на графике функции. Приращение значений функции будет равно нулю: . Поэтому , что и требовалось.
Теорема 7.3. Если каждая из функций и имеет производную в произвольной точке , то сумма , разность , произведение и частное ( при условии ) этих функций тоже имеет производную в этой точке , причем имеют место формулы
1) – производная суммы (разности) двух функций равна сумме (разности) производных каждой функции;
2) – производная произведения двух функций равна сумме производной первого множителя умноженной на второй множитель и первого множителя умноженного на производную второго множителя;
3) – производная частного двух функций равна частному от деления разности производной числителя умноженного на знаменатель и числителя умноженного на производную знаменателя, на квадрат знаменателя.
Следствие 7.1. Из второй формулы получаем свойство: постоянный множитель можно выносить за знак производной, если взять , тогда , и получаем или .
Доказательство формулы производной суммы (разности)
Обозначим .
Тогда .По определению производной и основным теоремах о пределах, получаем
Следствие 7.2. Свойство производной суммы (разности) двух функций можно распространить на любое конечное число функций: производная суммы (разности) функций равна сумме (разности) производных этих функций.
Доказательство формулы производной произведения двух функций.
Обозначим .
Тогда . По определению производной и основным теоремах о пределах, получаем
Прибавим и отнимем в числителе произведение , тогда
.
Отсюда
, или , что и требовалось.
Доказательство формулы производной частного двух функций.
Пусть
Отсюда
Прибавим и отнимем в числителе произведение , тогда
.
Переходим к пределу при и .
, что и требовалось.
Таблица дифференцирования основных функций
Вывод формулы производной степенной функции .
Рассмотрим функцию .
Тогда . Отношение
.
Заменяем бесконечно малый множитель в числителе на эквивалентную бесконечно малую и переходим к пределу при .
Частные случаи к формуле № 1:
Вывод формулы производной показательной функции . . Рассмотрим функцию ,тогда . Используя свойства показательной функции, преобразуем отношение
Отношение
.
Заменяем бесконечно малый множитель в числителе на эквивалентную бесконечно малую и переходим к пределу при .
.
В частном случае, когда основание показательной функции совпадает с Неперовым числом , то производная , т.к. .
Вывод формулы производной логарифмической функции
при .
Функция , тогда . Используя свойства логарифмов преобразуем отношение
.
Заменяя числитель на эквивалентную бесконечно малую и переходя к пределу при , получаем
.
В частном случае, когда основание логарифмической функции совпадает с Неперовым числом , то производная , т.к. .
Таблица дифференцирования тригонометрических функций
Вывод формулы .
Рассмотрим функцию . Отношение
.
В числителе заменили разность синусов на удвоенное произведение синуса полу-разности и косинус полу-суммы аргументов.
Переходим к пределу при , и учитывая, что , получаем
Аналогично, выводится формула .
Рассмотрим функцию .
Отношение
В числителе разность косинусов заменим на удвоенное произведение синуса полу-разности и синус полу-суммы аргументов, взятого со знаком минус.
Переходим к пределу при и учитывая, что , получаем
.
Вывод формулы осуществляется по правилу дифференцируемости отношения двух функций.
.
Аналогично,
Рекомендуемые страницы:
Поиск по сайту
poisk-ru.ru
