Формула уравнения окружности: 10.3. Уравнение окружности

Содержание

Уравнение Окружности Калькулятор — Mathcracker.Com

Инструкции: Используйте данный калькулятор для расчета формулы окружности, заданной радиусом и координатами x и y ее центра. Введите необходимую информацию в поля ниже.

Подробнее об этом уравнении окружности калькулятор

Данный калькулятор позволит вам получить уравнение окружности в стандартной форме и в общая форма , где показаны все шаги.

Вам необходимо указать правильный радиус окружности (правильное положительное числовое выражение), а также координаты x и y ее центра.

Числовые выражения, которые вы предоставите, могут быть чем-то вроде ‘1/2’ или составным выражением вроде ‘1/3+1/4’. Обратите внимание, что радиус должен быть положительным.

После того, как вы предоставите необходимую информацию с правильными данными, вам нужно будет нажать на кнопку «Рассчитать», и все этапы расчетов будут показаны вам.

Самый простой способ действовать в этом случае — сначала получить стандартная форма окружности с предоставленными данными, а затем просто расширить это выражение, чтобы получить общая форма уравнения окружности .

2\), где все, что вам нужно знать, это радиус r

Обратите внимание, что вышеописанный процесс заключается в нахождении уравнения окружности с заданными центром и радиусом. Другой способ получить уравнение окружности — начать с общего уравнения окружности, а затем сгруппировать и обработать выражение так, чтобы найти радиус и центр.

Уравнение окружности с пояснениями

У уравнения окружности есть два пути, обратных и в плане формулировки, и в плане интерпретации. С одной стороны, если вы знаете радиус r окружности и ее центр \((x_0, y_0)\), можно сказать, что вы уже знаете все, что вам нужно знать об окружности, по крайней мере, геометрически.

То есть, зная радиус и центр, вы можете нарисовать окружность. 2 \]

В таком случае вы знаете, что r — это радиус, а \((x_0, y_0)\) — его центр. Почему? Ну, это следует непосредственно из Теорема Пифагора .

Общее уравнение окружности калькулятор

Если уравнение дано в стандартной форме, вы будете знать все, что нужно знать об окружности, потому что вам напрямую известны радиус и центр. Но что если вам дано общее уравнение?

Шаг 1: Определите заданное общее уравнение. Это должно быть уравнение, квадратичное по x и y, иначе вы не сможете продолжить
Шаг 2: Получив общее уравнение, убедитесь, что коэффициенты умножения x^2 и y^2 одинаковы, иначе вы не сможете продолжить
Шаг 3: После того, как у вас есть действительное общее уравнение, вы выполняете процедуру Заполните квадраты процедура для x и y
Шаг 4: Получив стандартное уравнение путем заполнения квадратов и перестановки членов, вы определяете центр и радиус напрямую

Процедура заполнения квадрата может быть утомительной, но она является систематической, и ее проведение не должно быть слишком сложным. 2 = 1\). Все остальные окружности могут быть получены на основе единичной окружности путем преобразований и расширений или сужений.

Однако центром всех кругов является единичный круг, который прочно укоренился в алгебре и тригонометрии.

Пример: вычисление уравнения окружности

Вычислите следующее: Уравнение окружности с радиусом r = 3 и центром (3, -4).

Решение:

Нам нужно найти стандартную форму окружности, где заданный радиус равен \(r = \displaystyle 3\), а заданный центр — \(\left(\displaystyle 3, -4 \right)\). 2-6x+8y+16 = 0\).

Пример: подробнее о нахождении уравнения окружности

Вычислите следующее: \(\frac{1}{3} + \frac{5}{4} — \frac{5}{6}\)

Решение:

чем завершается расчет.

Пример: вычисления уравнения окружности

Рассчитайте \( \left(\frac{2}{3} \times \frac{6}{5} \right)+ \frac{2}{5} \).

Решение:

чем завершается расчет.

Другие полезные калькуляторы окружностей

Окружности и их свойства играют важнейшую роль в математике. Что можно сделать с помощью формула окружности ? Много! Например, вы можете использовать формула для площади круга или также использовать его формула окружности чтобы получить площадь и периметр, соответственно.

В кругах есть то, что неотъемлемо присуще математике. Его совершенная симметрия и тесная связь с \(\pi\) превратили их в увлекательный объект изучения для математиков всех времен.

Как найти уравнение окружности

Все математические ресурсы SAT

16 диагностических тестов 660 практических тестов Вопрос дня Карточки Learn by Concept

← Предыдущая 1 2 3 4 Следующая →

SAT Math Help » Геометрия » Координатная геометрия » Круги » Как найти уравнение окружности

Если центр окружности находится в точке (0,4) и диаметр окружности равен 6, каково уравнение этой окружности?

Возможные ответы:

x ² + (Y-4) ² = 9

(x-4) ² + Y ² =

x ² + (Y

0 =

x ² (у -4) ² = 36

x ² + Y ² =

(x-4) ² + Y ² = 36

Правильный ответ:

x ² + (у-4) ² = 9

Пояснение:

Формула уравнения окружности:

(x-h) ² + (y-k) ² = r ²

Где (h,k) — центр окружности.

h = 0 и k = 4

и диаметр = 6, поэтому радиус = 3

(x-0) ² + (y-4) ² = 3 ²

9 + 90 90 (y-4) ² = 9

Сообщить об ошибке

Круг A задается уравнением (x – 4) ² + (y + 3) ² = 29. Круг A сдвинут вверх на пять единиц и слева на шесть единиц. Затем его радиус удваивается. Какое новое уравнение для окружности A?

Возможные ответы:

(x — 10) ² + (Y + 8) ² = 116

(x + 2) ² + (Y — 2)

2 = 116

(х + 2) ² + (у – 2) ² = 58

(х – 10) ² + (у + 8) ² 1) 20 0

(–

) + (y + 2) ² = 58

Правильный ответ:

(x + 2) ² + (y – 2) ² = 116

5 Объяснение:

Общее уравнение окружности: (x – h) ² + (y – k) ² = r ² , где (h, k) представляет собой положение центра окружности, а r представляет собой длина его радиуса.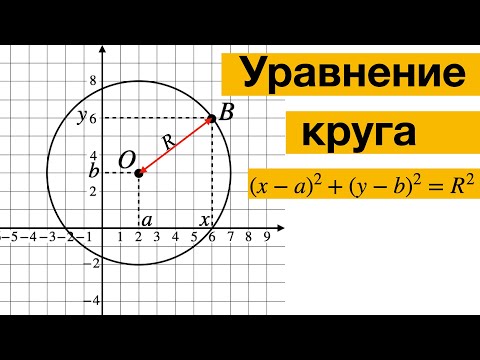

Окружность A сначала имеет уравнение (x – 4) ² + (y + 3) ² = 29. Это означает, что ее центр должен находиться в точке (4, –3), а ее радиус равен √ 29.

Затем нам сообщают, что окружность А сдвинулась вверх на пять единиц, а затем влево на шесть единиц. Это означает, что координата y центра увеличится на пять, а координата x центра уменьшится на 6. Таким образом, новый центр будет расположен в точке (4 – 6, –3 + 5), или ( –2, 2).

Затем нам сообщают, что радиус круга A удвоился, что означает, что его новый радиус равен 2√29.

Теперь, когда у нас есть новый центр и радиус окружности A, мы можем написать ее общее уравнение, используя (x – h) ² + (y – k) ² = r ² . 11 .

(x + 2) ² + (y – 2) ² = 116.

Ответ: (x + 2) ² + (y – 2) ² = 116.

Сообщить об ошибке

Какое из следующих уравнений описывает все точки (x, y) на координатной плоскости, которые находятся на расстоянии пяти единиц от точки (– 3, 6)?

Возможные ответы:

y + 6 = 5 – (x – 3) ²

(x – 3) ² + (y + 6) ^{2 0 9025 0 9 0 9 0 2 5 ) ² + (y + 6)}

2 = 5

(x – 3) ² – (y + 6) ² = 25

(x + 3) ² + (Y — 6) ² = 25

Правильный ответ:

(x + 3) ² + (Y — 6) ² = 25

Объяснение:

Мы пытаемся найти уравнение для всех точек, находящихся на одинаковом расстоянии (5 единиц) от (–3, 6). Геометрическое место всех точек, равноудаленных от одной точки, представляет собой окружность. Другими словами, нам нужно найти уравнение окружности. Центр круга будет (–3, 6), а радиус, который является расстоянием от (–3,6), будет равен 5.