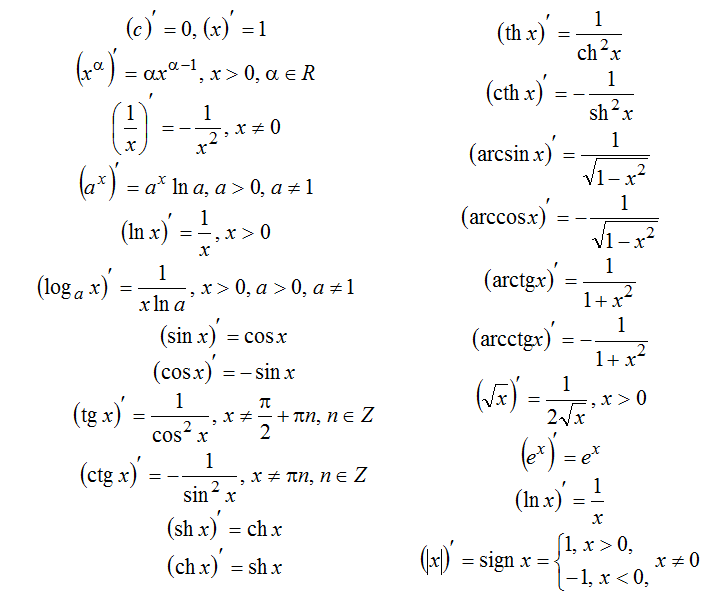Формулы для нахождения производной: Формулы производных функции

Содержание

Правила и формулы нахождения производных. Производная сложной функции.

Основные правила дифференцирования:

Производная постоянной равна нулю, т.е. .
Производная аргумента равна единице, т.е. .
Производная алгебраической суммы конечного числа дифференцируемых функций равна алгебраической сумме производных этих функций, т.е. .
Производная произведения двух дифференцируемых функций равна произведению производной первого сомножителя на второй плюс произведение первого сомножителя на производную второго, т.е. .

Следствие 1. Постоянный множитель можно выносить за знак производной: .

Следствие 2. Производная произведения нескольких дифференцируемых функций равна сумме произведений производной каждого из сомножителей на все остальные, например: .

Производная частного двух дифференцируемых функций может быть найдена по формуле (при условии, что ).
Производная сложной функции. Пусть задана сложная функция .

Теорема. Если и дифференцируемые функции от своих аргументов, то производная сложной функции существует и равна производной данной функции по промежуточному аргументу и умноженной на производную промежуточного аргумента по независимой переменной , т.е..

Производные основных элементарных функций (таблица производных):

Производная логарифмической функции.

А) и, где некоторая функция зависящая от .

Б) и.

Производная показательной функции.

А) и.

Б) и.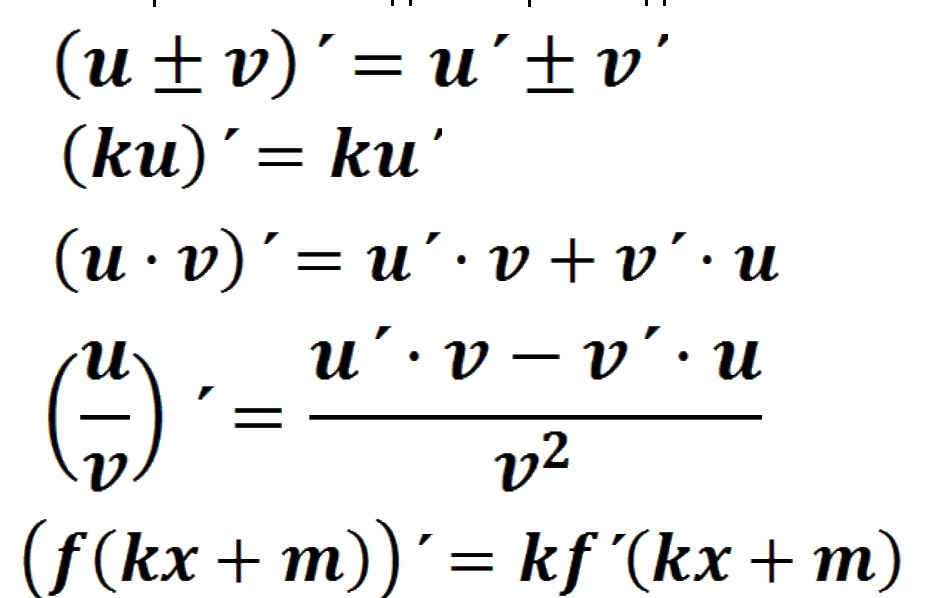

Производная степенной функции.

и .

Производная степенно-показательной функции.

Производная тригонометрических функций.

и ;

и .

Производная обратных тригонометрических функций.

и ;

и .

Пример. Найти производные следующих функций:

А) ;	Б) ;
В) ;	Г) .

Производные высших порядков.

Производной второго порядка или второй производной функции называется производная от ее первой производной, т. е., и обозначаетсяилиили.

Аналогично определяются и обозначаются: производная 3-го порядка ; производная 4-го порядка; ………… производная-го порядка.

Пример. Найти производную 2-го и 3-го порядка:

А)

Б)

Понятие дифференциала и его геометрический смысл.

Пусть функция определена на промежуткеи дифференцируема в окрестности точки,тогдаили по теореме о связи бесконечно малых с пределами функций имеем, где бесконечно малая величина при . Отсюда:. Таким образом, приращение функциисостоит из двух слагаемых: 1. линейного относительно , т.к.; 2. нелинейного относительно , т.к..

Дифференциалом функции называется главная, линейная относительно часть приращения функции, равная произведению производной на приращение независимой переменной:.

Пример. Найти приращение функции прии

Пример. Найти дифференциал функции .

Дифференциал независимой переменной равен приращению этой переменной:.

Тогда формулу для дифференциала функции можно записать в виде: . Откуда, поэтомуможно рассматривать не только как символическое обозначение производной, но и как обычную дробь с числителеми знаменателем.

Геометрический смысл. На графике функции (рис. 5.) возьмем произвольную точку . Дадим аргументуприращение, тогда функция получает приращение. В точкепроведем касательную, образующую уголс осью. Извидно, что. Изимеем:. Таким образом,и соответствует формуле.

Рис. 5.

Следовательно, с геометрической точки зрения дифференциал функции есть приращение ординаты касательной, проведенной к графику функции в данной точке, когдаполучает приращение.

Свойства дифференциала аналогичны свойствам производной:

1) .

4) .

2) .

3) .

5) .

Формула дифференциала не изменится, если вместо функции от независимой переменной рассматривать функцию от зависимой переменной. Это свойство дифференциала получило названиеинвариантности (т.е. неизменности) формы дифференциала, т.е. .

Приближенные вычисления с помощью дифференциала. Согласно формулы , т.е., при достаточно малых значенияхприращение функцииприблизительно равно ее дифференциалу,. Эту формулу часто используется в приближенных вычислениях.

Пример. Вычислить .

найти производную функции f(x)=x в четвертой степени

Ответ или решение2

Вера

Исходя из условия задачи нам необходимо найти производную следующей функции:

f(x) = x^4

Для нахождения производной данной рассматриваемой функции нам необходимо воспользоваться следующим свойством производной:

(x^a)’ = a * x^(a — 1)

Применим данное свойство производной к нашей исходной функции и получим, что решение будет иметь следующий вид:

f'(x) = (x^4)’ = 4 * x^(4 — 1) = 4 * x^3

Таким образом мы получили, что производная нашей функции f(x) = x^4 имеет следующий вид: f'(x) = 4 * x^3

Мария

По условию задачи нам необходимо вычислить производную функции y = x⁴.

Правила и формулы для вычисления производной

Для вычисления нашей производной будем использовать следующие правила и основные формулы дифференцирования

(xⁿ)’ = n * x^(n-1).
(с)’ = 0, где с – const.
(с * u)’ = с * u’, где с – const.

Вычисление производной

Найдём производную нашей данной функции: f(x) = x

Чтобы найти производную нашей данной функции будем использовать, основную формулу дифференцирования и запишем это так:

f(x)’ = (x⁴)’.

Для того чтобы вычислить нашу производную используем формулы дифференцирования и правила дифференцирования. Продифференцируем нашу данную функцию:

Вычислим производную от «x⁴»:

перед «x⁴» коэффициент 1;
производная от «x⁴» – это будет «4 * x^{(4 – 1)} = 4 * x³ = 4x³»;
следовательно, у нас получается, что «(x⁴)’ = 1 * 4x³ = 4x³».

Для полного закрепления данной темы рассмотрим несколько примеров, где будем применять основную формулу дифференцирования (xⁿ)’ = n * x^(n-1).

(x³)’ = 3 * x^{(3 – 1)}
= 3 * x² = 3x².
(x⁵)’ = 5 * x^{(5 – 1)} = 5 * x⁴ = 5x⁴.
(x⁶)’ = 6 * x^{(6 – 1)} = 6 * x⁵ = 6x⁵.
(x⁷)’ = 7 * x^{(7 – 1)} = 7 * x⁶ = 7x⁶.
(x⁸)’ = 8 * x^{(8 – 1)} = 8 * x⁷ = 8x⁷.
(x⁹)’ = 9 * x^{(9 – 1)} = 9 * x⁸ = 9x⁸.
(x¹⁰)’ = 10 * x^{(10 – 1)} = 10 * x⁹ = 10x⁹.

Таким образом, производная нашей данной функции будет следующая:

f(x)’ = (x⁴)’ = 4 * x^{(4 – 1)} = 4 * x³ = 4x³.

Выходит, что наша производная данной функции будет выглядеть таким образом:

f(x)’ = 4x³.

Ответ: Производная нашей данной функции будет равна f(x)’ = 4x³.

Знаешь ответ?

Как написать хороший ответ?Как написать хороший ответ?

Будьте внимательны!

Копировать с других сайтов запрещено. Стикеры и подарки за такие ответы не начисляются. Используй свои знания. 🙂
Публикуются только развернутые объяснения. Ответ не может быть меньше 50 символов!

0 /10000

Есть ли определенная формула для производных? + Пример

Да, но не одна формула. Есть много.

Производная (дифференцируемой функции) #y=f(x)# в точке #x=a# определяется следующим пределом

# f'(a) = lim_(x rarr a )(f(x)-f(a))/(x-a) #

С небольшим изменением записи можно написать:

# dy/dx = f'(x) = lim_(h rarr 0 ) (f(x+h)-f(x))/h #

В некоторых старых текстах обозначения могут включать #deltax# или #Deltax# вместо #h#, что дает идентичный результат:

# f'(x) = lim_(deltax rarr 0 ) (f(x+deltax)-f(x))/(deltax) = lim_(Deltaxrarr 0 ) (f(x+deltax)-f(x)) /(Дельтакс)#

Представляет как скорость изменения функции, так и градиент касательной в любой конкретной точке. Если предел не существует, то функция не дифференцируема.

На практике мы не выводим производную из первых принципов, используя определение предела, а вместо этого используем различные правила, истинность которых можно доказать; 92#

Вот несколько других полезных производных формул, которые, я думаю, вам следует знать.

#d/dx(lnx) = 1/x#
#d/dx(sinx) = cosx#
#d/dx(cosx) = -sinx#

После того, как вы освоите основные правила дифференцирования, вас могут попросить решить задачи, которые интересным образом комбинируют правила дифференцирования.

Пример: Найти #dy/dx# для #y = ln(secx)#

Прежде всего, обратите внимание, что #secx = 1/cosx#. Функция становится

9-1#, а затем дважды дифференцировать по цепному правилу.

c) вы можете использовать законы логарифмов, чтобы упростить, а затем дифференцировать. Я воспользуюсь этим методом.

По правилу #ln(a/b) = lna — lnb# имеем:

#y = ln(1/cosx) = ln1 — lncosx = 0 — ln(cosx) = -ln(cosx)#

По правилу цепочки имеем

#dy/dx = -1/cosx * -sinx = sinx/cosx = tanx#

Надеюсь, теперь вы понимаете, что такое дифференциация!