Презентация к уроку «Формулы корней квадратного уравнения»
| 12+ Свидетельство СМИ ЭЛ № ФС 77 — 70917 Лицензия на образовательную деятельность №0001058 | Пользовательское соглашение Контактная и правовая информация |
Педагогическое сообщество | Бесплатные всероссийские конкурсы | Бесплатные сертификаты | Нужна помощь? Инструкции для новых участников | Бесплатная онлайн-школа для 1-4 классов |
Всё для аттестацииПубликация в сборникеВебинарыЛэпбукиПрофтестыЗаказ рецензийНовости
Библиотека▪Публикации▪Статьи
Материал опубликовала
#8 класс #Алгебра #ФГОС #Учебно-дидактические материалы #Контрольные / проверочные работы #Учитель-предметник #Школьное образование #УМК А.
Г. Мордковича
Решите анаграммы (в словах изменен порядок букв) Таиимдкисрнн Ниваренуе Фэкоцинетиф Ерокнь дискриминант уравнение коэффициент корень
Математический диктант 1. Квадратным уравнением называется уравнение вида … 2. Числа а, в, с называются … квадратного уравнения. 5. Квадратное уравнение называется приведённым, если … 6. Дискриминант квадратного уравнения вычисляется по формуле D = … . 7. Если D > 0, то квадратное уравнение имеет … . 3. В уравнении 3х² – 5х + 2 = 0 а = …, в = …, с = … . 4. Составьте квадратное уравнение, если а = 2, в = 4, с = – 5.
8. Если D = 0, то квадратное уравнение имеет… .
11. Закончите решение уравнения:
3х² – 5х + 2 = 0.
D = в² – 4ac,
D = (–5)² – 4·3·2 = 25 – 24 = 1,
х1 = …, х2 = … .
Математический диктант
9. Если D < 0, то квадратное уравнение … .
10.Корни квадратного уравнения находятся по
формулам: х1 = …, х2 = … .
Проверяем 1. ах² + вх + с = 0, а ≠ 0 2. коэффициентами 5. a = 1 7. два корня 9. не имеет корней 10. 11. х1 = 1, х2 = Х 1= 3. a = 3, b = – 5, c = 2 6. в² – 4ac 4. 2х² + 4х – 5 = 0 8. один корень
х² – 3175 х + 3174 = 0 ? ?
Сначала я делал открытия всем давно известные, потом не так известные, а потом новые. К.Э.Циолковский
Связь между корнями квадратного уравнения и его коэффициентами
1-я группа
2-я группа
3-я группа
1.
5х² – 8х + 3 = 0
2. – х² + 4х – 3 = 0
3. 2х² + 3х – 5 = 0
4. х² – 3х + 2 = 0
1. х² – 4х – 5 = 0
2. – х² + 4х + 5 = 0
3. 2х² + 5х + 3 = 0
4. 5х² – 3х – 8 = 0
1. х² – 5х + 6 = 0
2. х² + 7х + 12 = 0
3. х² + 3х – 18 = 0
4. х² – 2х – 15 = 0
1-я группа 1. 5х² – 8х + 3 = 0 2. – х² + 4х – 3 = 0 3. 2х² + 3х – 5 = 0 4. х² – 3х + 2 = 0
2-я группа 1. х² – 4х – 5 = 0 2. – х² + 4х + 5 = 0 3. 2х² + 5х + 3 = 0 4. 5х² – 3х – 8 = 0
3-я группа 1. х² – 5х + 6 = 0 2. х² + 7х + 12 = 0 3. х² + 3х – 18 = 0 4. х² – 2х – 15 = 0
х² – 3175 х + 3174 = 0 х1 = 1, х2 = 3174
1.
3х² – 7х + 4 = 0
2. 5х² + 9х + 4 = 0
3. х² – 7х + 10 = 0
4. х² – х – 6 = 0
5. 4х² – 9х + 5 = 0
6. 2х² – 9х – 11 = 0
1. 3х² – 7х + 4 = 0
5. 4х² – 9х + 5 = 0
2. 5х² + 9х + 4 = 0
6. 2х² – 9х – 11 = 0
3. х² – 7х + 10 = 0
4. х² – х – 6 = 0
1. 3х² – 7х + 4 = 0 5. 4х² – 9х + 5 = 0 3 + (–7) + 4 = 0, х1 = 1, х2 = 4 + (–9)+ 5 = 0, х1 = 1, х2 =
2. 5х² + 9х + 4 = 0 6. 2х² – 9х – 11 = 0 2 – (– 9)+ (–11) = 0 или – 9 = 2 – 11, х1 = –1, х2 = 5 – 9 + 4 = 0 или 9 = 5 + 4, х1 = –1, х2 = –
3. х² – 7х + 10 = 0 4. х² – х – 6 = 0 х1 + х2 = 7, х1· х2 = 10, х1 = 2, х2 = 5 х1 + х2 = 1, х1 · х2 = – 6, х1 = 3, х2 = –2
«5» 16 и более «4» 14 — 15 «3» 13 и менее
А я и не знал .
..
8 класс. Алгебра. Квадратные уравнения. — Теорема Виета.
Комментарии преподавателяПознакомимся с теоремой Виета, с соотношениями между корнями квадратного уравнения и его коэффициентами, научимся раскладывать квадратный трёхчлен на множители.
Квадратным уравнением называют уравнение вида ax2 +bx + c = 0, где a, b, c-коэффициенты, х – переменная, причём a ≠ 0. Левая часть квадратного уравнения
ax2 + bx +c – это многочлен второй степени, его называютквадратным трехчленом. Если в квадратном уравнении коэффициент при х2 или, можно сказать, старший коэффициент a равен 1, то такое квадратное уравнение называют приведенным.
Теорема Виета справедлива и для квадратных уравнений, имеющих один корень. В этом случае считают, что уравнение имеет два одинаковых корня.
Теорему Виета удобно применять для приведенного квадратного уравнения:
Приведенное квадратное уравнение можно записать в виде:
Тогда сумма корней х1 +х2 равна второму коэффициенту, взятому с противоположным знаком, то есть – р, а произведение корней х1∙ х2 равно свободному члену q.
х1 +х2 = – р
х1∙ х2 = q
По теореме Виета можно подбором найти корни уравнения.
Например, решим квадратное уравнение х2 – х – 12 = 0.
Уравнение является приведенным, так как коэффициент a равен 1. Тогда сумма корней х1 + х2 = 1, а произведение х1 ∙ х2= –12. Если х1 и х2 целые числа, то они являются делителями числа –12. Нетрудно догадаться, что х1 = –3; х2 = 4.
По теореме обратной теореме Виета можно выполнить проверку правильности нахождения корней квадратного уравнения.
Обратное утверждение теоремы Виета:
Если х1 и х2 – корни квадратного уравнениятакие, чтох1 + х2 = –р, х1 ∙ х2 = q, то эти числа0 – корни уравнения х2 + рх + q = 0.
Решим уравнение 3х2 – 4х – 4 = 0.
Дискриминант D = (-4)2 -4 ∙ 3 ∙ (-4) = 64, D > 0.
Найдем корни:
Значит, квадратный трехчленможно разложить на множители ax2 + bx + c = a(х– х1) (х –х2),где х1и х2 – корни квадратного трехчлена, которые можно найти, решая квадратное уравнение ax2 + bx +c = 0.
Если х1 = х2 , т.е. дискриминант квадратного трехчлена равен нулю (D = 0), то доказанная формула будет иметь вид ax2 + bx + c = a(х– х1)2.
Разложим на множители квадратный трехчлен 3х2 – 10х + 3.
Для этого решим квадратное уравнение 3х2 – 10х + 3 = 0.
Дискриминант D = = (-10)2 – 4 ∙ 3 ∙ 3 = 64, D > 0.
Тогда сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком х1 +х2 = –р, а произведение корней равно свободному члену х1∙ х2 = q. Эти соотношения впервые обнаружил французский математик Франсуа Виет.
По теореме Виета можно подбором найти корни уравнения.
Если свободный член q – отрицательное число, то корни имеют разные знаки. По теореме, обратной теореме Виета, можно проверить правильность нахождения корней.
С помощью теоремы Виета выводится формула разложения квадратного трёхчлена на множители a x2 + bx +c= a(х — х1) (х -х2), где х1; х2 – корни квадратного трехчлена.
Источник конспекта: http://znaika.ru/catalog/8-klass/algebra/Teorema-Vieta.-Razlozhenie-kvadratnogo-tryokhchlena-na-mnozhiteli
Источник видео: http://www.youtube.com/watch?v=bO7s5qOo7zk
ФайлыНет дополнительных материалов для этого занятия.
Дискриминант
Дискриминант
Краткий обзор квадратичной формулы
Квадратное уравнение представляет собой уравнение вида любое такое квадратное уравнение, квадратная формула:
| Корни (x 1 , x 2 ) = | −b ± √ б2 — 4ас |
| 2a |
Объяснение дискриминанта
В приведенной выше квадратной формуле величина «b 2 — 4ac» , стоящая под знаком квадратного корня, называется дискриминантом квадратного уравнения.
Дискриминант = b 2 — 4ac
Пример вычисления дискриминанта
Для квадратного уравнения x 2 + 4x + 4 = 0, определите определятель
Ответ
x 2 + 5x + 5 = 0
Дискриминанту = B 2 — 4AC
, A = 1, B = 5 , c = 5
Дискриминант = b 2 — 4ac = 5 2 — 4(1)(5) = 5
Использование дискриминанта
говорит о природе квадратичных корней уравнение. Корни могут быть действительными, равными или мнимыми.
В зависимости от значения дискриминанта квадратное уравнение может иметь:
◾ два действительных и неравных корня при значении дискриминанта > 0
◾ только один действительный и равный корень при значении дискриминанта = 10 904
◾ нет действительных корней т.е. оба корня являются мнимыми, когда значение дискриминанта < 0
Случай I.
Когда дискриминант > 0
Для квадратного уравнения x 2 — 12x + 32 = 0, определить дискриминант и корни квадратного уравнения = 32
Дискриминант = (-12) 2 — 4(1)(32) = 144 — 128 = 16
Мы знаем, что квадратичная формула равна
| 2 ) = | −b ± √ б2 — 4ас |
| 2a |
| х 1 = | −(-12) + √ (-12)2 − 4(1)(32) | = 8 |
| 2(1) |
| х 1 = | −(-12) — √ (-12)2 — 4(1)(32) | = 4 |
| 2(1) |
Следовательно, для квадратного уравнения x 2 — 12x + 32 = 0 мы получаем два действительных и различных корня — 8 и 4
Следовательно, при Дискриминанте > 0 квадратное уравнение имеет 2 действительных и различные корни
Случай II – когда дискриминант = 0
Для квадратного уравнения x 2 — 12x + 36 = 0, определите дискриминанту и корни квадратного уравнения
Ответ
Дискриминанте = 1, b = -12 , c = 36
Дискриминант = (-12) 2 — 4(1)(36) = 144 — 144 = 0
Мы знаем, что квадратичная формула равна
| Корни(х 1 , х 2 ) = | −b ± √ б2 — 4ас |
| 2a |
| х 1 = | −(-12) + √ (-12)2 − 4(1)(36) | = 6 |
| 2(1) |
| х 1 = | −(-12) — √ (-12)2 — 4(1)(36) | = 6 |
| 2(1) |
Следовательно, для квадратного уравнения x 2 — 12x + 36 = 0 мы получаем только один действительный и равный корень, равный 6.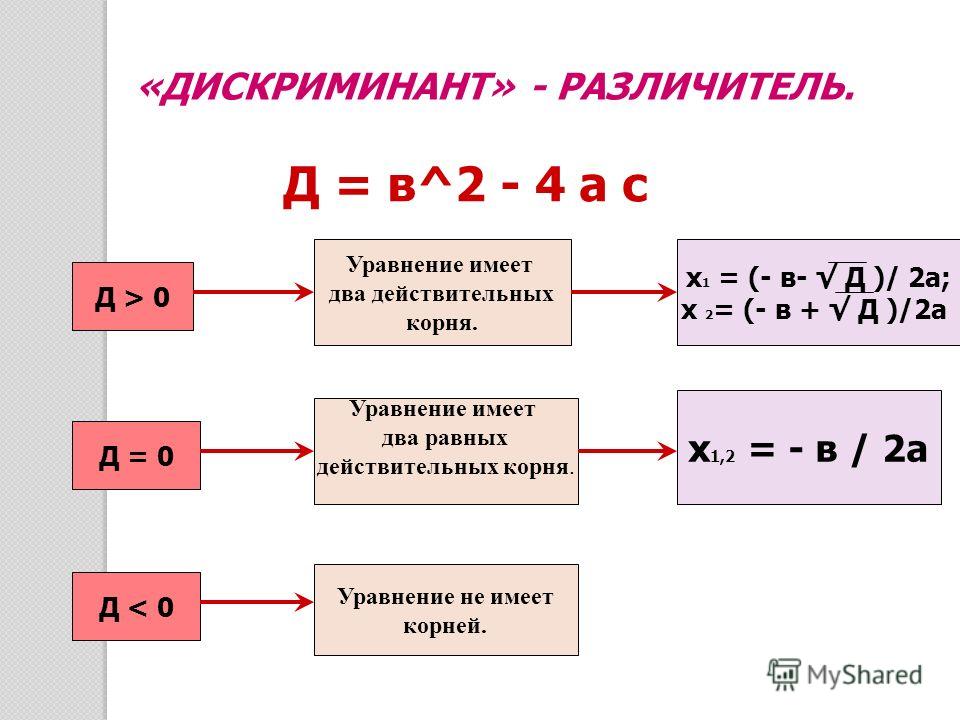
Следовательно, при Дискриминанте = 0 квадратное уравнение имеет только один действительный и равный корень
Случай III, когда дискриминантирует <0
для квадратного уравнения x 2 + 4x + 10 = 0, определите дискриминанту и корни квадратичного уравнения
Ответ
Дискриминант = b 2 – 4ac
Здесь a = 1, b = 4 , c = 10
Дискриминант = (4) 2 — 4(1)(10) = 16 — 40 = -24
Мы знаем что квадратичная формула равна
| Корни (х 1 , х 2 ) = | −b ± √ б2 — 4ас |
| 2a |
| х 1 = | −(4) + √(4)2 − 4(1)(10) | = | −(4) + √ -24 |
| 2(1) | 2 |
| х 1 = | −(4) — √(4)2 — 4(1)(10) | = | −(4) — √-24 |
| 2(1) | 2 |
Следовательно, для квадратного уравнения x 2 + 4x + 10 = 0 мы не получаем действительных корней
Следовательно, при Дискриминанте < 0 квадратное уравнение не имеет действительных корней
Резюме Значение дискриминанта Случаи Корни квадратного числа Факторизация квадратного числа Значение дискриминанта > 0 два действительных различных корня два различных линейных коэффициента Значение дискриминанта = 0 два одинаковых действительных корня два одинаковых линейных коэффициента Значение дискриминанта < 0 Нет настоящих корней Невозможно разложить на множители Решение квадратного уравнения в Excel (простой учебник)
Квадратное уравнение имеет вид ax 2 + bx + c = 0, где a ≠ 0.
Квадратное уравнение можно решить с помощью квадратной формулы. Вы также можете использовать функцию поиска цели Excel для решения квадратного уравнения.
1. Например, у нас есть формула у = 3х 2 — 12х + 9,5. Легко вычислить y для любого заданного x. Для x = 1, y = 0,5
2. Для x = 2, y = -2,5
3. Но что, если мы хотим узнать x для любого заданного y? Например, у = 24,5. Нам нужно решить 3x 2 — 12x + 9,5 = 24,5. Мы можем решить квадратное уравнение 3x 2 — 12x + 9,5 — 24,5 = 0, используя квадратную формулу.
3x 2 — 12x -15 = 0
а = 3, б = -12, с = -15
D = b 2 — 4ac = (-12) 2 — 4 * 3 * -15 = 144 + 180 = 324
| x = | -б + √D | или | х = | -b — √D |
| 2а | 2а |
| х = | 12 + √324 | или | х = | 12 — √324 |
| 6 | 6 |
| х = | 12 + 18 | или | х = | 12 — 18 |
| 6 | 6 |
| х = | 5 | или | х = | -1 |
4.