Интегрирование по частям: объяснение, решение примеров
- Суть метода интегрирования по частям
- Применяем интегрирование по частям вместе
- Применить интегрирование по частям самостоятельно, а затем посмотреть решение
- Снова применяем интегрирование по частям вместе
- Интегрирование по частям для вывода рекуррентных формул
Следующая формула называется формулой интегрирования по частям в неопределённом интеграле:
Для
применения формулы интегрирования по частям подынтегральное выражение нужно разбить на два множителя.
Один из них обозначается через u, а остальная часть относится ко второму множителю и
обозначается через dv. Затем дифференцированием находится du и интегрированием —
функция v. При этом за u следует брать такую часть подынтегральной функции,
которая при дифференцировании сильно не усложняется, а за dv — такую часть подынтегрального
выражения, которая легко интегрируется.
Когда выгодно применять метод интегрирования по частям? Тогда, когда подынтегральная функция содержит:
1) — логарифмические функции, а также обратные тригонометрические функции (с приставкой «arc»), тогда на основании продолжительного опыта интегрирования по частям эти функции обозначаются через u;
2) , , — синус, косинус и экспоненту, умноженные на P(x) — произвольный многочлен от икса, тогда эти функции обозначают через dv, а многочлен — через u;
3) , , , , в этом случае интегрирование по частям применяется дважды.
Поясним ценность метода интегрирования по частям на примере первого случая. Пусть выражение
под знаком интеграла содержит логарифмическую функцию (таким будет пример 1). Применением интегрирования по частям
такой интеграл сводится вычислению интеграла только алгебраических функций (чаще всего многочлена), то есть
не содержащих логарифмическую или обратную тригонометрическую функцию.
,
получаем в первом слагаемом (без интеграла) логарифмическую функцию, а во втором слагаемом (под знаком интеграла) — функцию, не содержащую логарифма. Интеграл алгебраической функции намного проще интеграла, под знаком которого находятся отдельно или вместе с алгебраическим множителем логарифмическая или обратная тригонометрическая функция.
Таким образом, с помощью формулы интегрирования по частям интегрирование не выполняется сразу: нахождение данного интеграла сводится к нахождению другого. Смысл формулы интегрирования по частям состоит в том, чтобы в результате её применения новый интеграл оказался табличным или хотя бы стал проще первоначального.
Метод интегрирования по частям основан на использовании формулы дифференцирования произведения двух функций:
Так как
то её можно записать в виде
,
который и был приведён в самом начале урока.
При нахождении интегрированием функции v для неё получается бесконечное множество первообразных функций. Чтобы применить формулу интегрирования по частям, можно взять любую из них, а значит, и ту, которая соответствует произвольной постоянной С, равной нулю. Поэтому при нахождении функции v произвольную постоянную С вводить не следует.
Есть у метода интегрирования по частям совершенно особенное применение: с его помощью
можно выводить рекуррентные формулы для нахождения первообразных функций, когда требуется понизить степень функций
под знаком интеграла. Понижение степени необходимо, когда не существует табличных интегралов для таких, например,
функций, как синусы и косинусы в степени более второй и их произведения. Рекуррентная формула — это формула для
нахождения очередного члена последовательности через предыдущий член. Для обозначенных случаев цель достигается
последовательным понижением степени. Так, если подынтегральная функция — синус в
четвёртой степени от икса, то методом интегрирования по частям можно найти формулу для интеграла синуса в третьей
степени и так далее. Описанной задаче посвящен последний параграф этого урока.
Так, если подынтегральная функция — синус в
четвёртой степени от икса, то методом интегрирования по частям можно найти формулу для интеграла синуса в третьей
степени и так далее. Описанной задаче посвящен последний параграф этого урока.
- Пригодится: тригонометрические тождества для преобразования выражений
Пример 1. Найти неопределённый интеграл методом интегрирования по частям:
.
Решение. В подынтегральном выражении — логарифм, который, как мы уже знаем, разумно обозначить через u. Полагаем, что , .
Тогда , .
Находим (как уже говорилось в пояснении к теоретической справке, сразу же получаем в первом слагаемом (без интеграла) логарифмическую функцию, а во втором слагаемом (под знаком интеграла) — функцию, не содержащую логарифма, сводящуюся к табличному интегралу (8)):
Для самопроверки при расчетах можно воспользоваться калькулятором неопределённых интегралов онлайн.
И снова логарифм…
Пример 2.
Найти неопределённый интеграл:.
Решение. Пусть , .
Логарифм присутствует в квадрате. Это значит, что его нужно дифференцировать как
сложную функцию. Находим, пользуясь производной 6 в таблице производных сложных функций:
,
.
Применяя формулу интегрирования по частям, получаем:
Второй интеграл вновь находим по частям и получаем уже упомянутое преимущество (в первом слагаемом (без интеграла) логарифмическую функцию, а во втором слагаемом (под знаком интеграла) — функцию, не содержащую логарифма, сводящуюся к табличному интегралу 9).
Находим изначальный интеграл:
Пример 3. Найти неопределённый интеграл методом интегрирования по частям:
.
Решение. Арктангенс, как и логарифм, лучше обозначить через u. Итак, пусть , .
Тогда, пользуясь табличной производной 12, получаем
,
.
Применяя формулу интегрирования по частям, получаем:
Второй интеграл находим методом замены переменной.
Возвращаясь к переменной x, получаем
.
Находим изначальный интеграл:
.
Для самопроверки при расчетах можно воспользоваться калькулятором неопределённых интегралов онлайн.
Пример 4. Найти неопределённый интеграл методом интегрирования по частям:
Решение. Экспоненту лучше обозначить через dv. Разбиваем подынтегральное выражение на два множителя. Полагая, что
находим
(воспользовались табличной производной 16).
- Пригодится: тригонометрические тождества для преобразования выражений
Проверить решение задач на неопределённый интеграл можно на калькуляторе неопределённых интегралов онлайн.
Нет времени вникать в решение? Можно заказать работу!
Пример 5. Найти неопределённый интеграл методом интегрирования по частям:
.
Решение. Пусть , . Тогда , (воспользовались табличной производной 4 в таблице производных сложной функции).
Используя формулу интегрирования по частям (1), находим:
Пример 6. Найти неопределённый интеграл методом интегрирования по частям:
.
Решение. Синус, как и экспоненту, удобно обозначить через dv. Пусть , .
Тогда , .
По формуле интегрирования по частям находим:
- Пригодится: тригонометрические тождества для преобразования выражений
Пример 7. Найти неопределённый интеграл методом интегрирования по частям:
Найти неопределённый интеграл методом интегрирования по частям:
.
Посмотреть правильное решение и ответ.
Пример 8. Найти неопределённый интеграл методом интегрирования по частям:
.
Посмотреть правильное решение и ответ.
Пример 9. Найти неопределённый интеграл методом интегрирования по частям:
.
Посмотреть правильное решение и ответ.
Для самопроверки при расчетах можно воспользоваться калькулятором неопределённых интегралов онлайн.
Пример 10. Найти неопределённый интеграл методом интегрирования по частям:
.
Решение. Как и во всех подобных случаях, косинус удобно обозначить через dv. Обозначаем
,
(производная 7 в
таблице производных сложной функции).
Тогда (табличные производные 3 и 2), ().
По формуле интегрирования по частям получаем:
Ко второму слагаемому также применяем интегрирование по частям. Обозначаем , .
Применив эти обозначения, интегрируем упомянутое слагаемое:
Теперь находим требуемый интеграл:
Среди интегралов, которые можно решить методом интегрирования по частям, есть и такие,
которые не входят ни в одну из трёх упомянутых в теоретической части групп, относительно которых из
практики известно, что лучше обозначать через u, а что через dv. Поэтому в этих случаях
нужно пользоваться соображением удобства, также приведённым в параграфе «Суть метода интегрирования по частям»:
за u следует брать такую часть подынтегральной функции,
которая при дифференцировании сильно не усложняется, а за dv — такую часть подынтегрального
выражения, которая легко интегрируется. Последний пример этого урока — решение именно такого интеграла.
Последний пример этого урока — решение именно такого интеграла.
Пример 11. Найти неопределённый интеграл методом интегрирования по частям:
.
Решение. Примем как руководство к действию общее соображение относительно обозначений. Обозначаем , (табличная производная 8).
Тогда , .
По формуле интегрирования по частям получаем:
- Пригодится: тригонометрические тождества для преобразования выражений
Случаев, когда требуется понижения степени подынтегральной функции, мы уже коснулись во вводной части урока. Теперь — практика использования для этой цели метода интегрирования по частям.
Пример 12. Используя интегрирование по частям, вывести рекуррентную формулу для
,
найти I4.
Решение. Для удобства приведём исходный интеграл к такому выражению, в котором присутствовали
бы и синус, и косинус. Используя тригонометрические тождества, получаем
Для удобства приведём исходный интеграл к такому выражению, в котором присутствовали
бы и синус, и косинус. Используя тригонометрические тождества, получаем
Ко второму слагаемому — интегралу — применяем метод интегрирования по частям. Для этого обозначим
Тогда
Находим это второе слагаемое — интеграл:
Теперь находим рекуррентную формулу для исходного интеграла:
С помощью полученной формулы найдём I4:
| Назад | Листать | Вперёд>>> |
К началу страницы
Пройти тест по теме Интеграл
Начало темы «Интеграл»
Неопределённый интеграл: основные понятия, свойства, таблица неопределённых интегралов
Найти неопределённый интеграл: начала начал, примеры решений
Метод замены переменной в неопределённом интеграле
Интегрирование подведением под знак дифференциала
Продолжение темы «Интеграл»
Интегрирование дробей
Интегрирование рациональных функций и метод неопределённых коэффициентов
Интегрирование некоторых иррациональных функций
Интегрирование тригонометрических функций
Определённый интеграл
Несобственные интегралы
Площадь плоской фигуры с помощью интеграла
Объём тела вращения с помощью интеграла
Вычисление двойных интегралов
Длина дуги кривой с помощью интеграла
Площадь поверхности вращения с помощью интеграла
Определение работы силы с помощью интеграла
Поделиться с друзьями
07.
 Метод интегрирования по частям в неопределенном интеграле
Метод интегрирования по частям в неопределенном интегралеПусть функции и дифференцируемы на множестве Х и функция имеет первообразную на Х. Тогда функция тоже имеет первообразную и
Чаще всего с помощью метода интегрирования по частям вычисляются интегралы вида:
1) ; | 2) ; | 3) ; |
4) ; | 5) ; | 6) ; |
7) . |
Здесь – многочлен степени . При вычислении интегралов первых четырех типов формулу интегрирования по частям приходится применять столько раз, какова степень многочлена, а для вычисления интеграла типа 7) раз.
Примеры. Вычислить неопределенные интегралы:
1) ; | 3) ; |
2) ; | 4) . |
Решение
В следующем примере степень многочлена и, метод интегрирования по частям придется применить дважды
2) | |
; | |
3) | |
; | |
4) | |
. |
С помощью метода интегрирования по частям можно получить уравнение относительно исходного интеграла или рекуррентное соотношение.
Примеры. Вычислить неопределенные интегралы:
1) ; | 3) ; |
2) ; | 4) . |
Решение
1) Обозначим
Интегралы 2) и 3) можно вычислять одновременно.
Таким образом, получаем систему:
Если степень многочлена достаточно высокая, то для вычисления интегралов вида:
1)
2)
3)
Получим такие формулы.
А)
Используя полученную формулу, несложно вычислить, например,
.
Б)
Аналогично может быть получена формула для
Используя формулы (2) и (3) вычислим:
А) Б)
А)
.
Б)
.
2. С помощью метода интегрирования по частям можно вывести так называемые рекуррентные формулы, дающие возможность свести некоторые интегралы к интегралам такого же типа, но более простым по структуре. Этот метод даёт возможность получить рекуррентную формулу для вычисления интеграла
Этот метод даёт возможность получить рекуррентную формулу для вычисления интеграла
.
Ко второму интегралу применим метод интегрирования по частям
Тогда
При
Используя полученную формулу, легко вычислить, например
| < Предыдущая | Следующая > |
|---|
Интегрирование по частям — формула, доказательство, вывод, примеры, часто задаваемые вопросы
Идея интегрирования по частям была предложена в 1715 году Бруком Тейлором, который также предложил знаменитую теорему Тейлора. Обычно интегралы вычисляются для функций, для которых существуют формулы дифференцирования. Здесь интегрирование по частям является дополнительным методом, используемым для нахождения интегрирования произведения функций, и его также называют частичным интегрированием. Он изменяет интегрирование произведения функций в интегралы, для которых можно легко вычислить решение.
Некоторые обратные тригонометрические функции и логарифмические функции не имеют интегральных формул, и здесь мы можем воспользоваться формулой интегрирования по частям. Здесь мы проверим доказательство, графическое представление, приложения и примеры интегрирования по частям.
| 1. | Что такое интеграция по частям? |
| 2. | Интегрирование по формуле частей |
| 3. | Интегрирование по формуле частей |
| 4. | Визуализация интеграции по частям |
| 5. | Применение интеграции по частям |
| 6. | Формулы, связанные с интегрированием по частям |
| 7. | Часто задаваемые вопросы об интеграции по частям |
Что такое интеграция по частям?
Интегрирование по частям используется для интегрирования произведения двух или более функций. Две интегрируемые функции f(x) и g(x) имеют вид \(\int\)f(x).g(x). Таким образом, его можно назвать продуктовым правилом интегрирования. Среди двух функций первая функция f(x) выбирается такой, что формула ее производной существует, а вторая функция g(x) выбирается такой, что интеграл от такой функции существует.
Две интегрируемые функции f(x) и g(x) имеют вид \(\int\)f(x).g(x). Таким образом, его можно назвать продуктовым правилом интегрирования. Среди двух функций первая функция f(x) выбирается такой, что формула ее производной существует, а вторая функция g(x) выбирается такой, что интеграл от такой функции существует.
\(\int f(x).g(x).dx = f(x) \int g(x).dx — \int (f'(x) \int g(x).dx).dx + С\)
Интегрирование (первая функция x вторая функция) = (первая функция) x (интегрирование второй функции) — интегрирование (дифференциация первой функции x интегрирование второй функции).
При интегрировании по частям формула разбивается на две части и мы можем наблюдать производную первой функции f(x) во второй части, и интеграл второй функции g(x) в обеих частях . Для простоты эти функции часто представляются как «u» и «v» соответственно. Интеграция формулы uv с использованием обозначений «u» и «v»:
∫ u dv = uv — ∫ v ду.
Интегрирование по формуле частей
Формула интегрирования по частям используется для нахождения интеграла от произведения двух различных типов функций, таких как логарифмическая, обратная тригонометрическая, алгебраическая, тригонометрическая и экспоненциальная функции. Формула интегрирования по частям используется для нахождения интеграла произведения. В правиле дифференцирования произведения, где мы дифференцируем произведение uv, u(x) и v(x) можно выбирать в любом порядке. Но при использовании формулы интегрирования по частям для выбора первой функции u(x) мы должны посмотреть, какая из следующих функций идет первой в следующем порядке, и затем принять ее за u.
Формула интегрирования по частям используется для нахождения интеграла произведения. В правиле дифференцирования произведения, где мы дифференцируем произведение uv, u(x) и v(x) можно выбирать в любом порядке. Но при использовании формулы интегрирования по частям для выбора первой функции u(x) мы должны посмотреть, какая из следующих функций идет первой в следующем порядке, и затем принять ее за u.
- Логарифмический (L)
- Обратный тригонометрический (I)
- Алгебраический (А)
- Тригонометрический (Т)
- Экспоненциальная (E)
Это можно запомнить с помощью правила LIATE . Обратите внимание, что этот заказ также может быть ILATE . Например, если нам нужно найти ∫ x ln x dx (где x — алгебраическая функция, а ln — логарифмическая функция), мы выберем ln x как u(x), как в LIATE, логарифмическая функция стоит перед алгебраической функцией. функция. Формула интегрирования по частям определяется двумя способами. Мы можем использовать любой из них для интегрирования произведения двух функций.
Мы можем использовать любой из них для интегрирования произведения двух функций.
Вывод формулы интегрирования по частям
Доказательство интегрирования по частям можно получить из формулы производной произведения двух функций. Для двух функций f(x) и g(x) производная произведения этих двух функций равна сумме производных первых функций, умноженных на вторую функцию, и производной второй функции, умноженной на первая функция.
Выведем формулу интегрирования по частям, используя правило дифференцирования произведения. Рассмотрим две функции u и v. Пусть их произведение равно y. т. е. у = ув. Применяя правило дифференцирования произведения, получаем
d/dx (uv) = u (dv/dx) + v (du/dx)
Здесь мы переставим термины.
u (dv/dx) = d/dx (uv) — v (du/dx)
Интегрируя в обе стороны по x,
∫ u (dv/dx) (dx) = ∫ d/dx (uv) dx — ∫ v (du/dx) dx
Сокращая члены,
∫ u dv = uv — ∫ v du
Отсюда выводится формула интегрирования по частям.
Визуализация интеграции по частям
Рассмотрим параметрическую кривую (x, y) = (f(θ), g(θ)). Будем считать эту кривую интегрируемой и взаимно однозначной функцией. Интегрирование по частям представляет площадь синей области на приведенной ниже кривой. Сначала рассмотрим области синей и желтой областей отдельно. 9{x_2}_{x_1}\)
Без определенных интегралов можно записать как.
∫ y.dx+ ∫ x.dy = xy
∫x.dy = xy — ∫ y.dx
Далее это можно изменить, чтобы получить формулу интегрирования по частям.
∫f(x).g(x).dx = f(x).∫ g(x).dx — ∫(f'(x) .∫ g(x).dx).dx
Применение интеграции по частям
Эта формула интегрирования по частям применяется к функциям или выражениям, для которых не существует формул интегрирования. Здесь мы пытаемся включить эту формулу интегрирования по частям и пытаемся вывести интеграл. Для логарифмических функций и для обратных тригонометрических функций интегральных ответов нет. Попробуем решить и найти интегрирование log x и tan -1 х.
Интегрирование логарифмической функции
∫ logx.dx = ∫ logx.1.dx
= logx. ∫1.dx — ∫ ((logx)’.∫ 1.dx).dx
=logx.x -∫ (1/x .x).dx
=xlogx — ∫ 1.dx
=x logx — x + C
Интегрирование обратной тригонометрической функции
∫ tan -1 x.dx = ∫tan -1 x.1.dx
= tan -1 x.∫1.dx — ∫1.dx ((tan -1 x)’.∫ 1.dx).dx
= tan -1 x. х — ∫(1/(1 + х 2 ).x).dx
= х. tan -1 x — ∫ 2x/(2(1 + x 2 )).dx
= x. tan -1 x — ½.log(1 + x 2 ) + C
Следующие формулы были получены из формулы интегрирования по частям и полезны в процессе интегрирования различных алгебраических выражений.
- ∫ e x (f(x) + f'(x)).dx = e x f(x) + C
- ∫√(x 2 + a 2 ).dx = ½ . х.√(х 2 + а 2 )+ а 2 /2. log|x + √(x 2 + a 2 )| С
- ∫√(x 2 — a 2 ).
 dx =½ . х.√(х 2 — а 2 ) — а 2 /2. log|x +√(x 2 — a 2 ) | С
dx =½ . х.√(х 2 — а 2 ) — а 2 /2. log|x +√(x 2 — a 2 ) | С - ∫√(a 2 — x 2 ).dx = ½ . х.√(а 2 — х 2 ) + а 2 /2. sin -1 х/а + С
☛ Также проверьте:
- Исчисление
- Формулы дифференцирования и интегрирования
- Дифференциальные уравнения
- Формулы интегрирования
Решенные примеры интегрирования по частям
Пример 1: Найдите интеграл от x 2 e x , используя формулу интегрирования по частям.
Решение:
Используя LIATE, u = x 2 и dv = e х дх.
Тогда du = 2x dx, v = ∫ e x dx = e x .
Using one of the integration by parts formulas,
∫ u dv = uv — ∫ v du
∫ x 2 e x dx = x 2 e x — ∫ e x ( 2x) dx
= x 2 e x — 2 ∫ x e x dx
Повторное применение формулы интегрирования по частям для вычисления ∫ x e x x dx,
3
2 e x dx = x 2 e x — 2 (x e x — ∫ e x dx) = x 2 e x — 2 x e x + 2 e x + C = e x (x 2 — 2 x + 2)+ C
Answer: ∫ x 2 e x dx = = e x (x 2 — 2 х + 2)+ С
Пример 2: Найдите интеграл от x sin2x, используя формулу интегрирования по частям.

Решение:
Для интегрирования данного выражения используем формулу интегрирования по частям: ∫ uv.dx = u∫ v.dx -∫( u’ ∫ v.dx).dx
Здесь u = x и v = Sin2x
∫x sin2x. dx
=x∫sin2xdx — d/dx. х.∫ sin2xdx. дх
=х. -cos2x/2 — ∫(1.-cos2x/2). дх
=-cos2x/2. dx + 1/2 cos2xdx
= -xcos2x/2 + sin2x/4 + C
Ответ: Таким образом, ∫x sin2x dx = -x cos2x/2 + sin 2x/4+ C
Пример 3: Вычислите интеграл ∫ x ln x dx, используя интегрирование по частям.
Решение:
Первый метод:
Используя LIATE, u = ln x и v = x.
С помощью одной из формул интегрирования по частям x) (∫ x dx) dx
= ln x (x 2 /2) — ∫ (1/x) (x 2 /2) dx
= (x 2 ln x)/2 — (1/2) ∫ x dx
= (x 2 ln x) / 2 — (1/2) (x 2 /2) + C
= (x 2 ln x) /2 — (x 2 / 4) + C
= (x 2 /4)(2 ln x -1) + C
Второй метод :
Используя LIATE, u = ln x и dv = x dx.

Тогда du = (1/x) dx и v = ∫ x dx = x 2 /2
Используя одну из формул интегрирования по частям,
∫ u dv = uv — ∫ v du
∫ x ln x dx = ln x (x 2 /2) — ∫ (x 2 /2) (1/x) dx
= (x 2 ln x)/2 — (1 /2) ∫ x dx
= (x 2 ln x) / 2 — (1/2) (x 2 /2) + C
= (x 2 ln x) /2 — ( x 2 / 4) + C
= (x 2 /4)(2 ln x -1) + C
Ответ: Оба метода ∫ x ln x dx = (x 2 /4)(2 п х -1) + С
перейти к слайдуперейти к слайдуперейти к слайду
Есть вопросы по основным математическим понятиям?
Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, почему математика стоит за нашими сертифицированными экспертами
Запишитесь на бесплатный пробный урок
Практические вопросы по интеграции по частям
перейти к слайдуперейти к слайду
Часто задаваемые вопросы об интеграции по частям
Что такое интеграция по частям?
Интегрирование по частям — это интегрирование произведения двух функций.
 Эти две функции обычно представляются как f(x) и g(x). Среди двух функций первая функция f(x) выбирается такой, что формула ее производной существует, а вторая функция g(x) выбирается такой, что интеграл от такой функции существует.
Эти две функции обычно представляются как f(x) и g(x). Среди двух функций первая функция f(x) выбирается такой, что формула ее производной существует, а вторая функция g(x) выбирается такой, что интеграл от такой функции существует.∫ f(x).g(x).dx = f(x) ∫ g(x).dx — ∫(f'(x) ∫g(x).dx).dx + C
Что такое Интеграция по формуле частей?
Формула интегрирования по частям — это формула, используемая для нахождения интеграла от произведения двух различных типов функций. Популярная формула интегрирования по частям:
∫ u dv = uv — ∫ v du
Здесь первая функция ‘u’ должна быть выбрана в соответствии с LIATE (логарифмическая (L), обратная тригонометрическая (I), алгебраическая (A ), тригонометрический (T), экспоненциальный (E)).
Как вывести формулу интегрирования по частям?
Используя правило дифференцирования произведения,
d/dx (uv) = u (dv/dx) + v (du/dx)
u (dv/dx) = d/dx (uv) — v (du /dx)
Взяв интеграл с обеих сторон,
∫ u (dv/dx) (dx) = ∫ d/dx (uv) dx — ∫ v(du/dx) dx
Это дает,
∫ u dv = uv — ∫ v du
Таким образом, получается формула интегрирования по частям.

Почему мы используем формулу интегрирования по частям?
Используется формула интегрирования частей, поскольку нормальная форма интегрирования невозможна. Интегрирование, как правило, возможно для функций, для которых доступна формула производной. Такие выражения, как логарифмические функции, обратные тригонометрические функции, не могут быть легко интегрированы, поэтому интегралы находятся с использованием формулы интегрирования по частям.
Какие существуют другие методы интеграции помимо интеграции по частям?
Для интеграции используются три различных метода.
(a) Интеграция путем замены
(b) Интегрирование неполных дробей
(c) Интеграция по частямКак узнать, когда использовать интеграцию по частям?
Интеграция по частям используется, когда простой процесс интеграции невозможен. Если есть две функции и произведение между ними, мы можем взять формулу интегрирования между частями. Также для одной функции мы можем взять 1 в качестве других функций и найти интегралы, используя интегрирование по частям.
 Например, мы можем интегрировать Sin -1 x, Logx, xCosx, используя эту формулу.
Например, мы можем интегрировать Sin -1 x, Logx, xCosx, используя эту формулу.Какая из функций должна быть выполнена в виде буквы «U» при интегрировании по частям?
Формула интегрирования по частям: \(\int uv.dx = u\int v.dx — \int( u’\int v.dx).dx\). Здесь функция «u» выбрана так, чтобы можно было вычислить формулу производной этой функции.
В чем разница между интеграцией по частям и заменой?
Интегрирование частей можно использовать для нахождения интегралов от произведения двух функций f(x).g(x). Интегрирование путем замены может быть рассчитано для функций, имеющих подфункции, f (g (x)). Интегрирование по частям можно использовать для таких функций, как xcosx, e 9b_a\)
Какое применение интегрирования по частям?
Эта формула интегрирования по частям применяется к функциям или выражениям, для которых не существует производной и которые не могут быть интегрированы с помощью простого процесса интегрирования. Здесь мы пытаемся использовать формулу интегрирования по частям и пытаемся найти интеграл от произведения двух или более функций.
 Мы можем применить эту формулу для логарифмических функций и для обратных тригонометрических функций, которые не могут быть интегрированы с помощью простого процесса интегрирования.
Мы можем применить эту формулу для логарифмических функций и для обратных тригонометрических функций, которые не могут быть интегрированы с помощью простого процесса интегрирования.Каковы применения формулы интегрирования по частям?
Формула интегрирования по частям используется для нахождения интеграла от произведения двух различных типов функций. Кроме того, эта формула используется для нахождения интеграла различных функций, таких как sin -1 x, ln x и т. д., принимая вторую функцию за 1.
Как узнать, когда использовать формулу интегрирования по частям?
Когда мы встречаем интеграл от произведения двух функций, то мы должны применить формулу интегрирования. Иногда мы используем формулу интегрирования по частям, когда есть одна функция, такая как ln x, sin -1 x, tan -1 x и т. д.
3.1 Интегрирование по частям – исчисление, том 2
Цели обучения
- 3.1.1
Знайте, когда использовать интегрирование по частям.

- 3.1.2 Используйте формулу интегрирования по частям для решения задач интеграции.
- 3.1.3 Используйте формулу интегрирования по частям для определенных интегралов.
К настоящему времени у нас есть довольно тщательная процедура вычисления многих основных интегралов. Однако, хотя мы можем интегрировать ∫xsin(x2)dx∫xsin(x2)dx, используя замену u=x2,u=x2, нечто настолько простое, как ∫xsinxdx∫xsinxdx, бросает нам вызов. Многие студенты хотят знать, существует ли правило продукта для интеграции. Нет, но есть метод, основанный на правиле произведения для дифференцирования, который позволяет нам заменить один интеграл на другой. Мы называем этот метод интеграцией по частям.
Формула интегрирования по частям
Если h(x)=f(x)g(x),h(x)=f(x)g(x), то, используя правило произведения, мы получаем h′(x)=f′(x )g(x)+g′(x)f(x).h′(x)=f′(x)g(x)+g′(x)f(x). Хотя на первый взгляд это может показаться контрпродуктивным, давайте теперь проинтегрируем обе части этого уравнения: ∫h′(x)dx=∫(g(x)f′(x)+f(x)g′(x))dx.
 ∫ h′(x)dx=∫(g(x)f′(x)+f(x)g′(x))dx.
∫ h′(x)dx=∫(g(x)f′(x)+f(x)g′(x))dx.Это дает нам
h(x)=f(x)g(x)=∫g(x)f′(x)dx+∫f(x)g′(x)dx.h(x)=f(x)g(x )=∫g(x)f′(x)dx+∫f(x)g′(x)dx.
Теперь находим ∫f(x)g′(x)dx: ∫f(x)g′(x)dx:
∫f(x)g′(x)dx=f(x)g(x)−∫g(x)f′(x)dx.∫f(x)g′(x)dx=f(x) g(x)−∫g(x)f′(x)dx.
Путем замены u=f(x)u=f(x) и v=g(x),v=g(x), что, в свою очередь, дает du=f′(x)dxdu=f′(x) dx и dv=g′(x)dx,dv=g′(x)dx имеем более компактную форму
∫udv=uv−∫vdu.∫udv=uv−∫vdu.
Теорема 3.1
Интеграция по частям
Пусть u=f(x)u=f(x) и v=g(x)v=g(x) — функции с непрерывными производными. Тогда формула интегрирования по частям для интеграла, включающего эти две функции, будет следующей:
∫udv=uv−∫vdu.∫udv=uv−∫vdu.
(3.1)
Преимущество использования формулы интегрирования по частям состоит в том, что мы можем использовать ее для замены одного интеграла на другой, возможно, более простой интеграл.
 Следующий пример иллюстрирует его использование.
Следующий пример иллюстрирует его использование.Пример 3.1
Использование интегрирования по частям
Используйте интегрирование по частям с u=xu=x и dv=sinxdxdv=sinxdx для вычисления ∫xsinxdx.∫xsinxdx.
Решение
Выбирая u=x,u=x, мы получаем du=1dx.du=1dx. Поскольку dv=sinxdx,dv=sinxdx, мы получаем v=∫sinxdx=−cosx.v=∫sinxdx=−cosx. Эти значения удобно отслеживать следующим образом:
u=xdv=sinxdxdu=1dxv=∫sinxdx=-cosx.u=xdv=sinxdxdu=1dxv=∫sinxdx=-cosx.
Применение формулы интегрирования по частям приводит к результату
∫xsinxdx=(x)(−cosx)−∫(−cosx)(1dx)Substitute.=−xcosx+∫cosxdxSimplify.=−xcosx+sinx+C.Use ∫cosxdx=sinx+C.∫xsinxdx=(x)(-cosx)-∫(-cosx)(1dx)Подставить.=-xcosx+∫cosxdxSimplify.=-xcosx+sinx+C.Использовать ∫cosxdx=sinx+C.
Анализ
На данный момент, вероятно, есть несколько моментов, требующих разъяснения.
 Прежде всего, вам может быть любопытно, что произошло бы, если бы мы выбрали u=sinxu=sinx и dv=x.dv=x. Если бы мы сделали это, то мы бы имели du=cosxdxdu=cosxdx и v=12×2.v=12×2. Таким образом, применив интегрирование по частям, мы имеем К сожалению, с новым интегралом мы не в лучшем положении, чем раньше. Важно иметь в виду, что когда мы применяем интеграцию по частям, нам может потребоваться попробовать несколько вариантов для uu и dvdv, прежде чем найти подходящий вариант.
Прежде всего, вам может быть любопытно, что произошло бы, если бы мы выбрали u=sinxu=sinx и dv=x.dv=x. Если бы мы сделали это, то мы бы имели du=cosxdxdu=cosxdx и v=12×2.v=12×2. Таким образом, применив интегрирование по частям, мы имеем К сожалению, с новым интегралом мы не в лучшем положении, чем раньше. Важно иметь в виду, что когда мы применяем интеграцию по частям, нам может потребоваться попробовать несколько вариантов для uu и dvdv, прежде чем найти подходящий вариант.Во-вторых, вы можете задаться вопросом, почему, когда мы находим v=∫sinxdx=−cosx,v=∫sinxdx=−cosx, мы не используем v=−cosx+K.v=−cosx+K. Чтобы увидеть, что это не имеет значения, мы можем переделать задачу, используя v=−cosx+K:v=−cosx+K:
∫xsinxdx=(x)(−cosx+K)−∫(−cosx+K) (1dx)=-xcosx+Kx+∫cosxdx-∫Kdx=-xcosx+Kx+sinx-Kx+C=-xcosx+sinx+C.∫xsinxdx=(x)(-cosx+K)-∫(-cosx+ K)(1dx)=-xcosx+Kx+∫cosxdx-∫Kdx=-xcosx+Kx+sinx-Kx+C=-xcosx+sinx+C.
Как видите, на окончательное решение это не влияет.
Наконец, мы можем проверить правильность нашей первообразной, дифференцируя −xcosx+sinx+C:−xcosx+sinx+C:
ddx(-xcosx+sinx+C)=(-1)cosx+(-x)(-sinx)+cosx=xsinx.
 ddx(-xcosx+sinx+C)=(-1)cosx+(-x)( −sinx)+cosx=xsinx.
ddx(-xcosx+sinx+C)=(-1)cosx+(-x)( −sinx)+cosx=xsinx.Следовательно, первообразная проверяется.
СМИ
Посмотрите это видео и посетите этот веб-сайт, чтобы ознакомиться с примерами интеграции по частям.
Контрольно-пропускной пункт 3.1
Вычислите ∫xe2xdx∫xe2xdx, используя формулу интегрирования по частям с u=xu=x и dv=e2xdx.dv=e2xdx.
В этот момент возникает естественный вопрос: откуда мы знаем, как выбирать uu и dv?dv? Иногда это вопрос проб и ошибок; тем не менее, аббревиатура LIATE часто помогает избавить нас от догадок при выборе. Эта аббревиатура означает L огарифмические функции, I обратные тригонометрические функции, A алгебраические функции, T ригонометрические функции и E экспоненциальные функции. Эта мнемоника помогает определить правильный выбор для u.u.
Тип функции в интеграле, который появляется первым в списке, должен быть нашим первым выбором u.
 u. Например, если интеграл содержит логарифмическую функцию и алгебраическую функцию, мы должны выбрать uu в качестве логарифмической функции, потому что L стоит перед A в LIATE. Интеграл в примере 3.1 имеет тригонометрическую функцию (sinx)(sinx) и алгебраическую функцию (x).(x). Поскольку в слове LIATE A стоит перед T, мы выбрали uu в качестве алгебраической функции. Когда мы выбрали u,u,dvdv, он становится оставшейся частью функции, которую необходимо интегрировать вместе с dx.dx.
u. Например, если интеграл содержит логарифмическую функцию и алгебраическую функцию, мы должны выбрать uu в качестве логарифмической функции, потому что L стоит перед A в LIATE. Интеграл в примере 3.1 имеет тригонометрическую функцию (sinx)(sinx) и алгебраическую функцию (x).(x). Поскольку в слове LIATE A стоит перед T, мы выбрали uu в качестве алгебраической функции. Когда мы выбрали u,u,dvdv, он становится оставшейся частью функции, которую необходимо интегрировать вместе с dx.dx.Почему эта мнемоника работает? Помните, что все, что мы выбираем для dvdv, должно быть чем-то, что мы можем интегрировать. Поскольку у нас нет формул интегрирования, позволяющих интегрировать простые логарифмические функции и обратные тригонометрические функции, имеет смысл не выбирать их в качестве значений для dv.dv. Следовательно, они должны быть во главе списка вариантов выбора для u.u. Таким образом, мы ставим LI в начале мнемоники. (С тем же успехом мы могли бы начать с IL, поскольку эти два типа функций не встречаются вместе в задаче интегрирования по частям.
 ) Экспоненциальные и тригонометрические функции находятся в конце нашего списка, потому что их довольно легко вычислить. интегрируйте и сделайте правильный выбор для dv.dv. Таким образом, у нас есть TE в конце нашей мнемоники. (Мы могли бы также легко использовать ET в конце, поскольку, когда эти типы функций появляются вместе, обычно не имеет большого значения, какая из них uu, а какая dv.)dv.) Алгебраические функции обычно легко интегрируются как с и различать, и они приходятся на середину мнемоники.
) Экспоненциальные и тригонометрические функции находятся в конце нашего списка, потому что их довольно легко вычислить. интегрируйте и сделайте правильный выбор для dv.dv. Таким образом, у нас есть TE в конце нашей мнемоники. (Мы могли бы также легко использовать ET в конце, поскольку, когда эти типы функций появляются вместе, обычно не имеет большого значения, какая из них uu, а какая dv.)dv.) Алгебраические функции обычно легко интегрируются как с и различать, и они приходятся на середину мнемоники.Пример 3.2
Использование интегрирования по частям
Оценить ∫lnxx3dx.∫lnxx3dx.
Решение
Начните с перезаписи интеграла:
∫lnxx3dx=∫x−3lnxdx.∫lnxx3dx=∫x−3lnxdx.
Поскольку этот интеграл содержит алгебраическую функцию x−3x−3 и логарифмическую функцию lnx,lnx, выберите u=lnx,u=lnx, так как L стоит перед A в LIATE. После того, как мы выбрали u=lnx,u=lnx, мы должны выбрать dv=x−3dx.
 dv=x−3dx.
dv=x−3dx.Далее, поскольку u=lnx,u=lnx, имеем du=1xdx.du=1xdx. Кроме того, v=∫x−3dx=−12x−2.v=∫x−3dx=−12x−2. Подводя итоги,
u=lnxdv=x−3dxdu=1xdxv=∫x−3dx=−12x−2.u=lnxdv=x−3dxdu=1xdxv=∫x−3dx=−12x−2.
Подстановка в формулу интегрирования по частям (уравнение 3.1) дает
∫lnxx3dx=∫x−3lnxdx=(lnx)(−12x−2)−∫(−12x−2)(1xdx)=− 12x−2lnx+∫12x−3dxSimplify.=−12x−2lnx−14x−2+CIntegrate.=−12x2lnx−14×2+C. Переписать положительными целыми числами.∫lnxx3dx=∫x−3lnxdx=(lnx)(−12x− 2)−∫(−12x−2)(1xdx)=−12x−2lnx+∫12x−3dxSimplify.=−12x−2lnx−14x−2+CIntegrate.=−12x2lnx−14×2+C. Перепишите с положительными целыми числами.
Контрольно-пропускной пункт 3.2
Оценка ∫xlnxdx.∫xlnxdx.
В некоторых случаях, как в следующих двух примерах, может потребоваться применить интегрирование по частям более одного раза.
Пример 3.3
Применение интегрирования по частям более одного раза
Оценить ∫x2e3xdx.
 ∫x2e3xdx.
∫x2e3xdx.Решение
Используя LIATE, выберите u=x2u=x2 и dv=e3xdx.dv=e3xdx. Таким образом, du=2xdxdu=2xdx и v=∫e3xdx=(13)e3x.v=∫e3xdx=(13)e3x. Следовательно,
u=x2dv=e3xdxdu=2xdxv=∫e3xdx=13e3x.u=x2dv=e3xdxdu=2xdxv=∫e3xdx=13e3x.
Подстановка в уравнение 3.1 дает
∫x2e3xdx=13x2e3x−∫23xe3xdx.∫x2e3xdx=13x2e3x−∫23xe3xdx.
Мы по-прежнему не можем напрямую интегрировать ∫23xe3xdx∫23xe3xdx, но интеграл теперь имеет меньшую степень по x.x. Мы можем вычислить этот новый интеграл, снова используя интегрирование по частям. Для этого выберите u=xu=x и dv=23e3xdx.dv=23e3xdx. Таким образом, du=dxdu=dx и v=∫(23)e3xdx=(29)e3x.v=∫(23)e3xdx=(29)e3x. Теперь у нас
u=xdv=23e3xdxdu=dxv=∫23e3xdx=29e3x.u=xdv=23e3xdxdu=dxv=∫23e3xdx=29e3x.
Подстановка обратно в предыдущее уравнение дает
∫x2e3xdx=13x2e3x−(29xe3x−∫29e3xdx).∫x2e3xdx=13x2e3x−(29xe3x−∫29e3xdx).
После вычисления последнего интеграла и упрощения получаем
∫x2e3xdx=13x2e3x−29xe3x+227e3x+C.
 ∫x2e3xdx=13x2e3x−29xe3x+227e3x+C.
∫x2e3xdx=13x2e3x−29xe3x+227e3x+C.Пример 3.4
Применение интеграции по частям, когда LIATE не работает
Оценка ∫t3et2dt.∫t3et2dt.
Решение
Если мы будем использовать строгую интерпретацию мнемонического LIATE для выбора u,u, мы получим u=t3u=t3 и dv=et2dt.dv=et2dt. К сожалению, этот вариант не сработает, потому что мы не можем вычислить ∫et2dt.∫et2dt. Однако, поскольку мы можем вычислить ∫tet2dx,∫tet2dx, мы можем попробовать выбрать u=t2u=t2 и dv=tet2dt.dv=tet2dt. С этими вариантами у нас есть
u=t2dv=tet2dtdu=2tdtv=∫tet2dt=12et2.u=t2dv=tet2dtdu=2tdtv=∫tet2dt=12et2.
Таким образом, получаем
∫t3et2dt=12t2et2−∫12et22tdt=12t2et2−12et2+C.∫t3et2dt=12t2et2−∫12et22tdt=12t2et2−12et2+C.
Пример 3,5
Применение интегрирования по частям более одного раза
Вычислить ∫sin(lnx)dx.∫sin(lnx)dx.
Решение
Похоже, что этот интеграл имеет только одну функцию, а именно, sin(lnx)sin(lnx), однако мы всегда можем использовать постоянную функцию 1 в качестве другой функции.
 В этом примере давайте выберем u=sin(lnx)u=sin(lnx) и dv=1dx.dv=1dx. (Решение использовать u=sin(lnx)u=sin(lnx) легко. Мы не можем выбрать dv=sin(lnx)dxdv=sin(lnx)dx, потому что, если бы мы могли его интегрировать, мы бы не используя в первую очередь интегрирование по частям!) Следовательно, du=(1/x)cos(lnx)dxdu=(1/x)cos(lnx)dx и v=∫1dx=x.v=∫1dx=x. После применения интегрирования по частям к интегралу и упрощения имеем
В этом примере давайте выберем u=sin(lnx)u=sin(lnx) и dv=1dx.dv=1dx. (Решение использовать u=sin(lnx)u=sin(lnx) легко. Мы не можем выбрать dv=sin(lnx)dxdv=sin(lnx)dx, потому что, если бы мы могли его интегрировать, мы бы не используя в первую очередь интегрирование по частям!) Следовательно, du=(1/x)cos(lnx)dxdu=(1/x)cos(lnx)dx и v=∫1dx=x.v=∫1dx=x. После применения интегрирования по частям к интегралу и упрощения имеем∫sin(lnx)dx=xsin(lnx)−∫cos(lnx)dx.∫sin(lnx)dx=xsin(lnx)−∫cos(lnx)dx.
К сожалению, этот процесс оставляет нам новый интеграл, который очень похож на оригинал. Однако давайте посмотрим, что произойдет, если мы снова применим интегрирование по частям. На этот раз давайте выберем u=cos(lnx)u=cos(lnx) и dv=1dx,dv=1dx, получив du=-(1/x)sin(lnx)dxdu=-(1/x)sin(lnx) dx и v=∫1dx=x.v=∫1dx=x. Подставляя, мы имеем
∫sin(lnx)dx=xsin(lnx)−(xcos(lnx)—∫−sin(lnx)dx).∫sin(lnx)dx=xsin(lnx)−(xcos (lnx)—∫−sin(lnx)dx).
После упрощения получаем
∫sin(lnx)dx=xsin(lnx)−xcos(lnx)−∫sin(lnx)dx.
 ∫sin(lnx)dx=xsin(lnx)−xcos( lnx)−∫sin(lnx)dx.
∫sin(lnx)dx=xsin(lnx)−xcos( lnx)−∫sin(lnx)dx.Последний интеграл теперь совпадает с исходным. Может показаться, что мы просто пошли по кругу, но теперь мы действительно можем вычислить интеграл. Чтобы лучше понять, как это сделать, замените I=∫sin(lnx)dx.I=∫sin(lnx)dx. Таким образом, уравнение принимает вид
I=xsin(lnx)−xcos(lnx)−I.I=xsin(lnx)−xcos(lnx)−I.
Сначала добавьте II к обеим частям уравнения, чтобы получить
2I=xsin(lnx)−xcos(lnx).2I=xsin(lnx)−xcos(lnx).
Затем разделите на 2:
I=12xsin(lnx)−12xcos(lnx).I=12xsin(lnx)−12xcos(lnx).
Снова подставив I=∫sin(lnx)dxI=∫sin(lnx)dx, мы получим
∫sin(lnx)dx=12xsin(lnx)−12xcos(lnx).∫sin(lnx) dx=12xsin(lnx)−12xcos(lnx).
Отсюда мы видим, что (1/2)xsin(lnx)−(1/2)xcos(lnx)(1/2)xsin(lnx)−(1/2)xcos(lnx) является первообразной sin (lnx)dx.sin(lnx)dx. Для самой общей первообразной добавьте +C:+C:
∫sin(lnx)dx=12xsin(lnx)−12xcos(lnx)+C.∫sin(lnx)dx=12xsin(lnx)−12xcos(lnx)+C.

Анализ
Если этот метод поначалу кажется немного странным, мы можем проверить ответ дифференцированием:
ddx(12xsin(lnx)−12xcos(lnx))=12(sin(lnx))+cos(lnx) · 1x·12x−(12cos(lnx)−sin(lnx)·1x·12x)=sin(lnx).ddx(12xsin(lnx)−12xcos(lnx))=12(sin(lnx))+cos(lnx) ·1x·12x−(12cos(lnx)−sin(lnx)·1x·12x)=sin(lnx).
Контрольно-пропускной пункт 3.3
Оценить ∫x2sinxdx.∫x2sinxdx.
Интегрирование по частям для определенных интегралов
Теперь, когда мы успешно использовали интегрирование по частям для вычисления неопределенных интегралов, мы обратим наше внимание на определенные интегралы. Техника интегрирования действительно такая же, только мы добавляем шаг для вычисления интеграла на верхнем и нижнем пределах интегрирования.
Теорема 3.2
Интегрирование по частям для определенных интегралов
Пусть u=f(x)u=f(x) и v=g(x)v=g(x) — функции с непрерывными производными на [a,b].
 [a,b]. Затем
[a,b]. Затем∫abudv=uv|ab−∫abvdu.∫abudv=uv|ab−∫abvdu.
(3.2)
Пример 3,6
Нахождение площади области
Найдите площадь области, ограниченной сверху графиком y=tan-1xy=tan-1x и снизу осью xx на интервале [0,1].[0, 1].
Решение
Этот регион показан на рис. 3.2. Чтобы найти площадь, мы должны вычислить ∫01tan-1xdx.∫01tan-1xdx.
Рисунок 3.2 Чтобы найти площадь заштрихованной области, мы должны использовать интегрирование по частям.
Для этого интеграла выберем u=tan−1xu=tan−1x и dv=dx,dv=dx, получив таким образом du=1×2+1dxdu=1×2+1dx и v=x.v=x. После применения формулы интегрирования по частям (уравнение 3.2) мы получаем
Area=xtan−1x|01−∫01xx2+1dx.Area=xtan−1x|01−∫01xx2+1dx.
Используйте u -подстановку, чтобы получить
∫01xx2+1dx=12ln|x2+1|01.∫01xx2+1dx=12ln|x2+1|01.

Таким образом,
Площадь=xtan−1x|01−12ln|x2+1||01=π4−12ln2. Площадь=xtan−1x|01−12ln|x2+1||01=π4−12ln2.
В этот момент неплохо было бы провести «проверку на реальность» разумности нашего решения. Поскольку π4−12ln2≈0,4388, π4−12ln2≈0,4388, а из рисунка 3.2 мы ожидаем, что наша площадь будет немного меньше 0,5, это решение кажется разумным.
Пример 3,7
Нахождение объема вращения
Найдите объем твердого тела, полученного путем вращения области, ограниченной графиком f(x)=e−x,f(x)=e−x, осью x , y -оси, и линия x=1x=1 вокруг и -ось.
Решение
Лучшим вариантом решения этой проблемы является использование метода оболочки. Начните с наброска области вращения вместе с типичным прямоугольником (см. следующий график).
Рисунок 3.3 Мы можем использовать метод оболочки, чтобы найти объем вращения.

Чтобы найти объем с помощью оболочек, мы должны вычислить 2π∫01xe-xdx.2π∫01xe-xdx. Для этого пусть u=xu=x и dv=e−x.dv=e−x. Эти варианты приводят к du=dxdu=dx и v=∫e−x=−e−x.v=∫e−x=−e−x. Подставляя в уравнение 3.2, получаем
Volume=2π∫01xe-xdx=2π(-xe-x|01+∫01e-xdx)Использовать интегрирование по частям.=-2πxe-x|01-2πe-x|01Evaluate∫01e-xdx=-e- x|01.=2π−4πe. Вычислить и упростить. Volume=2π∫01xe−xdx=2π(−xe−x|01+∫01e−xdx)Использовать интегрирование по частям.=−2πxe−x|01−2πe− x|01Evaluate∫01e−xdx=−e−x|01.=2π−4πe. Вычислите и упростите.
Анализ
Опять же, неплохо проверить разумность нашего решения. Заметим, что объем твердого тела немного меньше объема цилиндра радиуса 11 и высоты 1/e1/e, добавленного к объему конуса с радиусом основания 11 и высотой 1−1e.1−1e. Следовательно, твердое тело должно иметь объем чуть меньше
π(1)21e+(π3)(1)2(1−1e)=2π3e+π3≈1,8177.π(1)21e+(π3)(1)2(1−1e)=2π3e+π3≈1,8177.
Поскольку 2π−4πe≈1,6603,2π−4πe≈1,6603, мы видим, что наш расчетный объем является разумным.

Контрольно-пропускной пункт 3.4
Оценить ∫0π/2xcosxdx.∫0π/2xcosxdx.
Раздел 3.1 Упражнения
При использовании метода интегрирования по частям вы должны тщательно выбирать, какое выражение является u. Для каждой из следующих проблем используйте рекомендации в этом разделе, чтобы выбрать у.е. Вычислите интегралы с помощью , а не .
1.
∫x3e2xdx∫x3e2xdx
2.
∫x3ln(x)dx∫x3ln(x)dx
3.
∫y3cosydy∫y3cosydy
4.
∫x2arctanxdx∫x2arctanxdx
5.
∫e3xsin(2x)dx∫e3xsin(2x)dx
Найдите интеграл простейшим методом. Не все задачи требуют интегрирования по частям.
6.

∫vsinvdv∫vsinvdv
7.
∫lnxdx∫lnxdx ( Подсказка: ∫lnxdx∫lnxdx эквивалентно ∫1·ln(x)dx.)∫1·ln(x)dx.)
8.
∫xcosxdx∫xcosxdx
9.
∫tan-1xdx∫tan-1xdx
10.
∫x2exdx∫x2exdx
11.
∫xsin(2x)dx∫xsin(2x)dx
12.
∫xe4xdx∫xe4xdx
13.
∫xe-xdx∫xe-xdx
14.
∫xcos3xdx∫xcos3xdx
15.
∫x2cosxdx∫x2cosxdx
16.
∫xlnxdx∫xlnxdx
17.
∫ln(2x+1)dx∫ln(2x+1)dx
18.
∫x2e4xdx∫x2e4xdx
19.

∫exsinxdx∫exsinxdx
20.
∫excosxdx∫excosxdx
21.
∫xe-x2dx∫xe-x2dx
22.
∫x2e-xdx∫x2e-xdx
23.
∫sin(ln(2x))dx∫sin(ln(2x))dx
24.
∫cos(lnx)dx∫cos(lnx)dx
25.
∫(lnx)2dx∫(lnx)2dx
26.
∫ln(x2)dx∫ln(x2)dx
27.
∫x2lnxdx∫x2lnxdx
28.
∫sin-1xdx∫sin-1xdx
29.
∫cos−1(2x)dx∫cos−1(2x)dx
30.
∫xarctanxdx∫xarctanxdx
31.
∫x2sinxdx∫x2sinxdx
32.

∫x3cosxdx∫x3cosxdx
33.
∫x3sinxdx∫x3sinxdx
34.
∫x3exdx∫x3exdx
35.
∫xsec-1xdx∫xsec-1xdx
36.
∫xsec2xdx∫xsec2xdx
37.
∫xcoshxdx∫xcoshxdx
Вычисление определенных интегралов. Используйте графическую утилиту, чтобы подтвердить свои ответы.
38.
∫1/e1lnxdx∫1/e1lnxdx
39.
∫01xe−2xdx∫01xe−2xdx (Выразите ответ в точной форме.)
40.
∫01exdx(letu=x)∫01exdx(letu=x)
41.
∫1eln(x2)dx∫1eln(x2)dx
42.
∫0πxcosxdx∫0πxcosxdx
43.

∫−ππxsinxdx∫−ππxsinxdx (Выразите ответ в точной форме.)
44.
∫03ln(x2+1)dx∫03ln(x2+1)dx (Выразите ответ в точной форме.)
45.
∫0π/2x2sinxdx∫0π/2x2sinxdx (Выразите ответ в точной форме.)
46.
∫01x5xdx∫01x5xdx (Выразите ответ, используя пять значащих цифр.)
47.
Вычислить ∫cosxln(sinx)dx∫cosxln(sinx)dx
Выведите следующие формулы методом интегрирования по частям. Предположим, что n — целое положительное число. Эти формулы называются формулами приведения , потому что показатель степени в члене x был уменьшен на единицу в каждом случае. Второй интеграл проще исходного.
48.
∫xnexdx=xnex-n∫xn-1exdx∫xnexdx=xnex-n∫xn-1exdx
49.

∫xncosxdx=xnsinx-n∫xn-1sinxdx∫xncosxdx=xnsinx-n∫xn-1sinxdx
50.
∫xnsinxdx=______∫xnsinxdx=______
51.
Интегрировать ∫2x2x−3dx∫2x2x−3dx двумя способами:
- Используя части, полагая dv=2x−3dxdv=2x−3dx
- Подстановка, позволяющая u=2x−3u=2x−3
Укажите, будете ли вы использовать интегрирование по частям для вычисления интеграла. Если да, укажите у и дв . Если нет, опишите метод, использованный для выполнения интегрирования без фактического решения проблемы.
52.
∫xlnxdx∫xlnxdx
53.
∫ln2xxdx∫ln2xxdx
54.
∫xexdx∫xexdx
55.
∫xex2-3dx∫xex2-3dx
56.

∫x2sinxdx∫x2sinxdx
57.
∫x2sin(3×3+2)dx∫x2sin(3×3+2)dx
Нарисуйте область, ограниченную сверху кривой, x -оси, и x=1,x=1, и найдите площадь области. Укажите точную форму или округление ответов на указанное количество мест.
58.
y=2xe-xy=2xe-x (Приблизительный ответ до четырех знаков после запятой.)
59.
y=e−xsin(πx)y=e−xsin(πx) (Приблизительный ответ до пяти знаков после запятой.)
Найдите объем, полученный вращением области, ограниченной заданными кривыми, вокруг заданной линии. Ответы выражайте в точной форме или округляйте до указанного числа знаков после запятой.
60.
y=sinx,y=0,x=2π,x=3πy=sinx,y=0,x=2π,x=3π относительно оси y (Выразите ответ в точной форме.)
61.
у=е-ху=е-ху=0,х=-1х=0;у=0,х=-1х=0; о x=1x=1 (Выразите ответ в точной форме.
 )
)62.
Частица, движущаяся по прямой линии, имеет скорость v(t)=t2e−tv(t)=t2e−t через t сек. Какой путь он пройдет за первые 2 с? (Предположим, что единицы измерения указаны в футах, и представим ответ в точной форме.)
63.
Найдите площадь под графиком y=sec3xy=sec3x из x=0tox=1.x=0tox=1. (Округлите ответ до двух значащих цифр.)
64.
Найдите площадь между y=(x−2)exy=(x−2)ex и осью x- от x=2x=2 до x=5.x=5. (Выразите ответ в точной форме.)
65.
Найдите площадь области, ограниченной кривой y=xcosxy=xcosx и осью x для
11π2≤x≤13π2,11π2≤x≤13π2. (Выразите ответ в точной форме.)
66.
Найдите объем твердого тела, образованного вращением области, ограниченной кривой y=lnx,y=lnx, осью x и вертикальной линией x=e2x=e2 вокруг оси x .



 dx =½ . х.√(х 2 — а 2 ) — а 2 /2. log|x +√(x 2 — a 2 ) | С
dx =½ . х.√(х 2 — а 2 ) — а 2 /2. log|x +√(x 2 — a 2 ) | С
 Эти две функции обычно представляются как f(x) и g(x). Среди двух функций первая функция f(x) выбирается такой, что формула ее производной существует, а вторая функция g(x) выбирается такой, что интеграл от такой функции существует.
Эти две функции обычно представляются как f(x) и g(x). Среди двух функций первая функция f(x) выбирается такой, что формула ее производной существует, а вторая функция g(x) выбирается такой, что интеграл от такой функции существует.
 Например, мы можем интегрировать Sin -1 x, Logx, xCosx, используя эту формулу.
Например, мы можем интегрировать Sin -1 x, Logx, xCosx, используя эту формулу. Мы можем применить эту формулу для логарифмических функций и для обратных тригонометрических функций, которые не могут быть интегрированы с помощью простого процесса интегрирования.
Мы можем применить эту формулу для логарифмических функций и для обратных тригонометрических функций, которые не могут быть интегрированы с помощью простого процесса интегрирования.
 ∫ h′(x)dx=∫(g(x)f′(x)+f(x)g′(x))dx.
∫ h′(x)dx=∫(g(x)f′(x)+f(x)g′(x))dx. Следующий пример иллюстрирует его использование.
Следующий пример иллюстрирует его использование. Прежде всего, вам может быть любопытно, что произошло бы, если бы мы выбрали u=sinxu=sinx и dv=x.dv=x. Если бы мы сделали это, то мы бы имели du=cosxdxdu=cosxdx и v=12×2.v=12×2. Таким образом, применив интегрирование по частям, мы имеем К сожалению, с новым интегралом мы не в лучшем положении, чем раньше. Важно иметь в виду, что когда мы применяем интеграцию по частям, нам может потребоваться попробовать несколько вариантов для uu и dvdv, прежде чем найти подходящий вариант.
Прежде всего, вам может быть любопытно, что произошло бы, если бы мы выбрали u=sinxu=sinx и dv=x.dv=x. Если бы мы сделали это, то мы бы имели du=cosxdxdu=cosxdx и v=12×2.v=12×2. Таким образом, применив интегрирование по частям, мы имеем К сожалению, с новым интегралом мы не в лучшем положении, чем раньше. Важно иметь в виду, что когда мы применяем интеграцию по частям, нам может потребоваться попробовать несколько вариантов для uu и dvdv, прежде чем найти подходящий вариант. ddx(-xcosx+sinx+C)=(-1)cosx+(-x)( −sinx)+cosx=xsinx.
ddx(-xcosx+sinx+C)=(-1)cosx+(-x)( −sinx)+cosx=xsinx.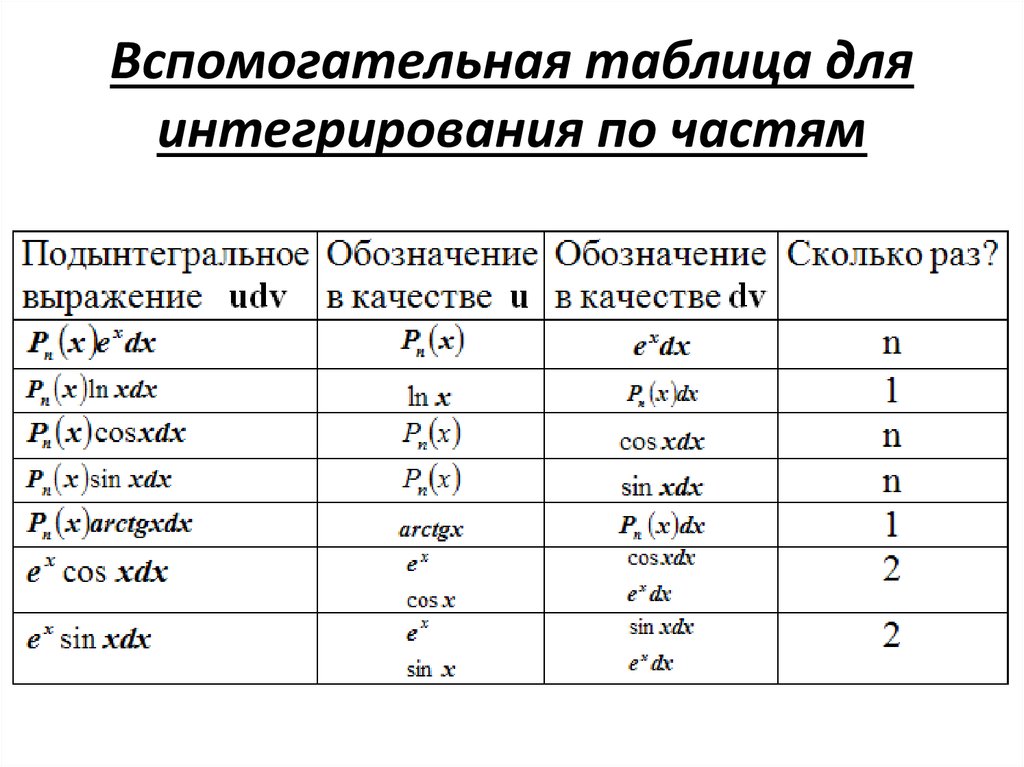 u. Например, если интеграл содержит логарифмическую функцию и алгебраическую функцию, мы должны выбрать uu в качестве логарифмической функции, потому что L стоит перед A в LIATE. Интеграл в примере 3.1 имеет тригонометрическую функцию (sinx)(sinx) и алгебраическую функцию (x).(x). Поскольку в слове LIATE A стоит перед T, мы выбрали uu в качестве алгебраической функции. Когда мы выбрали u,u,dvdv, он становится оставшейся частью функции, которую необходимо интегрировать вместе с dx.dx.
u. Например, если интеграл содержит логарифмическую функцию и алгебраическую функцию, мы должны выбрать uu в качестве логарифмической функции, потому что L стоит перед A в LIATE. Интеграл в примере 3.1 имеет тригонометрическую функцию (sinx)(sinx) и алгебраическую функцию (x).(x). Поскольку в слове LIATE A стоит перед T, мы выбрали uu в качестве алгебраической функции. Когда мы выбрали u,u,dvdv, он становится оставшейся частью функции, которую необходимо интегрировать вместе с dx.dx. ) Экспоненциальные и тригонометрические функции находятся в конце нашего списка, потому что их довольно легко вычислить. интегрируйте и сделайте правильный выбор для dv.dv. Таким образом, у нас есть TE в конце нашей мнемоники. (Мы могли бы также легко использовать ET в конце, поскольку, когда эти типы функций появляются вместе, обычно не имеет большого значения, какая из них uu, а какая dv.)dv.) Алгебраические функции обычно легко интегрируются как с и различать, и они приходятся на середину мнемоники.
) Экспоненциальные и тригонометрические функции находятся в конце нашего списка, потому что их довольно легко вычислить. интегрируйте и сделайте правильный выбор для dv.dv. Таким образом, у нас есть TE в конце нашей мнемоники. (Мы могли бы также легко использовать ET в конце, поскольку, когда эти типы функций появляются вместе, обычно не имеет большого значения, какая из них uu, а какая dv.)dv.) Алгебраические функции обычно легко интегрируются как с и различать, и они приходятся на середину мнемоники. dv=x−3dx.
dv=x−3dx. ∫x2e3xdx.
∫x2e3xdx. ∫x2e3xdx=13x2e3x−29xe3x+227e3x+C.
∫x2e3xdx=13x2e3x−29xe3x+227e3x+C. В этом примере давайте выберем u=sin(lnx)u=sin(lnx) и dv=1dx.dv=1dx. (Решение использовать u=sin(lnx)u=sin(lnx) легко. Мы не можем выбрать dv=sin(lnx)dxdv=sin(lnx)dx, потому что, если бы мы могли его интегрировать, мы бы не используя в первую очередь интегрирование по частям!) Следовательно, du=(1/x)cos(lnx)dxdu=(1/x)cos(lnx)dx и v=∫1dx=x.v=∫1dx=x. После применения интегрирования по частям к интегралу и упрощения имеем
В этом примере давайте выберем u=sin(lnx)u=sin(lnx) и dv=1dx.dv=1dx. (Решение использовать u=sin(lnx)u=sin(lnx) легко. Мы не можем выбрать dv=sin(lnx)dxdv=sin(lnx)dx, потому что, если бы мы могли его интегрировать, мы бы не используя в первую очередь интегрирование по частям!) Следовательно, du=(1/x)cos(lnx)dxdu=(1/x)cos(lnx)dx и v=∫1dx=x.v=∫1dx=x. После применения интегрирования по частям к интегралу и упрощения имеем ∫sin(lnx)dx=xsin(lnx)−xcos( lnx)−∫sin(lnx)dx.
∫sin(lnx)dx=xsin(lnx)−xcos( lnx)−∫sin(lnx)dx.
 [a,b]. Затем
[a,b]. Затем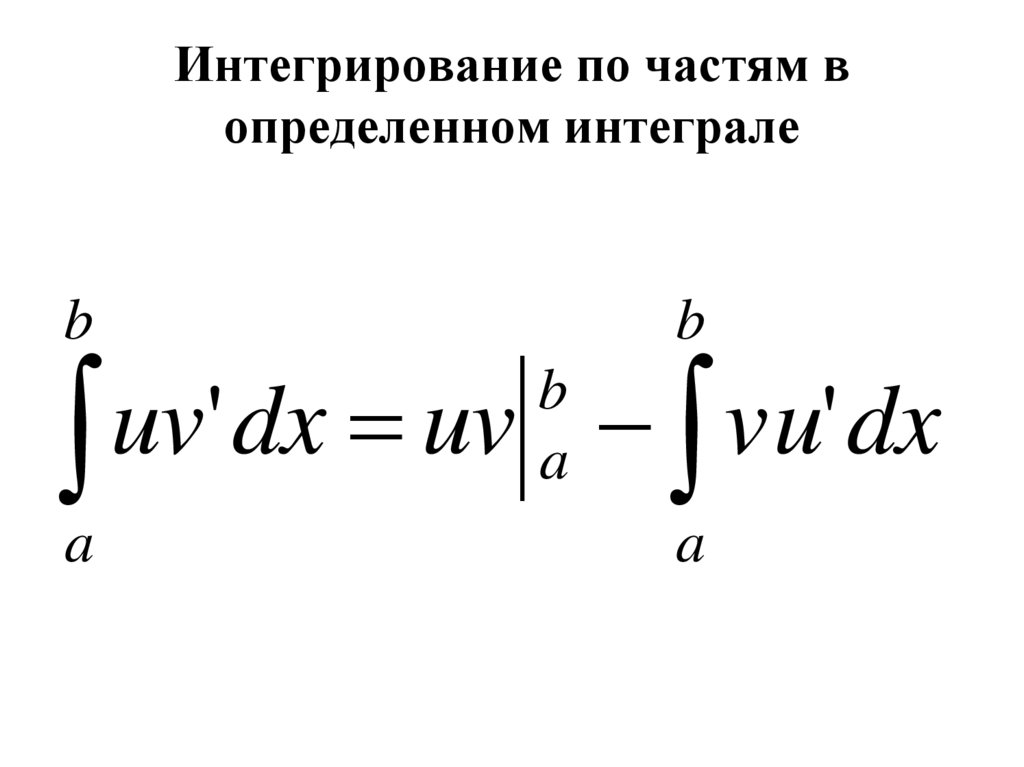








 )
)