Формулы мат логики: Формулы математической логики.

Формулы математической логики.

Формулой математической логики называется сложное высказывание, которое получено из элементарных высказываний с использованием логических операций.

Две формулы равносильны, если они принимают одинаковые логические значения на любом наборе значений входящих в формулу элементарных высказываний. Равносильность формул обозначается  A  B.

Формулы равносильности.

1. Коммутативность

АVВ  ВVА А&В  В&А

2. Ассоциативность

АV(ВVС)  (АVВ)VС А&(В&С)  (А&В) &С

3. Дистрибутивность

АV(В&С)  (АVВ)&(АVС) А&(ВVС)  (А&В)V(А&С)

4. Идемпотентность

АVА  А А&А  А

5. Поглощение

АV(А&В)  А А&(АVВ)  А

6. Закон де Моргана

& V

7. Закон исключающий третьего

АV1  1 А&1  A

8. Закон противоречия

AV  A A&  

9. Закон двойного отрицания

A

10. 1 ,  0

11. AB VB

12. AB  (AB)&(BA)

13. AB  A&V&B

14. A | B   V

15. AB   &

ПРИМЕР

Доказать:

Представление произвольной функции алгебры логики в виде формулы алгебры логики

Пусть — произвольная функция алгебры логикипеременных.

Рассмотрим формулу

(2.1)

которая составлена следующим образом: каждое слагаемое этой логической суммы представляет собой конъюнкцию, в которой первый член является значением функции при некоторых определенных значениях переменных, остальные же члены конъюнкции представляют собой переменные или их отрицания. При этом под знаком отрицания находятся те и только те переменные, которые в первом члене конъюнкции имеют значение 0..

Вместе с тем формула (2.1) содержит в виде логических слагаемых всевозможные конъюнкции указанного вида.

Ясно, что формула (2.1)полностью определяет функцию . Иначе говоря, значения функциии формулы (2.1) совпадают на всех наборах значений переменных. То есть функция

Составление формул по таблице истинности. может быть представлена в виде:

(2.2)

ПРИМЕР Пусть функция имеет следующую таблицу истинности:

0	0	0	1
0	0	1	0
0	1	0	0
0	1	1	1
1	0	0	0
1	0	1	1
1	1	0	1
1	1	1	0

Тогда функция может быть определена в следующем виде:

Нетрудно заметить, что для определении функции берутся только те наборы переменных , при которых функция принимает значения 1, что значительно упрощает процедуру определения функции.

Формула (2.1) обладает свойствами:

1. Каждое логическое слагаемое формулы содержит все переменные , входящие в функцию .

2. Все логические слагаемые формулы различны.

3. Ни одно логическое слагаемое формулы не содержит одновременно переменную и ее отрицание.

4. Ни одно логическое слагаемое формулы не содержит одну и ту же переменную дважды.

5. Перечисленные свойства называются свойствами совершенства.

Различные формы представления высказываний

Литерой

 называется элемент высказывания x или её отрицание.

Элементарной дизъюнкцией называется выражение следующего вида:

, (2.2)

где  литера.

Элементарной конъюнкцией называется выражение следующего вида:

, (2.3)

Дизъюнктивной нормальной формой (ДНФ) формулы называется выражение вида:

, (2.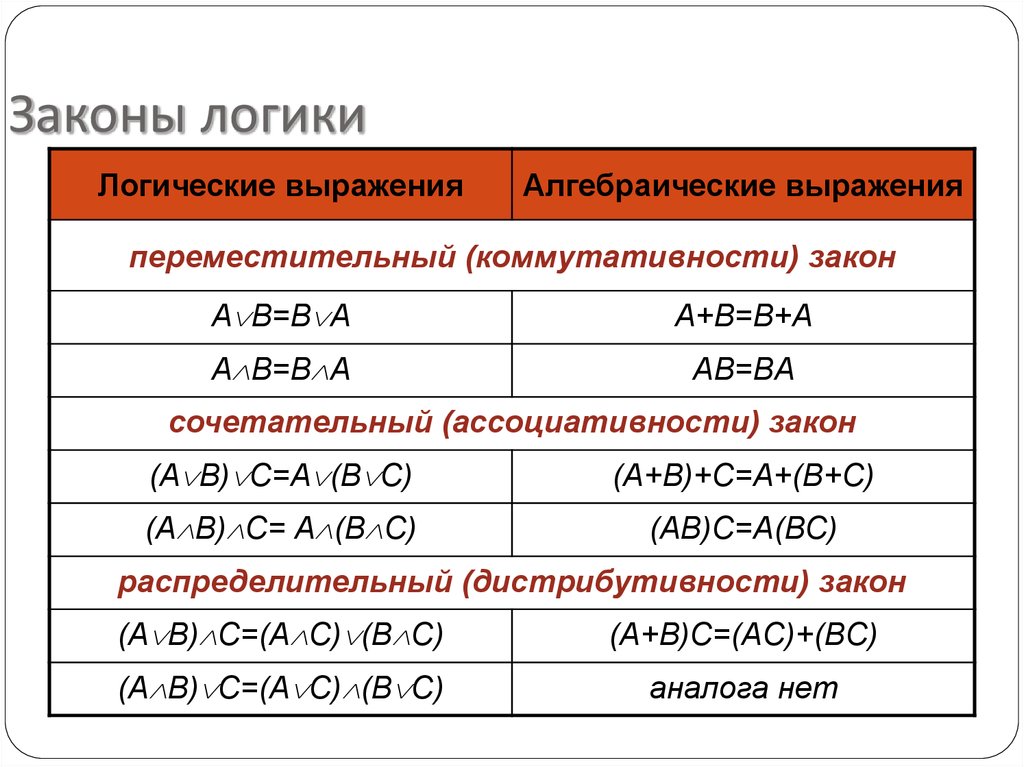 4)

где  элементарная конъюнкция.

Конъюнктивной нормальной формой (КНФ) формулы называется выражение вида:

, (2.5)

где  элементарная дизъюнкция.

Любую формулу можно представить в виде ДНФ или КНФ.

ПРИМЕР

Пусть дана формула

Требуется получить ДНФ и КНФ данной формулы.

Применяя формулы равносильности, получаем КНФ :

Применяя формулы равносильности, получаем ДНФ :

Совершенной дизъюнктивной нормальной формой (СДНФ) формулы называется такая ДНФ, для которой выполняются следующие условия:

1. Все элементарные конъюнкции, входящие в ДНФ , различны.

2. Все элементарные конъюнкции, входящие в ДНФ , содержат литеры, соответствующие всем переменным.

3. Каждая элементарная конъюнкция, входящая в ДНФ , не содержит двух одинаковых литер.

4. Каждая элементарная конъюнкция, входящая в ДНФ , не содержит переменную и ее отрицание.

СДНФ можно получить двумя способами:

1. по таблице истинности;

2. с помощью равносильных преобразований.

Первый способ получения СДНФ рассмотрен выше. Рассмотрим второй способ, который состоит в следующем:

С помощью равносильных преобразований формулы получают ДНФ . При этом в полученной ДНФ возможны следующие ситуации:

1. Элементарная конъюнкция ДНФ не содержит переменную , тогда используются следующие равносильные преобразования:

2. Если в ДНФ входят две одинаковые элементарные конъюнкции, то используя следующее равносильное преобразование:

,

одну элементарную конъюнкцию можно отбросить.

3. Если элементарная конъюнкция ДНФ содержит одновременно переменную и ее отрицание, то используя следующие равносильные преобразования:

,

эту элементарную конъюнкцию можно отбросить

4. Если элементарная конъюнкция ДНФ содержит дважды переменную , то используя следующее равносильное преобразование:

,

одну переменную можно отбросить

СДНФ формулы существует в единственном виде.

ПРИМЕР

Получить СДНФ формулы

С помощью равносильных преобразований получаем СДНФ :

С помощью таблицы истинности получаем СДНФ :

0	0	0	1	0	1
0	0	1	0	0	1
0	1	0	1	1	1
0	1	1	0	0	1
1	0	0	1	0	0
1	0	1	0	0	0
1	1	0	1	1	1
1	1	1	0	0	0

СДНФ

Очевидно, что в результат двух способов совпадает.

Совершенной конъюнктивной нормальной формой (СКНФ) формулы называется такая КНФ, для которой выполняются следующие условия:

1. Все элементарные дизъюнкции, входящие в КНФ , различны.

2. Все элементарные дизъюнкции, входящие в КНФ , содержат литеры, соответствующие всем переменным.

3. Каждая элементарная дизъюнкция, входящая в КНФ , не содержит двух одинаковых литер.

4. Каждая элементарная дизъюнкция, входящая в КНФ , не содержит переменную и ее отрицание.

СКНФ можно получить двумя способами:

1. по таблице истинности;

2. с помощью равносильных преобразований.

По первому способу по таблице истинности получаем СДНФ , а СКНФ можно получить, следуя следующему правилу

С помощью равносильных преобразований формулы получают КНФ . При этом в полученной КНФ возможны следующие ситуации:

1. Элементарная дизъюнкция КНФ не содержит переменную , тогда используются следующие равносильные преобразования:

2. Если в КНФ входят две одинаковые элементарные дизъюнкции, то используя следующее равносильное преобразование:

,

одну элементарную дизъюнкцию можно отбросить.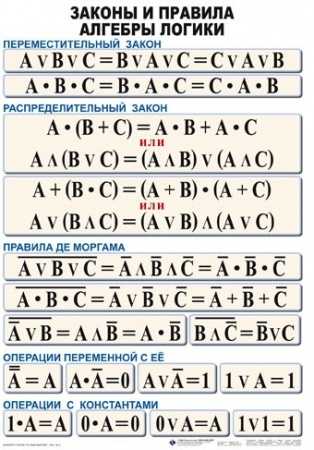

3. Если элементарная дизъюнкция КНФ содержит одновременно переменную и ее отрицание, то используя следующие равносильные преобразования:

,

эту элементарную дизъюнкцию можно отбросить.

4. Если элементарная дизъюнкция КНФ содержит дважды переменную , то используя следующее равносильное преобразование:

,

одну переменную можно отбросить.

СКНФ формулы существует в единственном виде.

ПРИМЕР

Получить СКНФ формулы

С помощью равносильных преобразований получаем СКНФ :

С помощью таблицы истинности получаем СДНФ :

0	0	0	1	0	1	0
0	0	1	0	0	1	0
0	1	0	1	1	1	0
0	1	1	0	0	1	0
1	0	0	1	0	0	1
1	0	1	0	0	0	1
1	1	0	1	1	1	0
1	1	1	0	0	0	1

СДНФ

Очевидно, что в результат двух способов совпадает.

СДНФ формулы можно получить из СКНФ, используя следующее правило:

Элементы теории доказательств в курсе математической логики

Библиографическое описание:

Иванисова, О. В. Элементы теории доказательств в курсе математической логики / О. В. Иванисова, И. В. Сухан, Г. Г. Кравченко. — Текст : непосредственный // Педагогика высшей школы. — 2016. — № 3 (6). — С. 37-38. — URL: https://moluch.ru/th/3/archive/43/1192/ (дата обращения: 13.03.2023).



Одной из основных задач математической логики является изучение понятия правильного рассуждения, или доказательства.

Доказательство (в широком смысле этого слова) — это логическое действие, в процессе которого истинность какого-либо суждения обосновывается с помощью других суждений.

Любое неформальное рассуждение (доказательство) представляет собой конечную последовательность повествовательных предложений (то есть высказываний), приводимых в обоснование того, что последнее повествовательное предложение (высказывание) в этой последовательности может быть выведено из начальных повествовательных предложений (высказываний).

Таким образом, изучение теории доказательств целесообразно начать с методов алгебры высказываний.

В алгебре высказываний обычно приходится доказывать, что некоторое высказывание B является логическим следствием некоторых высказываний A₁, A₂, …, A_n(в символической записи A₁, A₂, …, A_n |= B). Для этого применяют две схемы доказательств: прямое доказательство и косвенное.

Прямое доказательство того, что A₁, A₂, …, A_n|= B проводят по следующей схеме:

1. Формулы A₁,A₂, …,A_nсчитают входящими в доказательство.
2. К доказательству присоединяют ранее доказанные формулы, в частности тавтологии.
3. К доказательству присоединяют новые формулы, полученные по правилам вывода.
4. Доказательство закончено, если последняя формула есть B.

Эта схема обосновывается теоремой [5] о представлении доказательства в виде цепочки формул. Для доказательства этой теоремы требуется две леммы.

Лемма 1. A₁, A₂, …, A_n |=A_i, i = 1, 2, …, n.

Доказательство следует из определения логического следствия.

Лемма 2. Если A₁, A₂, …, A_n|= B_j, j = 1, 2, …, m, и если B₁, B₂, …, B_m |= C, то

A₁, A₂, …, A_n |= C.

Доказательство.

Доказательство проведем с помощью таблицы истинности высказываний A_i, B_j, C, построенной по переменным, входящим хотя бы в одну из формул A_i, B_j, C.

Рассмотрим строки таблицы, в которых все A_i принимают значение T (истина). Из определения логического следствия получаем, что все B_j в этих строках также получают значения T, следовательно, и C в этих строках принимает значение T, а это и означает, что A₁, A₂, …, A_n |= C.

Теорема о представлении доказательства в виде цепочки формул.

A₁, A₂, …, A_n |= B, если можно составить цепочку формул E₁, E₂, …, E_m= B, в которой либо E_k = A_j, либо в этой цепочке есть предшествующие формулы такие, что.

Другими словами, каждая формула цепочки либо есть посылка, либо получена из предыдущих формул цепочки по одному из правил вывода.

Доказательство.

Пусть такая цепочка построена, E_k удовлетворяют условию теоремы, т. е. либо E_k= A_j, либо существуют предшествующие формулы такие, что.

Докажем, что A₁, A₂, …, A_n|= E_k для k = 1…, m (E_m = B). Доказательство проведем методом математической индукции.

При k = 1 имеем: предшествующих формул нет, значит E_1— одна из посылок, т. е. E₁ = A_iдля некоторого i= 1, 2, …, n. По лемме 1 имеем: A₁, A₂, …, A_n |= A_i= E₁, i = 1, …, n.

Пусть это справедливо для E₁, E₂, …, E_k–1, т. е. A₁, A₂, …, A_n |= E_i, i= 1, …, k — 1.

Докажем, что это справедливо и для E_k.

Если E_{k— посылка, то применима лемма 1. Если Ekпосылкой не является, то из условия теоремы следует, что и так, как , то по предположению индукции A1, A2, …, An |= , j = 1, …, s и по лемме 2 имеем:}

A₁, A₂ …, A_n|= E_k.

Тогда A₁, A₂, …, A_n|= E_kдля любого k = 1, …, m.

Замечание. Очевидно, что в цепочку можно включать любую тавтологию. Если |=D (D — тавтология), то для любой формулы A имеем |=A→D. В качестве формулы A можно взять любую посылку A_i, тогда |=A_i→ D или A_i |=D.

Косвенное доказательство (или доказательство от противного) того, что

A₁, A₂, …, A_n|= B проводят по следующей схеме:

1. Формулы A₁,A₂, …,A_nсчитают входящими в доказательство.
2. К доказательству присоединяют формулу .
3. К доказательству присоединяют ранее доказанные формулы, в частности тавтологии.
4. К доказательству присоединяют новые формулы, полученные по правилам вывода.
5. Доказательство закончено, если в нем имеются две формулы и .

Для обоснования этой схемы нами была доказана следующая теорема.

Теорема (обоснование метода доказательства от противного).

A₁, A₂ …, A_n|= B, если из A₁, A₂, …, A_n, A_n+1 = можно составить цепочку формул E₁, E₂, …, E_m в которую входят две формулы и , и в которой либо E_k = A_j, либо в этой цепочке есть предшествующие формулы такие, что.

Доказательство.

Пусть такая цепочка построена.

После формул и вставим в цепочку тавтологию и применим правило отделения: Применим еще раз правило отделения .

Таким образом, в цепочке появилась формула . По теореме о представлении доказательства в виде цепочки формул имеем

A₁, A₂ …, A_n, |= . Отсюда получаем: A₁, A₂, …, A_n |= [5, с. 95].

Рассмотрим такой набор переменных, входящих во все формулы, что все A_iпринимают значение T, тогда и = T.

Так, как = F, то и = F, а следовательно B = T, а это означает, что

A₁, A₂, …, A_n |= B.

Замечание. Для присоединения к доказательству новых формул используют основные правила вывода алгебры высказываний [2]:

1. (правило отделения, правило заключения, modus ponens).
2. (правило отрицания, modus tollens).
3. (правило введения конъюнкции).
4. (правило удаления конъюнкции).
5. (правило введения дизъюнкции).
6. (правило удаления дизъюнкции).
7. (правило введения эквиваленции).
8. (правило удаления эквиваленции).
9. (правило контрапозиции).
10. (правило цепного заключения, правило силлогизма).
11. (правило перестановки посылок).
12. , (правило объединения и разъединения посылок).

Литература:

1. Успенский В. А., Верещагин Н. К., Плиско В. Е. Вводный курс математической логики. — М.: Физматлит, 2007. — 128 с.
2. Игошин В. И. Математическая логика и теория алгоритмов. М.: Издательский центр «Академия», 2010. — 448 с.
3. Колмогоров А. Н., Драгалин А. Г. Введение в математическую логику. М.: Издательство Московского университета, 1982. — 120 с.
4. Мендельсон Э. Введение в математическую логику. — М.: Наука, 1976. — 320 с.
5. Столл Р. Р. Множества. Логика. Аксиоматические теории. М.: Просвещение, 1968. — 232 с.

Основные термины (генерируются автоматически): доказательство, формула, вид цепочки формул, логическое следствие, правило вывода, правило отделения, представление доказательства, прямое доказательство, условие теоремы, цепочка формул.

Логические нормы обоснования в научном познании

доказательство, формула, представление доказательства, правило отделения, правило вывода, вид цепочки формул, логическое следствие, цепочка формул, условие теоремы, прямое доказательство.

Аксиоматические теории в курсе математической

логики

После этого, пользуясь правилами логического умозаключения, выводят новые утверждения о первоначальных и определяемых понятиях, которые называются теоремами. Доказательством называется конечная последовательность высказываний (формул)…

Методические аспекты обучения

доказательству студентов…

− Обучение умениям осуществлять цепочки логических шагов в доказательстве и применять эвристические приемы.

При работе над формулировкой и доказательством теорем можно придерживаться следующего плана [5]

Формирование метапредметных умений при обучении.

..

– доказательстве теорем и выводе формул; – решении уравнений, неравенств и их систем

В систему упражнений целесообразно включить задания, которые формируют умение строить цепочки логических рассуждений.

Доказательством называется конечная последовательность…

После этого, пользуясь правилами логического умозаключения, выводят новые утверждения о первоначальных и определяемых понятиях, которые называются теоремами. Доказательством называется конечная последовательность высказываний (формул)…

Построение формальной арифметики в рамках изучения…

Доказательство. Формула в стандартной интерпретации выражает невозможность вывода в теории S какой-либо формулы вместе с

Если , то по правилу отделения получаем, что . Из теоремы Гёделя следует, что если теория S непротиворечива, то формула в ней невыводима.

Целеполагание при проектировании курса «Дискретная…»

Доказательство в алгебре высказываний. Правила вывода.

Уметь представлять доказательство ЛС в виде цепочки формул.

Формировать умение формулировать прямую, обратную, противоположную, обратную противоположной теоремы.

Анализ существующих алгоритмов перевода функции алгебры…

Рекуррентный алгоритмоснован на использовании теоремы сложения вероятностей совместных событий, в качестве которых здесь

Согласно правилам теории вероятностей, вероятность реализации опасного состояния системы при развитии аварии можно вычислить по формуле

К вопросу об алгоритмической сложности задачи Рейдемейстера

Прародителем ее является К. Ф. Гаусс, который дал формулу для вычисления числа

Учитывая теорию особенностей (известную как теория катастроф) теорема Рейдемейстера вполне очевидна.

Как издать спецвыпуск? Правила оформления статей. Оплата и скидки.

Математическая логика. Правильно построенные формулы

Пропозициональная переменная похожа на любую реальную переменную, которую вы встречаете в математике. Например x — это переменная, которая может принимать любое математическое значение. Точно так же пропозициональная переменная, скажем, P, может принимать любое предложение в качестве значения. Предложение как значение называется пропозициональной константой.

Определение:

WFF производят предложение. Для построения WFF для логики предикатов применимы следующие правила:

(A) «Верно» (T) и «Ложно» (F) — это wffs.

(B)   Пропозициональная константа (т.е. конкретная пропозиция) и каждая пропозициональная переменная являются wffs.

(C)   Если P и Q являются wffs, то таковыми являются ¬P, P Ʌ Q, PV Q, P→Q и P ↔ Q.

(D)   Если x является переменной (представляющей объекты вселенной дискурса) и P является wff, то таковыми являются ∀P и ∃P. (Это кванторы существования, и они будут рассмотрены в отдельном разделе).

(E)    Строка пропозициональных переменных является wff тогда и только тогда, когда она получается конечным числом применений (A) – (D).

 

Таблица истинности для правильно построенной формулы

Если A  является WFF, состоящей из n пропозициональных переменных, то таблица, содержащая все возможные значения истинности для WFF A , полученная путем замены этих произвольных переменных значения истинности называется таблицей истинности для A .

Если WFF A имеет n пропозициональных переменных, то будет 2 ⁿ возможных комбинаций значений истинности для них и, следовательно, 2 ⁿ строки таблицы истинности для WFF A .

 

Пример:

Постройте таблицу истинности для следующего:

(P ∨ Q) → ((P ∨ R) → (R ∨ Q))

  Обозначим вышеприведенное решение:

по

А . A  содержит 3 пропозициональные переменные, следовательно, будет 2 ³ = 8

строк в таблице истинности A  , полученной ниже:

 

Р	Q	Р	П ∨ Q	П  ∨ Р	Р ∨ Q	(P  ∨ R) →  (R  ∨Q)	А
Ф	Ф	Ф	Ф	Ф	Ф	Т	Т
Ф	Ф	Т	Ф	Т	Т	Т	Т
Ф	Т	Ф	Т	Ф	Т	Т	Т
Ф	Т	Т	Т	Т	Т	Т	Т
Т	Ф	Ф	Т	Т	Ф	Ф	Ф
Т	Ф	Т	Т	Т	Т	Т	Т
Т	Т	Ф	Т	Т	Т	Т	Т
Т	Т	Т	Т	Т	Т	Т	Т

 

Тавтология и противоречие

(a)     Тавтология:  WFF α называется тавтологией, если в ее таблице истинности все значения в последнем столбце равны только T (Истина).

(b)    Противоречие:  WFF α называется противоречием, если в его таблице истинности все значения в последнем столбце равны только F (ложь).

 

Эквивалентность правильно построенных формул

Говорят, что две ВФФ α и β эквивалентны (или логически эквивалентны), если формула α ↔ β является тавтологией. Когда α и β эквивалентны, мы пишем α ≡ β.

Пример:

Докажите эквивалентность следующей:

P ≡ (P ∨ Q) ∧ (P ∨ ¬ Q)

Решение:

Пусть α обозначает P

и β -двойное двойное (

. P ∨ Q) ∧ (P ∨ ¬Q)

Тогда нам нужно доказать, что α ↔ β — тавтология. Это можно сделать с помощью следующей таблицы истинности:

 

П ( α)	Q	¬Q	П  ∨  Q	П  ∨   ¬Q	(P ∨  Q) ∧ (P ∨   ) 9Q) (β0006	α ↔   β
Ф	Ф	Т	Ф	Т	Ф	Т
Ф	Т	Ф	Т	Ф	Ф	Т
Т	Ф	Т	Т	Т	Т	Т
Т	Т	Ф	Т	Т	Т	Т

 

Поскольку мы видим, что последний столбец таблицы (значения для α ↔ β) содержит только значения истинности T (Истина), это означает, что α ↔ β является тавтологией, и, следовательно, эквивалентность выполняется.

 

Логические тождества

 

Определение: Логические тождества — это определенные эквивалентности, которые можно использовать для упрощения других сложных ВФФ.

 Процедура для этого основана на следующей парадигме: если WFF β является частью другого WFF α и β эквивалентен β’, то его можно заменить на β’ в α, и результирующий WFF по-прежнему будет эквивалентен к α.

 Все логические тождества могут быть доказаны методом доказательства эквивалентности, описанным выше.

Некоторые общепринятые логические идентичности перечислены в приведенном ниже:

1. Идентификационные законы

P ∨ P ≡ P, P ∧ P ≡ P

2. Коммутативный закон

P Q ≡ Q ∧ P

3.      Ассоциативный закон

P ∨ (Q ∨ R) ≡ (P ∨ Q) ∨ R,

P ∧ (Q ∧ R) ≡ 03 0 4 0 9,0 0 Распределительный закон

P ∨ (Q ∧ R) ≡ (P ∨ Q) ∧ (P ∨ R),

P ∧ (Q ∨ R) ≡ (P ∧ Q) ∨ (P ∧ R)

5.        Закон поглощения

6. Закон де Моргана

¬ (P ∨ q) ≡ ¬P ∧ Q,

¬ (P ∧ q) ≡ ¬P ∨ Q

7. Двойное отрицание

P ≡ O )

8. P ∨ �P ≡ T , P ∧ ¬P ≡ F

9. P ∨ T ≡ T , P ∨ F ≡ P, P ∧ T ≡ P, P ∧ F ≡ F ,

10. P → Q ≡ ¬P ∨ Q

11. (P → Q) ∧ (P → O Q) ≡ ¬P

12 .   Контрапозитив

P → Q ≡ ¬Q → ¬P

 ( ПРИМЕЧАНИЕ:  Постарайтесь запомнить как можно больше тождеств. Это реально поможет на экзаменах.)

Пример:

‘

We ve доказала следующую эквивалентность методом таблицы истинности выше:

P ≡ (P ∨ Q) ∧ (P ∨ ¬Q)

Теперь давайте докажем то же самое, используя логические тождества.

Решение:

Взятие правой руки:

правой руки ≡ (P ∨ q) ∧ (P ∨ ¬ Q)

≡ P ∨ (Q ∧ ¬ Q) (Закон распределения)

≡ P ∨ F

≡ P

≡ L.H.S.

Mathematical Logic:Know Определение, типы, формулы на примере

Изучение формальной логики в математике известно как математическая логика. Основными разделами являются теория моделей, теория доказательств, теория множеств и теория рекурсии. Исследования математической логики часто сосредотачиваются на математических свойствах систем формальной логики, таких как их выразительная или дедуктивная сила. Однако он также может включать применение логики для описания правильных математических рассуждений или для установления математических основ.

Для логических доказательств часто используется математическая логика. Доказательства — это действительные аргументы, которые оценивают истинностные значения математических утверждений. Аргумент представляет собой набор утверждений. Последнее утверждение является заключением, а утверждения перед ним называются посылками. В этой статье мы подробно узнаем о математической логике.

Математическая логика

В середине XIX века математическая логика возникла как предмет математики, объединивший две традиции: формально-философскую логику и математику. Раньше логика преподавалась с использованием риторики, расчетов, силлогизма и философии. В первой половине двадцатого века произошло множество значительных прорывов, сопровождавшихся жаркими спорами об основах математики. 9′ для конъюнкции и «v» для дизъюнкции являются символическими формами математической логики. Истинностное значение утверждений, установленное математической логикой, обеспечивает точное значение математических утверждений в рассуждениях. Эти правила используются для различения правильных и неправильных математических аргументов.

Помимо важности для понимания математических рассуждений, логика имеет множество применений в компьютерных науках, начиная от проектирования цифровых схем и заканчивая созданием компьютерных программ и проверкой правильности программ.

Математические логические операторы

Соединение

Операнд «И» может использоваться для соединения двух операторов. Он также идентифицируется как союз. Он имеет символ «∧». Если какое-либо из утверждений в этом операторе ложно, результат будет ложным. Если оба утверждения верны, результат будет верным. Он имеет несколько входов, но только один выход.

А И В = (А ∧ В)

Дизъюнкция.

Операнд «ИЛИ» может использоваться для соединения двух операторов. Его также называют дизъюнкцией. Он имеет символическую форму «∨». Если какое-либо из утверждений в этом операторе верно, то и результат верен. Если оба утверждения неверны, результат также будет неверным. Есть несколько входов, но только один выход.

A OR B = (A ∨ B)

Отрицание

Отрицание — это оператор, который возвращает оператор, обратный данному оператору. Он также известен как НЕ, что обозначается буквой «∼». Это операция, которая приводит к противоположному результату.

Отрицание A = (∼A)

Формулы математической логики

Логические правила можно использовать для упрощения логических формул.

Законы тождества

\( p\клин T \эквив p \)

\( p\vee F \эквив p \)

Законы доминирования

\( p\wedge F \equiv F \)

\( p\vee T \equiv T \)

Идемпотентные законы

\( p\wedge p\equiv )

\( p\vee p\equiv p \)

Закон двойного отрицания

\( \neg\left ( \neg p\right )\equiv p \)

Коммутативные законы

3 \ ( p\клин q\equiv q\клин p \)

\( p\vee q\equiv q\vee p \)

Ассоциативные законы

\( \left ( p\wee q \right )\wee r\equiv p\left ( q\wee r \right ) \)

\( \left ( p\vee q \right )\vee r\ Equiv p\left ( q\vee r \right ) \)

Распределительные законы

\( p\wedge \left ( q\vee r \right )\equiv \left ( p\wee q \right ) \ vee \left ( p\wee r \right ) \)

\( p\vee \left ( q\wee r \right )\equiv \left ( p\vee q \right )\weedge \left ( p\vee r \right ) \)

Законы Де Моргана

\( \neg\left ( p\wedge q \right )\equiv \neg p \vee \neg q \)

\( \neg\left ( p\vee q \right )\equiv \neg p \wedge \neg q \)

 Законы поглощения

\( p\wedge \left ( p\vee q \right )\equiv p \)

\( p\vee \left ( p\wedge q \right )\equiv p \)

 Законы отрицания

\( p\wedge\neg p\equiv F \)

\( p\vee \neg p\equiv T \)

Типы математической логики

Математическая логика состоит из четырех частей:

• Теория моделей
• Теория доказательств
• Теория рекурсии
• Теория множеств

Теория моделей

Модель — это упрощенная или сокращенная версия теории. Модели можно рассматривать как теории с более узкой областью объяснения. Модель носит описательный характер, тогда как теория является одновременно описательной и объяснительной.

Теория моделей — это изучение моделей различных формальных теорий. Теория — это набор уравнений с определенной формальной логикой и сигнатурой, тогда как модель — это структура, обеспечивающая осязаемую интерпретируемую интерпретацию теории.

Теория доказательств

Теория доказательств — это основная ветвь математической логики, которая представляет доказательства в виде формальных математических объектов, что упрощает анализ математических методов.

Доказательства обычно представляются в виде индуктивно определенных структур данных, таких как простые списки, рамочные списки или деревья, построенные в соответствии с аксиомами логической системы и правилами вывода. В результате теория доказательств носит синтаксический характер, тогда как теория моделей носит семантический характер. Структурная теория доказательств, порядковый анализ, логика доказуемости, обратная математика, анализ доказательств, автоматизированное доказательство теорем и сложность доказательства — вот некоторые из основных областей теории доказательств.

Теория рекурсии

Вычислимость функций из натуральных чисел в натуральные является предметом классической теории рекурсии. Используя машины Тьюринга, исчисление и другие системы, основные результаты позволяют построить надежный канонический класс вычислимых функций с несколькими независимыми эквивалентными характеристиками. Два более продвинутых вывода — это структура тьюринговых степеней и решетка рекурсивно перечислимых множеств.

Теория множеств

Теория множеств — это раздел математической логики, изучающий множества, которые можно неформально описать как наборы объектов. Хотя любой объект может быть скомпилирован в набор, теория множеств, символы теории множеств как раздел математики в основном связаны с теми, которые имеют отношение к математике в целом.

Таблица истинности математической логики

Таблица истинности — это математическая таблица, используемая в логике, особенно в связи с булевой алгеброй, булевыми функциями и исчислением высказываний, в которой перечислены функциональные значения логических выражений для каждого из их функциональных аргументов, т. е. для каждой комбинации значений, принимаемой их логическими переменными.

Таблицы истинности, в частности, могут использоваться для определения того, является ли пропозициональное выражение истинным для всех допустимых входных значений, т. е. логически верным.

Под таблицей истинности отображается результат объединения любых двух логических выражений с использованием операторов И и ИЛИ (или оператора НЕ).

Решенные примеры математической логики

Задача: 1
Рассмотрим утверждение \( x> 0\Rightarrow x+1> 0 \) это утверждение истинно или ложно?

Решение:

Чтобы определить его истинное значение, мы должны сначала проверить гипотезу: x> 0

Какой бы вывод мы ни сделали, он является результатом того факта, что x положителен.

Вывод следующий: x+ 1> 0 Поскольку x+1>x>0, это утверждение должно быть верным.

Это означает, что утверждение верно.

Задача: 2
Для данных двух утверждений вычислите значения таблицы истинности дизъюнкции.
А: p можно разделить на два.
B: p делится на три.

Решение:

Предположим: A: P делится на 2.

B: P делится на 3.

Предположим разные значения x, чтобы продемонстрировать таблицу истинности дизъюнкции.

Value of P	A	B	A OR B (A ∨ B)
P =12	T	T	T
P =4	T	F	T
P = 9	T	T	T
P =7	T	F	F

Хотите хорошо сдать экзамены по математике? Тогда вы находитесь в правильном месте. Платформа Testbook предлагает еженедельную подготовку к тестам, живые занятия и серию экзаменов. Подготовьте умную и высокорейтинговую стратегию к экзамену, скачав приложение Testbook прямо сейчас.

Часто задаваемые вопросы по математической логике

В.1 Как решить математическую логику?

Ответ 1 Например: Найдите отрицание данного утверждения «Число 6 — четное число». Решение: Пусть «S» представляет данное утверждение.
S — четное число.
В результате данный оператор инвертируется.
\( ∼S = 6 \) нечетное число.
В результате обратным утверждением будет «6 — нечетное число».

”

Q.2 Что такое элементарная логика в математике?

Ответ 2 Элементарная логика определяет логику, объясняет, как она работает и почему она может быть интересной. Книга охватывает самый важный аспект логики, который должны изучать все студенты: логику высказываний. Он призван дать четкое введение в то, что часто считается наиболее технически сложной областью философии.

Q.3 Для чего используется математическая логика?

Ans.3 Логическое мышление является полезным инструментом во многих областях, включая решение проблем. Логическое рассуждение — это процесс прихода к выводу о проблеме с использованием рациональных, системных шагов, основанных на математической процедуре.

Q.4 Что такое закон математической логики

Ответ 4 Многие логические законы аналогичны алгебраическим законам. Существует логический закон, соответствующий ассоциативному закону сложения, например, \( a+\left ( b+c \right ) = \left ( a+b \right )+c \) Действительно, ассоциативность конъюнкции и дизъюнкции является одним из законов логики.

Q.5 Является ли логика разделом математики?

Ответ 5 Логика и математика являются родственными дисциплинами, потому что логика является очень общей теорией вывода и рассуждения, а вывод и рассуждение играют очень важную роль в математике, потому что математики доказывают теоремы, что требует использования логических принципы и логические выводы.