Формулы нахождения производной: Формулы производных функции

Содержание

2.1.7. Вывод производных основных элементарных функций

Получим формулы для нахождения производных основных элементарных функций.

1. . При нахождении производной функции используем определение производной, формулы преобразования тригонометрических выражений и первый замечательный предел.

2. . Используем формулы приведения и производную сложной функции, получим

3. . Используем формулу дифференцирования частного, получим

4. . .

При выводе формул нахождения производных обратных тригонометрических функций используем взаимосвязь производных взаимно обратных функций и формулы взаимосвязи тригонометрических функций.

5. . Для обратной функцией является .

6. .

7. .

8..

9. .При нахождении производной логарифмической функции используем определение производной и второй замечательный предел.

В частном случае, когда a = e, .

10. При нахождении производной показательной функции используем так называемое логарифмическое дифференцирование. Для этого логарифмируем равенство , получаем . Это равенство дифференцируем; при этом учитываем, что сложная функция.

В частном случае, когда a = e , .

11. Производную степенной функции найдем так же, используя логарифмическое дифференцирование.

В практических задачах часто встречаются производные от функций и , которые полезно помнить.

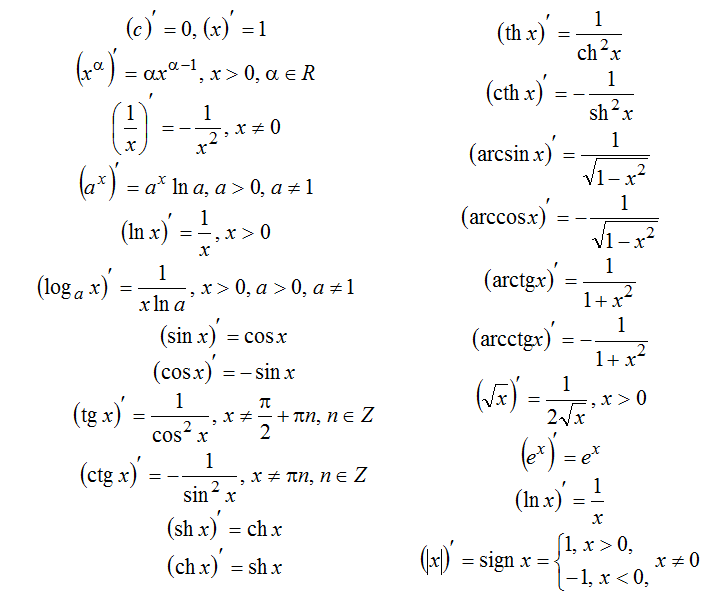12. Производная обобщенно-показательной (показательно-степенной) функции . Используем определение логарифма, представим функцию в виде Эту функцию дифференцируем как сложную показательную функцию.

= .

Как можно заметить производная обобщенно-показательной функции равняется сумме производных как показательной и как степенной функций.

Например: 1) ;

13. Производная функции, заданной неявно.

Функция называется заданной неявно, если она задана уравнением , не разрешенным относительно y. Чтобы найти производную функции , заданную неявно, необходимо каждое слагаемое уравнения продифференцировать по

x, учитывая, что y зависит от x, и из получившегося уравнения найти .

Пример 2. 1. Найти производные функций , заданных неявно.

1) . Находим .

2) . Получаем 

.

14. Производная функции, заданной параметрически.

Функция называется заданной параметрически, если функция y и аргумент x заданы в виде функций, зависящих от некоторого параметра t, т. е.

Найдем производную данной функции в общем случае

Здесь предполагается, что функция имеет обратную функцию .

Например, пусть функция в параметрической записи имеет вид

Исключим в этой системе параметр

t. Получим

т. е. данная функция представляет окружность в параметрической записи.

Найдем производную данной функции.

1. .

2. .

3. .

4. .

5. .

Таблица производных

1. .

2. . 2а. . 2б. . 2в. .

3. . 4. .

5. . 6. .

7. . 8. .

9. . 10. .

11. . 12. .

13. . 14. .

15. .

16. .

Дифференцирование. Основные правила дифференцирования. Формулы производных основных элементарных функций

Математика \ Дискретная математика

Страницы работы

3 страницы (Word-файл)

Посмотреть все страницы

Скачать файл

Содержание работы

Часть 2. Дифференцирование.

Контрольная работа №2. Цель данной контрольной работы помочь студентам в овладении навыками нахождения производных функций одной переменной. Операция нахождения производной называется дифференцированием функции. Производная функции y=f(x) обозначается либо , либо .

Сформулируем основные правила дифференцирования и приведем формулы производных основных элементарных функций:

1. 10.

2. 11.

3. 12.

4. 13.

5. 14.

6. 15.

7. 16.

8. 17.

Отметим, что полезно запомнить частный случай формулы 5

Большое значение для вычисления производных различных функций имеет следующая теорема:

Теорема о производной сложной функции. Пусть где , тогда

или эта формула записывается в виде

Так, например, если , то формулы 5, 6, 10, 13 принимают вид:

5а.

6а.

10а.

13а.

Задача 1a.

Основная цель данной задачи проверить навыки дифференцирования сложной функции. Рассмотрим примеры.

Найти , где .

Приведем подробное решение этой задачи. (Мы предполагаем, что студенты к моменту выполнения контрольной работы изучили таблицу производных основных элементарных функций.)

Функция имеет вид , где .

Воспользуемся формулой производной сложной функции. Тогда

, где . Функция u(x) имеет вид , где . Получаем . Функция имеет вид , где . Получаем ==

Теперь можем записать окончательный ответ

Ответ: =.

Отметим, что нет необходимости (если вы уверенно владеете техникой дифференцирования) при выполнении контрольной работы столь подробно проводить все выкладки.

Задача. Найти , где .

Используя последовательно формулы 10, 5, 6, 4 и 5, а также правило дифференцирования сложной функции, получим:

Отметим, что все производные по промежуточным аргументам можно выполнять в уме и непосредственно давать готовый ответ.

Задача. Найти , где .

Ответ: .

Задача 1б.

Целью данной задачи является закрепления навыков нахождения производной произведения функций.

Задача. Найти , если .

Используя формулу производной произведения, получаем

Далее воспользуемся формулой производной сложной функции. Получаем

Вычисляя табличные производные, получаем ответ.

Ответ:

Как мы уже упоминали ранее, при уверенном владении техникой дифференцирования в контрольной работе нет необходимости приводить столь подробное описание.

Рассмотрим еще один пример.

Задача. Найти , если

Сначала воспользуемся формулой производной произведения, а затем формулой дифференцирования сложной функции:

Приведем решение еще одного примера, где все промежуточные рассуждения проведены в уме.

Задача. Найти , если .

Задача 1в.

Целью данной задачи является закрепления навыков нахождения производной частного.

Задача. Найти , если .

Информация о работе

Скачать файл

Derivatives • Формулы CFA® Level 1 • 365 Financial Analyst

Нужен полный список с формулами Derivatives , включенными в экзамен CFA Level 1? Мы собрали их для вас здесь. Соответствующие формулы были организованы и представлены по главам. В этом разделе мы рассмотрим следующие темы: репликация , переадресация, свопы, параметры и биномиальная модель .

1. Репликация

Длинный безрисковый актив (кредитование)

 Длинный~безрисковый~актив~(кредитование) = Длинный~актив + Короткий~производный~

Длинный~производный~ Заимствование)

Короткий актив

 Короткий ~ Активу = Короткий ~ Дериватный + Короткий ~ БЕЗОПАСНОСТЬ - БЕЗОПАСНОСТЬ ~ (заимствование)

2. Ведл
FRA Урегулировал до долгого 7777
FRA.
FRA~расчет~долгой= \frac {Условная~основная сумма \times (Плавающая~ставка — Форвардная~ставка) \Big( \frac {Days}{360} \Big)}{1 + Floating \ Большой( \frac {Дней}{360} \Большой)} 9T
F_0(T) = Цена форварда
S_0 = Спотовая цена базового актива
r = Безрисковая процентная ставка
T = Время действия контракта
Стоимость
V_T(T) = S_T - F_0(T)
V_T(T) = стоимость форварда на момент времени T
S_T = спотовая цена базового актива на момент времени T
F_0(T) = цена форварда
Чистая стоимость Carry
Чистая~стоимость~перевозки = ϒ - θ
ϒ = Выгоды
θ = Затраты 9{-(T — t)}
V_t(T) = стоимость на момент времени t
S_t = спотовая цена базового актива на момент времени t
При деньгах : S_T > X
При деньгах : S_T = X
Вне денег : S_T < X
Опцион колл
03 Покупатель
04
C_T = макс. (0, S_T — X)
\Pi = C_T — P C_T = -Max (0, S_T — X)
\Pi = C_T + P
C_T = Стоимость опциона колл при экспирации (T)
S_T = Цена акции при экспирации ( T)
X = Цена исполнения/страйка опциона
\Pi = Прибыль
P = Выплаченная премия за опцион
Опционы пут
В деньгах : S_T < X
ST_04ey : At-04ey = X
Без денег : S_T > X
Покупатель опциона пут Продавец опциона пут
P_T = Макс. Pi = -P_T + P
P_T = стоимость опциона пут по истечении (T)
S_T = цена акции по истечении (T)
X = цена исполнения/страйка опциона
\Pi = прибыль
P = уплаченная премия по опциону
Паритет пут-колл
S_0 + p_0 = c_0 + \frac {X}{(1 + r)^T} 9-}{1 + r}
c_0 = Стоимость колл-опциона
1 — π = Синтетическая вероятность движения вниз
5. Свопы
Своп с фиксированной процентной ставкой 09 07 ~платеж~(t) = (Своп~FR — LIBOR) \times \frac {T}{360} \times NP~Обычная~Ванильная~Процентная~ставка~Своп
FR = Фиксированная ставка
T = Количество дней в расчетный период
NP = номинальная основная сумма
Перейдите по ссылкам, чтобы найти дополнительные формулы по количественным методам, экономике, корпоративным финансам, альтернативным инвестициям, финансовой отчетности и анализу, управлению портфелем, инвестициям в акционерный капитал и инвестициям с фиксированным доходом, включенным в экзамен CFA® уровня 1.
Дифференциация
с учетом функции y = ƒ ( x ), его производное , обозначается на y ′ или DY / DX , или DY / DX , или DY / DX , или DY 9035 / DX ′ или . до х . Геометрически это дает наклон кривой (то есть наклон касательной к кривой)
y = ƒ( x ).
Рисунок 1
Вторая производная идентифицирует вогнутость кривой y = ƒ( x ). Часть дифференцируемой кривой y = ƒ( x ) от x = a до x = b называется вогнутой вверх , если кривая лежит выше 09 касательной. a и b и вогнуты вниз , если он лежит ниже его касательных.
Кривая y = ƒ ( x ) вогнута вверх в этих точках x , где вторая производная положительная, и вогнутая, если вторая производная отрицательна. Points where the concavity changes are called inflection points and are located at those points x ₀ where ƒ ⁿ ( x
₀ ) = 0 but ƒ ^m ( x ₀ ) ≠ 0,
Рисунок 2
В Таблице 1 перечислены наиболее часто используемые свойства производных и, для последующего использования, соответствующие свойства интегралов.
ТАБЛИЦА 1 Вычислительные свойства дифференцирования и интегрирования

Помимо знакомства с определениями и фундаментальными свойствами, вы, конечно же, должны уметь различать функции. Хотя приведенная ниже таблица не содержит всех формул дифференцирования, ее, вероятно, будет достаточно, чтобы дифференцировать почти все функции, с которыми вы, вероятно, столкнетесь на практике. Опять же, для дальнейшего использования, формулы интегрирования перечислены рядом с соответствующими формулами дифференцирования. (Примечание: чтобы избежать повторения записи «+c» после каждого результата в правом столбце, произвольная аддитивная константа c опущено в каждой из формул интегрирования, как и в таблице 1.)
ТАБЛИЦА 2 Формулы дифференцирования и интегрирования

Пример 1 : Различайте каждое из следующего:
и . у = 3 х ² — 5 х + 8
б . у = х ² e ^х
с . у = В х / х
д . у = ( х ³ + х — 1) ⁴
эл.
ф . у = грех( х ² )
г . у = sin ² х
ч. у = е ^{тан х}
я.
Решения следующие:
и . у ′ = 6 х — 5
б. Using the product rule, y ′ = x ² · e ^x · e ^x · 2 x = xe ^x ( x + 2)
в. По частному правилу
Все остальные части используют цепное правило (как воплощено в формулах в ).
д . у ′ = 4( х ³ + х — 1) ³ · (3 х ² + 1)
эл.
ф . у ′ = 2 х потому что ( х ² )
г . y = (sin x ) ² ⟹ y ′ = 2 sin x cos x = sin 2 x
ч . y ′ = e ^{тангенс x} сек ² x
я.
Пример 2 : Уравнение касательной к кривой y = e ^x В x в точке (1, 0)?
Первый шаг — найти наклон касательной в точке x = 1, что является значением производной от y в этой точке:
уклон в точке
Поскольку формула точка-уклон говорит, что прямая линия с уклоном м , проходящая через точку ( x ₀ , y ₀ ) имеет уравнение
уравнение искомой касательной: y = e ( x −1).
Пример 3: Является ли кривая y = arcsin вогнутой вверх или вогнутой вниз в точке ( ?
Вогнутость определяется знаком второй производной.
С
первая производная от y = арксинус равен
Следовательно, его вторая производная равна 9.0007
Для x + ¼ знаменатель в приведенном выше выражении для y ″ положителен (как и для любых x в интервале 0 < x < 1), но числитель отрицателен. Следовательно, y ″(¼) < 0), и в точке кривая вогнута вниз.
Пример 4: рассмотрим кривую, неявно заданную уравнением
Каков наклон этой кривой в точке, где она пересекает х ось?
Чтобы найти наклон кривой, определенной неявно (как в данном случае), используется метод неявного дифференцирования : Продифференцируем обе части уравнения относительно x ; затем решите полученное уравнение для y ′.
Кривая пересекает ось x , когда y = 0, и из данного уравнения ясно следует, что x = — 1 при y = 0.
No related posts.