Формула объема в химии
Онлайн калькуляторы
На нашем сайте собрано более 100 бесплатных онлайн калькуляторов по математике, геометрии и физике.
Справочник
Основные формулы, таблицы и теоремы для учащихся. Все что нужно, чтобы сделать домашнее задание!
Заказать решение
Не можете решить контрольную?!
Мы поможем! Более 20 000 авторов выполнят вашу работу от 100 руб!
В химии, равно как и в физике очень важным является понятие объема, поскольку для решения задач, связанных с газообразными веществами, приходится оперировать именно этой величиной.
а) Закон Авогадро, молярный объем газа
Поскольку газы являются наиболее простым объектом для исследования, то их свойства и реакции между газообразными веществами изучены наиболее полно.
Французский ученый Ж. Л. Гей-Люссак установил закон объемных соотношений: объемы вступающих в реакцию газов при одинаковых условиях (температуре и давлении) относятся друг к другу как простые целые числа. Например, при взаимодействии 1 л хлора с 1 л водорода будет образовываться 2 л хлороводорода и т.д.
Например, при взаимодействии 1 л хлора с 1 л водорода будет образовываться 2 л хлороводорода и т.д.
Этот закон позволил итальянскому ученому А. Авогадро предположить, что молекулы простых газов состоят из двух одинаковых атомов (водород, кислород, азот и др.). Изучение свойств газов позволило ему высказать гипотезу, которая впоследствии получила экспериментальное подтверждение и стала называться законом Авогадро: в равных объемах различных газов при одинаковых условиях (температуре и давлении) содержится одинаковое число молекул. Следовательно, при нормальных условиях 1 моль различных газов занимает объем, равный 22,4 л. Этот объем называется молярным объемом газа:
Vm = V / n
б) Газовые законы объем газа
Кроме вышеуказанной формулы для решения расчетных химических задач, нередко приходится использовать газовые законы, известные из курса физики.
— Закон Бойля-Мариотта
При постоянной температуре объем данного количества газа обратно пропорционален давлению, под которым он находится:
pV = const
— Закон Гей-Люссака
При постоянном давлении изменение объема газа прямо пропорционально температуре:
V/T = const
— Объединенный газовый закон Бойля-Мариотта и Гей-Люссака
pV/T = const
Помимо этого, если известна масса или количество газа, его объем можно вычислить, используя уравнение Менделеева-Клапейрона:
pV = nRT;
pV = n/M ×RT,
где n–число молей вещества, m–масса (г), Ь – молярная масса газа (г/моль), R – универсальная газовая постоянная равная 8,31 Дж/(моль×К).
Примеры решения задач
| Понравился сайт? Расскажи друзьям! | |||
Объем полого цилиндра
Для полной функциональности сайта желательно включить JavaScript в настройках Вашего браузера.
Главная
→
Геометрия
→
Объем полого цилиндра
Объем полого цилиндра, формулы для вычисления объема и площадей правильного полого цилиндра.
Формула вычисления объема полого цилиндра часто применяются при расчете массы полой круглой трубы. Для вычисления массы трубы, необходимо вычисленный объем трубы (полого цилиндра) умножить на плотность материала из которого изготовлена труба (цилиндр).
Расчет площади поверхностей цилиндра, иногда необходим для определения расхода материала для нанесения защитного покрытия трубы (полого цилиндра).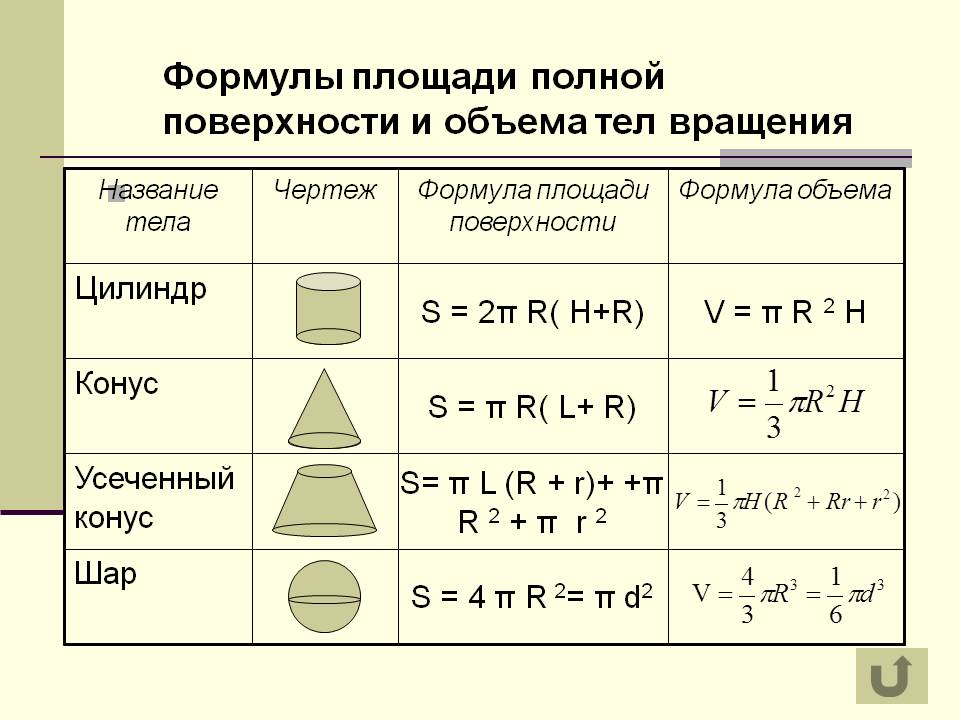
Объем полого цилиндра, вычисленный через внутренний и наружный радиусы
r1 — внешний радиус
r2 — внутренний радиус
h — высота цилиндра
… вычисление …
Площадь основания
… вычисление …
Площадь внутренней и внешней боковой поверхности
… вычисление …
Общая площадь
… вычисление …
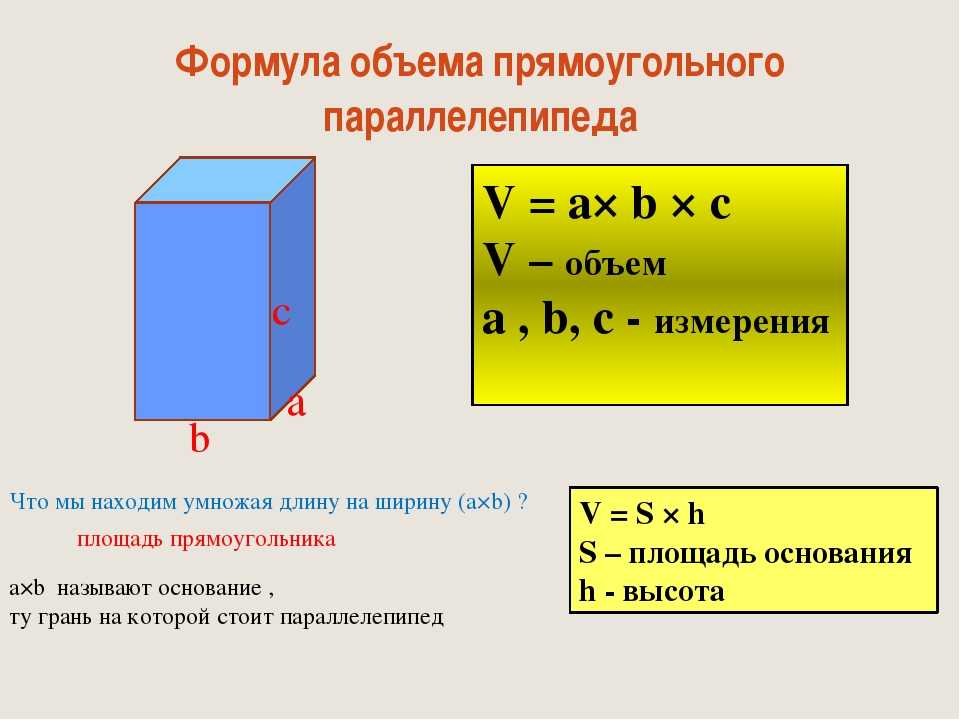
Объем полого цилиндра по толщине стенки и наружному диаметру
D — внешний диаметр
δ — толщина стенки
h — высота цилиндра
… вычисление …
Площадь основания
… вычисление …
Площадь внутренней и внешней боковой поверхности
. .. вычисление …
.. вычисление …
Общая площадь поверностей
… вычисление …
Объем полого цилиндра, вычисляемый по внутреннему диаметру и толщине стенки
δ — толщина стенки
h — высота цилиндра
… вычисление …
Упрощение формулы:
Площадь основания
… вычисление …
Площадь внутренней и внешней боковой поверхности
… вычисление …
Упрощение формулы:
Общая площадь поверностей
… вычисление …
Различия между разными видами цилиндров, а также со свойствами правильного цилиндра, можно ознакомиться в статье «Объем цилиндра» в разделе« Теория».
Объем и площадь других видов цилиндров рассмотрен в статьях:
Объем цилиндра
Объем части цилиндра
Объем части полого цилиндра
Вы можете скачать формулы объема и площади поверхностей правильного полого цилиндра в виде картинки.

скачать
скачать
скачать
скачать
скачать
скачать
Формулы объема
Здесь мы предлагаем вам формулы объема для некоторых распространенных трехмерных фигур, а также для эллипсоида и полого цилиндра, которые не так распространены.
Куб:
Объем = a 3 = a × a × a
Цилиндр:
Объем = π × r 2 × h
π = 3,14
h высота
r радиус
Прямоугольный сплошной или кубовидный:
Объем = l × w × h
l — длина
w — ширина
h — высота
Сфера:
Объем = (4 × π × r 3 )/3
π = 3,14
Конус:
Объем = (π × r 2 × h)/3
pi = 3,14
r — радиус
h — высота
Пирамида:
Объем = (Б × ч)/3·
B – площадь основания
h – высота
Немного менее распространенные формулы объема
Эллипсоид:
Объем = (4 × π × a × b × c)/3
Использование π = 3,14
Полый цилиндр:
Объем = π × R 2 × h — π × r 2 × h
Объем = π × h ( R 2 — r 2 )
Используйте π = 3,14.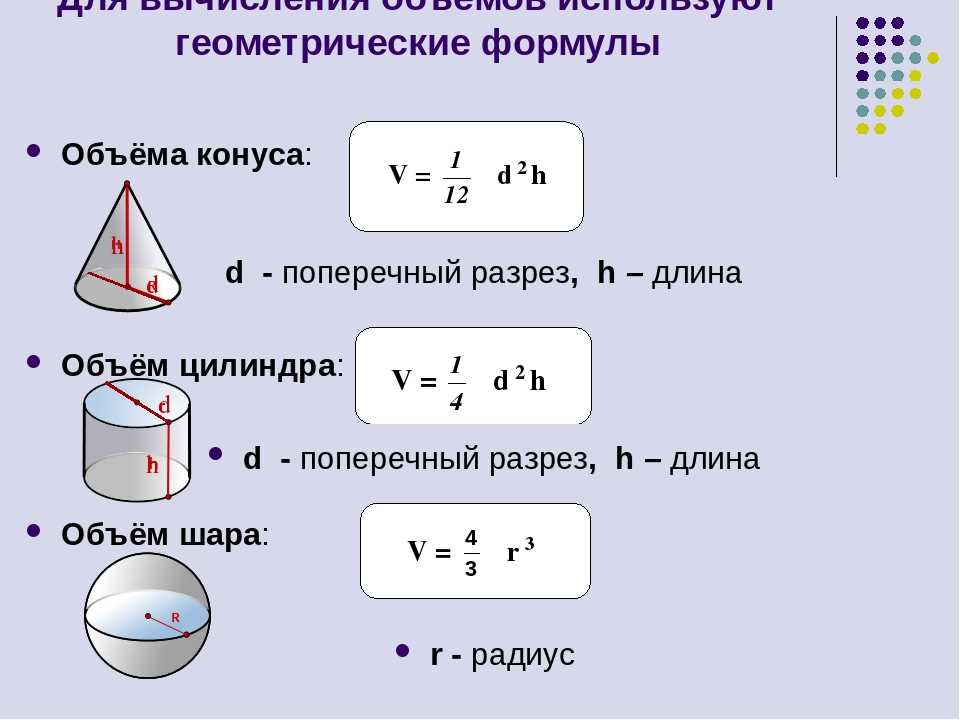
Как использовать формулы объема для расчета объема.
Куб
Длина стороны = a = 2 см
Объем = (2 см) = 2 см × 2 см × 2 см = 8 см дюймов, а радиус равен 2 дюймам.
Объем = π × r 2 × h = 3,14 × (2 дюйма) 2 × 8 дюймов = 3,14 × 4 × 8 дюймов 3
Объем = 3,14 × 32 дюймов 1 дюйм
1 3
=
Прямоугольный сплошной или кубовидный
Длина 6 см, ширина 3 см, высота 5 см.
Объем = l × w × h = 6 × 3 × 5 = 90 см = [4 × 3,14 × (20) 3 ]/3 = 3,14 × (20) 3 × 4
Объем = 3,14 × 8000 × 4 = 3,14 × 32000 = 100480
Объем = (π × r 2 × h)/3 = [3,14 × (3) 2 × 4]/3 = 3,14 × 9 × 4
Объем = 3,14 × 36 = 113,04
Пирамида
Пирамида имеет высоту 6 футов. Найдите объем, если основанием пирамиды является квадрат длиной 2 фута.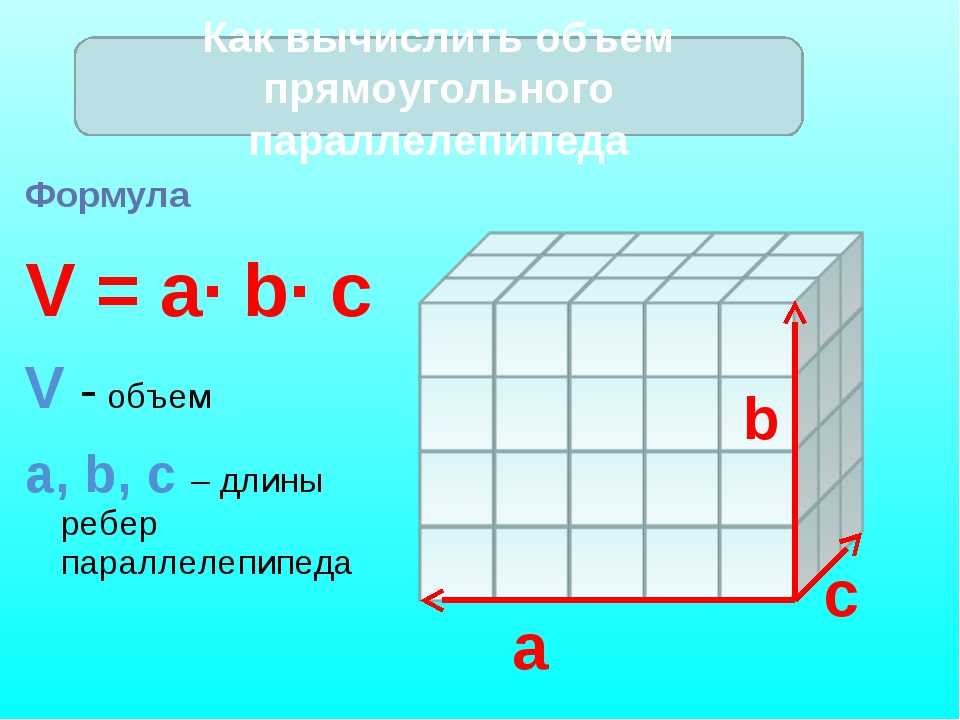
Объем = (B × h)/3
B = площадь основания = 2 фута × 2 фута = 4 фута 2
Объем = (4 × 6)/3 фута 3 = 24/3 фута 3 = 8 футов 3
Эллипсоид
Радиусы эллипсоида равны 1 см, 2 см и 3 см.
Объем = (4 × π × a × b × c)/3 = (4 × 3,14 × 1 × 2 × 3)/3
Объем = (3,14 × 4 × 6)/3 = (3,14 × 24)/ 3 = 81,64/3 = 25,12 см 3
Полый цилиндр
Внешний радиус равен 8, внутренний радиус равен 6, высота равна 10.
Объем = π × h ( R 2 — 4 r 2 ) = π × 10 ( 8 2 — 6 2 ) = π × 10 ( 64 — 36) Объем = π × 10(28) = π × 280 = 879,2 3 902 902 32 18, 22 ноября 08:20 Легко научитесь строить график прямоугольников и усов для набора данных, используя медианы и экстремальные значения. График прямоугольников и усов

Подробнее
Двоичная система счисления
17, 22 ноября 10:53
Этот урок познакомит вас с двоичной системой счисления.
Читать дальше
Формулы объемов – объяснение, единицы измерения, примеры решений и часто задаваемые вопросы
Для любого данного твердого объекта измеряется пространство, занимаемое таким объектом, которое называется объемом объекта. Кроме того, если объект полый, то известно, что его внутренняя часть пуста. Полая часть может быть заполнена воздухом или жидкостью. В этом случае объем вещества, которым можно заполнить внутреннее пространство, даст вместимость любой емкости.
Таким образом, объем объекта может быть определен как мера пространства, которое он занимает, или емкость объекта как объем вещества, которое может вместить его внутренняя часть. Здесь единицей измерения любого из двух является кубическая единица.
Единицы объема
Объем измеряется в «кубических» единицах. Объем любой заданной фигуры — это количество кубиков, необходимых для ее полного заполнения, например, кубиков в коробке.
Объем куба равен сторона х сторона х сторона. Поскольку все стороны квадрата равны, это может быть просто длина одной стороны в кубе.
Если предположить, что одна сторона квадрата равна 4 дюймам, объем будет равен 4 дюймам, умноженным на 4 дюйма x 4 дюйма, или 64 кубических дюйма. (Кубические дюймы также можно записать в 3.)
Some of the formulas to find out volumes of basic geometrical shapes are –
Shapes | Volume Formula | Variables | |||||||
Rectangular Solid or Cuboid | V = длина × ширина × высота | l = длина w = ширина h = высота | |||||||
4 куб 40281 V = A 3 | A = длина края или сторона | ||||||||
Цилиндр | V = π R 9000 | V = π r 9000 | V = π r 9000 | V = π r 9000 | V = π r 9000 | V = π r 289 | .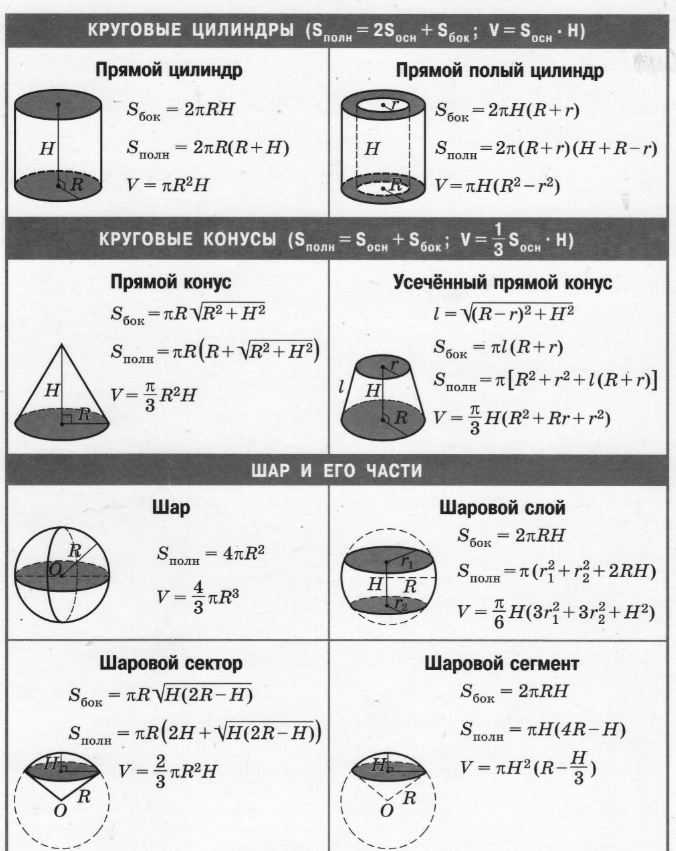 H = высота | ||
Призма | V = B × H | B = область основания, (B = сторона 2 или длина. | |||||||
Sphere | V = (4–3) π R 3 | R = радиус сферы | |||||||
Piramid | 4493|||||||||
| 4493 | |||||||||
| 493 | |||||||||
| 493 | |||||||||
| 493 | |||||||||
| 93 | |||||||||
| 3 | |||||||||
. | B = площадь основания, H = высота пирамиды | ||||||||
Правый циркулярный конус | V = (1⁄3) πr 2 | V = (1⁄3) πr 2 | V = (1⁄3) πr 2 | V = (1⁄3) πr 2 | V = (1⁄3) πr 2 | V = (1⁄3) πr 2 | .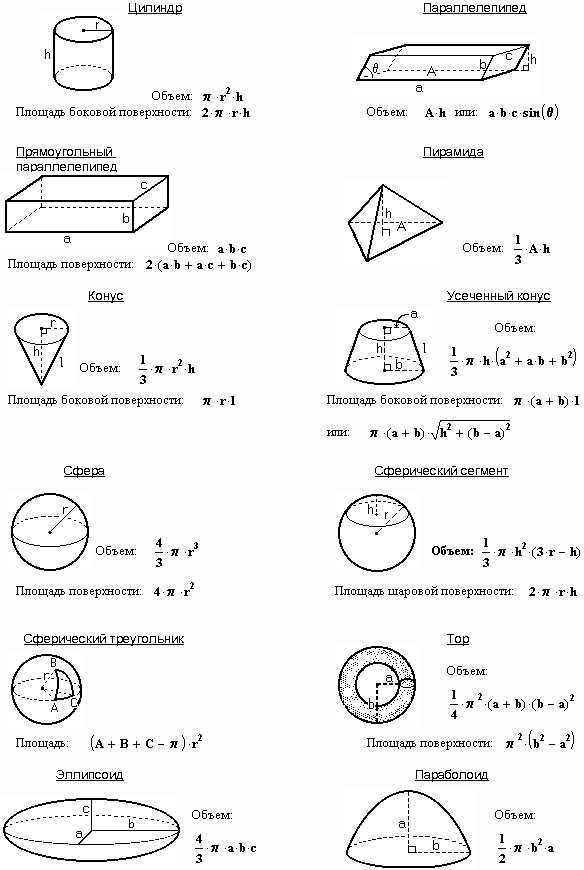 Радиус круглого основания Радиус круглого основанияh = Высота | ||
квадратная или прямоугольная пирамида | V = (1–3) × L × W × H | L = длина базы, | L = длина базы | W = ATHTTH изL = Длина базы W = AWTHSTHETS | L = Длина базового Высота (от основания до вершины) | ||||
Эллипсоид | V = (4⁄3) × π × a × b × c | a, b, c = полуоси 90 0 0 | |||||||
Тетраэдр | V = a 3 ⁄ (6 √2) | a = Длина края |
Решенные примеры
Вопрос 1) Размеры прямоугольного резервуара для воды даны как 2 м 4 см 75 см, 1 м 80 м. Сколько литров воды можно налить в бак данных размеров?
Решение) Как мы знаем, что 1м = 100см.
