Формулы площадь куба: Вычислите объём и площадь поверхности куба с ребром 6 дм.

alexxlab / / Разное

Диагональ грани куба при заданной площади боковой поверхности Калькулятор

✖Площадь боковой поверхности куба — это количество плоскостей, заключенных между всеми боковыми поверхностями (то есть верхняя и нижняя грани исключаются) куба.ⓘ Площадь боковой поверхности куба [SALateral]

акрАкко (служба США)НаходятсяАрпентамбарКарроКруговая дюймаКруговая MilCuerdaарамДунамРаздел электрон КрестаГаусадьбаMuпингплощадьPyongклочок землиСабинРазделКвадратный АнгстремПлощадь СантиметрПлощадь цепи Площадь декаметровойквадратный дециметрКвадратный футКвадратный фут (служба США)Площадь гектометровыеКвадратный дюймквадратный километрКвадратный метрПлощадь микрометраПлощадь MilКвадратная миляКвадратная миля (римская)Квадратная миля (Статут)Квадратная миля (служба США)Площадь МиллиметрПлощадь NanometreМера площадиПлощадь полюсаПлощадь РодКвадратный Rod (служба США)Квадратный дворрастяжениегородокВарас Castellanas CuadВарас Conuqueras Cuad

+10%

-10%

✖Диагональ грани куба — это расстояние между любой парой противоположных углов на конкретной квадратной грани куба. ⓘ Диагональ грани куба при заданной площади боковой поверхности [dFace]

створаАнгстремарпанастрономическая единицаАттометрAU длиныЯчменное зерноМиллиардный светБор РадиусКабель (международный)Кабель (UK)Кабель (США)калибрсантиметрцепьCubit (греческий)Кубит (Длинный)Cubit (Великобритания)ДекаметрДециметрЗемля Расстояние от ЛуныЗемля Расстояние от СолнцаЭкваториальный радиус ЗемлиПолярный радиус ЗемлиРадиус электрона (классическая)флигельЭкзаметрFamnВникатьFemtometerФермиПалец (ткань)ширина пальцаФутFoot (служба США)ФарлонгГигаметрРукаЛадоньгектометрдюймкругозоркилометркилопарсеккилоярдлигаЛига (Статут)Световой годСсылкаМегаметрМегапарсекметрмикродюйммикрометрмикронмилмилиМиля (Роман)Миля (служба США)МиллиметрМиллион светлого годаNail (ткань)нанометрМорская лига (международная)Морская лига ВеликобританииМорская миля (Международный)Морская миля (Великобритания)парсекОкуньпетаметрцицеропикометраПланка ДлинаТочкаполюскварталРидРид (длинный)прутРоман Actusканатныйрусский АрчинSpan (ткань)Солнечный радиусТераметрТвипVara КастелланаVara ConuqueraVara De ФаареяДворЙоктометрЙоттаметрЗептометрЗеттаметр

⎘ копия

👎

Формула

сбросить

👍

Диагональ грани куба при заданной площади боковой поверхности Решение

ШАГ 0: Сводка предварительного расчета

ШАГ 1. Преобразование входов в базовый блок

Площадь боковой поверхности куба: 400 Квадратный метр —> 400 Квадратный метр Конверсия не требуется

ШАГ 2: Оцените формулу

ШАГ 3: Преобразуйте результат в единицу вывода

14.142135623731 метр —> Конверсия не требуется

< 10+ Диагональ грани куба Калькуляторы

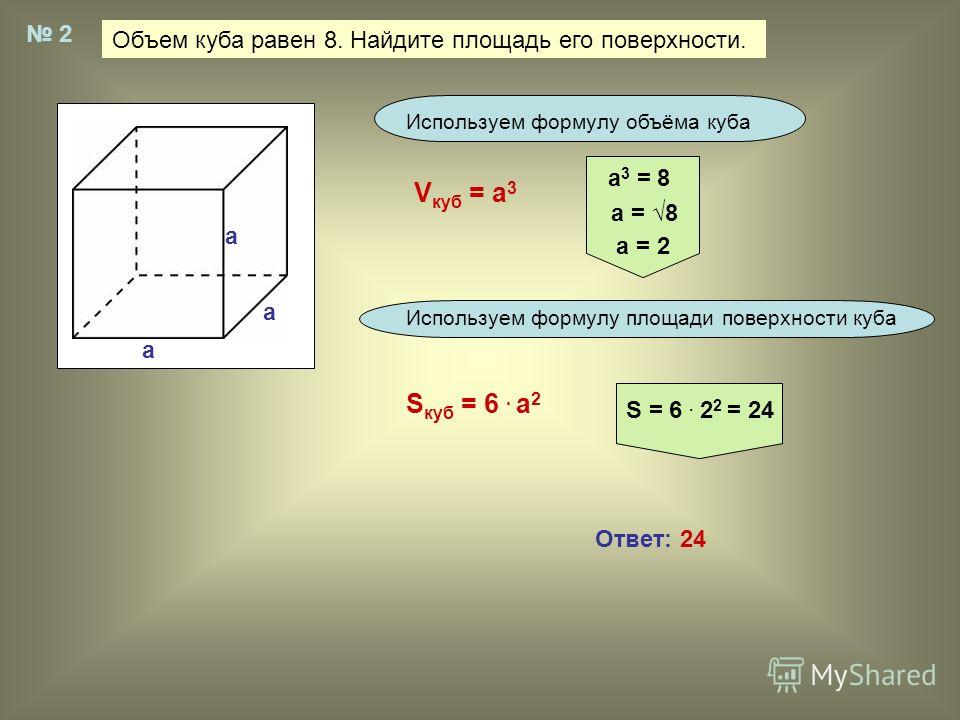
Диагональ грани куба при заданной площади боковой поверхности формула

Диагональ грани куба = sqrt(Площадь боковой поверхности куба/2)
dFace = sqrt(SALateral/2)

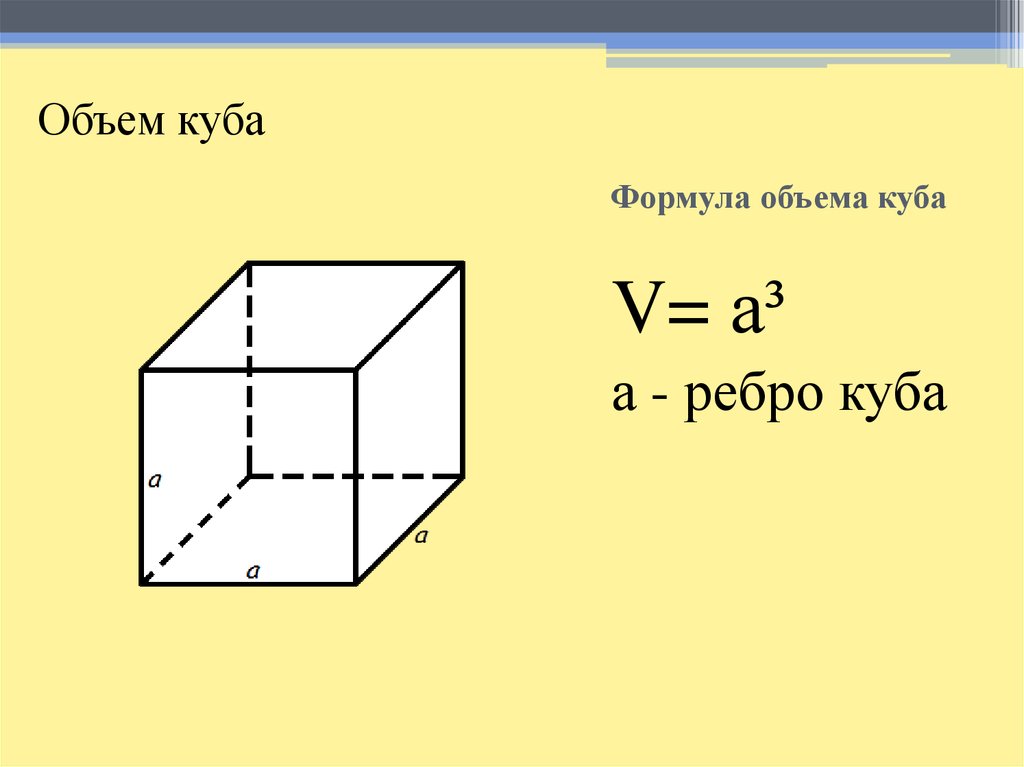
Что такое куб?

Куб — это симметричная замкнутая трехмерная фигура, имеющая 6 одинаковых граней квадратной формы. У него 8 углов, 12 ребер и 6 граней. И каждый угол разделяется на 3 грани, а каждое ребро — на 2 грани Куба. Другими словами, прямоугольный ящик, в котором длина, ширина и высота численно равны, называется кубом. 2. У прямоугольного параллелепипеда примерно та же история, у него 6 граней, только на этот раз грани — 3 пары прямоугольников. Поэтому формула площади поверхности будет состоять из суммы трёх пар площадей прямоугольников: Sпр = 2 • (ab + bc + ac).

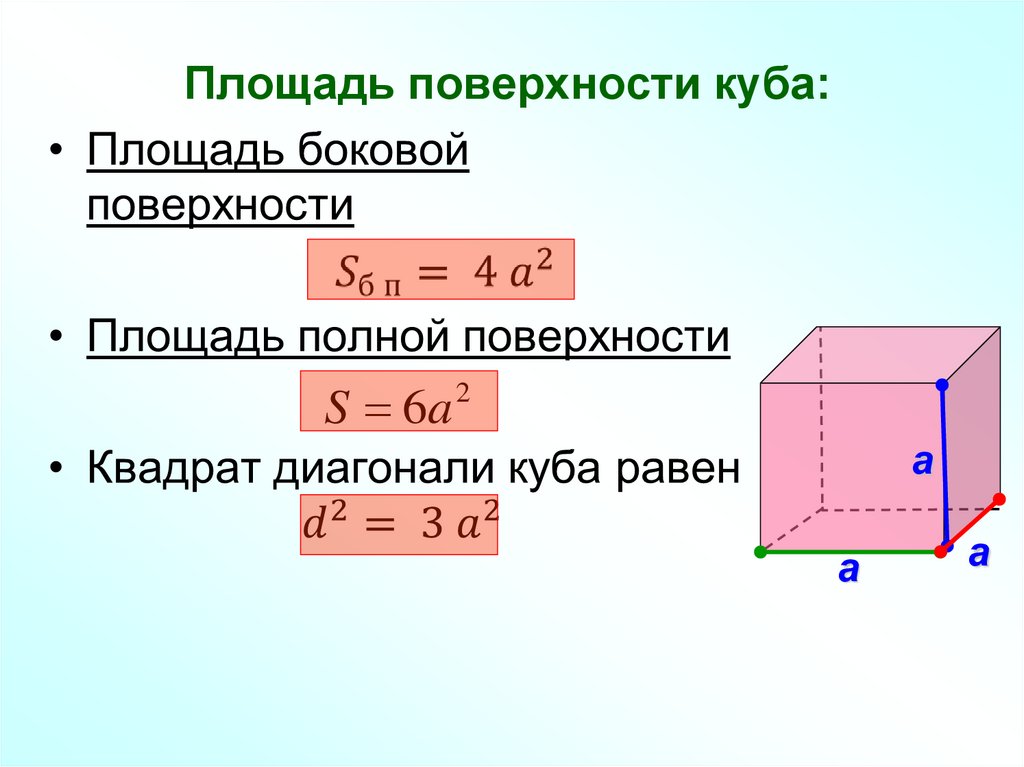
💁🏻‍♂ Площадь полной поверхности призмы состоит из суммы боковой поверхности и двух площадей основания. С основаниями все более менее понятно, а вот площадь боковой поверхности можно вычислить аж по двум формулам. Первая из них для прямой призмы, а вторая для наклонной призмы.

📌 У прямой призмы все грани — прямоугольники с одинаковой стороной в виде высоты. А вторая сторона каждого прямоугольника — сторона основания многоугольника в основании. Поэтому площадь боковой поверхности прямой призмы можно вычислить как произведение периметра основания на высоту.

📌 У наклонной призмы все грани — параллелограммы, поэтому базовый способ для нахождения площади поверхности — считать каждую грань по отдельности и суммировать все грани. Но это не сильно действенный способ потому, что долго и дорого так делать на экзамене, в задачах чаще всего работает другая формула.

✅ Площадь боковой поверхности наклонной призмы равна произведению бокового ребра на периметр перпендикулярного сечения этому ребру. То есть по сути это та же формула, что и для прямой призмы, только вместо периметра основания используем периметр перпендикулярного сечения, а вместо высоты используем ребро.

👉🏻 Последняя из действенных формул — площадь боковой поверхности правильной пирамиды. Площадь полной поверхности равна сумме площадей боковой поверхности и основания. Все грани правильной пирамиды – равные треугольники, у которых одинаковая высота в виде апофемы боковой грани, и равные стороны основания.

🌟 Поэтому площадь боковой поверхности равна произведению полупериметра на апофему. Одна вторая здесь возникает из-за того, что это коэффициент в каждой площади треугольника грани. 

На ЕГЭ нет подсказок в виде формул, поэтому сохраняй картинку, запоминай формулы и применяй их к задачам💕

Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter. Мы обязательно поправим!

Площадь поверхности куба — 2 формулы | Общая площадь поверхности куба

Содержание

Площадь поверхности трехмерной формы (твердого объекта) является мерой общей площади, которую занимает поверхность объекта. Площадь поверхности куба — это общая площадь, занимаемая всеми шестью гранями куба. Полную площадь поверхности куба можно вычислить, если вычислить площадь двух оснований и площадь четырех боковых (боковых) граней.

Важно знать и понимать площадь поверхности, так как это поможет вам узнать количество листов бумаги, необходимое для обертывания куба, покраски поверхностей куба и т. д. 

Куб имеет некоторые характерные особенности, которые используются для нахождения площади поверхности куба, например, все ребра куба равны, а все грани куба квадратны. Давайте узнаем, как найти площадь поверхности куба и его использование.

СКАЧАТЬ БЕСПЛАТНО КАРТОЧКИ ПО МАТЕМАТИКЕ:

Красиво оформленные карточки для печати, которые помогут вам запомнить все важные математические понятия и формулы. {2}$ кв. единиц. 9{2} = 64 => a = 8 см$

Длина ребра куба = 8 см$

Математика в реальной жизни

Разница между кубом и прямоугольным параллелепипедом

Хотя куб и прямоугольный параллелепипед являются похожими объектами $3D$ , есть несколько различий между этими двумя. Ниже приведены различия между кубом и прямоугольным параллелепипедом.

Практические задачи

  1. Если длина ребра куба $5 см$, вычислите его
    • площадь боковой поверхности
    • общую площадь поверхности 9{2}$, найдите площадь его боковой поверхности.
    • Куб со стороной $2$ см разделен на кубы со стороной $1$ см.
      • Сколько кубиков будет сделано?
      • Найдите общую площадь поверхности большего куба.
      • Найдите общую площадь поверхности меньших кубов.
      • Какая из двух указанных выше поверхностей больше?
    • Сплошной куб длиной $10 м$ нужно покрасить на $6$ гранях. Если стоимость покраски составляет 45 долларов США за квадратный метр, найдите общую стоимость покраски куба. 9{2}$, где $a$ — длина каждой стороны куба.

      Рекомендуемое чтение

      • Площадь прямоугольного параллелепипеда (определение, формула и примеры)
      • Площадь прямоугольника – определение, формула и примеры
      • Площадь квадрата – определение, формула и примеры
      • Площадь треугольника – формулы, методы и примеры
      • Площадь круга – формула, вывод и примеры
      • Площадь ромба – формулы, методы и примеры
      • Площадь воздушного змея – формулы, методы и примеры
      • Периметр многоугольника (с формулой и примерами)
      • Периметр трапеции – определение, формула и примеры
      • Периметр воздушного змея – определение, формула и примеры
      • Периметр ромба – Определение, формула и примеры
      • Окружность (периметр) круга – Определение, формула и примеры
      • Периметр квадрата – Определение, формула и примеры
      • Периметр прямоугольника – Определение, формула и примеры
      • Периметр треугольника — определение, формула и примеры
      • Что такое двумерные фигуры — названия, определения и свойства

      Вам также может понравиться

      Как решать линейные уравнения с помощью матриц (с методом18 и примерами) 9003 9003 903

      Содержание Как решать линейные уравнения с матрицамиУсловие непротиворечивости

      Читать далее

      Правило Крамера – определение, формулы и примеры

      Содержание Что такое правило Крамера?Формула правила КрамераПравило Крамера 2 x

      Читать далее

      Карточки по математике для бесплатной печати – скачать в формате PDF

      Карточки по математике – ценный инструмент для учащихся всех возрастов и Читать далее

      Площадь поверхности куба Формула

      Улучшить статью

      Сохранить статью

      • Последнее обновление: 31 мар, 2022

    • Читать
    • Обсудить

      • Улучшить статью

      Сохранить статью

      Куб — трехмерная коробчатая фигура, представленная в трехмерной плоскости. Куб имеет 6 равных граней квадратной формы. Каждая грань встречается с другой гранью под углом 90 градусов. Три грани куба сходятся в одной вершине. Куб — одна из пяти основных форм и единственный симметричный шестигранник.

      Площадь поверхности куба

      Вся площадь, занимаемая каждой гранью куба, называется площадью поверхности куба. Вычисление площади двух уровней и поверхности четырех противоположных ребер дает площадь поверхности куба. Куб — это твердая трехгранная фигура, состоящая из квадратных граней. В тех случаях, когда мы хотим заключить куб, раскрасить грани куба и т. д., знание площади поверхности имеет решающее значение.

      Formula

      The surface area of ​​a cube with side length ‘p’ units is given as:

      A = 6p 2

      Proof

      Since a cube is composed of 6 квадратов, соединенных встык, естественно, что площадь поверхности куба будет равна сумме площадей каждого из шести квадратов.

      Теперь, поскольку площадь квадрата определяется как: (сторона × сторона) = (сторона) 2 .

      Суммируя площади всех шести квадратов, получаем:

      A = 6 × (сторона) 2

      Отсюда доказано.

      Примеры задач

      Задача 1. Найдите площадь поверхности куба со стороной 4 см.

      Решение:

      Дано: P = 4 см

      С момента A = 6p 2

      = 6 × (4) 2

      = 6 × 16

      111111111111111111111111111111111111111111111111111111111111111111. 2

      Задача 2. Найдите сторону куба, если его площадь 21600 кв.см.

      Решение:

      Дано: A = 4800 кв.см.

      Since, A = 6p 2

      ⇒ 21600 = 6p 2

      ⇒ p 2 = 21600/6

      ⇒ p 2 = 3600

      ⇒ p = 60 cm

      Задача 3.

      No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *