Формулы расчета площади геометрических фигур: Формулы для расчета площади и объема геометрических фигур

Расчет площади геометрических фигур | International Institute of Care to Buildings

СПРАВОЧНИКИ

---

 

 

Площадь геометрической фигуры — часть поверхности, ограниченная замкнутым контуром данной фигуры. Величина площади выражается числом заключающихся в него квадратных единиц.

Формулы площади треугольника

1-ая формула

S — площадь треугольника

a, b — длины 2-х сторон треугольника

С — угол между сторонами a и b

2-ая формула

S — площадь треугольника

a — длина стороны треугольника

h — длина высоты, опущенной на сторону a

3-ья формула

S — площадь треугольника

a, b, c — длины 3-х сторон треугольника

p — полупериметр треугольника

4-ая формула

S — площадь треугольника

r — радиус вписанной окружности

p — полупериметр треугольника

5-ая формула

S — площадь треугольника

a, b, c — длины 3-х сторон треугольника

R — радиус описанной окружности

См. также: Онлайн калькулятор для расчета площади треугольника.

Формулы площади квадрата:

1) Площадь квадрата равна квадрату длины его стороны (a).

2) Площадь квадрата равна половине квадрата длины его диагонали (d).

S — площадь квадрата

a — длина стороны квадрата

d — длина диагонали квадрата

См. также: Онлайн кальклятор для расчета площади квадрата.

Формула площади прямоугольника:

1) Площадь прямоугольника равна произведению длин двух его смежных сторон (a, b).

S — площадь прямоугольника

a — длина 1-ой стороны прямоугольника

b — длина 2-ой стороны прямоугольника

См. также: Онлайн калькулятор для расчета площади прямоугольника.

Формула площади параллелограмма:

1) Площадь параллелограмма равна произведению длины его основания на длину высоты (a, h).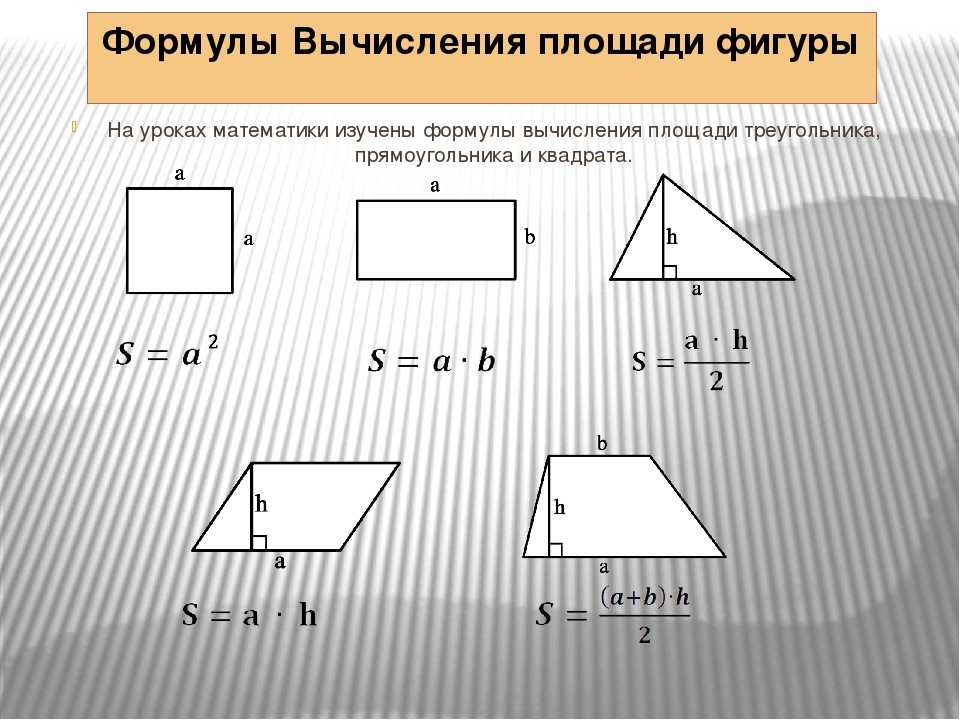

S — площадь параллелограмма

a — длина основания

h — длина высоты

См. также: Онлайн калькулятор для расчета площади параллелограмма.

Формула площади трапеции:

1) Площадь трапеции равна произведению полусуммы ее оснований на высоту (a, b, h).

S — площадь трапеции

a — длина 1-ого основания

b — длина 2-ого основания

h — длина высоты трапеции

См. также: Онлайн калькулятор для расчета площади трапеции.

Формулы площади ромба:

1) Площадь ромба равна произведению длины его стороны на высоту (a, h).

2) Площадь ромба равна половине произведения его диагоналей.

S — площадь ромба

a — длина основания ромба

h — длина высоты ромба

d₁ — длина 1-ой диагонали

d₂ — длина 2-ой диагонали

См. также: Онлайн калькулятор для расчета площади ромба.

Формула площади круга:

1) Площадь круга равна произведению квадрата радиуса на число пи (3.1415).

2) Площадь круга равна половине произведения длины ограничивающей его окружности на радиус.

S — площадь круга

π — число пи (3.1415)

r — радиус круга

См. также: Онлайн калькулятор для расчета площади круга.

Формула площади эллипса:

1) Площадь эллипса равна произведению длин большой и малой полуосей эллипса на число пи (3.1415).

S — площадь эллипса

π — число пи (3.1415)

a — длина большой полуоси

b — длина малой полуоси

См. также: Онлайн калькулятор для расчета площади эллипса.

 

---

 

 

список формул, описание, примеры / Справочник :: Бингоскул

Для решения практических задач иногда приходится вычислять площади геометрических фигур.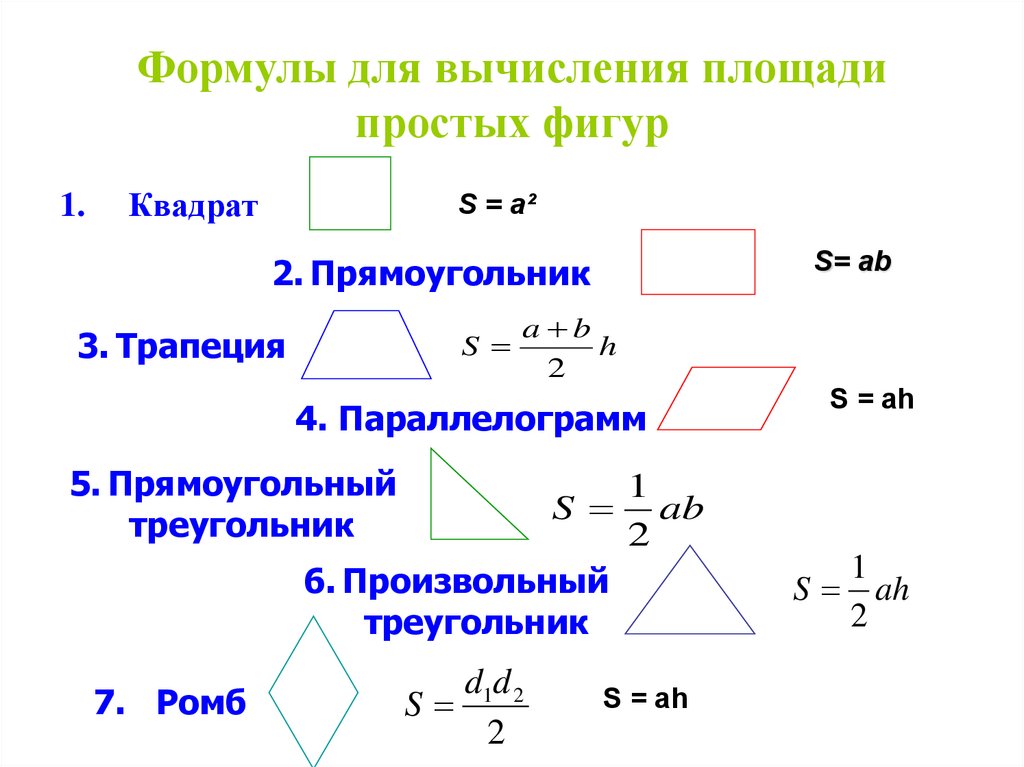 Они, например, нужны при измерениях земельных участков, поверхностей при проведении ремонтных и строительных работ. Рассмотрим, что такое площадь геометрической фигуры, по каким формулам она определяется в разных ситуациях.

Площади всех фигур в геометрии

Площадью называют численную характеристику поверхности, которая показывает сколько квадратов с размером 1 × 1 занимает объект на плоскости. Изменяется в квадратных единицах – метрах, сантиметрах, километрах и т. д.

Для нарисованного по клеточкам четырёхугольника с прямыми углами это делается простым подсчётом с перемножением полученных значений. Для квадрата на примере это 100 см2: 10 × 10 см.

В математике насчитывается менее десятка фигур – замкнутых множеств, сформированных точками, площадь которых можно вычислить. Общий принцип расчётов сформирован благодаря интегральному счислению. 

Формулы площадей фигур по геометрии

Начнём из самого интересного множества. 2 .

При наличии одной диагонали (полудиагонали) и стороны, неизвестные данные вычисляются по теореме Пифагора.

Трапеция: полусумма длин верхнего и нижнего оснований на высоту геометрической фигуры.

S = \frac {a+b}{2}h .

Когда даны средняя линия и высота, площадь находят путём перемножения их значений.

S = ch.

Выпуклый четырёхугольник: половина длины диагоналей, перемноженная на sin угла, который они образуют.

S = d₁d₂ * sinα.

Вписанный в окружность 4-угольник: площадь вычисляется как корень квадратный из произведения разности периметра на длину каждой стороны.

S = \sqrt { (p-a)*(p-b)*(p-c)*(p-d) } .

В случае с прямоугольником, квадратом формула упрощается.

Треугольники

Способов расчёта занимаемого треугольником места на плоскости множество. Это произведение:

Половины стороны на проведённую к ней высоту.

S = ½ ah_a.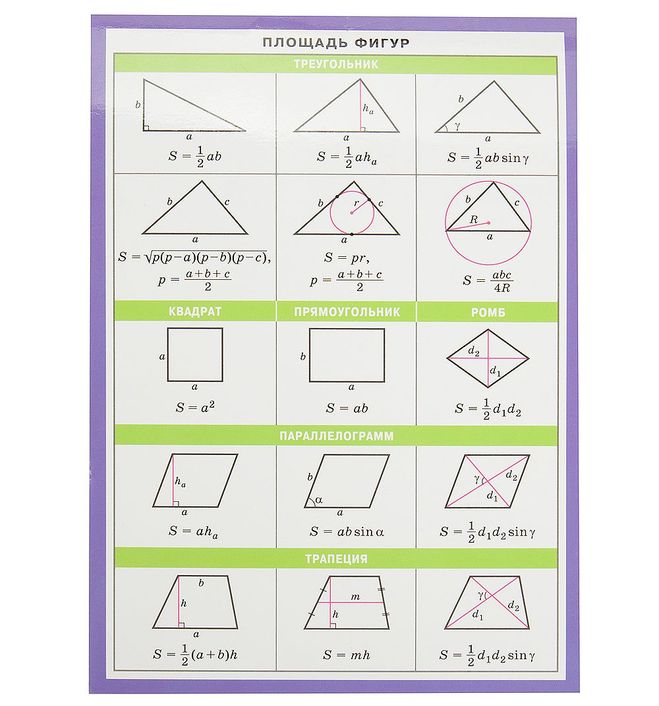 2 \ctg ( \frac { \pi }{ n }) .

 

Как найти площадь фигуры. Формулы и примеры.

Срок «площадь» в математике относится к количеству пространства, которое занимает двумерное пространство. форма занимает. Площадь может быть представлена ​​в сантиметрах, метрах, футах и ​​т. меры измерения. Потому что не все геометрические 2D-формы имеют одинаковый номер сторон, для вычисления площади каждой из сторон требуется своя формула. форма. На этой странице основное внимание будет уделено нахождению площади семи наиболее распространенных двухмерных формы. К ним относятся прямоугольник, квадрат, круг, треугольник, трапеция, эллипс и параллелограмм.

 

Потому что эти формулы включают 2D-формы, все расчеты площади имеют показатель «2» (также известный как надстрочный индекс или степень), чтобы указать, что форма имеет два стороны.

Как найти площадь прямоугольника

Формула для нахождения площади прямоугольника A = w x l , где «w» представляет ширину, а «l» представляет длину.

Пример :

A = Ш x Д

a = 32 x 52

A = 1664 FT ²

Как найти область квадратной

. формула чтобы найти площадь квадрата. «а» обозначает одну сторону квадрата. С квадрат имеет четыре равные стороны, измерение одной стороны дает вам измерения для остальных.

   

Example :

 
A = a ²

A = 12 ²

 

A = 144 in ²

 

How to Find Площадь круга

Чтобы найти площадь круга, используйте следующую формулу: A = πr ² . «r» в этой формуле представляет собой радиус круга.

Пример :

А = π 2

А = 14π 2

a = π 196

A ≈ 615,75 M ²

Как найти область Area of ​​A Area of ​​A Area of ​​A Area of ​​A at a Area of ​​A at a Area of ​​A at a Area of ​​A at a Area of ​​A at A Area of ​​A at A Area of ​​A at A Area of ​​A at A Area of ​​A at A Area of ​​A at A Area of ​​A at A Area at A найти площадь треугольника  где «b» представляет основание, а «h» представляет собой высоту.

 

Пример :

a = 58,5 см ²

Как найти площадь трапеции

. формула, чтобы найти площадь трапеции. В этой формуле «а» представляет собой более короткое основание (верхнее), «b» представляет собой более длинное основание (внизу), а «h» представляет собой высоту.

 

Пример :

A = 36 YD ²

Как найти площадь эллипса

AN эллипс похож на круг по своему внешнему виду, за исключением того, что он точно определенный. По сути, это круг, вытянутый горизонтально, с двумя симметричные оси. Овал это

а не точно определенный. Чтобы вычислить площадь эллипса, используйте A = π a x b формула. «а» представляет горизонтальную ось, а «b» представляет вертикальную ось.

 

Пример :

 

А = π a x b

А = π х 4 х 15

А ≈ 12,566 x 15

 

А ≈ 188,5 футов ²

 

 

Как найти площадь параллелограмма

формула для вычисления площади параллелограмма: A = b x h . «b» обозначает основу, а «b» обозначает высота.

 

Пример :

 

3 = b x h

А = 23 x 11

 

A = 253 дюйма ²

 

 

Формулы площади обычных геометрических фигур

В таблице ниже представлена ​​формула площади вышеупомянутые 2D-формы, в дополнение к некоторым другим распространенным формам.

Что такое площадь 2D-фигур? Определение, формулы, примеры, факты

Что такое площадь 2D-фигур?

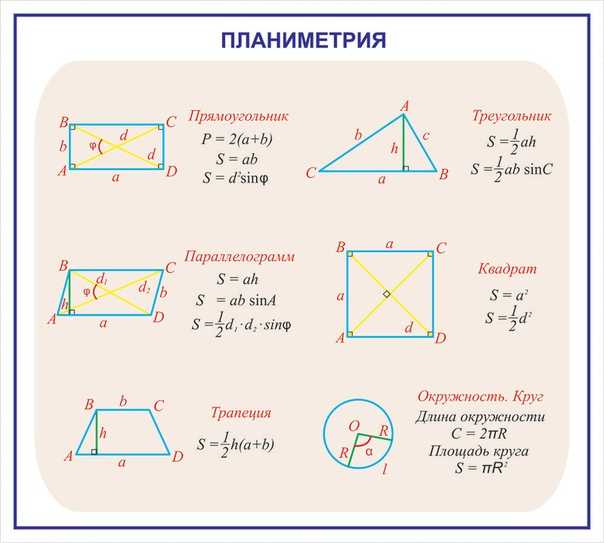
Площадь любой 2D-формы – это размер области, заключенной внутри нее. Существует несколько 2D-форм, таких как квадрат, прямоугольник, круг, ромб и треугольник. Цветная область в каждой фигуре представляет собой область соответствующей фигуры.

Единица площади называется квадратом. Разные фигуры имеют разную формулу расчета площади.

Площадь квадрата и прямоугольника:

Площадь квадрата и прямоугольника равна произведению двух его смежных сторон.

.0339	Площадь = 4 × 4 = 16 кв. см
Прямоугольник	Площадь прямоугольника = длина × ширина

Площадь треугольника:

Треугольники могут быть разных типов, например, равносторонний треугольник, равнобедренный треугольник и прямоугольный треугольник, но формула площади всех видов треугольников одинакова.

Площадь треугольника находим по формуле ¹ ⁄ ₂  × b × h, где основание (b) — длина любой стороны треугольника, а высота (h) — расстояние по перпендикуляру между основанием и вершиной треугольника.

Пример: 

В треугольнике ABC основание равно 6 единицам, а высота равна 4 единицам.

SO, площадь треугольника ABC =

1 ⁄ ₂ × B × H

= ¹ ⁄ ₂ × 6 × 4

= 12 кв. Бюлн

Круг :

Мы рассчитываем площадь круга по формуле π × r ² , где r — радиус круга, а π — это значение, 227 или 3,14

Пример: площадь вышеуказанного круга = π × r ²

= 3,14 × 4 ²

= 3,14 × 16

= 50,24 кв. См

Ромб :

Формула, чтобы найти площадь ромба составляет PQ/2, где P и Q — две диагонали ромба.

В Rhombus abcd мы можем рассчитать область следующим образом:

Площадь ромба = ¹ ⁄ ₂ PQ

= ¹ ⁄ ₂ × 3 ×

9002 = 7.5 SQM ₂ × 3 × 5

9003 = 7. 7.0003

Параллелограмм :

Чтобы найти площадь параллелограмма, мы используем формулу b × h, где b — основание, а h — высота.

No related posts.