Формулы разложить на множители: Применение формул сокращённого умножения для разложения многочлена на множители — урок. Алгебра, 7 класс.

Разложение многочлена на множители — intmag24.ru

Разложение многочлена на множители — это представление его его в виде произведения двух или нескольких многочленов. Перед изучением данной темы повторите: многочлены и формулы сокращенного умножения.

Разложение многочлена на множители способом

вынесения общего множителя за скобки

При вынесении общего множителя за скобки образуется произведение из двух множителей, один из которых является одночленом, а другой многочленом. Например: 6x + 3xy = 3x(2 + y)

Существуют также многочлены, в которых можно вынести за скобки такой общий множитель, который является двучленом. Например, рассмотрим многочлен 5a(x + y) + 7a(x + y). В этом многочлене общим множителем является двучлен (x + y). Вынесем его за скобки и получим (x + y) (5a+ 7a).

Разложение многочлена на множители способом

группировки

Некоторые многочлены содержат группу членов, имеющих общий множитель. Такие группы можно заключать в скобки и далее выносить в качестве общего множителя за эти скобки.

Пример 1. Разложить на множители многочлен ax + ay + 3x + 3y.
— члены ax и ay имеют общий множитель a: (ax + ay) 
— члены 3x и 3y имеют общий множитель 3: (3x + 3y)
— соединим выражения (ax + ay) и (3x + 3y) знаком «плюс»: (ax + ay) + (3x + 3y)
— вынесем за скобки общие множители, получим:  a(x + y)  и 3(x + y) 
— двучлен (x + y) является общим множителем, вынесем его за скобки. Получим: (x + y)(a + 3) 

Пример 2. Разложить на множители многочлен ab − 3b + b² − 3a.
— Сгруппируем первый член ab с четвёртым членом −3a, второй член −3b сгруппируем с третьим членом b². Получим: (ab − 3a) + (−3b + b²)
— В первой группе вынесем за скобки общий множитель a, во второй группе — общий множитель b. Получим: (ab − 3a) + (−3b + b²) = a(b − 3) + b(−3 + b)
— Во втором произведении b(−3 + b) в множителе (−3 + b) изменим порядок следования членов. Тогда получим b(b − 3)
— Получим: (ab − 3a) + (−3b + b²) = a(b − 3) + b(b − 3)
— Вынесем за скобки общий множитель (b − 3):  a(b − 3) + b(b − 3) = (b − 3)(a + b)

Разложение многочлена на множители

по формуле квадрата суммы двух выражений

Формулы сокращённого умножения можно применять для разложения многочленов на множители.

• Формула квадрата суммы двух выражений: (a + b)² = a² + 2ab + b²
• Поменяем местами левую и правую часть, получим: a² + 2ab + b² = (a + b)² — получим формулу разложения на множители.

a² + 2ab + b² = (a + b)(a + b)

Пример 3. Разложить на множители многочлен 4x² + 12xy + 9y²
— Первый член многочлена  является результатом возведения в квадрат одночлена 2x, так как  (2x)² = 4x².
— Третий член 9y² является результатом возведения в квадрат одночлена 3y, так как (3y)² = 9y²,
— Второй член 12xy это есть удвоенное произведение членов 2x и 3y, то есть 2 × 2x × 3y = 12xy.
— Получаем, что выражение 4x² + 12xy + 9y² = (2x + 3y)² =(2x + 3y)(2x + 3y)

Пример 4. Разложить на множители многочлен x² + 12x + 36
— Первый член — это результат возведения в квадрат одночлена x, так как  x² = x²,
— Третий член — это результат возведения в квадрат числа 6, поскольку 6² = 36,
— Второй а член — это удвоенное произведение членов x и 6, так как 2×x×6=12x.
— Получаем: x² + 12x + 36 = (x + 6)² = (x + 6)(x + 6)

Разложение многочлена на множители

по формуле квадрата разности двух выражений

• Формула квадрата разности двух выражений: ( a − b)² = a² − 2ab + b²
• Поменяем местами левую и правую часть, получим:  a² − 2ab + b² = (a − b)² — получим формулу разложения на множители.

a² − 2ab + b² = (a − b)(a − b)

Пример 5. Разложить на множители многочлен 9x² − 12xy + 4y²
— Первый член — это результат возведения в квадрат одночлена 3x, так как (3x)² = 9x².
— Третий член — результат возведения в квадрат одночлена 2y, так как (2y)² = 4y²,
— Второй член — это удвоенное произведение членов 3x и 2y, то есть 2×3x×2y= 2xy.
— Получаем: 9x² − 12xy + 4y² = (3x − 2y)² = (3x − 2y)(3x − 2y)

Разложение многочлена на множители

по формуле куба суммы двух выражений

• Формула куба суммы двух выражений: (a + b)³ = a³ + 3a
  2b + 3ab² + b³
• Поменяем местами левую и правую часть, получим: a³ + 3a²b + 3ab² + b³ = (a + b)³ — получим формулу разложения на множители.

a³ + 3a²b + 3ab² + b³ = (a + b)(a + b)(a + b)

Пример 6. Разложить на множители многочлен m³ + 6m²n + 12mn² + 8n³
Прежде чем применять формулу куба суммы, следует проанализировать данный многочлен и убедиться, что перед нами действительно куб суммы двух выражений.
— Первый член — это результат возведения в куб одночлена: m³ = m³
— Последний член — это результат возведения в куб одночлена: (2n)³ = 8n³
— Второй член — это утроенное произведение квадрата первого выражения m и последнего 2n: 
3 × m² × 2n = 6m²n
— Третий член — это утроенное произведение первого выражения m и квадрата последнего выражения 2n:
3 × m × (2n)² = 3 × m × 4n² = 12mn²
— Значит  исходный многочлен  соответствует кубу суммы двух выражений. Получаем: 
m³ + 6m²n + 12mn² + 8n³ = (m + 2n)³ = (m + 2n)(m + 2n)(m + 2n)

Пример 7. Разложить на множители многочлен 125x³ + 75x² + 15x + 1
— Первый член — это результат возведения в куб одночлена: (5x)³ = 125x³
— Последний член — это результат возведения в куб одночлена: 1³ = 1
— Второй член — это утроенное произведение квадрата первого выражения 5x и последнего 1:
3 × (5x)² × 1 = 3 × 25x² = 75x²
— Третий член — это утроенным произведением первого выражения 5x и квадрата второго выражения 1:
3 × 5x × 1² = 15x
— Получаем: 125x³ + 75x² + 15x + 1 = (5x + 1)³ = (5x + 1)(5x + 1)(5x + 1)

Разложение многочлена на множители

по формуле куба разности двух выражений

• Формула куба разности двух выражений:  (a − b)³ = a³ − 3a²b + 3ab² − b³
• Поменяем местами левую и правую часть, получим: a³ − 3a²b + 3ab² − b³ = (a − b)³  — получим формулу разложения на множители.

a³ − 3a²b + 3ab² − b³ = (a − b)(a − b)(a − b)

Пример 8. Разложить на множители многочлен 64 − 96x + 48x² − 8x³
— Первый член — это  результат возведения в куб одночлена: 4³ = 64
— Последний член — это результат возведения в куб одночлена: (2x)³ = 8x³
— Второй член — это утроенное произведение квадрата первого выражения 4 и последнего 2x:
3 × 4² × 2x = 3 × 16 × 2x = 96x
— Третий член — это утроенное произведение первого выражения 4 и квадрата второго выражения 2x: 
3 × 4 × (2x)² = 3 × 4 × 4x² = 48x²
— Получаем: 64 − 96x + 48x² − 8x³ = (4 − 2x)³ = (4 − 2x)(4 − 2x)(4 − 2x)

Разложение многочлена на множители

по формуле разности квадратов двух выражений

• Формула умножения разности двух выражений на их сумму: (a − b)(a + b) = a² − b²
• Поменяем местами левую и правую часть, получим: a² − b² = (a − b)(a + b) — получим формулу разложения на множители.

a² − b² = (a − b)(a + b)

Пример 9. Разложить на множители многочлен 16x² − 25y²
— Первый член — это результат возведения в квадрат одночлена: (4x)² = 16x²
— Второй член — это результат возведения в квадрат одночлена: (5y)² = 25y²
— Получаем: (4x)² − (5y)² = (4x − 5y)(4x + 5y)
— Проверка: (4x − 5y)(4x + 5y) = 16x² − 20xy + 20xy − 25y² = 16x² − 25y²

Разложение многочлена на множители

по формуле сумме кубов двух выражений

• Формула сокращенного умножения: (a + b)(a ² − ab + b²) = a³ + b³
• Поменяем местами левую и правую часть, получим: a³ + b³ = (a + b)(a² − ab + b²) — получим формулу разложения на множители.

a³ + b³ = (a + b)(a² − ab + b²)

Пример 10. Разложить на множители многочлен 27x³ + 64y³
— Представим члены 27x³ и 64y³ в виде одночленов, возведённых в куб: 27x³ + 64y³ = (3x)³ + (4y)³
— Воспользуемся формулой суммы кубов:
27x³ + 64y³ = (3x)³ + (4y)³ = (3x + 4y)((3x)² − 3x × 4y + (4y)²) = (3x + 4y)(9x² − 12xy + 16y²)

Разложение многочлена на множители

по формуле разности кубов двух выражений

• Формула сокращенного умножения:
  (a − b)(a² + ab + b²) = a³ − b³
• Поменяем местами левую и правую часть, получим: a³ − b³ = (a − b)(a² + ab + b²) — получим формулу разложения на множители.

a³ − b³ = (a − b)(a² + ab + b²)

Пример 11. Разложить на множители многочлен 64x³ − 27y³
— Представим члены 64x³ и 27y³ в виде одночленов, возведённых в куб: 64x³ − 27y³ = (4x)³ − (3y)³
— Воспользуемся формулой разности кубов:
64x³ − 27y³ = (4x)³ − (3y)³ = (4x − 3y)((4x)² + 4x × 3y + (3y)²) = (4x − 3y)(16x² + 12xy + 9y²)

Разложение многочлена на множители различными способами

К некоторым многочленам можно применять различные способы разложения на множители. Например, к одному многочлену можно применить способ вынесения общего за скобки, а затем воспользоваться одной из формул сокращённого умножения.

Пример 12. Разложить на множители многочлен ax² − ay² 
— В данном многочлене содержится общий множитель a. Вынесем его за скобки: ax² − ay² = a(x² − y²)
— В скобках образовался многочлен, который является разностью квадратов. Применив формулу разности квадратов. Тогда получим: ax² − ay² = a(x² − y²) = a(x − y)(x + y)

Пример 13. Разложить на множители многочлен 3x² + 6xy + 3y²
— Вынесем за скобки общий множитель 3: 3x² + 6xy + 3y² = 3(x² + 2xy + y²)
— В скобках образовался многочлен, который является квадратом суммы двух выражений. Применив формулу, получаем: 3x² + 6xy + 3y² = 3(x² + 2xy + y²) = 3(x + y)² = 3(x + y)(x + y).

Разложение многочлена на множителе особенно вам пригодится при делении многочленов и преобразовании выражений с многочленами.

 

Примеры разложения многочленов на множители

Примеры с решением квадратного уравнения

Пример 1.1

Разложить многочлен на множители:
x⁴ + x³ – 6x².

Решение

Выносим x² за скобки:
.
Решаем квадратное уравнение x² + x – 6 = 0:
.
Корни уравнения:
,   .

Отсюда получаем разложение многочлена на множители:
.

Ответ

.

Пример 1.2

Разложить на множители многочлен третьей степени:
x³ + 6x² + 9x.

Решение

Выносим x за скобки:
.
Решаем квадратное уравнение x² + 6x + 9 = 0:
Его дискриминант:   .
Поскольку дискриминант равен нулю, то корни уравнения кратные: ;
.

Отсюда получаем разложение многочлена на множители:
.

Ответ

.

Пример 1.3

Разложить на множители многочлен пятой степени:
x⁵ – 2x⁴ + 10x³.

Решение

Выносим x³ за скобки:
.
Решаем квадратное уравнение x² – 2x + 10 = 0.
Его дискриминант:   .
Поскольку дискриминант меньше нуля, то корни уравнения комплексные: ;
,   .

Разложение многочлена на множители имеет вид:
.

Если нас интересует разложение на множители с действительными коэффициентами, то:
.

Ответ

.

Примеры разложения многочленов на множители с помощью формул

Примеры с биквадратными многочленами

Пример 2.1

Разложить биквадратный многочлен на множители:
x⁴ +x² – 20.

Решение

Применим формулы:
a² + 2ab + b² = (a + b)²;
a² – b² = (a – b)(a + b).

;
.

Ответ

.

Пример 2.2

Разложить на множители многочлен, сводящийся к биквадратному:
x⁸ +x⁴ + 1.

Решение

Применим формулы:
a² + 2ab + b² = (a + b)²;
a² – b² = (a – b)(a + b):

;

;
.

Ответ

.

Пример 2.3 с возвратным многочленом

Разложить на множители возвратный многочлен:
.

Решение

Возвратный многочлен имеет нечетную степень. Поэтому он имеет корень x = –1. Делим многочлен на x – (–1) = x + 1. В результате получаем:
.
Делаем подстановку:
,   ;
;

;
.

Ответ

.

Примеры разложения многочленов на множители с целыми корнями

Пример 3.1

Разложить многочлен на множители:
.

Решение

Предположим, что уравнение

имеет хотя бы один целый корень. Тогда он является делителем числа 6 (члена без x). То есть целый корень может быть одним из чисел:
–6, –3, –2, –1, 1, 2, 3, 6.
Подставляем поочередно эти значения:
(–6)³ – 6·(–6)² + 11·(–6) – 6 = –504;
(–3)³ – 6·(–3)² + 11·(–3) – 6 = –120;
(–2)³ – 6·(–2)² + 11·(–2) – 6 = –60;
(–1)³ – 6·(–1)² + 11·(–1) – 6 = –24;
1³ – 6·1² + 11·1 – 6 = 0;
2³ – 6·2² + 11·2 – 6 = 0;
3³ – 6·3² + 11·3 – 6 = 0;
6³ – 6·6² + 11·6 – 6 = 60.

Итак, мы нашли три корня:
x₁ = 1, x₂ = 2, x₃ = 3.
Поскольку исходный многочлен – третьей степени, то он имеет не более трех корней. Поскольку мы нашли три корня, то они простые. Тогда
.

Ответ

.

Пример 3.2

Разложить многочлен на множители:
.

Решение

Предположим, что уравнение

имеет хотя бы один целый корень. Тогда он является делителем числа 2 (члена без x). То есть целый корень может быть одним из чисел:
–2, –1, 1, 2.
Подставляем поочередно эти значения:
(–2)⁴ + 2·(–2)³ + 3·(–2)³ + 4·(–2) + 2 = 6;
(–1)⁴ + 2·(–1)³ + 3·(–1)³ + 4·(–1) + 2 = 0;
1⁴ + 2·1³ + 3·1³ + 4·1 + 2 = 12;
2⁴ + 2·2³ + 3·2³ + 4·2 + 2 = 54.

Итак, мы нашли один корень:
x₁ = –1.
Делим многочлен на x – x₁ = x – (–1) = x + 1:

Тогда,
.

Теперь нужно решить уравнение третьей степени:
.
Если предположить, что это уравнение имеет целый корень, то он является делителем числа 2 (члена без x). То есть целый корень может быть одним из чисел:
1, 2, –1, –2.
Подставим x = –1:
.

Итак, мы нашли еще один корень x₂ = –1. Можно было бы, как и в предыдущем случае, разделить многочлен     на   , но мы сгруппируем члены:
.

Поскольку уравнение x ² + 2 = 0 не имеет действительных корней, то разложение многочлена на множители имеет вид:
.

Ответ

.

Расширение с помощью формул факторинга и полиномиальной факторизации ｜ Hatsudy

В математике мы изучаем алгебраические выражения, используя алфавит. Мы используем символы для выполнения вычислений, таких как сложение, вычитание, умножение и деление.

Скобки часто используются в математических вычислениях. При умножении скобок на скобки мы используем формулы факторинга.

Как только вы выучите формулы факторинга, вы также сможете их факторизовать. Факторизация — это способ преобразования многочленов в уравнения умножения с использованием скобок. При вычислении многочленов факторизация сложнее, чем расширение выражения с помощью формул факторинга, поэтому нужно понимать, как его вычислять.

Изучение формулы факторинга и факторизации вместе облегчит понимание математики. Мы объясним, как использовать формулу факторинга и решать задачи факторизации.

Содержание

• 1 Доказательство умножения полиномов на свойство распределения
  • 1. 1 Расширение уравнения с использованием четырех формул факторизации
  • 1.2 Если вы забудете формулы факторизации, вы все равно сможете вычислить
  : Факторизация: Создание уравнений в скобках
  • 2,1 Факторизация имеет множество вариантов
  • 2,2 Факторизация с использованием четырехэтажной формулы
• 3 Упражнения: Формулы факторинга и расчеты факторизации
• 4 Формаризации и факторизации для решения Polynomial.

. the Distributive Property

В полиномиальных вычислениях возникает так много проблем, которые требуют от нас расширения уравнений. Снятие скобок, чтобы уравнение приняло вид сложения и вычитания одночленов, называется расширяющим (или развивающим). В расширяющих уравнениях умножение двух скобок может быть сложным.

В частности, мы делаем следующий расчет.

• $(a+b)(c+d)$

Другими словами, умножьте $(a+b)$ на $(c+d)$. Как мы делаем такой полиномиальный расчет?

При умножении двух многочленов раскройте выражение следующим образом.

Почему можно составить уравнение таким образом? В математике нам нужно понять, почему. Итак, давайте попробуем доказать, что эта формула верна.

Как мы знаем из алгебраических выражений, цифры можно заменять буквами. Итак, давайте заменим $(c+d)$ на $N$. Тогда $(a+b)(c+d)$ становится $(a+b)N$. Следовательно, используя распределительное свойство (или распределительный закон), мы можем вычислить следующее.

• $(a+b)N=aN+bN$

$N$ равно $(c+d)$. Итак, подставляем $N=(c+d)$. В результате получается следующий расчет.

$aN+bN$

$=a(c+d)+b(c+d)$

$=ac+ad+bc+bd$

Из этого результата можно доказать, что $(a +b)(c+d)=ac+ad+bc+bd$. При умножении двух многочленов мы можем использовать эту формулу для расширения уравнения.

Однако нам не нужно доказывать приведенную выше формулу каждый раз, когда мы делаем математические вычисления. Итак, поймите, что эта формула верна, и запомните, как ее вычислить. Узнайте, как расширить уравнение. 2+(a+b)x+ab$. Это наиболее часто используемая формула факторинга в математике, и ее необходимо запомнить. 92-6x+9$

Если вы помните формулы факторинга, то можете пропустить эти расчеты и получить ответ. Однако, даже если вы забудете, вы все равно можете посчитать, чтобы получить ответ.

Факторизация: создание уравнений в скобках

Следующим шагом после изучения расширения выражений в математике является факторизация. Расширение выражения означает удаление скобок. С другой стороны, что такое факторизация? Факторизация противоположна расширению уравнения. Другими словами, вы создаете выражение со скобками из выражения без скобок.

Уравнение умножения называется коэффициентом. Для уравнения, состоящего из сложения и вычитания, мы разлагаем его так, чтобы оно стало произведением множителей.

При факторизации нам нужно найти общие факторы. Например, мы получаем следующее.

Разложение на множители сложнее, чем расширение выражений. В расширении выражения ясно, какие числа нужно умножить. С другой стороны, в факторинге нужно искать общие факторы. Поскольку общие факторы не записаны, вам необходимо выяснить, какие из них являются общими факторами.

Факторизация имеет несколько вариантов

Кроме того, в случае факторизации многие вопросы основаны на формулах факторинга. Другими словами, если вы забудете формулы факторинга, вы не сможете их решить. В расширении уравнения, даже если вы забудете формулы факторинга, вы все равно сможете получить ответ. С другой стороны, факторизация требует, чтобы вы помнили формулы факторинга.

При факторизации с использованием формул факторинга существует несколько вариантов. Вы должны найти лучший ответ из них. 92+(a+b)x+ab$, мы можем получить следующее.

• $a+b=4$
• $ab=3$

Нам нужно найти множители, которые удовлетворяют этим двум. Обратите внимание, что существует лучший способ факторизации. То есть нам нужно сосредоточиться на умножении.

-Сложение и вычитание имеют бесконечные ответы

Если мы применим $a$ и $b$ так, что $a+b=4$, то будет бесконечно много ответов. Например, у нас есть следующее.

• $2+2=4$
• $10-6=4$
• $-100+104=4$

Поэтому, когда мы факторизуем, мы не фокусируемся сначала на $a+b$. Вместо этого мы сосредоточимся на $ab$, то есть на умножении. Есть только два целых числа, которые удовлетворяют $ab=3$ следующим образом.

• $1×3=3$
• $-1×(-3)=3$

Другими словами, есть два кандидата на ответ при факторинге. Какой из них является правильным ответом? Итак, нам нужно найти число, удовлетворяющее условию $a+b=4$. Результат следующий.

• Если $a=1,b=3$, то $1+3=4$
• Если $a=-1,b=-3$, то $-1+(-3)=-4$

Если $a=1,b=3$, то оба $a+b=4 $ и $ab=3$ выполняются. Следовательно, мы можем разложить его следующим образом.

Таким образом, при факторизации мы должны вычислить правильный ответ из нескольких кандидатов. В этом примере мы использовали факторизацию простого уравнения в качестве примера. Однако, если выражение более сложное, факторинг усложняется.

Факторизация с использованием формулы с четырьмя шаблонами

Как упоминалось выше, существует четыре формулы факторинга. Поэтому, когда вы впервые изучаете факторизацию, вам нужно выбрать, какую из четырех формул факторинга использовать. Хотя существуют и другие формулы для факторизации, их следует выучить при изучении более сложной математики, например, в старшей школе.

Один из способов отличить формулы факторинга, используемые в факторинге, состоит в том, чтобы проверить, содержат ли они степени. Из четырех формул факторинга следующие три включают степени. 92=25$, и это уравнение содержит степень. Оно также имеет отрицательный знак и $2ax$ или $(a+b)x$ не существует. При соблюдении этих условий возможна следующая факторизация.

Таким образом, мы можем разложить на множители, используя формулы факторинга.

— Факторизация при отсутствии мощности

Часто бывают случаи, когда нельзя использовать три формулы факторизации, описанные ранее, например, когда в уравнение не включается мощность.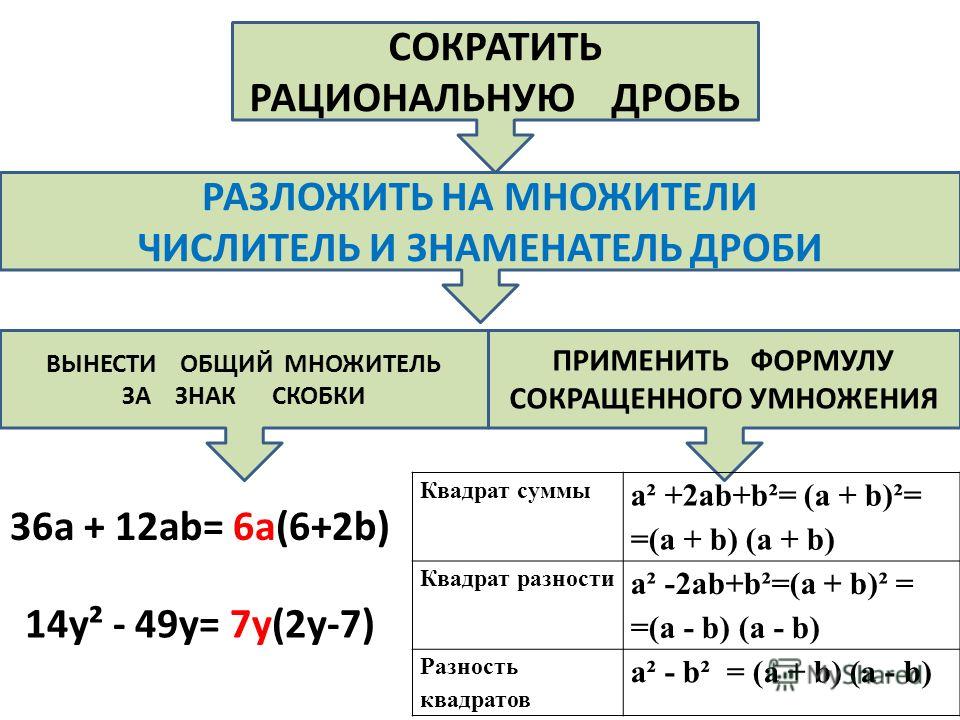 В таких случаях для факторизации уравнения можно использовать следующую формулу факторизации. 92=(N+2)(N-2)$

Однако $N=x+y$. Тогда, подставив $N=x+y$, мы можем завершить факторизацию следующим образом.

• $(N+2)(N-2)=(x+y+2)(x+y-2)$

Использование формул факторинга и факторизации для решения полиномиальных задач

В математике формулы факторинга и факторизацию следует понимать как множество. Таким образом, вы должны быть в состоянии факторизовать, а также разрабатывать уравнения, используя формулы факторинга.

Формулы факторинга необходимо запомнить; Вы должны быть в состоянии использовать четыре формулы факторинга. При построении уравнения вам не нужно запоминать формулы факторинга, чтобы получить ответ. С другой стороны, при факторизации вы должны помнить формулы факторинга, чтобы получить ответ.

По сравнению с расширением уравнения с использованием формул факторизации, факторизация имеет гораздо больше чисел-кандидатов, и на нее труднее ответить. Однако в смысле использования формул факторинга и расширение уравнения, и факторизация одинаковы.

Одним из наиболее важных разделов математики является расширение уравнения и факторизация с использованием формул факторинга. Попытайтесь понять, как использовать формулы факторинга для расширения и факторизации выражений.

Что такое формула факторизации | Расчет и примеры

Введение

В этой статье вы узнаете, что такое формула факторизации и как выполнять факторизацию.

Что такое факторизация?

Процесс нахождения множителей квадратных уравнений для нахождения решения называется факторизацией. Множитель числа относится к ненулевому числу, которое делит его, не оставляя остатка. Факторизация разбивает число, чтобы найти его кратное.

В алгебре факторизация используется для нахождения двух чисел, произведение и сумма которых заданы в уравнении. Он разбивает произведение двух чисел на два меньших числа, называемых множителями выражения.

Формула факторизации в алгебре

В алгебре формула факторизации помогает преобразовать алгебраическое выражение в простую форму с использованием его множителей. Например, если у нас есть квадратное уравнение,

x ² + bx + c = 0

Чтобы преобразовать его в простую форму, формула разложения разбивает среднее значение на два числа так, что

Формула факторизации используется для простого нахождения множителей любого числа или алгебраического выражения. Это метод разложения, который разбивает число на произведения других факторов.

Формула факторинга

В математике факторизация может относиться к простой факторизации, GCF или HCF. Это делает факторы числа или целых чисел. Например, простая факторизация числа 12 равна

12=12×1

12=6×2

12=4×3

12=3×4

12=2×6

Здесь 1, 2 , 3, 4 и 6 — делители 12, а 1, 2 и 3 — простые множители.

Как найти коэффициенты квадратного уравнения?

По сути, вы можете вычислить коэффициенты выражения, найдя два кратных среднего коэффициента. Но здесь мы предлагаем вам простой и пошаговый метод поиска факторов.

1. Приведите уравнение к стандартной форме так, что

x ²

+ bx + c = 0

2. Найдите множители b такие, что b ₁ x b ₂ = ac

3. Используйте коэффициенты b в уравнении, используя формулу факторизации.

4. Решите уравнение, чтобы найти решение x.

Как использовать первичную факторизацию для поиска LCM?

Вы можете легко найти LCM, используя простую факторизацию. Используйте следующие шаги, чтобы найти LCM.

1. Найдите простую факторизацию каждого числа.
2. Запишите каждое число как произведение простых множителей.
3. Уменьшите количество простых чисел в каждом столбце.
4. Найдите наименьший общий делитель.

Например, простая факторизация чисел 12 и 18 равна2)$$

Часто задаваемые вопросы

Как найти GCF с помощью простой факторизации?

GCF означает наибольший общий делитель, то есть наибольший общий делитель, на который можно разделить два или более чисел.