Дистанционный репетитор — онлайн-репетиторы России и зарубежья
КАК ПРОХОДЯТ
ОНЛАЙН-ЗАНЯТИЯ?
Ученик и учитель видят и слышат
друг друга, совместно пишут на
виртуальной доске, не выходя из
дома!
КАК ВЫБРАТЬ репетитора
Выбрать репетитора самостоятельно
ИЛИ
Позвонить и Вам поможет специалист
8 (800) 333 58 91
* Звонок является бесплатным на территории РФ
** Время приема звонков с 10 до 22 по МСК
ПОДАТЬ ЗАЯВКУ
Россия +7Украина +380Австралия +61Белоруссия +375Великобритания +44Израиль +972Канада, США +1Китай +86Швейцария +41
Выбранные репетиторы
Заполните форму, и мы быстро и бесплатно подберем Вам дистанционного репетитора по Вашим пожеланиям.
Менеджер свяжется с Вами в течение 15 минут и порекомендует специалиста.
Отправляя форму, Вы принимаете Условия использования и даёте Согласие на обработку персональных данных
Вы также можете воспользоваться
расширенной формой подачи заявки
Как оплачивать и СКОЛЬКО ЭТО СТОИТ
от
800 до 5000 ₽
за 60 мин.
и зависит
ОТ ОПЫТА и
квалификации
репетитора
ОТ ПОСТАВЛЕННЫХ ЦЕЛЕЙ ОБУЧЕНИЯ
(например, подготовка к олимпиадам, ДВИ стоит дороже, чем подготовка к ЕГЭ)
ОТ ПРЕДМЕТА (например, услуги репетиторовиностранных языков дороже)
Оплата непосредственно репетитору, удобным для Вас способом
Почему я выбираю DisTTutor
БЫСТРЫЙ ПОДБОР
ИНДИВИДУАЛЬНЫЙ ПОДХОД
ОПТИМАЛЬНОЕ
СООТНОШЕНИЕ ЦЕНЫ И
КАЧЕСТВА
ПРОВЕРЕНЫ ДОКУМЕНТЫ ОБ ОБРАЗОВАНИИ У ВСЕХ РЕПЕТИТОРОВ
НАДЕЖНОСТЬ И ОПЫТ.
DisTTutor на рынке с 2008 года.
ПРОВЕДЕНИЕ БЕСПЛАТНОГО, ПРОБНОГО УРОКА
ЗАМЕНА РЕПЕТИТОРА, ЕСЛИ ЭТО НЕОБХОДИМО
376070 УЧЕНИКОВ ИЗ РАЗНЫХ СТРАН МИРА
уже сделали свой выбор
И вот, что УЧЕНИКИ ГОВОРЯТ
о наших репетиторах
Владимир Александрович Кузьмин
«
Тренинг у Кузьмина В. А. проходил в экстремальных условиях. Мой модем совершенно не держал соединение. За время часового тренинга связь прерывалась практически постоянно. Ясно, что в таких условиях чрезвычайно непросто чему-то учить.
Однако Владимир Александрович проявил удивительную выдержку и терпение. Неоднократно он перезванивал мне на сотовый телефон, чтобы дать пояснения или комментарии.
Ценой больших усилий нам удалось рассмотреть три программы: ConceptDraw MINDMAP Professional Ru, GeoGebra и Ultra Flash Video FLV Converter. Владимир Александрович открыл мне курс на платформе dist-tutor.info и научил подключать и настраивать Виртуальный кабинет, порекомендовав изучать возможности этого ресурса, чтобы постепенно уходить от использования Skype.
«
Вячеслав Юрьевич Матыкин
Чулпан Равилевна Насырова
«
Я очень довольна репетитором по химии. Очень хороший подход к ученику,внятно объясняет. У меня появились сдвиги, стала получать хорошие оценки по химии. Очень хороший преподаватель. Всем , кто хочет изучать химию, советую только её !!!
«
Алина Крякина
Надежда Васильевна Токарева
«
Мы занимались с Надеждой Васильевной по математике 5 класса. Занятия проходили в удобное для обоих сторон время. Если необходимо было дополнительно позаниматься во внеурочное время, Надежда Васильевна всегда шла навстречу. Ей можно было позванить, чтобы просто задать вопрос по непонятной задачке из домашнего задания.
Моя дочь существенно подняла свой уровень знаний по математике и начала демонстрировать хорошие оценки. Мы очень благодарны Надежде Васильевне за помощь в этом учебном году, надеемся на продолжение отношений осенью.
«
Эльмира Есеноманова
Ольга Александровна Мухаметзянова
«
Подготовку к ЕГЭ по русскому языку мой сын начал с 10 класса. Ольга Александровна грамотный педагог, пунктуальный, ответственный человек. Она всегда старается построить занятие так, чтобы оно прошло максимально плодотворно и интересно. Нас абсолютно все устраивает в работе педагога. Сотрудничество приносит отличные результаты, и мы его продолжаем. Спасибо.
«
Оксана Александровна
Клиентам
- Репетиторы по математике
- Репетиторы по русскому языку
- Репетиторы по химии
- Репетиторы по биологии
- Репетиторы английского языка
- Репетиторы немецкого языка
Репетиторам
- Регистрация
- Публичная оферта
- Библиотека
- Бан-лист репетиторов
Партнеры
- ChemSchool
-
PREPY.
RU
- Class
RU
решение уравнений, понижение степени, сумма и разность
Описание тригонометрических формул
Определения
Тригонометрия — раздел математики, который изучает зависимости между углами и сторонами треугольников.
Основные тригонометрические формулы — это формулы, устанавливающие связи между основными тригонометрическими функциями.
Термин «тригонометрия» дословно означает «измерение треугольников». Его ввел в употребление немецкий математик и богослов Варфоломей Питиск, автор учебника по тригонометрии и тригонометрических таблиц. Но саму тригонометрию — ее основные функции и их таблицы — придумали еще до нашей эры, в Древнем Вавилоне.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления).
{}\left(\alpha\right)\;\times\;ctn\left(\alpha\right)\;=\;1\)
Формулы приведения
Что позволяют формулы
С их помощью значение тригонометрической функции любого угла можно привести к значению как той же, так и другой функции острого угла. Это позволяет, имея тупой угол, перейти к работе с острым, что намного удобнее для решения задач.
Часто в таблицах приводятся формулы только для синуса и косинуса, из которых легко получить формулы для тангенса и котангенса. При необходимости их можно переписать, заменяя радианы на градусы. Для этого нужно подставить вместо числа пи 180 градусов
.Формулы приведения не нужно заучивать наизусть. Достаточно запомнить закономерность, известную как мнемоническое правило:
- Представить аргумент исходной функции в виде:
\(\pm\;\alpha\;+\;2\pi\;\times\;z,\;\frac{\mathrm\pi}2\;\pm\;\alpha\;+\;2\pi\;\times\;z,\;\pi\;\pm\;\alpha\;+\;2\pi\;\times\;z,\;\frac{3\mathrm\pi}2\;\pm\;\alpha\;+\;2\pi\;\times\;z,\;\)
-
Определить знак исходной функции — тот же знак будет иметь функция в правой части формулы приведения.
-
Сохранить название исходной функции для углов:
\( \pm\;\alpha\;+\;2\pi\;\times\;z,\;\pi\;\pm\;\alpha\;+\;2\pi\;\times\;z\)
-
\(\frac{\mathrm\pi}2\;\pm\;\alpha\;+\;2\pi\;\times\;z,\;\frac{3\mathrm\pi}2\;\pm\;\alpha\;+\;2\pi\;\times\;z\)
Важно, чтобы угол \(\alpha\) был не больше 90 градусов.
Следствием чего являются
Формулы приведения следуют из свойств тригонометрических функций:
- периодичности;
- симметричности;
- сдвига на данный угол.
Формулы сложения
Эти формулы обычно группируют попарно, используя знаки «плюс-минус» и «минус-плюс».
\(\sin\left(\alpha\pm\beta\right)\;=\;\sin\left(\alpha\right)\cos\left(\beta\right)\;\pm\;\cos\left(\alpha\right)\sin\left(\beta\right)\)
\(\cos\left(\alpha\pm\beta\right)\;=\;\cos\left(\alpha\right)\cos\left(\beta\right)\;\mp\;\sin\left(\alpha\right)\sin\left(\beta\right)\)
\(\tan\left(\alpha\pm\beta\right)\;=\;\frac{\tan\left(\alpha\right)\;\pm\;\tan\left(\beta\right)}{1\;\mp\;\tan\left(\alpha\right)\tan\left(\beta\right)}\)
\(ctn\left(\alpha\pm\beta\right)\;=\;\frac{ctn(\alpha)ctn(\beta)\mp\;1}{ctn(\alpha)\;\pm\;ctn(\beta)}\)
Для чего применяются
Формулы сложения показывают, как функции суммы или разности двух углов выражаются через функции самих углов. Так можно решить тригонометрическое выражение, когда точные значения функций рассматриваемых углов отсутствуют в таблицах.
Например, тангенс угла 15 градусов можно представить, как разность углов 45 и 30 градусов или любых других углов, тангенсы которых известны.
Это означает число сочетаний из p элементов по q.
Сумма и разность функций
В каком виде можно представить действия
Использование этих формул позволяет перейти от суммы или разности функций углов \(\alpha\) и \(\beta\) к произведению функций углов \(\frac{\alpha\;+\;\beta}2\;\) и \(\;\frac{\alpha\;-\;\beta}2\).
Примеры формул
\(\sin\left(\alpha\right)\;+\;\sin\left(\beta\right)\;=\;2\;\times\;\sin\left(\frac{\alpha\;+\;\beta}2\right)\;\times\;\cos\left(\frac{\alpha\;-\;\beta}2\right)\)
\(\sin\left(\alpha\right)\;-\;\sin\left(\beta\right)\;=\;2\;\times\;\sin\left(\frac{\alpha\;-\;\beta}2\right)\;\times\;\cos\left(\frac{\alpha\;+\;\beta}2\right)\)
\(\cos\left(\alpha\right)\;+\;\cos\left(\beta\right)\;=\;2\;\times\;\cos\left(\frac{\alpha\;+\;\beta}2\right)\;\times\;\cos\left(\frac{\alpha\;-\;\beta}2\right)\)
\(\cos\left(\alpha\right)\;-\;\cos\left(\beta\right)\;=\;-2\;\times\;\sin\left(\frac{\alpha\;+\;\beta}2\right)\;\times\;\sin\left(\frac{\alpha\;-\;\beta}2\right)\)
Произведение тригонометрических функций
Для чего используются
В некоторых случаях применение формул произведения помогает упростить преобразование тригонометрического выражения.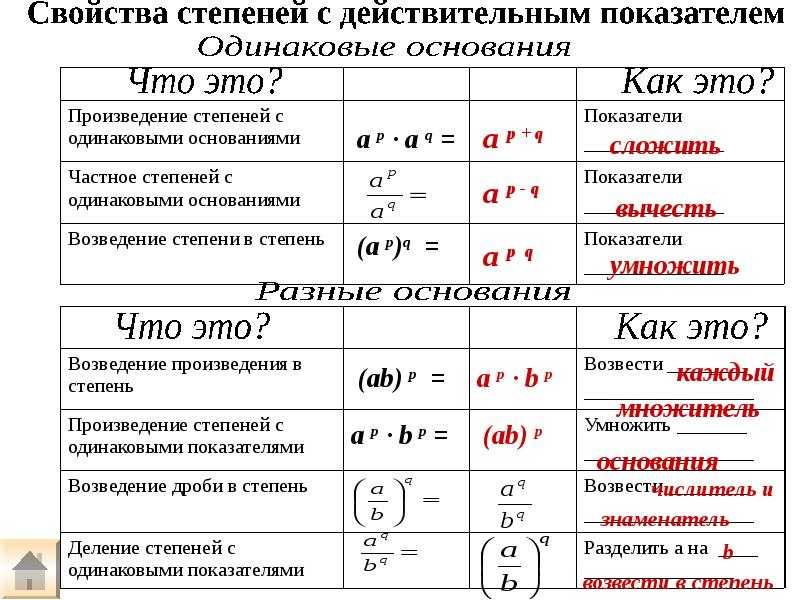
Переход к сумме, примеры
Формулы умножения выводятся из формул суммы и разности. Рассмотрим, как от этих формул можно перейти к формулам произведения и наоборот.
Применив вычитание из косинуса суммы косинуса разности, мы получим:
\(\sin\left(\alpha\right)\sin\left(\beta\right)\;=\;\frac12(\cos\left(\alpha-\beta\right)\;-\;\cos\left(\alpha+\beta\right))\)
Сложим косинус суммы и косинус разности:
\(\cos\left(\alpha-\beta\right)\;=\;\cos\left(\alpha\right)\cos\left(\beta\right)\;+\;\sin\left(\alpha\right)\sin\left(\beta\right)\)
\(\cos\left(\alpha+\beta\right)\;=\;\cos\left(\alpha\right)\cos\left(\beta\right)\;-\;\sin\left(\alpha\right)\sin\left(\beta\right)\)
\(\cos\left(\alpha+\beta\right)\;+\;\cos\left(\alpha-\beta\right)\;=\;2\cos\left(\alpha\right)\cos\left(\beta\right)\)
Следовательно:
\(\cos\left(\alpha\right)\cos\left(\beta\right)\;=\;\frac12(\cos\left(\alpha-\beta\right)\;-\;\cos\left(\alpha+\beta\right))\)
Сложим синус суммы и синус разности:
\(\sin\left(\alpha+\beta\right)\;=\;\sin\left(\alpha\right)\cos\left(\beta\right)\;+\;\sin\left(\beta\right)\cos\left(\alpha\right)\)
\(\sin\left(\alpha-\beta\right)\;=\;\sin\left(\alpha\right)\cos\left(\beta\right)\;-\;\sin\left(\beta\right)\cos\left(\alpha\right)\)
\(\sin\left(\alpha\right)\cos\left(\beta\right)\;=\;\frac12(\cos\left(\alpha-\beta\right)\;-\;\cos\left(\alpha+\beta\right))\)
Формулы тройного угла
Эти тригонометрические формулы позволяют выразить функции двойных и тройных углов через функцию одинарного угла.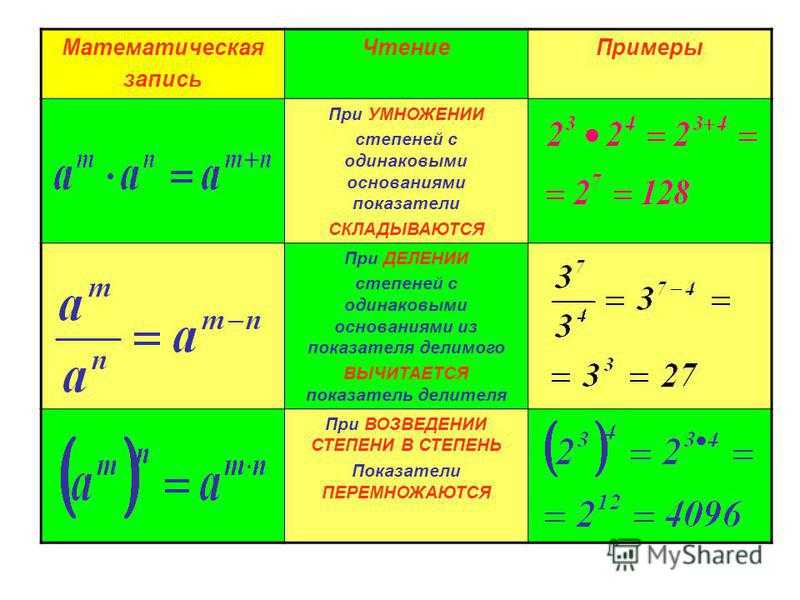
2\left(\alpha\right)}\)
из формулы Эйлера
Cedron Dawg●16 марта 2019 г.●Tweet
ВведениеМы надеемся, что эта статья поможет лучше понять дискретное преобразование Фурье (ДПФ), но только косвенно. Основная цель состоит в том, чтобы немного привыкнуть к ним тех, кому не нравятся комплексные числа, и связать их с уже известными тригонометрическими отношениями, выполненными в действительных значениях. По сути, это продолжение моей первой статьи в блоге «Экспоненциальная природа комплексного единичного круга».
Полярные координаты Более распространенным способом указания местоположения точки на плоскости является использование декартовых координат. Они выражаются в виде пары действительных значений, таких как $(x,y)$, где $x$ указывает (по соглашению) расстояние по горизонтальной оси пары ортогональных осей. Значение $y$ указывает расстояние по вертикальной оси. Точку можно найти, перемещаясь либо по горизонтальной оси на $x$ единиц, либо по вертикали на $y$ единиц.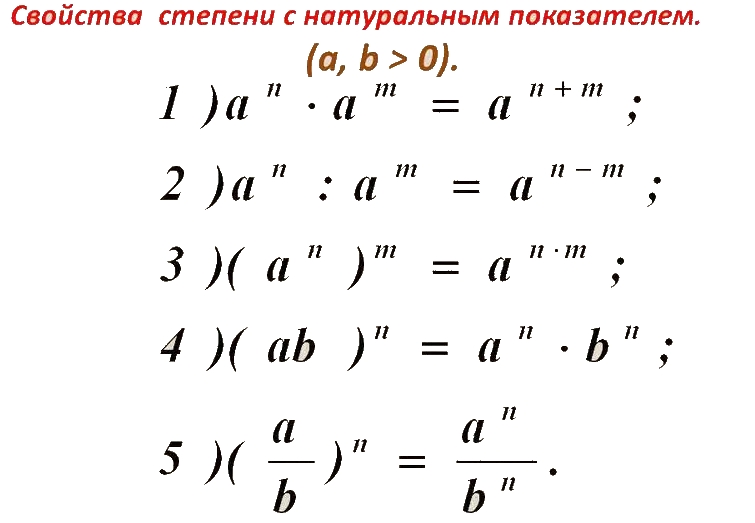
Или наоборот. В любом случае вы окажетесь в одной и той же точке. В декартовых координатах представление точки уникально. Это означает, что если $(a,b)$ и $(x,y)$ относятся к одной и той же точке, $x=a$ и $y=b$.
Полярные координаты другие. Они задают точку, задавая расстояние до начала координат и угол сегмента линии, соединяющего начало координат с точкой и горизонтальной осью. Нулевой угол направлен вправо, а угол в 180 градусов или $\pi$ радиан — влево. 90 градусов, или $\pi/2$ радиан вверх. Это также по соглашению. Они также указываются как пара координат, часто называемая $(r,\theta)$.
Первое, на что следует обратить внимание, это то, что если расстояние до начала координат, также называемое радиусом, равно нулю, то значение угла не имеет смысла. Второе, на что следует обратить внимание, это то, что представление точки не уникально. Вы можете инвертировать $r$ и добавить $\pi$ к углу и вернуться к той же точке. Или вы можете добавить или вычесть любое число, кратное $2\pi$, к углу, и все равно ссылаться на ту же точку.
{-1} \left( \frac{y}{x} \right) \tag {6} $$
Но не так быстро. Существует проблема, связанная с разными квадрантами: $(-x,-y)$ даст тот же ответ, что и $(x,y)$, хотя они явно разнесены на $\pi$ радиан, также называемых противоположными друг другу. Вы можете решить эту проблему с помощью дополнительных тестов, что означает операторы «если» при программировании, или вы можете использовать специальную функцию под названием «atan2». Большинство языков программирования и электронных таблиц поддерживают такую функцию, хотя ее название может немного отличаться.
$$ \theta = \text{atan2} \left( y , x \right) \tag {7} $$
Эта функция заботится о расположении квадрантов и возвращает правильный угол.
Мнимое число — это действительный скаляр, умноженный на $\sqrt{-1}$. Вы возражаете, что невозможно извлечь квадратный корень из отрицательного числа. Отрицательное, умноженное на отрицательное, является положительным, и положительное, умноженное на положительное, также является положительным.
Итак, как я могу умножить что-то на что-то и получить отрицательное число? Ответ: Для этого нужно мнимое число. Например, «представьте число, которое может», а не то, что их не существует. Ну, насколько существует любое математическое понятие. Из любого такого числа можно вынести $\sqrt{-1}$, и тогда оно станет обычным действительным числом. Математики обычно обозначают $\sqrt{-1}$ как $i$, а инженеры-электрики — как $j$. Это не американо-европейская вещь, как я сказал в своей первой статье. В этой и во всех моих статьях используется $i$.
Комплексное число – это сумма действительного числа и мнимого числа. Итак, если $x$ и $y$ оба действительны, то $x + i y$ — комплексное число. Его также можно было бы выразить как $x + y i $, поскольку умножение коммутативно. Также по соглашению действительная часть пишется перед мнимой частью.
Комплексная плоскость — это представление полного набора возможных комплексных чисел. Горизонтальная ось используется для реальной части, а вертикальная ось — для мнимой части.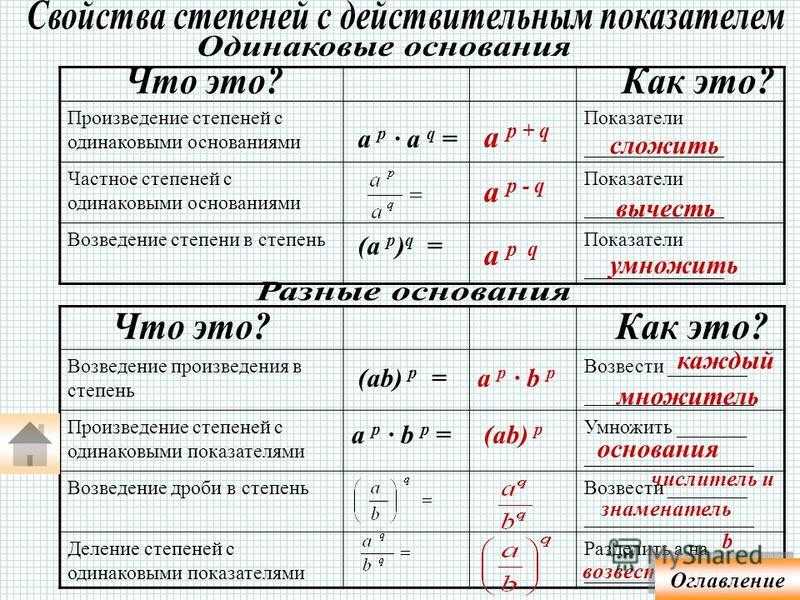
{i(\alpha + \beta)} &= \cos(\alpha + \beta) + i\cdot \sin(\alpha + \beta)
\end{выровнено} \tag {17} $$
Правая часть — декартовы координаты. Помните уникальность декартова представления? Это означает, что:
$$ \cos( \alpha + \beta ) = \cos( \alpha ) \cos( \beta ) — \sin( \alpha ) \sin( \beta ) \tag {18} $$
А также:
$$ \sin(\alpha + \beta) = \cos(\alpha) \sin(\beta) + \sin(\alpha) \cos(\beta) \tag {19} $$
Это ваши формулы сложения углов для синуса и косинуса. Довольно аккуратно, да?
Важно отметить, что это не вывод этих формул, а просто подтверждение. Цепочка вывода выглядит так.
1) Формула сложения углов косинуса от расстояний на единичной окружности
2) Формула сложения угла синуса из формулы косинуса
3) Производные синуса и косинуса из формул сложения углов и пределов
4) Ряды Тейлора для синуса и косинуса от производных
5) Формула Эйлера из ряда Тейлора
6) Формулы сложения косинуса и синуса угла из формулы Эйлера
Нет «7) Перейти к 3».
{i (\theta_1 + \theta_2) }
\end{выровнено} \tag {21} $$
Теперь давайте посмотрим, действительно ли это работает. (У вас есть сомнения?)
92 } = \sqrt{1089 + 3136} = \sqrt{4225} = 65 \\
\end{выровнено} \tag {23} $$
Да, я выбрал пифагорейские тройки для $z_1$ и $z_2$, чтобы числа получались красивыми. Но смотрите, получается тоже пифагорейская тройка. Разум затуманивается. Вернемся к проверке. 5$\cdot 13 = 65$. Проверять.
Теперь посмотрим на углы, они не такие чистые. Вот небольшой код Gambas для выполнения вычислений:
Размер z1, z2, z3 Как Комплекс
z1 = 3 + 4i
z2 = 5 + 12i
z3 = z1 * z2
Вывести "|z1| = "; Абс (z1)
Вывести "|z2| = "; Абс (z2)
Вывести "|z3| = "; Абс (z3)
Распечатать
Вывести "arg(z1) = "; z1.Arg(), Дег(z1.Arg())
Вывести "arg(z2) = "; z2.Arg(), градус(z2.Arg())
Вывести "arg(z3) = "; z3.Arg(), градус(z3.Arg())
Распечатать
Вывести "z3 = "; z3
Распечатать
Вывести "atan2( 4, 3) = "; ATan2(4, 3)
Вывести "atan2(12, 5) = "; ATan2(12, 5)
Вывести "atan2(56,-33) = "; АТан2(56, -33)
И вот результаты:
|z1| = 5 |z2| = 13 |z3| = 65 arg(z1) = 0,92729521800161 53,130102354156 арг(z2) = 1,17600520709514 67,3801350519596 аргумент(z3) = 2,10330042509675 120,510237406116 z3 = -33+56i atan2( 4, 3) = 0,92729521800161 атан2(12, 5) = 1,17600520709514 атан2(56,-33) = 2,10330042509675
Неважно, радианы или градусы, углы все равно складываются.
Эта статья должна была познакомить вас с комплексными числами и их представлением как в декартовой, так и в полярной форме. Эти концепции необходимы для понимания многих концепций DSP и, в частности, DFT (дискретного преобразования Фурье). Фраза «Одно комплексное число можно повернуть, умножив его на другое» должна иметь смысл. Если это не так, перечитайте статью и поиграйте с цифрами, пока это не произойдет.
ПосвящениеЭта статья посвящена некой мисс М.Б., которая явно никогда не обращала внимания на то, что «девушкам не положено любить математику». Иди ты, девочка!
О ГамбасеGambas — это основанный на Linux (на момент написания этой статьи) диалект платформы разработки BASIC, частично основанный (но значительно улучшенный) Microsoft VB5 и VB6. Я призываю всех программистов, от новичков до экспертов, проверить это.
Технические детали:
Версия в моем дистрибутиве (3.
1.1) устарела. Последняя версия 3.12.2
.
PPA: gambas-team/gambas3
- Документация Wiki
- Gambas.One Форум
- Источник в Gitlab
[1] Дог, Седрон, Экспоненциальный характер сложной единичной окружности.
Полные формулы сложения для эллиптических кривых простого порядка
Paper 2015/1060
Полные формулы сложения для эллиптических кривых простого порядка
Джуст Ренес, Крейг Костелло и Лейла Батина
Abstract
Закон сложения эллиптических кривых называется полным, если он правильно вычисляет сумму любых двух точек в группе эллиптических кривых. Одна из основных причин возросшей популярности кривых Эдвардса в сообществе ECC заключается в том, что они могут позволить полный групповой закон, который также является относительно эффективным (например, по сравнению со всеми известными законами сложения для кривых Эдвардса). Такие полные формулы сложения могут упростить задачу разработчика ECC и в то же время могут значительно снизить потенциальные уязвимости криптосистемы.
К сожалению, до сих пор полные законы сложения, которые относительно эффективны, были предложены только для кривых составного порядка и, таким образом, были несовместимы со всеми стандартизированными в настоящее время кривыми простого порядка.
В этой статье мы представляем оптимизированные формулы сложения, которые полны на каждой короткой кривой Вейерштрасса простого порядка, определенной над полем k с char(k), отличным от 2 или 3. По сравнению с их неполными аналогами, эти формулы требуют большего количества сложений полей, но интересно, требуется меньше умножений полей. Мы обсудим, как эти формулы можно использовать для достижения безопасных и свободных от исключений реализаций всех кривых простого порядка в стандартах NIST (и многих других).
Примечание: EUROCRYPT 2016 версия для камеры
Метаданные
- Доступный(е) формат(ы)
- Категория
- Криптография с открытым ключом
- Информация о публикации
- Опубликовано IACR в EUROCRYPT 2016
- Ключевые слова
- криптография с открытым ключомэллиптические кривыекороткая форма Вейерштрассаполные формулы сложения
- Связаться с автором(ами)
- Джей Ренес @ cs ru nl
- История
- 08.
