Формулы сложения тригонометрических функций примеры: доказательство, примеры, формулы сложения синусов и косинусов, tg суммы и разности

Mathway | Популярные задачи

1	Найти точное значение	sin(30)
2	Найти точное значение	sin(45)
3	Найти точное значение	sin(30 град. )
4	Найти точное значение	sin(60 град. )
5	Найти точное значение	tan(30 град. )
6	Найти точное значение	arcsin(-1)
7	Найти точное значение	sin(pi/6)
8	Найти точное значение	cos(pi/4)
9	Найти точное значение	sin(45 град. )
10	Найти точное значение	sin(pi/3)
11	Найти точное значение	arctan(-1)
12	Найти точное значение	cos(45 град. )
13	Найти точное значение	cos(30 град. )
14	Найти точное значение	tan(60)
15	Найти точное значение	csc(45 град. )
16	Найти точное значение	tan(60 град. )
17	Найти точное значение	sec(30 град. )
18	Найти точное значение	cos(60 град. )
19	Найти точное значение	cos(150)
20	Найти точное значение	sin(60)
21	Найти точное значение	cos(pi/2)
22	Найти точное значение	tan(45 град. )
23	Найти точное значение	arctan(- квадратный корень из 3)
24	Найти точное значение	csc(60 град. )
25	Найти точное значение	sec(45 град. )
26	Найти точное значение	csc(30 град. )
27	Найти точное значение	sin(0)
28	Найти точное значение	sin(120)
29	Найти точное значение	cos(90)
30	Преобразовать из радианов в градусы	pi/3
31	Найти точное значение	tan(30)
32	Преобразовать из градусов в радианы	45
33	Найти точное значение	cos(45)
34	Упростить	sin(theta)^2+cos(theta)^2
35	Преобразовать из радианов в градусы	pi/6
36	Найти точное значение	cot(30 град. )
37	Найти точное значение	arccos(-1)
38	Найти точное значение	arctan(0)
39	Найти точное значение	cot(60 град. )
40	Преобразовать из градусов в радианы	30
41	Преобразовать из радианов в градусы	(2pi)/3
42	Найти точное значение	sin((5pi)/3)
43	Найти точное значение	sin((3pi)/4)
44	Найти точное значение	tan(pi/2)
45	Найти точное значение	sin(300)
46	Найти точное значение	cos(30)
47	Найти точное значение	cos(60)
48	Найти точное значение	cos(0)
49	Найти точное значение	cos(135)
50	Найти точное значение	cos((5pi)/3)
51	Найти точное значение	cos(210)
52	Найти точное значение	sec(60 град. )
53	Найти точное значение	sin(300 град. )
54	Преобразовать из градусов в радианы	135
55	Преобразовать из градусов в радианы	150
56	Преобразовать из радианов в градусы	(5pi)/6
57	Преобразовать из радианов в градусы	(5pi)/3
58	Преобразовать из градусов в радианы	89 град.
59	Преобразовать из градусов в радианы	60
60	Найти точное значение	sin(135 град. )
61	Найти точное значение	sin(150)
62	Найти точное значение	sin(240 град. )
63	Найти точное значение	cot(45 град. )
64	Преобразовать из радианов в градусы	(5pi)/4
65	Найти точное значение	sin(225)
66	Найти точное значение	sin(240)
67	Найти точное значение	cos(150 град. )
68	Найти точное значение	tan(45)
69	Вычислить	sin(30 град. )
70	Найти точное значение	sec(0)
71	Найти точное значение	cos((5pi)/6)
72	Найти точное значение	csc(30)
73	Найти точное значение	arcsin(( квадратный корень из 2)/2)
74	Найти точное значение	tan((5pi)/3)
75	Найти точное значение	tan(0)
76	Вычислить	sin(60 град. )
77	Найти точное значение	arctan(-( квадратный корень из 3)/3)
78	Преобразовать из радианов в градусы	(3pi)/4
79	Найти точное значение	sin((7pi)/4)
80	Найти точное значение	arcsin(-1/2)
81	Найти точное значение	sin((4pi)/3)
82	Найти точное значение	csc(45)
83	Упростить	arctan( квадратный корень из 3)
84	Найти точное значение	sin(135)
85	Найти точное значение	sin(105)
86	Найти точное значение	sin(150 град. )
87	Найти точное значение	sin((2pi)/3)
88	Найти точное значение	tan((2pi)/3)
89	Преобразовать из радианов в градусы	pi/4
90	Найти точное значение	sin(pi/2)
91	Найти точное значение	sec(45)
92	Найти точное значение	cos((5pi)/4)
93	Найти точное значение	cos((7pi)/6)
94	Найти точное значение	arcsin(0)
95	Найти точное значение	sin(120 град. )
96	Найти точное значение	tan((7pi)/6)
97	Найти точное значение	cos(270)
98	Найти точное значение	sin((7pi)/6)
99	Найти точное значение	arcsin(-( квадратный корень из 2)/2)
100	Преобразовать из градусов в радианы	88 град.

Математика: Справ. материалы

Математика: Справ. материалы

Гусев В. А., Мордкович А. Г. Математика: Справ. материалы: Кн. для учащихся.— М.: Просвещение, 1988.— 416 с. В книге дано краткое изложение основных разделов школьных курсов алгебры и начал анализа, геометрии. Книга окажет помощь в систематизации и обобщении знаний по математике. Оглавление СЛОВО К УЧАЩИМСЯ ГЛАВА I. ЧИСЛА § 1. Натуральные числа 2. Арифметические действия над натуральными числами. 3. Деление с остатком. 4. Признаки делимости. 5. Разложение натурального числа на простые множители. 6. Наибольший общий делитель нескольких натуральных чисел. 7. Наименьшее общее кратное нескольких натуральных чисел. 8. Употребление букв в алгебре. Переменные. § 2. Рациональные числа 10. Равенство дробей. Основное свойство дроби. Сокращение дробей. 11. Приведение дробей к общему знаменателю. 12. Арифметические действия над обыкновенными дробями. 13. Десятичные дроби. 14. Арифметические действия над десятичными дробями. 15. Проценты. 16. Обращение обыкновенной дроби в бесконечную десятичную периодическую дробь. 17. Обращение бесконечной десятичной периодической дроби в обыкновенную дробь. 18. Координатная прямая. 19. Множество рациональных чисел. § 3. Действительные числа 21. Действительные числа. Числовая прямая. 22 Обозначения некоторых числовых множеств. 23. Сравнение действительных чисел. 25. Числовые промежутки. 26. Модуль действительного числа. 27. Формула расстояния между двумя точками координатной прямой. 28. Правила действий над действительными числами. 29. Свойства арифметических действий над действительными числами. 30. Пропорции. 31. Целая часть числа. Дробная часть числа. 32. Степень с натуральным показателем. 33. Степень с нулевым показателем. Степень с отрицательным целым показателем. 34. Стандартный вид положительного действительного числа. 35. Определение арифметического корня. 36. Корень нечетной степени из отрицательного числа. 37. Степень с дробным показателем. 38. Свойства степеней с рациональными показателями. 39. Приближенные значения чисел. Абсолютная и относительная погрешности. 40. Десятичные приближения действительного числа по недостатку и по избытку. 41. Правило извлечения квадратного корня из натурального числа. 42. Понятие о степени с иррациональным показателем. 43. Свойства степеней с действительными показателями. § 4. Комплексные числа 45. Арифметические операции над комплексными числами. 46. Алгебраическая форма комплексного числа. 47. Отыскание комплексных корней уравнений. ГЛАВА II. АЛГЕБРАИЧЕСКИЕ ВЫРАЖЕНИЯ 49. Допустимые значения переменных. 50. Понятие тождественного преобразования выражения. Тождество. § 6. Целые рациональные выражения 52. Многочлены. Приведение многочленов к стандартному виду. 53. Формулы сокращенного умножения. 54. Разложение многочленов на множители. 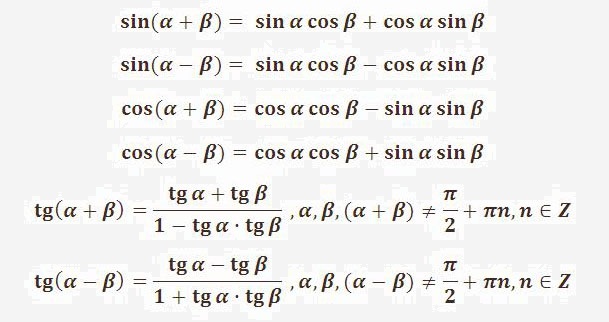3. 112. Построение графика функции y = f(x-m)+n 113. График квадратичной функции. 114. Способы построения графика квадратичной функции 115. Построение графика функции y = f(kx). 116. Сжатие и растяжение графиков тригонометрических функций. 117. График гармонического колебания ГЛАВА IV. ТРАНСЦЕНДЕНТНЫЕ ВЫРАЖЕНИЯ § 12. Преобразование выражений, содержащих переменную под знаком логарифма 119. Определение логарифма положительного числа по данному основанию. 120. Свойства логарифмов. 121. Переход к новому основанию логарифма. 122. Логарифмирование и потенцирование. 123. Десятичный логарифм. Характеристика и мантисса десятичного логарифма. § 13. Формулы тригонометрии и их использование для преобразования тригонометрических выражений 125. Формулы сложения и вычитания аргументов. 126. Формулы приведения. 127. Соотношения между тригонометрическими функциями одного и того же аргумента. 128. Формулы двойного угла. 129. Формулы понижения степени. 130. Преобразование суммы тригонометрических функций в произведение. 131. Преобразование произведения тригонометрических функций в сумму. 132. Преобразование выражения a cos t + b sin t к виду A sin (t + a). 133. Примеры преобразований выражений, содержащих обратные тригонометрические функции. ГЛАВА V. УРАВНЕНИЯ И СИСТЕМЫ УРАВНЕНИЙ § 14. Уравнения с одной переменной 135. Равносильность уравнений. 136. Линейные уравнения. 137. Квадратные уравнения. 138. Неполные квадратные уравнения. 139. Теорема Виета. 140. Системы и совокупности уравнений. 141. Уравнения, содержащие переменную под знаком модуля. 142. Понятие следствия уравнения. Посторонние корни. 143. Уравнения с переменной в знаменателе. 144. Область определения уравнения. 145. Рациональные уравнения. 146. Решение уравнения p(x) = 0 методом разложения его левой части на множители. 147. Решение уравнений методом введения новой переменной. 148. Биквадратные уравнения. 149. Решение задач с помощью составления уравнений. 150. Иррациональные уравнения. 151. Показательные уравнения. 152. Логарифмические уравнения. 153. Примеры решения показательно-логарифмических уравнений. 154. Простейшие тригонометрические уравнения. 155. Методы решения тригонометрических уравнений. 156. Универсальная подстановка (для тригонометрических уравнений). 157. Метод введения вспомогательного аргумента (для тригонометрических уравнений). 158. Графическое решение уравнений. 159. Уравнения с параметром. § 15. Уравнения с двумя переменными 161. График уравнения с двумя переменными. 162. Линейное уравнение с двумя переменными и его график. § 16. Системы уравнений 164. Решение систем двух уравнений с двумя переменными методом подстановки. 165. Решение систем двух уравнений с двумя переменными методом сложения. 167. Графическое решение систем двух уравнений с двумя переменными. 168. Исследование системы двух линейных уравнений с двумя переменными. 169. Решение систем двух уравнений с двумя переменными методами умножения и деления. 170. Системы показательных и логарифмических уравнений. 171. Системы тригонометрических уравнений с двумя переменными. 172. Системы трех уравнений с тремя переменными. 173. Решение задач с помощью составления систем уравнений. Глава VI. НЕРАВЕНСТВА § 17. Решение неравенств с переменной 175. Графическое решение неравенств с одной переменной. 176. Линейные неравенства с одной переменной. 177. Системы неравенств с одной переменной. 178. Совокупность неравенств с одной переменной. 179. Дробно-линейные неравенства. 180. Неравенства второй степени. 181. Графическое решение неравенств второй степени. 182. Неравенства с модулями. 183. Решение рациональных неравенств методом промежутков. 184. Показательные неравенства. 185. Логарифмические неравенства. 186. Иррациональные неравенства. 187. Решение тригонометрических неравенств. 188. Неравенства и системы неравенств с двумя переменными. § 18. Доказательство неравенств 190. Синтетический метод доказательства неравенств. 191. Доказательство неравенств методом от противного. 192. Использование неравенств при решении уравнений. ГЛАВА VII. ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОГО АНАЛИЗА § 19. Числовые последовательности 194. Способы задания последовательности. 195. Возрастание и убывание последовательности. 196. Определение арифметической прогрессии. 197. Свойства арифметической прогрессии 198. Определение геометрической прогрессии. 199. Свойства геометрической прогрессии. 200. Понятие о пределе последовательности. 201. Вычисление пределов последовательностей. 202. Сумма бесконечной геометрической прогрессии при |q| § 20. Предел функции 204. Вычисление пределов функции при х->оо. 205. Предел функции в точке. Непрерывные функции. 206. Вертикальная асимптота. 207. Вычисление пределов функций в точке. § 21. Производная и ее применения 209. Определение производной. 210. Формулы дифференцирования. Таблица производных. 211. Дифференцирование суммы, произведения, частного. 212. Сложная функция и ее дифференцирование. 213. Физический смысл производной. 214. Вторая производная и ее физический смысл. 215. Касательная к графику функции. 216. Применение производной к исследованию функций на монотонность. 217. Применение производной к исследованию функций на экстремум. 218. Отыскание наибольшего и наименьшего значений непрерывной функции на отрезке. 219. Отыскание наибольшего или наименьшего значения непрерывной функции на незамкнутом промежутке. 220. Задачи на отыскание наибольших или наименьших значений величин. 221. Применение производной для доказательства тождеств. 222. Применение производной для доказательства неравенств. 223. Общая схема построения графика функции. § 22. Первообразная и интеграл 225. Таблица первообразных. 226. Правила вычисления первообразных. 227. Интеграл. 228. Связь между интегралов и первообразной (формула Ньютона—Лейбница). 229. Правила вычисления интегралов. 230. Использование интеграла для вычисления площадей плоских фигур. ГЕОМЕТРИЯ. ГЛАВА I. ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ НА ПЛОСКОСТИ 2. Точка. Прямая. 3. Определения. Аксиомы. Теоремы. § 2. Основные свойства простейших геометрических фигур 5. Луч. 6. Окружность. Круг. 7. Полуплоскость. 8. Угол. Градусная мера угла. 9. Смежные и вертикальные углы. 10. Центральные и вписанные углы. 11. Параллельные прямые. 12. Признаки параллельности прямых. 13. Перпендикулярные прямые. 14. Касательная к окружности. 15. Треугольники. 16. Равенство треугольников. 17. Равнобедренный треугольник. 18. Сумма углов треугольника. 19. Прямоугольный треугольник. Теорема Пифагора. 20. Окружности, вписанные в треугольник и описанные около треугольника. § 3. Геометрические построения на плоскости 22. Простейшие задачи на построение. 23. Геометрическое место точек на плоскости. § 4. Четырехугольники 25. Параллелограмм. 26. Прямоугольник. Ромб. Квадрат. 27. Трапеция. § 5. Многоугольники 29. Выпуклые многоугольники. 30. Правильные многоугольники. 31. Длина окружности. § 6. Решение треугольников 33. Соотношения между сторонами и углами в прямоугольном треугольнике. 34. Теорема косинусов. Теорема синусов. 35. Решение треугольников. § 7. Площади плоских фигур 37. Площади многоугольников. 38. Площади подобных фигур. 39. Площадь круга. ГЛАВА II. Прямые и плоскости в пространстве § 9. Параллельность прямых и плоскостей 42. Параллельность прямой и плоскости. 43. Параллельные плоскости. § 10. Перпендикулярность прямых и плоскостей 45. Перпендикуляр и наклонная к плоскости. 46. Перпендикулярность плоскостей. ГЛАВА III. ТЕЛА В ПРОСТРАНСТВЕ § 11. Многогранники 48. Многогранные углы. Многогранники. 49. Призма. Параллелепипед. Куб. 50. Пираприда. 51. Правильные многогранники. § 12. Тела вращения 53. Конус. 54. Шар. § 13. Изображение пространственных фигур на плоскости 56. Ортогональное проектирование. 57. Геометрическое место точек в пространстве. § 14. Объемы тел 59. Объем параллелепипеда, призмы и пирамиды. 60. Объем цилиндра и конуса. 61. Общая формула объемов тел вращения. § 15. Площади поверхностей тел 63. Понятие площади поверхности. 64. Площади поверхностей тел вращения. ГЛАВА IV. ДЕКАРТОВЫ КООРДИНАТЫ § 16. Координаты на плоскости и в пространстве 66. Координаты середины отрезка. § 17. Уравнения фигур на плоскости 68. Пересечение двух окружностей. 69. Уравнение прямой. 70. Пересечение прямой и окружности. § 18. Уравнения фигур в пространстве 72. Уравнение сферы. 73. Взаимное расположение сферы и плоскости. 74. Пересечение двух сфер. ГЛАВА V. РЕОБРАЗОВАНИЯ ФИГУР 76. Понятие движения. § 20. Подобие фигур 78. Подобные фигуры. ГЛАВА VI. ВЕКТОРЫ 80. Понятие вектора. 81. Координаты вектора. § 22. Операции над векторами 83. Умножение вектора на число. Коллинеарные векторы. 84. Скалярное произведение векторов. ПРИЛОЖЕНИЯ ГЕОМЕТРИЯ

Определения формул тригонометрических функций и примеры

Определения формул тригонометрических функций и примеры

Тригонометрия — это раздел математики, изучающий отношения между сторонами и углами треугольников. Слово «тригонометрия» происходит от греческих слов «треугольник» и «мера». Существует шесть тригонометрических функций, которые обычно обозначаются буквами синус (sin), косинус (cos), тангенс (tan), косеканс (csc), секанс (sec) и котангенс (cot). Эти шесть инверсий тригонометрических функций, углы и тождества необходимы для понимания при изучении тригонометрии. В этом сообщении блога мы подробно рассмотрим эти темы с определениями, формулами и примерами. 92 – 2bc cosA

Список формул тригонометрии

Тригонометрические функции определяются как отношения сторон прямоугольного треугольника. Тремя основными тригонометрическими функциями являются синус (sin), косинус (cos) и тангенс (tan). Эти функции имеют множество приложений в математике, физике, технике и других науках.

Существует ряд различных формул тригонометрии, которые можно использовать для решения различных задач. Ниже приведен список некоторых наиболее часто используемых формул: 92

Формулы сложения углов: sin(x+y) = sin(x)cos(y)+cos(x)sin(y) и cos(x+y)= cos(x)cos(y)-sin( x)sin(y)

Основные формулы тригонометрии

Основные формулы тригонометрии

Sin, cos и tan являются основными функциями тригонометрии. Функция синуса, обозначаемая как sin(?), определяется как отношение длины стороны, противоположной углу ? на длину гипотенузы. Функция косинуса, обозначаемая как cos(?), определяется как отношение длины стороны, прилегающей к углу ? на длину гипотенузы. Касательная функция, обозначаемая tan(?), определяется как отношение длины стороны, противоположной углу ? к соседней стороне.

Ниже приведены некоторые основные формулы тригонометрии:

1. sin2? + cos2? = 1 ……………………….(тождество)
2. cosec2? = 1 + тангенс2? ……………………. (взаимное тождество)
3. сек2? = 1 + детская кроватка2? ……………………… (взаимное тождество)
4. cosec ? = 1/грех? ……………………. (определение)
5. сек ? = 1/cos ? …………………….. (определение)
6. загар ? = 1/детская кроватка? ……………………. (определение)

Тригонометрические формулы, включающие взаимные тождества

Существует несколько тригонометрических формул, включающих взаимные тождества. Это тождества, которые можно использовать для упрощения выражений, содержащих обратные числа. Вот несколько примеров:

1. Обратная величина синусу равна косекансу:

Обратная величина косинуса равна секансу:

2. Обратная величина тангенса равна котангенсу:

3. Обратная величина косинуса равна синусу:

косинус:

5. Обратная величина котангенса равна тангенсу:

Эти соотношения между обратными величинами тригонометрических функций могут быть полезны при упрощении выражений или решении уравнений. Например, если вам нужно найти значение sin15°, вы можете использовать тот факт, что sin15° = 1/2, а затем использовать обратное тождество для синуса, чтобы записать его как 2sinx=1. Затем вы можете найти x, используя базовую алгебру, и найти, что x = 30°.

Таблица тригонометрических отношений

Тригонометрические отношения — отношения сторон прямоугольного треугольника. Отношения не зависят от размера треугольника.

Тригонометрические соотношения для прямоугольного треугольника:

Синус (sin) = противолежащее/гипотенуза
Косинус (cos) = прилежащее/гипотенуза
Тангенс (tan) = противоположное/прилежащее

Тригонометрические формулы, включающие периодические тождества (в радианах) )

1. sin(x+y) = sin x cos y + cos x sin y 92 года

Тригонометрические формулы, включающие тождества кофункций (в градусах)

Существует несколько тригонометрических формул, включающих тождества кофункций, которые важно знать при работе со степенями. К ним относятся:

– sin(90° – x) = cos(x)
– cos(90° – x) = sin(x)
– tan(90° – x) = cot(x)

Каждый из эти формулы можно вывести из основного определения кофункции: f(x) = 1/f(?/2 – x). Используя это определение, легко увидеть, как работают приведенные выше формулы.

Например, давайте посмотрим на первую формулу: sin(90° – x) = cos(x). Мы можем подставить наши известные значения и изменить порядок, чтобы получить: cos(x) = 1/sin(?/2 – x). Отсюда мы можем заменить 90° на ?/2 и упростить, чтобы получить окончательный результат.

Тригонометрические формулы, включающие тождества суммы и разности

При работе с тригонометрическими функциями необходимо знать несколько основных тождеств. Эти тождества, включающие суммы и разности, могут быть очень полезны при упрощении выражений или решении уравнений.

Вот самые основные тождества суммы и разности:

sin(x + y) = sin(x)cos(y) + cos(x)sin(y)
cos(x + y) = cos(x) cos(y) – sin(x)sin(y)
tan(x + y) = tan(x) + tan(y)/[1 – tan(x)*tan(y)]

Эти тождества могут быть получены из более фундаментальных формул сложения для синуса и косинуса:

sin(x + y)= sin x cos y + cos x sin y
cos (x+y)= cos x cos y – sin x sin y
и может использоваться для получения многих других тригонометрических тождеств.

92А)

Эти формулы можно использовать для нахождения значений тригонометрических функций для углов, кратных или дольных другим углам. Например, если известно значение sin60°, можно использовать формулу для sin(2A), чтобы найти значение sin120°.

Тригонометрические формулы, использующие тождества половин углов

Тригонометрия — это раздел математики, изучающий отношения между углами и сторонами треугольников. Наиболее распространенными тригонометрическими функциями являются синус, косинус и тангенс. Эти функции имеют множество приложений в науке и технике.

Тождества половинного угла представляют собой набор тригонометрических тождеств, включающих определение синуса, косинуса или тангенса половины угла. Эти тождества можно использовать для упрощения выражений и решения задач.

Вот несколько примеров тождеств половинного угла:

sin(?/2) = ?( (1 – cos(?)) / 2 )
cos(?/2) = ?( (1 + cos(?) )) / 2 )
tan(?/2) = 1 / ?( (1 – cos(?)) / (1 + cos(?)) )

Эти тождества можно использовать для упрощения выражений, включающих тригонометрические функции. Например, если вы хотите найти синус угла ?, вы можете использовать тождество sin(?) = 2sin(?/2)cos(?/2). Это может быть полезно, если вы знаете значение sin(?/2), но не знаете значение sin(?).

Тригонометрические формулы с тождествами двойных углов

Для начала давайте вспомним определение тригонометрической функции. Тригонометрическая функция — это функция, которая принимает угол в качестве входных данных и возвращает отношение сторон прямоугольного треугольника. Наиболее распространенными тригонометрическими функциями являются синус, косинус и тангенс, хотя их гораздо больше.

Теперь давайте перейдем к тождествам с двойным углом. Тождество двойного угла — это тождество, верное для всех углов. Например, для всех углов x верно следующее тождество: 92(x) = 1

Тригонометрические формулы, использующие тождества тройного угла

При работе с тригонометрическими функциями важно помнить, что они периодические. Это означает, что они повторяются снова и снова. Период функции — это время, за которое функция повторяется. Например, функция косинуса имеет период 2pi радиан, что означает, что она будет повторяться каждые 2pi радиан (или 360 градусов).

Существует ряд различных тождеств с тройными углами, о которых вам следует знать при работе с тригонометрическими функциями. Эти тождества можно использовать для упрощения уравнений или для помощи в решении задач. 93(?)

Тригонометрические формулы – тождества суммы и произведения

В математике тригонометрические тождества – это уравнения, включающие тригонометрические функции и истинные для всех значений встречающихся переменных, когда обе части равенства определены. Тригонометрические функции важны при изучении треугольников и моделировании периодических явлений, а также во многих других приложениях.

Существует бесконечное количество тригонометрических тождеств, но есть несколько особенно полезных, включая тождества суммы и произведения. В этом разделе мы рассмотрим эти удостоверения и несколько примеров их использования.

Тождество суммы утверждает, что для любых углов A и B верно следующее равенство: углы. Например, рассмотрим выражение sin(30° + 45°). Используя тождество суммы, мы можем переписать это следующим образом:

sin(30° + 45°) = sin30°cos45° + cos30°sin45°
= 0,5cos45° + 0,866sin45°
= 0,7378640776699029…

тождество произведения утверждает, что для любых углов A и B верно следующее уравнение:

sinAcosB = 1/2[cos(A – B) – cos(A + B)]

Это тождество можно использовать для для решения проблем. К ним относятся синус и косинус суммы или разности, формулы двойного угла и формула половинного угла.

Синус и косинус суммы или разности можно найти по следующим формулам:

sin(A+B) = sinAcosB + cosAsinB 92 A)/cos A) // знак положительный, если A находится в квадранте I или IV,

Тригонометрические формулы, включающие тождества суммы в произведение

Существует множество формул тригонометрии, включающих тождества суммы в произведение, которые можно использовать для решения различных проблемы. Эти формулы можно использовать для упрощения уравнений, решения неизвестных углов или сторон треугольника и многого другого. Ниже перечислены некоторые из наиболее часто используемых тригонометрических формул, включающих тождества суммы и произведения:

— Тождество суммы произведения для Sin: sin(A + B) = sinAcosB + cosAsinB
— Сумма идентичности продукта для Cos: cos(A + B) = cosAcosB – sinAsinB
— Формула разности для Sin: sin(A – B) = sinAcosB – cosAsinB
— Формула разности для Cos: cos(A – B) = cosAcosB + sinAsinB
— Формула двойного угла для Sin: sin2A = 2sinAcosA
— Формула двойного угла для Cos: cos2A = cos2A – sin2A

Обратные тригонометрические формулы

Обратные тригонометрические функции используются для решения задач, связанных с измерением углов в радианах или градусах. Эти функции позволяют вычислить величину угла, не зная длины сторон треугольника. Наиболее распространенными обратными тригонометрическими функциями являются:

– арккосинус (acos)
– арксинус (asin)
– арктангенс (atan)
– котангенс (cot)
– секанс (sec)
– синус (sin)
– тангенс (tan)

Тригонометрические формулы, включающие синус и Законы косинуса

Законы синуса и косинуса — это две тригонометрические формулы, которые позволяют нам находить неизвестные стороны и углы в треугольнике. Эти законы важны для всех, кто изучает тригонометрию, поскольку они позволяют вычислять всевозможные свойства треугольников.

Закон синусов гласит:

sin(A)/a = sin(B)/b = sin(C)/c

где A, B и C — углы треугольника, а a, b , c — длины соответствующих сторон. Итак, если мы знаем два угла и длину одной стороны в треугольнике, мы можем использовать закон синусов для определения длин двух других сторон. Например, если мы знаем, что угол A равен 60 градусам, угол B равен 30 градусам, а длина стороны a равна 10 единицам, мы можем найти сторону b и сторону c, используя следующие уравнения:0003

sin(60)/10 = sin(30)/b ~~> b = 5 единиц
sin(60)/10 = sin(C)/c ~~> c = 10/sin(60) ~~> c = 16,97 единиц

Что такое тригонометрические функции?

Тригонометрическая функция — это функция, связывающая угол с отношением двух сторон прямоугольного треугольника. Наиболее распространенными тригонометрическими функциями являются синус, косинус и тангенс.

Синус угла – это отношение длины стороны, противоположной углу, к длине гипотенузы. Косинусом угла называется отношение длины стороны, прилежащей к углу, к длине гипотенузы. Тангенс угла – это отношение длины стороны, противолежащей углу, к длине стороны, прилежащей к углу.

Эти соотношения можно использовать для решения задач, связанных с треугольниками, таких как нахождение неизвестных длин или углов. Тригонометрические функции также можно изображать в виде графиков, и эти графики можно использовать для решения задач, связанных с периодическим движением.

Различные типы тригонометрических функций

Существуют три общие тригонометрические функции: синус, косинус и тангенс. Каждая из этих функций имеет определенное определение и формулу, которая используется для вычисления различных свойств углов.

Синус (sin): Синус угла – это отношение длины противоположной стороны к длине гипотенузы.

Косинус (cos): Косинусом угла называется отношение длины прилежащего катета к длине гипотенузы.

Тангенс (tan): Тангенс угла представляет собой отношение длины противоположной стороны к длине прилежащей стороны.

Формула для тригонометрических функций

Когда мы говорим о тригонометрических функциях, мы имеем в виду группу функций, которые помогают нам понять отношения между углами и сторонами в треугольниках. Наиболее распространенными тригонометрическими функциями являются синус, косинус и тангенс, хотя есть и другие (такие как косеканс, секанс и котангенс). Эти функции можно представить с помощью следующих формул:

Синус (sin): sin(?) = противоположный / гипотенуза
Косинус (cos): cos(?) = смежный / гипотенуза
Тангенс (tan): tan(?) = противоположный / смежный

Эти формулы позволяют нам вычислить значения этих функций для любого заданного угла. Например, если мы знаем, что угол ? равен 30°, мы можем подставить это значение в каждую из вышеприведенных формул, чтобы найти соответствующие значения функции:

sin(30°) = противоположность / гипотенуза
=> sin(30°) = 0,5 / 1
=> sin(30°) = 0,5

cos(30°) = смежный / гипотенуза
=> cos(30°) = ?3/2 / 1
=> cos(30°) = ?3/2

tan(30°) = противоположный / смежный
=> tan(30°) = 0,5/?3 / 1
=> tan(

Заключение

Тригонометрические функции очень важны в математике и имеют множество приложений в физике и технике. В этой статье мы кратко изложили введение в тригонометрические функции, их формулы и некоторые примеры.Мы надеемся, что эта информация оказалась для вас полезной и вы будете использовать ее для дальнейшего понимания этих важных концепций.

Примеры тригонометрических функций

Существует множество тригонометрических функций, каждая из которых определяется как отношение двух сторон прямоугольного треугольника. Наиболее распространенными тригонометрическими функциями являются синус, косинус и тангенс, но есть также секанс, косеканс и котангенс. Эти шесть функций обозначаются как sin, cos, tan, sec, csc и cot.

Функция синуса определяется как отношение длины стороны, противоположной углу, к длине гипотенузы. Функция косинуса определяется как отношение длины стороны, примыкающей к углу, к длине гипотенузы. Касательная функция определяется как отношение длины стороны, противоположной углу, к длине стороны, прилегающей к углу.

Чтобы найти секанс, косеканс или котангенс, мы берем обратную (обратную) величину синуса, косинуса или тангенса соответственно. Итак, секанс равен 1/синус, косеканс равен 1/косинус, а котангенс равен 1/тангенс.

Вот несколько примеров:

Sin(30°)=0,5, потому что в прямоугольном треугольнике 30-60-90 (особый тип прямоугольного треугольника, где все углы равны 60° или 90°) длина стороны, противоположной 30° ° составляет половину гипотенузы Cos(45°)=

Как составить уравнение с тригонометрическими функциями

Этот совет показывает, как добавить уравнение с тригонометрическими функциями, например, Формула Эйлера .

Как добавить уравнение в документ см. Работа с Microsoft Equation.

Чтобы вставить, например, формулу Эйлера , выполните следующие действия:

В формате

Professional :

   1.   В собственном уравнении в разделе Инструменты для формул , на вкладке Проект в группе Конструкции нажмите кнопку Скрипт :

В списке Script выберите Верхний индекс :

   2.    В базовое поле сценария введите e .

   3.   В нижней части скрипта введите ix .

   4.   Введите = .

   5.   В разделе Equation Tools на вкладке Design , в группе Конструкции нажмите кнопку Функция :

В списке Функция выберите Функция косинуса :

   6.   В базовом блоке тригонометрической функции введите х .

   7.   Введите +i .

   8.   В разделе Equation Tools на вкладке Design , в группе Конструкции нажмите кнопку Функция и затем в списке Функция , выберите Синусоидальная функция :

9(ix) и затем нажмите пробел.