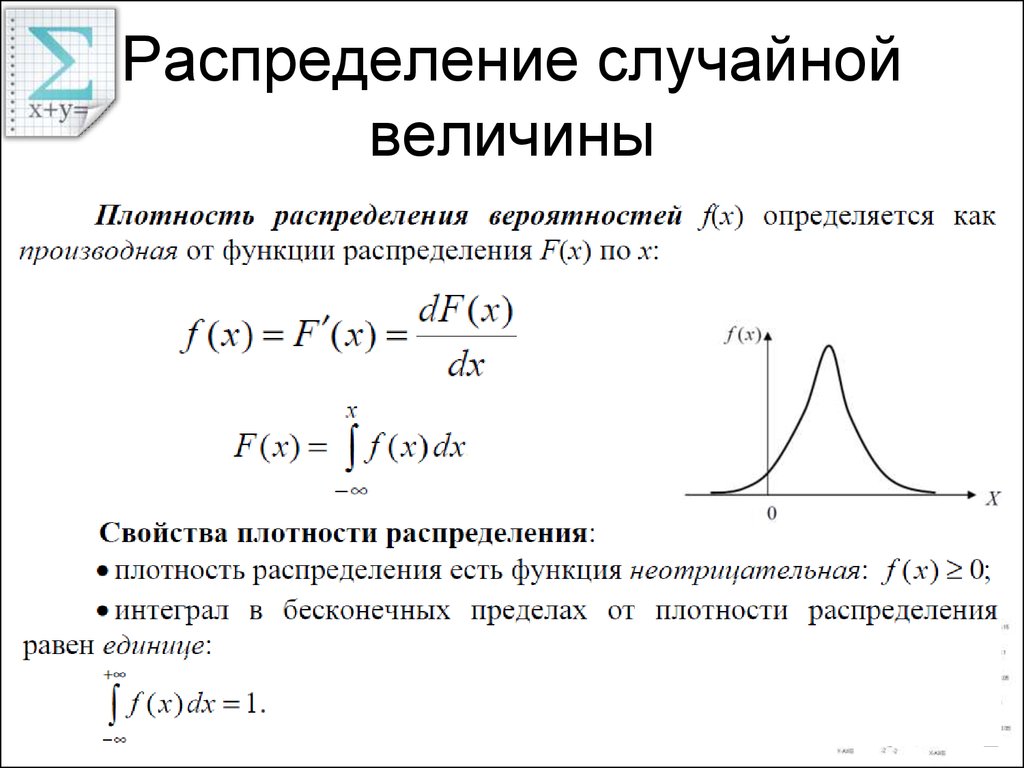
ряд распределения, функция распределения, функция плотности распределения
Способы или формы представления закона распределения случайной величины могут быть различны.
Наиболее просто решается задача вероятностной оценки для дискретной случайной величины. Для этого достаточно указать, какой вероятностью обладает каждое из событий х1, х2, х3, … хn: Р(Х = х1) = р1; Р(Х = х2) = р2; Р(Х = х3) = р3; Р(Х = хn) = рn.
Рассмотрим дискретную случайную величину Х = {число попаданий при 3 выстрелах}.
Пусть вероятность попадания в цель равна 0,3 и от выстрела к выстрелу не изменяется.
Возможные частные
значения случайной величины Х = {число
попаданий при 3 выстрелах } могут быть
следующими: ни одного попадания – х1 = 0; одно попадание – х2 = 1; два попадания – х
Вероятности частных значений случайной величины найдем по формуле Бернулли:
Проведем проверку учета всех гипотез:
0,343 + 0,441 + 0,189 + 0,027 = 1
Таким образом, мы определили вероятность наступления каждого из всех несовместных событий и с вероятностной точки зрения полностью охарактеризовали случайную величину Х = {число попаданий при 3 выстрелах}, поставив в соответствие каждому частному значению случайной величины х1= 0; х2= 1; х3= 2; х4= 3 вероятность его появления:=0,343,=0,441,=0,189,=0,027.
Такая форма закона распределения дискретной случайной величины называется рядом распределения.
Закон распределения дискретной случайной величины, когда каждому частному значению х1, х2
, х3, … хn случайной величины Х ставится в соответствие её вероятность: Р(Х = х1)
= р1;
Р(Х = х2)
= р2;
Р(Х = х3)
= р3;
Р(Х = хn)
= рn.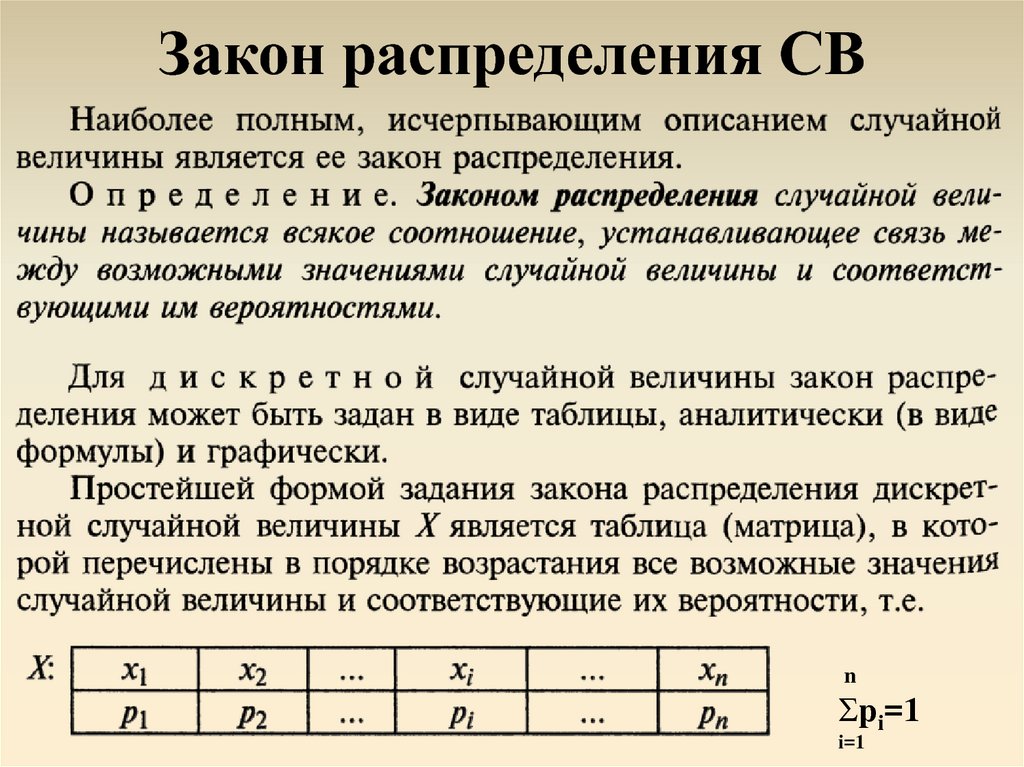
называется рядом распределения дискретной случайной величины.
Ряд распределения, как правило, представляют в виде таблицы, где в верхней строке в порядке возрастания размещают возможные частные значения случайных величин, а в нижней – соответствующие им вероятности.
хi
1
2
3
Р(Х = хi)
0,343
0,441
0,189
0,027
При составлении
ряда распределения следует иметь в
виду, что все события являются
несовместными, т.к. случайная величина
Х может принять в результате испытания
только одно значение. Эти события
случайны, т.к. нельзя указать, какое
значение примет случайная величина и,
последнее, все события должны образовывать
полную группу событий, т.
к. никаких
других событий, кроме перечисленных, в
результате опыта произойти не может.
На основании вышеизложенного, что события Х = хi(i= 1, 2, 3, …n) образуют полную группу несовместных событий, сумма вероятностей всех возможных частных значений должна удовлетворять условию:
Ряд распределения можно представить графически, для этого по оси абсцисс откладывают возможные значения случайной величины, а по оси ординат – вероятности этих значений (рис. 4).
1
0,4
0
0,441
,3
0,189
0
0,343
,2
0,1
0,027
0 х
1 2 3
Рис. 4
Для
наглядности вершины полученных ординат
соединяют пунктирными отрезками. Следует
помнить, что соединение вершин прямыми
делается только в целях наглядности,
т.
к. в промежутках между х1их2;х2их
Рассмотренный ряд распределения является весьма удобной формой представления закона распределения. Однако основным недостатком данной формы закона распределения является то, что область его применения ограничивается распределением дискретной случайной величины с конечным числом возможных значений.
Для
непрерывной случайной величины, когда
возможные значения случайной величины
заполняют всю числовую ось или какой-то
ее интервал, поставить в соответствие
каждому частному значению случайной
величины соответствующую ему вероятность,
невозможно. Множество возможных значений
такой случайной величины несчетно (их
невозможно перечислить в верхней части
таблицы).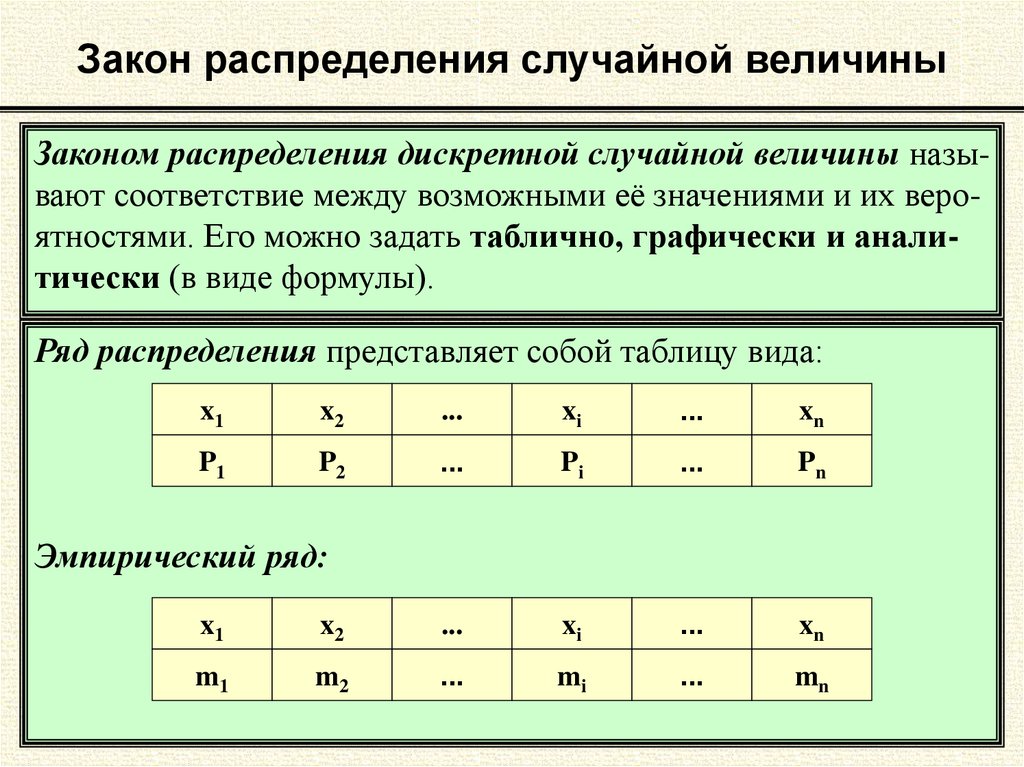
То есть, иметь какую то универсальную форму закона распределения для всех типов случайной величины.
Для количественной характеристики распределения как дискретной, так и непрерывной случайной величины, удобно воспользоваться не вероятностью события Х = хi, а вероятностью события Х < х, где х – некоторая текущая переменная. Вероятность такого события есть некоторая функция от х –F(x). Эта функция носит название функции распределения случайной величины Х.
Функцией распределения случайной величины Х называется функция аргумента х, равная вероятности того, что случайная величина примет любое значение, меньше чем х.
На
примере дискретной случайной величины
Х = {число попаданий при 3 выстрелах}
покажем, как возможно составить фикцию
распределения.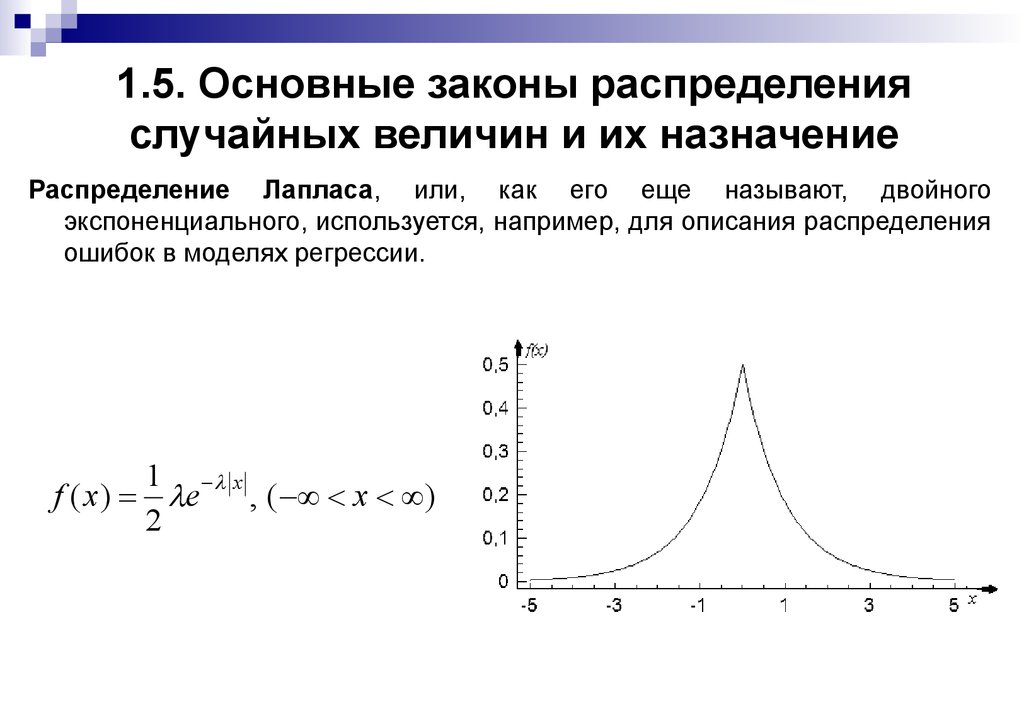
(Однако здесь необходимо
несколько абстрагироваться от того,
что число попаданий может быть только
натуральными числами: 0, 1, 2, 3, но и иметь
дробное значение, а также меньше 0 и
больше 3, т.е. рассмотреть все возможные
значения числовой оси)
Рассчитаем функцию распределения дискретной случайной величины Х = {число попаданий при 3 выстрелах}:
, событие невозможное
,
Таким образом, функция распределения случайной величины Х= {число попаданий при 3 выстрелах} будет иметь следующий вид:
Отобразим полученную функцию распределения F(x) в виде графика (рис. 5):
F(х)
1
0,9
0,8
0,7
0,6
0,5
0,4
0,3
0.2
0,1
х
0 1 2 3 4
Рис.
5
Функция распределения дискретной случайной величины является ступенчатой функцией.
Из графика функции распределения (рис. 5) видно, что в возможных частных значениях дискретной случайной величины Х функция разрывается и поднимается скачками на величину вероятности соответствующего значения случайной величины.
Значение функции распределения в точке разрыва определяется при подходе к этой точке слева по оси Ох.
Сумма всех скачков функции F(x) равна 1 (в соответствии с условием:).
По мере увеличения числа возможных значений случайной величины и уменьшения интервалов между ними число скачков становится больше, а сами скачки – меньше, ступенчатая кривая становится более плавной, дискретная случайная величина постепенно приближается к непрерывной, а ее функция распределения – к непрерывной функции.
В
принципе, любую непрерывную величину
можно рассматривать как дискретную.
Ведь измеряя какое-то ее значение по
результатам опыта, например, удаление
точки падения снаряда от цели, мы всегда
выражаем ее в каких-то единицах измерения
(метрах, сантиметрах).
В реальности такая
замена не всегда оправдана так как,
во-первых, всегда имеется потенциальная
возможность повысить точность измерения,
а во-вторых, частные значения случайной
величины могут быть очень тесно
расположены на числовой оси. В этих
случаях проще рассматривать случайную
величину не как дискретную, а как сплошь
занимаемую какой-то интервал числовой
оси.
На рис. 6 приведена функция распределения для непрерывной случайной величины, имеющей нормальное распределение.
F(х)
1
х
Рис. 6
Вероятный смысл функции распределения состоит в том, что она определяет распределение вероятности между отдельными включающими друг друга участками интервала возможных значений случайной величины.
Сформулируем общие свойства функции распределения:
1. Функция распределения F(x) есть неотрицательная функция, заключенная между 0 и 1
.
2. Функция распределения F(x) есть неубывающая функция своего аргумента
при .
3. На минус бесконечности функция распределения равна нулю
.
4. На плюс бесконечности функция распределения равна 1
.
Кроме того, из графика функции распределения F(x) (рис. 6) видно, что значение функции распределения в точке разрыва определяется при подходе к этой точке слева по оси 0х. Это означает, что функция распределения непрерывна слева.
Таким образом, функция распределения F(x) любой случайной величины есть неотрицательная, неубывающая, непрерывная слева функция своего аргумента, значения которой заключены между нулем и единицей, причем ;. В отдельных точках эта функция может иметь скачки, на некоторых участках она может быть постоянной, на других – постоянно возрастать.
Следует
также отметить, что имеет место и обратное
утверждение: каждая функция, удовлетворяющая
вышеперечисленным условиям, является
функцией распределения некоторой
случайной величины.
Функция распределения самая универсальная форма представления закона распределения случайной величины и может характеризовать как дискретные, так и непрерывные случайные величины.
Существенным недостатком такой формы закона распределения случайной величины, как функция распределения, является то, что она не позволяет ответить на вопрос в окрестностях какой из точек аилиbбудет чаще появляться непрерывная величина (рис.7).
F(х)
1
F(а) F(b)
х
а b
Рис.7
Для более наглядного характера распределения непрерывной случайной величины в окрестностях различных точек вводится особая функция, называемая плотностью вероятности или плотностью распределения.
Предел
отношения вероятности попадания
непрерывной случайной величины на
элементарный участок от х до х+х
к длине этого участка х,
когда х
стремится к нулю, называется плотностью
распределения случайной величины в
точке Х.
Функцию плотности распределения обозначают как f(x).
Кривая, изображающая плотность распределения случайной величины, называется кривой распределения
На рис.8 приведена кривая плотности распределения непрерывной случайной величины имеющей нормальное распределение.
f(х)
0 х
Рис. 8
Физический смысл плотности распределения заключается в том, что она указывает на то, как часто появляется случайная величина в малой окрестности точки х при повторении испытаний (рис. 9).
F(х)
1
F(а) F(b)
х
а b
f(х)
f(а)
f(b)
а b х
Рис. 9
Если
в точке Х = а плотность распределения
больше, чем в точке Х = b(f(а) >f(b)),
то это означает, что в небольшой
окрестности точкиапри повторении
испытаний случайная величина Х будет
появляться чаще, чем в такой же по
величине окрестности вокруг точки Х =b(приа
=b).
Плотность распределения так же, как и функция распределения, есть одна из форм закона распределения. Однако, в противоположность функции распределения, являющейся универсальной формой закона распределения, плотность распределения существует только для непрерывных случайных величин.
Сформулируем основные свойства плотности распределения:
1. Плотность распределения неотрицательна.
.
2. Интеграл в бесконечных пределах от плотности распределения равен 1.
Геометрически это свойство плотности распределения означает, что вся площадь, ограниченная кривой распределения и осью абсцисс, равна 1 (рис. 10).
f(х)
0 х
Рис 10
Таким образом, подводя итог вышесказанному, закон распределения дискретной случайной величины может быть задан одним из следующих способов:
формулой, с помощью которой можно вычислить вероятность всех возможных значений случайной величины;
рядом распределения;
функцией распределения.
Закон распределения непрерывной случайной величины может быть задан:
формулой, с помощью которой можно вычислить вероятность попадания случайной величины в заданный интервал;
функцией распределения;
функцией плотности распределения.
Раздел недели: Скоропись физического, математического, химического и, в целом, научного текста, математические обозначения. Математический, Физический алфавит, Научный алфавит. | ||||||||
| Поиск на сайте DPVA Поставщики оборудования Полезные ссылки О проекте Обратная связь Ответы на вопросы. Оглавление Таблицы DPVA.ru — Инженерный Справочник | Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация/ / Математический справочник / / Теория вероятностей. Математическая статистика. Комбинаторика. / / Формы закона распределения случайной величины. Ряд распределения, Функция распределения, Функция плотности распределения верятностей. Математическое ожидание, Дисперсия, Среднее квадратическое отклонение, моменты случайных величин. Поделиться:
 Введите свой запрос: | |||||||
Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста. | ||||||||
Коды баннеров проекта DPVA.ru Консультации и техническая | Проект является некоммерческим. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса. Free xml sitemap generator | |||||||
Определение формы распространения | Law Insider
означает форму, устанавливаемую время от времени Администратором Плана, которую Директор заполняет, подписывает и возвращает Администратору Плана для указания времени и формы распространения.
(a) В случае наступления Случая неисполнения обязательств (как определено в Соглашении о базовых ценных бумагах) по Базовым ценным бумагам в соответствии с пунктами (1) или (2) Раздела 5.01 Соглашения о базовых ценных бумагах, то Доверительный управляющий в случае получив уведомление о таком событии, должен на 30-й день после такого события или сразу после него дать указание Агенту рынка продать Базовые ценные бумаги и пропорциональную часть Связанных активов, находящихся в собственности Траста, в соответствии с Процедурами продажи, и Поступления от ликвидации, если таковые имеются, должны быть разделены между Классами в соответствии с Коэффициентом распределения, и часть каждого Класса должна быть депонирована на Сертификатный счет такого Класса и распределена среди Держателей Сертификатов такого Класса пропорционально в первый Рабочий день после такого депозита. в такую учетную запись сертификата.
означает план распределения долей в капитале Компании, подготовленный Доверительными управляющими в соответствии с пунктом 4;
означает форму, устанавливаемую время от времени Комитетом, которую Участник заполняет, подписывает и возвращает в Комитет для проведения выборов в соответствии с Планом.
означает водонепроницаемый компонент, который принимает сточные воды из септического резервуара или другого очистного сооружения и распределяет сточные воды под действием силы тяжести примерно равными порциями к двум или более распределительным отводам в зоне обработки почвы.
означает план распределения Суммы расчетов и начисленных процентов, полностью или частично, утвержденный судами.
означает любую форму заявки, которая должна быть заполнена подписчиками на Акции, как время от времени предписано Компанией.
рассчитывается, как указано в подпункте (A) ниже, если только Проспект не предусматривает усреднение распределения доходов, и в этом случае «Распределение доходов» рассчитывается, как указано в подпункте (B) , ниже. Соответственно, «Распределение дохода» Пайщика будет равно:
означает каждую форму, устанавливаемую время от времени Администратором, которую Исполнитель заполняет, подписывает и возвращает Администратору для определения суммы Отсрочки.
означает Форму заявки на получение личного счета для международного банковского обслуживания физических лиц или Wealth and Investment, в зависимости от обстоятельств;
означает форму, устанавливаемую время от времени Администратором Плана, которую Исполнитель заполняет, подписывает и возвращает Администратору Плана для назначения одного или нескольких Бенефициаров.
Субсчет Распределительного счета, который должен быть активом Трастового фонда и REMIC верхнего уровня.
означает план распределения реинвестиций Компании, утвержденный Советом и изложенный в Проспекте.
В совокупности Счет распределения REMIC верхнего уровня, Счет распределения REMIC нижнего уровня, Счет распределения избыточного процента (и в каждом случае любой его субсчет), все из которых могут быть субсчетами одного Правомочного счета.
имеет значение, присвоенное этому термину в Разделе 5.01.
означает соглашение, в соответствии с которым Правомочный сотрудник может по своему выбору зарегистрироваться в Плане, разрешить новый уровень отчислений из заработной платы или прекратить отчисления из заработной платы и выйти из Периода предложения.
означает часть любой магистрали, с которой служебная линия соединена или должна быть непосредственно соединена;
Субсчет Счета распределения, который должен быть активом Трастового фонда и REMIC нижнего уровня.
означает каждое 15 июня и каждое 15 декабря, начиная с 15 декабря 2016 года; при условии, однако, что, если какой-либо такой день не является Рабочим днем, соответствующее распределение должно быть произведено на следующий последующий Рабочий день без дополнительных процентов.
означает Дату подтверждения.
В отношении распределения Плановых платежей в отношении Сертификатов означает каждую дату, обозначенную в качестве Даты регулярного распределения в Сертификатах, выпущенных в соответствии с настоящим Соглашением, до момента оплаты всех Плановых платежей, которые должны быть произведены по имеющимся Облигациям на оборудование. в Доверии были сделаны; при условии, однако, что, если какой-либо такой день не является Рабочим днем, соответствующее распределение должно быть произведено на следующий последующий Рабочий день без дополнительных процентов.
означает время вступления Распределения в силу в Дату распространения, которое считается 23:59 по восточному летнему времени в Дату распространения.
означает регистрацию ценной бумаги, в которой указывается нынешний владелец ценной бумаги и намерение владельца относительно лица, которое станет владельцем ценной бумаги после смерти владельца.
имеет значение, указанное в Разделе 5.02(c) Трастового соглашения.
означает «дистрибьюторскую сеть», как определено в Специальном условии E2A Лицензии перевозчика, принадлежащей каждому Оператору DN;
означает платеж или распределение держателям разрешенных требований, разрешенных долей или другим правомочным организациям в соответствии с Планом.
Форма распространения Определение | Law Insider
означает время, когда отказ от участия вступит в силу при владении или пользовании.
имеет значение, указанное в Разделе 2(а).
(a) В случае наступления Случая неисполнения обязательств (как определено в Соглашении о базовых ценных бумагах) по Базовым ценным бумагам в соответствии с пунктами (1) или (2) Раздела 5.01 Соглашения о базовых ценных бумагах, то Доверительный управляющий в случае получив уведомление о таком событии, должен на 30-й день после такого события или сразу после него дать указание Агенту рынка продать Базовые ценные бумаги и пропорциональную часть Связанных активов, находящихся в собственности Траста, в соответствии с Процедурами продажи, и Поступления от ликвидации, если таковые имеются, должны быть разделены между Классами в соответствии с Коэффициентом распределения, и часть каждого Класса должна быть депонирована на Сертификатный счет такого Класса и распределена среди Держателей Сертификатов такого Класса пропорционально в первый Рабочий день после такого депозита. в такую учетную запись сертификата.
означает форму, устанавливаемую время от времени Администратором Плана, которую Директор заполняет, подписывает и возвращает Администратору Плана для указания времени и формы распространения.
или «MDF» означает распределительную раму CenturyLink (например, раму COSMIC™), используемую для соединения кабельных пар CenturyLink и терминалов линейного и магистрального оборудования в системе коммутации CenturyLink. «Техническое обслуживание и ремонт» включает обмен информацией между перевозчиками, когда один из них инициирует запрос на техническое обслуживание или ремонт существующих продуктов и услуг или отдельных сетевых элементов или их комбинаций от другого с сопутствующими подтверждениями и отчетами о состоянии для обеспечения надлежащей работы и функциональности. объектов. «Плата за техническое обслуживание» — это разные сборы, относящиеся к работе по устранению неполадок, выполняемой компанией CenturyLink. Плата за базовое техническое обслуживание взимается, когда технический специалист CenturyLink выполняет работу в стандартное рабочее время. Плата за обслуживание в сверхурочное время применяется, когда технический специалист CenturyLink выполняет работу в рабочий день, но в нерабочее время или в субботу.
Плата за техническое обслуживание премиум-класса применяется, когда технический специалист CenturyLink выполняет работу либо в воскресенье, либо в праздничный день, признанный CenturyLink.имеет значение, указанное в Разделе 5.02(c) Трастового соглашения.
означает в отношении любого Залогового займа на каждую Дату платежа запланированную выплату основной суммы долга и/или процентов и/или сборов, причитающихся в такой Срок платежа в отношении такого Залогового займа.
означает «Форму Уведомления о существенном изменении покупки», приложенную в Приложении 2 к Форме уведомления, прилагаемой к настоящему документу в качестве Приложения A.
означает серьезные финансовые трудности для Участника в результате внезапной и неожиданной болезни или несчастного случая. Участника или его или ее иждивенца (как это определено в Разделе 152(а) Кодекса), утрата имущества Участника в результате несчастного случая или других подобных или чрезвычайных и непредвиденных обстоятельств, возникших в результате событий, не зависящих от контроля Участник.
Обстоятельства, которые могут представлять собой непредвиденную чрезвычайную ситуацию, будут зависеть от фактов каждого случая, но, в любом случае, распределение трудностей не может быть произведено в той степени, в которой такие трудности облегчаются или могут быть уменьшены (i) посредством возмещения или компенсации за счет страхования. или иным образом, (ii) путем ликвидации активов Участника в той мере, в какой ликвидация активов сама по себе не вызовет серьезных финансовых затруднений, или (iii) путем прекращения отсрочек по настоящему Плану.означает соединительную раму для внешнего оборудования и межстанционного офисного оборудования в CO. Выборы
имеет значение, указанное в параграфе 4(e) Приложения I.
означает раздел настоящей политики, который показывает, среди прочего, квалификационные требования, квалификационный период ожидания, квалификационный период, сумму Страхование, минимальное пособие и максимальный период пособия.
Доступная сумма распределения REMIC III на любую Дату распределения распределяется между Сертификатами и Остаточной долей участия Класса R-3 в следующих количествах и в следующем порядке:
(I) На любую Дату распределения до Кредита Дата исчерпания поддержки, Доступная сумма распределения REMIC II на такую Дату распределения распределяется между Регулярными долями REMIC II и Остаточной долей класса R-2 в следующих количествах и в следующем порядке:
означает аннуитет, предусматривающий равные ежемесячные платежи в течение всей жизни Участника без выплаты пособий в связи с потерей кормильца.
означает распределение Компанией всех держателей ее Обыкновенных акций денежных средств, кроме любых денежных средств, которые распределяются при слиянии или консолидации, к которым применяется Раздел 2(h), или как часть распределения, указанного в параграфе (4) Раздела 2(b).
имеет значение, указанное в Разделе 2.
2(b).означает форму соглашения, содержащуюся в Части D RFP;
имеет значение, указанное в Разделе 14.12(а).
означает «Форму уведомления о преобразовании», приложенную в Приложении 1 к Форме уведомления, приложенную к настоящему документу в качестве Приложения A.
означает водонепроницаемый компонент, который принимает сточные воды из септиктенка или другой очистной установки и распределяет сточные воды под действием силы тяжести примерно равными порциями к двум или более распределительным отводам в зоне обработки почвы.
означает выбор в четвертый вторник июня
означает выбор, описанный в Разделе 338(h)(10) Кодекса в отношении приобретения Покупателем Акций в соответствии с настоящим Соглашением. Раздел 338(h)(10) Выборы включают любые соответствующие выборы в соответствии с законодательством штата или местным законодательством, в соответствии с которыми разрешены отдельные выборы в отношении приобретения Акций Покупателем в соответствии с настоящим Соглашением.
Плата за техническое обслуживание премиум-класса применяется, когда технический специалист CenturyLink выполняет работу либо в воскресенье, либо в праздничный день, признанный CenturyLink.
Обстоятельства, которые могут представлять собой непредвиденную чрезвычайную ситуацию, будут зависеть от фактов каждого случая, но, в любом случае, распределение трудностей не может быть произведено в той степени, в которой такие трудности облегчаются или могут быть уменьшены (i) посредством возмещения или компенсации за счет страхования. или иным образом, (ii) путем ликвидации активов Участника в той мере, в какой ликвидация активов сама по себе не вызовет серьезных финансовых затруднений, или (iii) путем прекращения отсрочек по настоящему Плану.
2(b).