НОУ ИНТУИТ | Лекция | Функция распределения случайной величины. Виды распределения
< Практическая работа 4 || Лекция 5: 12345
Аннотация: Подробно рассматриваются основные характеристики случайной величины и виды распределения.
Ключевые слова: дискретная случайная величина, функция, выражение, случайная величина, значение, вероятность, полная группа, ПО, интервал, определение, площадь, дисперсия, график, ось абсцисс, ось ординат, максимум, параметр, прямой, вывод, ветвь, графика, точность, математика, метода наименьших квадратов, бифуркация, нормальная функция, пункт, нормальное распределение, погрешность, Биноминальное распределение, операции, связь, Распределение Пуассона, равенство
Функция распределения
Известно, что если события составляют полную совокупность, то . Тогда совокупность всех возможных значений случайной величины и соответствующих им вероятностей составляет распределение случайной величины.
Определение. Законом распределения или функций распределения случайной величины называется всякое соответствие между всевозможными значениями случайной величины и соответствующим им вариантом.
Определение. Случайные величины называются независимыми, если закон распределения одной не зависит от закона распределения другой.
В противном случае величины будут зависимыми.
Для дискретной случайной величины, которая может принимать значения _ функция распределения имеет вид:
| ( 1) |
Выражение (1) читается так: «функция распределения численно равна вероятности того, что случайная величина примет значение не больше, чем «.
Пусть теперь некоторая случайная величина примет значения из ряда с вероятностями , соответственно. Тогда очевидно, что вероятность того, что значение случайной величины будет меньше равно 0: , а вероятность того, что будет меньше , равна : . Вероятность, что случайная величина будет меньше будет равна , так как — это вероятность варианты , а — вероятность варианты . Случайная величина принимает одно значение из двух либо , потому . Но тогда, рассуждая аналогично, получаем:
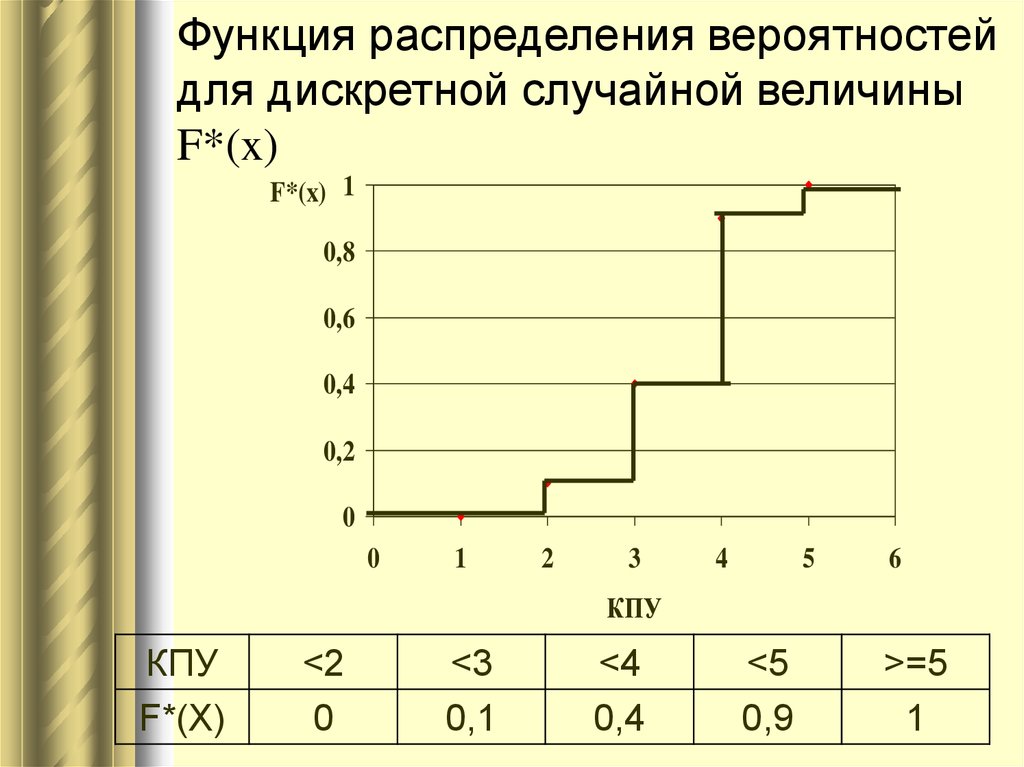
Последнее выражение равно 1, так как все пять событий образуют полную группу. Здесь любое число, которое просто больше , . Сказанное можно изобразить графически ( рис.9.1 ), если по оси ординат откладывать вероятности по оси абсцисс – сами значения случайной величины.
Рис. 9.1. Дискретная функция распределения случайной величины
intuit.ru/2010/edi»>Очевидно, чтоЕсли бы наша случайная величина была бы непрерывной, то тогда распределенное выглядела несколько бы иначе ( рис.9.2 ).
Свойства функции F(x)
Функции распределения для дискретной и непрерывной величин обладают рядом одинаковых очевидных свойств, в вытекающих из ее определения.
Свойство 1. Функция распределения есть не отрицательная функция, значение которой изменяются от 0 до 1:
| ( 2) |
| ( 3) |
Следствие. Вероятность попадания непрерывной случайной величины в не конкретный интервал равна нулю.
Свойство 3. Функция распределения случайной величиной есть не убы-вающая функция, т. е. при имеем
или
Свойство 4. Значение функции распределения на равно нулю, и единице ? на , т.е.
Пример 1. Построить функцию распределения вариационного ряда
| Xi | 1 | 2 | 3 | 4 | 5 | 6 |
| Mi | 3 | 2 | 6 | 7 | 5 | 2 |
Теперь построим функцию распределения математически (4)
| ( 4) |
и графически (рис.9.3 ).
Рис. 9.3. Функция распределения
Дальше >>
< Практическая работа 4 || Лекция 5: 12345
Введение в теорию случайных сигналов и шумов
Введение в теорию случайных сигналов и шумов
ОглавлениеПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДАПРЕДИСЛОВИЕ Глава 1.  ВВЕДЕНИЕ ВВЕДЕНИЕ1.1. Системы связи и статистика 1.2. Эта книга Глава 2. ВЕРОЯТНОСТЬ 2.2. Основы 2.3. Совместные вероятности 2.4. Условные вероятности 2.5. Статистическая независимость 2.6. Примеры 2.7. Задачи Глава 3. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ И РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ 3.2. Функции распределения случайных величин 3.3. Дискретные случайные величины 3.4. Непрерывные случайные величины 3.5. Независимые случайные величины 3.6. Функции от случайных величин 3.7. Вероятностные процессы 3.8. Задачи Глава 4. СРЕДНИЕ ЗНАЧЕНИЯ 4.1. Математические ожидания 4.2. Моменты 4.3. Характеристические функции 4.4. Корреляция 4.5. Корреляционные функции 4.6. Сходимость 4.7. Интегралы от вероятностных процессов 4.8. Временные средние 4.9. Задачи Глава 5. ВЫБОР 5.2. Выборочное среднее 5.3. Сходимость выборочных средних 5.5. Относительная частота 5.6. Задачи Глава 6.  СПЕКТРАЛЬНЫЙ АНАЛИЗ СПЕКТРАЛЬНЫЙ АНАЛИЗ6.2. Спектральная плотность периодической функции 6.3. Спектральная плотность периодического вероятностного процесса 6.4. Разложение вероятностных процессов в ортогональные ряды 6.5. Спектральная плотность произвольной функции 6.6. Спектральный анализ стационарных в широком смысле вероятностных процессов 6.7. Взаимные спектральные плотности 6.8. Задачи Глава 7. ДРОБОВОЙ ШУМ 7.2. Распределение вероятностей для моментов вылета электронов 7.3. Средний ток в диоде, работающем в режиме насыщения 7.4. Спектральная плотность дробового шума диода, работающего в режиме насыщения 7.5. Плотность распределения вероятностей для дробового шума диода в режиме насыщения 7.6. Ток диода, работающего не в режиме насыщения 7.7 . Дробовой шум диода, работающего не в режиме насыщения 7.8 Дробовой шум триодов и пентодов, работающих не в режиме насыщения 7.9. Задачи Глава 8. ГАУССОВСКИЙ ПРОЦЕСС 8.2. Двумерное распределение 8.  3. Многомерное распределение 3. Многомерное распределение8.4. Гауссовский вероятностный процесс 8.5. Узкополосный гауссовский вероятностный процесс 8.6. Сумма синусоидального сигнала и узкополосного гауссовского вероятностного процесса 8.7. Задачи Глава 9. ЛИНЕЙНЫЕ СИСТЕМЫ 9.2. Случайные воздействия 9.3. Корреляционная функция и спектр отклика 9.4. Тепловой шум 9.5. Распределения вероятностей отклика 9.6. Задачи Глава 10. ШУМФАКТОР 10.2. Шумфактор 10.3. Многокаскадный усилитель 10.4. Пример 10.5. Задачи Глава 11. ОПТИМАЛЬНЫЕ ЛИНЕЙНЫЕ СИСТЕМЫ 11.2. Сглаживание и прогнозирование стационарных воздействий с использованием бесконечной предыстории (теория Винера) 11.4. Решение уравнения прогнозирования и фильтрации 11.5. Другие задачи фильтрации, использующие критерий среднеквадратичной ошибки 11.6. Сглаживание и прогнозирование при конечном времени наблюдения 11.7. Максимизация отношения сигнал/шум; согласованный фильтр 11.  8. Задачи 8. ЗадачиГлава 12. НЕЛИНЕЙНЫЕ СИСТЕМЫ; ПРЯМОЙ МЕТОД 12.2. Квадратичный детектор 12.3. Квадратичный детектор; сигнал плюс шум на входе 12.4. Однополупериодный линейный детектор 12.5. Задачи Глава 13. НЕЛИНЕЙНЫЕ СИСТЕМЫ; МЕТОД ПРЕОБРАЗОВАНИЙ 13.2. Устройства v-й степени 13.3. Корреляционная функция и спектральная плотность отклика 13.4. Спектральная плотность отклика 13.5. Узкополосное воздействие 13.6. Детекторы v-й степени 13.7. Задачи Глава 14. СТАТИСТИЧЕСКОЕ ОБНАРУЖЕНИЕ СИГНАЛОВ 14.1. Применение статистических понятий в вопросах радиосвязи и радиолокации 14.2. Проверка статистических гипотез 14.3. Критерии отношения правдоподобия 14.4. Статистические оценки 14.5. Передача информации фиксированными сигналами на фоне гауссовского шума 14.6. Сигналы с неизвестными параметрами в белом шуме 14.7. Радиолокационные сигналы на фоне гауссовского шума 14.8. Задачи ПРИЛОЖЕНИЕ 1. ИМПУЛЬСНЫЕ ФУНКЦИИ ПРИЛОЖЕНИЕ 2.  ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯЛИТЕРАТУРА |
Функции случайных величин и их распределение
Марко Табога, доктор философии
Позволять быть случайной величиной с известным распределением. Позволять другая случайная величина быть функцией :где . Как мы получаем распределение от распределения ?
На этот вопрос нет общего ответа. Однако есть несколько частные случаи, в которых легко получить распределение . Мы обсудим эти случаи ниже.
СОДЕРЖАНИЕ
Строго увеличивающиеся функции
Строго увеличение функций дискретной случайной переменной
Строго увеличивающихся функций
Строго увеличивающихся функций 9 0003
Строго увеличивающихся функций 9 0003
.
Строго убывающие функции дискретной случайной величины
Строго убывающие функции непрерывной случайной величины
Invertible functions
One-to-one functions of a discrete random variable
One-to-one functions of a continuous random variable
Solved exercises
Упражнение 1
Упражнение 2
Упражнение 3
Строго возрастающие функции
Когда функция
строго возрастает на
поддержка
(т. е.
),
затем
допускает обратный, определенный на носителе
,
то есть функция
такой
чтоКроме того
сама строго возрастает.
е.
),
затем
допускает обратный, определенный на носителе
,
то есть функция
такой
чтоКроме того
сама строго возрастает.
Функция распределения строго возрастающей функции случайного переменная может быть вычислена следующим образом.
Предложение (распределение возрастающей функция) Позволять быть случайной величиной с носителем и функция распределения . Позволять строго возрастать на опоре . Тогда поддержка со стороны остров функция распределения
Доказательство
Конечно, поддержка определяется и по всем значениям могу взять. Функция распределения можно вывести следующим образом:
если ниже минимального значения можно взять, то , так
если относится к поддержке , затем можно вывести следующим образом:
если выше, чем самое высокое значение можно взять, то , так
Поэтому в случае возрастающей функции знание
и верхних и нижних границ носителя
это все, что нам нужно, чтобы вывести функцию распределения
из функции распределения
.
Пример Позволять быть случайной величиной с носителем и распространение функцияLetThe функция строго возрастает и допускает обратную на носителе : поддержка является . Функция распределения
В тех случаях, когда является дискретным или непрерывным, существуют специальные формулы для функции массы вероятности и плотности вероятности, о которых сообщается ниже.
Строго возрастающие функции дискретной случайной величины
Когда является дискретным случайным переменная, вероятностная масса функция можно вычислить следующим образом.
Предложение (вероятностная масса возрастающего функция) Позволять — дискретная случайная величина с носителем и функция массы вероятности . Позволять строго возрастать на опоре . Тогда поддержка со стороны остров его функция массы вероятности
Доказательство
Это предложение является тривиальным следствием тот факт, что строго возрастающая функция обратимый:
Пример Позволять — дискретная случайная величина с носителем и функция массы вероятности Позволять поддержка это функция строго возрастает и обратно это функция массы вероятности is
Строго возрастающие функции непрерывного случайная величина
Когда
является непрерывным
случайная величина и
дифференцируема, то и
является непрерывным и его
плотность вероятности
функция легко вычисляется следующим образом.
Предложение (плотность возрастающего функция) Позволять быть непрерывной случайной величиной с носителем и функция плотности вероятности . Позволять быть строго возрастающей и дифференцируемой на носителе . Тогда поддержка со стороны остров его функция плотности вероятности
Доказательство
Это предложение является тривиальным следствием тот факт, что функция плотности является первой производная функции распределения: она может быть получена дифференцируя выражение для функции распределения нашел выше.
Пример Позволять быть непрерывной случайной величиной с поддержка и плотность вероятности функцияLet поддержка это функция строго возрастает и обратно это с производнаяThe функция плотности вероятности
Строго убывающие функции
Когда функция
строго убывает на поддержке
(т. е.
),
затем
допускает обратный, определенный на носителе
,
то есть функция
такой
чтоКроме того
сама строго убывает.
е.
),
затем
допускает обратный, определенный на носителе
,
то есть функция
такой
чтоКроме того
сама строго убывает.
Функция распределения строго убывающей функции случайного переменная может быть вычислена следующим образом.
Предложение (распределение убывающей функция) Позволять быть случайной величиной с носителем и функция распределения . Позволять строго убывать на носителе . Тогда поддержка со стороны остров функция распределения
Доказательство
Конечно, поддержка определяется и по всем значениям могу взять. Функция распределения можно вывести следующим образом:
если ниже минимального значения можно взять, то , так
если относится к поддержке , затем можно вывести следующим образом:
если выше, чем самое высокое значение можно взять, то , так
Поэтому и в случае убывающей функции знание
и верхних и нижних границ носителя
это все, что нам нужно, чтобы вывести функцию распределения
из функции распределения
.
Пример Позволять быть случайной величиной с носителем и распространение функцияLetThe функция строго убывает и допускает обратную на носителе : поддержка является . Функция распределения это здесь равно когда и иначе (потому что всегда равен нулю, за исключением случаев, когда и ).
Ниже мы приводим формулы для частных случаев, когда либо дискретно, либо непрерывно.
Строго убывающие функции дискретной случайной величины
Когда — дискретная случайная величина, функция массы вероятности можно вычислить следующим образом.
Предложение (вероятностная масса убывающей
функция)
Позволять
— дискретная случайная величина с носителем
и функция массы вероятности
.
Позволять
строго убывать на носителе
. Тогда поддержка со стороны
остров
его функция массы вероятности
Тогда поддержка со стороны
остров
его функция массы вероятности
Доказательство
Доказательство этого предложения идентично к доказательству предложения для строго возрастающих функций. Фактически, единственное свойство, которое имеет значение, это то, что строго убывающая функция обратимый:
Пример Позволять — дискретная случайная величина с носителем и функция массы вероятности Позволять поддержка это функция строго убывает и обратно ему это функция массы вероятности
Строго убывающие функции непрерывного случайная величина
Когда является непрерывной случайной величиной и дифференцируема, то и является непрерывным, и его функция плотности вероятности выводится следующим образом.
Предложение (плотность убывающей
функция)
Позволять
быть непрерывной случайной величиной с носителем
и функция плотности вероятности
. Позволять
быть строго убывающей и дифференцируемой на носителе
.
Тогда поддержка со стороны
остров
его функция плотности вероятности
Позволять
быть строго убывающей и дифференцируемой на носителе
.
Тогда поддержка со стороны
остров
его функция плотности вероятности
Доказательство
Это предложение легко выводится: 1) памятуя о том, что вероятность того, что непрерывная случайная величина принимает любое конкретное значение и, как следствие, для любого ; 2) используя тот факт, что функция плотности является первой производной функция распределения; 3) дифференцируя выражение для распределения функция нашел выше.
Пример
Позволять
быть равномерной случайной величиной на интервале
,
т. е. непрерывная случайная величина с
поддержка и
плотность вероятности
функцияLet
где
является константой. Поддержка
это здесь
мы можем смело игнорировать тот факт, что
,
потому что
событие с нулевой вероятностью (см. Непрерывные случайные величины и
события с нулевой вероятностью). Функция
строго убывает и обратно ему
это с
производнаяThe
функция плотности вероятности
следовательно является,
имеет экспоненциальное распределение с параметром
(см. лекцию «Экспоненциальная
распределение).
Непрерывные случайные величины и
события с нулевой вероятностью). Функция
строго убывает и обратно ему
это с
производнаяThe
функция плотности вероятности
следовательно является,
имеет экспоненциальное распределение с параметром
(см. лекцию «Экспоненциальная
распределение).
Обратимые функции
В случае, когда функция не является ни строго возрастающей, ни строго убывающей, формулы, приведенные в предыдущие разделы для дискретных и непрерывных случайных величин по-прежнему применимо, при условии является взаимно однозначным и, следовательно, обратимым. Мы приводим эти формулы ниже.
Однозначные функции дискретной случайной величины
Когда — дискретная случайная величина, функция массы вероятности дается следующим.
Предложение (вероятностная масса однозначного
функция)
Позволять
— дискретная случайная величина с носителем
и функция массы вероятности
. Позволять
быть один на один при поддержке
.
Тогда поддержка со стороны
остров
его функция массы вероятности
is
Позволять
быть один на один при поддержке
.
Тогда поддержка со стороны
остров
его функция массы вероятности
is
Доказательство
Доказательство этого предложения идентично к доказательству утверждений о строгом возрастании и строгом найдены убывающие функции выше:
Однозначные функции непрерывной случайной величины
Когда является непрерывной случайной величиной и дифференцируема, то и является непрерывным, и его функция плотности вероятности задается следующим предложение.
Предложение (плотность однозначного функция) Позволять быть непрерывной случайной величиной с носителем и функция плотности вероятности . Позволять быть взаимно однозначной и дифференцируемой на носителе . Тогда поддержка со стороны Еслито функция плотности вероятности
Доказательство
Доказательство этого предложения см. :
Пуарье, Д. Дж. (1995) Промежуточная статистика и
эконометрика: сравнительный подход, Массачусетский технологический институт
Нажимать.
:
Пуарье, Д. Дж. (1995) Промежуточная статистика и
эконометрика: сравнительный подход, Массачусетский технологический институт
Нажимать.
Решенные упражнения
Ниже вы можете найти несколько упражнений с поясненными решениями.
Упражнение 1
Позволять быть непрерывной случайной величиной с поддержка и плотность вероятности функцияLet Находить функция плотности вероятности .
Решение
Поддержка это функция строго возрастает и обратно это с производнаяThe функция плотности вероятности
Упражнение 2
Позволять быть непрерывной случайной величиной с поддержка и плотность вероятности функцияLet Находить функция плотности вероятности .
Решение
Поддержка это функция строго убывает и обратно ему это с производнаяThe функция плотности вероятности
Упражнение 3
Позволять
быть дискретной случайной величиной с
поддержка и
вероятностная масса
функцияLet
Находить
функция массы вероятности
.
Решение
Поддержка это функция строго возрастает и обратно это функция массы вероятности
Как указывать
Пожалуйста, указывайте как:
Taboga, Marco (2021). «Функции случайных величин и их распределение», Лекции по теории вероятностей и математической статистике. Прямая публикация Kindle. Онлайн приложение. https://www.statlect.com/fundamentals-of-probability/functions-of-random-variables-and-their-distribution.
1.4 – Кумулятивная функция распределения
Предыдущая: 1.3 – Дискретная функция плотности вероятности
Следующая: 1.5 – Некоторые общие дискретные распределения
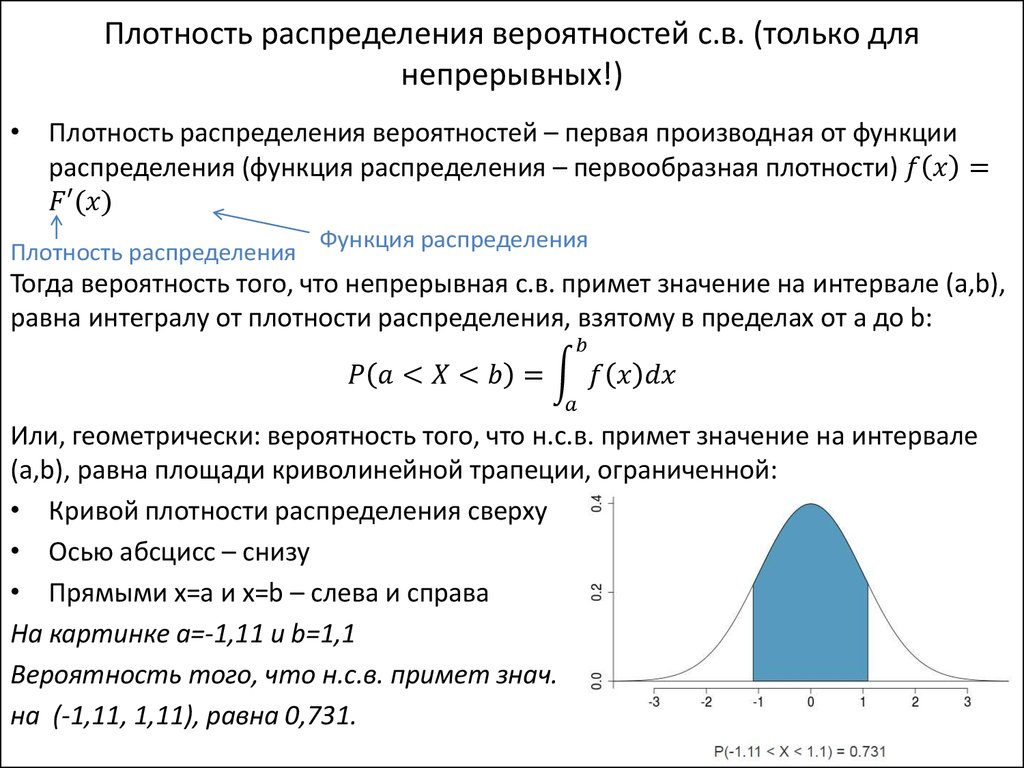
Учитывая функцию плотности вероятности, мы определяем кумулятивную функцию распределения (CDF) следующим образом .
| Кумулятивная функция распределения дискретной случайной величины |
|---|
Кумулятивная функция распределения (CDF) случайной величины X обозначается как F ( x ) и определяется как F ( x ) = Pr( X ≤ x ).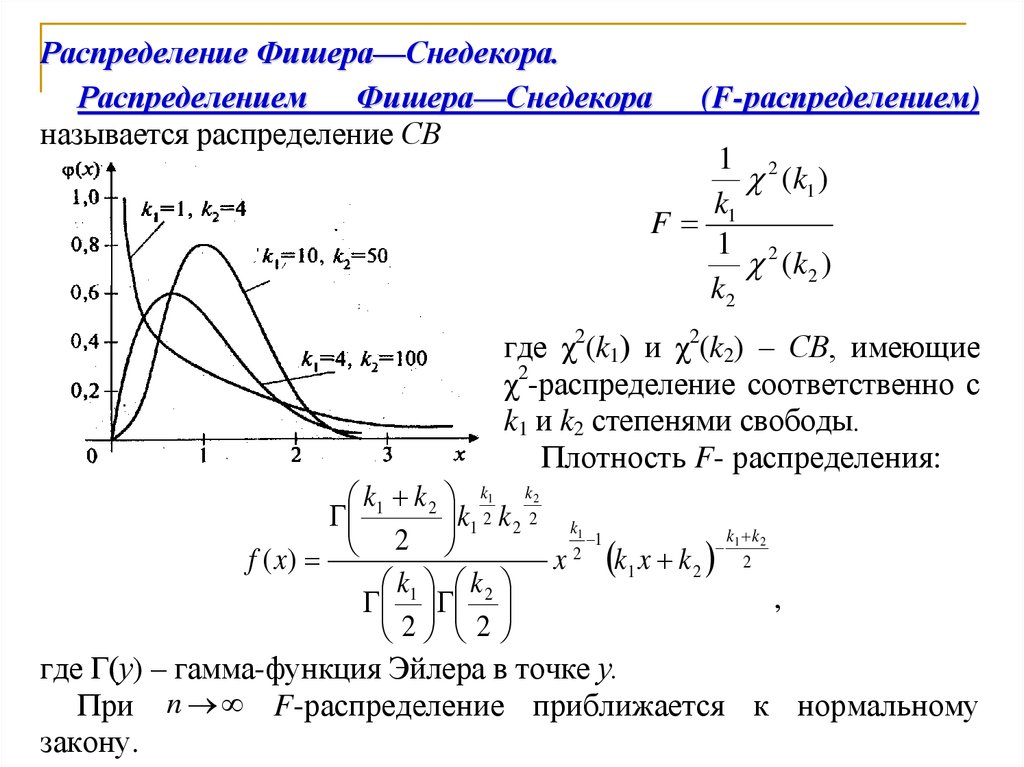 Используя наше тождество для вероятности непересекающихся событий, если X является дискретной случайной величиной, мы можем написать где x n — максимальное возможное значение X , меньшее или равное x . |
Другими словами, кумулятивная функция распределения для случайной величины в x дает вероятность того, что случайная величина X меньше или равна этому числу x . Обратите внимание, что в формуле для CDF дискретных случайных величин мы всегда имеем , где N число возможных исходов X .
Заметим также, что CDF дискретной случайной величины останется постоянной на любом интервале вида . То есть, .
Следующие свойства являются прямым следствием нашего определения случайной величины и вероятности, связанной с событием.
| Свойства CDF |
|---|
Recall that a function f ( x ) is said to be nondecreasing if f ( x 1 ) ≤ f ( x 2 ) whenever х 1 < х 2 .
Пример: Бросание одной игральной кости
Если X — это случайная величина, которую мы связали ранее с броском правильного шестигранного кубика, то мы можем легко записать CDF X .
Мы уже вычислили, что плотность вероятности X определяется как Pr( X = k ) = 1/6 для k = 1,2,…,6. CDF можно вычислить путем последовательного суммирования этих вероятностей; резюмируем следующим образом:
- Pr( X ≤ 1) = 1/6
- Пр( Х ≤ 2) = 2/6
- Pr( X ≤ 3) = 3/6
- Pr( X ≤ 4) = 4/6
- Pr( X ≤ 5) = 5/6
- Pr( X ≤ 6) = 6/6 = 1
Обратите внимание, что Pr( X ≤ x ) = 0 для любых x < 1, поскольку X не может принимать значения меньше 1. Также обратите внимание, что Pr( X ≤ x
2 ) = для любого x > 6. Наконец, заметим, что вероятности Pr( X ≤ x ) постоянны на любом интервале формы [ k , k + 1) по мере необходимости.
Пример: бросание двух игральных костей
Предположим, что у нас есть две правильные шестигранные кости, одна желтая и одна красная, как на изображении ниже.
Мы бросаем оба кубика одновременно и складываем два числа, указанные на верхних гранях.
Пусть X будет дискретной случайной величиной, связанной с этой суммой.
- Сколько возможных исходов? То есть, сколько различных значений может быть X предположим?
- Как распространяется X ? То есть, что такое PDF X ?
- Какова вероятность того, что X меньше или равно 6?
- Что такое CDF X ?
Решение
Часть 1)
Каждый кубик может принимать 6 возможных значений. Два кубика бросают независимо (т. е. значение одного из кубиков не влияет на значение другого кубика), поэтому мы видим, что = существует 6 ✕ 6 = 36 различных исходов при одном броске двух кубиков. Обратите внимание, что все 36 исходов различимы, поскольку два кубика разного цвета. Таким образом, мы можем различать бросок, который дает 4 на желтом кубике и 5 на красном кубике, и бросок, который дает 5 на желтом кубике и 4 на красном кубике.
Таким образом, мы можем различать бросок, который дает 4 на желтом кубике и 5 на красном кубике, и бросок, который дает 5 на желтом кубике и 4 на красном кубике.
Однако нас интересует количество возможных исходов для суммы значений на двух игральных костях, т. е. количество различных значений для случайной величины X . Наименьшая сумма может быть равна 1 + 1 = 2, а наибольшая — 6 + 6 = 12. Ясно, что X также может принимать любое значение между этими двумя крайними значениями; таким образом, мы заключаем, что возможные значения для X равны 2,3,…,12.
Часть 2)
Построить распределение вероятностей для X , сначала рассмотрим вероятность того, что сумма игральных костей равна 2. Это может произойти только одним способом: обе кости должны выбросить 1. Существует 36 различимых бросков игральных костей, поэтому вероятность того, что сумма равна равно 2 это 1/36.
Аналогичным образом можно вычислить другие возможные значения случайной величины X и соответствующие им вероятности. Некоторые из них перечислены в таблице ниже.
Некоторые из них перечислены в таблице ниже.
| Исход (желтый, красный) | Сумма = Желтый + Красный | Вероятность |
|---|---|---|
| (1,1) | 2 | 1/36 |
| (1,2), (2,1) | 3 | 2/36 |
| (1,3), (2,2), (3,1) | 4 | 3/36 |
| (1,4), (2,3), (3,2), (4,1) | 5 | 4/36 |
| (1,5), (2,4), (3,4), (4,2), (5,1) | 6 | 5/36 |
| . . . | . . . | . . . |
| (6,6) | 12 | 1/36 |
Функция плотности вероятности X показана на следующем графике.
В качестве альтернативы, если мы допустим p k = Pr( X = k ), вероятность того, что случайная сумма X равна k , тогда PDF может быть задана одним формула:
Часть 3)
Вероятность того, что сумма меньше или равна 6, может быть записана как Pr( X ≤ 6), что равно F (6), значение кумулятивного функция распределения при x = 6. Используя наше тождество для вероятностей непересекающихся событий, мы вычисляем
Используя наше тождество для вероятностей непересекающихся событий, мы вычисляем
Часть 4)
Чтобы найти CDF X вообще, нам нужно дать таблицу, график или формулу для Pr( X ≤ 6) для любого данного к . Используя нашу таблицу для PDF X , мы можем легко построить соответствующую таблицу CDF:
| Х = к | F ( k ) = Pr( X ≤ k ) |
|---|---|
| 2 | 1/36 |
| 3 | 3/36 |
| 4 | 6/36 |
| 5 | 36/10 |
| 6 | 15/36 |
| . . . | . . . |
| 12 | 36/36 = 1 |
Эта таблица определяет ступенчатую функцию, начинающуюся с 0 для x < 2 и постепенно увеличивающуюся до 1 для x ≥ 12.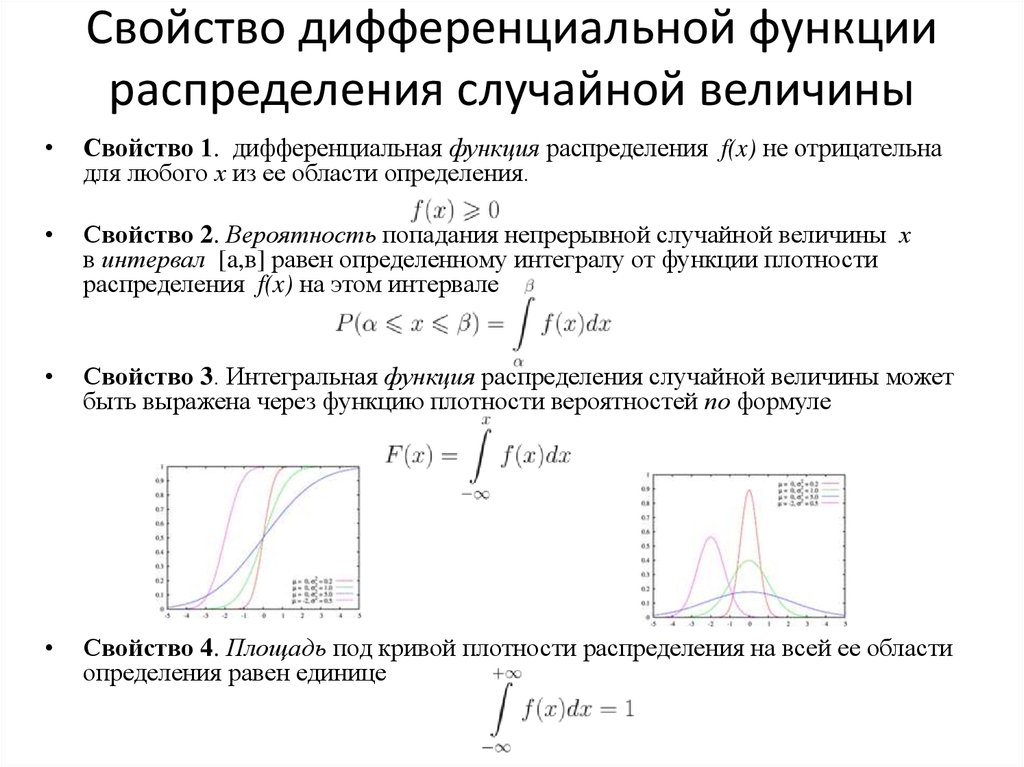

 Б., Рут В.Л. Введение в теорию случайных сигналов и шумов. М.: ИЛ, 1960. — 467 с.
Б., Рут В.Л. Введение в теорию случайных сигналов и шумов. М.: ИЛ, 1960. — 467 с.