Функция тангенса: Функция y = tgx и её свойства — урок. Алгебра, 11 класс.

Свойства функции синуса, косинуса, тангенса, котангенса, арксинуса, арккосинуса. Графики. Тест

Математика->Тригонометрия->тригонометрические функции->

Тестирование онлайн

• Функция синуса, косинуса

• Функция тангенса, котангенса

Функция синуса

На рисунке показано построение графика синуса на отрезе .

Рассмотрим основные свойства функции y=sinx:

1) Область определения функции — множество всех действительных чисел

2) Множеством значений функции является промежуток

3) Функция является нечетной, график симметричен относительно начала координат (0;0).

4) Функция периодическая. Наименьший положительный период равен

5) График функции пересекает ось Ох (нули функции) в точках

6) График функции пересекает ось Оy в точке (0; 0).

7) Функция принимает положительные значения на промежутках

8) Функция принимает отрицательные значения на промежутках

9) Функция возрастает на промежутках

10) Функция убывает на промежутках

11) Точки минимума:

12) Точки максимума:

13) Графиком функции является синусоида

Функция косинуса

График косинуса получается из графика синуса с помощью параллельного переноса на расстояние влево.

Основные свойства функции y=cosx:

1) Область определения функции — множество всех действительных чисел

2) Множеством значений функции является промежуток

3) Функция является четной, график симметричен относительно оси Оу.

4) Функция периодическая. Наименьший положительный период равен

5) График функции пересекает ось Ох (нули функции) в точках

6) График функции пересекает ось Оy в точке (0; 1).

7) Функция принимает положительные значения на промежутках

8) Функция принимает отрицательные значения на промежутках

9) Функция возрастает на промежутках

10) Функция убывает на промежутках

11) Точки минимума:

12) Точки максимума:

13) Графиком функции является косинусоида

Функция тангенса

Основные свойства функции y=tgx:

1) Область определения функции:

2) Множеством значений функции:

3) Функция является нечетной, график симметричен относительно начала координат (0;0).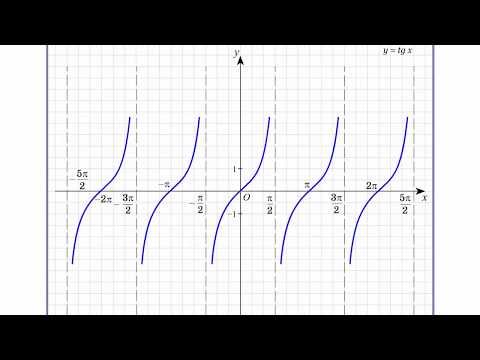

4) Функция периодическая. Наименьший положительный период равен

5) График функции пересекает ось Ох (нули функции) в точках

6) График функции пересекает ось Оy в точке (0; 0).

7) Функция принимает положительные значения на промежутках

8) Функция принимает отрицательные значения на промежутках

9) Функция возрастает на промежутках

10) Промежутки убывания отсутствуют.

11) Точек минимума нет.

12) Точек максимума нет.

13) Графиком функции является тангенсоида:

Функция котангенса

Основные свойства функции y=сtgx:

1) Область определения функции:

2) Множеством значений функции:

3) Функция является нечетной, график симметричен относительно начала координат (0;0).

4) Функция периодическая. Наименьший положительный период равен

5) График функции пересекает ось Ох (нули функции) в точках

6) Функции не пересекает ось Оy.

7) Функция принимает положительные значения на промежутках

8) Функция принимает отрицательные значения на промежутках

9) Функция не имеет промежутков возрастания.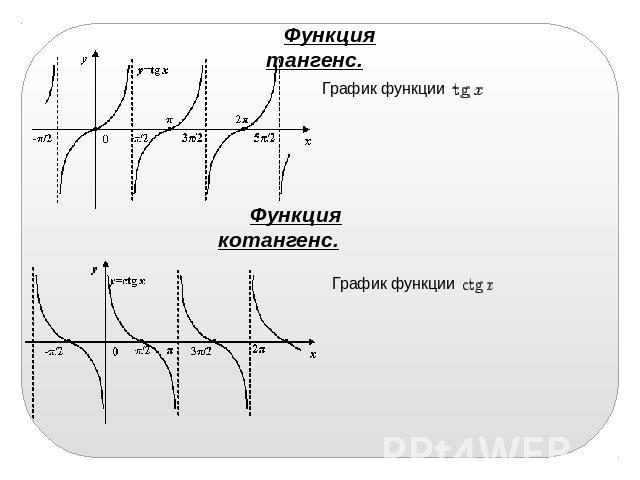

10) Промежутки убывания:

11) Точек минимума нет.

12) Точек максимума нет.

13) Графиком функции является котангенсоида:

Период функции

1) Если T — основной период функции y=f(x), то число является основным периодом функции y=f(ax), где a — любое положительное число.

2) Если периодические функции y=f(x) и y=g(x) имеют один и тот же период T, то их сумма, разность и произведение тоже будет иметь период T.

3) Если периодические функции y=f(x) и y=g(x) имеют соизмеримые периоды T₁ и T₂, то они имеют общий период.

4) Период сложной функции y=g(f(x)) совпадает с периодом функции y=f(x).

что это, формула, свойства, график, примеры

Содержание:

• Что такое тангенс
• Что такое функция тангенса: формула
• Свойства функции
• Как построить график
• Примеры решения задач

Содержание

• Что такое тангенс
• Что такое функция тангенса: формула
• Свойства функции
• Как построить график
• Примеры решения задач

Что такое тангенс

Тангенсом какого-либо острого угла \(\alpha (tg \alpha)\) называют величину, выражающую отношение противоположного катета (а) к прилегающему катету (b) в треугольнике с углом 90°, то есть: \(tg \alpha = \frac{a}{b}\) 

Понятие тангенса угла можно проиллюстрировать таким образом:

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Источник: microexcel.ru

Пример 1

Рассмотрим наглядный пример. Предположим, что катеты в треугольнике из определения тангенса имеют следующие значения: a = 3 b = 4 В таком случае справедливо записать выражение для расчета тангенса угла: \(tg \alpha = \frac{a}{b} = \frac{3}{4} = 0,75\) 

Что такое функция тангенса: формула

При решении задач можно нередко встретить примеры с тригонометрическими функциями, в том числе, функцией тангенса. Эта функция обладает специфическими свойствами, которые значительно упрощают вычисления. Запись имеет следующий вид:

\(у = tg х\)

Здесь х обозначает аргумент тригонометрической функции и играет роль независимой переменной, а у определяет непосредственно функцию, то есть зависимую переменную.

Свойства функции

С помощью знаний свойств функций в тригонометрии достаточно просто решать самые сложные и громоздкие примеры.

Перечислим закономерности, характерные для функции тангенса:

1. Функция тангенса определяется в области \((x\ne\frac\pi2+\pi k)\), то есть на множестве, в состав которого включены действительные числа, за исключением точек, характеризующихся нулевым значением для косинуса.
2. Функция на графике не имеет ограничений в верхней и нижней части, поэтому ее область значений можно записать как \(y\in\mathbb{R}\).
3. Функция тангенса является нечетной, что целесообразно записать в виде соотношения \(tg(-x)=-tgx\).
4. Тригонометрическая функция тангенса является периодической, а ее период составляет pi. Таким образом:\(tg(x+\pi k)=tgx\) .
5. Стремление функции \(к +\infty\) можно наблюдать при сближении с левой стороны с точками \(x=\frac\pi2+\pi k\). Приближение к точке, обозначенной за a, слева формулируют таким образом: \(x\rightarrow\) \(a-0 \lim_{x\rightarrow\frac\pi2+\pi k-0} tgx=+\infty\) .
6. Стремление функции \(к -\infty\) можно наблюдать при сближении с правой стороны с точками \(x=\frac\pi2+\pi k\). Приближение к точке, обозначенной за а, справа следует зафиксировать как \(x\rightarrow\) \(a+0 \lim_{x\rightarrow\frac\pi2+\pi k+0} tgx=-\infty\).
7. Нули рассматриваемой функции \(y_{0}=0\) определены точками \(x_0=\pi k\).
8. Возрастание функции можно наблюдать на всей области, где она определена.
9. Функция разрывается в точках \(x=\frac\pi2+\pi k\), которые пересечены вертикальными асимптотами. На отрезках между ними функция не прерывается, то есть \(\left(-\frac\pi2+\pi k;\ \frac\pi2+\pi k\right).\)
10. Функция не обладает максимальными и минимальными значениями.

Как построить график

Как и любую другую тригонометрическую функцию, тангенс достаточно просто изобразить в системе координат. Графическое изображение функции тангенса в обобщенном виде представлено на рисунке ниже:

Источник: microexcel.ru

Построить график функции тангенса несложно. Нужно лишь последовательно выполнять действия согласно стандартному алгоритму:

• определить контрольные точки для построения;
• начертить плавную кривую линию на плоскости координат;
• для выбранного промежутка построить значения, которые расположены симметрично по отношению к началу координат;
• так как для значений функции характерны повторы с некоторым периодом, то целесообразно скопировать график для каждого из промежутков области определения;
• в результате получен график под названием тангенсоида.

Примеры решения задач

Задача 1

Требуется путем применения свойств тригонометрической функции, изученных в теоретическом разделе, записать область определения для следующей функции: \(y=\text{tg}\left( 2x+\frac{\pi }{3} \right)\) 

Решение

Зная, что функция тангенса не может быть определена в точках при нулевом значении косинуса, запишем справедливое соотношение и выполним необходимые преобразования:

\(\cos \left( 2x+\frac{\pi }{3} \right)=0\)

\(2x+\frac{\pi }{3}\ne \frac{\pi }{2}+\pi n,n\in Z\)

\(x\ne \frac{\pi }{12}+\frac{\pi n}{2},n\in Z\)

В результате получена область, в которой определена функция из условия задания:

\(D(y)=\left( -\frac{\pi }{12}+\frac{\pi n}{2},\frac{\pi }{12}+\frac{\pi n}{2} \right),n\in Z\)

Ответ: \(D(y):x\in \left( -\frac{\pi }{12}+\frac{\pi n}{2},\frac{\pi }{12}+\frac{\pi n}{2} \right),n\in Z\) 

Задача 2

Дано уравнение, решение которого требуется найти: \(\sin 2x-\sqrt{3}\cos 2x=0\) 

Решение

Выполним преобразования исходного соотношения. В результате получим:

\(\sin 2x=\sqrt{3}\cos 2x\)

После деления всех частей записи на выражение \(\cos 2x\) соотношение изменится таким образом:

\(\text{tg}2x=\sqrt{3}\)

При этом ОДЗ для полученного выражения примет следующий вид:

\(\left( -\frac{\pi }{4}+\frac{\pi n}{2},\frac{\pi }{4}+\frac{\pi n}{2} \right),n\in Z.\)

Далее целесообразно приступить к решению уравнения:

\(2=\frac{\pi }{3}+\pi n,n\in Z\)

\(x=\frac{\pi }{6}+\frac{\pi n}{2},n\in Z\)

Заметим, что корни, которые получились по итогам расчетов, соответствуют ОДЗ. Можно записать ответ.

Ответ: \(x=\frac{\pi }{6}+\frac{\pi n}{2},n\in Z\)

Насколько полезной была для вас статья?

У этой статьи пока нет оценок.

Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»

Поиск по содержимому

Тангенциальная функция

Горячая математика

Касательная функция представляет собой периодический функция, которая очень важна в тригонометрии.

Самый простой способ понять функцию касательной — использовать единичную окружность. Для заданной угловой меры θ нарисуйте единичный круг на координатной плоскости и нарисуйте угол с центром в начале координат, с одной стороной как положительной Икс -ось. Икс -координата точки пересечения другой стороны угла с окружностью потому что ( θ ) и у -координата грех ( θ ) .

Есть несколько значений синуса и косинуса, которые следует запомнить, основываясь на 30 ° − 60 ° − 90 ° треугольники и 45 ° − 45 ° − 90 ° треугольники. Основываясь на них, вы можете определить соответствующие значения тангенса.

грех ( θ )	потому что ( θ )	загар ( θ )
грех ( 0 ° ) «=» 0	потому что ( 0 ° ) «=» 1	загар ( 0 ° ) «=» 0 1 «=» 0
грех ( 30 ° ) «=» 1 2	потому что ( 30 ° ) «=» 3 2	загар ( 30 ° ) «=» 1 2 ⋅ 2 3 «=» 3 3
грех ( 45 ° ) «=» 2 2	потому что ( 45 ° ) «=» 2 2	загар ( 45 ° ) «=» 2 2 ⋅ 2 2 «=» 1
грех ( 60 ° ) «=» 3 2	потому что ( 60 ° ) «=» 1 2	загар ( 60 ° ) «=» 3 2 ⋅ 2 1 «=» 3
грех ( 90 ° ) «=» 1	потому что ( 90 ° ) «=» 0	загар ( 90 ° ) «=» 1 0 «=» недеф .

Обратите внимание, что:

• для углов с конечным плечом в квадранте II, поскольку синус положительный, а косинус отрицательный, тангенс отрицательный.
• для углов с конечным плечом в квадранте III, поскольку синус отрицательный, а косинус отрицательный, тангенс положительный.
• для углов с конечным плечом в квадранте IV, поскольку синус отрицательный, а косинус положительный, тангенс отрицательный.

Вы можете нанести эти точки на координатную плоскость, чтобы показать часть функции, часть между 0 и 2 π .

Для значений θ меньше, чем 0 или больше, чем 2 π можно найти значение θ используя опорный угол .

График функции на более широком интервале показан ниже.

Обратите внимание, что областью определения функции является вся действительная линия, а диапазон − ∞ ≤ у ≤ ∞ .

APC Тангенциальная функция

Мотивирующие вопросы

• Как определяется функция тангенса с помощью функций синуса и косинуса?

• Почему график функции тангенса так отличается от графиков функций синуса и косинуса?

• Каковы важные применения функции тангенса?

В упражнении 4.1.4 мы определили расстояние между двумя точками \(A\) и \(B\) на противоположных сторонах реки, зная длину вдоль одного берега реки и угол, образованный между точкой ниже по течению и точку на противоположном берегу, как показано на рисунке 4.2.1. Сначала используя косинус угла, мы определили значение \(z\) и оттуда смогли использовать синус угла, чтобы найти \(w\text{,}\) ширину реки, которая оказывается быть

\begin{уравнение*} w = 50 \cdot \frac{\sin(56.4)}{\cos(56.4)}\text{.} \end{equation*}

Рисунок 4.2.1. Нахождение ширины реки.

Оказывается, нам регулярно нужно вычислять отношение функций синуса и косинуса под одним и тем же углом, поэтому удобно определить новую функцию как их отношение.

Определение 4.2.2. Касательная функция.

Для любого действительного числа \(t\), для которого \(\cos(t) \ne 0\text{,}\) мы определяем тангенс \(t\) , обозначенный \(\tan(t)\text{,}\)

\begin{уравнение*} \ tan (t) = \ frac {\ sin (t)} {\ cos (t)} \ text {.} \end{уравнение*}

Предварительный просмотр 4.2.1.

Ответив на следующие вопросы, мы пытаемся понять специальные значения и общее поведение функции тангенса.

1. Без использования вычислительного устройства найти точное значение \(\tan(t)\) при следующих значениях: \(t = \frac{\pi}{6}, \frac{\pi}{4 }, \frac{\pi}{3}, \frac{2\pi}{3}, \frac{3\pi}{4}, \frac{5\pi}{6}\text{.}\ )

2. Почему \(\tan \left( \frac{\pi}{2} \right)\) не определено? Какие еще три входных значения \(x\), для которых \(\tan(x)\) не определены?

3. Откройте в браузере страницу http://gvsu.edu/s/0yO ¹ («zero-y-Oh»), чтобы найти рабочий лист Desmos с уже введенными данными функции тангенса. Нажмите на несколько оранжевых точек, чтобы сравнить ваши точные значения в (а) с десятичными значениями, заданными Desmos . Добавьте в таблицу одну запись: \(x = \frac{11\pi}{24}\text{,}\) \(y = T(\frac{11\pi}{24})\text{.} \) Примерно в каких координатах лежит эта точка? Каковы соответствующие значения \(\sin(\frac{11\pi}{24})\) и \(\cos(\frac{11\pi}{24})\text{?}\) Почему значение \(\tan(\frac{11\pi}{24})\) такое большое?

4. В верхней части списка ввода в левой части рабочего листа Desmos щелкните кружок, чтобы выделить функцию \(T(x) = \tan(x)\) и, таким образом, отобразить ее график вместе с точками данных. в оранжевом. Используйте график и свою работу выше, чтобы ответить на следующие важные вопросы о функции тангенса:

   • Каков домен \(y = \tan(x)\text{?}\)

   • Каков период \(y = \tan(x)\text{?}\)

   • Каков диапазон \(y = \tan(x)\text{?}\)

Подраздел 4.2.1 Два взгляда на касательную функцию

Рисунок 4. 2.3. Угол \(t\) в стандартном положении в единичной окружности, пересекающий дугу из \((1,0)\) в \((a,b).\)Рисунок 4.2.4. Прямоугольный треугольник со смежными катетами и противоположным углом \(\theta\text{.}\)

Поскольку функция тангенса определяется через две фундаментальные круговые функции по правилу \(\tan(t) = \frac{\sin(t)}{\cos(t)}\text{,}\), мы можно использовать наше понимание функций синуса и косинуса, чтобы понять функцию тангенса. В частности, мы можем рассматривать тангенс угла с двух разных точек зрения: как угол в стандартном положении в единичной окружности или как угол в прямоугольном треугольнике.

С точки зрения рисунка 4.2.3, поскольку точка, соответствующая углу \(t\), пересекает окружность и порождает точку \((a,b)\text{,}\), мы знаем, что \(\cos(t ) = a\) и \(\sin(t) = b\text{,}\) и, следовательно, функция тангенса отслеживает отношение этих двух величин и определяется как

\begin{уравнение*} \ tan (t) = \ frac {\ sin (t)} {\ cos (t)} = \ frac {b} {a} \ text {. } \end{уравнение*}

С точки зрения любого прямоугольного треугольника (не обязательно в единичной окружности) с гипотенузой «hyp» и катетами «adj» и «opp», которые соответственно примыкают и противоположны известному углу \(\theta\text{,}\) как видно на рисунке 4.2.4, мы знаем, что \(\sin(\theta) = \frac{\text{opp}}{\text{hyp}}\) и \(\cos(\theta) = \frac {\text{adj}}{\text{hyp}}\text{.}\) Подставив эти выражения вместо \(\sin(\theta)\) и \(\cos(\theta)\) в правиле для касательной функции, мы видим, что

\begin{уравнение*} \ tan (\ theta) = \ frac {\ sin (\ theta)} {\ cos (\ theta)} = \ frac {\ frac {\ text {opp}} {\ text {hyp}}} {\ frac { \text{adj}}{\text{hyp}}} = \frac{\text{opp}}{\text{adj}}\text{.} \end{уравнение*}

Обычно мы используем первую перспективу отслеживания отношения \(y\)-координаты к \(x\)-координате точки, пересекающей единичный круг, чтобы думать об общем поведении и графике касательной функции , и используйте вторую перспективу в прямоугольном треугольнике всякий раз, когда мы работаем над определением пропущенных значений в треугольнике.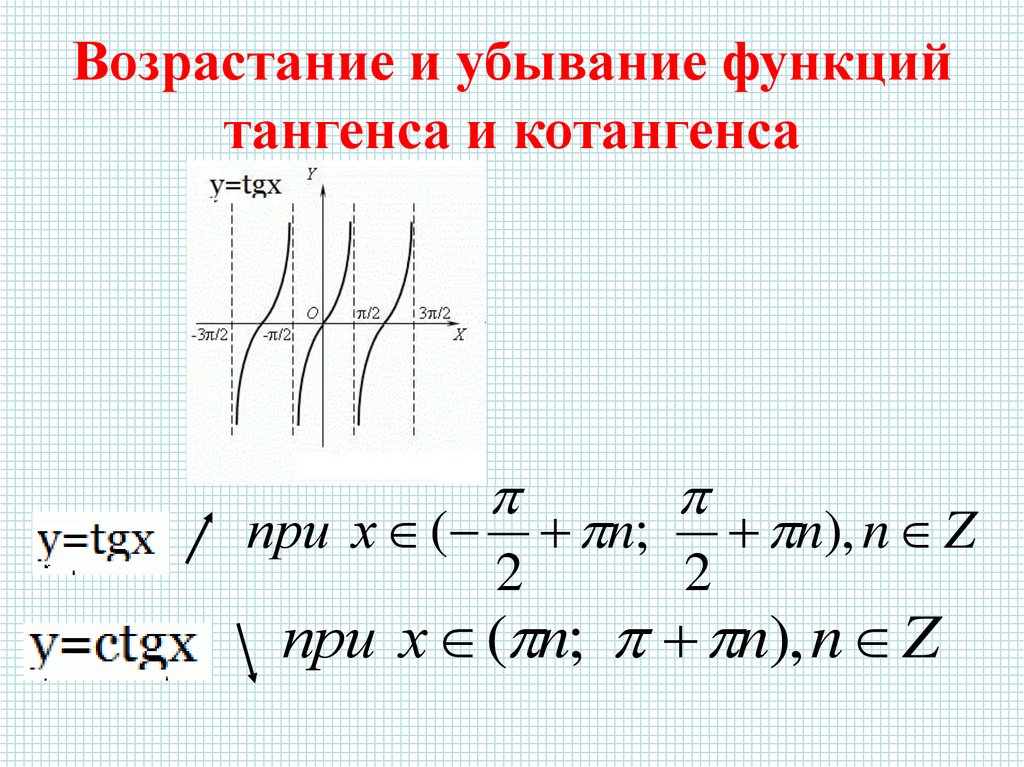

Подраздел 4.2.2 Свойства касательной функции

Поскольку функция тангенса определяется в терминах функций синуса и косинуса, ее значения и поведение полностью определяются этими двумя функциями. Для начала мы знаем значение \(\tan(t)\) для каждого специального угла \(t\) на единичной окружности, который мы определили для функций синуса и косинуса. Например, мы знаем, что

\begin{уравнение*} \tan \left(\frac{\pi}{6} \right) = \frac{ \sin \left(\frac{\pi}{6} \right)}}{\cos \left(\frac{\pi {6} \right) } = \ frac{ \ frac {1} {2} }{ \ frac {\ sqrt {3}} {2} } = \ frac {1} {\ sqrt {3}} \ text {.} \end{уравнение*}

Выполняя аналогичные вычисления для каждого известного специального угла на единичной окружности, мы получаем результаты, показанные в Таблице 4.2.5 и Таблице 4.2.6. Отметим также, что в любом месте \(\cos(t) = 0\text{,}\) значение \(\tan(t)\) не определено. Записываем такие экземпляры в таблицу, записывая «u».

Таблица 4.2.5.

\(т\)	\(0\)	\(\ гидроразрыва {\pi}{6}\)	\(\ гидроразрыва {\pi}{4}\)	\(\ гидроразрыва {\pi}{3}\)	\(\frac{\pi}{2}\)	\(\frac{2\pi}{3}\)	\(\frac{3\pi}{4}\)	\(\frac{5\pi}{6}\)	\(\пи\)
\(\sin(t)\)	\(0\)	\(\ гидроразрыва{1}{2}\)	\(\ гидроразрыва {\ sqrt {2}} {2} \)	\(\ гидроразрыва {\ sqrt {3}} {2} \)	\(1\)	\(\ гидроразрыва {\ sqrt {3}} {2} \)	\(\ гидроразрыва {\ sqrt {2}} {2} \)	\(\ гидроразрыва{1}{2}\)	\(0\)
\(\cos(t)\)	\(1\)	\(\frac{\sqrt{3}}{2}\)	\(\ гидроразрыва {\ sqrt {2}} {2} \)	\(\ гидроразрыва{1}{2}\)	\(0\)	\(-\frac{1}{2}\)	\(-\frac{\sqrt{2}}{2}\)	\(-\frac{\sqrt{3}}{2}\)	\(-1\)
\(\загар(т)\)	\(0\)	\(\frac{1}{\sqrt{3}}\)	\(1\)	\(\frac{3}{\sqrt{3}}\)	и	\(-\frac{3}{\sqrt{3}}\)	\(-1\)	\(-\frac{1}{\sqrt{3}}\)	\(0\)

Таблица 4. 2.6.

\(т\)	\(\frac{7\pi}{6}\)	\(\frac{5\pi}{4}\)	\(\frac{4\pi}{3}\)	\(\frac{3\pi}{2}\)	\(\frac{5\pi}{3}\)	\(\frac{7\pi}{4}\)	\(\frac{11\pi}{6}\)	\(2\пи\)
\(\sin(t)\)	\(-\frac{1}{2}\)	\(-\frac{\sqrt{2}}{2}\)	\(-\frac{\sqrt{3}}{2}\)	\(-1\)	\(-\frac{\sqrt{3}}{2}\)	\(-\frac{\sqrt{2}}{2}\)	\(-\frac{1}{2}\)	\(0\)
\(\cos(t)\)	\(-\frac{\sqrt{3}}{2}\)	\(-\frac{\sqrt{2}}{2}\)	\(-\frac{1}{2}\)	\(0\)	\(\ гидроразрыва{1}{2}\)	\(\ гидроразрыва {\ sqrt {2}} {2} \)	\(\ гидроразрыва {\ sqrt {3}} {2} \)	\(0\)
\(\загар(т)\)	\(\frac{1}{\sqrt{3}}\)	\(1\)	\(\frac{3}{\sqrt{3}}\)	и	\(-\frac{3}{\sqrt{3}}\)	\(-1\)	\(-\frac{1}{\sqrt{3}}\)	\(0\)

Таблица 4. 2.5 и Таблица 4.2.6 помогают нам определить тренды касательной функции. Например, мы наблюдаем, что знак \(\tan(t)\) положительный в квадранте I, отрицательный в квадранте II, положительный в квадранте III и отрицательный в квадранте IV. Это верно, потому что функции синуса и косинуса имеют одинаковый знак в первом и третьем квадрантах и ​​противоположные знаки в двух других квадрантах.

Кроме того, мы наблюдаем, что по мере приближения \(t\)-значений в первом квадранте к \(\frac{\pi}{2}\text{,}\) \(\sin(t)\) становится ближе к \(1\text{,}\), а \(\cos(t)\) ближе к \(0\) (всегда положительное). Отметив, что \(\frac{\pi}{2} \приблизительно 1,57\text{,}\), мы наблюдаем, что

\begin{уравнение*} \ tan (1,47) = \ frac {\ sin (1,47)} {\ cos (1,47)} \ приблизительно \ frac {0,995} {0,101} = 9,887 \end{уравнение*}

и

\begin{уравнение*} \ tan (1,56) = \ frac {\ sin (1,56)} {\ cos (1,56)} \ приблизительно \ frac {0,9994}{0,0108} = 92,6205\текст{.} \end{уравнение*}

Поскольку отношение чисел ближе и ближе к \(1\), деленное на числа ближе и ближе к \(0\) (но положительное), неограниченно возрастает, это означает, что \(\tan(t)\) неограниченно увеличивается когда \(t\) приближается к \(\frac{\pi}{2}\) с левой стороны. Как только \(t\) немного превышает \(\frac{\pi}{2}\) в квадранте II, значение \(\sin(t)\) остается близким к \(1\text{,} \), но теперь значение \(\cos(t)\) отрицательно (и близко к нулю). Например, \(\cos(1,58) \приблизительно -0,0092\text{.}\) Это делает значение \(\tan(t)\) неограниченно уменьшающимся (отрицательным и удаляющимся от \(0\)) при \(t\), приближающемся к \(\frac{ \pi}{2}\) с правой стороны и приводит к тому, что \(h(t) = \tan(t)\) имеет вертикальную асимптоту в точке \(t = \frac{\pi}{2}\text {.}\) Периодичность и знаковое поведение \(\sin(t)\) и \(\cos(t)\) означают, что это асимптотическое поведение функции тангенса будет повторяться.

Нанеся данные в таблицу вместе с ожидаемыми асимптотами и интуитивно соединив точки, мы увидим график функции тангенса на рисунке 4.2.7.

Рисунок 4.2.7. График функции касательной вместе со специальными точками, исходящими из единичной окружности.

Из таблиц 4.2.5 и 4.2.6, а также из рисунка 4.2.7 видно, что касательная функция имеет период \(P = \pi\) и что функция возрастает на любом интервале, на котором она определена. Подытожим нашу недавнюю работу следующим образом.

Свойства функции касательной.

Для функции \(h(t) = \tan(t)\text{,}\)

• его областью определения является множество всех действительных чисел, кроме \(t = \frac{\pi}{2} \pm k\pi\), где \(k\) — любое целое число;

• его диапазон — это набор всех действительных чисел;

• его период равен \(P = \pi\text{;}\)

• увеличивается на любом интервале, на котором функция определена в каждой точке интервала.

Хотя функция тангенса сама по себе является интересной математической функцией, ее наиболее важные применения связаны с определением прямоугольных треугольников, и в оставшейся части этого раздела мы сосредоточимся на этой перспективе.

Подраздел 4.2.3 Использование функции касательной в прямоугольных треугольниках

Функция касательной предлагает нам дополнительный выбор при работе с прямоугольными треугольниками с ограниченной информацией. В ситуации, когда у нас есть прямоугольный треугольник с одним дополнительным известным углом, если мы знаем длину гипотенузы, мы можем использовать либо синус, либо косинус угла, чтобы легко найти оставшиеся длины сторон. Но в условиях, когда мы знаем только длину одного катета, функция тангенса теперь позволяет нам таким же простым способом определить значение оставшегося катета, а оттуда — гипотенузу.

Пример 4.2.8.

Используйте функцию касательной, чтобы определить ширину \(w\text{,}\) реки на рисунке 4.2.9. (Обратите внимание, что здесь мы возвращаемся к задаче из упражнения 4.1.4, которую ранее решили без использования функции касательной.) Какую еще информацию мы теперь можем легко определить?

Рисунок 4.2.9. Прямоугольный треугольник с известным углом и катетом.

Раствор.

Используя перспективу, что \(\tan(\theta) = \frac{\text{opp}}{\text{adj}}\) в прямоугольном треугольнике, в этом контексте мы имеем 9\circ) = \frac{w}{50} \end{equation*}

и, таким образом, \(w = 50\tan(56.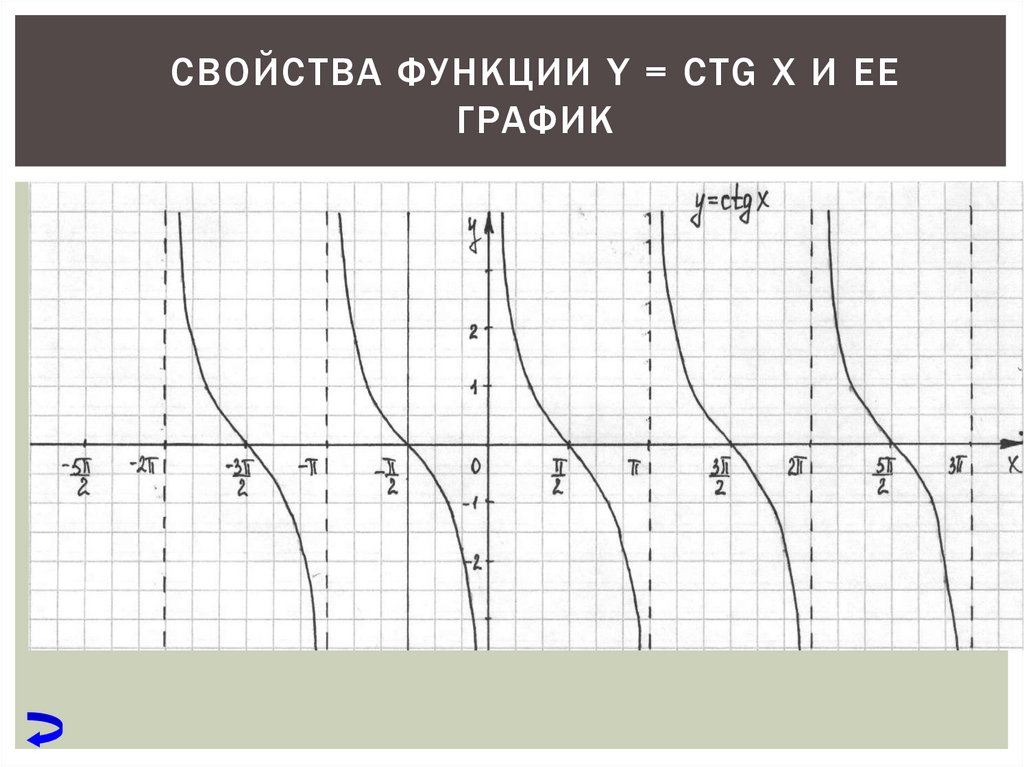 4)\) — точная ширина реки. Используя вычислительное устройство, мы находим, что \(w \приблизительно 75,256\текст{.}\)

Зная ширину реки, мы можем использовать теорему Пифагора или функцию синуса для определения расстояния от \(P\) к \(A\text{,}\), в которой известны все \(6\) частей треугольника.

Функция касательной находит широкое применение при поиске недостающей информации в прямоугольных треугольниках, где известна информация об одной или нескольких сторонах треугольника. 9{\circ}\) с землей. Какой длины должны быть кабели и на каком расстоянии от основания башни они должны быть закреплены?

Мероприятие 4.2.3.

Supertall ² высотных зданий изменили горизонт Манхэттена. Эти небоскребы известны своей небольшой площадью по сравнению с их высотой, с их отношением ширины к высоте самое большее \(1:10\text{,}\), а некоторые даже достигают \(1:24\text{.} \) Предположим, что относительно невысокий сверхвысокий объект высотой \(635\) футов, как показано на рис. 4.2.10, и второй сверхвысокий объект построен поблизости. Учитывая два угла, которые вычисляются от нового здания, какова высота \(s\text{,}\) нового здания и как далеко друг от друга \(d\text{,}\) две башни? 9угол \circ\), найдите второе уравнение, связывающее \(x\) и \(h\text{.}\)

Наша работа в (a) и (b) приводит к системе двух уравнений с двумя неизвестными \(x\) и \(h\text{.}\) Решите каждое из двух уравнений относительно \(h\ ), а затем соответствующим образом подставить, чтобы найти одно уравнение в переменной \(x\text{.}\)

Решите уравнение из (c), чтобы найти точное значение \(x\) и определить приблизительное значение с точностью до \(3\) знаков после запятой.

Используйте предыдущую работу, чтобы точно определить \(h\), а также определить оценку с точностью до \(3\) знаков после запятой.

Если первоначальные измерения геодезистов были сделаны на высоте \(78\) футов над уровнем моря, на какой высоте над уровнем моря находится вершина холма?

Подраздел 4.

2.4 Резюме

• Функция тангенса определена как отношение функций синуса и косинуса в соответствии с правилом

  \begin{уравнение*} \ тангенс (т) = \ гидроразрыва {\ грех (т)} {\ соз (т)} \end{уравнение*}

  для всех значений \(t\), для которых \(\cos(t) \ne 0\text{.}\)

• График функции тангенса существенно отличается от графиков функций синуса и косинуса прежде всего тем, что вблизи значений, где \(\cos(t) = 0\text{,}\) отношение \(\frac{\ sin(t)}{\cos(t)}\) неограниченно увеличивается или уменьшается, образуя вертикальные асимптоты. Кроме того, в то время как период функций синуса и косинуса равен \(P = 2\pi\text{,}\), период функции тангенса равен \(P = \pi\) из-за того, как функции синуса и косинуса повторять одни и те же значения (с разными знаками), когда точка пересекает единичный круг.

• Функция тангенса находит одно из наиболее важных применений при построении прямоугольных треугольников, когда известен один катет треугольника и известен один из непрямых углов. Вычисление тангенса известного угла, скажем, \(\alpha\text{,}\) и использование того факта, что

  \begin{уравнение*} \ загар (\ альфа) = \ гидроразрыва {\ текст {опп}} {\ текст {прил}} \end{уравнение*}

  мы можем найти длину недостающего катета через другой и тангенс угла.

Упражнения 4.2.5 Упражнения

1.

По полученной информации найдите квадрант, в котором находится конечная точка, определяемая \(t\). Введите I, II, III или IV.

(a) \(\sin (t)\lt 0\) и \(\cos (t)\lt 0\text{,}\) квадрант ;

(b) \(\sin (t)>0\) и \(\cos (t)\lt 0\text{,}\) квадрант ;

(c) \(\sin (t)>0\) и \(\cos (t)>0\text{,}\) квадрант ;

(d) \(\sin (t)\lt 0\) и \(\cos (t)>0\text{,}\) квадрант ; 9\circ\text{,}\) найти недостающие углы или стороны. Дайте ответ не менее чем с 3 десятичными знаками.

АВ =

ВС =

\(\альфа\)=

4.

Если \(\cos(\phi) = 0,8347\) и \(3 \pi /2 \leq \phi \leq 2 \pi\text{,}\) аппроксимируйте следующее число до четырех знаков после запятой.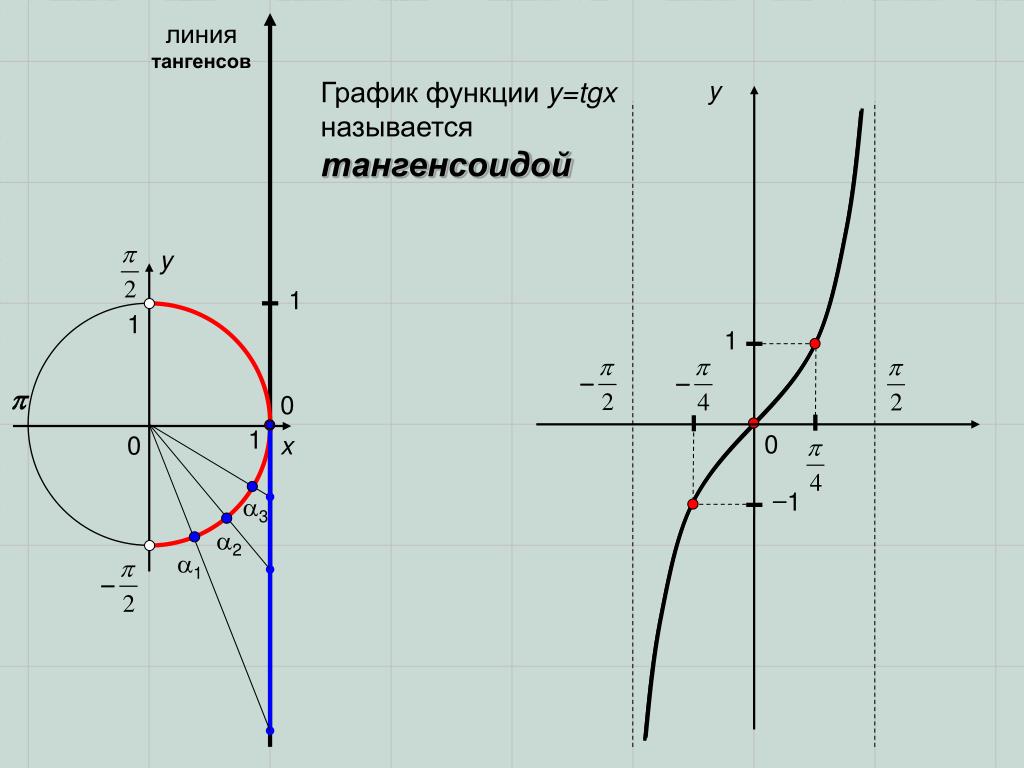

(a) \(\sin( \phi )\) = (Округлить до четырех знаков после запятой.)

(b) \(\tan( \phi )\) = (Округлить до четырех знаков после запятой.)

5.

Предположим, что \(\displaystyle \sin{ \theta } = \frac{x}{8}\) и угол \(\theta\) находится в первом квадранте. Запишите алгебраические выражения для \(\cos(\theta)\) и \(\tan(\theta)\) через \(x\text{.}\)

(a) \(\cos(\theta)\) =

(b) \(\tan(\theta)\) =

6.

Точно решите приведенные ниже уравнения. Дайте ответы в радианах и найдите все возможные значения \(t\) в интервале \(0 \leq t \leq 2 \pi\text{.}\) Если имеется более одного ответа, введите свои решения в список, разделенный запятыми.

(a) \(\displaystyle \sin{(t)} = \frac{\sqrt{2}}{2}\), когда \(t =\)

(b) \(\displaystyle \cos{ (t)} = — \frac{\sqrt{2}}{2}\), когда \(t =\) 9{\circ}\text{.}\) Если пандус будет подниматься от ровного тротуара до крыльца на высоте \(3\) футов над землей, какой длины должен быть пандус? На каком расстоянии от крыльца он будет упираться в тротуар? Какой уклон пандуса?

8.