исследование функции y=x-lnx — @дневники: асоциальная сеть
четверг, 15 декабря 2011
доброго времени сутокделаю исследование функции. пока всё норм или нет?
y=x-lnx
y=x-lnx1) область определения функции
x принадлежит (0; + бесконечность)
2) четность, нечетность, периодичность
y(-x)=-x-ln(-x) — не существует, т.к. ооф x>0
y(-x) не равно y(x) не равно -y(x)
следовательно функция не четная и не нечетная
также функция не является периодической
т.к. (x+T)-ln(x+T) не равно x-lnx
3) точки пересечения с осями координат
oy: т.к. x не может быть = 0 (см. ооф), следовательно нет пересечения
ox: x-lnx=0
lnx=x — неверное
следовательно нет пересечения
продолжение исследования
читать дальше
4) асимптотывертикальная:
lim (при x->0) (x-lnx) = — бесконечность
x=0
горизонтальная:
не понимаю, как сделать
наклонная:
не понимаю, как сделать
5) монотонность и экстремумы
y’=1-1/x
критические точки:
x=0 (точка разрыва)
x=1 (1-1/x=0 -> x=1)
при x от 0 до 1, y’ меньше 0
при x от 1 до бесконечности, y` больше 0
следовательно, функция y на интервале x (0; 1) убывает
на интервале x (1; бесконечность) возрастает
точка минимума: x=1, y=1
6) выпуклость и точки перегиба
y»=1/x2
критические точки:
x=0
при x>0, y»>0
следовательно функция выпукла вверх
точек перегиба нет
@темы: Исследование функций
- ← Предыдущая запись
- Следующая запись →
Этот пост будет безвозвратно удален:
Вы уверены в том, что действительно хотите это сделать?
Да Нет
Вычисление производных первого порядка.
 2+1}.$$
2+1}.$$
3) $ y-x=\varepsilon\sin y $
Решение.
$$\frac{d}{dx}(y-x-\varepsilon\sin y)=0\Rightarrow\,\, y’-1-\varepsilon\cos y\cdot y’=0 \Rightarrow y’=\,\frac{1}{1-\varepsilon\cos y}.$$
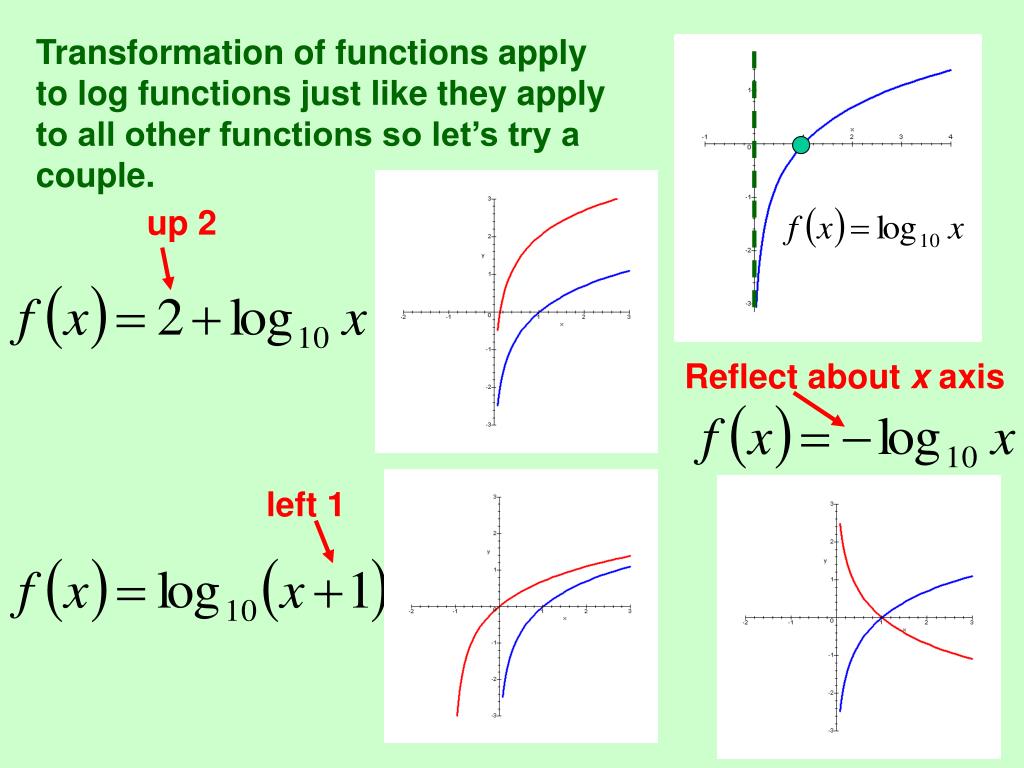
Внеклассный урок — Функция y = ln x
Функция y = ln x
Графиком функции y = ln x является экспонента, у которой в точке х = 1 угол между касательной и осью абсцисс равен 45º.
Не следует путать с функцией у = ех, у которой: а) касательная под углом 45º пересекает ось абсцисс в точке х = 0; б) экспонента выпукла вниз.
В отличие от функции у = ех, экспонента функции y = ln x выпукла вверх.
График функции y = ln x симметричен графику функции у = ех относительно прямой у = х.
Свойства функции y = ln x:
1) Областью определения являются все положительные числа: D(f) = (0; +∞). 2) Область значений функции – все числа от –∞ до +∞: E(f) = (–∞; +∞) 3) Функция ни четная, ни нечетная. 4) Возрастает на промежутке (0; +∞). 5) Не ограничена ни снизу, ни сверху. 6) Не имеет наибольшего и наименьшего значений. 7) Непрерывна. 8) Выпукла вверх. 9) Дифференцируема. |
Производная функции y = ln x:
1 |
Логарифмическая производная.
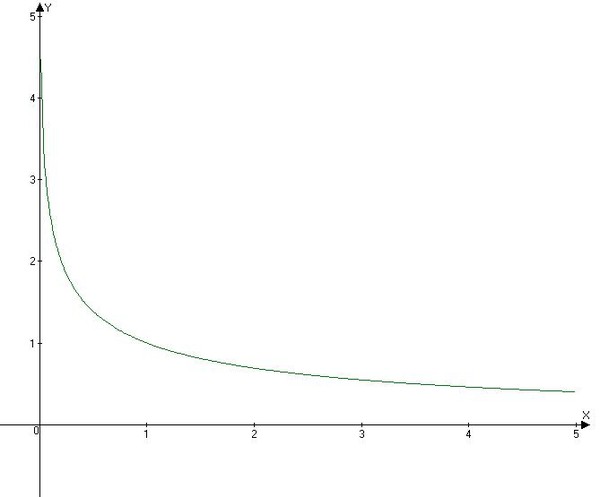 Дифференцирование показательно степенной функции.
Дифференцирование показательно степенной функции.Когда нам нужно выполнить дифференцирование показательно степенной функции вида y=(f(x))g(x) или преобразовать громоздкое выражение с дробями, можно использовать логарифмическую производную. В рамках этого материала мы приведем несколько примеров применения этой формулы.
Чтобы понять эту тему, необходимо знать, как пользоваться таблицей производных, быть знакомым с основными правилами дифференцирования и представлять себе, что такое производная сложной функции.
Как вывести формулу логарифмической производной
Для получения этой формулы нужно сначала произвести логарифмирование по основанию e, а затем упростить получившуюся функцию, применив основные свойства логарифма. После этого надо вычислить производную неявно заданной функции:
y=f(x)ln y=ln(f(x))(ln y)’=(ln(f(x)))’1y·y’=(ln(f(x)))’⇒y’=y·(ln(f(x)))’
Примеры использования формулы
Покажем на примере, как это делается.
Вычислить производную показательно степенной функции переменной x в степени x.
Решение
Проводим логарифмирование по указанному основанию и получаем ln y=ln xx. С учетом свойств логарифма это можно выразить как ln y=x·ln x. Теперь дифференцируем левую и правую части равенства и получаем результат:
ln y=x·ln xln y’=x·ln x’1y·y’=x’·ln x+·ln x’⇒y’=y·1·ln x+x·1x=y·(ln x+1)=xx·(ln x+1)
Ответ: xx’=xx·(ln x+1)
Такую задачу можно решить и другим способом, без логарифмической производной. Сначала нам надо преобразовать исходное выражение так, чтобы перейти от дифференцирования показательно степенной функции к вычислению производной сложной функции, например:
y=xx=eln xx=ex·ln x⇒y’=(ex·ln x)’=ex·ln x·x·ln x’=xx·x’·ln x+x·(ln x)’==xx·1·ln x+x·1x=xx·ln x+1
Рассмотрим еще одну задачу.
Пример 2Вычислите производную функции y=x2+13×3·sin x.
Исходная функция представлена в виде дроби, значит, мы можем решить задачу с помощью дифференцирования. Однако эта функция довольно сложная, значит, преобразований потребуется много. Значит, нам лучше использовать здесь логарифмическую производную y’=y·ln(f(x))’. Поясним, почему такое вычисление удобнее.
Однако эта функция довольно сложная, значит, преобразований потребуется много. Значит, нам лучше использовать здесь логарифмическую производную y’=y·ln(f(x))’. Поясним, почему такое вычисление удобнее.
Начнем с нахождения ln(f(x)). Для дальнейшего преобразования нам потребуются следующие свойства логарифма:
- логарифм дроби можно представить в виде разности логарифмов;
- логарифм произведения можно представить в виде суммы;
- если у выражения под логарифмом есть степень, мы можем вынести ее в качестве коэффициента.
Преобразуем выражение:
ln(f(x))=ln(x2+1)13×3·sin x12=ln(x2+1)13-ln(x3·sin x)12==13ln(x2+1)-32ln x-12ln sin x
В итоге у нас получилось достаточно простое выражение, производную которого вычислить несложно:
(ln(f(x)))’=13ln(x2+1)-32ln x-12ln sin x’==13ln(x2+1)’-32ln x’-12ln sin x’==13(ln(x2+1))’-32(ln x)’-12(ln sin x)’==13·1×2+1·x2+1′-32·1x-12·1sin x·(sin x)’==13·2xx2+1-32x-cos x2 sin x
Теперь то, что у нас получилось, нужно подставить в формулу логарифмической производной.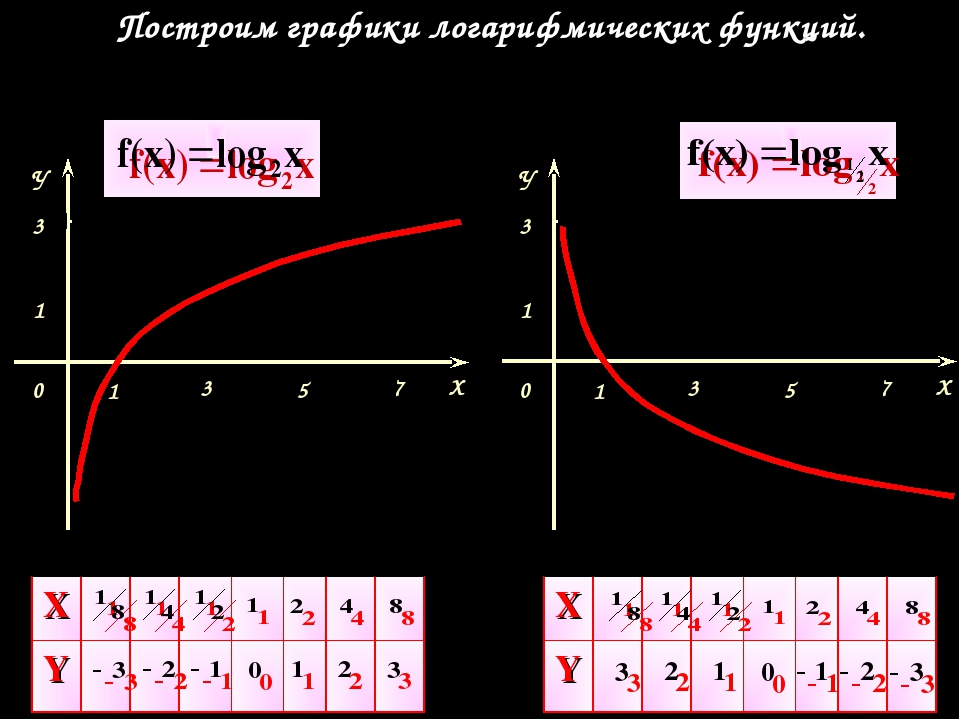
Ответ: y’=y·ln(f(x))’=x2+13×3·sin x·13·2xx2+1-32x-cos x2 sin x
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать заданиеЧтобы закрепить материал, изучите еще пару следующих примеров. Здесь будут приведены только вычисления с минимумом комментариев.
Пример 3Дана показательно степенная функция y=(x2+x+1)x3. Вычислите ее производную.
Решение:
y’=y·(ln(f(x)))’=(x2+x+1)x3·ln(x2+x+1)x3’==(x2+x+1)x3·x3·(x2+x+1)’==(x2+x+1)x3·x3’·ln(x2+x+1)+x3ln(x2+x+1)’==(x2+x+1)x3·3×2·ln(x2+x+1)+x3·1×2+x+1·x2+x+1’==(x2+x+1)x3·3×2·ln(x2+x+1)+x32x+1×2+x+1==(x2+x+1)x3·3×2·ln(x2+x+1)+2×4+x3x2+x+1
Ответ: y’=y·(ln(f(x)))’=(x2+x+1)x3·3×2·ln(x2+x+1)+2×4+x3x2+x+1
Пример 4Вычислите производную выражения y=x2+13·x+1·x3+14×2+2x+2.
Решение
Применяем формулу логарифмической производной.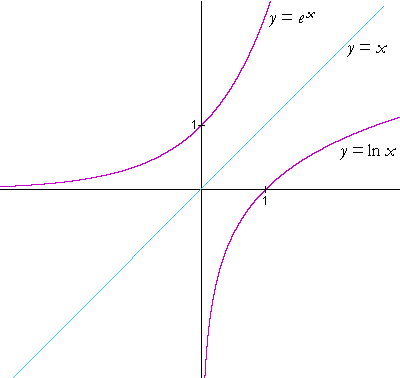
y’=y·lnx2+13·x+1·x3+14×2+2x+2’==y·lnx2+13+lnx+1+lnx3+14-lnx2+2x+2’==y·13ln(x2+1)+12lnx+1+14ln(x3+1)-12ln(x2+2x+2)’==y·(x2+1)’3(x2+1)+x+1’2(x+1)+(x3+1)’4×3+1-x2+2x+2’2×2+2x+2==x2+13·x+1·x3+14×2+2x+2·2×3(x2+1)+12(x+1)+3×24(x3+1)-2x+22(x2+2x+2)
Ответ:
y’=x2+13·x+1·x3+14×2+2x+2·2×3(x2+1)+12(x+1)+3×24(x3+1)-2x+22(x2+2x+2).
Производные некоторых основных элементарных функций (Лекция №5)
- y = xn.
Если n – целое положительное
число, то, используя формулу бинома Ньютона:
(a + b)n
= an+n·an-1·b + 1/2∙n(n – 1)an-2∙b2+ 1/(2∙3)∙n(n – 1)(n – 2)an-3b3+…+
bn,
можно доказать, что
Итак, если x получает приращение Δx, то f(x+Δx) = (x + Δx)n, и, следовательно,
Δy=(x+Δx)n – xn =n·xn-1·Δx + 1/2·n·(n–1)·xn-2·Δx2 +…+Δxn.

Заметим, что в каждом из пропущенных слагаемых есть множитель Δx в степени выше 3.
Найдем предел
Мы доказали эту формулу для n Î N. Далее увидим, что она справедлива и при любом n Î R.
- y= sin x. Вновь воспользуемся определением производной.
Так как, f(x+Δx)=sin(x+Δx), то
Таким образом,
- Аналогично можно показать, что
- Рассмотрим функцию y= ln x.
Имеем f(x+Δx)=ln(x+Δx). Поэтому
Итак,
- Используя свойства логарифма можно показать, что
Формулы 3 и 5 докажите самостоятельно.
ОСНОВНЫЕ ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ
Применяя общий способ
нахождения производной с помощью предела можно получить простейшие формулы
дифференцирования.
- .
- (справедлива для любого конечного числа слагаемых).
- .
- .
а) .
б) .
Формулы 1 и 2 докажите самостоятельно.
Доказательство формулы 3.
Пусть y = u(x) + v(x). Для значения аргумента x+Δx имеем y(x+Δx)=u(x+Δx) + v(x+Δx).
Тогда
Δy=y(x+Δx) – y(x) = u(x+Δx) + v(x+Δx) – u(x) – v(x) = Δu +Δv.
Следовательно,
.
Доказательство формулы 4.
Пусть y=u(x)·v(x). Тогда y(x+Δx)=u(x+Δx)·v(x
Δy=u(x+Δx)·v(x+Δx) – u(x)·v(x).
Заметим, что поскольку каждая из функций u и v дифференцируема в точке x, то они непрерывны в этой точке, а значит u(x+Δx)→u(x), v(x+Δx)→v(x), при Δx→0.
Поэтому можем записать
На основании этого свойства можно получить правило дифференцирования произведения любого числа функций.
Пусть, например, y=u·v·w. Тогда,
y ‘ = u ‘·(v·w) + u·(v ·w) ‘ = u ‘·v·w + u·(v ‘·w +v·w ‘) = u ‘·v·w + u·v ‘·w + u·v·w ‘.
Доказательство формулы 5.
Пусть . Тогда
При доказательстве воспользовались тем, что v(x+Δx)→v(x) при Δx→0.
Примеры.
- Если , то
- y = x3 – 3x2 + 5x + 2.
Найдем y ‘(–1).

y ‘ = 3x2 – 6x+ 5. Следовательно, y ‘(–1) = 14.
- y = ln x · cos x, то y ‘ = (ln x) ‘ cos x + ln x (cos x) ‘ =1/x∙cos x – ln x · sin x.
Таким образом,
- Аналогично для y= ctgx,
ТЕОРЕМА О ПРОИЗВОДНОЙ СЛОЖНОЙ ФУНКЦИИ
Пусть y = f(u), а u= u(x). Получаем функцию y, зависящую от аргумента x: y = f(u(x)). Последняя функция называется функцией от функции или сложной функцией.
Областью определения функции
y = f(u(x))
является либо вся область определения функции u=u(x) либо та ее часть, в которой определяются значения u, не выходящие из области
определения функции y= f(u).
Операция «функция от функции» может проводиться не один раз, а любое число раз.
Установим правило дифференцирования сложной функции.
Теорема. Если функция u= u(x) имеет в некоторой точке x0 производную и принимает в этой точке значение u0 = u(x0), а функция y= f(u) имеет в точке u0 производную y ‘u= f ‘(u0), то сложная функция y = f(u(x)) в указанной точке x0 тоже имеет производную, которая равна y ‘x= f ‘(u0)·u ‘(x0), где вместо u должно быть подставлено выражение u= u(x).
Таким образом, производная
сложной функции равна произведению производной данной функции по промежуточному
аргументу u на производную
промежуточного аргумента по x.
Доказательство. При фиксированном значении х0 будем иметь u0=u(x0), у0=f(u0). Для нового значения аргумента x0+Δx:
Δu= u(x0 + Δx) – u(x0), Δy=f(u0+Δu) – f(u0).
Т.к. u – дифференцируема в точке x0, то u – непрерывна в этой точке. Поэтому при Δx→0 Δu→0. Аналогично при Δu→0 Δy→0.
По условию . Из этого соотношения, пользуясь определением предела, получаем (при Δu→0)
,
где α→0 при Δu→0, а, следовательно, и при Δx→0.
Перепишем это равенство в виде:
Δy= y ‘uΔu+α·Δu.
Полученное равенство
справедливо и при Δu=0 при произвольном
α, так как оно превращается в
тождество 0=0. При Δu=0 будем полагать α=0. Разделим все члены
полученного равенства на Δx
При Δu=0 будем полагать α=0. Разделим все члены
полученного равенства на Δx
.
По условию . Поэтому, переходя к пределу при Δx→0, получим y ‘x= y ‘u·u ‘x . Теорема доказана.
Итак, чтобы продифференцировать сложную функцию y = f(u(x)), нужно взять производную от «внешней» функции f, рассматривая ее аргумент просто как переменную, и умножить на производную от «внутренней» функции по независимой переменной.
Если функцию y=f(x) можно представить в виде y=f(u), u=u(v), v=v(x), то нахождение производной y ‘x осуществляется последовательным применением предыдущей теоремы.
По доказанному правилу имеем y ‘x= y ‘u·u ‘x . Применяя эту же теорему для u ‘x получаем , т.е.
y ‘x = y ‘x· u ‘v· v ‘x = f ‘u (u)·u ‘v (v)·v ‘x (x).
Примеры.
- y = sin x2. Тогда .
ПОНЯТИЕ ОБРАТНОЙ ФУНКЦИИ
Начнем с примера. Рассмотрим функцию y= x3. Будем рассматривать равенство y= x3 как уравнение относительно x. Это уравнение для каждого значения у определяет единственное значение x: . Геометрически это значит, что всякая прямая параллельная оси Oxпересекает график функции y= x3 только в одной точке. Поэтому мы можем рассматривать x как функцию от y. Функция называется обратной по отношению к функции y= x3.
Прежде чем перейти к общему случаю, введем определения.
Функция y = f(x) называется
возрастающей на некотором отрезке,
если большему значению аргумента x из
этого отрезка соответствует большее значение функции, т. е. если x2>x1, то f(x2) > f(x1).
е. если x2>x1, то f(x2) > f(x1).
Аналогично функция называется убывающей, если меньшему значению аргумента соответствует большее значение функции, т.е. еслих2 < х1 , то f(x2) > f(х1).
Итак, пусть дана возрастающая или убывающая функция y= f(x), определенная на некотором отрезке [a; b]. Для определенности будем рассматривать возрастающую функцию (для убывающей все аналогично).
Рассмотрим два различных
значения х1
и х2. Пусть y1=f(x1), y2=f(x2). Из
определения возрастающей функции следует, что если x1<x2, то у1<у2. Следовательно, двум различным значениям х1 и
х2 соответствуют два
различных значения функции у1
и у2. Справедливо и обратное,
т.е. если у1<у2, то из определения
возрастающей функции следует, чтоx1<x2. Т.е. вновь двум различным
значениям у1
и у2 соответствуют два
различных значенияx1 и x2. Т.о.,
между значениями x и соответствующими им значениями y устанавливается взаимно однозначное
соответствие, т.е. уравнение y=f(x) для каждого y (взятого из области
значений функции y=f(x)) определяет единственное значение x, и можно
сказать, что x есть
некоторая функция аргумента y: x= g(у).
Справедливо и обратное,
т.е. если у1<у2, то из определения
возрастающей функции следует, чтоx1<x2. Т.е. вновь двум различным
значениям у1
и у2 соответствуют два
различных значенияx1 и x2. Т.о.,
между значениями x и соответствующими им значениями y устанавливается взаимно однозначное
соответствие, т.е. уравнение y=f(x) для каждого y (взятого из области
значений функции y=f(x)) определяет единственное значение x, и можно
сказать, что x есть
некоторая функция аргумента y: x= g(у).
Эта функция называется обратной для функции y=f(x). Очевидно, что и функция y=f(x) является обратной для функции x=g(у).
Заметим, что обратная
функция x=g(y) находится
путем решения уравнения y=f(x) относительно
х.
Пример. Пусть дана функция y = ex. Эта функция возрастает при –∞ < x <+∞. Она имеет обратную функцию x = lny. Область определения обратной функции 0 < y < + ∞.
Сделаем несколько замечаний.
Замечание 1. Если возрастающая (или убывающая) функция y=f(x) непрерывна на отрезке [a; b], причем f(a)=c, f(b)=d, то обратная функция определена и непрерывна на отрезке [c; d].
Замечание 2. Если функция y=f(x) не является ни возрастающей, ни убывающей на некотором интервале, то она может иметь несколько обратных функций.
Пример. Функция y=x2 определена при –∞<x<+∞. Она не является ни
возрастающей, ни убывающей и не имеет обратной функции. Однако, если мы рассмотриминтервал 0≤x<+∞, то здесь функция является
возрастающей и обратной для нее будет . На интервале – ∞ <x≤ 0 функция – убывает и обратная
для нее .
На интервале – ∞ <x≤ 0 функция – убывает и обратная
для нее .
Замечание 3. Если функции y=f(x) и x=g(y) являются взаимно обратными, то они выражают одну и ту же связь между переменными x и y. Поэтому графикомих является одна и та же кривая. Но если аргумент обратной функции мы обозначим снова через x, а функцию через y и построим их в одной системе координат, то получим уже два различных графика. Легко заметить, что графики будут симметричны относительно биссектрисы 1-го координатного угла.
ТЕОРЕМА О ПРОИЗВОДНОЙ ОБРАТНОЙ ФУНКЦИИ
Докажем теорему, позволяющую находить производную функции y=f(x), зная производную обратной функции.
Теорема. Если для функции y=f(x) существует
обратная функция x=g(y), которая в некоторой точке
у0 имеет
производную g ‘(v0), отличную от нуля, то в
соответствующей точке x0=g(x0) функция y=f(x) имеет
производную f ‘(x0), равную ,
т. е. справедлива формула.
е. справедлива формула.
Доказательство. Т.к. x=g(y) дифференцируема в точке y0, то x=g(y) непрерывна в этой точке, поэтому функция y=f(x) непрерывна в точке x0=g(y0). Следовательно, при Δx→0 Δy→0.
Покажем, что .
Пусть . Тогда по свойству предела . Перейдем в этом равенстве к пределу при Δy→0. Тогда Δx→0 и α(Δx)→0, т.е. .
Следовательно,
,
что и требовалось доказать.
Эту формулу можно записать в виде .
Рассмотрим применение этой теоремы на примерах.
Примеры.
- y = ex. Обратной для этой функции
является функция x= ln y. Мы уже доказали, что .
Поэтому согласно сформулированной выше теореме
Итак, (ex) ‘ = ex
- Аналогично можно показать, что (ax) ‘ = ax·lna.
 Докажите самостоятельно.
Докажите самостоятельно. - y = arcsin x.
Рассмотрим обратную функцию x = sin y. Эта функция в интервале – π/2<y<π/2 монотонна. Ее производная
x ‘ = cos y не
обращается в этом интервале в нуль. Следовательно, по теореме о производной
обратной функции
.
Но на (–π/2; π/2) .
Поэтому
- Аналогично
Докажите самостоятельно.
- y = arctg x.
Эта функция по определению удовлетворяет условию существования обратной функции
на интервале –π/2< y < π/2. При этом обратная функция x = tg y монотонна.
По ранее доказанному .
Следовательно, y ‘ = cos2y . Но .
Поэтому
- Используя эти формулы, найти производные следующих функций:
Специфика работы с логарифмами в задаче B15
Вообще говоря, для решения задачи B15 с логарифмом надо знать две формулы:
Первая формула — классическая производная натурального логарифма, вторая — производная сложной функции. Обратите внимание: в числителе стоит число k, это не опечатка.
Обратите внимание: в числителе стоит число k, это не опечатка.
Добавьте к этим формулам стандартные правила вычисления производных — и задача B15 решена:
(f ± g) ’ = f ’ ± g ’;
(c · f) ’ = c · f ’, c ∈ R.
В настоящих задачах логарифмы никогда не встречаются сами по себе. Поэтому обязательно приводите всю производную к общему знаменателю. Почему это важно, узнаете из примеров.
Задача. Найдите наименьшее значение функции на отрезке [0,5; 4]:
y = 2x2 − 4 ln x + 5
Находим производную:
Выясняем, когда производная равна к нулю. Дробь равна нулю, когда ее числитель равен нулю. Имеем:
4(x2 − 1) = 0;
x2 = 1;
x = ±1.
Корень x = −1 не принадлежит отрезку [0,5; 4], поэтому нас интересует только x = 1. Кроме того, рассмотрим концы отрезка — числа 0,5 и 4. Итого три числа: 0,5; 1; 4. Поскольку требуется найти наименьшее значение функции, подставляем эти числа в исходную функцию:
y (0,5) = 2 · 0,52 − 4 ln 0,5 + 5 = 0,5 − 4 ln 0,5 + 5 = 5,5 − 4 ln 0,5;
y (1) = 2 · 12 − 4 ln 1 + 5 = 2 − 0 + 5 = 7;
y (4) = 2 · 42 − 4 ln 4 + 5 = 32 − 4 ln 4 + 5 = 37 − 4 ln 4.
В общем, выбирать особо не из чего. Ответ: 7. Потому что числа 5,5 − 4ln 0,5и 37 − 4ln 4 иррациональны, их нельзя записать в виде конечной десятичной дроби.
Задача. Найдите точку минимума функции:
y = 2x − 5 ln (x − 7) + 3
Снова считаем производную:
Под логарифмом стоит линейная функция y = x − 7. Коэффициент при переменной x равен k = 1, поэтому в числителе никаких дополнительных множителей не возникнет — только множитель 5, который стоит перед логарифмом.
Поскольку требуется найти точку минимума, считаем нули числителя и знаменателя:
2x − 19 ⇒ x = 19 : 2 = 9,5;
x − 7 = 0 ⇒ x = 7.
Отмечаем эти точки на прямой, расставляем знаки производной между точками:
Итак, в точке x = 9,5 производная меняет знак с минуса на плюс, если считать слева — направо, в направлении стрелки. Это и есть точка минимума.
Задача. Найдите наибольшее значение функции на отрезке [−1,5; 1]:
y = 3 ln (x + 2) − 3x + 10
Считаем производную:
Находим нули числителя:
−3x − 3 = 0;
x = −1.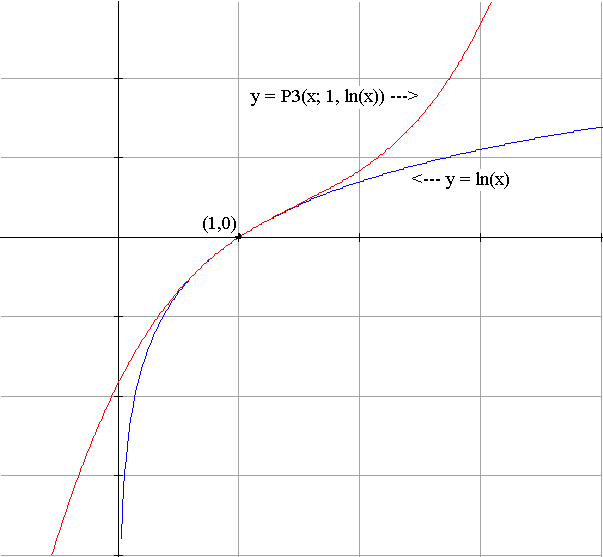
Нули знаменателя нас не интересуют, поскольку требуется найти значение функции. А когда знаменатель равен нулю, значение функции не определено.
Поскольку корень x = −1 ∈ [−1,5; 1], получаем три точки: −1,5; −1; 1. Подставляем их в исходную функцию:
y (−1,5) = 3 ln (−1,5 + 2) − 3 · (−1,5) + 10 = 3 ln 0,5 + 14,5;
y (−1) = 3 ln (−1 + 2) − 3 · (−1) + 10 = 3 ln 1 + 13 = 0 + 13 = 13;
y (1) = 3 ln (1 + 2) − 3 · 1 + 10 = 3 ln 3 + 7.
Понятно, что числа 3 ln 0,5 + 14,5и 3 ln 3 + 7 нельзя записать в ответ. Остается только число 13 — это и будет наибольшее значение.
Вынесение степени за знак логарифма
Еще одна полезная фишка, которая избавит вас от сложных производных:
ln (f (x))k = k · ln f (x)
Обратите внимание: в первом случае внутри логарифма стоит степень, для которой потребуется производная сложной функции. Во втором случае все намного проще, поскольку чаще всего f (x) — это обычная линейная функция.
Этот прием часто встречается в задачах на вычисление максимального и минимального значения. В задачах на точки экстремума его почти не применяют. Прежде чем решать такую задачу, обязательно найдите ОДЗ логарифма. Если забыли, что это такое, см. «Что такое логарифм».
В задачах на точки экстремума его почти не применяют. Прежде чем решать такую задачу, обязательно найдите ОДЗ логарифма. Если забыли, что это такое, см. «Что такое логарифм».
Задача. Найдите наименьшее значение функции на отрезке [−4; 1]:
y = 5x − ln (x + 5)5
Итак, область допустимых значений логарифма — аргумент должен быть больше нуля. Имеем:
(x + 5)5 > 0;
x + 5 > 0;
x > −5;
x ∈ (−5; +∞).
Теперь решаем задачу. Сначала немного преобразуем исходное выражение:
y = 5x − 5 ln (x + 5)
Это и есть вынесение степени за знак логарифма. Считаем производную:
Дальше все стандартно. Нас интересует значение функции, поэтому приравниваем числитель к нулю:
5x + 20 = 0;
x = −4.
Полученное число x = −4 ∈ [−4; 1] совпадает с концом отрезка, поэтому кандидатов на наименьшее значение всего два: −4 и 1. Оба числа подходят по ОДЗ. Поскольку требуется найти наименьшее значение, подставляем эти числа в исходную функцию:
y (−4) = 5 · (−4) − 5 · ln (−4 + 5) = −20 − 5 · ln 1 = −20;
y (1) = 5 · 1 − 5 · ln (1 + 5) = 5 − 5 ln 6.
Второе число — точно не ответ, поскольку его нельзя представить в виде десятичного числа. Значит, наименьшее значение функции равно −20.
Задача. Найдите точку максимума функции:
y = 18 ln x − x2 + 5
ОДЗ логарифма: x > 0 ⇒ x ∈ (0; +∞). Считаем производную:
Поскольку требуется найти точку максимума, нас интересует и числитель, и знаменатель. Приравниваем их к нулю:
2 · (9 − x2) = 0 ⇒ x2 = 9 ⇒ x = ±3 — числитель;
x = 0 — знаменатель.
Получили три точки. Отмечаем эти точки и знаки производной на числовой прямой:
Требуется найти точку максимума — там, где плюс меняется на минус. Таких точек две: x = −3и x = 3. Но вспомним ОДЗ: x ∈ (0; +∞). Значит, точка x = −3 не подходит. Остается точка x = 3 — это и будет ответ.
Смотрите также:
- Показательные функции в задаче B15
- Задача B15: частный случай при работе с квадратичной функцией
- Что такое числовая дробь
- Основное тригонометрическое тождество
- Пробный ЕГЭ по математике 2015: 5 вариант
- Формула простого процента: неизвестно конечное значение
| 1 | Найдите производную — d / dx | натуральное журнал x | |
| 2 | Оцените интеграл | интеграл натурального логарифма x относительно x | |
| 3 | Найдите производную — d / dx | е ^ х | |
| 4 | Оцените интеграл | интеграл от e ^ (2x) относительно x | |
| 5 | Найдите производную — d / dx | 1 / х | |
| 6 | Найдите производную — d / dx | х ^ 2 | |
| 7 | Найдите производную — d / dx | 1 / (х ^ 2) | |
| 8 | Найдите производную — d / dx | грех (х) ^ 2 | |
| 9 | Найдите производную — d / dx | сек (x) | |
| 10 | Оцените интеграл | интеграл e ^ x относительно x | |
| 11 | Оцените интеграл | интеграл x ^ 2 относительно x | |
| 12 | Оцените интеграл | интеграл квадратного корня x относительно x | |
| 13 | Найдите производную — d / dx | соз (х) ^ 2 | |
| 14 | Оцените интеграл | интеграл от 1 / x по отношению к x | |
| 15 | Оцените интеграл | интеграл sin (x) ^ 2 относительно x | |
| 16 | Найдите производную — d / dx | х ^ 3 | |
| 17 | Найдите производную — d / dx | сек (x) ^ 2 | |
| 18 | Оцените интеграл | интеграл cos (x) ^ 2 относительно x | |
| 19 | Оцените интеграл | интеграл от sec (x) ^ 2 относительно x | |
| 20 | Найдите производную — d / dx | е ^ (х ^ 2) | |
| 21 | Оцените интеграл | интеграл от 0 до 1 кубического корня из 1 + 7x относительно x | |
| 22 | Найдите производную — d / dx | грех (2x) | |
| 23 | Найдите производную — d / dx | загар (x) ^ 2 | |
| 24 | Оцените интеграл | интеграл 1 / (x ^ 2) относительно x | |
| 25 | Найдите производную — d / dx | 2 ^ х | |
| 26 | График | натуральное бревно из | |
| 27 | Найдите производную — d / dx | cos (2x) | |
| 28 | Найдите производную — d / dx | хе ^ х | |
| 29 | Оцените интеграл | интеграл от 2x относительно x | |
| 30 | Найдите производную — d / dx | (натуральный логарифм x) ^ 2 | |
| 31 | Найдите производную — d / dx | натуральный логарифм (x) ^ 2 | |
| 32 | Найдите производную — d / dx | 3x ^ 2 | |
| 33 | Оцените интеграл | интеграл xe ^ (2x) относительно x | |
| 34 | Найдите производную — d / dx | 2e ^ x | |
| 35 | Найдите производную — d / dx | натуральное бревно 2x | |
| 36 | Найдите производную — d / dx | -sin (х) | |
| 37 | Найдите производную — d / dx | 4x ^ 2-x + 5 | |
| 38 | Найдите производную — d / dx | y = 16 корень четвертой степени из 4x ^ 4 + 4 | |
| 39 | Найдите производную — d / dx | 2x ^ 2 | |
| 40 | Оцените интеграл | интеграл e ^ (3x) относительно x | |
| 41 | Оцените интеграл | интеграл cos (2x) относительно x | |
| 42 | Найдите производную — d / dx | 1 / (квадратный корень из x) | |
| 43 | Оцените интеграл | интеграл e ^ (x ^ 2) относительно x | |
| 44 | Оценить | e ^ бесконечность | |
| 45 | Найдите производную — d / dx | х / 2 | |
| 46 | Найдите производную — d / dx | -cos (x) | |
| 47 | Найдите производную — d / dx | грех (3x) | |
| 48 | Найдите производную — d / dx | 1 / (х ^ 3) | |
| 49 | Оцените интеграл | интеграл от tan (x) ^ 2 относительно x | |
| 50 | Оцените интеграл | интеграл 1 по x | |
| 51 | Найдите производную — d / dx | х ^ х | |
| 52 | Найдите производную — d / dx | x натуральное бревно x | |
| 53 | Найдите производную — d / dx | х ^ 4 | |
| 54 | Оценить предел | предел, когда x приближается к 3 из (3x-5) / (x-3) | |
| 55 | Оцените интеграл | интеграл x ^ 2 натуральный логарифм x относительно x | |
| 56 | Найдите производную — d / dx | f (x) = квадратный корень из x | |
| 57 | Найдите производную — d / dx | х ^ 2sin (х) | |
| 58 | Оцените интеграл | интеграл sin (2x) относительно x | |
| 59 | Найдите производную — d / dx | 3e ^ x | |
| 60 | Оцените интеграл | интеграл xe ^ x относительно x | |
| 61 | Найдите производную — d / dx | у = х ^ 2 | |
| 62 | Найдите производную — d / dx | квадратный корень из x ^ 2 + 1 | |
| 63 | Найдите производную — d / dx | грех (x ^ 2) | |
| 64 | Оцените интеграл | интеграл от e ^ (- 2x) относительно x | |
| 65 | Оцените интеграл | интеграл натурального логарифма квадратного корня x относительно x | |
| 66 | Найдите производную — d / dx | е ^ 2 | |
| 67 | Найдите производную — d / dx | х ^ 2 + 1 | |
| 68 | Оцените интеграл | интеграл sin (x) относительно x | |
| 69 | Найдите производную — d / dx | арксин (х) | |
| 70 | Оценить предел | предел, когда x приближается к 0 of (sin (x)) / x | |
| 71 | Оцените интеграл | интеграл e ^ (- x) относительно x | |
| 72 | Найдите производную — d / dx | х ^ 5 | |
| 73 | Найдите производную — d / dx | 2 / х | |
| 74 | Найдите производную — d / dx | натуральное бревно из 3х | |
| 75 | Найдите производную — d / dx | х ^ (1/2) | |
| 76 | Найдите производную — d / d @ VAR | f (x) = квадратный корень из x | |
| 77 | Найдите производную — d / dx | соз (x ^ 2) | |
| 78 | Найдите производную — d / dx | 1 / (х ^ 5) | |
| 79 | Найдите производную — d / dx | кубический корень из x ^ 2 | |
| 80 | Оцените интеграл | интеграл cos (x) относительно x | |
| 81 | Оцените интеграл | интеграл e ^ (- x ^ 2) относительно x | |
| 82 | Найдите производную — d / d @ VAR | е (х) = х ^ 3 | |
| 83 | Оцените интеграл | интеграл от 0 до 10 из 4x ^ 2 + 7 по x | |
| 84 | Оцените интеграл | интеграл (натуральный логарифм x) ^ 2 относительно x | |
| 85 | Найдите производную — d / dx | журнал x | |
| 86 | Найдите производную — d / dx | арктан (x) | |
| 87 | Найдите производную — d / dx | натуральное бревно 5x | |
| 88 | Найдите производную — d / dx | 5e ^ x | |
| 89 | Найдите производную — d / dx | cos (3x) | |
| 90 | Оцените интеграл | интеграл x ^ 3 относительно x | |
| 91 | Оцените интеграл | интеграл x ^ 2e ^ x относительно x | |
| 92 | Найдите производную — d / dx | Корень четвертой степени из 4x ^ 4 + 4 (16) | |
| 93 | Найдите производную — d / dx | х / (е ^ х) | |
| 94 | Оценить предел | предел, когда x приближается к 3 от arctan (e ^ x) | |
| 95 | Оцените интеграл | интеграл от (e ^ x-e ^ (- x)) / (e ^ x + e ^ (- x)) относительно x | |
| 96 | Найдите производную — d / dx | 3 ^ х | |
| 97 | Оцените интеграл | интеграл xe ^ (x ^ 2) относительно x | |
| 98 | Найдите производную — d / dx | 2sin (х) | |
| 99 | Оценить | сек (0) ^ 2 | |
| 100 | Найдите производную — d / dx | натуральный логарифм x ^ 2 |
| 1 | Найдите производную — d / dx | натуральное журнал x | |
| 2 | Оцените интеграл | интеграл натурального логарифма x относительно x | |
| 3 | Найдите производную — d / dx | е ^ х | |
| 4 | Оцените интеграл | интеграл от e ^ (2x) относительно x | |
| 5 | Найдите производную — d / dx | 1 / х | |
| 6 | Найдите производную — d / dx | х ^ 2 | |
| 7 | Найдите производную — d / dx | 1 / (х ^ 2) | |
| 8 | Найдите производную — d / dx | грех (х) ^ 2 | |
| 9 | Найдите производную — d / dx | сек (x) | |
| 10 | Оцените интеграл | интеграл e ^ x относительно x | |
| 11 | Оцените интеграл | интеграл x ^ 2 относительно x | |
| 12 | Оцените интеграл | интеграл квадратного корня x относительно x | |
| 13 | Найдите производную — d / dx | соз (х) ^ 2 | |
| 14 | Оцените интеграл | интеграл от 1 / x по отношению к x | |
| 15 | Оцените интеграл | интеграл sin (x) ^ 2 относительно x | |
| 16 | Найдите производную — d / dx | х ^ 3 | |
| 17 | Найдите производную — d / dx | сек (x) ^ 2 | |
| 18 | Оцените интеграл | интеграл cos (x) ^ 2 относительно x | |
| 19 | Оцените интеграл | интеграл от sec (x) ^ 2 относительно x | |
| 20 | Найдите производную — d / dx | е ^ (х ^ 2) | |
| 21 | Оцените интеграл | интеграл от 0 до 1 кубического корня из 1 + 7x относительно x | |
| 22 | Найдите производную — d / dx | грех (2x) | |
| 23 | Найдите производную — d / dx | загар (x) ^ 2 | |
| 24 | Оцените интеграл | интеграл 1 / (x ^ 2) относительно x | |
| 25 | Найдите производную — d / dx | 2 ^ х | |
| 26 | График | натуральное бревно из | |
| 27 | Найдите производную — d / dx | cos (2x) | |
| 28 | Найдите производную — d / dx | хе ^ х | |
| 29 | Оцените интеграл | интеграл от 2x относительно x | |
| 30 | Найдите производную — d / dx | (натуральный логарифм x) ^ 2 | |
| 31 | Найдите производную — d / dx | натуральный логарифм (x) ^ 2 | |
| 32 | Найдите производную — d / dx | 3x ^ 2 | |
| 33 | Оцените интеграл | интеграл xe ^ (2x) относительно x | |
| 34 | Найдите производную — d / dx | 2e ^ x | |
| 35 | Найдите производную — d / dx | натуральное бревно 2x | |
| 36 | Найдите производную — d / dx | -sin (х) | |
| 37 | Найдите производную — d / dx | 4x ^ 2-x + 5 | |
| 38 | Найдите производную — d / dx | y = 16 корень четвертой степени из 4x ^ 4 + 4 | |
| 39 | Найдите производную — d / dx | 2x ^ 2 | |
| 40 | Оцените интеграл | интеграл e ^ (3x) относительно x | |
| 41 | Оцените интеграл | интеграл cos (2x) относительно x | |
| 42 | Найдите производную — d / dx | 1 / (квадратный корень из x) | |
| 43 | Оцените интеграл | интеграл e ^ (x ^ 2) относительно x | |
| 44 | Оценить | e ^ бесконечность | |
| 45 | Найдите производную — d / dx | х / 2 | |
| 46 | Найдите производную — d / dx | -cos (x) | |
| 47 | Найдите производную — d / dx | грех (3x) | |
| 48 | Найдите производную — d / dx | 1 / (х ^ 3) | |
| 49 | Оцените интеграл | интеграл tan (x) ^ 2 относительно x | |
| 50 | Оцените интеграл | интеграл 1 по x | |
| 51 | Найдите производную — d / dx | х ^ х | |
| 52 | Найдите производную — d / dx | x натуральное бревно x | |
| 53 | Найдите производную — d / dx | х ^ 4 | |
| 54 | Оценить предел | предел, когда x приближается к 3 из (3x-5) / (x-3) | |
| 55 | Оцените интеграл | интеграл x ^ 2 натуральный логарифм x относительно x | |
| 56 | Найдите производную — d / dx | f (x) = квадратный корень из x | |
| 57 | Найдите производную — d / dx | х ^ 2sin (х) | |
| 58 | Оцените интеграл | интеграл sin (2x) относительно x | |
| 59 | Найдите производную — d / dx | 3e ^ x | |
| 60 | Оцените интеграл | интеграл xe ^ x относительно x | |
| 61 | Найдите производную — d / dx | у = х ^ 2 | |
| 62 | Найдите производную — d / dx | квадратный корень из x ^ 2 + 1 | |
| 63 | Найдите производную — d / dx | грех (x ^ 2) | |
| 64 | Оцените интеграл | интеграл от e ^ (- 2x) относительно x | |
| 65 | Оцените интеграл | интеграл натурального логарифма квадратного корня x относительно x | |
| 66 | Найдите производную — d / dx | е ^ 2 | |
| 67 | Найдите производную — d / dx | х ^ 2 + 1 | |
| 68 | Оцените интеграл | интеграл sin (x) относительно x | |
| 69 | Найдите производную — d / dx | арксин (х) | |
| 70 | Оценить предел | предел, когда x приближается к 0 of (sin (x)) / x | |
| 71 | Оцените интеграл | интеграл e ^ (- x) относительно x | |
| 72 | Найдите производную — d / dx | х ^ 5 | |
| 73 | Найдите производную — d / dx | 2 / х | |
| 74 | Найдите производную — d / dx | натуральное бревно из 3х | |
| 75 | Найдите производную — d / dx | х ^ (1/2) | |
| 76 | Найдите производную — d / d @ VAR | f (x) = квадратный корень из x | |
| 77 | Найдите производную — d / dx | соз (х ^ 2) | |
| 78 | Найдите производную — d / dx | 1 / (х ^ 5) | |
| 79 | Найдите производную — d / dx | кубический корень из x ^ 2 | |
| 80 | Оцените интеграл | интеграл cos (x) относительно x | |
| 81 | Оцените интеграл | интеграл e ^ (- x ^ 2) относительно x | |
| 82 | Найдите производную — d / d @ VAR | е (х) = х ^ 3 | |
| 83 | Оцените интеграл | интеграл от 0 до 10 из 4x ^ 2 + 7 по x | |
| 84 | Оцените интеграл | интеграл (натуральный логарифм x) ^ 2 относительно x | |
| 85 | Найдите производную — d / dx | журнал x | |
| 86 | Найдите производную — d / dx | арктан (x) | |
| 87 | Найдите производную — d / dx | натуральное бревно 5x | |
| 88 | Найдите производную — d / dx | 5e ^ x | |
| 89 | Найдите производную — d / dx | cos (3x) | |
| 90 | Оцените интеграл | интеграл x ^ 3 относительно x | |
| 91 | Оцените интеграл | интеграл x ^ 2e ^ x относительно x | |
| 92 | Найдите производную — d / dx | 16 корень четвертой степени из 4x ^ 4 + 4 | |
| 93 | Найдите производную — d / dx | х / (е ^ х) | |
| 94 | Оценить предел | предел, когда x приближается к 3 от arctan (e ^ x) | |
| 95 | Оцените интеграл | интеграл от (e ^ x-e ^ (- x)) / (e ^ x + e ^ (- x)) относительно x | |
| 96 | Найдите производную — d / dx | 3 ^ х | |
| 97 | Оцените интеграл | интеграл xe ^ (x ^ 2) относительно x | |
| 98 | Найдите производную — d / dx | 2sin (х) | |
| 99 | Оценить | сек (0) ^ 2 | |
| 100 | Найдите производную — d / dx | натуральный логарифм x ^ 2 |
Производные логарифмических функций | Блестящая вики по математике и науке
Исходя из первых принципов, ddxf (x) = limh → 0f (x + h) −f (x) h \ frac {d} {dx} f (x) = \ displaystyle \ lim_ {h \ rightarrow 0} {\ dfrac {f (x + h) -f (x)} {h}} dxd f (x) = h → 0lim hf (x + h) −f (x).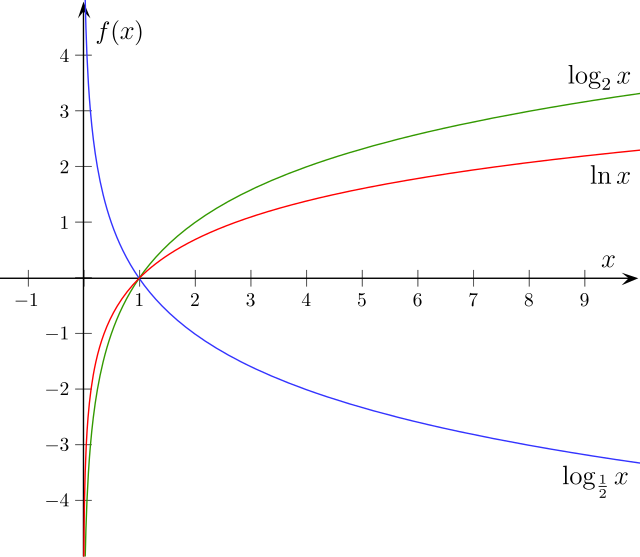 {\ frac {x} {h}}}} {x}}
\\ & = \ lim_ {h \ rightarrow 0} {\ dfrac {\ ln {e}} {x}}
\\ & = \ dfrac {1} {x}. \ _ \ квадрат
\ end {align} dxd f (x) = h → 0lim hln (x + h) −lnx = h → 0lim xhx ln (1 + xh) = h → 0lim xln (1+ xh) hx = h → 0lim xlne = x1. □
{\ frac {x} {h}}}} {x}}
\\ & = \ lim_ {h \ rightarrow 0} {\ dfrac {\ ln {e}} {x}}
\\ & = \ dfrac {1} {x}. \ _ \ квадрат
\ end {align} dxd f (x) = h → 0lim hln (x + h) −lnx = h → 0lim xhx ln (1 + xh) = h → 0lim xln (1+ xh) hx = h → 0lim xlne = x1. □
Найти производную lnx \ ln {x} lnx при x = 2x = 2x = 2.
У нас
ddxlnx = 1x. \ dfrac {\ text {d}} {\ text {d} x} \ ln {x} = \ dfrac {1} {x} .dxd lnx = x1.
Отсюда
ddxlnx∣x = 2 = 12. □ \ dfrac {\ text {d}} {\ text {d} x} \ ln x \ Bigg | _ {x = 2} = \ dfrac {1} {2}.\ _ \ в квадрате xd lnx 2 x = 2 = 21. □
Дифференцировать ln5x \ ln 5xln5x
Решение 1: Используйте правило цепочки.
Пусть f (x) = lnxf (x) = \ ln xf (x) = lnx и g (x) = 5xg (x) = 5xg (x) = 5x. Затем нас просят найти (f∘g) ′ (f \ circ g) ‘(f∘g) ′.
Используя цепное правило, мы знаем, что (f∘g) ′ = (f′∘g) × g ′. (F \ circ g) ‘= (f’ \ circ g) \ times g ‘. (f∘g) ′ = (f′∘g) × g ′.
Поскольку f′∘g = 15xf ‘\ circ g = \ frac {1} {5x} f′∘g = 5×1 и g ′ (x) = 5, g’ (x) = 5, g ′ (x) = 5, имеем (f∘g) ′ = 15x × 5 = 1x.□ (f \ circ g) ‘= \ frac {1} {5x} \ times 5 = \ frac {1} {x}. \ _ \ Square (f∘g) ′ = 5×1 × 5 = x1. □
Решение 2: Используйте свойства логарифмов.
Нам известно свойство логарифмов logab + logac = logabc \ log_a b + \ log_a c = \ log_a bcloga b + loga c = loga bc. Используя это свойство,
ln5x = lnx + ln5. \ ln 5x = \ ln x + \ ln 5. ln5x = lnx + ln5.
Если мы различим обе стороны, мы увидим, что
ddxln5x = ddxlnx \ dfrac {\ text {d}} {\ text {d} x} \ ln 5x = \ dfrac {\ text {d}} {\ text {d} x} \ ln xdxd ln5x = dxd lnx
, поскольку дифференцирование ln5 \ ln 5ln5, которое является константой, равно 0.0,0.
Мы видели, что ddxlnx = 1x \ frac {\ text {d}} {\ text {d} x} \ ln x = \ frac {1} {x} dxd lnx = x1, и это ответ на этот вопрос. □ _ \ квадрат □
Обобщение: Для любого положительного действительного числа ppp мы можем заключить, что ddxlnpx = 1x \ frac {\ text {d}} {\ text {d} x} \ ln px = \ frac {1} {x} dxd Lnpx = x1. Обратите внимание, что производная не зависит от ppp. Это можно проверить, написав ppp вместо 555 в приведенных выше решениях.
Обратите внимание, что производная не зависит от ppp. Это можно проверить, написав ppp вместо 555 в приведенных выше решениях.
Mathscene — Показатели и логарифмы
Mathscene — Показатели и логарифмы — Урок 3| 2007 Rasmus ehf и Джанн Сак Птурссон | Экспоненты и логарифмы | печать |
Урок 3
Естественный логарифмы
Поскольку калькуляторы и компьютеры стали инструменты для большинства числовых операций, логарифмы с основанием 10 стали менее полезно.С другой стороны, логарифм с другим основанием чем 10, становится все более полезным во многих науках.
Эта функция называется функцией натурального логарифма и имеет символ пер.
f (x) = ln x
Основание натурального логарифма — число e
что вы можете увидеть на своем калькуляторе.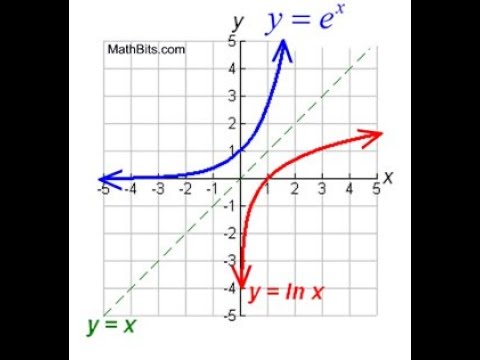
e — иррациональное число e2.718
| Пример 1 |
Вот как вы находите натуральный логарифм 2 на калькуляторе CASIO:
Ответ примерно 0.693 — это степень, в которую нам нужно возвести е, чтобы получить 2.
е 0 . 693 ≈ 2
Проверь это на себе калькулятор:
Ответ: 1.9997 ≈ 2.
Функции f (x) = ln x и g (x) = e x отменяют каждый other out, когда одна функция используется для результата другой. Это то же, что и с f (x) = log x и g (x) = 10 x или возведение числа в квадрат, а затем извлечение квадратного корня из результата.Другими словами функция f (x) = ln x является обратной функцией g (x) = e x .
Верно следующее: ln e x = x og e ln х = х
Число е иррационально
и поэтому мы не можем найти для него точное значение.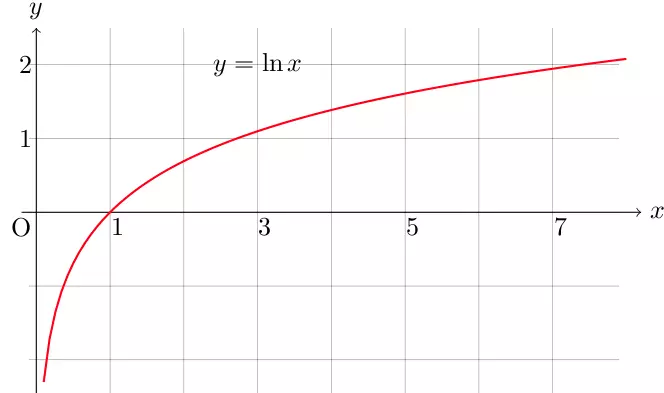
Мы можем вычислить его значение до любого количества десятичных знаков, выбрав большее
и большие значения x и поместив их в следующую формулу.
Пример 2
Вычислите e, положив x = 1000 в формулу и с помощью калькулятора.
Используя EXCEL получаем значение 2.7182818284591 для e. Таким образом, выбор x = 1000 дает нам только два правильных цифры. Теперь попробуйте вычислить e, используя x = 1000000.
Теперь у нас есть пять правильных цифр. Чем выше значение x тем больше точность в нашем вычислении e.
Пример 3
Нарисуйте графики функции f (x) = ln x и g (x) = e x .
Первый составить таблицу значений:
| x | f (x) = e x | x | г (х) = ln x | |
| -3 | 0,05 | -1. 39 39 | ||
| -2 | 0,14 | -0,69 | ||
| -1 | 0,37 | 1 | 0 | |
| 0 | 1 | 2 | 0,69 | |
| 1 | 2,72 | 4 | 1.39 | |
| 2 | 7,39 | 8 | 2,08 |
Обратите внимание, что нет отрицательного
значения в столбце для g (x) = e x и нет отрицательных значений в столбце x для обратной функции g (x) =
ln x.
Область для f (x) = ln x есть множество {xR | х> 0}.
Обратите внимание, что когда мы рисуем оба графика в одном
система координат они зеркальное отображение каждого
прочее (симметричное) в строке проведенный через точки, где y = x.
Это верно для графиков любых двух функций, обратных друг другу.
Те же правила действуют для натуральная логарифмическая функция
Следующие примеры показывают как используются эти правила.
Пример 4
Решите следующие уравнения:
а)
| Двигаться
2 и напишите как степень.Введите число e с обеих сторон уравнения. e и ln отменяют друг друга оставляя нас с квадратным уравнением. Перемещение x над знаком равенства. Разложите на множители и решите относительно x |
x = 0 невозможно, так как там
это не способ записать 0 как степень.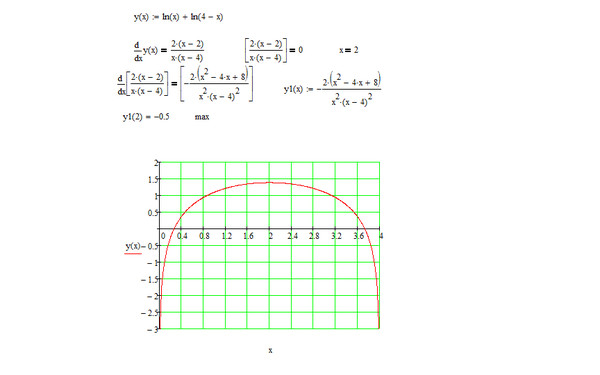
б)
| Написать
левая часть как один логарифм. Положить в базовом числе e. ln и e нейтрализуют друг друга. |
c)
| Упростить слева, записав как один логарифм. |
| Вставить основание е с двух сторон. | |
Пример 5
Решите следующие уравнения:
а)
| Взять логарифм обеих сторон . |
б)
Использование правила: a x a y = a x + y , a x / a y = a x − y a n d(a n ) m = a нм к
запишите каждую сторону как степень e . |
c)
Использование правила: a x a y = a x + y и x / a y = a x − y для записи каждой стороны как мощность эл. |
Пример 6
Решите уравнения:
а)
Взять логарифм обеих сторон уравнения, затем используйте правило а x = x ln a для перемещения неизвестное значение вниз перед пер. |
б)
Взять
члены в x к одной стороне уравнения и другие члены к другой
боковая сторона. |
c)
Отдельно силы 5.разделите обе стороны на 25, затем решите относительно x, как и раньше . |
Попробуйте пройти тест 3 по показателям экспонент и логарифмы.
Не забудьте использовать контрольный список, чтобы отслеживать свою работу.
Логарифмическое дифференцирование
Метод дифференцирования функций путем сначала логарифмирования, а затем дифференцирования называется логарифмическим дифференцированием.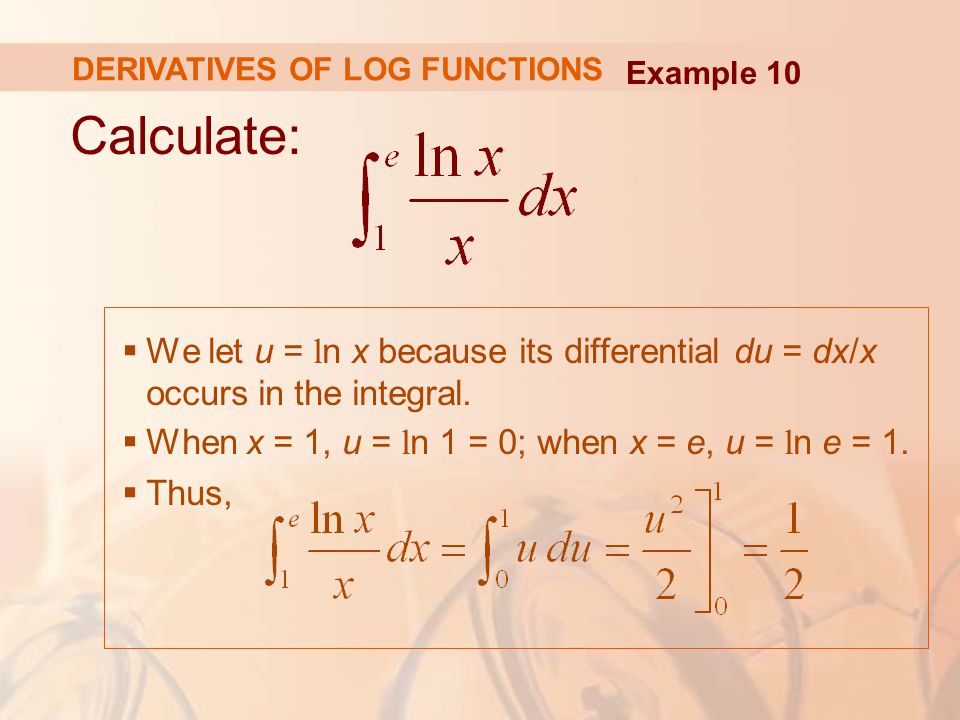 Мы используем логарифмическое дифференцирование в ситуациях, когда легче дифференцировать логарифм функции, чем дифференцировать саму функцию. Такой подход позволяет эффективно вычислять производные от степенных, рациональных и некоторых иррациональных функций.
Мы используем логарифмическое дифференцирование в ситуациях, когда легче дифференцировать логарифм функции, чем дифференцировать саму функцию. Такой подход позволяет эффективно вычислять производные от степенных, рациональных и некоторых иррациональных функций.
Рассмотрим этот способ подробнее. Пусть \ (y = f \ left (x \ right) \). Возьмите натуральный логарифм от обеих сторон:
\ [\ ln y = \ ln f \ left (x \ right). \]
Затем мы дифференцируем это выражение с помощью цепного правила и помня, что \ (y \) является функцией \ (x.{2x}} \ left ({\ ln x + 1} \ right).}
\]
графическое представление функции x * ln (x) -x
× Программное обеспечение для построения графиков онлайн , также известное как графопостроитель ,
представляет собой онлайн-плоттер кривых , который позволяет строить графики функций в интерактивном режиме.
Просто введите выражение в соответствии с x функции, которую нужно построить, используя обычные математические операторы. Для мощности
Для мощности
Это программное обеспечение для построения кривых позволяет использовать следующие стандартные математические функции :
- абс (абсолютное значение), абсолютное значение графика
- arccos (арккосинус), сюжет арккосинус
- арксин (арксинус), сюжет арксинус
- арктангенс (арктангенс), арктангенс графика
- ch (гиперболический косинус), построить гиперболический косинус
- cos (косинус), сюжетный косинус
- котан (котангенс), котангенс участка
- котангенс (гиперболический котангенс), гиперболический котангенс графика
- cube_root (кубический корень), Построить кубический корень
- exp (экспонента), сюжет экспоненциальный
- ln (наперский логарифм), график наперовского логарифма
- лог (логарифм), логарифм графика
- ш (гиперболический синус), график гиперболический синус
- sin (синус), сюжетный синус
- sqrt (квадратный корень), квадратный корень из участка
- загар (тангенс), касательная к сюжету
- -я (гиперболический тангенс), построить гиперболический тангенс
- График функций онлайн
Этот онлайн-плоттер позволяет рисовать несколько кривых одновременно ,
просто введите выражение функции, которую нужно построить, и нажмите «Добавить», графическое представление функции появляется мгновенно, можно повторить операцию , чтобы построить другие кривые онлайн .
Для представления функций используется переменная «x».
С помощью курсора можно получить координаты точек на кривой . Для этого щелкните кривую, чтобы появился курсор, а затем перетащите ее вдоль кривой, чтобы увидеть ее координаты.
Кривые можно снимать с плоттера:
- Чтобы удалить кривую, выберите кривую, затем нажмите кнопку удаления в меню.
- Чтобы удалить все кривые с графика, нажмите кнопку «Удалить все» в меню.
Можно изменить кривую, представленную на графике, выбрав ее, отредактировав ее выражение, а затем щелкнув на кнопке редактирования.
Онлайн-плоттер имеет несколько опций, которые позволяют настраивать график.
Чтобы получить доступ к этим параметрам, нажмите кнопку параметров.Затем можно определить границы графиков,
чтобы подтвердить эти изменения, необходимо еще раз нажать кнопку «Параметры».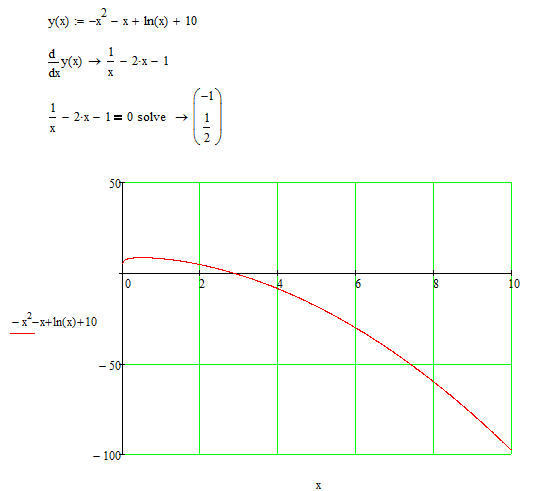
- Проведите касательную функции к точке
- Построить график производной функции
Онлайн-плоттер позволяет построить касательную функции в точке , чтобы сделать это, вы просто нарисуете желаемую функцию, а затем, когда функция будет нарисована, щелкните меню, параметры, а затем кнопку касательной, которая появляется на экране, затем рисуется касательная, можно изменить точку касательной, что приведет к перерисовке касательной.Калькулятор позволяет определить уравнение касательной очень просто, с уравнением кривой.
Онлайн-плоттер позволяет вам построить производную функции для этого,
вы просто рисуете желаемую функцию, а затем после ее рисования
щелкните по меню, по опциям, затем по появившейся производной кнопке,
затем строится производная функции.
Графопостроитель может также использоваться для вычисления производной функции и участок это для этого, вам нужно построить желаемую функцию, затем, когда функция будет нарисована, выберите ее, щелкнув по ней, красный курсор появится на кривой. Затем нажмите на меню, на опции, затем на производную кнопку «выражение», которая появляется на экране, затем строится и вычисляется производная функции.(«Выражение» представляет выражение, которое будет выведено и нанесено на график).
Плоттер позволяет построить параметрическую кривую , для этого
вам просто нужно ввести абсциссу, ординату как функцию от t,
затем нажмите кнопку «построить параметрическую кривую»,
кривая автоматически отображается с двумя курсорами для отображения желаемых точек.
Графопостроитель можно использовать для построения полярной кривой . Для этого просто введите выражение полярной кривой как функцию от t, затем нажмите кнопку «построить полярную кривую», кривая автоматически отобразится с двумя курсорами для отображения желаемых точек.
Есть возможность перемещаться по кривым и получать координаты точки, на которой находится курсор, Для этого необходимо ввести курсор и перемещать его по графику, координаты X и Y отображаются под графиком.
Можно изменить область графика, для этого необходимо войти в меню, затем щелкнуть по опциям,
Затем можно изменить пределы графического отображения.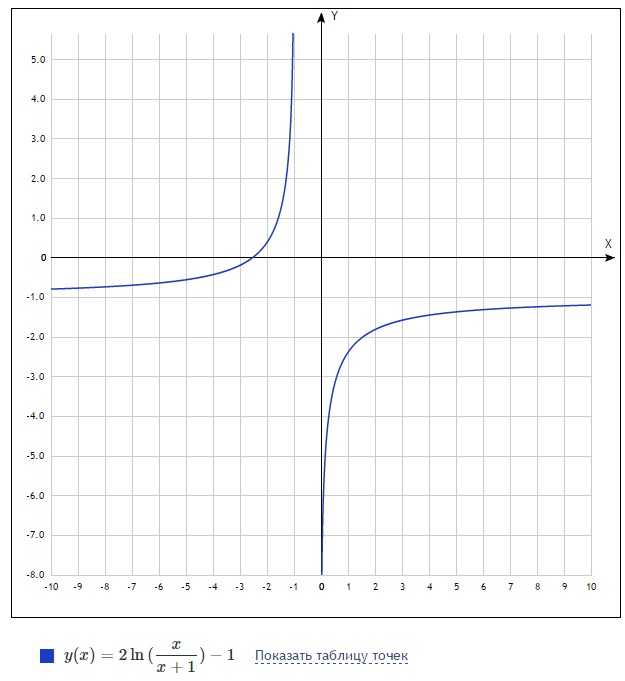
Графический калькулятор предлагает возможность масштабировать и перемещать область графика. Сделать это, используйте область в правом нижнем углу графиков.
- Кнопка + позволяет увеличить масштаб кривых,
- — позволяет уменьшить масштаб кривых,
- Стрелки используются для перемещения кривых,
Построенные кривые можно экспортировать с помощью графического калькулятора , экспорт выполняется как
изображение в формате PNG.Для этого вам нужно перейти в меню графика, затем в подменю экспорта графиков.
Калькулятор затем отображает построенные кривые в виде изображения, просто щелкните правой кнопкой мыши, чтобы экспортировать изображение,
также возможно копирование изображения. Чтобы вернуться к нормальному отображению калькулятора, используйте кнопку «Выйти из режима изображения».
Чтобы вернуться к нормальному отображению калькулятора, используйте кнопку «Выйти из режима изображения».
Справочник логарифмических функций
Это логарифмическая функция:
f (x) = журнал a (x)
— любое значение больше 0, кроме 1
Свойства зависят от значения «а»
- Когда a = 1 , график не определен
- Кроме того, есть два случая, на которые стоит обратить внимание:
| a от 0 до 1 | a выше 1 | |
Пример: f (x) = log ½ (x) | Пример: f (x) = log 2 (x) | |
Для a от 0 до 1 | Для и и выше 1: |
Постройте график здесь (используйте ползунок «a»)
В общем, логарифмическая функция:
- всегда находится на положительной стороне (и никогда не пересекает) оси Y
- всегда пересекает ось x при x = 1.
 .. другими словами он проходит через (1,0)
.. другими словами он проходит через (1,0) - равно 1 , когда x = a , другими словами, он проходит через (a, 1)
- — это инъективная (однозначная) функция
Его домен — положительные действительные числа: (0, + ∞)
Его диапазон — действительные числа:
Обратный
Таким образом, логарифмическая функция может быть «обращена» экспоненциальной функцией.
Функция натурального логарифма
Это «Натуральный» логарифм Функция:
f (x) = журнал e (x)
Где e — «число Эйлера» = 2.718281828459 … и т. Д.
Но чаще пишут так:
f (x) = ln (x)
«ln» означает «бревно, натуральное»
Итак, когда вы видите ln (x), просто помните, что это логарифмическая функция с основанием e : log e (x).
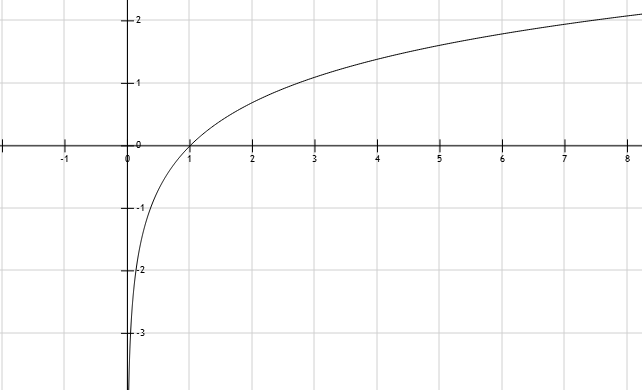
График f (x) = ln (x)
В точке (e, 1) наклон линии равен 1 / e , и прямая касается кривой.

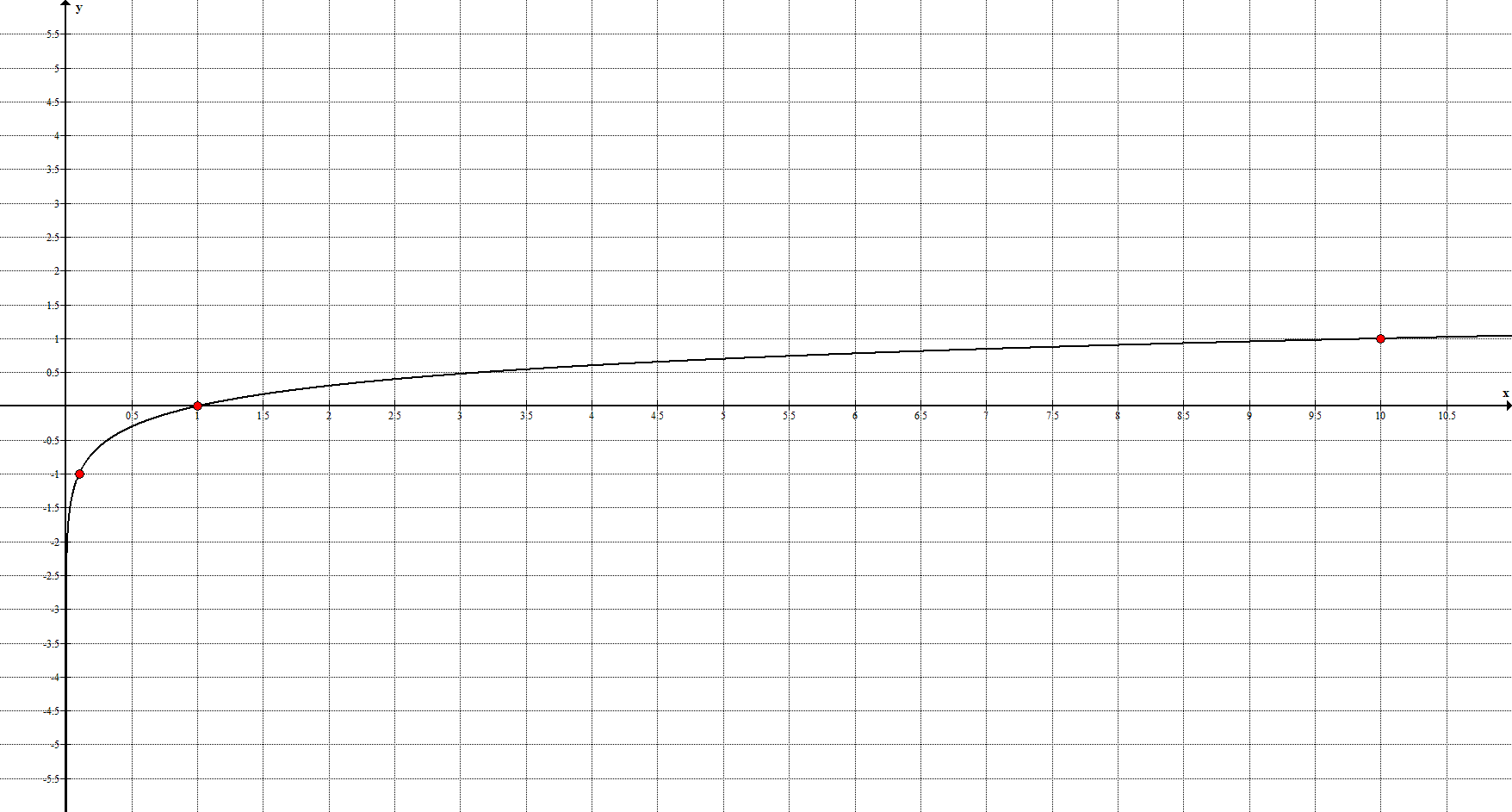
 Докажите самостоятельно.
Докажите самостоятельно.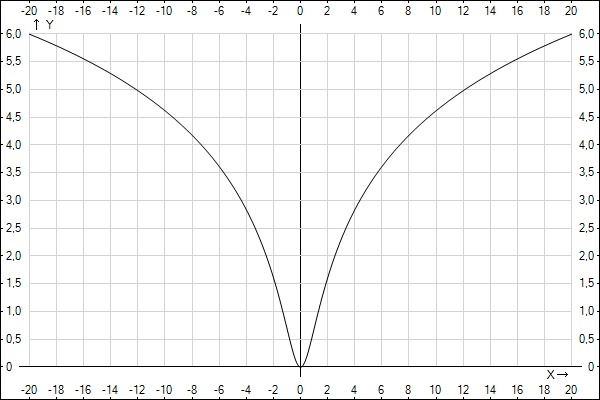
 Упростите использование правил для индексов.
Упростите использование правил для индексов.