Функция y 1 2 x: Mathway | Популярные задачи

2

Математическая грубость (в хорошем смысле слова)

Андроник Арутюнов,
cтарший научный сотрудник ИПУ РАН им. В. А. Трапезникова,
преподаватель Свободного университета,
куратор раздела «Математика» в «Яндекс.Кью»
«Троицкий вариант» №2(370), 24 января 2023 года

Оригинал статьи на сайте «Троицкого варианта»

Когда я (помыв предварительно шею, конечно) заявился рассказывать про грубую геометрию в свою родную «Вторую школу», встреченные коллеги, узнав тему, немедленно хихикнули: «Ну, чего от тебя еще ожидать-то…» Если чуть более серьезно, то грубая геометрия — это достаточно новый раздел математики. Причем, как мне кажется, идеи, заложенные в него, не просто красивы математически, но и в целом чрезвычайно перспективны. Так что я надеюсь, что этот текст не только будет популярно-интересен неспециалистам, но, возможно, заинтересует и побудит коллег к поиску приложений.

Место действия — метрические пространства

Перед тем, как перейти к главному герою — грубым отображениям, сначала нужно определиться с тем, где же будут разворачиваться дальнейшие события. Нудно говоря, метрическое пространство это такая пара (M, ρ) из множества M и функции ρ: M × M → \(\mathbb{R}\), называемой метрикой (иначе — расстоянием), что выполнены следующие свойства:

• ρ(a; b) ≥ 0, ρ(a; b) = 0 ↔ a = b — расстояние неотрицательно и между не совпадающими точками отлично от нуля;
• ρ(a; b) = ρ(b; a) — расстояние симметрично;
• ρ(a; b) + ρ(b; c) ≥ ρ(a; c) — неравенство треугольника.

Сразу скажем, что привычная нам евклидова метрика и другие ее близкие родственники уже соответствуют нашему определению. То же касается и расстояния в графе — минимальной длины пути, соединяющего вершины.

2}}{2 \;\sqrt{y_1 y_2}};
$$

3. Ненаправленный граф γ и функция ρ(a, b) = длина минимального пути из a в b.

Обратим внимание на первый пример. Если p = 2, то мы получаем обычную евклидову метрику. А если p = 1, то так называемую манхеттенскую, или городскую, как иногда говорят. А вот метрика ρ\(\mathcal{H}\) задает геометрию Лобачевского (это когда через данную точку можно провести бесконечно много прямых, параллельных данной). Больше о геометрии Лобачевского можно прочитать в [1].

Перед тем, как мы двинемся дальше, заметим вот еще что. Хоть для разных p метрики и «похожи», но соответствующие метрические пространства заметно отличаются друг от друга. К примеру, кратчайшее расстояние на евклидовой плоскости — это прямая. И между любыми двумя точками существует ровно одна кривая, вдоль которой оно достигается (такая кривая называется геодезической). А вот на плоскости с метрикой 

ρ₁ геодезических между любыми двумя точками уже сколько угодно!

Для аккуратности скажем, что все метрические пространства, о которых мы будем толковать, — так называемые геодезические, т. 2\), ρ_p) изометрическими не будут, хотя с точки зрения внутреннего устройства они друг на друга достаточно похожи. А вот на геометрию Лобачевского, к примеру, они совсем не похожи. Точно так же понятно, что прямую \(\mathbb{R}\) уместно сравнивать с целыми числами \(\mathbb{Z}\), а плоскость — с целочисленной решеткой \(\mathbb{Z}\) × \(\mathbb{Z}\).

Возникает естественное желание найти какое-нибудь условие «равенства», более слабое, чем изометричность, но все-таки имеющее понятный геометрический смысл. При этом хотелось бы, чтобы похожие метрические пространства были «равными», а непохожие — не были. В таком случае мы сможем искать разные инварианты, которые позволят нам отличать похожее от непохожего. Такое условие называется квазиизометричностью.

Итак, назовем отображение F : (M₁, ρ¹) → (M₂, ρ²) квазиизометрией (или грубой изометрией), если:

1. Найдутся константы A, B такие, что

$$
\forall x,y\in M_1: \frac{1}{A}\; \rho^1(x,y)-B\leq \rho^2(f(x),f(y))\leq A\; \rho^1(x,y)+B;
$$

2.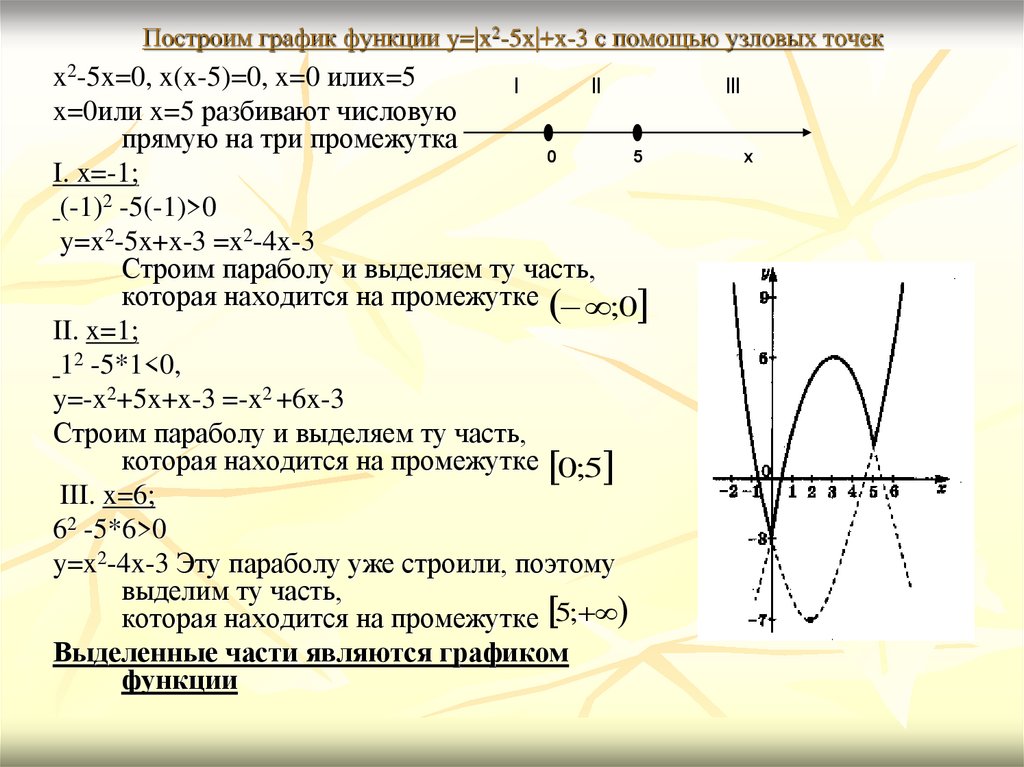 2\), ρ_p) квазиизометричны относительно тождественного отображения id: x ⟼ x. Куда сложнее проверить (но все-таки можно), что они не квазиизометричны геометрии Лобачевского.

Так же заметим, что прямая R (с обычной метрикой) квазиизометрична целым числам \(\mathbb{Z}\) так же, как плоскость (с метриками ρ_p) всегда грубо изометрична целочисленной решетке. Но ни в коем случае не грубо эквивалентна прямой, что тоже можно проверить непосредственно, но ниже мы предложим способ сделать это «автоматически».

Еще можно установить, что разные графы Кэли для одной группы (о которых я рассказывал в [2]) обязательно будут квазиизометричными, хоть и не будут изометричными.

Важная особенность: любое конечное метрическое пространство (в том числе и граф) обязательно грубо эквивалентно точке. Так что вся та наука, которую мы тут обсуждаем, касается только бесконечных пространств и бесконечных графов. И все свои рассуждения мы на самом деле ведем на «большом масштабе» — локально, в отдельной точке, может произойти что угодно.

Конец близок?

Чем отличается прямая от плоскости? Или они обе от пучка лучей, исходящих из одной точки «по всем румбам»? Крупномасштабно, т. е. если посмотреть издалека («вооруженным взглядом»), становится понятно, что разница — в торчащих в разные стороны бесконечных «хвостах», по каждому из которых можно уйти на бесконечность. Строго выражаясь, речь идет о занятном грубом инварианте — числе концов. Дадим сначала определение для графов.

Определение. Будем называть числом концов данного графа γ максимально число бесконечных (!) компонент связности в графах вида γ \ Q, где Q — всевозможные конечные подграфы.

Легко проверить, что число концов (конечное или бесконечное) у разных грубо изометричных пространств обязано совпадать.

Понятно, что у целочисленной решетки на плоскости конец один (как ни вырезай конечную дырку, бесконечный остаток графа будет связен), у прямой — концов два (после вырезания конечной дырки останется два бесконечных луча), а у связки лучей концов столько, сколько лучей.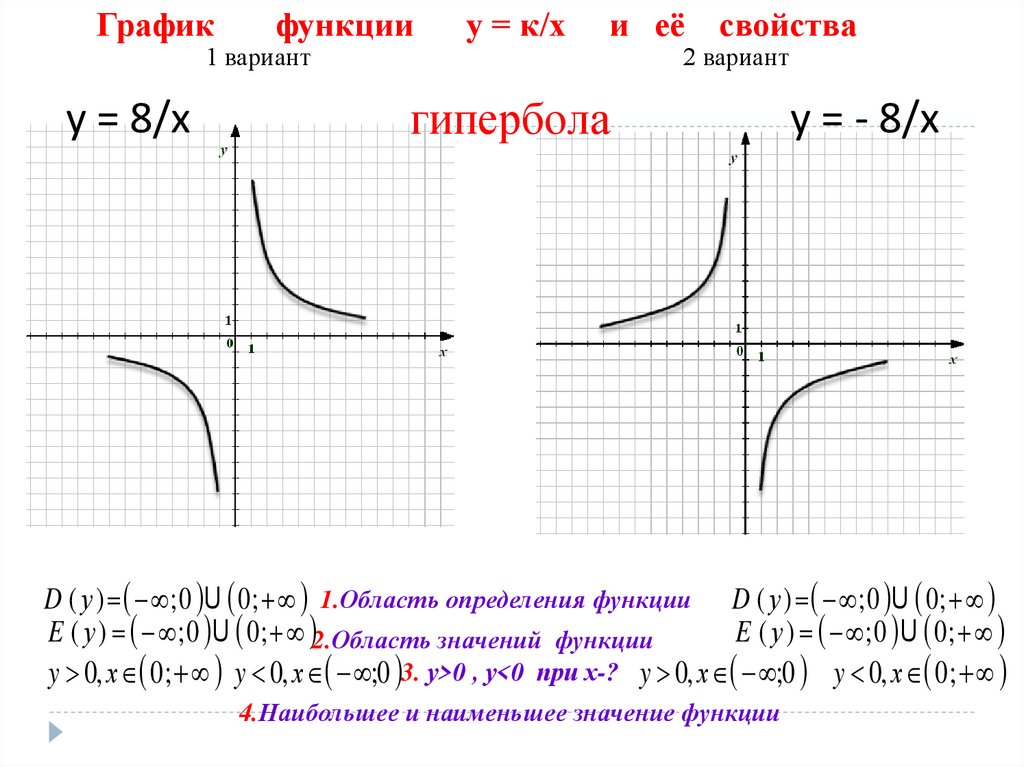 Так что все эти графы не будут грубо эквивалентными, потому что у них число концов разное.

Есть и более занятный пример. Например, у дерева (граф без циклов), в котором есть бесконечно много вершин со степенью три (т. е. вершин, из которых выходит три ребра), концов будет бесконечно много, потому как, вырезая всё больший и больший кусок, мы можем получить сколь угодно много бесконечных компонент связности.

Понятие конца можно обобщить и на случай произвольных метрических пространств.

Определение. Будем называть числом концов данного метрическое пространства (M, ρ) максимальное число бесконечных (!) компонент связности в метрических пространствах вида (M, ρ) \ Q, где Q — всевозможные конечные метрические подпространства.

Как и для графов, легко проверить следующее утверждение. Если два метрических пространства грубо изометричны, то у них число концов одинаково. Обратное, конечно, не верно. Сложный, но важный пример: геометрия Лобачевского имеет один конец, но не грубо изометрична обычной плоскости (у которой снова один конец). Простой (но тоже важный, конечно) пример: целочисленная решетка в трехмерном пространстве и целочисленная решетка на плоскости. Например, ниже нам пригодится гексагональная решетка на плоскости

Внимательный читатель, наверное, заметил, что пока мы оперируем только «числом концов», но сами концы пока не определили. Неформально говоря, конец — это такой способ уйти на бесконечность. Дадим и ученое определение для графов (на метрические пространства оно легко обобщается).

Во-первых, лучом в графе будем называть упорядоченную последовательность соседних вершин. Во-вторых, назовем два луча эквивалентными, если есть третий луч, у которого бесконечно много пересечений с обоими лучами.

В-третьих, концом мы назовем классы эквивалентных концов. Таким образом, конец — это не какой-то отдельный подграф, а некая система внутри графа. Хотя геометрически можно говорить, что на прямой, скажем, есть два конца — «левый» и «правый».

Еще один смешно звучащий термин — это «толстый конец» (иначе, простите, жирный конец — fat end, см. [3], это не я придумал). Собственно говоря, конец называется толстым, если в него входит бесконечно много непересекающихся лучей. Ну и несложно видеть, что, к примеру, на плоскости конец один, но толстый. А в луче конец тоже один, но не толстый (иначе говоря — тонкий).

Оказывается, что верно и обратное. Сформулируем теорему Рудольфа Халина (см. оригинальную работу [4], а излагаем мы по [3]).

Теорема. Если в графе есть толстый конец, то в нем есть подграф, изоморфный подразделению гексагональной решетки.

Иными словами, если есть толстый конец, то в некотором подграфе, лежащем в толстом конце, есть структура гексагональной сетки. Доступное доказательство этой теоремы можно прочитать в [3].

Вообще, решетки — это очень важный элемент грубой геометрии. Фактически речь идет о том, что мы можем любое метрическое пространство свести к решетке, т. е. к системе точек пространства, расстояние между которыми равно всегда целому числу, причем для любой точки пространства найдется хотя бы одна точка решетки на расстоянии не более единицы. Решетки еще тесно связаны с такими вещами, как мозаики и паркеты (и вообще покрытия разных пространств). А если говорить о, что называется, пользе для народного хозяйства, то без них не обойдется кристаллография.

Собственно, теорема Халина позволяет в сложно (и, вообще говоря, непонятно как) устроенном толстом конце найти хорошую внутреннюю структуру.

Добавлю еще, что идея, как по множеству концов понять, каким образом можно достигать бесконечности, крайне продуктивна и позволяет строить «грубые» компактификации метрического пространства. Про три разных варианта таких конструкций можно почитать в препринте исследовательницы Элизы Хартман [5].

Скорости роста

Мы уже говорили, что геометрия Лобачевского не будет грубо изометричной евклидовой. Доказывать это в лоб непросто, и нам потребуется еще один сюжет из грубой геометрии — понятие скорости роста метрического пространства. Кстати, любители теории алгоритмов сейчас увидят много знакомых терминов (и неспроста).

Пусть мы имеем решетку в нашем пространстве M.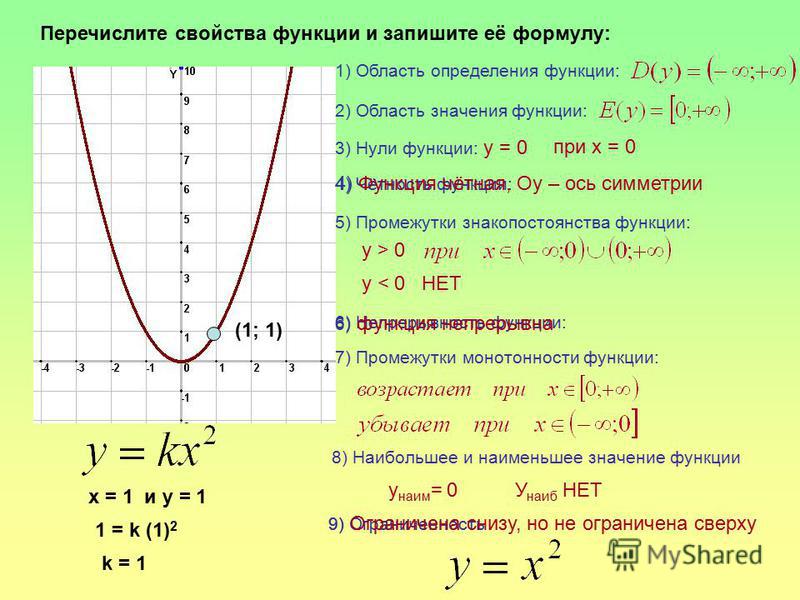  Зафиксируем какую-нибудь точку O и посмотрим на количество точек решетки на расстоянии не более, чем N от O. Получится некоторая функция f_M, O(N). Оказывается, любые две функции роста f, g (при фиксированной метрике и разных точках — началах координат) эквивалентны в следующем смысле

$$
f(n) \leq ag(bn), \quad g(n)\leq c f(dn),
$$

для всех достаточно больших n и некоторых положительных констант a, b, c, d. Короче говоря, функция роста может меняться, но если для одной точки она линейна (квадратична, экспоненциальна, etc), то будет линейной (квадратичной, экспоненциалной, etc) и для любой другой точки. Более того, можно показать, что у двух грубо изометричных пространств функции роста также будут эквивалентны.

Например, для \(\mathbb{Z}\) функция роста линейна, для \(\mathbb{Z}\) × \(\mathbb{Z}\) — квадратична, а для дерева, у которого все вершины имеют степень три, — экспоненциальна.

Если внимательно посчитать (ну или обратиться к соответствующей литературе, например [6]), то окажется, что у пространства с геометрией Лобачевского скорость роста экспоненциальная. А значит, геометрия Лобачевского не может быть грубо изометричной евклидовой.

Кстати, отметим, что вопреки ожиданиям людей, знакомых с проблемой P = N P (подробнее см., например [7]), функции роста даже «интересных» метрических пространств бывают не только полиномиальными и экспоненциальными. Оказывается, бывают регулярно устроенные пространства промежуточного роста (граф Кэли некоторой группы) — соответствующий пример построил в 1983 году Ростислав Григорчук. Подробнее об этом результате и вообще о функциях роста см. в [8].

Вернемся к геометрии Лобачевского и заодно разберемся, почему ее называют гиперболической геометрией. Для этого нам потребуется понятие кривизны.

Строгое определение кривизны требует определенных знаний, которых мы от уважаемого читателя совсем не требуем, поэтому попробуем дать понятие кривизны пространства неформально. Сразу скажу, что в журнале «Квант» есть две замечательные статьи про кривизну, на которые можно обратить внимание [10, 11] для лучшего понимания.

Неформально понятие кривизны на поверхности можно воспринимать следующим образом. Возьмем треугольник, у которого стороны — геодезические. И нарисуем треугольник с такими же сторонами на обычной евклидовой плоскости. Если углы треугольника на плоскости меньше исходного — значит, кривизна отрицательна, если больше — положительна. К примеру, сфера — поверхность положительной кривизны. Там бывают треугольники, у которых все углы прямые (и вообще сумма углов всегда больше 180°). А вот на гиперболоиде (на котором реализуется геометрия Лобачевского, откуда и название) кривизна отрицательна, и углы у гиперболического треугольника всегда меньше углов его плоского аналога.

Как при грубых изометриях устроена кривизна, в своем время исследовал Михаил Громов в [9]. Одним из результатов была «кошачья» классификация пространств CAT(k) по параметру k, отвечающему кривизне.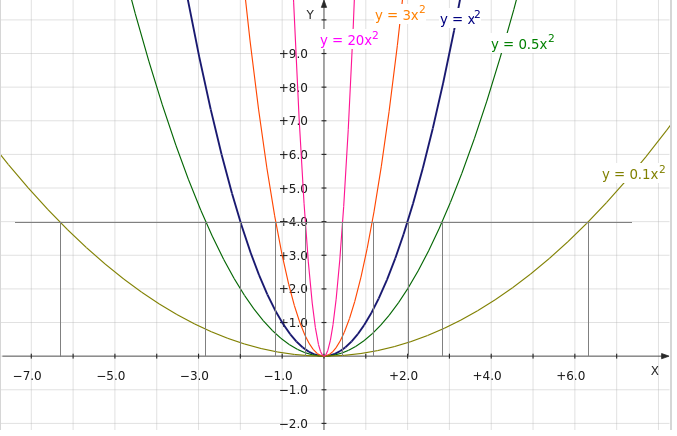  CAT в данном случае — акроним фамилий Эли Жозефа Картана, Александра Даниловича Александрова и Виктора Андреевича Топоногова, чьи работы в свое время и легли в основу этой теории.

Отметим, что при таком подходе работает идея, которую мы описывали выше. Чтобы определить CAT(k)-структуру пространства, тоже достаточно рассмотреть его решетку. К примеру, находясь в нашей вселенной, можно понять, является ли ее пространство гиперболическим или сферическим, изучив его решетку (фактически — распределение массы, как нас учит теория относительности). Главное, чтобы хватило данных!

Заключение

Так чем же занимается грубая геометрия, что она изучает? Сформулируем так: бесконечные метрические пространства и их инварианты, определяющие их крупномасштабную структуру. Нам не важно происходящее локально, в окрестностях точек, важно происходящее в пространстве в целом. Если совсем коротко, то мы не можем грубыми методами исследовать происходящее локально, но зато можем исследовать, если можно так выразиться, космологию пространства.

В современном мире нахождения достаточно точных решений уравнений часто можно добиться «силовыми» вычислительными методами, благо вычислительные мощности сейчас сравнительно доступны. В связи с этим становится куда актуальнее вопрос изучения макроскопических свойств пространств. Некоторые из них мы описали выше. О приложениях к разнообразным математическим вопросам можно почитать в цитированной литературе (особенно рекомендую [6, 9]) и других современных работах по грубой геометрии.

Но интересно подумать и о приложениях грубой геометрии и в целом «крупномасштабного подхода» в естественных науках. Я выше обозначил одно возможное приложение в космологии, но аналогичные вопросы наверняка есть и в других разделах естественнонаучного знания. Например, весьма естественно выглядит грубая структура в кристаллографии. Ну или, к примеру, если мы посмотрим на общество как на граф (люди — вершины, ребра — социальные связи), который при достаточно большом количестве вершин можно условно считать бесконечным, то социологические задачи начинают выглядеть именно как вопросы о грубой структуре этого человеческого графа.

Но постановка более конкретных вопросов и поиск приложений — задача будущих междисциплинарных штудий.

Так что желаю всем нам удачи в исследованиях!

Иллюстрации подготовлены художником и мультипликатором Ксенией Никитиной.

---

1. Прасолов В. Геометрия Лобачевского // МЦНМО, 2004.

2. Арутюнов А. Как правильно гулять по графам Кэли // «Троицкий вариант» №9(353), 17 мая 2022 года.

3. Dlestel R. A short proof of Halin’s grid theorem // Abhandlungen aus dem Mathematischen Seminar der Universitat Hamburg. Vol. 74. P. 237–242 (2004).

4. Halin R. Uber die Maximalzahl fremder unendlicher Wege in Graphen // Math. Nachr. 30 (1965). P. 63–85.

5. Hartmanm E. Coarse compactifications of proper metric spaces // arxiv:2009.08147, 2020.

6. Roe J. Lectures on coarse geometry // Pennsylvania State University, University Park, PA, 2003.

7. Шень А. Проблема перебора // Postnauka, 04.03.2015.

8. Grigorchuk R. , Pak I. Groups of Intermediate Growth, an Introduction // L’Enseignement Mathematique. 2008. Vol. 54. P. 251–272.

9. Gromov M. Hyperbolic groups // Essays in group theory. Math. Sci. Res. Inst. Publ. 8. New York: Springer, 1987. P. 75–263.

10. Виленкин Н. О кривизне // Квант. 1992. № 4. С. 2–9, 15.

11. Табачников С. Л. О кривизне // Квант. 1989. № 6. С. 15–21.

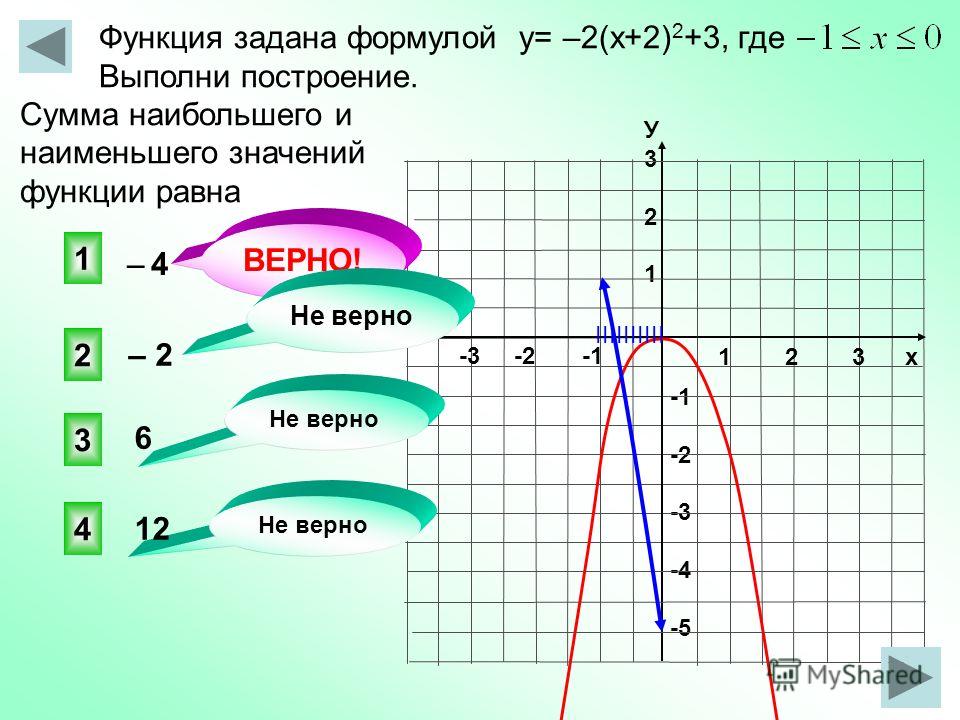
3-8 9 Оценить квадратный корень из 12 10 Оценить квадратный корень из 20 11 Оценить квадратный корень из 50 94 18 Оценить квадратный корень из 45 19 Оценить квадратный корень из 32 20 Оценить квадратный корень из 18 92

Решить Свойства прямой линии y=-1/2x-7 Tiger Algebra Solver

Переставить:

Переставить уравнение, вычитая то, что находится справа от знака равенства из обеих частей уравнения:

                     y -(-1/2*x-7)=0 

Шаг 1 :

 1
 Упростить —
            2
 

Уравнение в конце шага 1 :

 1
  у - ((0 - (— • х)) - 7) = 0
               2
 

Шаг 2 :

Преобразование целого в виде эквивалентной дроби:

 2. 1   Вычитание целого из дроби

Преобразование целого в виде дроби с использованием 2 в качестве знаменателя:

 7 7 • 2
    7 = — = —————
         1 2
 

Эквивалентная дробь: Полученная таким образом дробь выглядит иначе, но имеет то же значение, что и целое

Общий знаменатель: Эквивалентная дробь и другая дробь, участвующая в расчете, имеют один и тот же знаменатель

Сложение дробей, имеющих общий знаменатель:

 2.2       Сложение двух эквивалентных дробей
Сложение двух эквивалентных дробей, которые теперь имеют общий знаменатель самые низкие условия, если это возможно:

 -x - (7 • 2) -x - 14
 "="
      2 2
 

Уравнение в конце шага 2 :

 (-x - 14)
  у - ————————— = 0
           2
 

Шаг 3 :

Преобразование целого в виде эквивалентной дроби:

 3.1   Вычитание дроби из целого

Преобразование целого в виде дроби с использованием 2 в качестве знаменателя:

 y y • 2
     у = — = —————
          1 2
 Шаг 40917 
  4. 2       Сложение двух эквивалентных дробей 
 
 
 y • 2 - ((-x-14)) 2y + x + 14
 "="
         2 2
 
 Уравнение в конце шага 4 : 
 2y + x + 14
  ——————————— = 0
       2
 
   
   
 Шаг 5  : 
 Когда дробь равна нулю : 
  5.1    Когда дробь равна нулю ... 
 Если дробь равна нулю, ее числитель, часть над чертой дроби, должен быть равен нулю.
 Теперь, чтобы избавиться от знаменателя, Тигр умножает обе части уравнения на знаменатель.
 Вот как:
 2y+x+14
  ——————— • 2 = 0 • 2
     2
 
 Теперь в левой части 2 уравновешивает знаменатель, а в правой части ноль, умноженный на что-либо, по-прежнему равен нулю.
 Уравнение теперь принимает форму: 
    2y+x+14  = 0
 Уравнение прямой линии 
  5.2     Решите   2y+x+14  = 0
 Тайгер понимает, что перед нами уравнение прямой линии. Такое уравнение обычно записывается как y=mx+b («y=mx+c» в Великобритании).
 "y=mx+b" - это формула прямой линии в декартовой системе координат, в которой "y" - вертикальная ось, а "x" - горизонтальная ось.
 В этой формуле:
 y говорит нам, как далеко вверх идет линия 
 x говорит нам, как далеко вдоль 
 м находится уклон или уклон, т.е. насколько крута линия 
 b это точка пересечения Y, т.е. Ось Y
 Точки пересечения по осям X и Y, а также наклон называются свойствами линии. Теперь нарисуем линию  2y+x+14  = 0 и вычислим ее свойства
 График прямой линии: 
 
 Вычисление точки пересечения Y: 
 Обратите внимание, что при x = 0 значение y равно -7/1, поэтому эта линия «пересекает» ось y при y = -7,00000
   y-intercept = -14/2 = -7 
 Вычислить X-Intercept : 
 Когда y = 0 значение x равно -14/1 Таким образом, наша линия "пересекает" ось x в точке x=-14,00000
   x-intercept = -14/1 = -14,00000 
 Рассчитать наклон: 
 Наклон определяется как изменение y, деленное на изменение x. Отметим, что для x=0 значение y равно -7,000, а для x=2,000 значение y равно -8,000. Таким образом, для изменения x на 2.
No related posts.