Функції одз: Область допустимых значений (ОДЗ): теория, примеры, решения

Что такое ОДЗ

Важное замечание!
Если вместо формул ты видишь абракадабру, почисти кэш. Как это сделать в твоем браузере написано здесь: «Как почистить кэш браузера».

Что такое ОДЗ?

Это область допустимых значений, то есть это все значения переменной, при которых выражение имеет смысл.

Например, если перед тобой уравнение  , то ни  , ни   не могут быть отрицательными:

 

Часто в задачах бывает очень важно учесть ОДЗ. То есть некоторые из решений на самом деле решениями не являются.

Давай разберем пример, наглядно показывающий что такое ОДЗ:

Решим уравнение  .

Все очень просто, если ты уже освоил тему «Иррациональные уравнения». Возводим левую и правую части уравнения в квадрат:

 .

Теперь решаем квадратное уравнение. Я воспользуюсь теоремой Виета (если забыл что это такое — посмотри тему «Квадратные уравнения»). Получаем корни:

 

Вроде все? А давай-ка теперь сделаем проверку – подставим полученные значения в начальное уравнение:

  – все верно.

  – неверно! А все почему?

Да потому, что мы не учли ОДЗ: ведь по определению квадратный корень из любого числа не может быть отрицательным. Значит, глядя на уравнение   мы должны сразу же написать:

 

Если помнишь тему «Иррациональные уравнения», ты сразу скажешь, что второе условие в этой системе писать необязательно. И правда, мы ведь потом возведем все в квадрат, и получится, что  , а значит – автоматически неотрицательно. Итак, с помощью этих рассуждений приходим к такой области допустимых значений:

 .

Тогда сразу становится ясно, что корень   не подходит. И остается единственный ответ  .

Функции, для которых важна ОДЗ

Всего мы изучаем несколько разных функций, для которых важна ОДЗ. Вот они:

Тип функции	ОДЗ
Обратная зависимость	.
Степенная функция (корень)
Показательная функция
Логарифмическая функция
Тригонометрическая функция	\[y = {\mathop{\rm tg}\nolimits} x:{\rm{ }}x \ne \frac{\pi }{2} + \pi n,{\rm{ }}n \in \mathbb{Z};\] \[y = {\mathop{\rm ctg}\nolimits} x:{\rm{ }}x \ne \pi n,{\rm{ }}n \in \mathbb{Z}{\rm{.}}\]

Рассмотрим примеры с каждой из этих функций:

1. ОДЗ обратной зависимости

 .

Замечаем, что в знаменателе правой части формула сокращенного умножения:

 .

ОДЗ:  

Теперь можно спокойно избавляться от одинаковых знаменателей:

 

Согласно ОДЗ второй корень не подходит.

Ответ:  .

2. ОДЗ степенной функции

 .

Такой пример мы уже рассматривали, поэтому реши его самостоятельно.

Ответ:  .

3. ОДЗ показательной функции

 

Не пугайся, тут все просто:

ОДЗ:  

Обе части уравнения строго положительны, поэтому делим все на правую часть:

 

Теперь возможны два варианта: либо основание степени равно  , либо показатель равен  :

 

(квадратное уравнение реши сам)

Теперь вспомним ОДЗ: корень   – «сторонний».

Ответ:  .

4. ОДЗ логарифмической функции

 .

ОДЗ:  

 

С учетом ОДЗ нужно отбросить отрицательный корень:

Ответ:  .

5. ОДЗ тригонометрической функции

\[\frac{{{{\sin }^2}x}}{{\cos x}} = {\mathop{\rm tg}\nolimits} x\]

ОДЗ:  .

Для наглядности изображу область допустимых значений на единичной окружности в виде выколотых точек:

\[\frac{{{{\sin }^2}x}}{{\cos x}} = {\mathop{\rm tg}\nolimits} x \Leftrightarrow \frac{{\sin x}}{{\cos x}} \cdot \sin x = {\mathop{\rm tg}\nolimits} x \Leftrightarrow {\mathop{\rm tg}\nolimits} x \cdot \sin x = {\mathop{\rm tg}\nolimits} x \Leftrightarrow {\mathop{\rm tg}\nolimits} x\left( {\sin x — 1} \right) = 0 \Leftrightarrow \]

\[\left[ \begin{array}{l}{\mathop{\rm tg}\nolimits} x = 0\\\sin x = 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \pi n,{\rm{ }}n \in \mathbb{Z}\\x = \frac{\pi }{2} + 2 \pi k,{\rm{ }}k \in \mathbb{Z}\end{array} \right.\]

Очевидно, что вторая группа корней не подходит по ОДЗ.

ОБЛАСТЬ ДОПУСТИМЫХ ЗНАЧЕНИЙ. КОРОТКО О ГЛАВНОМ

ОДЗ — это область допустимых значений, то есть это все значения переменной, при которых выражение имеет смысл.

Функции, для которых важна ОДЗ:

Тип функции	ОДЗ
Обратная зависимость	.
Корень
Показательная функция
Логарифмическая функция
Тригонометрические функции	\[y = {\mathop{\rm tg}\nolimits} x:{\rm{ }}x \ne \frac{\pi }{2} + \pi n,{\rm{ }}n \in \mathbb{Z};\] \[y = {\mathop{\rm ctg}\nolimits} x:{\rm{ }}x \ne \pi n,{\rm{ }}n \in \mathbb{Z}{\rm{.}}\]

Ответ:  .

ОСТАВШИЕСЯ 2/3 СТАТЬИ ДОСТУПНЫ ТОЛЬКО УЧЕНИКАМ YOUCLEVER!

Стать учеником YouClever,

Подготовиться к ОГЭ или ЕГЭ по математике по цене «чашка кофе в месяц», 

А также получить бессрочный доступ к учебнику «YouClever», Программе подготовки (решебнику) «100gia», неограниченному пробному ЕГЭ и ОГЭ, 6000 задач с разбором решений и к другим сервисам YouClever и 100gia.

можно кликнув по этой ссылке.

 

 

 

 

Область допустимых значений

Область допустимых значений (ОДЗ) — важное математическое понятие, которое нужно учитывать при решении выражений с переменными, поскольку на практике часто можно столкнуться с выражениями, значения которых вычислить невозможно (например, $1:a$ при $a=0$). Поэтому существует термин «выражение, имеющее смысл при заданных значениях переменных». Он означает, что при данных значениях переменных выражение можно вычислить. Напротив, выражение не имеет смысла, если на данном множестве переменных нельзя найти его значение.

Определение 1

Область допустимых значений — множество переменных, при которых выражение имеет смысл. Значения переменных, при которых выражение теряет смысл, называют недопустимыми.

Когда выражение содержит две, три, и большее число переменных, можно говорить о парах, тройках и т.п. допустимых значений. Рассмотрим, например, выражение

$\frac{1}{x — y + z}$

со значениями $x=0$, $y=1$, $z=2$. Здесь мы имеем дело с тройкой переменных, которую можно обозначить как $(0, 1, 2)$. Эта совокупность является допустимой, поскольку в данном случае можно найти значение выражения:

Готовые работы на аналогичную тему

$\frac{1}{0 — 1 + 2} = 1$

Тройка же (1, 2, 1) недопустима, поскольку при подстановке значений в выражение в знаменателе окажется ноль.

Для выражения $\frac{6}{x — 4}$ ОДЗ можно выразить как $(−∞, 4)∪(4, +∞)$, т.е. объединение числовых открытых множеств от отрицательной бесконечности до $4$ и от $4$ до бесконечности. Иными словами, как множество всех действительных чисел за исключением числа $4$.

ОДЗ можно определить не только через множества, но и через уравнения и неравенства, например $\frac{z}{x — y}$, где ОДЗ $x \neq y$ при произвольном $z$.

Следует иметь в виду, что термины «ОДЗ» и «область определения» не совпадают по смыслу. Область определения относится к функциям, а область допустимых значений — к выражениям с переменными. Однако при этом справедливо утверждение: область допустимых значений переменной $x$ для выражения $f(x)$ совпадает с областью определения функции $y=f(x)$.

ОДЗ для элементарных выражений (умножение, деление, возведение в степень, логарифмы, тригонометрические операции) хорошо изучены. Так, выражение, стоящее под знаком корня чётной степени (например, квадратного), должно быть неотрицательным, поскольку не существует действительных чисел, которые при возведении в четную степень давали бы отрицательное число.

Замечание 1

Изучением корней четной степени из отрицательных чисел занимается особый раздет математики — теория комплексных чисел.

Пример 1

Как найти ОДЗ переменных для выражения $x^3 + 2xy − 4$?.

Возвести в куб можно любое число, равно как выполнить другие встречающиеся в данном примере арифметические операции (умножение, сложение, вычитание). Следовательно, можно вычислить значение данного выражения при любых значениях $x$ и $y$. Иными словами, выражение $x^3 + 2xy − 4$ имеет смысл при любых значениях его переменных. ОДЗ для него представляет собой множество пар $(x, y)$, где как $x$, так и $y$ могут быть любым числом.

Ответ:

$(x, y)$, где $x$ – любое, $y$ — любое.

Пример 2

Найти ОДЗ переменной x для выражения $\frac{1}{3} — \frac{x + 1}{0} $.

В знаменателе одной из дробей, входящих в состав данного выражения, присутствует ноль, следовательно, ни одно значение переменной $x$ не позволит составить имеющее смысл выражение. Следовательно, данное выражение не определено ни при каких значениях переменной $x$.

Ответ:

Пустое множество ($∅$).

ОДЗ | Алгебра

Найти ОДЗ — область допустимых значений — задание, которое в алгебре встречается как в виде самостоятельных примеров, так и при решении уравнений, неравенств и их систем.

   

   

ОДЗ многочлена — любое значение переменной.

   

Дробь имеет смысл, если знаменатель отличен от нуля.

Следовательно, ОДЗ дроби — все значения переменной, за исключением тех, в которых знаменатель обращается в нуль.

   

Выражение, стоящее под знаком корня чётной степени (в том числе, под знаком квадратного корня), должно быть неотрицательным.

Следовательно, ОДЗ выражения, содержащего переменную под знаком корня чётной степени — все значения переменной, при которых это выражение больше либо равно нуля.

   

Выражение, стоящее под знаком корня чётной степени (в том числе, под знаком квадратного корня) в знаменателе дроби, должно быть положительным.

То есть ОДЗ выражения с корнем чётной степени в знаменателе — множество значений переменной, при котором это выражение строго больше нуля.

   

Выражение, стоящее под знаком логарифма, должно быть положительным.

Выражение, стоящее в основании логарифма, должно быть положительным и не равным единице.

   

Выражение, стоящее под знаком синуса, может принимать любые значения (ОДЗ синуса — любые значения переменной).

   

Выражение, стоящее под знаком косинуса, может принимать любые значения (ОДЗ косинуса — любые значения переменной).

   

ОДЗ тангенса можно рассматривать как ОДЗ дроби

   

   

ОДЗ котангенса находим как ОДЗ дроби

   

   

Выражение, стоящее под знаком арксинуса, должно быть не меньшим -1 и не большим 1 (то есть ОДЗ арксинуса — промежуток [-1;1]).

   

Выражение, стоящее под знаком арккосинуса, должно быть не меньшим -1 и не большим 1 (ОДЗ арккосинуса — промежуток [-1;1]).

   

Выражение, стоящее под знаком арктангенса, может принимать любые значения (ОДЗ арктангенса — любые значения f(x)).

   

Выражение, стоящее под знаком арккотангенса, может принимать любые значения (ОДЗ арккотангенса — любые значения f(x)).

   

   

Выражение, стоящее в показателе степени, основание которой — положительное число, может принимать любые значения.

В ходе изучения темы «Степенная функция» обобщается информация по области допустимых значений степени и корня.

   

• Если α — натуральное число, то f(x)∈R.
• Если α — целое отрицательное число или нуль, то f(x)≠0.
• Если α — нецелое положительное число, то то f(x)≥0.
• Если α — нецелое отрицательное число, то то f(x)>0.

ОДЗ. Зачем, когда и как?

ОДЗ. Зачем, когда и как?

Шамшурин  А.В. 1

---

1Муниципальное бюджетное общеобразовательное учреждение «Средняя общеобразовательная школа №31»

Гагарина  Н.А. 1

---

1Муниципальное бюджетное общеобразовательное учреждение «Средняя общеобразовательная школа №31»

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF

Введение

Я начал работу с того, что в Интернете пересмотрел множество тем по математике и выбрал эту тему, потому что уверен, что важность нахождения ОДЗ играет огромную роль в решении уравнений и задач. В своей исследовательской работе я рассмотрел уравнения, в которых достаточно только нахождения ОДЗ, опасность, необязательность, ограниченность ОДЗ, некоторые запреты в математике. Самое главное для меня хорошо сдать ЕГЭ по математике, а для этого надо знать: когда, зачем и как находить ОДЗ. Это и подтолкнуло меня к исследованию темы, целью которой, стало показать, что овладение данной темой поможет учащимся правильно выполнить задания на ЕГЭ. Чтобы достичь этой цели, я исследовал дополнительную литературу и другие источники. Мне стало интересно, а знают учащиеся нашей школы: когда, зачем и как находить ОДЗ. Поэтому я провёл тест по теме «Когда, зачем и как находить ОДЗ?» (было дано 10 уравнений). Количество учащихся – 28. Справились – 14 %, опасность ОДЗ (учли) – 68 %, необязательность (учли) – 36 %.

Цель: выявление: когда, зачем и как находить ОДЗ.

Проблема: уравнения и неравенства, в которых нужно находить ОДЗ, не нашли места в курсе алгебры систематического изложения, возможно поэтому я и мои сверстники часто делаем ошибки при решении таких примеров, уделив много времени их решению, забыв при этом об ОДЗ.

Задачи:

1. Показать значимость ОДЗ при решении уравнений и неравенств.
2. Провести практическую работу по данной теме и подвести её итоги.

Я думаю полученные мною, знания и навыки помогут мне решить вопрос: искать ОДЗ или не надо?  Я перестану делать ошибки, научившись правильно делать ОДЗ. Получится ли у меня это, покажет время, точнее ЕГЭ[4].

Глава 1

Что такое ОДЗ?

 ОДЗ — это область допустимых значений, то есть это все значения переменной, при которых выражение имеет смысл.

Важно. Для нахождения ОДЗ мы не решаем пример! Мы решаем кусочки примера для нахождения запретных мест.

Некоторые запреты в математике. Таких запретных действий в математике очень мало. Но их не все помнят…

• Выражения, состоящие под знаком чётной кратности или должно быть>0 или равно нулю , ОДЗ:f(x)
• Выражение, стоящее в знаменателе дроби не может быть равно нулю , ОДЗ:f(x)
• |f(x)|=g(x), ОДЗ: g(x) 0

 Как записать ОДЗ? Очень просто. Всегда рядом с примером пишите ОДЗ. Под этими известными буквами, глядя на исходное уравнение, записываем значения х, которые разрешены для исходного примера. Преобразование примера может изменить ОДЗ и, соответственно ответ.

 Алгоритм нахождения ОДЗ:

1. Определите вид запрета.
2. Найти значения, при которых выражение не имеет смысла.
3. Исключить эти значения из множества действительных чисел R[6].

Решить уравнение: =

Без ОДЗ	С ОДЗ
= = х-9=1-х х+х=9+1 2х=10 х=5 Ответ: х=5 Оценка  2	= ОДЗ: => =>   Ответ: корней нет Оценка 5

Область допустимых значений оберегает нас от таких серьёзных ошибок. Честно говоря, именно из-за ОДЗ многие «ударники» превращаются в «троечников». Считая, что поиск и учёт ОДЗ малозначимым шагом в решении, они пропускают его, а потом удивляются: «почему учитель поставил 2?». Да потому и поставил, что ответ неверен! Это не «придирки» учителя, а вполне конкретная ошибка, такая же как неверное вычисление или потерянный знак[7].

Дополнительные уравнения:

а) = ;      б) -42=14х+ ;      в) =0;       г) |x-5|=2x-2 [5]

Глава 2

 ОДЗ. Зачем? Когда? Как?

 Область допустимых значений – есть решение

1. ОДЗ представляет собой пустое множество, а значит, исходный пример не имеет решений

Ответ: корней нет.

Ответ: корней нет.

ОДЗ:   х 0

0, уравнение не имеет корней

Ответ: корней нет.

Дополнительные примеры:

а) + =5;   б) + =23х-18;   в) =0[6].

2. В ОДЗ находится одно или несколько чисел, и несложная подстановка быстро определяет корни.

ОДЗ: х=2, х=3

Проверка: х=2, + ,  0<1,   верно

Проверка: х=3, + , 0<1, верно.

Ответ: х=2, х=3[8].

Проверка: х=0, > , 0>0, неверно

Проверка: х=1, > , 1>0, верно

Ответ: х=1.

Проверка:  + =3, 0=3, неверно.

Ответ: корней нет.

Дополнительные примеры:

а) = ;   б) + =0;   в) + =х -1[5]

 Опасность ОДЗ

Заметим, тождественные преобразования могут:

• не влиять на ОДЗ;
• приводить к расширенному ОДЗ;
• приводить к сужению ОДЗ.

Известно также, что в результате некоторых преобразований, изменяющих исходное ОДЗ, может привести к неверным решениям.

Давайте поясним каждый случай примером.

1)   Рассмотрим выражение х +4х+7х, ОДЗ переменной х для этого есть множество R. Приведём подобные слагаемые. В результате оно примет вид x

2+11x. Очевидно, ОДЗ переменной x этого выражения тоже является множество R. Таким образом, проведенное преобразование не изменило ОДЗ.

2)   Возьмем уравнение x+ — =0. В этом случае ОДЗ: x≠0.  Это выражение тоже содержит подобные слагаемые, после приведения которых, приходим к выражению x, для которого ОДЗ есть R. Что мы видим: в результате проведенного преобразования произошло расширение ОДЗ (к ОДЗ переменной x для исходного выражения добавилось число нуль).

3)   Возьмем выражение .    ОДЗ переменной x определяется неравенством (x−5)·(x−2)≥0, ОДЗ: (−∞, 2]∪[5, +∞).   А теперь преобразуем исходное выражение к виду .    ОДЗ переменной x для этого выражения определяет система линейных неравенств , решение которой дает множество [5, +∞). Таким образом, в результате проведенного преобразования произошло сужение ОДЗ с множества (−∞, 2]∪[5, +∞) до множества [5, +∞)[9].

Решим уравнение:

а)   3х+ = +15.  Перенесём дробь

ОДЗ: х-5 0,  х 5

3х+ — =15

х=5,    5 ОДЗ.       Ответ: корней нет.

б)   =0        х-х=0        =0.      Снова ловушка!

ОДЗ: х-3 0, х 3.     Ответ: х-любое число, кроме х=3.

в)   ,   ОДЗ: х .

Сокращение дробей даёт =0,  х=0. Ловушка!   Ответ: корней нет[6].

Дополнительные примеры: а) =0,   б) =0;

в) 214х+ = +642,   г) + =92[5].

Вывод. Итак, на каждом шаге преобразования выражения постоянно спрашивайте себя: «Не изменяет ли это преобразование ОДЗ»? Если не изменяет, то выполняйте его. Если сужает, то откажитесь от него. А если расширяет, то выполняйте его, но оставайтесь в рамках ОДЗ переменных для исходного выражения. Самый верный шаг – найдите сразу ОДЗ[2].

 Необязательность ОДЗ

Решим уравнение:

а) — =2

=2+ ,   f(x)=  — убывает, g(x)=2+ — возрастает

Значит, уравнение имеет не более одного корня. Решаем методом подбора: х=-1.  Ответ: х=-1.

б) =13-х,   f(x)=  —  возрастает,    g(x)= 13-х – убывает, значит, уравнение имеет не более одного корня. Решаем методом подбора: х=11.

ОДЗ:  х-7≥0 х≥7   

Квадратный корень всегда неотрицателен, значит 13-х>0.

Ответ: х=11.

в) + =0

Так как система, достаточно решить одно из уравнений и проверить, подставив во второе.

х +3х-4=0       а+в+с=0 х =1,  х = , значит х =-4

х=1:    1 +12 1 -11 1-2=0

х=-4:  (-4)  +12 (-4) -11 (-4)-2 0.    Ответ: х=1.

Вывод: нахождение ОДЗ не всегда является обязательным, часто не нужно, а иногда и невозможно — и всё это без какого бы то ни было ущерба для решения примера. Но я согласен с тем, что на уроках математики от нас требуют нахождения ОДЗ в каждом примере[3].

 Нестандартные уравнения

1)|х+4|=2х-10   ОДЗ: 2х-10 0, х 5

х+4=2х-10	-х-4=2х-10
х-2х=-10-4 -х=-14 х=14	-х-2х=4-10 -3х=-6 х=2, 2 ОДЗ

Ответ: х=14.

2) — =23х-18    ОДЗ:  

Так как полученная система решений не имеет, то область решений не имеет, таким образом, область определения уравнения не содержит ни одного корня, значит, данное уравнение не имеет корней[8].

3) + = —           ОДЗ: х

— = =

+ =

f(x)= +  — возрастает ,    g(x)=  — убывает

(так как если h(x) возрастает, то — убывает).

Уравнение имеет не более одного корня. Метод подбора. Ответ: х=2[4].

4) + + + =2

ОДЗ: х=2,х=0. Подставляем числа 2 и 0 в уравнение.

+ + + =2,  2=2

+ + + .

Ответ: х=2[4].

Глава 3

Практическая работа «ОДЗ: когда, зачем и как?»

 Было дано 10 уравнений, 2 неравенства. Количество учащихся – 28. Справились — 14 %, опасность ОДЗ(учли) – 68 %, необязательность (учли)-36%.

	ОДЗ -решение	Опасность ОДЗ	Необязательность ОДЗ	Нестандартные уравнения и неравенства
Иррациональные уравнения	61%	68%	82%	43%
Дробные уравнения	69%	89%	86%	50%
Неравенства	50%	89%	82%	64%
Уравнения, содержащие модуль	86%	96%	43%	61%

Заключение

 Тема работы раскрыта. Цель: выявление: когда, зачем и как находить ОДЗ – раскрыта. В исследовательской работе рассмотрены уравнения, в которых достаточно только нахождения ОДЗ, опасность, необязательность, ограниченность ОДЗ, некоторые запреты в математике. Самое главное для выпускников хорошо сдать ЕГЭ по математике, а для этого надо знать: когда, зачем и как находить ОДЗ.

Задачи, поставленные в работе, решены. Разобраны стандартные и нестандартные уравнения и неравенства. Проведена практическая работа по теме «ОДЗ. Когда? Зачем и как?» И подведены итоги. Полученные читателями, знания и навыки помогут им решить вопрос- искать ОДЗ или не надо?[10]

Каждому выражению с переменными соответствует область допустимых значений (ОДЗ) переменных, которую ОБЯЗАТЕЛЬНО нужно учитывать при работе с этим выражением. Акцент на слове «обязательно» сделан не случайно: при решении примеров и задач халатное отношение к ОДЗ может привести к получению неверных результатов.

Овладение данной темой поможет учащимся правильно выполнить задания на ЕГЭ[4].

Литература

 М.Я. Выгодский «Справочник по элементарной математике». М.: «Наука», 1966.

1. Газета «Математика» №17. 2002.
2. Г.И. Глейзер «История математики в школе VII-VIII классы». М.: «Просвещение», 1982.
3. Л.О. Денищева и др. «ЕГЭ. Математика. Универсальные материалы для подготовки учащихся/ФИПИ» — М.: «Интеллект-центр», 2009.
4. [Электронный ресурс]/Режим доступа: Материалы сайтов www.fipi.ru, www.eg
5. Область допустимых значений – есть решение [Электронный ресурс]/Режим доступа: rudocs.exdat.com›docs/index-16853.html
6. ОДЗ – область допустимых значений, как найти ОДЗ [Электронный ресурс]/Режим доступа: cleverstudents.ru›expressions/odz.html
7. Область допустимых значений: теория и практика [Электронный ресурс]/Режим доступа: pandia.ru›text/78/083/13650.php
8. Что такое ОДЗ [Электронный ресурс]/ Режим доступа: www.cleverstudents.ru›odz.html
9. Что такое ОДЗ и как его искать — объяснение и пример. Электронный ресурс]/ Режим доступа: cos-cos.ru›math/82/

Приложение 1

Практическая работа «ОДЗ: когда, зачем и как?»

Вариант 1	Вариант 2
	= 0
9х+  =  + 27	≤ +
+  = –1
│х+14│= 2 – 2х	=
	8х +  =  – 32
≥  +	+  = 1
= 0	│3-х│=1 – 3х

Приложение 2

Ответы к заданиям практической работы «ОДЗ: когда, зачем и как?»

Вариант 1	Вариант 2
Ответ: корней нет	ОДЗ: х 5 Ответ: х-любое число, кроме х=5
9х+ = +27  ОДЗ: х≠3 Ответ: корней нет	≤+ ОДЗ:→ ОДЗ: х=-3, х=5. Ответ:-3;5.
+=-1 у=  –убывает, у=  –возрастает Значит, уравнение имеет не более одного корня.    Ответ: х=6.	ОДЗ: → →х≥5 → Ответ:х≥5, х≤-6.
│х+14│=2-2х  ОДЗ:2-2х≥0, х≤1 х=-4, х=16, 16 не принадлежит ОДЗ Ответ:-4	=  – убывает,  –возрастает Уравнение имеет не более одного корня.  Ответ: корней нет.
0,  ОДЗ: х≥3,х≤2 Ответ: х≥3,х≤2	8х+ = -32, ОДЗ: х≠-4. Ответ:  корней нет.
≥+ ОДЗ:→ х=7, х=1. Ответ: решений нет	+=1 — возрастает, — убывает Ответ: х=2.
=0     ОДЗ: х≠15 Ответ: х- любое число, кроме х=15.	│3-х│=1-3х, ОДЗ: 1-3х≥0, х≤ х=-1, х=1 не принадлежит ОДЗ.  Ответ:  х=-1.

Просмотров работы: 3218

Находить ли ОДЗ?

В уравнениях и неравенствах вида , , , ,  пересечение областей определения функций  и  называют областью допустимых значений (ОДЗ) переменной, а также ОДЗ уравнения или неравенства соответственно.

При решении уравнений (неравенств) с одной переменной, когда встает вопрос – находить ли ОДЗ, часто можно услышать категоричное «да» и не менее категоричное «нет». «Сначала нужно найти ОДЗ, а затем приступать к решению уравнения (неравенства)», — утверждают одни. «Незачем тратить время на ОДЗ, по ходу решения будем переходить к равносильному уравнению (неравенству) или к равносильной системе уравнений и неравенств или только неравенств. В конце концов, если это уравнение, то можно сделать проверку», — утверждают другие.

Так находить ли ОДЗ?

Конечно, однозначного ответа на этот вопрос не существует. Нахождение ОДЗ уравнения или неравенства не является обязательным элементом решения. В каждом конкретном примере этот вопрос решается индивидуально.

В одних случаях нахождение ОДЗ упрощает решение уравнения или неравенства (примеры 1-5), а в ряде случаев даже является необходимым этапом решения (примеры 1, 2, 4).

В других случаях (примеры 6, 7) от предварительного нахождения ОДЗ стоит отказаться, так как оно делает решение более громоздким.

Пример 1. Решить уравнение .

Решение.

Возведение обеих частей уравнения в квадрат не упростит, а усложнит его и не позволит избавиться от радикалов. Нужно искать другой способ решения.

Найдем ОДЗ уравнения:

Таким образом, ОДЗ содержит только одно значение , а, следовательно, корнем исходного уравнения может служить только число 4. Непосредственной подстановкой убеждаемся, что  – единственный корень уравнения.

Ответ: 4.

Пример 2. Решить уравнение .

Решение.

Наличие в уравнении радикалов различных степеней – второй, третьей и шестой – делает решение сложным. Поэтому, прежде всего, найдем ОДЗ уравнения:

Непосредственной подстановкой убеждаемся, что  является корнем исходного уравнения.

Ответ: 2.

Пример 3. Решить неравенство .

Решение.

Конечно, можно решать это неравенство, рассматривая случаи: , , но нахождение ОДЗ сразу же упрощает это решение.

ОДЗ:

Подставляя это единственное значение  в исходное неравенство, получим ложное числовое неравенство . Следовательно, исходное неравенство не имеет решения.

Ответ: нет решения.

Пример 4. Решить уравнение .

Решение.

Запишем уравнение в виде .

Уравнение вида  равносильно смешанной системе  т.е.

Конечно, здесь нахождение ОДЗ излишне.

В нашем случае получим равносильную систему  т.е.

Уравнение  равносильно совокупности  Уравнение  рациональных корней не имеет, но оно может иметь иррациональные корни, нахождение которых вызовет у учащихся затруднения. Поэтому поищем другой способ решения.

Вернемся к первоначальному уравнению, запишем его в виде .

Найдем ОДЗ: .

При  правая часть уравнения , а левая часть . Следовательно, исходное уравнение в области допустимых значений переменной х равносильно системе уравнений  решением которой является только одно значение .

Таким образом, в данном примере именно нахождение ОДЗ позволило решить исходное уравнение.

Ответ: 0.

Пример 5. Решить уравнение .

Решение.

Так как , а , то при решении исходного уравнения нужно будет избавляться от модулей (раскрывать их).

Поэтому, сначала имеет смысл найти ОДЗ уравнения:

Итак, ОДЗ:

Упростим исходное уравнение, воспользовавшись свойствами логарифмов.

,

,

.

Так как в области допустимых значений переменной х  и , то , а , тогда получим равносильное уравнение:

,

.

Учитывая, что в ОДЗ , перейдем к равносильному уравнению  и решим его, разделив обе части на 3.

Ответ: − 4,75.

Замечание.

Если не находить ОДЗ, то при решении уравнения  необходимо было бы рассмотреть четыре случая: , , , . На каждом из этих промежутков знакопостоянства выражений, стоящих под знаком модуля, нужно было бы раскрыть модули и решить полученное уравнение. Кроме того еще и выполнить проверку. Мы видим, что нахождение ОДЗ исходного уравнения значительно упрощает его решение.

При решении следующих примеров предварительно ОДЗ находить не будем, так как это сделает решение более громоздким.

Пример 6. Решить неравенство .

Решение.

Исходное неравенство запишем в виде . Учитывая, что функция  непрерывна и убывающая при , перейдем к равносильной системе неравенств:

Решением последнего неравенства, а, значит, и исходного является множество .

Ответ: .

Замечание. Если бы мы находили ОДЗ, то нужно было бы решать систему неравенств  Все эти неравенства вошли в рассматриваемую при решении систему неравенств, причем, в процессе преобразования этой системы, все неравенства, из которых и состоит ОДЗ, оказались лишними. Таким образом, в данном примере нахождение ОДЗ только сделало бы решение более громоздким.

Пример 7. Решить неравенство .

Решение.

Так как переменная х входит и в основание  логарифма, то при решении этого неравенства необходимо будет рассмотреть два случая:  и . Поэтому отдельно находить ОДЗ нецелесообразно.

Итак, представим исходное неравенство в виде  и оно будет равносильно совокупности двух систем:

Ответ: .

ОДЗ. Область Допустимых Значений. Область определения функции. Примеры

Если где-то нет чего-то, значит, где-то что-то есть

Продолжаем изучение раздела «Функции и графики», и следующая станция нашего путешествия – . Активное обсуждение данного понятия началось в статье о множествах и продолжилось на первом уроке о графиках функций , где я рассмотрел элементарные функции, и, в частности, их области определения. Поэтому чайникам рекомендую начать с азов темы, поскольку я не буду вновь останавливаться на некоторых базовых моментах.

Предполагается, читатель знает область определения следующих функций: линейной, квадратичной, кубической функции, многочленов, экспоненты, синуса, косинуса. Они определены на (множестве всех действительных чисел) . За тангенсы, арксинусы, так и быть, прощаю =) – более редкие графики запоминаются далеко не сразу.

Область определения – вроде бы вещь простая, и возникает закономерный вопрос, о чём же будет статья? На данном уроке я рассмотрю распространённые задачи на нахождение области определения функции. Кроме того, мы повторим неравенства с одной переменной , навыки решения которых потребуются и в других задачах высшей математики. Материал, к слову, весь школьный, поэтому будет полезен не только студентам, но и учащимся. Информация, конечно, не претендует на энциклопедичность, но зато здесь не надуманные «мёртвые» примеры, а жареные каштаны, которые взяты из настоящих практических работ.

Начнём с экспресс-вруба в тему. Коротко о главном: речь идёт о функции одной переменной . Её область определения – это множество значений «икс» , для которых существуют значения «игреков». Рассмотрим условный пример: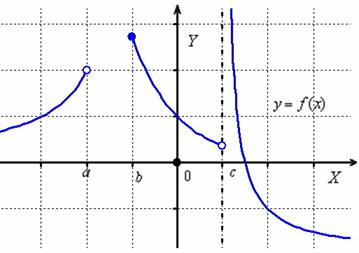

Область определения данной функции представляет собой объединение промежутков:
(для тех, кто позабыл: – значок объединения). Иными словами, если взять любое значение «икс» из интервала , или из , или из , то для каждого такого «икс» будет существовать значение «игрек».

Грубо говоря, где область определения – там есть график функции. А вот полуинтервал и точка «цэ» не входят в область определения и графика там нет.

Как найти область определения функции? Многие помнят детскую считалку: «камень, ножницы, бумага», и в данном случае её можно смело перефразировать: «корень, дробь и логарифм». Таким образом, если вам на жизненном пути встречается дробь, корень или логарифм, то следует сразу же очень и очень насторожиться! Намного реже встречаются тангенс, котангенс, арксинус, арккосинус, и о них мы тоже поговорим. Но сначала зарисовки из жизни муравьёв:

Область определения функции, в которой есть дробь

Предположим, дана функция, содержащая некоторую дробь . Как вы знаете, на ноль делить нельзя: , поэтому те значения «икс», которые обращают знаменатель в ноль – не входят в область определения данной функции .

Не буду останавливаться на самых простых функциях вроде и т.п., поскольку все прекрасно видят точки, которые не входят в их области определения. Рассмотрим более содержательные дроби:

Пример 1

Найти область определения функции

Решение : в числителе ничего особенного нет, а вот знаменатель должен быть ненулевым. Давайте приравняем его к нулю и попытаемся найти «плохие» точки:

Полученное уравнение имеет два корня: 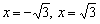. Данные значения не входят в область определения функции . Действительно, подставьте или в функцию и вы увидите, что знаменатель обращается в ноль.

Ответ : область определения: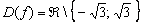

Запись читается так: «область определения – все действительные числа за исключением множества, состоящего из значений 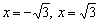». Напоминаю, что значок обратного слеша в математике обозначает логическое вычитание , а фигурные скобки – множество . Ответ можно равносильно записать в виде объединения трёх интервалов:

Кому как нравится.

В точках 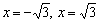функция терпит бесконечные разрывы , а прямые, заданные уравнениями являются вертикальными асимптотами для графика данной функции. Впрочем, это уже немного другая тема, и далее я на этом не буду особо заострять внимание.

Пример 2

Найти область определения функции

Задание, по существу, устное и многие из вас практически сразу найдут область определения. Ответ в конце урока.

Всегда ли дробь будет «нехорошей»? Нет. Например, функция определена на всей числовой оси. Какое бы значение «икс» мы не взяли, знаменатель не обратится в ноль, более того, будет всегда положителен: . Таким образом, область определения данной функции: .

Все функции наподобие 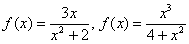определены и непрерывны на .

Чуть более сложнА ситуация, когда знаменатель оккупировал квадратный трёхчлен:

Пример 3

Найти область определения функции

1. Функция, одз

Пусть заданы 2 множества Х,У функцией или отображением из Х в У

называется правило, по которому каждому значению их Х ставится в соотвествие

значение из У.

Числовые функции характеризуются тем, что оба множества Х и У являются

подмножествами множества действительных чисел (или совпадают с ними). Область

определения функции — множество возможных значений, которые может принимать

аргумент.

Графиком функции с областью определения называется множетсво точек

Г={(x,f(x)|xÎX}.

2. Свойства функции.

1. Чётность. Если облать определения функции симметричня относительно

нуля и f(-x)=f(x) «xÎD(f), то функция у=f(x) называется чётной.

Если

f(-x)= — f(x) «xÎD(f), то функция у=f(x) называется нечётной.

Если не выполняется ни первое, ни второе условие, то функция обшего вида.

2. Монотонность. функция у=f(x) – возрастающая , если для

любого х₁ и х₂ из области определения функции (х₁

<х₂) выполняется неравенство f(x₁)<f(x₂)

Функция у=f(x) – убывающая, если для любого х₁ и х₂

из области определения функции (х₁>х₂) выполняется

неравенство f(x₁)>f(x₂).

Возрастающие или убывающие функции называются монотонными.

3. Ограниченность. Функция у=f(x) называется ограниченной на некотором

промежутке , если существует М>0, MÎR|»xÎданному промежутку

|f(x)|£M.

Функция у=f(x) называется ограниченной снизу, если существует mÎR

|»xÎданному промежутку m£f(x). Функция у=f(x) называется

ограниченной сверху, если существует mÎR |»xÎданному промежутку

m³f(x).

4. Периодичность. Функция у=f(x) называется периодической с

периодом Т не равным нулю, если выволняется условие f(x+ — T)=f(x).

3. Обратная функция.

Пусть Функция у=f(x) задана на множестве Х=D(f) и Y=E(f). Предположим, что

различным значениям х₁ и х₂ соответствуют различные

значения функции f(x₁) и f(x₂). Тогда для любого

уÎУ мы сможем поставить в соответсвие хÎХ| y=f(x). Получает

отображение f^-1: У®Х. Это отображение называется обратным.

График прямой и обратной функции симметричен относительно биссектрисы первой и

третьей координатной четверти.

4. Сложная функция.

Пусть заданы две функции t=h(x), [xÎD(h), T=E(h)] и y=g(t),

[tÎT=D(g), Y=E(g)] (область определения одной функции совпадает с

областью значений другой функции и наоборот) Тогда справедливо следующее

правило: из любого хÎХ по правилу ставится в соответствие y=g(h(x)).

Это правило называется сложной функцией.

5. Основные элементарные функции.

1. Степенная. y=x^a, a=const, aÎR. D(f)=(0;+¥). Если aÎNÞD(f)=R.

2. Показательная. y=a^x

, a>0,a не равно 1. D(f)=R/ E(f)=(0;+¥). Если a>1, следовательно,

функция возрастает. Если аÎ(0;1), функция убывает.

3. Логарифмическая. y=log_ax, a>0, a не равно 1. D(f)=(0;+¥),

E(f)=R. Если a>1, следовательно, функция возрастает. Если аÎ(0;1),

функция убывает.

4. Тригонометрические.

5. Обратные тригонометрические.

6. Предел функции

Опр. Пределом функции у=f(x) в точке х₀ (или при х →х

₀ )называют число а, если для любой последовательности { х_n}

значений аргумента , сходящейся к (при этом все х_n≠ х₀

) последовательность значений функции сходится к пределу а. Это записывают в

виде:

(*)

Аналогично определяеся предел при х →∞ (случаи когда х₀

есть +∞ или -∞). А именно, равенство (*) во всех случаях означает

следующее: для любой последовательности { х_n}, сходящейся к х₀

, соответствующая последовательность {f(х_n)} сходится к а.

Инъективный, сюръективный и биективный

«Инъективный, сюръективный и биективный» рассказывает нам о том, как ведет себя функция.

Функция — это способ сопоставления элементов набора «A» до набора «B»:

Давайте посмотрим на это более внимательно:

A Общая функция баллов от каждого члена «A» к члену «B».

Это никогда не имеет один «A», указывающий на более чем один «B», поэтому «один ко многим» не подходит в функции (например, «f (x) = 7 или 9 «не допускается)

Но более одного «A» могут указывать на одну и ту же «B» ( «многие к одному» )

Injective означает, что у нас не будет двух или более «A», указывающих на одну и ту же «B».

Итак, многие-к-одному НЕ ОК (что нормально для общей функции).

Так как это тоже функция «один ко многим» не работает

Но у нас может быть «B» без соответствия «A»

Injective также называется « One-to-One »

Surjective означает, что каждый «B» имеет по крайней мере один , соответствующий «A» (возможно, более одного).

Не останется «B».

Биективное одновременно означает и инъективное, и сюръективное.

Думайте об этом как об «идеальной паре» между наборами: у каждого есть партнер, и никто не остается в стороне.

Итак, существует идеальное « однозначное соответствие » между членами множеств.

(Но не путайте это с термином «один к одному», который означает инъективный).

Биективные функции имеют обратный !

Если каждый «A» переходит в уникальный «B», и каждый «B» имеет соответствующий «A», то мы можем двигаться назад и вперед, не сбиваясь с пути.

Подробнее см. Обратные функции.

На графике

Итак, давайте посмотрим на несколько примеров, чтобы понять, что происходит.

Когда A и B являются подмножествами вещественных чисел, мы можем построить график зависимости.

Пусть у нас есть A по оси x и B по y, и посмотрите на наш первый пример:

Это , а не функция , потому что у нас есть A с множеством B . Это как сказать f (x) = 2 или 4

Он не прошел «Тест вертикальной линии» и поэтому не является функцией.Но это все еще действительные отношения, так что не сердитесь на это.

Теперь общая функция может быть такой:

A Общая функция

Он МОЖЕТ (возможно) иметь B с множеством A . Например, синус, косинус и т.д. Совершенно правильные функции.

Но « Injective Function » строже и выглядит так:

«Injective» (индивидуально)

Фактически мы можем провести «Тест горизонтальной линии»:

Чтобы быть Injective , горизонтальная линия никогда не должна пересекать кривую в 2 или более точках.

(Примечание: строго возрастающие (и строго убывающие) функции являются инъективными, вы можете прочитать о них для получения дополнительной информации)

Итак:

• Если он проходит тест вертикальной линии , это функция
• Если он также проходит тест горизонтальной линии , это инъективная функция

Формальные определения

Хорошо, ждите, чтобы узнать обо всем этом подробнее:

Впрыск

Функция f является инъективной тогда и только тогда, когда всякий раз, когда f (x) = f (y) , x = y .

Пример: f ( x ) = x + 5 из набора действительных чисел в является инъективной функцией.

Верно ли, что всякий раз, когда f (x) = f (y) , x = y ?

Представьте, что x = 3, тогда:

Теперь я говорю, что f (y) = 8, каково значение y? Может быть только 3, поэтому x = y

Пример: f ( x ) = x ² от набора действительных чисел до , а не , инъективная функция из-за такого рода вещей:

Это противоречит определению f (x) = f (y) , x = y , потому что f (2) = f (-2), но 2 ≠ -2

Другими словами, существует , два значения из A , которые указывают на одно B .

НО если бы мы сделали его из набора натуральных числа к тогда это инъективно, потому что:

• f ( 2 ) = 4
• нет f (-2), потому что -2 не является естественным число

Значит домен и кодомен каждого набора важны!

Сюръективное (также называется «Онто»)

A функция f (из набора A до B ) сюръективное значение тогда и только тогда, когда на каждые y in B , есть хотя бы один x in A такой, что f ( x ) = y , другими словами f является сюръективным если и только если f (A) = B .

Проще говоря: у каждого B есть несколько A.

Пример: Функция f ( x ) = 2x из набора натуральных чисел в набор неотрицательных , четных чисел — это сюръективная функция .

А ф ( х ) = 2х из набора натуральных Числа в не являются сюръективными , потому что, например, ни один член в не может быть сопоставлен с 3 этой функцией.

Биективный

Функция f (из набора A до B ) имеет значение bijective , если для каждых y в B существует ровно один x дюйм A такой, что f ( x ) = y

В качестве альтернативы f является биективным, если это взаимно однозначное соответствие между этими наборами, другими словами, инъективное и сюръективное.

Пример: Функция f ( x ) = x ² из множества положительных вещественных числа в положительные реальные числа одновременно инъективны и сюръективны. Таким образом, это также биективное .

Но одна и та же функция из набора всех действительных чисел не является биективной, потому что мы могли бы иметь, например, оба

,

Четные и нечетные функции

Это особые типы функций

Четные функции

Функция «даже», когда:

f (x) = f (−x) для всех x

Другими словами, существует симметрия относительно оси Y (как отражение):

Это кривая f (x) = x ² +1

Их назвали «четными» функциями, потому что функции x ² , x ⁴ , x ⁶ , x ⁸ и т. Д. Ведут себя так же, но есть и другие функции, которые ведут себя так же, например, cos (х):

Косинусная функция: f (x) = cos (x)
Это четная функция

Но четный показатель не всегда дает четную функцию, например (x + 1) ² — это , а не — четная функция.

Нечетные функции

Функция считается «нечетной», если:

−f (x) = f (−x) для всех x

Обратите внимание на минус перед f (x): −f (x) .

И получаем симметрию начала координат:

Это кривая f (x) = x ³ −x

Их назвали «нечетными», потому что функции x, x ³ , x ⁵ , x ⁷ и т. Д. Ведут себя так же, но есть и другие функции, которые ведут себя так же, например sin (x ) :

Функция синуса: f (x) = sin (x)
Это нечетная функция

Но нечетная экспонента не всегда дает нечетную функцию, например x ³ +1 — это , а не — нечетная функция.

Ни нечетное, ни четное

Пусть вас не вводят в заблуждение имена «нечетный» и «четный» … это всего лишь имен … и функция не обязательно должна быть четной или нечетной.

На самом деле большинство функций не являются ни нечетными, ни четными. Например, просто добавив 1 к приведенной выше кривой, получим:

Это кривая f (x) = x ³ −x +1

Это не нечетная функция , и это не четная функция .
Нечетно и нечетно

Четное или нечетное?

Пример: является ли f (x) = x / (x ² −1) четным или нечетным или ни одним?

Давайте посмотрим, что произойдет, если мы подставим −x :

f (−x) = (−x) / ((- x) ² −1)

= −x / (x ² −1)

= −f (х)

Итак, f (−x) = −f (x), что делает его нечетной функцией

Четное и нечетное

Единственная функция, которая является четной и нечетной , это f (x) = 0

Особые свойства

Добавляем:

• Сумма двух четных функций равна
• Сумма двух нечетных функций нечетная
• Сумма четной и нечетной функции не является ни четной, ни нечетной (если одна функция не равна нулю).

Умножение:

• Произведение двух четных функций является четной функцией.
• Произведение двух нечетных функций является четной функцией.
• Произведение четной функции и нечетной функции является нечетной функцией.

,

функций существительных | Owlcation

Существительное можно определить как слово, которое используется для обозначения человека, места, животного или предмета. Он также может называть состояние, действие, действие или качество.

Какова грамматическая функция существительного?

Произведение, которое существительное выполняет в предложении, называется его грамматической функцией. В этой статье мы подробно рассмотрим пять грамматических функций существительных.

Существительное может выполнять любую из следующих пяти функций:

• подлежащее глагола
• Объект глагола
• Дополнение к глаголу
• Объект предлога
• Быть в приложении к другому существительному

Давайте теперь посмотрим на приведенные выше функции одну за другой.

Существительное в качестве подлежащего глагола

Существительное действует как подлежащее глагола, когда оно является подлежащим предложения и стоит перед основным глаголом предложения. Чаще всего предложение начинается с существительного.

Пример: Стейси вчера ночью убила змею . (Здесь существительное «Стейси» функционирует как подлежащее глагола «убит».)

Другие примеры:

• Джон преподает английский язык в Китае.
• Дети иногда могут быть очень непослушными.
• Обама был избран президентом.
• Политик — лжец.

Все выделенные существительные в приведенных выше предложениях функционируют как подлежащие соответствующим глаголам. Они действуют как подлежащие глаголов просто потому, что стоят перед главными глаголами в предложениях, а также являются субъектами в своих соответствующих предложениях.

Существительное функционирует как объект глагола

Существительное функционирует как объект глагола, когда оно стоит после глагола действия и принимает действие глагола.Существительное, выступающее в качестве объекта глагола в предложении, всегда будет получателем действия.

Пример : Том ударил Джерри . (Здесь, поскольку существительное «Джерри» стоит после глагола действия «пощечину» и принимает действие глагола, мы говорим, что это объект глагола «пощечину».)

Другие примеры:

• Я ударил по мячу .
• Ненавижу Джанет .
• Учитель наказал учеников .
• Я написал письмо .
• Я знаю Лондон , потому что был там несколько раз.
• Роберта приготовила еды .

Все выделенные слова в предложениях выше являются существительными, функционирующими как объекты глаголов. Они функционируют как объекты своих соответствующих глаголов просто потому, что являются получателями действий своих глаголов.

Существительное как дополнение к глаголу

Существительное будет функционировать как дополнение глагола, если оно стоит после связующего глагола или глагола состояния и не получает никакого действия от глагола.Вот некоторые примеры связывания глаголов в английском языке: is, are, am, be, are, was, were, been, being, звучать, вкушать, назначать, становиться, чувствовать, обонять, звучать, появляться и т. Д.

Пример: Джон — лжец . (Здесь существительное «лжец» функционирует как дополнение к глаголу «есть».)

Другие примеры существительных, функционирующих как дополнения к глаголам:

• Мужчина — торговец .
• Я был учителем , живя в Китае.
• Джон — победитель .
• Наши друзья из Пакистана были проигравшими .
• Я думаю, это зверь .
• Фил Коллинз — легендарный музыкант .

Все выделенные существительные в приведенных выше предложениях функционируют как дополнения к своим соответствующим глаголам-связям.

Существительное в качестве объекта предлога

Когда существительное выступает в качестве объекта предлога, оно следует после предлога в предложении.По определению, любое существительное, идущее сразу после предлога, является объектом этого предлога. Например, «Джон» является объектом предлога «к» в этом предложении: Я дал книгу Иоанну .

Таким образом, мы можем сказать, что существительное «Джон» функционирует как объект предлога «к».

Теперь, когда у нас есть хорошее представление о том, как выглядит существительное, выступающее в качестве объекта предлога, давайте рассмотрим еще несколько примеров ниже.

• Я ходатайствовал за мальчика .
• Я куплю книги для детей сегодня, когда приду в книжный магазин.
• Надо отдать учителю .
• Давайте возьмем Иоанна .
• Я верю в Бог .
• Это не мое; это для домовладельца .

Из приведенных выше примеров вы можете видеть, что каждое из выделенных существительных идет после предлогов, что делает их объектами соответствующих предлогов.

Существительное в приложении к другому существительному

Это последняя, ​​но не менее важная грамматическая функция существительного.Существительное может быть добавлено к другому существительному. По определению, слово «аппозиция» означает размещение существительного рядом с другим существительным для объяснения этого. Итак, каждый раз, когда вы видите существительное, помещенное рядом с другим существительным, и это существительное объясняет другое существительное, тогда у вас есть хороший пример того, как существительное находится в приложении к другому существительному.

Например: Игрок , Суарес дисквалифицирован . (Здесь вы заметили, что рядом друг с другом поставлены два существительных, а именно «футболист» и «Суарес».Теперь вы заметили, что существительное «Суарес» может использоваться для замены «футболист», а также дает некоторую информацию о другом существительном «футболист». Таким образом, мы можем сказать, что существительное «Суарес» находится в приложении к существительному «футболист»)

Другие примеры включают следующее:

• Медсестра, Джанет вышла на пенсию.
• Его книга « Скотный двор » считается одной из величайших когда-либо написанных книг.
• Пастор, Илия , арестован.
• Мой родной город Манчестер — прекрасное место.

Все выделенные существительные в приведенных выше предложениях являются существительными в приложении к существительным, идущим перед ними.

Я надеюсь, что, прочитав эту статью от начала до конца, вы теперь имеете хотя бы элементарное представление о функциях существительных и о том, как каждое из них выглядит. Если вы все еще не поняли, я предлагаю вам еще раз прочитать эту статью. Я считаю, что понимание обязательно начнет постепенно приходить.

Давайте теперь попробуем наши руки на следующих ниже примерах и посмотрим, сможем ли мы определить грамматические функции выделенных существительных в предложениях:

1. Ненавижу ездить в мой родной город .
2. Джон очень хорошо сдал экзамены.
3. Не тратьте свое драгоценное время на Иоанна .
4. Президент поддержал акцию .
5. Забастовка длилась более недели.
6. Демократия дает власть людям .
7. Лисица перепрыгнула через стену .
8. Он профессор .
9. Страна, Швеция , очень мирная.
10. Это было написано Джорджем Оруэллом .

ПРИМЕЧАНИЕ : Грамматическая функция существительного очень похожа на грамматическую функцию местоимения. Помните, что местоимения ведут себя так же, как и существительные — где бы ни могло быть помещено существительное, там также может быть помещено местоимение и исключение существительного.По этой причине грамматики говорят, что местоимения также могут выполнять все пять грамматических функций существительного. Вы можете прочитать наш урок о грамматических функциях местоимений здесь: Функции местоимений. Я рекомендую вам также прочитать этот урок.

,

FiSe (ISFP) — Тип в уме

Каждый тип личности имеет четыре когнитивные функции. Функции выражают язык тому, как они обрабатывают информацию и принимают решения. Каждый тип обозначается двумя главными функциями. Внутренние функции — это те, которые вы используете в своей голове, а внешние — это те, которые вы используете для взаимодействия с окружающим миром.

Функции FiSe:
1. Fi — интровертное чувство
Хотя это называется «чувство», Fi — это не внутренние эмоции, а ценности, которые приходят изнутри.FiSe может испытать уйму эмоций, но это не корень Fi. Это процесс принятия решений, который очень заинтересован в определении своего собственного морального кодекса и правильности того, что инстинкт FiSe подсказывает им, что часто основывается на том, как они хотели бы, чтобы с ними обращались. Они, как правило, очень внимательны к другим и могут долго обдумывать свои собственные убеждения, чтобы убедиться, что они кажутся правильными. Процесс уточнения ценностей может занять довольно много времени и требует душевного одиночества.Фай обычно высоко ценит аутентичность и отталкивается от всего, что кажется сфабрикованным или мелким.

2. Se — экстравертное восприятие
Se — это основной способ, которым FiSe получает информацию. Это означает, что они используют свои чувства, чтобы понять окружающий мир. Они живут настоящим моментом и предпочитают иметь дело с реальными и твердыми вещами, а не с чисто гипотетическими. Se — это часть FiSe, которая заставляет их искать новые игровые ощущения.

3.Ni — интровертный iNtuition
Ni — это третья функция FiSe, которая позволяет им извлекать из каждой области своего мозга ценные данные, искать закономерности в собираемой информации или пропустить десять шагов вперед и предсказать, что произойдет. случится в будущем. Ni делает внутренний мир, управляемый Fi, очень абстрактным и может включать в себя множество интуитивных прыжков.

4. Te — экстравертное мышление
Te — подчиненная функция FiSe. Эта функция может быть их ахиллесовой пятой и по своей сути не так сильна, как другие их функции, потому что их высший приоритет и внимание сосредоточены на Fi.Te — это очень логичный способ решения проблем. Это их сторона, которая, естественно, стремится найти лучшее решение проблемы, повысить эффективность процесса или критиковать и уточнять то, что уже существует. FiSe обычно предпочитают использовать Te только при необходимости, а не принимать все свои решения. Чрезмерное использование подчиненных функций может быть очень истощающим и может быть вредным для здоровья, если постоянно уделяется приоритетное внимание другим функциям.

Доминирующая функция и ядро ​​внутреннего мира:

Интровертное чувство
Фи-доминирующие типы очень теплые и заботливые по отношению к своим близким, поскольку они могут подсознательно полагать, что у каждого есть внутренний мир, похожий на глубину к их.Однако им нужно время, чтобы открыться людям, и они вряд ли подойдут к кому-то, если этот человек каким-то образом не заинтересует их. После того, как пользователь Fi впустил кого-то в свой мир, он, вероятно, будет поддерживать это соединение, пока сохраняется гармония между ними, то есть если другой человек показывает, что он не соответствует действительности или живет в сильной оппозиции к ценности FiSe. держит, FiSe отступит от отношений. До тех пор, пока их близкие остаются верными своему представлению о себе и не оскорбляют их мораль, FiSe, вероятно, будет привязан к этому человеку на всю жизнь, независимо от того, видят ли они его регулярно.

В лучшем случае, Fi-доминантные типы (FiSe и FiNe) являются мастерами самообслуживания и отлично умеют устанавливать здоровые границы. Они очень чуткие люди, поэтому видят потребности других и хотят заботиться о них. Однако здоровые фи-домы знают, что они не могут эффективно заботиться о других, если сначала не позаботятся о себе. Они знают свои пределы и обычно не боятся сказать «нет», когда они не могут что-то сделать или вписать что-то в свою жизнь.

Fi отличается от Fe (экстравертное чувство) тем, что Fe сфокусирован внешне и постоянно спрашивает: «Как группа думает по этому поводу?», Тогда как Fi сосредоточен внутри себя и постоянно спрашивает: «Как я к этому отношусь? » FiSe также склонны оттачивать одно или два важных отношения, которые они естественным образом ищут, когда удовлетворяются их собственные потребности — партнер, лучший друг и т. Д.Они сильно защищают свой «внутренний круг», чувствуя, что те, с кем они разделяют интимные детали своей личности, в некотором смысле являются частью их самих. Они будут без колебаний защищать себя или своих близких, когда чувствуют, что на них нападают или им угрожают.

В своих лучших проявлениях FiSe отлично знает себя, поскольку они тратят много времени на саморефлексию. Их очень волнуют глубина и нюансы своих ценностей; они тратят большую часть своего умственного пространства на прояснение, отсеивание и уточнение своих убеждений.Этот процесс может быть очень связан с глубокими эмоциями, и они могут смеяться или плакать над красотой, казалось бы, случайного объекта, который имеет для них значение, в то время как сторонние наблюдатели, заметившие их реакцию, могут быть весьма сбиты с толку их внезапной вспышкой. У некоторых людей с сильным Fi эмоции настолько глубоки, что для того, чтобы они вырвались наружу, в течение некоторого времени должно было быть много чувств, зарождающихся под поверхностью. Они склонны искать вещи (фильмы, книги и т. Д.), Которые вызовут их эмоции, потому что следование за персонажами, которые им небезразличны в эмоциональном путешествии, может быть очень полезным.

Стоит отметить, что когда мы говорим о чувствах (Fi или Fe) как о когнитивной функции, мы не имеем в виду эмоции. Эмоциональные переживания или выражения могут быть связаны с Чувством (Fe или Fi), но они не являются корнем «Чувства». Корень Fi или Fe сводится к ценностям человека (то есть, что человек считает важным, исходя из его собственной совести и почему). Моральный кодекс пользователя Fi основан на том, что его совесть или инстинкт подсказывают ему, что он прав, обычно относясь к другим так, как они сами хотят, чтобы относились к ним.Это значение Fi не основано на эмоциях, но и не должно быть на 100% логичным. Его не слишком заботит ПРИЧИНА справедливого обращения с другими … Это просто «кажется» хорошим и правильным поступком, потому что они сами хотят, чтобы с ними обращались справедливо.

Инстинкт Фи — достичь внутренней гармонии, оставаясь верным себе и своим ценностям, сводя к минимуму влияние внешних факторов (социальных ожиданий и, возможно, даже мнения друзей и семьи) на их ценности.FiSe могут любить обсуждать или даже обсуждать свои ценности с другими, если при этом они остаются верными себе. Но после продолжительного обсуждения им потребуется время, чтобы самостоятельно оценить беседу и подумать о том, что сказал другой человек, и как они могут вписать это в свою систему ценностей. Они находят свои собственные принципы заслуживающими доверия и ценными, и по своей сути скептически относятся к тому, что другие пытаются им навязать. Если что-то не соответствует их собственным убеждениям, они не могут действовать в соответствии с ними.Идти против собственных ценностей — значит вызвать внутренний разлад, который им очень трудно вынести.

Типы с преобладанием Fi могут потеряться в своем собственном мире, пытаясь понять, что думает незнакомец, который сидит в 200 футах от них в кафе, как проходит их день, какой должна быть их жизнь, и т. д. Они любят наблюдать за людьми, но обычно не заинтересованы в близких и личных отношениях с большинством людей. Они чувствуют необходимость реагировать и должным образом реагировать на реальные взаимодействия, что может быть для них очень утомительным.Они могут предпочесть воображаемый разговор с кем-то, чем на самом деле разговаривать с кем-то, поскольку у воображаемых людей нет требований или ожиданий от них.

FiSe, как правило, проявляют активное воображение в зрелом возрасте. Типы с доминированием Fi очень озабочены историей различных вещей. Например, они могут увидеть большое крепкое дерево и задаться вопросом, сколько времени оно там существует, пытаясь представить себе события, ради которых оно существовало, или кто еще сидел в его тени, какая мудрость могла быть связана с этим деревом или внутри него и т. Д. ,Они автоматически ищут смысл повсюду — в книгах, фильмах, в мимолетном замечании друга, в специальной чашке, которую они любят использовать, или даже в том, почему это дерево было посажено в определенном месте. Fi придает смысл всему.

Поскольку они настолько увлечены глубиной и нюансами значения всего, и как значение чего-то связано со всем остальным, они могут быть невероятно увлечены правильной идеей или историей. Когда что-то пробуждает их воображение или затрагивает какой-то аспект значения, который имеет для них большой вес, они очаровываются историей или идеей.Даже сам процесс разворачивания истории может иметь для них большее значение, чем сумма частей истории.

Вторая функция и ядро ​​внешнего мира:

Экстравертное восприятие
Хотя FiSe могут обрабатывать абстрактные идеи, концепции и разговоры, они могут быстро устать от такого типа мыслей, если не видят практического, реального мира ценность для этого. В то время как бесконечные размышления о каждой возможности под солнцем утомят их, если вы дадите им одну абстрактную концепцию, они часто смогут с ней работать — опираясь на нее и чувствуя, как сделать ее осязаемой реальностью.

ФиСи, как правило, очень приземленные, их привлекают таинственные, интуитивные аспекты окружающего мира из-за их Ni. Все они посвящены текущим, осязаемым, конкретным переживаниям и восприятиям реального мира, а также тому, как они могут связать свое физическое окружение со своим изменчивым, мистическим внутренним миром. Возможно, что люди с сильным Се — единственные люди, которые в некотором смысле действительно живут «настоящим моментом». Они рассматривают мир как твердую силу и предпочитают воспринимать информацию конкретным и надежным образом.Поскольку они не ощущают внутри себя твердости, они ищут эту стабильность в окружающем их мире.

FiSe особенно чувствует, что каждое мгновение следует тратить на что-то стоящее и интересное, а делать все, что они считают «работой», утомительно и утомительно, даже если это работа, которая им нравится. Все они хотят веселиться и получать новые впечатления, поэтому даже приятная работа редко бывает для них любимым занятием. Они хотят иметь возможность делать именно то, что они хотят, в тот момент, когда они думают об этом.Все, что мешает этой свободе, расстраивает их Se.

Фисам нужен определенный уровень импульсивности в жизни, чтобы быть счастливыми. Чрезмерная привязка к расписанию может показаться им пыткой, а слишком много планирования может привести к большому стрессу. Им может нравиться время от времени нарушать правила, особенно если они чувствуют, что другие пытаются навязать им слишком много нежелательной структуры. Они хотят делать то, что хотят, и когда хотят, и жаждут веселья и спонтанности в своей жизни. Даже если их работа приносит большое удовлетворение и удовлетворение, если она не задействует их в физическом плане, им быстро надоест.

Несмотря на то, что они прекрасные слушатели, им действительно нравится общаться с людьми, чтобы познакомиться. Они жаждут острых ощущений и приключений. FiSe необходимо взаимодействовать с окружающим миром. Изучение природы, занятия физическими видами спорта, пачкание рук и занятия физическим миром — это очень катарсис для них. Se сторона FiSe заставляет их очень высоко ценить красоту и искать красивые, безмятежные окрестности, особенно на природе. Их окружение оказывает на них сильное влияние, и они хорошо осведомлены о своем физическом окружении.

FiSe обычно очень креативны. Се нравится очень осязаемый опыт с пятью чувствами (зрение, осязание, вкус, запах, звук), поэтому создание искусства своими руками (например, игра на музыкальном инструменте, рисование, рисование, лепка, фотография и т. Д.) Доставляет им большое удовольствие. Создавая осязаемое искусство, они могут использовать Fi и Se, выражая смысл всевозможными способами реального мира, которые могут испытать другие люди.

Когда FiSe делает что-то, чтобы задействовать их чувства, оно возбуждает их и дает им энергию.Без красивых переживаний «5 чувств» их энергия и творческий потенциал сходятся на нет, и они могут обратиться к нездоровым порокам, таким как переедание, алкоголь, телевизор или видеоигры, чтобы попытаться удовлетворить эту потребность в физическом взаимодействии. Эту потребность лучше удовлетворять упражнениями, исследованиями и играми.

FiSe рады тому, что происходит здесь и сейчас. Они очень присутствуют, и им может быть трудно планировать будущее. Они настолько полно присутствуют в моменте, что текущая ситуация, в которой они оказались, кажется, будто это весь их мир.Если бы вы спросили FiSe, какова их жизнь, они, вероятно, расскажут вам о своих нынешних обстоятельствах, а не об общей картине.

Когда FiSe находятся в кризисном режиме, они чувствуют, что им нужно подготовиться к тому, что может произойти дальше («Чего мне ожидать на работе завтра, исходя из того, что произошло сегодня?»), И особенно как они могут относиться к тому, что они могут встреча. Поскольку они очень внимательны, они, вероятно, не будут думать обо всех возможностях через 5 лет в будущем.Их интуиция проникает в ближайшее будущее, поэтому они знают, что делать дальше. Если их текущая ситуация кажется неспокойной, стрессовой или подавляющей, у них возникает ощущение, что их жизнь в целом находится вне их контроля. Если выход не сразу очевиден, они могут почувствовать себя совершенно безнадежными. Им кажется, что их обстоятельства никогда не изменятся, и что их нынешняя реальность навсегда останется их реальностью.

Третья функция и вспомогательная роль во внутреннем мире:

Introverted iNtuition
FiSe познает свой внутренний мир очень интуитивно.В своем постоянном поиске смысла во всем, что они видят, делают и переживают, они всегда развиваются и меняются внутри. Их внутренний мир открыт и изменчив, хотя они видят внешний мир очень твердым и неизменным. Когда они рассматривают различные концепции или идеи, они, естественно, видят их с разных сторон и точек зрения.

Они интуитивно исследуют свои чувства и эмоции и твердо уверены, что все связано со всем остальным. Разум FiSe похож на созвездие ценностей, эмоций и предчувствий.Все в их внутреннем мире связано через постоянно меняющиеся и развивающиеся сети. У них может быть интуитивный инстинкт, что что-то должно произойти, часто прямо перед тем, как этот сценарий разыграется перед ними. Это немного похоже на экстрасенсорное ощущение, потому что их интровертная интуиция (Ni) подсознательно пытается понять, что будет дальше. Они подсознательно рассчитывают несколько возможностей, основываясь на том, что происходит вокруг них в данный момент. Когда дело доходит до прошлого, большая часть того, что они вспоминают, — это общее ощущение своего опыта, а не яркие детали.На протяжении всего опыта (будь то жизнь в целом, история книги или фильма и т. Д.) Их разум естественным образом выделяет темы и видит закономерности смысла в общей истории.

Фисы обычно очень духовные люди. Даже если они не придерживаются определенной религиозной доктрины, у них обычно есть врожденное чувство, что существуют другие сферы и силы, выходящие за рамки того, что большинство людей приняли бы за чистую монету. Они удивляются скептикам духовности, потому что это часть их самих себя, которую они так сильно и очевидно чувствуют.Им комфортно с неизвестным, и они чувствуют, что никогда не смогут быть на 100% уверены или достичь абсолютной правды о большинстве вещей в жизни, хотя у них, вероятно, есть горстка вещей, которые они постоянно считают истинными и реальными для них. Они постоянно переоценивают вещи и подходят к различным вопросам с разных сторон. Их Ни похож на утешающего друга, который гладит их по плечу и говорит: «Ничего страшного. Вам не нужно все выяснять «.

FiSe естественно видит закономерности и устанавливает связи.Например, они могут прочитать сложную теорию, которая не сразу имеет смысл, но после перехода к новой деятельности их подсознание соединит точки. Все будет синтезироваться в их уме, и у них будет момент «ага!», Когда все станет ясно.

Из-за постоянно меняющейся природы своего внутреннего мира им может потребоваться несколько дней, чтобы разобраться в своих эмоциях. Они могут поспорить со своим другом и знать, что в данный момент они расстроены, но после этого им придется потратить много времени на то, чтобы распутать различные эмоции, которые они испытывали, и их причины.Поскольку они так глубоко переживают свой внутренний мир, их эмоции очень глубоки и могут быть очень подавляющими, и временами с ними трудно справиться.

FiSe всегда ищут основную суть вещей, пытаются получить инстинкт того, как все работает, и пытаются выяснить следующий уровень глубины — духовно, эмоционально и ментально. В ходе размышлений они естественно рассматривают вещи с нескольких разных точек зрения. Их воображение и понимание постоянно развиваются, чтобы учесть эти точки зрения, и они часто находят новые разработки или идеи.

Люди обычно чувствуют себя в безопасности с FiSe’s. Они могут представить другим разные, необычные концепции в удобной для них форме. Они могут объяснить чужие идеи, которые обычно могут оттолкнуть людей, таким образом, чтобы они вовлекались и чувствовали себя комфортно. Их доставка нежная и продуманная, уникальная для их типа.

Последняя функция и вспомогательная роль внутреннего мира:

Экстравертное мышление
Te — последняя функция и вспомогательная роль во внешнем мире FiSe.Te — это процесс, который позволяет им получать информацию из реального мира, быстро принимать решения о том, какое решение является наиболее эффективным, и сразу же применять это решение. Это самая слабая ахиллесова пята FiSe. Хотя для них было бы утомительно и вредно полагаться на этот аспект себя все время, они могут использовать свои навыки устранения неполадок, когда это необходимо для эффективного выполнения работы.

Поскольку эта их сторона заставляет их ценить превосходство и эффективность, у них могут возникнуть проблемы с началом новых хобби, карьерного роста или других серьезных изменений в жизни.Хотя они знают, что на самом деле это невозможно, они хотят быть мастерами во всем, что они пробуют, когда делают это в первый раз.

Хотя они предпочитают не торопиться с принятием решений, это не всегда возможно или практично. В таких ситуациях полезно иметь Те, чтобы они могли принять быстрое и срочное решение. Поскольку они могут полагаться на свой внутренний компас Fi в фоновом режиме, чтобы сообщить им, когда что-то не так, они могут чувствовать себя комфортно в своем решении, даже если они не могут сформулировать вескую причину для этого в то время, пока оно проходит. их «проверка кишки».Например, если у них есть ощущение, что кто-то, кого они видят идущим по улице, может причинить им какой-то вред, у них нет времени, чтобы понять, почему у них такое чувство. Они просто знают, что не чувствуют себя в безопасности рядом с этим человеком, и лучшее решение — перейти улицу или сделать объезд, чтобы избежать их.

Во многих случаях Te является защитной функцией FiSe. Когда одна из их ценностей подвергается нападкам, они полагаются на прямой, практичный стиль общения Те, чтобы защитить ее.Когда они настолько сильно относятся к предмету, что знают, что должны принять меры по нему, они подключаются к этой части себя, которая является сильной и властной, чтобы отстоять то, что они считают правильным. Он также может быть их частью, которая говорит им просто выбрать что-то (карьеру, хобби, одежду и т. Д.) И придерживаться этого, по крайней мере, на короткий период времени. Именно меньшая их часть подталкивает их к выводу и решимости. Если бы это было исключительно их Fi, они бы постоянно размышляли о том, что они думают по этому поводу.

В общем, FiSe ненавидит резкость и осуждение. Они хорошо осведомлены о мыслях и эмоциях других людей и всегда подходят к людям с глубокого понимания. Хотя они могут проявлять чрезмерную критику, когда устают или находятся в стрессе, они сожалеют о каждом случае, когда сталкиваются с таким образом, который, по их мнению, не отражает их истинный характер.

Физик, который вынужден действовать исходя из этого решения проблем, критикуя сторону своей личности в течение большей части своего времени (для работы, воспитания детей и т. Д.), Скорее всего, выгорит и может испытать усталость от принятия решений. очень быстро.Как правило, у них получается лучше всего, когда они могут позволить кому-то другому принимать решения по крайней мере в какой-то части своей жизни. Если они должны принимать все решения в своей работе, все решения в отношении родителей, все решения в отношении отношений и т. Д., Тогда, когда приходит время для простых решений, касающихся самопомощи, таких как решение, что есть на ужин или какой маршрут поехать домой от работы они уже вымотаны и будут бороться за то, чтобы понять, чего они хотят.

FiSe лучше всего используют свой Te, когда система уже существует, поскольку им проще всего использовать простейшую версию Te — критику и уточнение.Когда что-то уже существует и нуждается в улучшении, может быть проще проанализировать это и увидеть решение. Когда они начинают с нуля, у них может быть много идей, но внедрение систем и структур эффективности для них труднее.

.