2+n-72)=1/(n+9)| 1 | Найти точное значение | грех(30) | |
| 2 | Найти точное значение | грех(45) | |
| 3 | Найти точное значение | грех(30 градусов) | |
| 4 | Найти точное значение | грех(60 градусов) | |
| 5 | Найти точное значение | загар (30 градусов) | |
| 6 | Найти точное значение | угловой синус(-1) | |
| 7 | Найти точное значение | грех(пи/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | грех(45 градусов) | |
| 10 | Найти точное значение | грех(пи/3) | |
| 11 | Найти точное значение | арктан(-1) | |
| 12 | Найти точное значение | cos(45 градусов) | |
| 13 | Найти точное значение | cos(30 градусов) | |
| 14 | Найти точное значение | желтовато-коричневый(60) | |
| 15 | Найти точное значение | csc(45 градусов) | |
| 16 | Найти точное значение | загар (60 градусов) | |
| 17 | Найти точное значение | сек(30 градусов) | |
| 18 | Найти точное значение | cos(60 градусов) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | грех(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | загар (45 градусов) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 градусов) | |
| 25 | Найти точное значение | сек(45 градусов) | |
| 26 | Найти точное значение | csc(30 градусов) | |
| 27 | Найти точное значение | грех(0) | |
| 28 | Найти точное значение | грех(120) | |
| 29 | Найти точное значение | соз(90) | |
| 30 | Преобразовать из радианов в градусы | пи/3 | |
| 31 | Найти точное значение | желтовато-коричневый(30) | |
| 32 | 92|||
| 35 | Преобразовать из радианов в градусы | пи/6 | |
| 36 | Найти точное значение | детская кроватка(30 градусов) | |
| 37 | Найти точное значение | арккос(-1) | |
| 38 | Найти точное значение | арктан(0) | |
| 39 | Найти точное значение | детская кроватка(60 градусов) | |
| 40 | Преобразование градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2 шт. )/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | тан(пи/2) | |
| 45 | Найти точное значение | грех(300) | |
| 46 | Найти точное значение | соз(30) | |
| 47 | Найти точное значение | соз(60) | |
| 48 | Найти точное значение | соз(0) | |
| 49 | Найти точное значение | соз(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | сек(60 градусов) | |
| 53 | Найти точное значение | грех(300 градусов) | |
| 54 | Преобразование градусов в радианы | 135 | |
| 55 | Преобразование градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5 дюймов)/6 | |
| 57 | Преобразовать из радианов в градусы | (5 дюймов)/3 | |
| 58 | Преобразование градусов в радианы | 89 градусов | |
| Преобразование градусов в радианы | 60 | ||
| 60 | Найти точное значение | грех(135 градусов) | |
| 61 | Найти точное значение | грех(150) | |
| 62 | Найти точное значение | грех(240 градусов) | |
| 63 | Найти точное значение | детская кроватка(45 градусов) | |
| 64 | Преобразовать из радианов в градусы | (5 дюймов)/4 | |
| 65 | Найти точное значение | грех(225) | |
| 66 | Найти точное значение | грех(240) | |
| 67 | Найти точное значение | cos(150 градусов) | |
| 68 | Найти точное значение | желтовато-коричневый(45) | |
| 69 | Оценить | грех(30 градусов) | |
| 70 | Найти точное значение | сек(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | КСК(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | загар((5pi)/3) | |
| 75 | Найти точное значение | желтовато-коричневый(0) | |
| 76 | Оценить | грех(60 градусов) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3 пи)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | угловой синус(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | КСК(45) | |
| 83 | Упростить | арктан(квадратный корень из 3) | |
| 84 | Найти точное значение | грех(135) | |
| 85 | Найти точное значение | грех(105) | |
| 86 | Найти точное значение | грех(150 градусов) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | загар((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | пи/4 | |
| 90 | Найти точное значение | грех(пи/2) | |
| 91 | Найти точное значение | сек(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | угловой синус(0) | |
| 95 | Найти точное значение | грех(120 градусов) | |
| 96 | Найти точное значение | желтовато-коричневый ((7pi)/6) | |
| 97 | Найти точное значение | соз(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразование градусов в радианы | 88 градусов |
Давайте изучим единицу окружности/углов в стандартном положении/длине дуги 92=1\text{.
}\) Единичный круг — самый важный график во всей тригонометрии, поскольку он является основой для определения всех тригонометрических функций. Рисунок 16.1.1. Единичный кругИспользуя формулу длины окружности \(C=2\pi r\text{,}\), мы можем легко определить, что длина окружности единичного круга равна \(2 \pi\) (единица измерения). Итак, если мы начнем с любой точки по окружности и совершим один полный оборот по окружности, мы проедем расстояние \(2\pi\) (единица измерения).
Как упоминалось выше, все тригонометрические функции определяются относительно этой окружности, и в этих определениях отправной точкой для вращения всегда является \((1,0)\text{.}\). Мы будем называть дуги вдоль единицы окружность, которая исходит из точки \((1,0)\) как дуг в стандартной позиции . Когда мы удаляемся от этой точки в направлении против часовой стрелки, мы определяем размер результирующей дуги (части окружности) как положительное число. Когда мы движемся от точки \((1,0)\) и движемся по часовой стрелке, мы определяем измерение дуги как отрицательное число.
Для дуг, которые не исходят из точки \((1,0)\text{,}\), измерение всегда указывается как положительное число.
Рассмотрим дугу в стандартном положении, которая вращается на четверть оборота против часовой стрелки. Эта дуга показана на рисунке 16.1.2. Поскольку длина одного полного оборота равна \(2\pi\) (единица), длина одной четверти оборота равна \(\frac{2\pi}{4}\), что упрощается до \(\frac{\ pi}{2}\text{.}\) Поскольку изображенная дуга вращается против часовой стрелки, мы измеряем ее положительным значением.
Рисунок 16.1.2. Дуга \(\frac{\pi}{2}\) (единицы) в стандартном положенииКогда дуга находится в стандартном положении, угол от начала координат, стороны которого являются положительной осью \(x\) и линией от начала координат до конечной точки дуги, имеет измерение в радианах, численно эквивалентное измерению дуги . Мы называем такие углы углов в стандартном положении .
Рассмотрим угол в стандартном положении, который поворачивается на три восьмых оборота по часовой стрелке.
Этот угол показан на рисунке 16.1.3. В стандартном положении угол, который поворачивается на четверть оборота по часовой стрелке, заканчивается на отрицательной оси \(y\), а угол, который поворачивается на половину оборота по часовой стрелке, заканчивается на отрицательной оси \(x\). Поскольку \(\frac{3}{8}\) находится на полпути между \(\frac{1}{2}\) и \(1\text{,}\), угол в стандартном положении, который поворачивает на три восьмых оборот по часовой стрелке должен заканчиваться на полпути в квадранте III.
Поскольку угол, показанный на рисунке 16.1.3, вращается по часовой стрелке, его измерение в радианах отрицательно. Поскольку вращение составляет три восьмых оборота, абсолютное значение его измерения в радианах равно \(\frac{3}{8}(2\pi)\), что упрощается до \(\frac{3\pi}{4 }\text{.}\) Мы часто используем греческую букву \(\theta\) (тета), когда обозначаем углы в стандартном положении, поэтому, используя эту ссылку, мы будем называть угол на рис.
16.1.3 как \(\theta =-\frac{3\pi}{4}\) rad (читается как «радианы»). Мы будем называть аффилированную дугу вдоль единичной окружности как \(t=-\frac{3\pi}{4}\text {.}\)
Давайте проиллюстрируем \(\theta=\frac{\pi}{4}\) рад. Поскольку измерение положительное, мы знаем, что вращение от положительной оси \(x\) происходит против часовой стрелки. Поскольку за один полный оборот приходится \(2\pi\) рад, мы можем определить величину вращения в \(\frac{\pi}{4}\) рад, решив уравнение \(\frac{\pi} {4}=2\pi x\), что дает нам \(x=\frac{1}{8}\text{.}\) Таким образом, конечная сторона угла попадает на полпути в квадрант I. Угол показан на рисунке 16.1.4.
Рисунок 16.1.4. Угол \(\frac{\pi}{4}\), нарисованный в стандартном положении По причинам, которые станут очевидными, когда мы начнем вычислять тригонометрические функции, мы часто разбиваем единичный круг на 24 равные части. Это показано на рис. 16.1.5–рис. 16.1.12. В каждом из четырех квадрантов есть три угла интереса, которые заканчиваются в квадранте.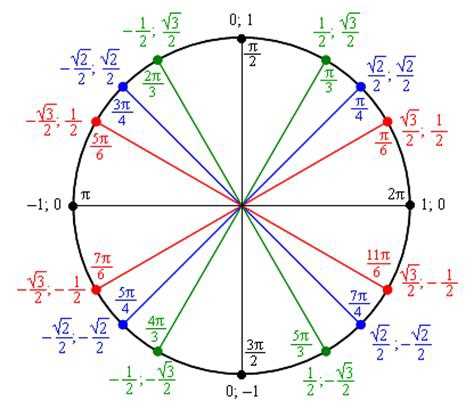
На рисунках слева каждая интересующая конечная сторона помечена своим наименьшим положительным измерением в радианах как доля \(2\pi\text{.}\). На рисунках справа дроби были уменьшены — это способ, которым ценности будут изложены в будущем.
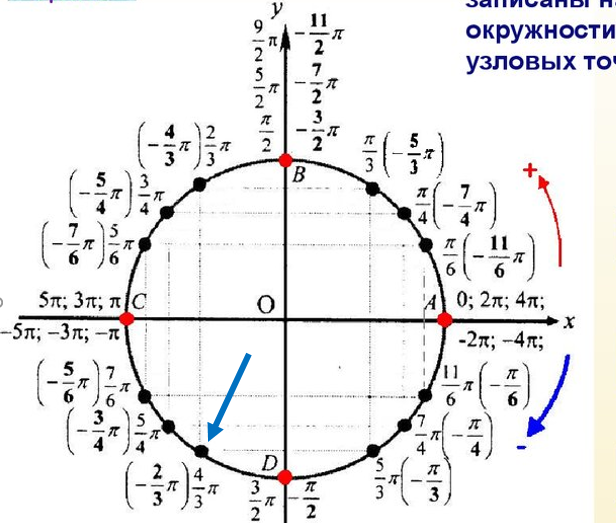
На рис. 16.1.13 показаны точки, упомянутые выше, а также точки, в которых единичная окружность пересекает оси. На рис. 16.1.14 показан круг с ключевыми точками, помеченными отрицательными значениями (результат вращения по часовой стрелке).
В следующем разделе мы добавим координаты каждой точки на график, и эта картинка станет основой для всей тригонометрии. Как вы, наверное, догадались, запоминание местоположения этих ключевых точек и их координат жизненно важно, если вы действительно хотите понять и освоить тригонометрию.
Как показано выше, при рисовании в стандартном положении несколько углов имеют одну и ту же конечную сторону. На самом деле нет ограничений на количество углов, заканчивающихся в любой заданной позиции. Углы, начерченные в стандартном положении и имеющие общую конечную сторону, называются котерминальными углами . Измерения котерминальных углов в радианах всегда отличаются на целое число, кратное \(2\pi\), а углы, измерения которых в радианах отличаются на целое число, кратное \(2\pi\), всегда котерминальны.
Пример 16.1.15.
Определите четыре угла, два положительных измерения и два отрицательных измерения, котерминальные углу \(\theta=\frac{5\pi}{7}\text{.
}\)
Решение
Нам нужно сложить и вычесть целые числа, кратные \(2\pi\), к \(\frac{5\pi}{7}\), чтобы получить котерминальные углы к \(\theta\text{.}\ ) Это делается ниже.
\begin{выравнивание*} \frac{5\pi}{7}+2\pi\amp=\frac{5\pi}{7}+\frac{14\pi}{7}\\ \amp=\frac{19\pi}{7} \end{выравнивание*}
\begin{выравнивание*} \frac{5\pi}{7}+2 \cdot 2\pi\amp=\frac{5\pi}{7}+4\pi\\ \amp=\frac{5\pi}{7}+\frac{28\pi}{7}\\ \amp=\frac{33\pi}{7} \end{выравнивание*}
\begin{выравнивание*} \frac{5\pi}{7}-2\pi\amp=\frac{5\pi}{7}-\frac{14\pi}{7}\\ \amp=-\frac{9\pi}{7} \end{выравнивание*}
\begin{выравнивание*} \frac{5\pi}{7}-2 \cdot 2\pi\amp=\frac{5\pi}{7}-4\pi\\ \amp=\frac{5\pi}{7}-\frac{28\pi}{7}\\ \amp=-\frac{23\pi}{7} \end{align*}
В некоторых случаях предпочтительно измерять углы в градусах, а не в радианах. (На самом деле, некоторые студенты предпочли бы, чтобы это было сделано во всех контекстах. 🙂 Вы можете вспомнить, что в одном полном обороте есть \(360^{\circ}\).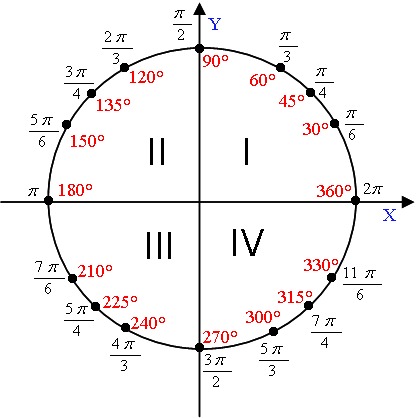
{\circ}\text{.}\) 9{\circ}\text{.}\) Первое, что нам нужно определить, это количество раз, когда 360 делится на 21 254. Это скажет нам, сколько полных оборотов сделано до окончательного частичного оборота.
\begin{уравнение*} \ гидроразрыва {21 254} {60} \ приблизительно 59,039 \end{equation*}
Это говорит нам о том, что угол составляет 59 полных оборотов плюс чуть больше. Поскольку вращение происходит против часовой стрелки, угол заканчивается в квадранте I.
Чтобы определить желаемый котерминальный угол, давайте вычтем 59{\ круг} \конец{выравнивание*}
Длина дуги, s, проведенной по окружности с радиусом r и отрезанной под углом с вершиной в центре окружности с радианным измерением \(\theta\), определяется уравнением \( s=r\theta\text{.}\) Это показано на рисунке 16.1.19. Когда мы решаем уравнение длины дуги для \(\theta\text{,}\), мы получаем следующее уравнение, которое имеет поразительное значение в отношении радиана.
\begin{уравнение*} \ тета = \ гидроразрыва {s} {r} \end{уравнение*}
Рисунок 16.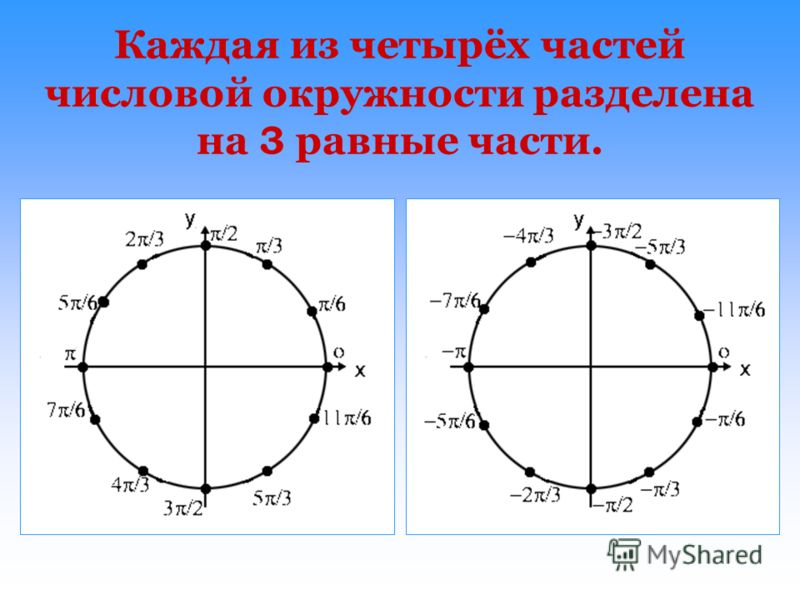
1.19. Длина дуги: \(s=r\theta\)Предположим, вы начертили дугу длиной 7 см на окружности радиусом 21 см. Тогда измерение центрального угла выводится следующим образом.
\begin{выравнивание*} \тета\амп=\фрак{с} {r}\\ \amp=\frac{7\,\text{см}}{21\,\text{см}}\\ \amp=\frac{1}{3} \конец{выравнивание*}
Где блок? Единицы нет! Единицы cm делились на единицу и не оставляли ничего (по единицам) после себя.
Оказывается, единица измерения радиан — это что-то вроде бутафории. Когда мы говорим «три радиана», на самом деле мы имеем в виду «три». Так почему же мы вообще используем слово радиан? Чтобы контекстуал читателя к тому факту, что мы имеем в виду «три» как измерение угла или величины вращения. Поскольку радианы не являются реальным значением, мы обычно не пишем его — например, мы пишем \(\frac{\pi}{2}\) и контекстуально распознаем, что мы ссылаемся на «радианное измерение». При указании угловых измерений пропуск единицы измерения всегда указывает на то, что мы должны интерпретировать значение как измерение в радианах.
По этой причине очень важно, чтобы вы включали символ градуса при указании измерения в градусах. 9{\circ}\) угол
Для каждого установленного значения \(\theta\text{,}\) определите квадрант, в котором заканчивается угол, и определите угол с измерением между \(0\) и \(2\pi\), котерминальный с \(\тета\текст{.}\)
5.
\(\theta=\frac{226\pi}{3}\)
Решение
Начнем с определения количества оборотов, оставшихся после совершения всех полных оборотов. Мы делаем это, разделив значение \(\theta\) на \(2\pi\) — количество радиан за один полный оборот.
\begin{уравнение*} \ гидроразрыва {\ гидроразрыва {226 \ пи} {3}} {2 \ пи} \ приблизительно 37,67 \end{equation*}
Таким образом, угол составляет 37 полных оборотов плюс чуть меньше трех четвертей оборота. Поскольку вращение происходит против часовой стрелки (\(\theta\) положительна), угол заканчивается в квадранте III.
\begin{уравнение*} \frac{226\pi}{3}-37 \cdot 2\pi=\frac{4\pi}{3} \end{equation*}
Это говорит нам о том, что угол измерения \(\frac{226\pi}{3}\) совпадает с углом измерения \(\frac{4\pi}{3} \текст{.
}\)
6.
\(\тета=3,356\)
Решение
Начнем с определения количества оборотов, оставшихся после совершения всех полных оборотов. Мы делаем это, разделив значение \(\theta\) на \(2\pi\) — количество радиан за один полный оборот.
\begin{уравнение*} \frac{3,356}{2\pi} \ приблизительно 534,12 \end{equation*}
Таким образом, угол составляет 534 полных оборота плюс менее четверти оборота. Поскольку вращение происходит против часовой стрелки (\(\theta\) положительна), угол заканчивается в квадранте I.
\begin{уравнение*} 3,356-37 \cdot 2\pi \примерно 0,779 \end{equation*}
Это говорит нам о том, что угол измерения \(3,356\) угол (очень близок к тому, чтобы быть) сотерминальным с углом измерения \(0,779\text{.}\)
7.
\(\theta=-\frac{1781\pi}{2}\)
Решение
Начнем с определения количества оборотов, оставшихся после совершения всех полных оборотов.
Мы делаем это, разделив значение \(\theta\) на \(2\pi\) — количество радиан за один полный оборот.
\begin{уравнение*} \ гидроразрыва {\ гидроразрыва {1781 \ пи} {2}} {2 \ пи} \ приблизительно 445,25 \end{equation*}
Таким образом, угол составляет 445 полных оборотов плюс ровно четверть оборота. Поскольку вращение происходит по часовой стрелке (\(\theta\) отрицательно), угол заканчивается на отрицательной оси \(y\) и совпадает с \(\frac{3\pi}{2}\)
8.
\(\тета=-250\)
Решение
Начнем с определения количества оборотов, оставшихся после совершения всех полных оборотов. Мы делаем это, разделив значение \(\theta\) на \(2\pi\) — количество радиан за один полный оборот.
\begin{уравнение*} \frac{250}{2\pi} \ приблизительно 39,79 \end{equation*}
Таким образом, угол составляет 39 полных оборотов плюс немногим более трех четвертей оборота. Поскольку вращение происходит по часовой стрелке (\(\theta\) отрицательно), угол заканчивается в квадранте I.