Геометрический и физический смысл определённого интеграла. — Мегаобучалка
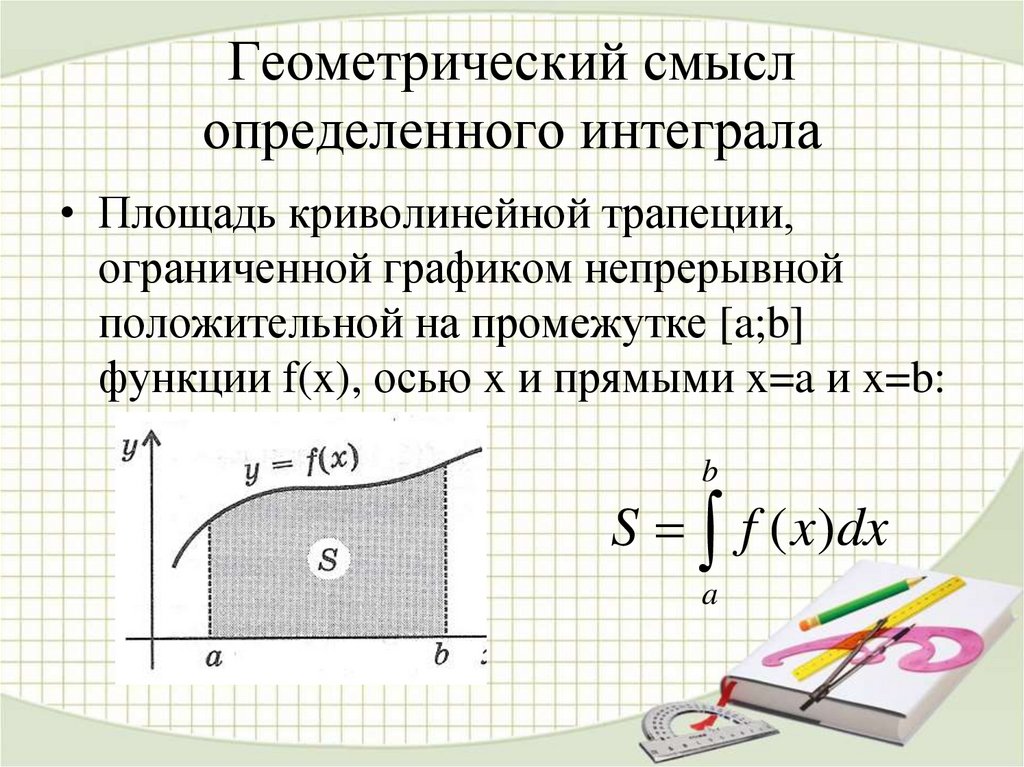
Геометрический смысл определенного интеграла. Если f ( x ) непрерывна и положительна на [ a , b ], то интеграл представляет собой площадь криволинейной трапеции, ограниченной линиями y = 0, x = a , x = b , y = f ( x ) (см. рис. 5.).
Физический смысл определенного интеграла: пусть материальная точка M движется вдоль числовой оси со скоростью V ( t ), V ( t )≥0 . Тогда путь, пройденный точкой за промежуток времени от t = a до t = b , равен определенному интегралу от скорости: S =
Замена переменной в определённом интеграле.
Пусть для вычисления интеграла от непрерывной функции сделана подстановка х = φ(t).
Теорема 1. Если: 1) функция х = φ(t) и ее производная х’ =φ’(t) непрерывны при t ϵ [α;β]; 2) множеством значений функции х = φ(t) при t ϵ [α,β] является отрезок [а; b ]; 3) φ(α) = а и φ(β) = b, то = * φ ’( t ) dt
Формула называется формулой замены переменной в определенном интеграле. Отметим, что:
Отметим, что:
1) при вычислении определенного интеграла методом подстановки возвращаться к старой переменной не требуется
2) часто вместо подстановки х = φ(t) применяют подстановку t = g(x)
3) не следует забывать менять пределы интегрирования при замене переменных!
Интегрирование по частям при вычислении определённого интеграла.
Пусть U(x) и V(x) — дифференцируемые функции. Тогда d ( U ( x ) V ( x )) = U ( x ) dV ( x ) + V ( x ) dU ( x ) . Поэтому U ( x ) dV ( x ) = d ( U ( x ) V ( x )) – V ( x ) dU ( x ) . Вычисляя интеграл от обеих частей последнего равенства, с учетом того, что ∫ d ( U ( x ) V ( x ))= U ( x ) V ( x )+ C , получаем соотношение
Называемое формулой интегрирования по частям. Понимают его в том смысле, что множество первообразных, стоящее в левой части, совпадает со множеством первообразных, получаемых по правой части.
Понимают его в том смысле, что множество первообразных, стоящее в левой части, совпадает со множеством первообразных, получаемых по правой части.
Вычисление площадей плоских фигур в прямоугольных и полярных координатах
Допустим, что фигура D предполагает наличие границы ծ D : y = f ( x ), x = a , x = b ( a < b ), f ( x )ϵ C [ a , b ]
D является криволинейной трапецией и , при условии, что f ( x )>0 на [ a , b ].
Если D находится ниже оси [ a , b ] (рис. 18.1), то
Под полярной системой координат понимается совокупность т. O (полюса) и исходящей из данной точки направленной полупрямой l (полярной оси). В качестве полярных координат т. M обозначают числа (полярный радиус) и (полярный угол) (рис. а).
Вычисление длины дуги плоской кривой.
Кривой линией l -наз. непрерывное отображение отрезка трехмерного пространства. Кривая наз. плоской если она целиком лежит в какой-то плоскости.
Кривая наз. плоской если она целиком лежит в какой-то плоскости.
Замечание: Кривую L можно задавать в виде( параметрическое задание кривой) :
На плоскости бывает задана в таком виде: или в явном виде y = f ( x ) a Предположим, что функция y = f ( x ) непрер. дифференц. Разобьем отрезок [ a , b ] на n частичных отрезков и рассм.точки на кривой с координатами. Рассмотрим ломаную соверш.в этих точках, тогда длина кривой L =
Навигация: Главная Случайная страница Обратная связь ТОП Интересно знать Избранные Топ: Оценка эффективности инструментов коммуникационной политики: Внешние коммуникации — обмен информацией между организацией и её внешней средой… Теоретическая значимость работы: Описание теоретической значимости (ценности) результатов исследования должно присутствовать во введении. Когда производится ограждение поезда, остановившегося на перегоне: Во всех случаях немедленно должно быть ограждено место препятствия для движения поездов на смежном пути двухпутного… Интересное: Мероприятия для защиты от морозного пучения грунтов: Инженерная защита от морозного (криогенного) пучения грунтов необходима для легких малоэтажных зданий и других сооружений… Берегоукрепление оползневых склонов: На прибрежных склонах основной причиной развития оползневых процессов является подмыв водами рек естественных склонов… Лечение прогрессирующих форм рака: Одним из наиболее важных достижений экспериментальной химиотерапии опухолей, начатой в 60-х и реализованной в 70-х годах, является… Дисциплины: Автоматизация Антропология Археология Архитектура Аудит Биология Бухгалтерия Военная наука Генетика География Геология Демография Журналистика Зоология Иностранные языки Информатика Искусство История Кинематография Компьютеризация Кораблестроение Кулинария Культура Лексикология Лингвистика Литература Логика Маркетинг Математика Машиностроение Медицина Менеджмент Металлургия Метрология Механика Музыкология Науковедение Образование Охрана Труда Педагогика Политология Правоотношение Предпринимательство Приборостроение Программирование Производство Промышленность Психология Радиосвязь Религия Риторика Социология Спорт Стандартизация Статистика Строительство Теология Технологии Торговля Транспорт Фармакология Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Экономика Электроника Энергетика Юриспруденция | ⇐ ПредыдущаяСтр 2 из 2 1. 2. Если переменная сила F=f(x) действует в направлении оси Ox (f(x) – непрерывна на [a; b]), то работа этой силы на отрезке [a; b] оси Ох равна . 3. Если функция f(x) непрерывна и неотрицательна на отрезке [a; b], то геометрически представляет собой площадь криволинейной трапеции, ограниченной сверху графиком функции y=f(x), снизу – отрезком [ Пример 3.5.11.Найти площадь фигуры, ограниченной параболой и гиперболой . ○ Найдем точки пересечения параболы и гиперболы, для этого решим систему уравнений: ; ; ; , ; , . Таким образом, заданные кривые пересекаются в точках А(1; 0) и В(3; 4) (рис. 3.27). Следовательно, 4,58 (кв. ед.). ● Замена переменной в определенном интеграле Формула замены переменной в определенном интеграле: , где , α и β определяются из условий соответственно. Пример 3.5.12. Вычислить . ○ ● Теорема 3.5.6. (Теорема о среднем)Если функция f(x) непрерывна на отрезке [a ; b], то в интервале (a; b) найдется такая точка с, что. Интегрирование по частям в определенном интеграле Пусть u=u(x), v=v(x) – непрерывно дифференцируемые на отрезке [a; b] функции. Тогда . Определенный интеграл с переменным верхним пределом Пусть функция f(x) непрерывна на отрезке [a; b]. , где х – любая точка из [a; b]. Если F(x) – первообразная функции f(x), т.е. F′(x)=f(x), то согласно формуле Ньютона-Лейбница имеем: . Отсюда . Таким образом, производная определенного интеграла с переменным верхним пределом по этому пределу равна значению подынтегральной функции от этого предела.
Несобственные интегралы Интегралы с одним или обоими бесконечными пределами получили название несобственных интегралов первого рода. Здесь также, как при вычислении определенных интегралов, можно на практике использовать формулу Ньютона-Лейбница, однако следует помнить, что символ ∞ – не число, а условное обозначение неограниченного возрастания (или убывания) аргумента в процессе его изменения. То есть, со строгих позиций, вычисление несобственного интеграла первого рода – это вычисление некоторого предела, с постоянным использованием теорем о бесконечно малых и бесконечно больших величинах. Таким образом: ; ; . То есть, символы бесконечности условно заменяются буквенными параметрами, применяется формула Ньютона-Лейбница, после чего обычным образом вычисляются указанные пределы. Если в результате такого расчета получится конечное число А (включая 0), то ответ следует записать в форме: интеграл сходится к значению А. Если же результатом будет +∞ (или –∞) или предел не существует, то ответ: интеграл расходится. В практических вычислениях, вполне допустимо не использовать в явной форме операторы lim, но не следует забывать о том, что на самом деле вычисляются пределы, а не конкретные числовые значения. Следующим видом несобственных интегралов являются интегралы от функций с разрывом на одном конце (или обоих концах) интервала интегрирования или с разрывом внутри интервала интегрирования. Например: , и т.п. Такие интегралы носят название несобственных интегралов второго рода. Эти интегралы очень опасны, т. Вычисление несобственных интегралов второго рода осуществляется приведением к интегралам первого рода (или сумме таких интегралов), то есть, ставится задача вычисления предела относительно точки, в которой подынтегральная функция разрывна.
Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции… Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого… Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим… Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ — конструкции, предназначенные для поддерживания проводов на необходимой высоте над землей, водой. |
Геометрическая интерпретация определенных интегралов
- Математические сомнения
- Определенные интегралы
Объяснение определенного интеграла математическим уравнением определенно сбивает с толку всех на начальном уровне, но геометрическая интерпретация ни для кого не создает проблем. Итак, всем всегда рекомендуется понимать концепцию определенного интегрирования по геометрической системе.
График функции необходим для объяснения понятия определенного интеграла в геометрической системе. Итак, давайте сначала нарисуем график для функции, а затем выполним еще несколько геометрических шагов для подготовки графика для поддержки геометрической интерпретации.
- Пусть $x$ — переменная, представляющая действительные числа по горизонтальной оси $x$.
- Давайте рассмотрим функцию, и это функция в терминах $x$. Итак, в математике это записывается как $f(x)$. Соответствующие значения функции для всех значений $x$ отложены по вертикальной оси $y$.
 Таким образом, математическая связь между значениями $x$ и соответствующими значениями функции $f(x)$ выражается кривой.
Таким образом, математическая связь между значениями $x$ и соответствующими значениями функции $f(x)$ выражается кривой. - Теперь возьмем точку $P$ на оси $x$ и проведем прямую, пересекающую кривую в точке $Q$. Аналогичным образом рассмотрим другую точку на оси $x$, обозначенную как $R$, а затем проведем прямую линию, пересекающую кривую в точке $S$. Помните, что две прямые линии должны быть перпендикулярны горизонтальной оси.
- Предположим, что $x$-координата точек $P$ и $R$ обозначена через $a$ и $b$ соответственно.
Интерпретация
Образуется замкнутая геометрическая фигура $PQSR$. Площадь замкнутой геометрической формы равна площади, ограниченной кривой функции $f(x)$, прямыми $x = a$ и $x = b$ и осью $x$.
Область $PQSR$ не является идеальным четырехугольником. Таким образом, найти площадь области по формулам площади невозможно, потому что она не является ни квадратом, ни прямоугольником, ни каким-либо другим четырехугольником. Однако разбиение области на несколько прямоугольников одинаковой длины помогает нам найти ее площадь. Итак, разделите область на несколько прямоугольников одинаковой длины, как показано на рисунке.
Итак, разделите область на несколько прямоугольников одинаковой длины, как показано на рисунке.
Теперь длина каждого прямоугольника одинакова, и его можно обозначить дифференциальным элементом $\Delta x$ согласно дифференциальному исчислению, но ширина каждого прямоугольника различна. Однако площадь любого прямоугольника можно вычислить по формуле его площади. Интегрирование площадей всех прямоугольников — это концепция нахождения всей площади области $PQSR$.
Площадь каждого прямоугольника может быть легко вычислена по формуле площади прямоугольника, но мы можем заметить, что мы игнорируем некоторые части области над прямоугольниками. По этой причине сумма площадей всех прямоугольников не равна в точности площади замкнутой геометрической фигуры $PQSR$.
Если мы уменьшим длину каждого прямоугольника наполовину, то игнорируемая часть области всех прямоугольников уменьшится по сравнению с предыдущим случаем. Теперь сумма площадей всех прямоугольников близка к площади области $PQSR$, но не совсем равна. Однако сумма площадей всех прямоугольников текущего случая больше площадей всех прямоугольников предыдущего случая.
Однако сумма площадей всех прямоугольников текущего случая больше площадей всех прямоугольников предыдущего случая.
Два случая показали, что уменьшение длины прямоугольника минимизирует неучтенную площадь над каждым прямоугольником. Следовательно, если длина каждого прямоугольника приблизительно равна нулю, то не учитываемая площадь над каждым прямоугольником также равна нулю. В этом случае сумма площадей всех прямоугольников в точности равна площади замкнутой геометрической фигуры $PQSR$.
Теперь разделите область области $PQSR$ на несколько прямоугольников одинаковой длины.
- Длина каждого прямоугольника очень мала, приблизительно равна нулю, а его длина математически обозначается дифференциалом $dx$. Из-за очень маленькой длины прямоугольник выглядит как прямая линия. Помните, что для удобства мы показываем на рисунке только два прямоугольника.
- Ширина каждого прямоугольника является переменной, и ее можно узнать, сравнив ширину двух прямоугольников.
 Однако ширину любого прямоугольника можно вычислить с помощью функции $f(x)$.
Однако ширину любого прямоугольника можно вычислить с помощью функции $f(x)$.
Следовательно, площадь одного прямоугольника равна произведению длины и ширины прямоугольника.
$A_R$ $\,=\,$ $dx \times f(x)$
$\имплицит$ $A_R$ $\,=\,$ $f(x) \times dx$
$\ ,\,\,\следовательно\,\,\,\,\,\,$ $A_R$ $\,=\,$ $f(x)dx$
Площадь каждого прямоугольника выражается приведенной выше формулой математически. Итак, складываем площади всех прямоугольников, и их сумма обозначается интегральным символом в исчислении.
$\implies$ $A$ $\,=\,$ $\displaystyle \int{f(x)}\,dx$
Функция $f(x)$ является непрерывной функцией. Таким образом, кривая продолжается бесконечно в обоих направлениях. Интеграл от произведения $f(x)$ и $dx$ вычисляет площадь под всей кривой.
В этом случае площадь под кривой должна быть рассчитана между пределами. Итак, границы должны быть определены, чтобы найти интеграл функции. По этой причине границы $a$ и $b$ отображаются ниже и выше символа интеграла соответственно. {\displaystyle b} {f(x)}\,dx$
{\displaystyle b} {f(x)}\,dx$
Интеграл функции $f(x)$ от $a$ до $b$ точно вычисляет площадь, ограниченную кривой $f(x)$, линиями $x = a$ и $x = b$, и горизонтальная ось $x$.
| Определенный интеграл Ваш браузер не поддерживает видео тег. Интегральное понятие связано с понятием площади. Хотя Кавальери не знал термина «функция», мы можем сказать, что одним из его вкладов было рассмотрение проблемы вычисления функции. площадь, ограниченная графиком положительной функции, осью x и двумя вертикальными линиями («криволинейная трапеция» или «площадь под кривой»): Мы хотим присвоить этой области число, которое представляет ее площадь, когда функция положительна. Мы будем называть это число определенным интегралом f между a и b. Этот интеграл не всегда представляет собой площадь «криволинейной трапеции». Это только случай
когда f неотрицательно.
Когда f отрицательно, интеграл будет минус площадь. В общем,
интеграл — это площадь криволинейной трапеции, лежащей над осью x, уменьшенная на площадь частей, которые
лежат ниже оси x. Если мы хотим интегрировать линейные функции, проблема проста. Проблема усложняется, когда график функции не является линией. «Мы будем следовать идее Архимеда. Она состоит в том, чтобы аппроксимировать функцию f горизонтальными (постоянными) функциями, а площадь под f — функцией сумма маленьких прямоугольников» (Ланг) В этих случаях мы хотим построить определенный интеграл (число) как результат некоторого предельного процесса. Мы можем начать делить [a,b] на подынтервалы и взять сумма площадей некоторых прямоугольников, аппроксимирующих функцию f в различных точках отрезка. Площадь этих прямоугольников аппроксимирует интеграл. Интеграция – это процесс суммирования. Это обозначение, которое мы используем: Символ S (удлиненная буква S для суммы) называется знаком интеграла и был введен Лейбницем в 1675 году. Процесс, в результате которого получается результат, называется
интеграция. Числа а и b, которые стоят перед знаком интеграла, называются нижним и верхним пределами интегрирования. Лейбниц использовал этот символ, потому что считал интеграл суммой бесконечного числа прямоугольников с высотой f (x) и «бесконечно малым». ширина. Его с готовностью приняли многие ранние математики, потому что им нравилось думать об интегрировании как о своего рода «процесс суммирования», который позволял им складывать вместе бесконечно много «бесконечно малых величин». Мы попытаемся показать некоторые идеи, лежащие в основе строгого определения интеграла, данного Бернхардом Риманом (1826-1866). P является разбиением [a,b]. Раздел определяет некоторые подынтервалы. Ширина этих подынтервалов может быть разной: Учитывая раздел [a,b], мы можем добавить больше чисел к разделу, и тогда мы получим новый раздел с небольшими интервалами. Если мы добавьте достаточное количество промежуточных чисел, тогда интервалы можно сделать сколь угодно малыми. Одним из ограничений является использование регулярных подразделений интервала. В этом случае основания прямоугольников равны: Для каждого i мы выбираем некоторую точку x i * в [x i , x i+1 ]. «Основная идея, которую мы собираемся осуществить, состоит в том, что по мере того, как мы будем делать интервалы нашего разбиения все меньше и меньше, сумма площадей прямоугольников приблизится к пределу, и этот предел можно использовать для определения площади под кривой» (Ланг). Мы можем выбрать, что x i * будет точкой в середине подынтервала (как в матлете и в предыдущих примерах). Одним из популярных вариантов является x i * , равный x i , левому концу подынтервала. Тогда высота прямоугольника будет f(x i ): Или мы можем выбрать x i * равным x i+1 , правому концу подынтервала. Тогда высота прямоугольника будет f(x я+1 ): Выбор этих x i * в [x i , x i+1 ] является произвольным. Любая из этих сумм называется суммой Римана функции f для P. Геометрическая интерпретация: «Это общая площадь n прямоугольников, которая лежит частично под графиком f и частично над ним. Из-за каким бы образом ни были выбраны высоты прямоугольников, мы не можем с уверенностью сказать, меньше ли та или иная сумма Римана или больше интеграла. Но кажется, что перекрытие не должно иметь большого значения; если основания всех прямоугольников узкие достаточно, то сумма Римана должна быть близка к интегралу». (Спивак) Если мы увеличим количество прямоугольников, мы (интуитивно) будем иногда ближе к значению, которое является определенным интегралом. Тогда можно сказать, что определенный интеграл является пределом сумм Римана при стремлении числа подразделений к бесконечности и ширины каждого подинтервала стремится к нулю. И неважно, какую точку x i * мы выберем в каждом подинтервале. «Мораль этой басни состоит в том, что все, что выглядит как хорошее приближение к интегралу, на самом деле им является, при условии, что все длины
интервалы в разбиении достаточно малы». В математике мы можем изменить функцию и количество прямоугольников. Хотя в каждом интервале высота прямоугольника может быть любым значением функции в точке подынтервала, здесь мы рассматриваем только одну простую возможность: x i * является средней точкой подынтервала. В этом случае суммы Римана называются средними суммами Римана. «Интегралы большинства функций невозможно точно определить (хотя их можно вычислить с любой желаемой степенью точности). путем вычисления нижней и верхней сумм). Тем не менее [как мы узнаем позже, например, при изучении основной теоремы исчисления] интеграл от многих функций может быть вычисляется очень легко» (Спивак). Аксиоматический подход к интегралу (вслед за Сержем Лангом) В своей книге «Первый курс исчисления», прежде чем объяснять суммы Римана, он подчеркивает важность двух свойств, которые будут определять интеграл. для f на [a,b]: Пусть a, b — два числа, причем a удовлетворяющие следующим свойствам: Свойство 1. |

 ..
.. Путь S, пройденный точкой по прямой за время T – t0 со скоростью v=v(t) (v(t) непрерывна на [t0; T]), есть .
Путь S, пройденный точкой по прямой за время T – t0 со скоростью v=v(t) (v(t) непрерывна на [t0; T]), есть .
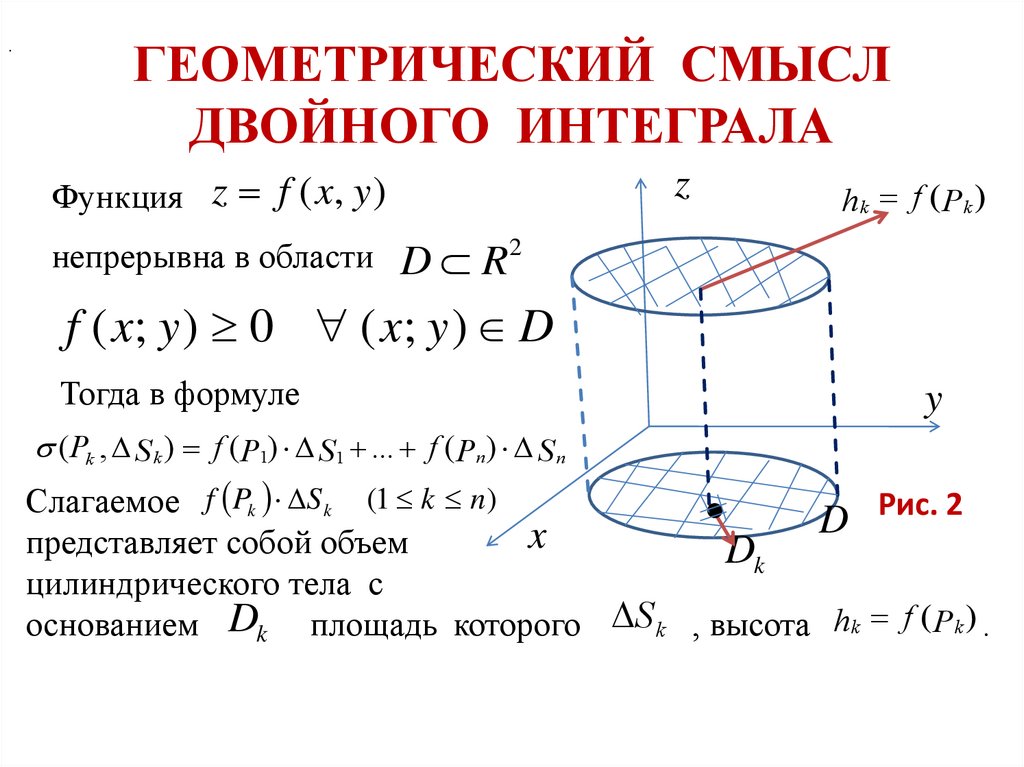
 Рассмотрим интеграл
Рассмотрим интеграл
 к. часто выглядят вполне безобидно (по невнимательности забываем особые точки подынтегральной функции), но применение формулы Ньютона-Лейбница приводит к неверным результатам.
к. часто выглядят вполне безобидно (по невнимательности забываем особые точки подынтегральной функции), но применение формулы Ньютона-Лейбница приводит к неверным результатам.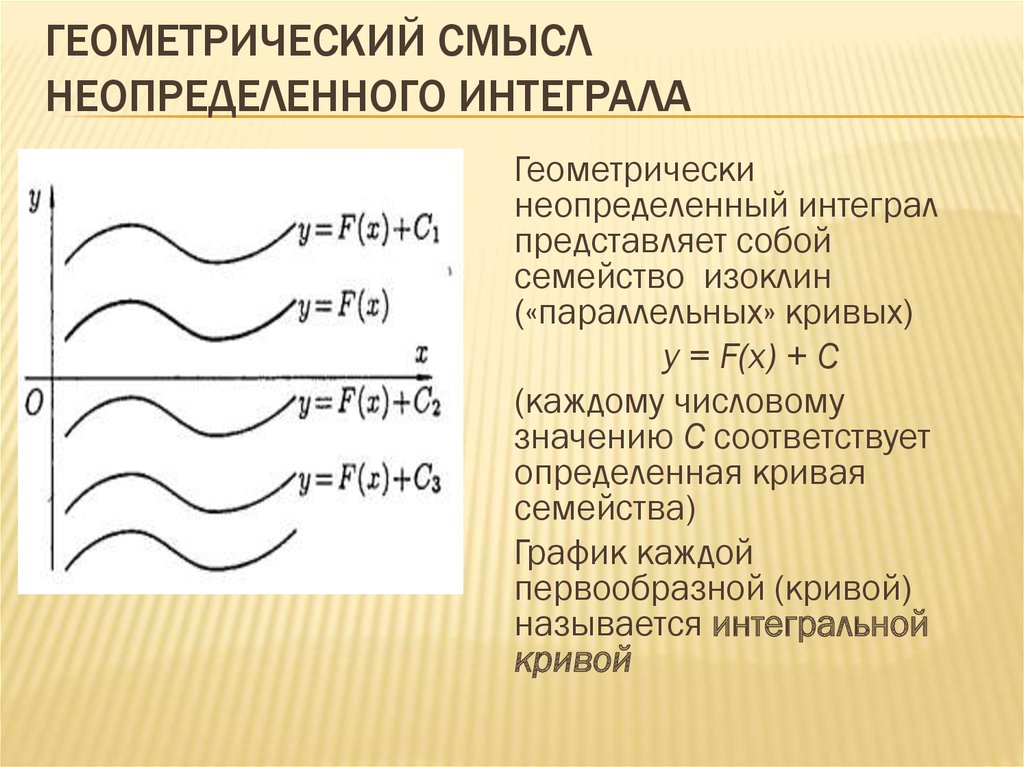
 Таким образом, математическая связь между значениями $x$ и соответствующими значениями функции $f(x)$ выражается кривой.
Таким образом, математическая связь между значениями $x$ и соответствующими значениями функции $f(x)$ выражается кривой. Однако ширину любого прямоугольника можно вычислить с помощью функции $f(x)$.
Однако ширину любого прямоугольника можно вычислить с помощью функции $f(x)$. Когда плоская фигура ограничена прямыми линиями, легко вычислить ее площадь.
Однако области, ограниченные изогнутыми линиями, сложнее найти (и даже определить).
9n) от n=1 до n=9.
Общий результат для произвольного n был получен Ферма.
Когда плоская фигура ограничена прямыми линиями, легко вычислить ее площадь.
Однако области, ограниченные изогнутыми линиями, сложнее найти (и даже определить).
9n) от n=1 до n=9.
Общий результат для произвольного n был получен Ферма.

 Значение f(x i * )
можно рассматривать как высоту прямоугольника.
Значение f(x i * )
можно рассматривать как высоту прямоугольника.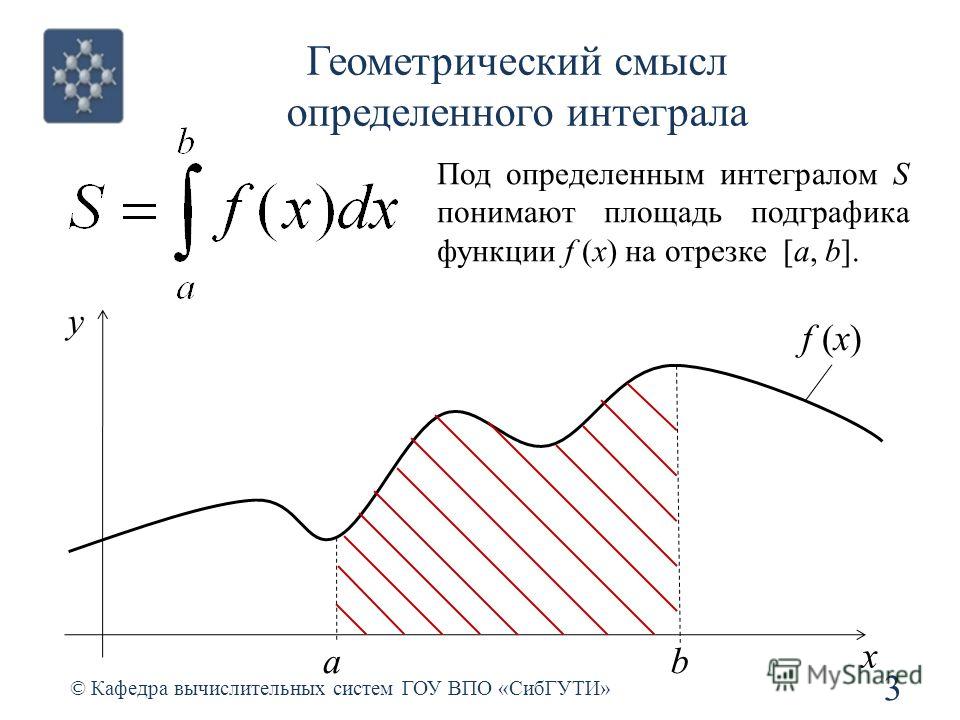 Затем Риман считал
Затем Риман считал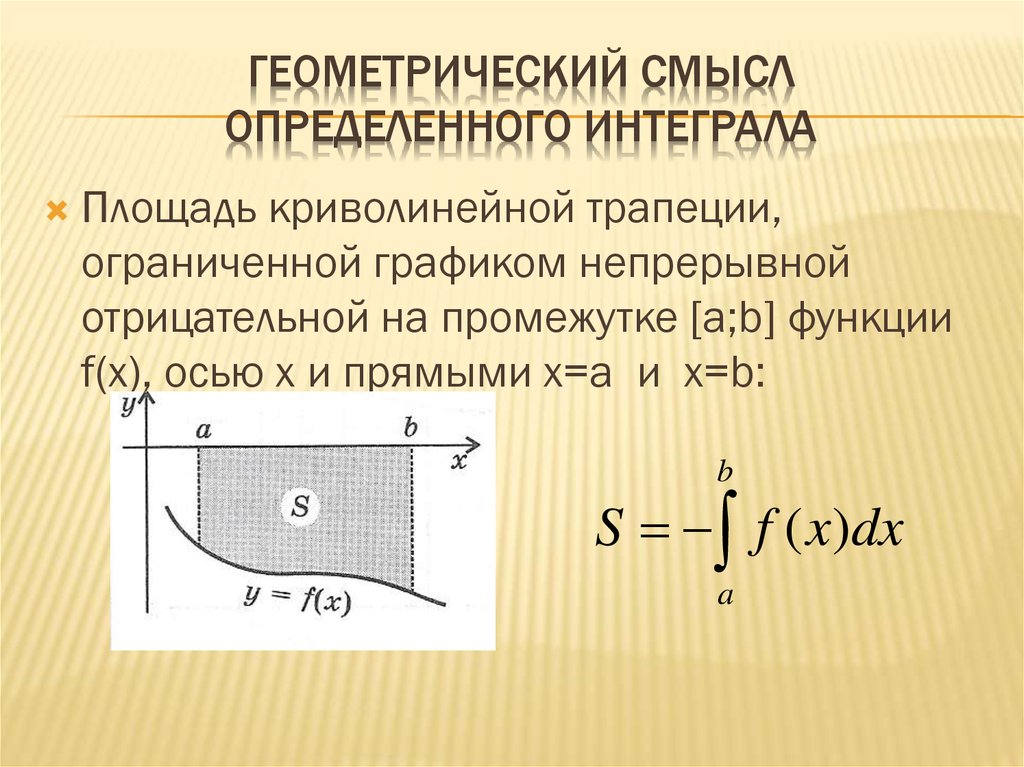 (Спивак)
(Спивак)