Что такое вектор, как найти длину? Координаты? Формулы
Поможем понять и полюбить математику
Начать учиться
Сегодня нас ждёт увлекательное путешествие, которое можно озаглавить словосочетанием «векторы в геометрии». Да, достаточно самонадеянно думать, что меньше чем за час можно стать экспертом в этой теме. Но познакомиться, выяснить нюансы, а главное, увидеть всю картину целиком — можно! Мы постараемся стать вашими проводниками в этот удивительный мир и охватить все темы о векторах, которые могут встретиться в школе.
Определение и обозначение вектора
Вектор в геометрии — это отрезок, для которого указано, какая из его граничных точек считается началом, а какая — концом. В некоторых учебниках вектор могут называть направленным отрезком.
Вектор обозначается одной строчной буквой латинского алфавита или двумя заглавными со стрелкой (в некоторых случаях — прямой линией) сверху.
Интересно, что порядок букв в названии вектора имеет значение! Первая буква отвечает за начало вектора, а последняя — за его конец. Поэтому и — абсолютно разные векторы.
Узнай, какие профессии будущего тебе подойдут
Пройди тест — и мы покажем, кем ты можешь стать, а ещё пришлём подробный гайд, как реализовать себя уже сейчас
Виды векторов
Во-первых, векторы бывают коллинеарными и неколлинеарными.
Коллинеарными называют те векторы, которые лежат на одной прямой или параллельных прямых. На рисунке и и являются коллинеарными, а и относительно друг друга — нет.
Векторы различаются и по направлению. Если векторы уже являются коллинеарными, они могут быть сонаправленными или противоположно направленными. Сонаправленные векторы обозначаются так: Если же они противоположно направлены, мы можем записать это следующим образом:
Равными являются те векторы, которые одновременно и коллинеарны, и сонаправлены, а также имеют одинаковую длину.
Нулевой вектор — вектор, длина которого равна нулю. Чаще всего его обозначают так: Он считается коллинеарным любому вектору.
Иногда в геометрии вводят дополнительные понятия, рассмотрим и их:
Закреплённый вектор — отрезок с упорядоченными концами: если С — точка начала вектора, а Е — точка конца, тогда (это то, что мы понимаем под обычным вектором в школьной геометрии).
Свободный вектор — вектор, начало и конец которого не закреплены. Его можно перемещать как вдоль прямой, на которой он находится, так и параллельно этой прямой. По сути под свободным вектором понимают множество закреплённых векторов.
Сложение и вычитание векторов
Действия с векторами описываются и в алгебре, и в геометрии.
Сложение: метод треугольника
Представим, что в пространстве заданы векторы и которые нам необходимо сложить. Эта задача особенно актуальна для физиков, поскольку такие векторные величины, как сила, часто приложены к одному и тому же телу. В таком случае возникает вопрос: а как же рассчитать результирующее действие всех этих сил?
В этом на помощь физикам приходит математика — царица наук! Чтобы сложить два вектора, необходимо:
Отложить начало одного вектора от конца другого.
Вектор их суммы будет совпадать с вектором , который соединяет начало вектора с концом вектора
Сложение: метод параллелограмма
Сложить векторы можно и по-другому, используя метод параллелограмма:
Совместим между собой концы и
Отложим от конца вектор, равный
Отложим от конца вектор, равный
Благодаря пунктам 2 и 3 мы получили параллелограмм (четырёхугольник, противоположные стороны которого параллельны и равны).

Проведём диагональ параллелограмма между и на которой будет лежать вектор, равный сумме и
Задача решена, вы великолепны!
Обратите внимание
Как метод параллелограмма, так и метод треугольника подразумевает перемещение векторов в пространстве: мы или совмещаем их концы, или откладываем от конца одного вектора начало другого. Получить сумму векторов, не имеющих общей точки, с этими методами не представляется возможным.
Сложение: метод многоугольника
А что если векторов больше, чем два? На эту проблему математика уже подготовила решение: воспользуемся расширенным методом треугольника, который получил название «метод многоугольника».
Согласно этому методу мы последовательно совмещаем конец и начало векторов, а после изображаем суммирующий вектор, начало которого совпадает с началом первого вектора, а конец — с концом последнего. Лучше всего рассмотреть это на чертеже:
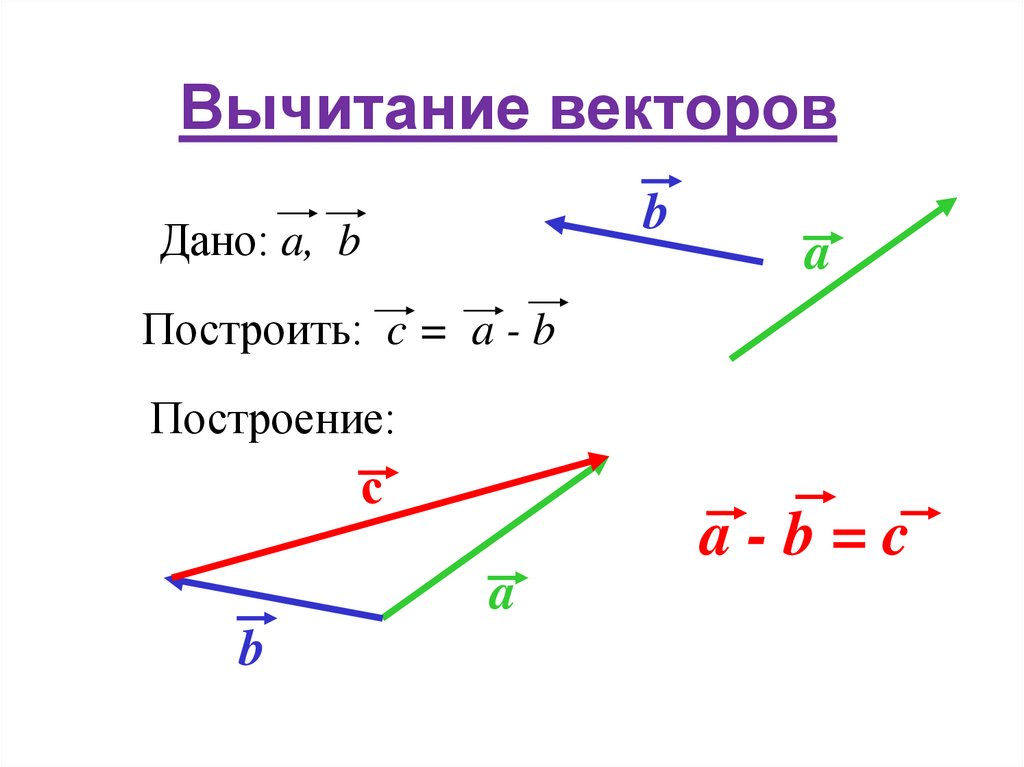
Вычитание векторов
Продолжаем проделывать с векторами всевозможные действия, на этот раз вычитание.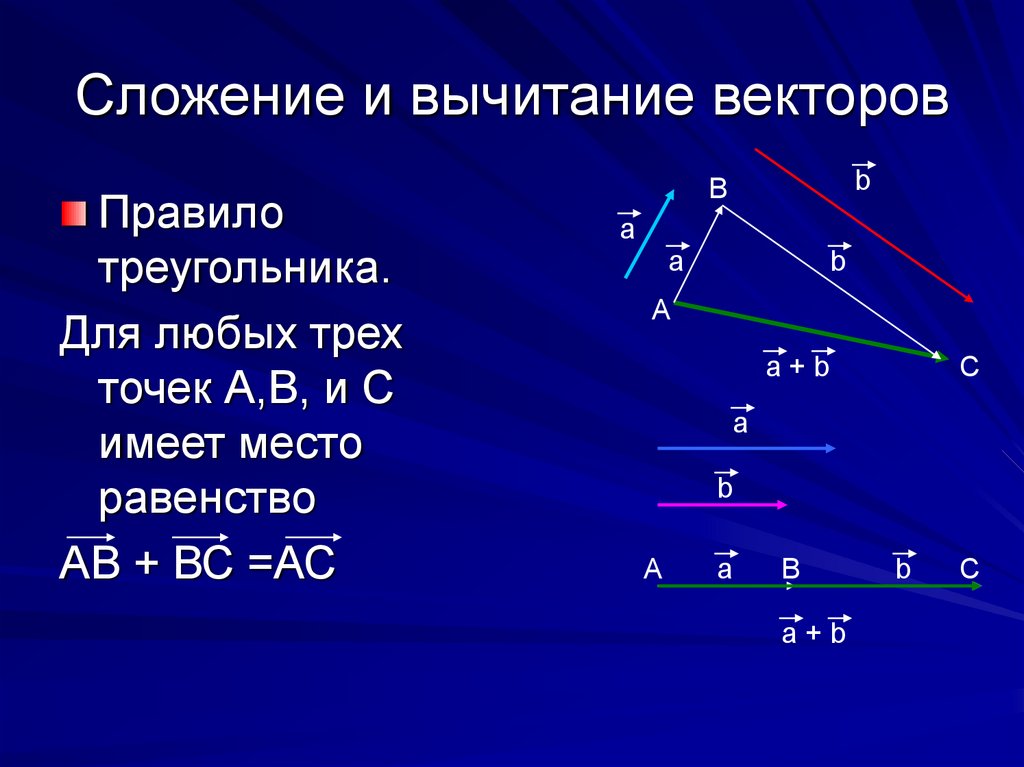 Математики знают, что вычитание — это по своей сути то же сложение, но с обратным числом.
Математики знают, что вычитание — это по своей сути то же сложение, но с обратным числом.
С векторами работает та же штука: вместо вычитания попробуем прибавить вектор, противоположно направленный исходному:
Изобразим разность векторов с помощью уже знакомого нам правила треугольника:
Боитесь запутаться в векторах сонаправленных и противоположно направленных? Существует отдельное правило для их вычитания:
Отложим один вектор от начала другого.
Тогда вектор их разности совпадает с вектором, начало которого совмещено с концом вычитаемого вектора, а начало — с концом уменьшаемого.
Этот метод схож и с методом параллелограмма, но в этом случае мы берём другую диагональ.
Координаты вектора на плоскости и в пространстве
Для выполнения остальных действий с векторами нам необходимо поместить их в такую систему координат, чтобы можно было
определить их положение относительно друг друга.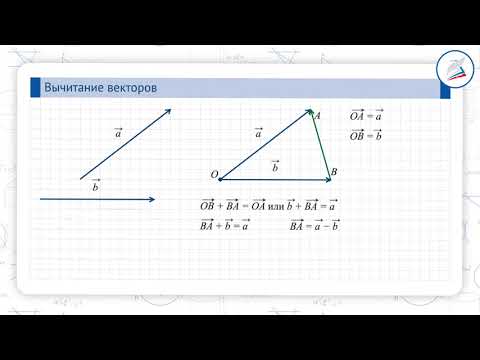
Тогда, если находится на плоскости, его координаты можно выразить как если в пространстве —
Базисные векторы — это векторы, каждый из которых направлен вдоль своей оси координат, в трёхмерном пространстве их обозначают
Любой вектор в трёхмерном пространстве можно разложить по трём базисным векторам.
с координатами можно записать так:
Умножение вектора на число
Представьте, что нам необходимо растянуть вектор в два раза или же сжать, но уже в три. За все эти действия отвечает
одна простая задача: умножение вектора на число.
Для того чтобы увеличить или уменьшить вектор в некоторое количество раз, необходимо умножить все координаты вектора на это число.
Таким образом, если задан координатами то — Кстати, подобным образом можно перевернуть вектор, направив его в противоположную сторону:
Длина вектора
Длина вектора — одно из основных понятий в этом разделе. И неудивительно, ведь она характеризует его протяженность в пространстве и выражается числом.
Итак, длина вектора
— это расстояние между его началом и концом. Её часто называют модулем, что отражается и в обозначении. Если нам необходимо найти длину мы так и запишем:Длину вектора можно найти разными способами, вот основные:
через координаты вектора;
через координаты точек начала и конца вектора;
через теорему косинусов.

Давайте вместе разберём все методы!
Длина вектора через его координаты
Если задан через координаты то его длину можно найти как
Почему мы можем быть уверены, что эта формула правильная? Рассмотрим вектор в декартовой системе координат.
Отложим вектор от точки с координатами Тогда этот вектор можно назвать , и так как мы строили его из начала координат, координаты вектора могут быть найдены как
Рассчитаем длину через теорему Пифагора:
Задача 1
Посчитайте, чему равен модуль , если его координаты
Решение:
Модуль вектора — это его длина, а значит,
Задача 2
Длина Чему равна координата по оси , если координата по оси
Решение:
Длина вектора через координаты точек начала и конца
Для начала давайте вспомним, как задать координаты вектора через координаты его начала и конца.
Рассмотрим где и Тогда координаты вектора можно выразить так:
Мы уже знаем, как найти длину вектора через его координаты, поэтому подставим полученное выражение в формулу:
Задача 3
Найдите длину если и
Решение:
Задача 4
Рассчитайте координату по точки вектора , если его длина равна а
Решение:
Остановимся здесь и подставим известные числа в формулу:
или
Длина вектора через теорему косинуса
К сожалению, в задачах не всегда даны координаты точек вектора или его самого. В таком случае мы воспользуемся теоремой косинуса. Давайте вспомним её формулировку.
Теорема косинусов звучит так: квадрат стороны треугольника равен сумме квадратов двух других его сторон минус
удвоенное произведение этих сторон на косинус угла между ними.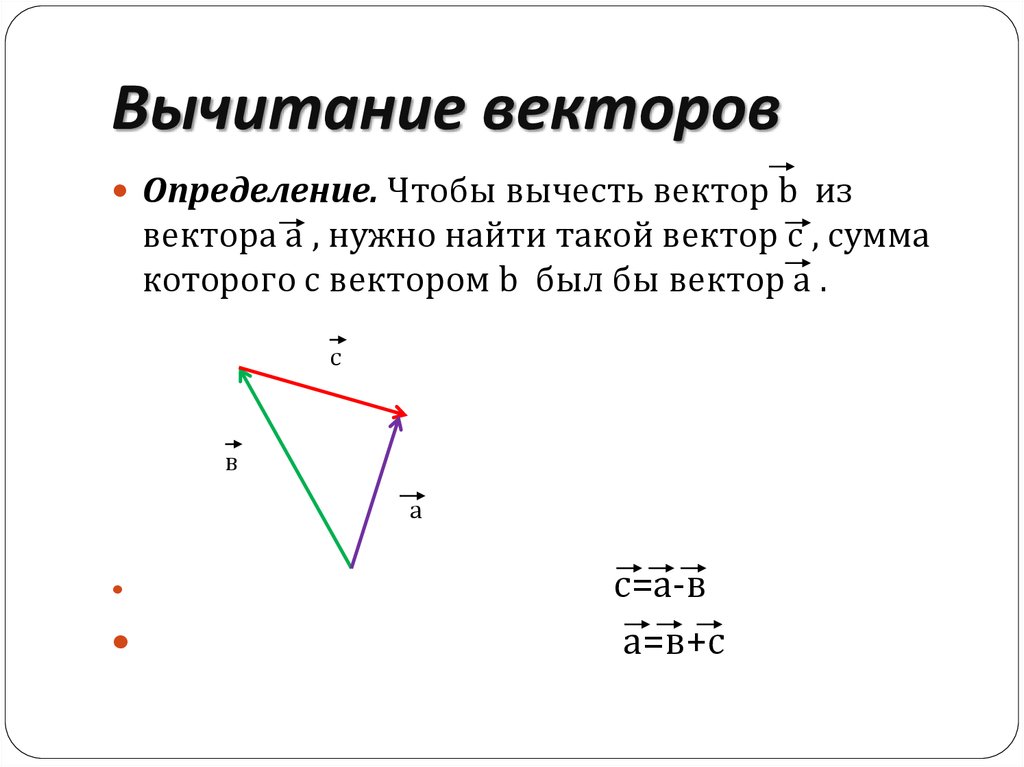
Формула теоремы косинусов:
Эту теорему можно применить и в векторной форме. Немного изменим рисунок:
Тогда, чтобы найти длину , необходимо знать (или иметь возможность вычислить) длины и , знать угол между ними, а также уметь рассчитать произведение длин этих векторов.
Задача 5
Длины и равны 4 и 6 соответственно, а угол между ними равен Вычислите длину
Решение:
Задача 6
Рассчитайте модуль вектора в треугольнике, если длина = 8, длина = 10, а угол между ними равен
Решение:
Скалярное произведение векторов
Мы практически дошли до финала нашего путешествия по царству векторов. 👑 Нам осталось изучить только скалярное произведение векторов. Что это?
Скалярное произведение — это операция над двумя векторами, результатом которой является скаляр, то
есть число,
которое не зависит от выбора системы координат.
Скалярным произведением и будет скалярная величина, равная произведению модулей этих векторов, умноженная на косинус угла между ними:
Вспомним, что в той же физике величины делятся на скалярные (не имеющие направления, например, масса) и векторные (имеющие направление, например, сила, ускорение, скорость). В математике под вектором подразумевают направленный отрезок, а понятие скаляра хоть и не равно, но очень близко к понятию числа.
Скалярное произведение показывает, насколько синхронизированы, скоординированы направления векторов. Так, чем больше угол между векторами, тем меньше согласованности, а значит, скалярное произведение будет уменьшаться с ростом угла:
Скалярное произведение вектора на само себя равно квадрату его модуля: В данном случае значение скалярного произведения является наибольшим из возможных.
Если угол между векторами острый и векторы ненулевые, то скалярное произведение положительно, так как
Если угол между векторами прямой, то скалярное произведение равно 0, так как
Если угол между векторами тупой и векторы ненулевые, то скалярное произведение отрицательно, так как
Cкалярное произведение вектора на противоположно направленный ему вектор равно отрицательному произведению их длин .
 В данном случае значение скалярного произведения является наименьшим из возможных.
В данном случае значение скалярного произведения является наименьшим из возможных.
Конечно, вы можете возразить: «Согласованность направлений отлично показывает угол, для чего нам эти сложные вычисления?». А всё дело в том, что в пространстве порой очень сложно измерить угол, а вот посчитать скалярное произведение — просто, особенно если рассмотреть его через координаты.
Если выражен координатами а то скалярное произведение этих векторов описывается формулой: В пространстве скалярное произведение через координаты векторов будет задаваться так:
Где применяется скалярное произведение? Благодаря ему выполняется большое количество математических операций, таких
как нахождение угла между векторами и любых расстояний, если они заданы через координаты. Благодаря скалярному
произведению можно описать даже характеристику криволинейных поверхностей, но это мы обсудим как-нибудь в другой
раз. 🙂
🙂
Чтобы закрепить пройденный материал, нужно больше, чем пара заданий. Поэтом приглашаем на онлайн-уроки математики в школу Skysmart. За короткое время благодаря особенной платформе и учителям-профессионалам вы сможете улучшить школьные отметки, подготовиться к экзаменам и олимпиадам, и самое главное — понять и полюбить математику.
Шпаргалки для родителей по математике
Все формулы по математике под рукой
Дарья Вишнякова
К предыдущей статье
421.9K
Длина окружности
К следующей статье
Нахождение наибольшего и наименьшего значения функции
Получите план обучения, который поможет понять и полюбить математику
На вводном уроке с методистом
Выявим пробелы в знаниях и дадим советы по обучению
Расскажем, как проходят занятия
Подберём курс
Вычитание векторов.
 Правило вычитания векторов. Геометрия вычитание векторов.
Правило вычитания векторов. Геометрия вычитание векторов.- Альфашкола
- Статьи
- Правила вычитания векторов
В этой статье мы узнаем как вычесть вектора. Вектор — это величина, имеющая величину размер и направление. Вычитание вектора равносильно добавлению вектора с отрицательным знаком. Разность векторов \(\overline{a}\) и \(\overline{-b}\) равна сумме \(\overline{a}\) и \(\overline{-b}\):
Перемещение векторов
Наша задача — найти способ четко и последовательно представлять векторы. Графически это просто: поскольку мы можем перемещать вектор в любом месте, давайте всегда будем располагать «хвост» вектора в начале координатной плоскости.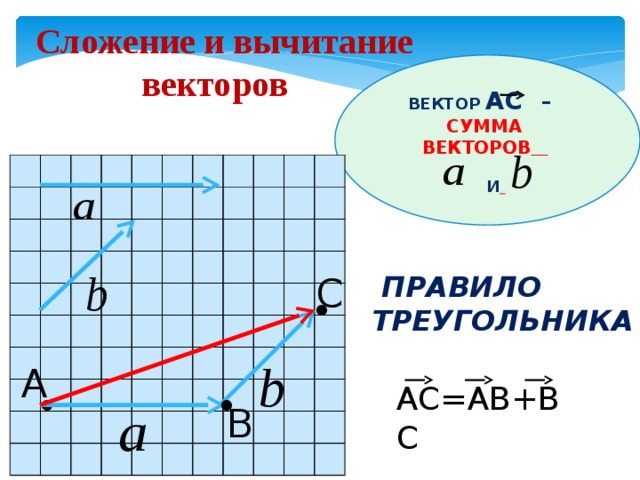 Теперь, когда хвост вектора помещен в конец другого вектора (помните, мы можем перемещать вектор в любом месте, пока мы сохраняем его направление и длину). Проводим от начала вектора \(\overline{b}\) (вычитаемого вектора) вектор \(\overline{c}\) к началу вектора \(\overline{a}\) (уменьшаемого вектора) получаем разость вектор \(\overline{c}\) :
Теперь, когда хвост вектора помещен в конец другого вектора (помните, мы можем перемещать вектор в любом месте, пока мы сохраняем его направление и длину). Проводим от начала вектора \(\overline{b}\) (вычитаемого вектора) вектор \(\overline{c}\) к началу вектора \(\overline{a}\) (уменьшаемого вектора) получаем разость вектор \(\overline{c}\) :
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Наши преподаватели
Наталья Михайловна Алипчикова
Репетитор по математике
Стаж (лет)
Образование:
Могилевский педагогический институт
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Аида Робертовна Алтунян
Репетитор по математике
Стаж (лет)
Образование:
Самаркандский государственный университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Юрий Алексеевич Алексеенко
Репетитор по математике
Стаж (лет)
Образование:
Кубанский государственный университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Предметы
- Математика
- Репетитор по физике
- Репетитор по химии
- Репетитор по русскому языку
- Репетитор по английскому языку
- Репетитор по обществознанию
- Репетитор по истории России
- Репетитор по биологии
- Репетитор по географии
- Репетитор по информатике
Специализации
- Репетитор по химии для подготовки к ЕГЭ
- Репетитор по химии для подготовки к ОГЭ
- Репетитор для подготовки к ОГЭ по физике
- Репетитор по русскому языку для подготовки к ЕГЭ
- Репетитор по русскому языку для подготовки к ОГЭ
- Подготовка к олимпиадам по английскому языку
- Репетитор для подготовки к ЕГЭ по истории
- Репетитор по биологии для подготовки к ОГЭ
- Репетитор по географии для подготовки к ЕГЭ
- Подготовка к ОГЭ по литературе
Похожие статьи
- Свойства интегралов
- Движение навстречу друг другу
- Решение дробно-рациональных уравнений
- ЕГЭ по математике, профильный уровень.
 Задачи по планиметрии
Задачи по планиметрии - ЕГЭ по математике, базовый уровень. Планиметрия. Прямоугольный треугольник (вариант 3)
- Вместе — все по плечу: фильмы и мультики о братьях и сестрах
- 10 познавательных YouTube-каналов для детей
- Как вести себя со сложными подростками?
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Текст с ошибкой:
Расскажите, что не так
векторное вычитание — примеры | Как вычитать векторы?
Мы можем выполнять вычитание векторов точно так же, как мы делаем вычитание скаляров. Мы вычитаем соответствующие компоненты векторов при вычитании векторов. Графическую интерпретацию вычитания векторов можно понять, используя закон параллелограмма и закон сложения треугольника.
Графическую интерпретацию вычитания векторов можно понять, используя закон параллелограмма и закон сложения треугольника.
Давайте узнаем больше о вычитании векторов вместе с геометрической интерпретацией и примерами.
| 1. | Что такое векторное вычитание? |
| 2. | Вычитание векторов по закону параллелограмма |
| 3. | Вычитание векторов по закону треугольника |
| 4. | Как вычитать векторы? |
| 5. | Свойства векторного вычитания |
| 6. | Часто задаваемые вопросы о векторном вычитании |
Что такое векторное вычитание?
Вычитание вектора из двух векторов a и b представляется как a — b , и это не что иное, как сложение отрицательного значения вектора b с вектором a .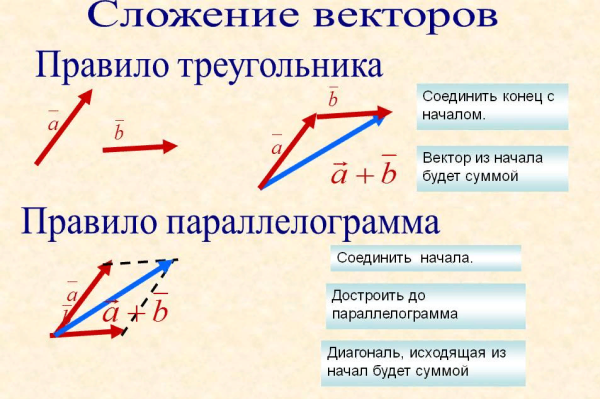 т. е. a — b = a + (- b ). Таким образом, вычитание векторов включает в себя сложение векторов и отрицание вектора. Результат векторного вычитания снова является вектором. Ниже приведены правила вычитания векторов:
т. е. a — b = a + (- b ). Таким образом, вычитание векторов включает в себя сложение векторов и отрицание вектора. Результат векторного вычитания снова является вектором. Ниже приведены правила вычитания векторов:
- Следует выполнять только между двумя векторами (не между одним вектором и одним скаляром).
- Оба вектора в вычитании должны представлять одну и ту же физическую величину.
Давайте разберемся, как вычитать векторы графически в следующих разделах.
Вычитание векторов по закону параллелограмма
Предположим, что a и b — два вектора. Как можно графически интерпретировать вычитание этих векторов? То есть какой смысл мы придаем а — б ? Для начала отметим, что a — b будет вектором, который при добавлении к b должен вернуть a . то есть,
то есть,
( A — B ) + B = A
Но как мы определили вектор A — B , дали Vectors A и B , дали Vectors A и B ? На следующем рисунке показаны векторы a и b (мы нарисовали их совпадающими).
Используя закон сложения векторов параллелограмма, мы можем определить вектор следующим образом. Мы интерпретируем a — b как a + (- b ), то есть векторную сумму a и — b . Теперь мы обращаем вектор b , а затем складываем a и — b , используя закон параллелограмма:0051 a и − b .
Вычитание векторов по закону треугольника
Теперь мы интерпретируем вычитание векторов, используя треугольный закон сложения векторов. Обозначим вектор, проведенный из конечной точки b в конечную точку a , через c .
Обозначим вектор, проведенный из конечной точки b в конечную точку a , через c .
Обратите внимание, что b + c = a . Таким образом, c = a — b . Другими словами, вектор a — b — это вектор, проведенный от вершины b к вершине a (если a и b совпадают с начальными).
Обратите внимание, что оба описанных выше способа (с использованием закона параллелограмма и закона треугольника) дают нам один и тот же вектор для a — b . Это становится яснее из рисунка ниже:
Вектор PT получается сложением a и − b по закону параллелограмма. Вектор RQ получается путем рисования вектора от вершины b до вершины — a . Ясно, что оба вектора одинаковы (поскольку их величины и направления одинаковы).
Ясно, что оба вектора одинаковы (поскольку их величины и направления одинаковы).
Как вычитать векторы?
Вот несколько способов вычитания векторов:
- Чтобы вычесть два вектора a и b графически (т. кончик b до наконечника a .
- Мы можем добавить — b (отрицательное значение вектора b , полученное путем умножения b на -1) к a , чтобы выполнить вычитание вектора a — b . то есть a — b = a + ( -b ).
- Если векторы находятся в компонентной форме, мы можем просто вычесть их соответствующие компоненты в порядке вычитания векторов.
Вот пример.
Пример: Если a = <4, -2, 3> и b = <1, -2, 5>, то найдите a — b .
Решение:
а — б = <4, -2, 3> — <1, -2, 5>
= <4 - 1, -2 - (-2), 3 - 5>
= <3, 0, -2>
Следовательно, a — b = <3, 0, -2>.
Свойства векторного вычитания
Вот некоторые важные свойства векторного вычитания.
- Любой вектор, вычтенный из самого себя, дает нулевой вектор. то есть a — a = 0 для любого вектора a .
- Вычитание векторов НЕ является коммутативным. т. е. a — b не обязательно равно b — a.
- Вычитание векторов НЕ является ассоциативным. т. е. ( a — b ) — c не обязательно должен быть равен a — ( b — c ).
- ( a — b ) · ( a + b ) = | и | 2 — | б | 2 .

- ( а — б ) · ( а — б ) = | а — б | 2 = | и | 2 + | б | 2 — 2 а · б .
☛ Связанные темы:
- Типы векторов
- Калькулятор добавления векторов
- Калькулятор векторного вычитания
- Угол между векторами
Часто задаваемые вопросы о векторном вычитании
Что означает векторное вычитание?
Векторное вычитание двух векторов a и b — это просто сложение векторов a и -b . т. е. a — b = a + (- b ). Чтобы найти — b , мы должны умножить каждый компонент вектора b на -1.
Как вычитать векторы?
- Чтобы вычесть вектор b из другого вектора a , просто сделайте их совпадающими по началу и затем нарисуйте вектор от вершины b до вершины a .
- Чтобы вычесть вектор b из другого вектора a , когда их компоненты заданы, просто вычтите каждый компонент b из соответствующего компонента a .
Как найти разность векторов графически?
Чтобы найти разность векторов двух векторов a и b графически:
- Нарисуйте оба вектора, чтобы начать с одной и той же начальной точки.
- Нарисуйте вектор разности a — b от наконечника b до наконечника a .
Как вычитать векторы в компонентной форме?
Если два вектора a =  то есть a — b =
то есть a — b =
Что такое параллелограммный закон вычитания векторов?
Закон вычитания параллелограмма гласит: «Если два вектора a и -b начинаются из точки P и являются двумя смежными сторонами параллелограмма, то их сумма, равная a + (- b ) (который также может быть записан как a — b ) — это вектор, который представляет собой диагональ параллелограмма, начинающегося с P».
Что такое треугольный закон вычитания векторов?
Треугольный закон вычитания векторов гласит: «Чтобы найти разность a — b двух векторов a и b (которые совпадают по началу), просто начертите вектор от хвоста b к хвост и «.
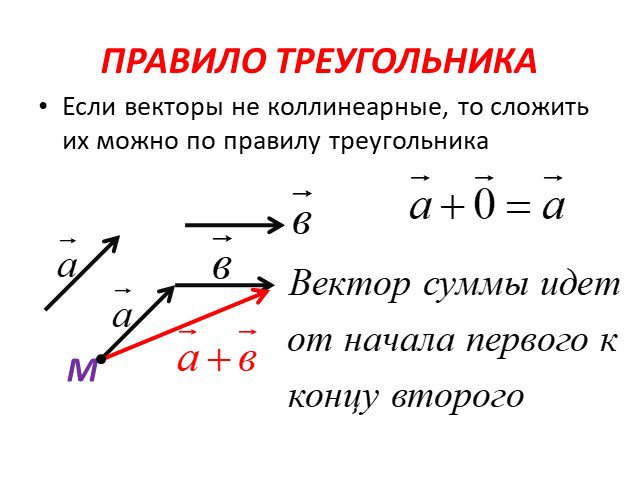
Сложение и вычитание векторов
Горячая математика Чтобы добавить или вычесть два вектора, добавьте или вычтите соответствующие компоненты.
Позволять ты → «=» 〈 ты 1 , ты 2 〉 и в → «=» 〈 в 1 , в 2 〉 быть два вектора.
Тогда сумма ты → и в → это вектор
ты → + в → «=» 〈 ты 1 + в 1 , ты 2 + в 2 〉
Разница ты → и в → является
ты → − в → «=» ты → + ( − в → ) «=» 〈 ты 1 − в 1 , ты 2 − в 2 〉
Сумма двух и более векторов называется равнодействующей. Результат двух векторов можно найти с помощью метод параллелограмма или метод треугольника .
Результат двух векторов можно найти с помощью метод параллелограмма или метод треугольника .
Метод параллелограмма:
Нарисуйте векторы так, чтобы их начальные точки совпадали. Затем нарисуйте линии, чтобы сформировать полный параллелограмм. Диагональ из начальной точки в противоположную вершину параллелограмма является равнодействующей.
Добавление вектора:
- Поместите оба вектора ты → и в → в той же начальной точке.
- Завершите параллелограмм. Результирующий вектор ты → + в → является диагональю параллелограмма.
Вычитание векторов:
- Завершите параллелограмм.

- Проведите диагонали параллелограмма из начальной точки.
Метод треугольника:
Нарисуйте векторы один за другим, помещая начальную точку каждого последующего вектора в конечную точку предыдущего вектора. Затем проведите равнодействующую от начальной точки первого вектора до конечной точки последнего вектора. Этот метод также называют метод «голова к хвосту» .
Добавление вектора:
Вычитание векторов:
Пример:
Найди)
ты
→
+
в
→
и (б)
ты
→
−
в
→
если
ты
→
«=»
〈
3
,
4
〉
и
в
→
«=»
〈
5
,
−
1
〉
.
Подставить заданные значения ты 1 , ты 2 , в 1 и в 2 в определение сложения векторов.
ты → + в → «=» 〈 ты 1 + в 1 , ты 2 + в 2 〉 «=» 〈 3 + 5 , 4 + ( − 1 ) 〉 «=» 〈 8 , 3 〉
Перепишите разницу
ты
→
−
в
→
как сумма
ты
→
+
(
−
в
→
)
. Нам нужно определить компоненты
−
в
→
.
Нам нужно определить компоненты
−
в
→
.
Напомним, что − в → является скалярным множителем − 1 раз в . Из определения скалярного умножения имеем:
− в → «=» − 1 〈 в 1 , в 2 〉 «=» − 1 〈 5 , − 1 〉 «=» 〈 − 5 , 1 〉
Теперь добавьте компоненты
ты
→
и
−
в
→
.


 В данном случае значение скалярного произведения является наименьшим из возможных.
В данном случае значение скалярного произведения является наименьшим из возможных.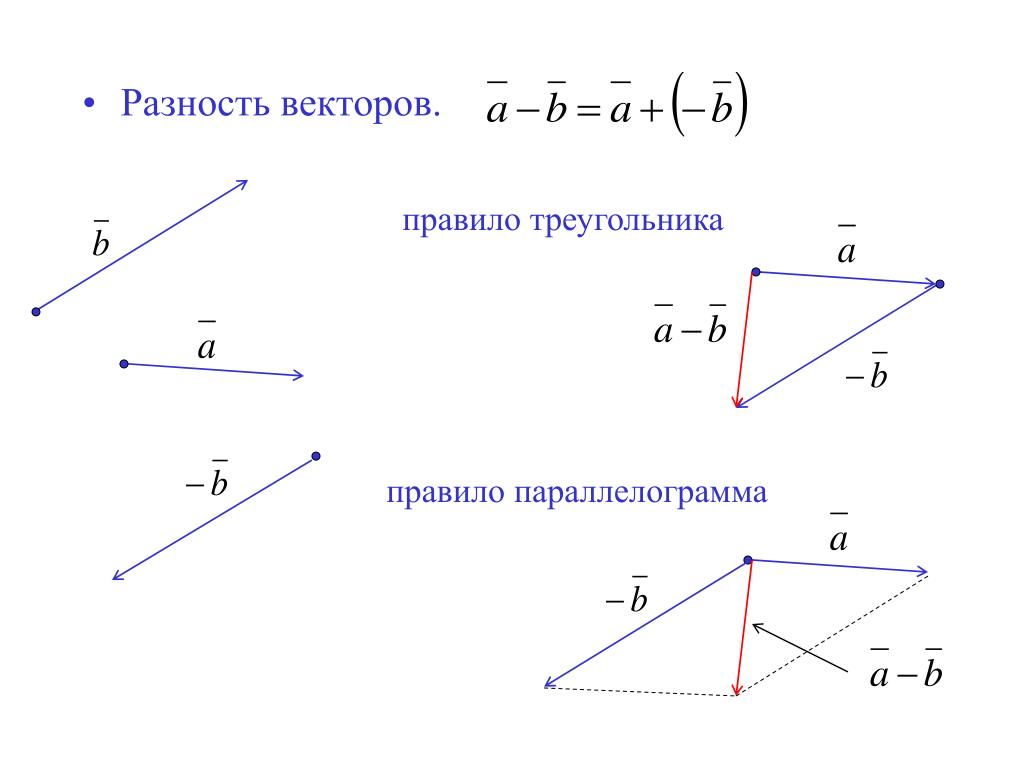 Задачи по планиметрии
Задачи по планиметрии