Асимптоты — определение; вертикальная, горизонтальная, наклонная асимптота; алгоритм исследования поведения функции
- Понятие асимптоты
- Вертикальная асимптота
- Горизонтальная асимптота
- Наклонная асимптота
- Алгоритм исследования асимптотического поведения функции
- Примеры
п.1. Понятие асимптоты
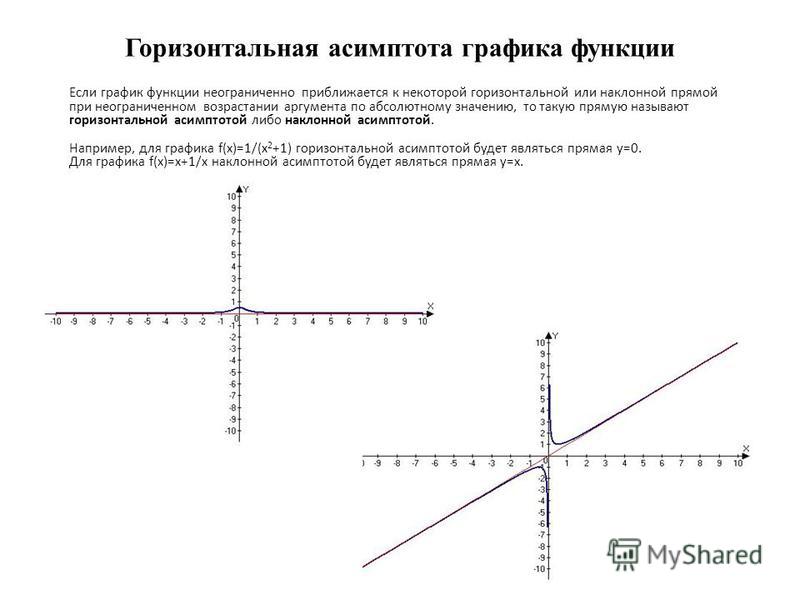
Асимптота прямая, расстояние от которой до точки кривой стремится к нулю при удалении точки вдоль ветви кривой на бесконечность.
Различают вертикальные, горизонтальные и наклонные асимптоты.
Например:
Вертикальная асимптота x=3 | Горизонтальная асимптота y=1 |
Наклонная асимптота y=x | |
п.2. Вертикальная асимптота
Вертикальная асимптота кривой \(y=f(x)\) имеет вид: \(x=a\)
где \(a\) — точка разрыва 2-го рода функции \(f(x)\), для которой хотя бы один односторонний предел существует и равен бесконечности.
Таким образом, практически каждой точке разрыва 2-го рода (см. §40 данного справочника) соответствует вертикальная асимптота.
Вертикальных асимптот может быть сколько угодно, в том числе, бесконечное множество (например, как у тангенса – см. §6 данного справочника).
Например:
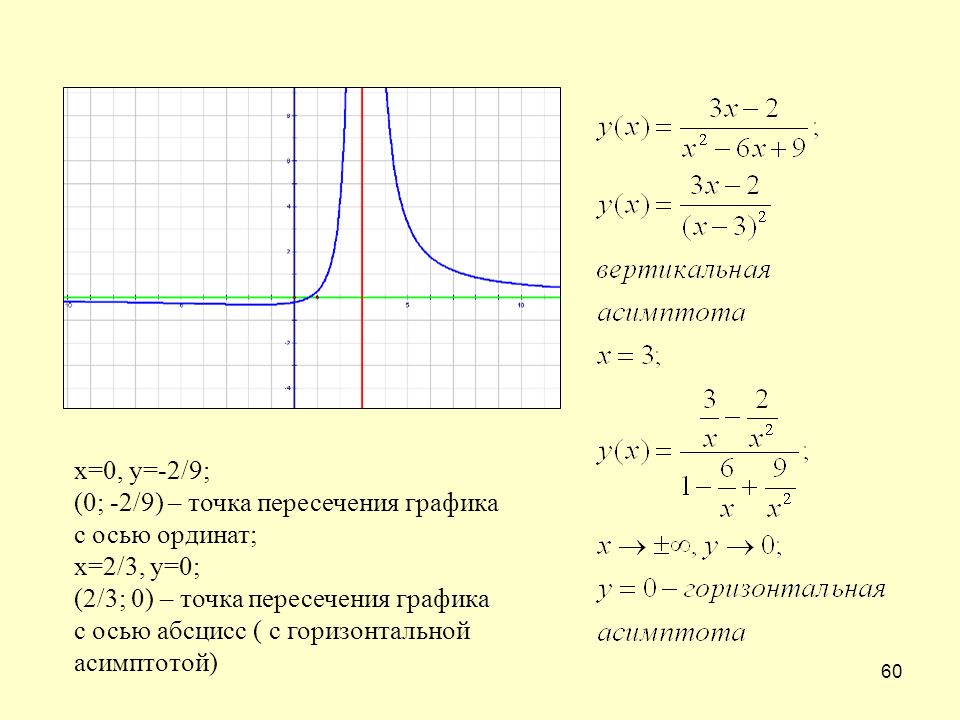
Исследуем непрерывность функции \(y=\frac{1}{(x-1)(x+3)}\)
ОДЗ: \(x\ne \left\{-3;1\right\}\)
\(\left\{x_0=-3,\ x_1=1\right\}\notin D\) — точки не входят в ОДЗ, подозрительные на разрыв.
Исследуем \(x_0=-3\). Найдем односторонние пределы: \begin{gather*} \lim_{x\rightarrow -3 -0}\frac{1}{(x-1)(x+3)}=\frac{1}{(-3-0-1)(-3-0+3)}=\frac{1}{-4\cdot(-0)}=+\infty\\ \lim_{x\rightarrow -3 +0}\frac{1}{(x-1)(x+3)}=\frac{1}{(-3+0-1)(-3+0+3)}=\frac{1}{-4\cdot(+0)}=-\infty \end{gather*} Односторонние пределы не равны и бесконечны.
Точка \(x_0=-3\) — точка разрыва 2-го рода.
Исследуем \(x_1=1\). Найдем односторонние пределы: \begin{gather*} \lim_{x\rightarrow 1 -0}\frac{1}{(x-1)(x+3)}=\frac{1}{(1-0-1)(1-0+3)}=\frac{1}{-0\cdot 4}=-\infty\\ \lim_{x\rightarrow 1 +0}\frac{1}{(x-1)(x+3)}=\frac{1}{(1+0-1)(1+0+3)}=\frac{1}{+0\cdot 4}=+\infty \end{gather*} Односторонние пределы не равны и бесконечны.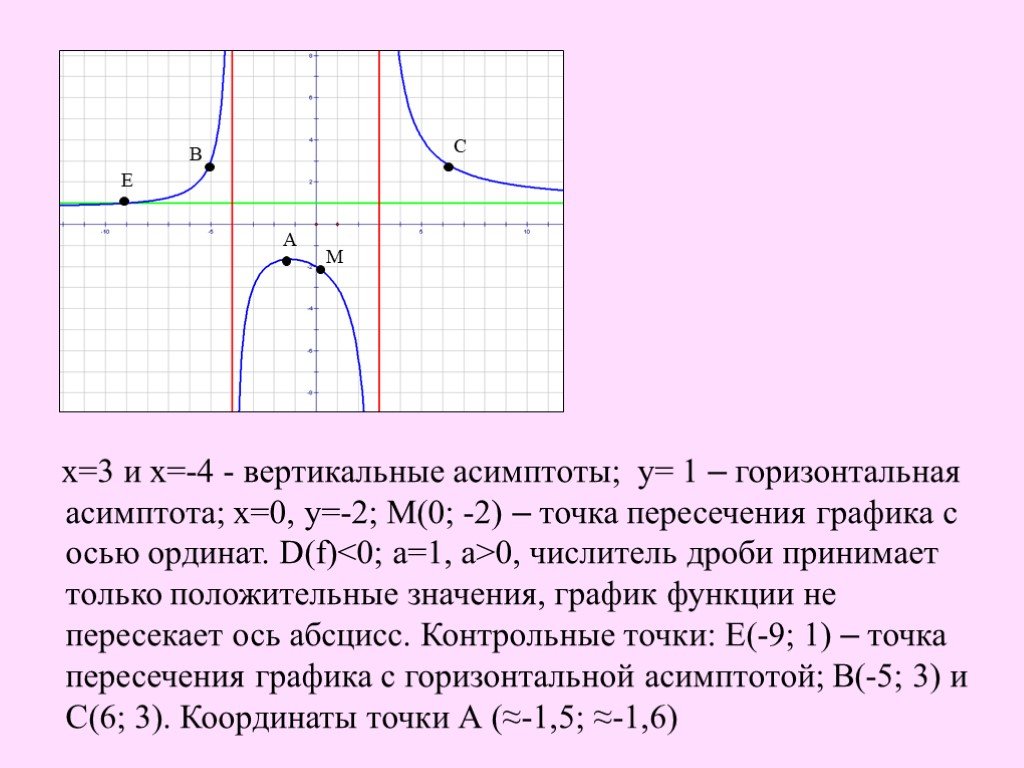
Точка \(x_1=1\) — точка разрыва 2-го рода.
Вывод: у функции \(y=\frac{1}{(x-1)(x+3)}\) две точки разрыва 2-го рода \(\left\{x_0=-3, x_1=1\right\}\), соответственно – две вертикальные асимптоты с уравнениями \(x=-3\) и \(x=1\).
п.3. Горизонтальная асимптота
Горизонтальная асимптота кривой \(y=f(x)\) имеет вид: \(y=b\)
где \(b\) — конечный предел функции \(f(x)\) на бесконечности: \(b=\lim{x\rightarrow \pm\infty}f(x),\ b\ne\infty\)
Число горизонтальных асимптот не может быть больше двух.
Например:
Исследуем наличие горизонтальных асимптот у функции \(y=\frac{1}{(x-1)(x+3)}\)
Ищем предел функции на минус бесконечности: \begin{gather*} \lim_{x\rightarrow -\infty}\frac{1}{(x-1)(x+3)}=\frac{1}{(-\infty)(-\infty)}=+0 \end{gather*} На минус бесконечности функция имеет конечный предел \(b=0\) и стремится к нему сверху (о чем свидетельствует символическая запись +0).
Ищем предел функции на плюс бесконечности: \begin{gather*} \lim_{x\rightarrow +\infty}\frac{1}{(x-1)(x+3)}=\frac{1}{(+\infty)(+\infty)}=+0 \end{gather*} На плюс бесконечности функция имеет тот же конечный предел \(b=0\) и также стремится к нему сверху. 2+3}{x-1}\):
2+3}{x-1}\):
п.5. Алгоритм исследования асимптотического поведения функции
На входе: функция \(y=f(x)\)
Шаг 1. Поиск вертикальных асимптот
Исследовать функцию на непрерывность. Если обнаружены точки разрыва 2-го рода, у которых хотя бы один односторонний предел существует и бесконечен, сопоставить каждой такой точке вертикальную асимптоту. Если таких точек не обнаружено, вертикальных асимптот нет.
Найти пределы функции на плюс и минус бесконечности. Каждому конечному пределу сопоставить горизонтальную асимптоту. Если оба предела конечны и равны, у функции одна горизонтальная асимптота. Если оба предела бесконечны, горизонтальных асимптот нет.
Шаг 3. Поиск наклонных асимптот
Найти пределы отношения функции к аргументу на плюс и минус бесконечности.
Каждому конечному пределу k сопоставить наклонную асимптоту, найти b. Если только один предел конечен, у функции одна наклонная асимптота.
 3
3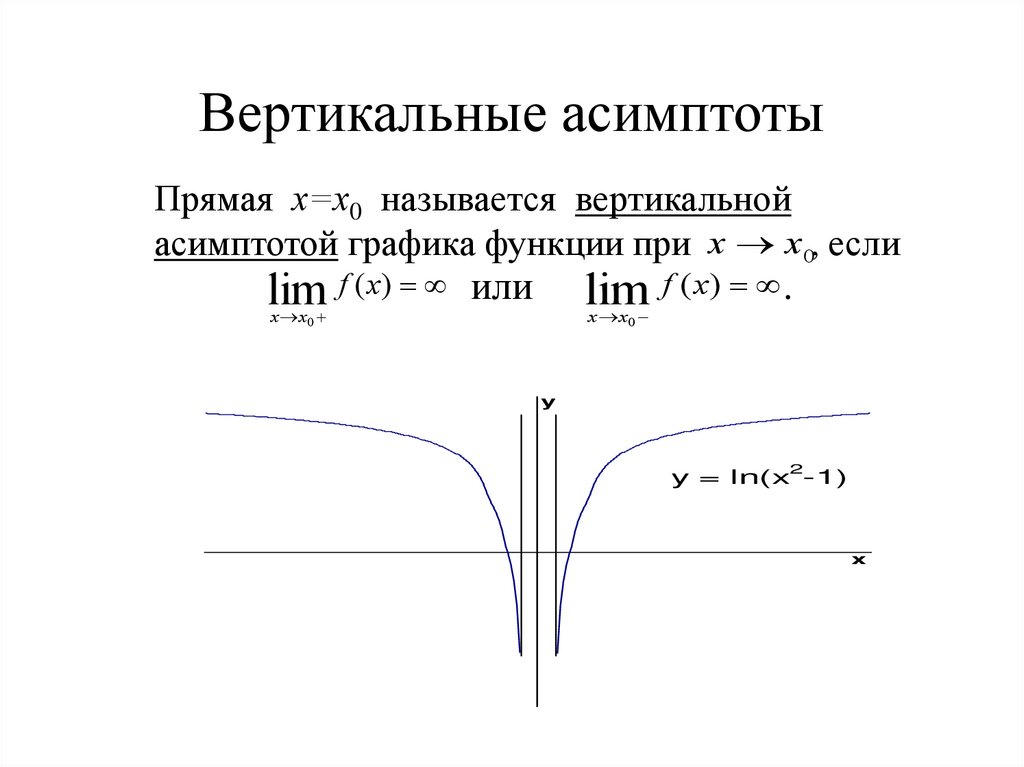 2+n-72)=1/(n+9)
2+n-72)=1/(n+9)Горизонтальная асимптота — Правила | Нахождение горизонтальной асимптоты
Горизонтальная асимптота функции — это горизонтальная линия, с которой график функции кажется совпадающим, но на самом деле он не совпадает. Горизонтальная асимптота используется для определения конечного поведения функции.
Давайте узнаем больше о горизонтальной асимптоте, а также о правилах ее нахождения для различных типов функций.
| 1. | Что такое горизонтальная асимптота? |
| 2. | Может ли горизонтальная асимптота пересечь кривую? |
| 3. | Как найти горизонтальную асимптоту? |
| 4. | Нахождение горизонтальной асимптоты рациональной функции |
| 5. | Нахождение горизонтальной асимптоты показательной функции |
6. | Правила горизонтальной асимптоты |
| 7. | Часто задаваемые вопросы о горизонтальной асимптоте |
Что такое горизонтальная асимптота?
Горизонтальная асимптота функции y = f(x) представляет собой прямую y = k, если либо lim ₓ→∞ f(x) = k, либо lim ₓ→ -∞ f(x) = k. т. е. это линия, к которой график (кривая) функции, кажется, приближается при x→∞ или x→ -∞. Обычно он обозначается как HA . Здесь k — действительное число, к которому приближается функция, когда значение x чрезвычайно велико или чрезвычайно мало. Функция может иметь или не иметь горизонтальную асимптоту. Но максимальное количество асимптот, которое может иметь функция, равно 2. То есть функция может иметь 0, 1 или 2 асимптоты. Вот несколько примеров горизонтальных асимптот, которые дадут нам представление о том, как они выглядят. Горизонтальная линия обычно изображается пунктирной горизонтальной линией. Когда сама ось X представляет собой ГК, мы обычно не используем для нее пунктирную линию.
Когда сама ось X представляет собой ГК, мы обычно не используем для нее пунктирную линию.
Обратите внимание, что мы находим HA при построении кривой только для того, чтобы представить значение, к которому приближается функция. Но его не обязательно рисовать при построении графика кривой, потому что он НЕ является частью кривой. Даже графические калькуляторы не показывают горизонтальную линию для горизонтальной асимптоты. Другими словами, горизонтальная линия — это воображаемая линия.
Может ли горизонтальная асимптота пересечь кривую?
Да, горизонтальная асимптота y = k функции y = f(x) может пересекать кривую (график). т. е. может существовать значение x такое, что f(x) = k. Обратите внимание, что это НЕ относится к любой вертикальной асимптоте, поскольку вертикальная асимптота никогда не пересекает кривую. Вот пример, когда горизонтальная асимптота (HA) пересекает кривую.
Здесь кривая имеет горизонтальную асимптоту по оси x (уравнение которой y = 0) и пересекает кривую в точке (0, 0).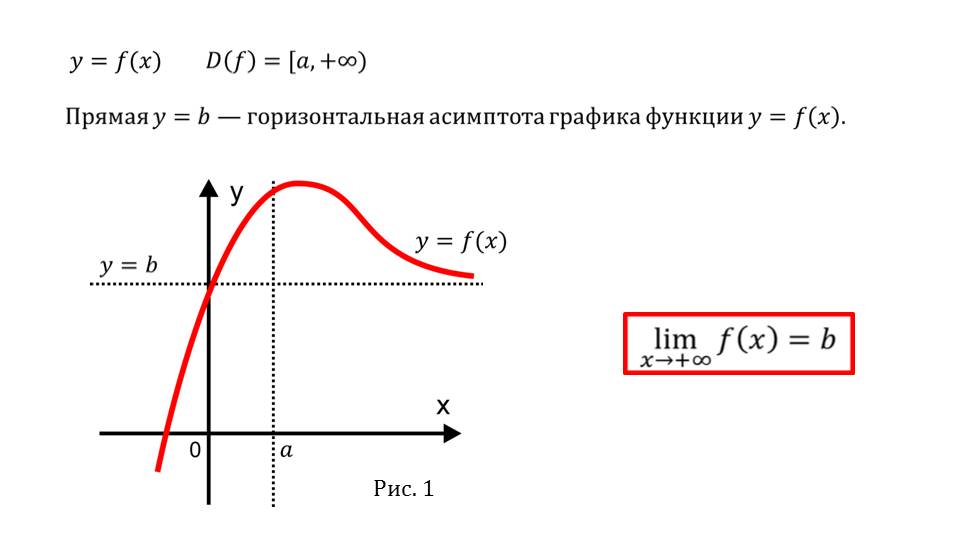 Попробуйте решить уравнение x/(x 2 +1) = 0, и мы получим x = 0.
Попробуйте решить уравнение x/(x 2 +1) = 0, и мы получим x = 0.
Как найти горизонтальную асимптоту?
Вот шаги для нахождения горизонтальной асимптоты любого типа функции y = f(x).
- Шаг 1: Найдите lim ₓ→∞ f(x). т. е. применить предел для функции при x→∞.
- Шаг 2: Найти lim ₓ→ -∞ f(x). т. е. применить предел для функции при x→ -∞.
- Шаг 3: Если один (или оба) из приведенных выше пределов являются действительными числами, то представить горизонтальную асимптоту как y = k, где k представляет собой значение предела.
Если один (или оба) из приведенных выше случаев дают ∞ или -∞ в качестве ответа, просто игнорируйте их, и они НЕ являются горизонтальными асимптотами. Иногда каждый из пределов может давать одно и то же значение, и в этом случае (как в следующем примере) у нас есть только один HA. Чтобы узнать, как оценить ограничения, нажмите здесь.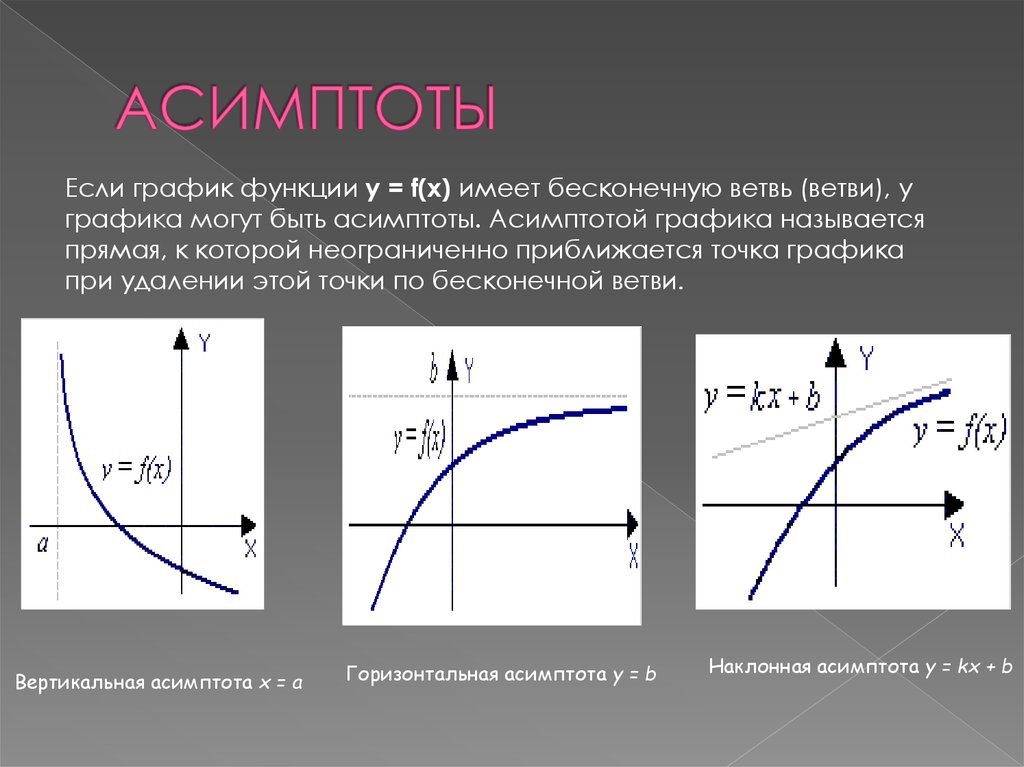
Нахождение горизонтальной асимптоты по графику
На всех вышеприведенных графиках мы видим нечто общее. Горизонтальная асимптота — это параллельная линия, к которой часть кривой параллельна и очень близка. Но обратите внимание, что HA никогда не должен касаться какой-либо части кривой (но он может пересекать кривую).
Пример: Найдите горизонтальную асимптоту функции f(x) = 2x / (x — 3).
Решение:
lim ₓ→∞ f(x) = lim ₓ→∞ 2x / (x — 3)
= lim ₓ→∞ 2x / [x (1 — 3/x)]
= lim ₓ→∞ 2 / (1 — 3/x)
= 2 / (1 — 0)
= 2
Итак, y = 2 — это HA функции. Теперь найдем другой предел.
lim ₓ→-∞ f(x) = lim ₓ→-∞ 2x / (x — 3)
= lim ₓ→-∞ 2x / [x (1 — 3/x)]
= lim ₓ→-∞ 2 / (1 — 3/x)
= 2 / (1 + 0)
= 2
Опять же, у нас есть 2, что дает тот же HA быть y = 2.
Таким образом, функция имеет только одну горизонтальную асимптоту, которая равна y = 2. Вот графическая проверка.
Фактически, мы используем горизонтальную асимптоту, чтобы найти диапазон рациональной функции. Мы просто используем тот факт, что HA НЕ является частью графика функции. Из приведенного выше графика диапазон f (x) равен {y ∈ R | у ≠ 2}.
Но нужно ли всегда применять ограничения, чтобы найти HA? Нет ли какого-либо простого метода? Вот несколько приемов/ярлыков для нахождения горизонтальных асимптот некоторых конкретных типов функций.
Нахождение горизонтальной асимптоты рациональной функции
Рациональная функция может иметь максимум 1 горизонтальную асимптоту. Хотя мы можем применить пределы для нахождения HA, другой более простой способ найти горизонтальные асимптоты рациональных функций состоит в том, чтобы применить следующие приемы:
- Если степень числителя > степени знаменателя, то функция не имеет ХА.
- Если степень числителя < степени знаменателя, то функция имеет один HA, который равен y = 0.
- Если степень числителя = степени знаменателя, то функция имеет один HA, который равен y = отношению старших коэффициентов числителя и знаменателя.

В приведенном выше примере из предыдущего раздела (где f(x) = 2x / (x — 3) ) степень числителя = степени знаменателя ( = 1). Таким образом, HA для f(x) равен y = 2/1 = 2. Обратите внимание, что мы получили тот же ответ, даже когда применили ограничения. Вот еще несколько примеров.
- у = (х 2 +3) / (2x) не имеет HA.
- HA для y = (2x) / (x 2 + 3) равно y = 0,
- га y = (2x 2 ) / (x 2 + 3) равно y = 2,
Нахождение горизонтальной асимптоты показательной функции
Экспоненциальная функция всегда имеет ровно одну горизонтальную асимптоту. Родительская экспоненциальная функция имеет вид f(x) = b x , но когда происходят преобразования, она может иметь вид f(x) = ab кх + с. Здесь «с» представляет вертикальное преобразование исходной экспоненциальной функции, и это само по себе является горизонтальной асимптотой. В заключение:
- HA f(x) = b x равно y = 0,
- HA f(x) = ab kx + c равно y = c.

Используя подсказку выше, горизонтальная асимптота экспоненциальной функции f(x) = 4 x + 2 равна y = 2 (технически y = lim ₓ→ -∞ 4 x + 2 = 0 + 2 = 2).
Вот несколько примеров.
- HA f(x) = 2 x — 3 равно y = -3.
- HA f(x) = 3 -x + 5 равно y = 5.
- HA f(x) = 0,5 2x — (2/3) равно y = -2/3.
Правила горизонтальной асимптоты
Давайте обобщим все правила горизонтальной асимптоты, которые мы видели до сих пор.
- Чтобы найти горизонтальную асимптоту рациональной функции, найдите степени числителя (n) и степени знаменателя (d).
Если n < d, то HA равно y = 0,
. Если n > d, то HA нет.
Если n = d, то HA равно y = отношению старших коэффициентов. - Горизонтальная асимптота показательной функции вида f(x) = ab kx + c равна y = c.
- Полиномиальная функция (например, f(x) = x+3, f(x) = x 2 -2x+3 и т.
 {2}-1}}\).
{2}-1}}\). - Ни одна полиномиальная функция не имеет горизонтальной асимптоты. т. е. линейные функции, квадратичные функции, кубические функции и т. д. не имеют HA.
- Ни одна базовая тригонометрическая функция не имеет горизонтальной асимптоты.
- Ни одна базовая логарифмическая функция не имеет горизонтальной асимптоты.
☛ Связанные темы:
- Калькулятор горизонтальной асимптоты
- Графический калькулятор
- Калькулятор графических функций
Часто задаваемые вопросы о горизонтальной асимптоте
Что такое горизонтальная асимптота функции?
Горизонтальная асимптота (HA) функции y = f(x) является пределом функции f(x) при x→∞ или x→ -∞. Функция может иметь максимум 2 HA.
Что такое правила горизонтальной асимптоты?
Общее правило нахождения горизонтальной асимптоты (HA) y = f(x) обычно задается как y = lim ₓ→∞ f(x) и/или y = lim ₓ→ -∞. Но вот несколько приемов, которые могут оказаться полезными при нахождении HA некоторых конкретных функций:
Но вот несколько приемов, которые могут оказаться полезными при нахождении HA некоторых конкретных функций:
- ГК рациональной функции
равен y = 0, когда степень его числителя меньше степени знаменателя
не существует, когда степень числителя больше степени знаменателя
равен y = k, когда обе степени равны, а k = отношение старших коэффициентов. - HA экспоненциальной функции f(x) = a x + k равно y = k.
В чем разница между вертикальной и горизонтальной асимптотами?
Асимптоты – это линии, которым функция кажется совпадающей, но на самом деле не совпадает. Горизонтальная асимптота представляет собой горизонтальную линию и имеет форму y = k. Вертикальная асимптота представляет собой вертикальную линию и имеет форму x = k.
Как рассчитать горизонтальную асимптоту?
Для нахождения горизонтальных асимптот функции y = f(x) воспользуемся формулами y = lim ₓ→∞ f(x) и y = lim ₓ→ -∞. Если какое-либо из этих ограничений приводит к недействительному числу, просто игнорируйте это ограничение.
Как найти горизонтальную асимптоту рациональной функции?
Степень числителя (n) и степень знаменателя (d) очень полезны при нахождении HA рациональной функции y = f(x).
- если n = d, то HA есть, y = отношение старших коэффициентов.
- , если n > d, то f(x) не имеет HA.
- , если n < d, то HA равно y = 0.
Как найти горизонтальную асимптоту показательной функции?
Основная экспоненциальная функция имеет вид y = a х . Если происходит какое-то вертикальное преобразование, то функция имеет вид y = a x + k. Его HA просто y = k.
Как найти диапазон функции с помощью горизонтальной асимптоты?
Горизонтальная асимптота используется для определения диапазона функции только в случае рациональной функции. Например, HA f(x) = (2x) / (x 2 +1) равен y = 0, а его диапазон равен {y ∈ R | у ≠ 0}.
3.5 — Рациональные функции и асимптоты
3.5 — Рациональные функции и асимптоты Рациональная функция – это функция, которая
можно записать как отношение двух
полиномы, где знаменатель
не ноль.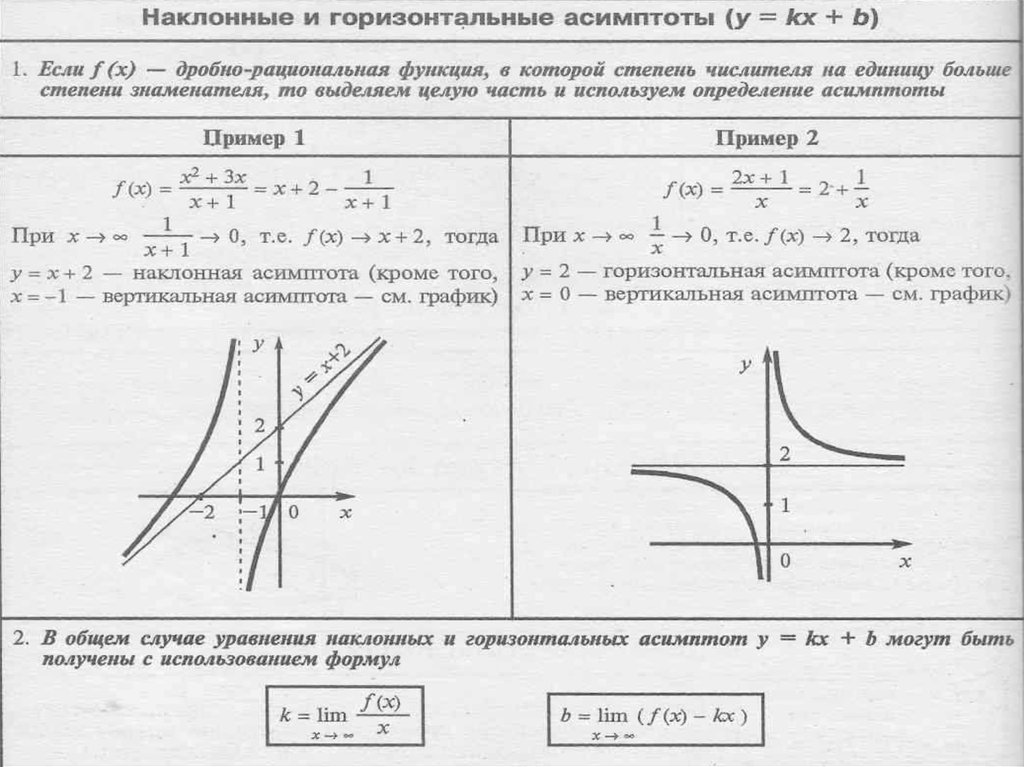
f(x) = p(x) / q(x)
Домен
Областью определения рациональной функции являются все действительные значения, кроме тех, где знаменатель q(x) = 0.
Корни
Корни, нули, решения, x-отрезки (называйте их как хотите) рациональной функции будут места, где p(x) = 0. То есть полностью игнорируем знаменатель. Что бы ни делал ноль числителя будет корнями рациональной функции, точно так же, как они были корнями полиномиальная функция ранее.
Если вы можете записать его в факторизованной форме, то вы можете сказать, будет ли он пересекать или касаться оси x в точке каждый x-отрезок от того, является ли кратность фактора нечетной или четной.
Вертикальные асимптоты
Асимптота — это линия, к которой кривая приближается, но не пересекает. Уравнения вертикали асимптоты можно найти, найдя корни q ( x ). Полностью игнорировать числитель, когда при поиске вертикальных асимптот имеет значение только знаменатель.
Если вы можете записать его в факторизованной форме, то вы можете сказать, будет ли график асимптотическим в
в одном и том же направлении или в разных направлениях в зависимости от того, является ли кратность четной или нечетной.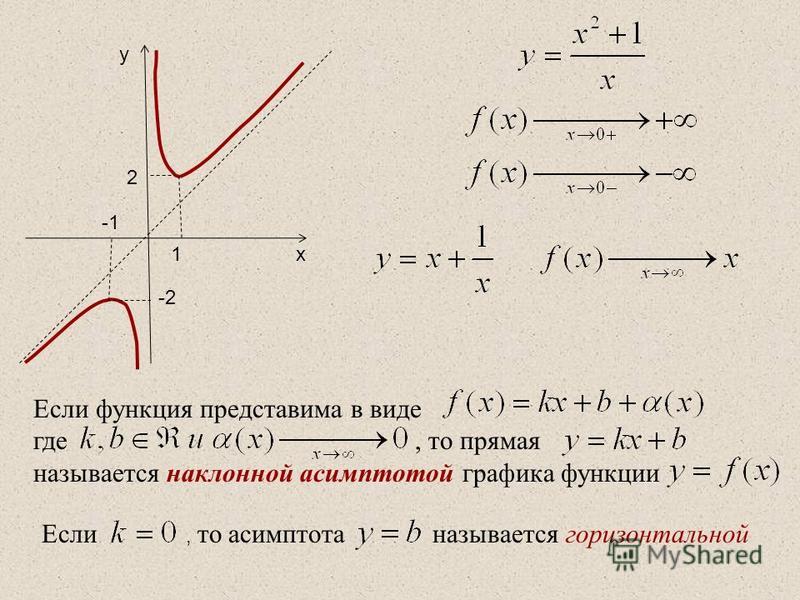
Асимптотика в одном направлении означает, что кривая будет идти вверх или вниз как слева, так и слева. правые части вертикальной асимптоты. Асимптотика в разные стороны означает, что одна сторона кривой пойдет вниз, а другая сторона кривой пойдет вверх по вертикальной асимптоте.
Горизонтальные асимптоты
Горизонтальная линия является асимптотой только крайнего левого и крайнего правого график. «Далеко» слева или «дальний» правый определяется как все, что находится за пределами вертикальных асимптот или пересечений по оси x. Горизонтальные асимптоты не являются асимптотами в середине. Это нормально, чтобы пересечь горизонтальная асимптота в середина.
Положение горизонтальной асимптоты определяется по градусам числитель (n) и знаменатель (m).
- Если n
- Если n=m, то y=a n / b m — горизонтальная асимптота. То есть соотношение ведущих коэффициенты.

- Если n>m, горизонтальной асимптоты нет. Однако, если n=m+1, имеется косая или наклонная асимптота.
- Если n=m, то y=a n / b m — горизонтальная асимптота. То есть соотношение ведущих коэффициенты.
Отверстия
Иногда в числителе и знаменателе появляется множитель. Предположим, коэффициент (xk) находится в числителе и знаменателе. Поскольку множитель стоит в знаменателе, x=k не будет находиться в области определения функции. Это означает, что может произойти одно из двух. Там будет либо вертикальная асимптота при x=k, либо будет дыра при x=k.
Давайте посмотрим, что произойдет в каждом из этих случаев.
- В знаменателе больше (x-k) множителей. После разделения всех повторяющихся факторов (xk) по-прежнему находится в знаменателе. Факторы в знаменателе приводят к вертикальным асимптотам. Следовательно, будет вертикальная асимптота при x=k.
- В числителе больше (x-k) множителей. После разделения всех повторяющихся факторов
(xk) все еще находится в числителе. Факторы в числителе приводят к x-перехватам. Но потому что
вы не можете использовать x=k, на графике по оси x будет дыра.

- В числителе и знаменателе одинаковое количество (x-k) множителей. После деления если исключить все множители (поскольку их количество равно), то (xk) вообще не останется. Потому что там нет (x-k) в знаменателе, нет вертикальной асимптоты при x=k. Потому что нет (х-к) в числителе нет точки пересечения x в точке x=k. Где-то на графике просто дыра кроме как на оси x. Чтобы найти точное местоположение, подставьте x=k в сокращенную функцию. (вы не можете подключить его к оригиналу, там он не определен) и посмотрите, какое значение y вы получите.
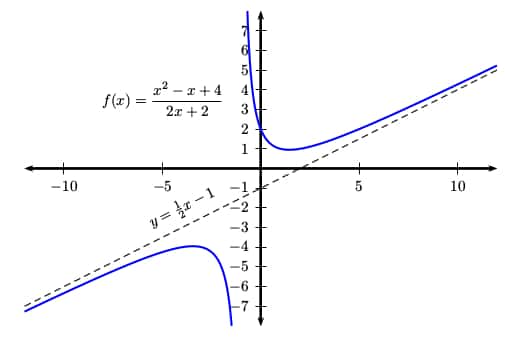
Наклонные асимптоты
Когда степень числителя ровно на единицу больше степени знаменателя, график рациональной функции будет иметь наклонную асимптоту. Другое название наклонной асимптота – наклонная асимптота.
Чтобы найти уравнение наклонной асимптоты, выполните длинное деление (синтетическое, если оно будет работать) на
деление знаменателя на числитель. Поскольку x становится очень большим (это крайний левый или крайний правый
о чем я говорил), оставшаяся часть становится очень маленькой, почти нулевой.


 {2}-1}}\).
{2}-1}}\).