«Радианная мера угла»
| 12+ Свидетельство СМИ ЭЛ № ФС 77 — 70917 Лицензия на образовательную деятельность №0001058 | Пользовательское соглашение Контактная и правовая информация |
Педагогическое сообщество | Бесплатные всероссийские конкурсы | Бесплатные сертификаты | Нужна помощь? Инструкции для новых участников | Бесплатная онлайн-школа для 1-4 классов |
Всё для аттестацииПубликация в сборникеВебинарыЛэпбукиПрофтестыЗаказ рецензийНовости
Библиотека▪Публикации▪Статьи
Материал опубликовала
#ФГОС #Методические разработки #Урок #Учитель-предметник #Среднее профессиональное образование
«Математика выявляет порядок, симметрию и определённость, а это – важнейшие виды прекрасного».
(Аристотель)
«Радианная мера угла»
УГОЛ РАДИАН ГРАДУСНАЯ МЕРА РАДИАННАЯ МЕРА
Найдите ошибку: 1 2 3 4 5 1 — полный угол 2 — тупой угол 3 — развёрнутый угол 4 — прямой угол 5 — острый угол
Угол поворота х у 1 -1 1 -1 II IV I III ОР0 — неподвижный луч ОР — подвижный луч Р Р0 Угол поворота соответствует длине пути, пройденного точкой Р от начального положения Р0 Угол поворота можно измерить двумя мерами : градусной и радианной О
Радианная мера угла у О Р х 1 радиан это центральный угол, длина дуги которого равна радиусу окружности 1 радиан 1 радиан 57 ° 90° 270° 180° 0° 360° 180°= рад 180° развёрнутый угол 90° прямой угол 360° полный угол 2 Формула перехода от радианной меры к градусной : Формула перехода от градусной меры к радианной:
100
180
=
=
Нужно умножить число градусов на
т.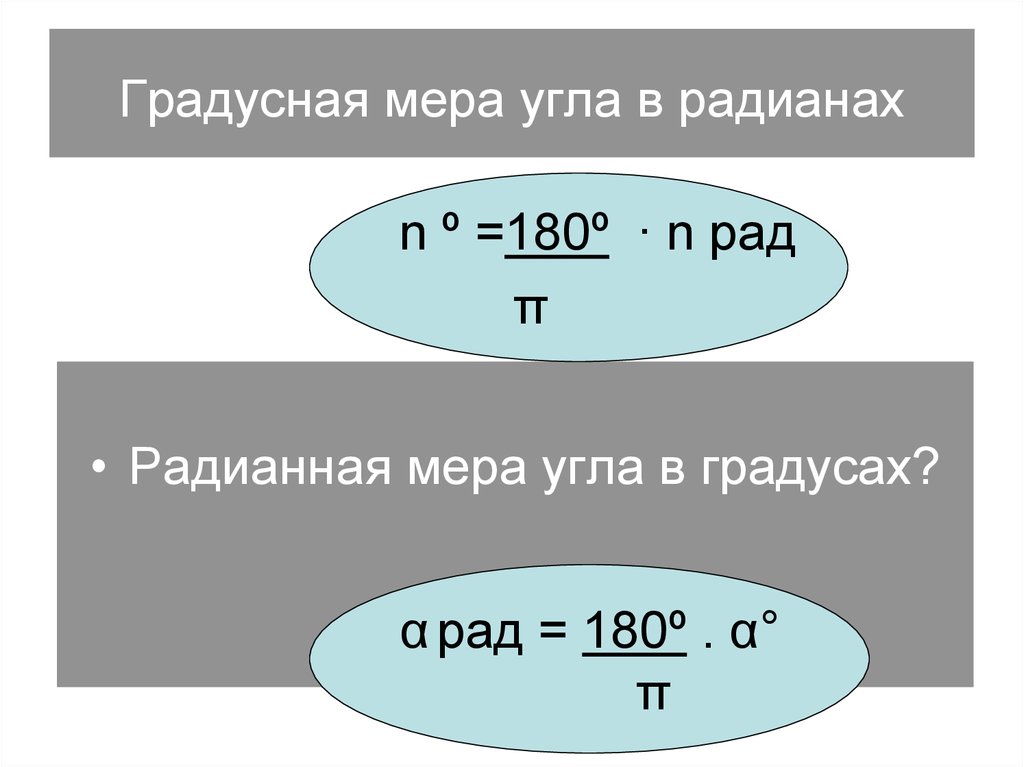
Нужно умножить число радиан на т. е. на величину одного радиана в градусах. = = = 90 60 1200
100
150
200
180
300
360
450
600
750
900
1800
2700
3600
1350
2250
=
=
=
=
=
=
=
=
=
=
=
=
=
=
=
Нужно умножить число градусов на
т.
Нужно умножить число радиан на т. е. на величину одного радиана в градусах. = = = = = = = = = = = = = = = 150 900 600 450 360 200 180 120 100 90 60 1200 1350
ОглавлениеВВЕДЕНИЕЧасть первая. АРИФМЕТИКА, АЛГЕБРА И ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ Глава I. ДЕЙСТВИТЕЛЬНЫЕ И КОМПЛЕКСНЫЕ ЧИСЛА 2. Простые и составные числа. Признаки делимости. 3. Наибольший общий делитель и наименьшее общее кратное.  4. Целые числа. Рациональные числа. 5. Десятичные дроби. Представление рациональных чисел десятичными дробями. 6. Иррациональные числа. Действительные числа. 7. Действия с приближенными числами. 8. Числовая ось. Координаты точки на плоскости. 9. Степени с натуральными показателями. 10. Степени с целыми показателями. 11. Корни. 12. Степени с рациональными показателями. Степени с действительными показателями. 13. Алгоритм извлечения квадратного корня. § 3. Комплексные числа 14. Основные понятия и определения. 15. Рациональные действия с комплексными числами. 16. Геометрическое изображение комплексных чисел. Тригонометрическая форма комплексного числа. 17. Действия с комплексными числами, заданными в тригонометрической форме. Формула Муавра. 18. Извлечение корня из комплексного числа. Глава II. ТОЖДЕСТВЕННЫЕ ПРЕОБРАЗОВАНИЯ 19. Алгебраические выражения. Одночлены и многочлены. 20. Формулы сокращенного умножения. 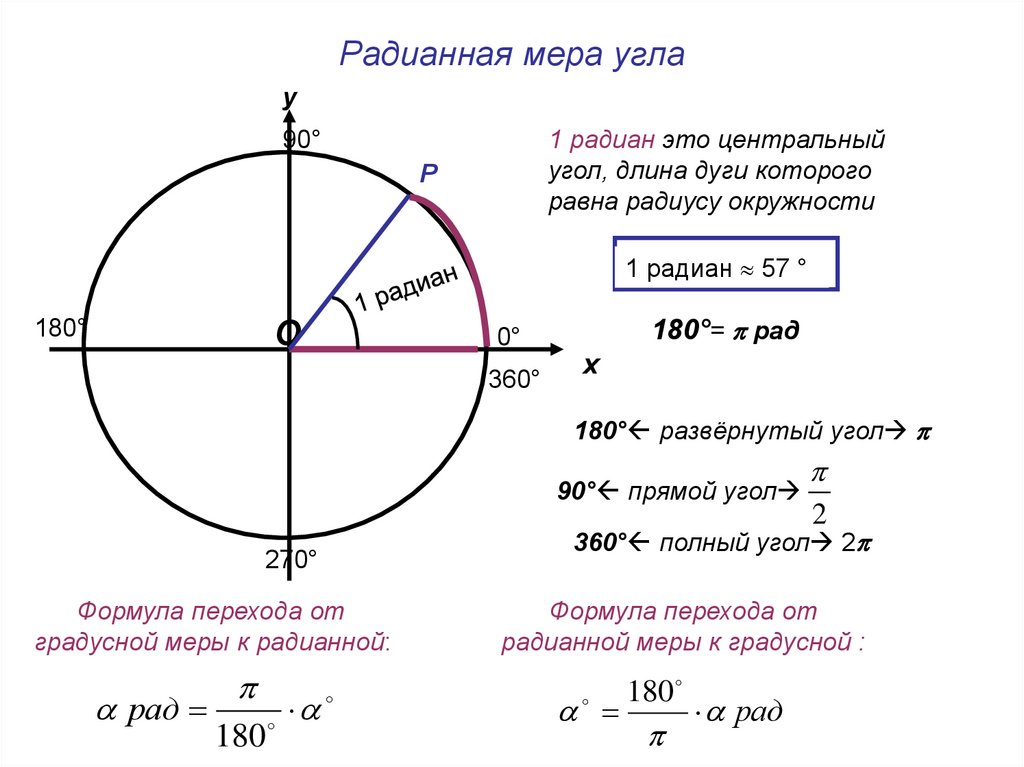 n.41. Обратная пропорциональная зависимость. Степенная функция с рациональным показателем степени. 42. Показательная функция. 43. Логарифмическая функция. § 3. Преобразование графиков 44. Параллельный сдвиг графика. 45. График квадратного трех члена. 46. График дробно-линейной функции. 47. Преобразование симметрии. Сжатие и растяжение графика. 48. Построение графиков функций. 49. Сложение графиков. § 4. Некоторые сведения о рациональных функциях 50. Целые и дробные рациональные функции. Деление многочленов. 51. Схема Горнера. Теорема Безу. 52. Нули многочлена. Разложение многочлена на множители. Глава V. УРАВНЕНИЯ 53. Уравнение. Корни уравнения. 54. Равносильные уравнения. 55. Системы уравнений. 56. Графическое решение уравнений. §. 2. Алгебраические уравнения с одной неизвестной 57. Число и кратность корней. 58. Уравнения первой степени (линейные уравнения). 59. Уравнения второй степени (квадратные уравнения).  60. Формулы Виета. Разложение квадратного трехчлена на множители. 61. Исследование квадратного уравнения. 62. Уравнения высших степеней. Целые корни. 63. Двучленные уравнения. 64. Уравнения, сводящиеся к квадратным. 65. Возвратные уравнения. § 3. Системы алгебраических уравнений 66. Линейные системы. 67. Определители второго порядка. Исследование линейных систем двух уравнений с двумя неизвестными. 68. Системы, состоящие из уравнения второй степени и линейного уравнения. 69. Примеры систем двух уравнений второй степени. Системы уравнений высших степеней. § 4. Иррациональные, показательные и логарифмические уравнения 70. Иррациональные уравнения. 71. Показательные уравнения. 72. Логарифмические уравнения. 73. Разные уравнения. Системы уравнений. Глава VI. НЕРАВЕНСТВА 74. Свойства неравенств. Действия над неравенствами. 75. Алгебраические неравенства. § 2. Решение неравенств 76. Множество решений неравенства.  Равносильные неравенства.77. Графическое решение неравенств. 79. Квадратные неравенства. 80. Неравенства высших степеней. Неравенства, содержащие дробные рациональные функции от х. 81. Иррациональные, показательные и логарифмические неравенства. 82. Неравенства с двумя неизвестными. Глава VII. ПОСЛЕДОВАТЕЛЬНОСТИ 83. Числовая последовательность. 84. Предел числовой последовательности. 85. Бесконечно малые. Правила предельного перехода. § 2. Арифметическая прогрессия 86. Арифметическая прогрессия. Формула общего члена. 87. Свойства арифметической прогрессии. 88. Формула для суммы n членов арифметической прогрессии. § 3. Геометрическая прогрессия 89. Геометрическая прогрессия. Формула общего члена. 90. Свойства геометрической прогрессии. 91. Формулы для суммы n членов геометрической прогрессии. Глава VIII. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ УГЛА (ДУГИ) 93. Вектор, проекция вектора.  94. Положительные углы и дуги, меньшие 360°. 95. Углы и дуги, большие 360°. 96. Отрицательные углы. Сложение и вычитание углов. § 2. Тригонометрические функции произвольного угла 97. Определение основных тригонометрических функций. 98. Изменение основных тригонометрических функций при изменении угла от 0 до 2pi. § 3. Соотношения между тригонометрическими функциями одного и того же угла 99. Основные тригонометрические тождества. 100. Вычисление значений тригонометрических функций по значению одной из них. 101. Значения тригонометрических функций некоторых углов. § 4. Четность, нечетность и периодичность тригонометрических функций 102. Четность и нечетность. 103. Понятие периодической функции. 104. Периодичность тригонометрических функций. § 5. Формулы приведения 105. Зависимость между тригонометрическими функциями дополнительных углов. 106. Формулы приведения. Глава IX. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ ЧИСЛОВОГО АРГУМЕНТА И ИХ ГРАФИКИ § 1.  Тригонометрические функции числового аргумента108. Области определения и области изменения значений тригонометрических функций. 109. Некоторые неравенства и их следствия. § 2. Графики тригонометрических функций 110. Первоначальные сведения о таблицах тригонометрических функций. 111. Основные графики. 112. Примеры построения графиков некоторых других тригонометрических функций. 113. Дальнейшие примеры построения графиков функций. Глава X. ПРЕОБРАЗОВАНИЕ ТРИГОНОМЕТРИЧЕСКИХ ВЫРАЖЕНИЙ 114. Расстояние между двумя точками на плоскости. 115. Косинус суммы и разности двух аргументов. 116. Синус суммы и разности двух аргументов. 117. Тангенс суммы и разности двух аргументов. 118. О формулах сложения для нескольких аргументов. § 2. Формулы для двойного и половинного аргумента. Выражение sin na и cos na через степени sin a и cos a 119. Тригонометрические функции двойного аргумента. 120. Выражение sin na и cos na через степени sin a и cos a при натуральном числе n.  121. Тригонометрические функции половинного аргумента. 122. Выражение основных тригонометрических функций аргумента а через tg(a/2). § 3. Преобразование в сумму выражений вида sina•cosb, cosa•cosb и sinа•sinb § 4. Преобразование в произведение сумм вида § 5. Преобразование некоторых выражений в произведения с помощью введения вспомогательного аргумента 127. Преобразование в произведение выражения a•sina + b•cosa. 128. Преобразование в произведение выражений a•sina+b и a•cosa+b 129. Преобразование в произведение выражения a•tga+b. Глава XI. ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ И ИХ ГРАФИКИ 130. Функция у = arcsin x (арксинус). 131. Функция y = arccos x (арккосинус). 132. Функция y = arctg x (арктангенс). 133. Функция y = arcctg x (арккотангенс). 134. Пример. § 2. Операции над обратными тригонометрическими функциями 135. Тригонометрические операции. 136. Операции сложения (вычитания). § 3. Обратные тригонометрические операции над тригонометрическими функциями 137. 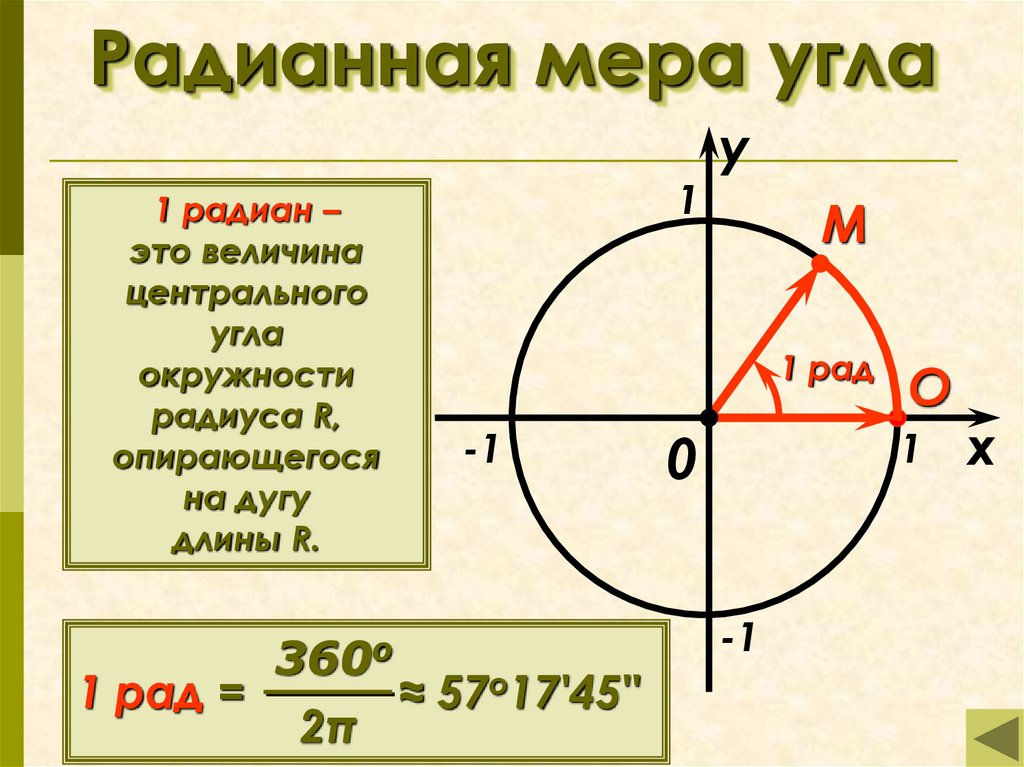 Функция у = arcsin (sin x).138. Функция y = arctg (tg x). Глава XII. ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ И НЕРАВЕНСТВА 139. Уравнение sin х = а. 140. Уравнение cos х = a. 141. Уравнение tg x = a. 142. Уравнение ctg x = a. 143. Некоторые дополнения. § 2. Способ приведения к одной функции одного и того же аргумента 145. Некоторые типы уравнений, приводящихся к уравнениям относительно функции одного аргумента. 146. Способ разложения на множители. 147. Решение рациональных тригонометрических уравнений с помощью универсальной тригонометрической подстановки tg(x/2) = t. § 3. Некоторые частные приемы решения тригонометрических уравнений и систем 148. Введение вспомогательного аргумента. 149. Преобразование произведения в сумму или разность. 150. Переход к функциям удвоенного аргумента. 151. Решение уравнения типа… 152. Применение подстановок sinx ± соsx = y. § 4. Решение тригонометрических неравенств 154. Простейшие тригонометрические неравенства.  155. Примеры тригонометрических неравенств, сводящихся к простейшим. Часть вторая. ГЕОМЕТРИЯ 156. Точка. Прямая. Луч. Отрезок. 157. Плоскость. Фигуры и тела. 160. Равенство фигур. Движение. 161. Равенство тел. § 2. Измерение геометрических величин 162. Сложение отрезков. Длина отрезка. 163. Общая мера двух отрезков. 164. Сравнительная длина отрезков и ломаных. 165. Измерение углов. 166. Радианная мера угла. 167. Измерение площадей. 168. Площадь прямоугольника. Объем прямоугольного параллелепипеда. Глава XIV. ПЕРПЕНДИКУЛЯРНЫЕ И ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ. ЗАДАЧИ НА ПОСТРОЕНИЕ 169. Перпендикуляр и наклонные. 170. Свойство перпендикуляра, проведенного к отрезку в его середине. 171. Параллельные прямые. 172. Углы, образованные двумя параллельными прямыми и секущей. 173. Углы с параллельными или перпендикулярными сторонами. § 2. Геометрические места точек. Окружность 174. Геометрическое место точек. 175. Свойство биссектрисы угла.  176. Окружность. 177. Взаимное расположение прямой и окружности. Касательная и секущая. 178. Хорда и диаметр. Сектор и сегмент. 179. Взаимное расположение двух окружностей. § 3. Основные задачи на построение 181. Деление отрезка пополам. Построение перпендикуляров. 182. Построение углов. 183. Другие задачи на построение. Глава XV. ТРЕУГОЛЬНИКИ, ЧЕТЫРЕХУГОЛЬНИКИ 184. Стороны и углы треугольника. 185. Биссектрисы треугольника. Вписанная окружность. 186. Оси симметрии сторон треугольника. Описанная окружность. 187. Медианы и выcоты треугольника. 188. Равенство треугольников. 189. Построение треугольников. 190. Равнобедренные треугольники. 191. Прямоугольные треугольники. § 2. Параллелограммы 192. Четырехугольники. 193. Параллелограмм и его свойства. 194. Прямоугольник. § 3. Трапеция 196. Трапеция. 197. Средняя линия треугольника. 198. Средняя линия трапеции. 199. Деление отрезка на равные части.  § 4. Площади треугольников и четырехугольников 200. Площадь параллелограмма. 201. Площадь треугольника. 202. Площадь трапеции. Глава XVI. ПОДОБИЕ ГЕОМЕТРИЧЕСКИХ ФИГУР 203. Пропорциональные отрезки. 204. Свойства биссектрис внутреннего и внешнего углов треугольника. § 2. Подобное преобразование фигур (гомотетия) 205. Определение гомотетичных фигур. 206. Свойства преобразования подобия. § 3. Общее подобное соответствие фигур 207. Подобные фигуры. 208. Периметры и площади подобных треугольников. 209. Применение подобия к решению задач на построение. Глава XVII. МЕТРИЧЕСКИЕ СООТНОШЕНИЯ В ТРЕУГОЛЬНИКЕ И КРУГЕ 210. Углы с вершиной на окружности. 211. Углы с вершиной внутри и вне круга. 212. Угол, под которым виден данный отрезок. 213. Четырехугольники, вписанные в окружность. 214. Пропорциональные отрезки в круге. 215. Задачи на построение. § 2. Метрические соотношения в треугольнике 216. Пропорциональные отрезки в прямоугольном треугольнике.  Теорема Пифагора.218. Теорема синусов. Формула Герона. 217. Квадрат стороны, лежащей против острого или тупого утла и треугольнике. Теорема косинусов. 218. Теорема синусов. Формула Герона. 219. Радиусы вписанной и описанной окружностей. § 3. Решение треугольников 220. Таблицы функций. 221. Решение треугольников. Сводка основных формул. 222. Решение прямоугольных треугольников. 223. Решение косоугольных треугольников. Глава XVIII. ПРАВИЛЬНЫЕ МНОГОУГОЛЬНИКИ. ДЛИНА окружности И ПЛОЩАДЬ КРУГА 224. Выпуклые многоугольники. 225. Правильные многоугольники. 226. Соотношения между стороной, радиусом и апофемой. 227. Периметр и площадь правильного n-угольника. 228. Удвоение числа сторон правильного многоугольника. § 2. Длина окружности. Площадь круга и его частей 229. Длина окружности. 230. Площадь круга и его частей. Глава XIX. ПРЯМЫЕ И ПЛОСКОСТИ В ПРОСТРАНСТВЕ 231. Взаимное расположение двух прямых в пространстве.  232. Взаимное расположение прямой линии и плоскости. 233. Взаимное расположение двух плоскостей. 234. Свойства параллельных прямых и плоскостей. 235. Построения в стереометрии. § 2. Перпендикулярность прямых и плоскостей 236. Перпендикуляр к плоскости. 237. Перпендикуляр и наклонные. 238. Угол между прямой и плоскостью. 239. Связь между перпендикулярностью и параллельностью прямых и плоскостей. 240. Общий перпендикуляр двух скрещивающихся прямых. § 3. Двугранные и многогранные углы 241. Двугранный угол. 242. Взаимно перпендикулярные плоскости. 243. Трехгранные углы. 244. Многогранные углы. § 4. Многогранники 245. Многогранники. 246. Правильные многогранники. Глава XX. МНОГОГРАННИКИ И КРУГЛЫЕ ТЕЛА 247. Цилиндры и призмы. 248. Параллелепипеды. 249. Объемы призм и цилиндров. 250. Площадь боковой поверхности призмы. 251. Площадь поверхности цилиндра. § 2. Пирамида. Конус 252. Свойства пирамиды и конуса.  253. Объем пирамиды и конуса. 254. Площадь боковой поверхности правильной пирамиды и конуса. 255. Усеченный конус и усеченная пирамида. § 3. Шаровая поверхность. Шар 256. Шар и шаровая поверхность. 257. Объем шара и его частей. 258. Площадь поверхности шара и ее частей. 259. Понятие телесного угла. Ответы к упражнениям Приложения |
И. Элементарная математика. 2-е изд., перераб. и доп., М.: 1974г. — 592с.
градусов и радианской измерения Формулы
- Формула
определяется количеством поворота от исходной стороны до конечной стороны. В радианах один полный оборот против часовой стрелки равен 2π. В то время как в градусах один полный оборот против часовой стрелки равен 360°. Таким образом, градусная мера и радианная мера связаны уравнениями
360°= 2π радиан
и
180°= π радиан
Из последнего получаем уравнение 1° = π180 радиан.
Это приводит к правилу преобразования градусной меры в радианную. Чтобы перевести градусы в радианы, умножьте градусы на π180° радиан.
Как преобразовать градусы в радианы?
Значение 180° эквивалентно π радианам. Чтобы преобразовать любой заданный угол из градусов в радианы, значение необходимо умножить на π/180. Стандартная формула преобразования градусов в радианы состоит в том, чтобы просто умножить количество градусов на π/180
Таким образом, угол в радианах = угол в градусах × π / 180°
Формула измерения в радианах
В любой окружности радиуса r отношение длины дуги ℓ к длине окружности эквивалентно отношению угла θ, стягиваемого дугой в средней точке и углом за один оборот. Следовательно, формула радиана для измерения углов в радианах ℓ2πr=θ2π⟹ ℓ=rθ.
Формула расчета градусов
Угол измеряется в градусах (°). Радиан часто учитывается при вычислении углов тригонометрических функций или периодических функций.
Радианы всегда обозначаются числом пи (π), где значение числа пи эквивалентно 22/7 или 3,14.
Градус также состоит из частей, выраженных в виде минут и секунд. Это преобразование является важнейшим компонентом приложений тригонометрии. Таким образом, формула степени: — Радианы × 180/π = градусы
Решенные примеры того, как найти меру в радианах из градусов
Пример:
Преобразование 135° в меру в радианах
Решение:
Дано = угол 135 градусов
135∘× π/180∘
=3π/4 радиана
≈2,35 радиана
Пример:
Преобразование 210 градусов в радианы.
Решение: Дано = Угол в 210 градусов
Угол в радианах = Угол в градусах x (π/180)
= 210 x (π/180)
= 7π/6
≈3,67
0,
градус равен 7π/6 (3,67) в радианах.
Недавно обновленные страницы.0009 Формула среднего — Методы отклонения, примеры решений и часто задаваемые вопросы
Формула процентного выхода — APY, атомная экономика и пример решения
Формула ряда — определение, примеры решения и часто задаваемые вопросы
Формула площади поверхности квадратной пирамиды — определение и вопросы
Диагональ квадратной формулы – значение, вывод и примеры решения
Формула дисперсионного анализа – определение, полная форма, статистика и примеры
Формула среднего значения – методы отклонения, примеры решения и часто задаваемые вопросы
Формула доходности в процентах — APY, атомная экономика и пример решения
Формула серии — определение, примеры решения и часто задаваемые вопросы
Формула площади поверхности квадратной пирамиды — определение и вопросы
- Степень
Актуальные темы0 Радианные меры связаны друг с другом- unacademy
Градус и радианная мера угла связаны друг с другом.
Градусная мера указывает размер угла относительно полного круга, тогда как радианная мера указывает размер угла относительно самого себя. Хотя большие углы могут быть указаны с меньшим размером градуса, это не означает, что их будет легче рисовать или строить. Далее в этой статье мы также собираемся обсудить решенные примеры степени и радиана.
Радиан — это единица измерения, которая обычно используется в тригонометрии. Радиан равен половине длины дуги окружности или расстоянию между двумя точками на окружности, где одна точка находится в центре, а другая — на окружности.
Градус — еще одна единица измерения, обычно используемая в тригонометрии. Он равен одной сотой дуги окружности или тремстам шестидесяти пяти градусам, деленным на два. Градусы также могут быть определены как углы от нуля до девяноста градусов, где ноль эквивалентен обращению прямо на север.
Метры, футы, дюймы и другие традиционные единицы измерения основаны на этих двух единицах измерения.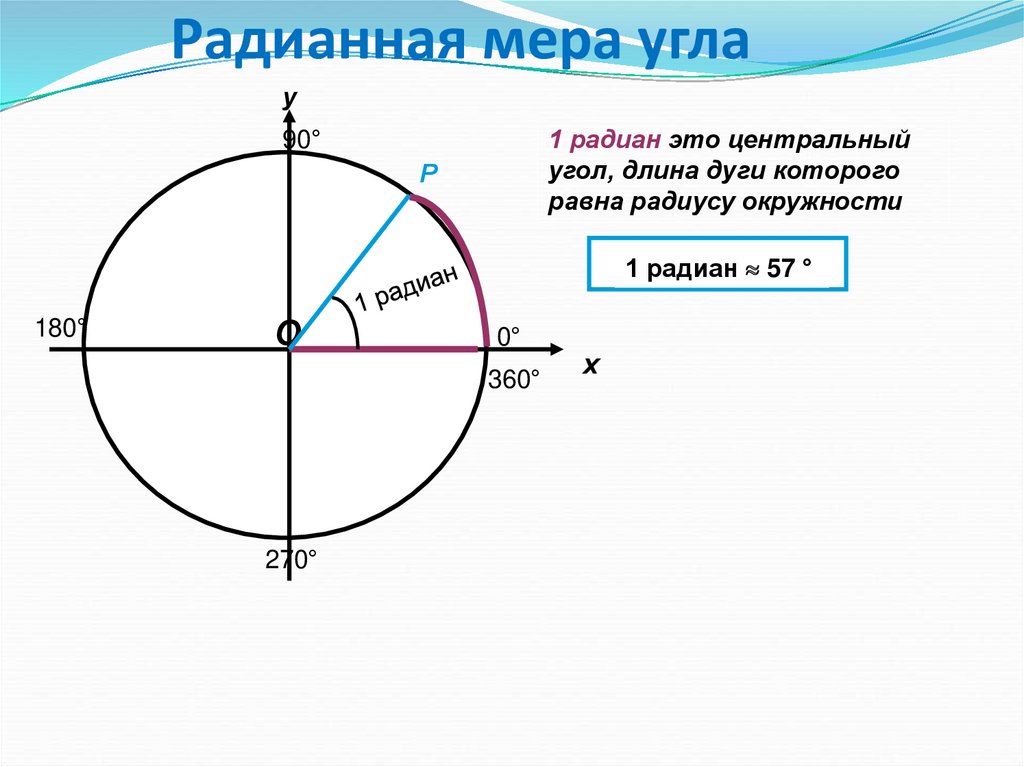
Радиан обозначается как «рад», а его аббревиатура — «рад». Символ градусов — «градус», а его аббревиатура — «°».
Формула радиана:
В любой окружности радиуса r отношение длины дуги ℓ к длине окружности эквивалентно отношению угла θ, образуемого дугой в средней точке, и угла за один оборот. Следовательно, (tanθ=r△y/x△z)
Формула расчета градусов:
Чтобы рассчитать градусы, сначала нужно найти меру угла. Мерой является величина угла, то есть его градусная мера. Чтобы определить это, используйте следующую формулу:
радианы × 180/π = градусы Преобразование 135° в радианы
Решение: Дано = Угол 135 градусов135°× π/180°=3π/4 радиана≈2,35 радиана
Пример 2: Преобразовать 210 градусов в радианы.
Решение: Дано = Угол 210 градусов Угол в радианах = Угол в градусах x (π/180)= 210 x (π/180)= 7π/6≈3,67 Следовательно, 210 градусов равно 7π/6 ( 3.
67) в радианах.
Пример 3: Преобразование 200 градусов в радианы.
Решение: По формуле знаем;
Угол в радианах = Угол в градусах × π/180
Таким образом,
200 градусов в радианах = 200 × π/180 = 10π/9 = 3,491 рад
Пример 4: Преобразование 450 градусов в радианы.
Решение: По формуле знаем;
Угол в радианах = Угол в градусах × π/180
Таким образом,
450 градусов в радианах = 450 × π/180 = 7,854 Рад
Таким образом, с помощью решенных выше примеров степени и радиана мы пришли к с двумя важными формулами:
- Радиан × 180/π = Градус
- ℓ2πr=θ2π⟹ ℓ=rθ
Ответ на вопрос, какова связь между радианом и градусом, состоит в том, что один радиан равен 180/π градусам. Когда радиус поворачивается на один радиан, длина дуги равна радиусу, умноженному на косинус угла, что можно упростить следующим образом:
Косинус угла равен его прилежащей стороне относительно гипотенузы.
Зная радиус и угол, можно найти длину дуги, перемножив их. Угол в радианах равен его градусам, умноженным на π. Таким образом, вы можете сказать, что один градус равен π/180 радианам, что равно 0,0174533… радианам. Разделив 180 на π, вы получите 180/π, что упрощается до 60°. Это означает, что в каждом градусе 60/π радиан или 0,0174533…радиан. Это упрощает преобразование между градусами и радианами, но они не являются взаимозаменяемыми, поскольку являются разными единицами измерения — вы не можете просто заменить число на «градусы» или «радианы», чтобы преобразовать его из одной единицы измерения в другую, не зная каким должен быть правильный ответ.
Мы постоянно используем радианы. Есть много важных применений степени и радиана. Радиан – это единица измерения углов. Как известно, в окружности 360°. Если вы разделите это на 2π, вы получите 57,3° на радиан. Если вы думаете об этом буквально как об измерении угла, это будет означать, что один радиан равен углу, образованному окружностью в ее центре.
Градус и радиан являются полезными способами измерения углов; это просто разные единицы измерения.
Мы используем градусные меры при написании педагогических материалов для студентов, изучающих основы тригонометрии. Это связано с тем, что учащиеся в этих классах, как правило, лучше знакомы с градусами, чем с радианами, а градусная мера занимает меньше места в уравнениях и на странице, чем радианная мера (напротив, мы часто используем радианы для научных работ, потому что они занимают много места). меньше места, чем градусов).
Как правило, использование степени или радиана зависит от личных предпочтений и контекста.
Заключение Градусы и радианы — это оба способа измерения углов. Мы используем степени, потому что с ними удобно работать и большинство людей с ними знакомы. Радианы основаны на количестве пройденного расстояния по окружности, поэтому они используются для описания функций синуса, косинуса и тангенса. В прямоугольном треугольнике, где одна сторона касается центра круга, а другая сторона охватывает край круга, гипотенуза равна 1, а отношение сторон этого прямоугольного треугольника равно тригонометрической функции его угла.