1 градус долготы в км. Перевести километры в градусы и обратно
Главная Выживание
Содержание
- 1 Как измерить расстояние на карте с помощью градусной сетки?
- 1.0.1 Не нашли, то что искали? Используйте форму поиска по сайту
- 1.0.2 Понравилась статья? Оставь комментарий и поделись с друзьями
- 2 Длина дуги параллелей и меридианов на эллипсоиде Красовского, с учетом искажений от полярного сжатия Земли
- 2.1 В сервисе maps.google.ru, поддерживаемые форматы определяются правилами
- 2.2 Числовое значение большой экваториальной полуоси – a современных земных эллипсоидов и референц-эллипсоида Красовского
- 2.3 Таблицы дуг в 1°, 1′, 1″
Как измерить расстояние на карте с помощью градусной сетки?
С помощью карты можно определять расстояние между точками на земной поверхности, но точность таких вычислений невысока.
Ситуация относительно проста, если точки лежат на одном меридиане. Все меридианы имеют одинаковую длину. Можно подсчитать, что одному градусу широты соответствует примерно 111,3 км реальной длины. Поэтому надо найти разницу в долготе между точками и умножить ее на 111,3 км. Например, если точка А находится на северной широте 50°, а Б располагается на северной широте 32°, и при этом у них совпадает долгота, то расстояние между ними составит.
Все меридианы имеют одинаковую длину. Можно подсчитать, что одному градусу широты соответствует примерно 111,3 км реальной длины. Поэтому надо найти разницу в долготе между точками и умножить ее на 111,3 км. Например, если точка А находится на северной широте 50°, а Б располагается на северной широте 32°, и при этом у них совпадает долгота, то расстояние между ними составит.
111,3х(50° – 32°) = 111,3х16 = 1780,8 км
Ситуация меняется, когда одна точка имеет северную, а другая – южную широту. В этом случае широты уже надо складывать. Так, если бы точка Б из предыдущего примера располагалась бы на южной широте 32°, то расстояние от А до Б составило бы:
111,3х(50° + 32°) = 111,3х82 = 9126,6 км
Ситуация усложняется, когда точки находятся на разных меридианах, но на одной параллели. Если у обеих точек долгота западная (или, наоборот, восточная), то сначала надо найти разницу их долгот. Если же одна точка имеет восточную, а другая западную долготу, то их надо суммировать.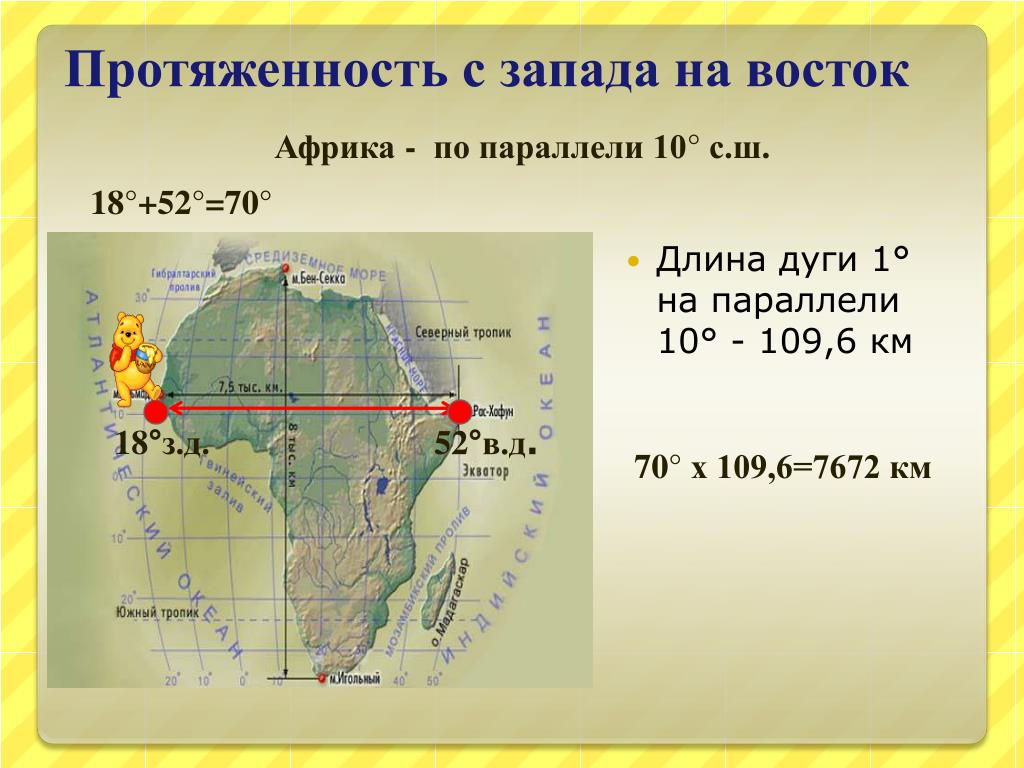 Далее результат надо умножить на длину 1° параллели. Эта длина у параллелей различна и зависит от их широты. Можно воспользоваться таблицей ниже:
Далее результат надо умножить на длину 1° параллели. Эта длина у параллелей различна и зависит от их широты. Можно воспользоваться таблицей ниже:
Например, нужно найти расстояние между точками, имеющими координаты:
А – 60° с. ш, 39° з. д.
Б – 60° с. ш, 25° з. д.
Широты у них одинаковы, поэтому смотрим на долготу. Она у обеих точек западная, поэтому надо найти их разницу:
39° – 25° = 14°
Полученный результат надо умножить на длину 1° параллели, широта которой составляет 60°. По табличке определяем, что на широте 60° дуга в 1° имеет длину 55,8 км. Перемножаем два числа:
14°х 55,8 км = 781,2 км
Список использованных источников
• https://www.yaklass.ru/p/geografiya/5-klass/izobrazheniia-zemnoi-poverkhnosti-i-ikh-ispolzovanie-131512/geograficheskie-koordinaty-161116/re-d77ff3cc-0858-4fd8-aabd-69f1fdffb41d • https://interneturok.ru/lesson/geografy/5-klass/plan-i-karta/gradusnaya-setka-geograficheskaya-dolgota-i-shirota
Не нашли, то что искали? Используйте форму поиска по сайту
Понравилась статья? Оставь комментарий и поделись с друзьями
Длина дуги параллелей и меридианов на эллипсоиде Красовского,
с учетом искажений от полярного сжатия Земли
2020 г. Минисправочники – Мобильная версия
Минисправочники – Мобильная версия
Для определения расстояния по туристической карте, в километрах между пунктами, число градусов умножают на длину дуги 1° параллели и меридиана (по долготе и широте, в системе географических координат), точные расчётные значения которых берутся из таблиц. Приблизительно, с определённой погрешностью, их можно посчитать по формуле, на калькуляторе.
Пример из школьного урока географии (по старому учебнику и из учебного пособия для факультативного курса)
Частный м-б может быть и больше и меньше главного, в зависимости от расположения выбранного участка на карте.
Чтобы добавить символ градуса ( ° ) – нажмите Альт+248 (цифрами в правой цифровой панели клавиатуры; в ноутбуке – с нажатой спец.кнопкой Fn или включив NumLk). Так делается в операционных системах Windows и Linux, а в ОС Mac – с помощью клавиш Shift+Option+8
Координаты широты всегда указываются перед координатами долготы (и печатая на компьютере, и записывая на бумаге).
Задача. Определить длину параллели на заданной широте, например, 50°
с помощью таблиц длин дуг (референц-эллипсоид Красовского)
Решение. Из таблицы («Длина дуги параллели в 1°»), для широты 50 градусов, находим соответствующее значение для дуги 1° – 71697 метров.
В окружности – 360 градусов, поэтому, умножаем табличное значение на 360
В сервисе maps.google.ru, поддерживаемые форматы определяются правилами
Примеры, как будет правильно:
Полная форма записи угла (градусы, минуты, секунды с долями):
Сокращённые формы записи угла:
Градусы и минуты с десятичными долями –
Десятичные градусы (DDD) –
Сервис Гугл-мап имеет онлайн-конвертер для преобразований координат и перевода их в нужный формат.
В качестве десятичного разделителя числовых величин, на сайтах в Интернет и в компьютерных программах – рекомендуется использовать точку.
Числовое значение большой экваториальной полуоси – a
современных земных эллипсоидов и референц-эллипсоида Красовского
Референц-эллипсоид Ф. Н.Красовского, применявшийся в СССР (с 1942 года)
Н.Красовского, применявшийся в СССР (с 1942 года)
в системах отсчета СК-42 и в РФ (СК-42/95, до 1 января 2017 г.)
a= 6 378 245
ГСК-2011 – эллипсоид и Российская геодезическая система координат 2011 года,
для осуществления геодезических и картографических работ.
a= 6 378 136.5
WGS-84 – современный Международный общеземной эллипсоид отсчетной системы,
почти идентичен ITRF(2008)
a= 6 378 137
Таблицы дуг в 1°, 1′, 1″
Чтобы убедиться, что таблица рассчитана по Красовскому,
посчитаем для нулевой широты (экватор), зная числовое значение
большой экваториальной полуоси для референц-эллипсоида Красовского
a= 6 378 245 метров
Приведённые на странице таблицы, будут ещё актуальны, в качестве учебных материалов (к имеющимся учебникам), при использовании старых, советских времён, карт и для приблизительных вычислений.
Длина дуги параллели в 1°, 1′ и 1″ по долготе (по линии запад-восток), метров
| Широта, градус | Длина дуги параллели в 1° по долготе, м | Длина дуги паралл в 1′,м | Длина дуги пар. в 1″,м в 1″,м |
|---|---|---|---|
| 111321 | 1855 | 31 | |
| 1 | 111305 | 1855 | 31 |
| 2 | 111254 | 1854 | 31 |
| 3 | 111170 | 1853 | 31 |
| 4 | 111052 | 1851 | 31 |
| 5 | 110901 | 1848 | 31 |
| 6 | 110716 | 1845 | 31 |
| 7 | 110497 | 1842 | 31 |
| 8 | 110245 | 1837 | 31 |
| 9 | 109960 | 1833 | 31 |
| 10 | 109641 | 1827 | 30 |
| 11 | 109289 | 1821 | 30 |
| 12 | 108904 | 1815 | 30 |
| 13 | 108487 | 1808 | 30 |
| 14 | 108036 | 1801 | 30 |
| 15 | 107552 | 1793 | 30 |
| 16 | 107036 | 1784 | 30 |
| 17 | 106488 | 1775 | 30 |
| 18 | 105907 | 1765 | 29 |
| 19 | 105294 | 1755 | 29 |
| 20 | 104649 | 1744 | 29 |
| 21 | 103972 | 1733 | 29 |
| 22 | 103264 | 1721 | 29 |
| 102524 | 1709 | 28 | |
| 24 | 101753 | 1696 | 28 |
| 25 | 100952 | 1683 | 28 |
| 26 | 100119 | 1669 | 28 |
| 27 | 99257 | 1654 | 28 |
| 28 | 98364 | 1639 | 27 |
| 29 | 97441 | 1624 | 27 |
| 30 | 96488 | 1608 | 27 |
| 31 | 95506 | 1592 | 27 |
| 32 | 94495 | 1575 | 26 |
| 33 | 93455 | 1558 | 26 |
| 34 | 92386 | 1540 | 26 |
| 35 | 91290 | 1522 | 25 |
| 36 | 90165 | 1503 | 25 |
| 37 | 89013 | 1484 | 25 |
| 38 | 87834 | 1464 | 24 |
| 39 | 86628 | 1444 | 24 |
| 40 | 85395 | 1423 | 24 |
| 41 | 84137 | 1402 | 23 |
| 42 | 82852 | 1381 | 23 |
| 43 | 81542 | 1359 | 23 |
| 44 | 80208 | 1337 | 22 |
| 45 | 78848 | 1314 | 22 |
| 46 | 77465 | 1291 | 22 |
| 47 | 76057 | 1268 | 21 |
| 48 | 74627 | 1244 | 21 |
| 49 | 73173 | 1220 | 20 |
| 50 | 71697 | 1195 | 20 |
| 51 | 70199 | 1170 | 19 |
| 52 | 68679 | 1145 | 19 |
| 53 | 67138 | 1119 | 19 |
| 54 | 65577 | 1093 | 18 |
| 55 | 1067 | 18 | |
| 56 | 62394 | 1040 | 17 |
| 57 | 60773 | 1013 | 17 |
| 58 | 59134 | 986 | 16 |
| 59 | 57476 | 958 | 16 |
| 60 | 55801 | 930 | 16 |
| 61 | 54108 | 902 | 15 |
| 62 | 52399 | 873 | 15 |
| 63 | 50674 | 845 | 14 |
| 64 | 48933 | 816 | 14 |
| 65 | 47176 | 786 | 13 |
| 66 | 45405 | 757 | 13 |
| 67 | 43621 | 727 | 12 |
| 68 | 41822 | 697 | 12 |
| 69 | 40011 | 667 | 11 |
| 70 | 38187 | 636 | 11 |
| 71 | 36352 | 606 | 10 |
| 72 | 34505 | 575 | 10 |
| 73 | 32647 | 544 | 9 |
| 74 | 30780 | 513 | 9 |
| 75 | 28902 | 482 | 8 |
| 76 | 27016 | 450 | 8 |
| 77 | 25122 | 419 | 7 |
| 78 | 23219 | 387 | 6 |
| 79 | 21310 | 355 | 6 |
| 80 | 19394 | 323 | 5 |
| 81 | 17472 | 291 | 5 |
| 82 | 15544 | 259 | 4 |
| 83 | 13612 | 227 | 4 |
| 84 | 11675 | 195 | 3 |
| 85 | 9735 | 162 | 3 |
| 86 | 7791 | 130 | 2 |
| 87 | 5846 | 97 | 2 |
| 88 | 3898 | 65 | 1 |
| 89 | 1949 | 32 | 1 |
| 90 |
Упрощённая формула расчёта дуг параллелей (без учета искажений от полярного сжатия):
l пар = l экв * cos(Широта).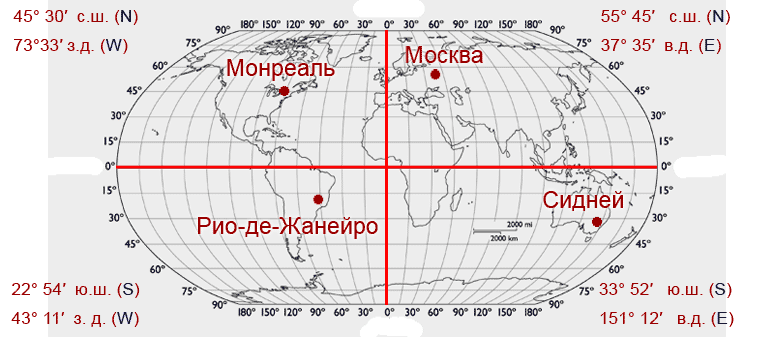
Длина дуги меридиана в 1°, 1′ и 1″ по широте (по линии север-юг), метров
| Широта, градус | Длина дуги меридиана в 1° по широте, м | в 1′, м | 1″,м |
|---|---|---|---|
| 110579 | 1843 | 31 | |
| 5 | 110596 | 1843 | 31 |
| 10 | 110629 | 1844 | 31 |
| 15 | 110676 | 1845 | 31 |
| 20 | 110739 | 1846 | 31 |
| 25 | 110814 | 1847 | 31 |
| 30 | 110898 | 1848 | 31 |
| 35 | 110989 | 1850 | 31 |
| 40 | 111085 | 1851 | 31 |
| 45 | 111182 | 1853 | 31 |
| 50 | 111278 | 1855 | 31 |
| 55 | 111370 | 1856 | 31 |
| 60 | 111455 | 1858 | 31 |
| 65 | 111531 | 1859 | 31 |
| 70 | 111594 | 1860 | 31 |
| 75 | 111643 | 1861 | 31 |
| 80 | 111677 | 1861 | 31 |
| 85 | 111694 | 1862 | 31 |
| 90 |
Рисунок.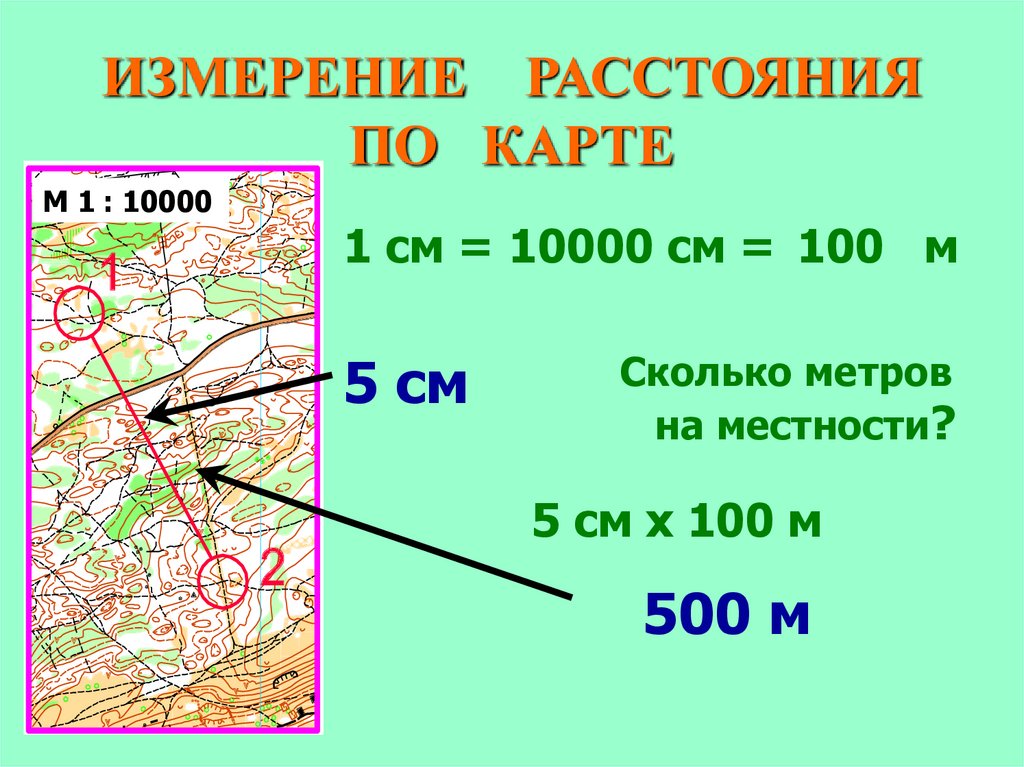 1-секундные дуги меридианов и параллелей (упрощённая формула).
1-секундные дуги меридианов и параллелей (упрощённая формула).
Практический пример использования таблиц. Например, если на карте не указан численный масштаб и нет масштабной линейки, но есть линии градусной картографической сетки – можно графически определить расстояния, из расчёта, что один градус дуги соответствует числовой величине протяжённости, полученной из таблицы. В направлениях «север-юг» (между горизонтальными линиями географической сетки на карте) – значения длин дуг меняются, от экватора до полюсов Земли, незначительно и составляют, приблизительно, 111 километров в одном градусе. Далее, вычислив, сколько содержится в сантиметровом отрезке, можно определить протяжённость произвольного профиля.
Список использованной литературы и ссылки на Интернет-ресурсы
Андреев Н.В. Топография и картография: Факультативный курс. М., Просвещение, 1985
Учебник по математике. Формулы для вычисления длины окружности по её диаметру или радиусу.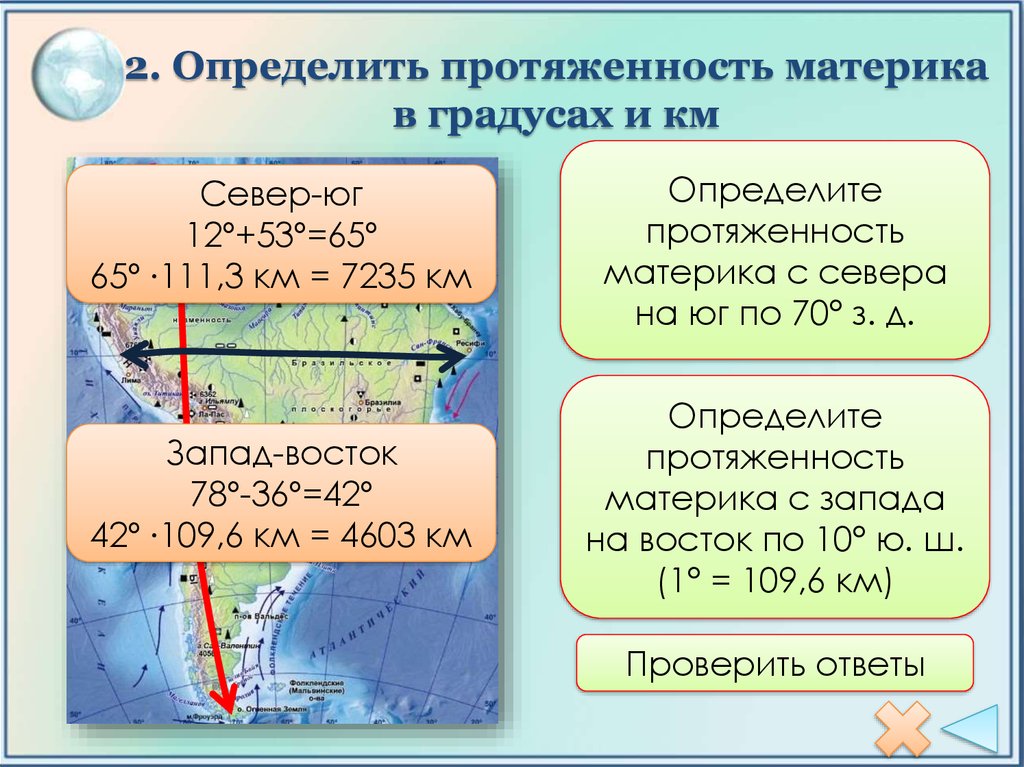
Блог сайта
[ на главную страницу ]
Туристический минисправочник по прикладной топографии – определение расстояния между двумя соседними параллелями по «размеру градуса». Здесь можно найти ответ на вопрос из задачи – сколько километров в одном градусе по линии долготы?
Copyright © 2007-2020, KAKRAS.RU
Post Views: 664
НРАВИТСЯ ЛЮДЯМ
Градусная сеть и ее элементы
|
Как перевести градусы в километры? – Обзоры Вики
Точно так же широта и долгота в метрах? На любой другой широте, 1° занимаемой долготы: 111319. 488*cos(широта) метров. Расстояние от Северного полюса до экватора около 10,000 90 км. Поскольку это охватывает 111.111 градусов широты, мы можем сделать вывод, что каждый градус широты составляет около 111,111 км или XNUMX метра.
488*cos(широта) метров. Расстояние от Северного полюса до экватора около 10,000 90 км. Поскольку это охватывает 111.111 градусов широты, мы можем сделать вывод, что каждый градус широты составляет около 111,111 км или XNUMX метра.
Как перевести градусы в сантиметры?
- Как перевести градусы в сантиметры? …
- нельзя перевести градусы в см. …
- измерения, если они одного типа.
- На самом деле можно при определенных обстоятельствах. …
- измеряя, как далеко поворачивается колесо от градусов до сантиметров, сейчас.
- ЭТО можно сделать.
- Просто получите Окружность колеса * 360.
Сколько градусов составляет метр? Значение в десятичных градусах с точностью до 4 знаков после запятой соответствует 11.1 метрам (+/- 5.55 м) на экваторе. Значение в десятичных градусах с точностью до 5 знаков после запятой соответствует 1.11 метра на экваторе.
…
Точность.
| десятичные знаки | степени | расстояние |
|---|---|---|
| 0 | 1. 0 0 | 111 км |
| 1 | 0.1 | 11.1 км |
| 2 | 0.01 | 1.11 км |
| 3 | 0.001 | 111 m |
• 24 мая 2011 г.
Во-вторых, сколько нм в градусе долготы? Расстояние между градусами долготы составляет около 60 морские мили на экваторе. Чем дальше на север или юг, тем меньше линии долготы сходятся к полюсам. Градусы широты всегда отстоят друг от друга на 60 морских миль. На экваторе сетка 1° долготы на 1° широты покрывает около 3,600 квадратных миль.
Как перевести DM в метры?
тогда каково расстояние между двумя долготами? Градус долготы самый широкий на экваторе с расстоянием 2 мили (69.172 км). Расстояние постепенно сокращается до нуля по мере того, как они встречаются на полюсах. На 111.321 градусах северной или южной широты расстояние между градусами долготы составляет 53 мили (85 км).
На 111.321 градусах северной или южной широты расстояние между градусами долготы составляет 53 мили (85 км).
Как вы рассчитываете градусы?
Каждая степень разделить на 60 равных частей, называемых минутами. Итак, семь с половиной градусов можно назвать 7 градусами и 30 минутами, записанными как 7 ° 30 ′. Каждая минута делится на 60 равных частей, называемых секундами, и, например, 2 градуса 5 минут 30 секунд записывается как 2 ° 5 ′ 30 ″.
Сколько дюймов в высоту составляет 30 градусов? Чтобы получить угол 30 градусов, вам нужно будет поднять изголовье кровати примерно на 41 дюймов… Или вы можете спать на одной из наших клиньев для взрослых, которые поднимают вашу верхнюю часть тела только на угол 30 градусов. У нас также есть клинья с малым и большим градусом.
Какой угол 45 градусов?
Угол 45 градусов — это ровно половина угла в 90 градусов, образованного двумя лучами. Это острый угол, и два угла, равные 45 градусам, образуют прямой угол золото имеет угол 90 градусов. Мы знаем, что угол образуется, когда два луча встречаются в вершине.
Это острый угол, и два угла, равные 45 градусам, образуют прямой угол золото имеет угол 90 градусов. Мы знаем, что угол образуется, когда два луча встречаются в вершине.
Какое расстояние составляет 1 градус долготы? Один градус широты равен примерно 364,000 69 футов (6,068 миль), одна минута равна 1.15 футам (101 мили), а одна секунда равна XNUMX футу. Один градус долготы равен 288,200 футов (54.6 миль), одна минута равна 4,800 футам (0.91 мили), а одна секунда равна 80 футам.
Как вы читаете широту и долготу?
Сколько км составляет градус широты?
Приблизительные метрические эквиваленты градусов. На экваторе для долготы и для широты в любом месте действительны следующие приближения: 1 = 111 км (или 60 морских миль)
Какое расстояние составляет 1 градус широты? Один градус широты равен примерно 364,000 футов (69 миль), одна минута равна 6,068 футам (1. 15 мили), а одна секунда равна 101 футу. Один градус долготы равен 288,200 54.6 футам (4,800 мили), одна минута равна 0.91 футам (80 мили), а одна секунда равна XNUMX футам.
15 мили), а одна секунда равна 101 футу. Один градус долготы равен 288,200 54.6 футам (4,800 мили), одна минута равна 0.91 футам (80 мили), а одна секунда равна XNUMX футам.
Сколько градусов в миле? Каждый градус широты составляет примерно 69 миль (111 километров) друг от друга. Диапазон варьируется (из-за слегка эллипсоидной формы Земли) от 68.703 миль (110.567 км) на экваторе до 69.407 (111.699 км) на полюсах. Это удобно, поскольку каждая минута (1/60 в А градус) составляет примерно одну [морскую] милю.
Который находится на расстоянии 23.5 с от Земли?
Тропик Козерога расположен примерно на 23.5 градуса южной широты или на 23.5 градуса южнее экватора. Эта линия широты является южной границей области, именуемой тропиками. Эта линия отмечает самую дальнюю к югу точку, в которой солнце в полдень висит прямо вверх.
Как преобразовать DD в DMM? Чтобы преобразовать координаты широты и долготы в десятичных градусах в градусы с минутами и секундами или градусы с десятичными минутами, выполните следующие три шага:
- Возьмем целое число — это градусы.

- Умножьте десятичную часть на 60. Хотите десятичные минуты — вот они! …
- Умножьте остальные на 60.
Как перевести градусы в NM?
нм = град2нм (градус, радиус) преобразует расстояния из градусов в морские мили, измеренные вдоль большого круга на сфере с указанным радиусом.
Чему равно расстояние между 2 долготами и 2 широтами? По мере продвижения к полюсам расстояние между каждой линией долготы становится меньше, пока не сойдутся на Северном и Южном полюсах. Расстояние между долготами на экваторе такое же, как широта, примерно 69 миль. На 45 градусах северной или южной широты расстояние между ними составляет около 49 миль (79 км).
Как рассчитать расстояние?
Чтобы найти расстояние, используйте формулу для расстояния д = ст, или расстояние равно скорости, умноженной на время. Скорость и скорость аналогичны, поскольку они оба представляют собой расстояние в единицу времени, например мили в час или километры в час.
Как вычислить долготу? Земля делает один полный оборот (360º долготы) за один день.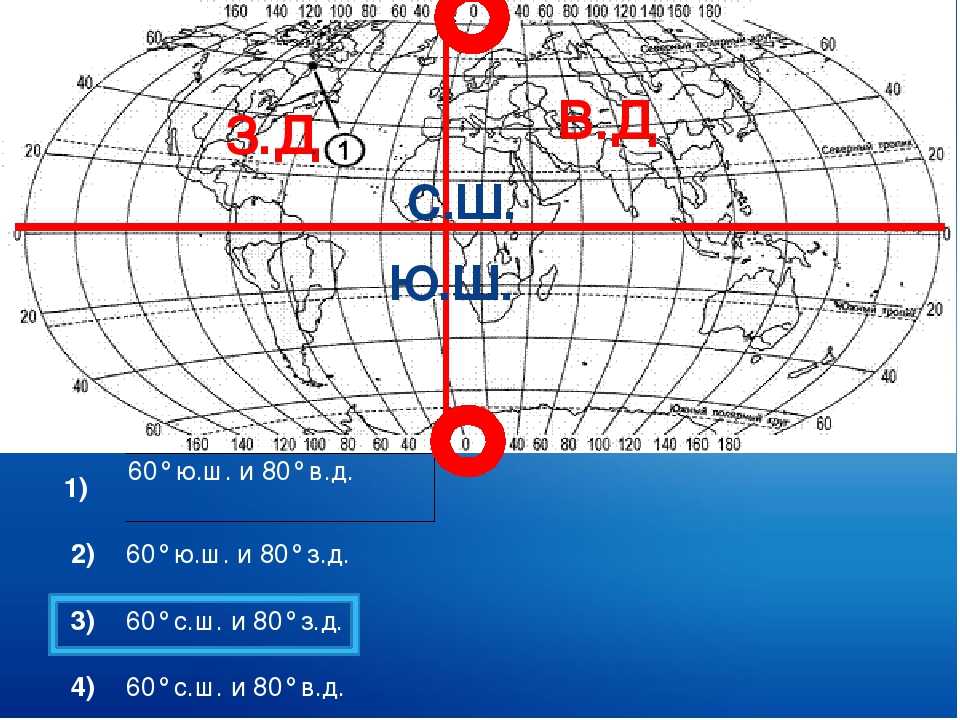 Следовательно, он поворачивается на один градус долготы за 1/360 дня, или каждые четыре минуты. Поэтому, чтобы рассчитать долготу, вам просто нужно рассчитать разницу во времени между полуднем в вашем местоположении и полуднем на нулевом меридиане.
Следовательно, он поворачивается на один градус долготы за 1/360 дня, или каждые четыре минуты. Поэтому, чтобы рассчитать долготу, вам просто нужно рассчитать разницу во времени между полуднем в вашем местоположении и полуднем на нулевом меридиане.
Что такое долгота в математике?
Воображаемые линии, идущие от полюса к полюсу. Они показывают положение восток-запад на Земле.
§ 18. Градусная сетка. Географические координаты
§ 18.Градусная сетка. Географические координаты
Вы узнаете
•Что такое географическая широта и долгота.
•Как определять географические координаты точки по градусной сетке.
Вспомните
•Одинаковую ли длину имеют параллели и меридианы?
•В каких единицах измеряют углы и дуги окружностей?
Обратитесь к электронному приложению
Рис. 53. Сетка параллелей и меридианов на глобусе
Градусная сетка. Пересекающиеся параллели и меридианы образуют на глобусах и картах сетку (рис. 53). Каждая «ячейка» сетки состоит из дуг окружностей. Дуги окружностей, как и углы, можно измерять в градусах, поэтому систему параллелей и меридианов называют градусной сеткой. Градусная мера окружности составляет 360°. (Вспомните компас!) Полуокружность — это дуга величиной 180°.
53). Каждая «ячейка» сетки состоит из дуг окружностей. Дуги окружностей, как и углы, можно измерять в градусах, поэтому систему параллелей и меридианов называют градусной сеткой. Градусная мера окружности составляет 360°. (Вспомните компас!) Полуокружность — это дуга величиной 180°.
Градусная сетка — это система пересекающихся линий — параллелей и меридианов, которые нанесены на глобус или географическую карту.
С помощью градусной сетки определяют географические координаты точек на земной поверхности: географическую широту и географическую долготу.
Рис. 54. Географическая широта
Географическая широта. Все параллели, нанесённые на глобус и карты, имеют обозначения в градусах (0°, 10°, 20° и т. д.). На глобусе они подписаны вдоль начального меридиана, на карте полушарий — на круглой рамке карты. Эти числа указывают географическую широту параллелей (рис. 54).
Географическая широта — это величина дуги меридиана в градусах от экватора до заданной точки.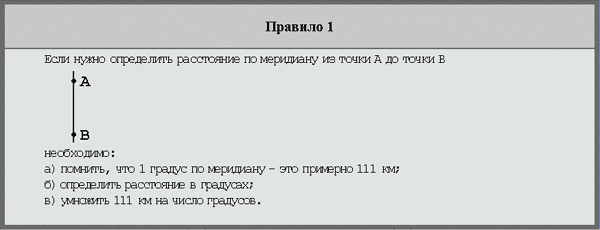
Все точки, лежащие на одной параллели, имеют одинаковую широту. Поскольку географическую широту отсчитывают от экватора, его широта — 0° ш. Значения широты на полюсах — 90° ш.
Рис. 55. Географическая долгота
Все точки, лежащиев Северном полушарии, имеют северную широту (с. ш.), а точки, лежащие в Южном полушарии, — южную широту (ю. ш.).
Географическая долгота. Чтобы определить местоположение какого-либо пункта, недостаточно знать только его широту. Ведь на одной и той же параллели много разных объектов! Поэтому приходится определять географическую долготу (рис. 55).
Географическая долгота — это величина дуги параллели в градусах от начального меридиана до заданной точки.
Все точки, лежащие на одном меридиане, имеют одинаковую долготу. Поскольку географическую долготу отсчитывают от начального (Гринвичского) меридиана, его долгота — 0° д. Поэтому этот меридиан часто называют нулевым. Значения долготы изменяются от 0 до 180°.
Все точки, находящиеся к востоку от начального (нулевого) меридиана, имеют восточную долготу (в. д.), а точки, лежащие к западу от него, — западную долготу (з. д.). Значения долготы в градусах на глобусе и карте полушарий подписывают вдоль экватора у его пересечения с меридианами.
д.), а точки, лежащие к западу от него, — западную долготу (з. д.). Значения долготы в градусах на глобусе и карте полушарий подписывают вдоль экватора у его пересечения с меридианами.
Определение географических координат. Чтобы определить географическую широту объекта, нужно определить параллель, на которой он находится. Например, Санкт-Петербург расположен в Северном полушарии на параллели 60°, поэтому его широта 60° с. ш. А как определить широту, если объект расположен между параллелями? Для этого нужно определить широту ближайшей к объекту параллели со стороны экватора и к ней прибавить число градусов дуги меридиана от этой параллели до объекта. Например, Москва располагается севернее параллели 50°. Число градусов по меридиану между этой параллелью и Москвой равно шести. Значит, географическая широта Москвы будет 56° с. ш.
Так же нужно поступать при определении географической долготы объекта. Если он располагается между двумя меридианами, то сначала узнают долготу ближайшего к объекту меридиана со стороны Гринвича.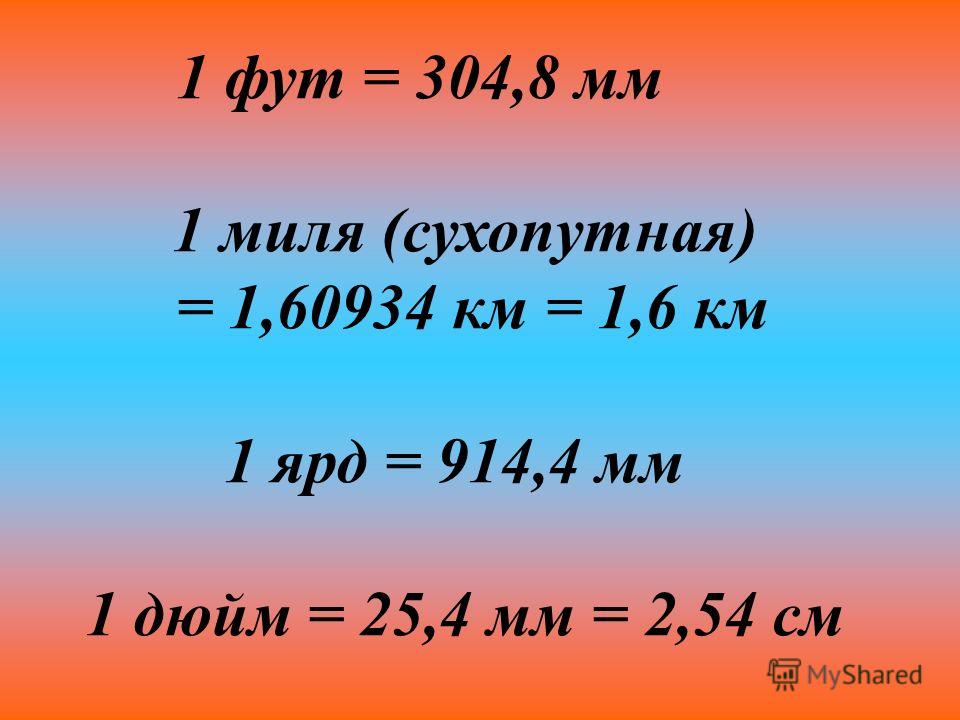 Затем к ней прибавляют число градусов дуги параллели между этим меридианом и самим пунктом. Например, Москва находится восточнее меридиана 30°. Дуга параллели между меридианом 30° и Москвой составляет 8°. Это значит, что географическая долгота Москвы 38°. Так как город расположен к востоку от нулевого меридиана, его долгота восточная — 38° в. д.
Затем к ней прибавляют число градусов дуги параллели между этим меридианом и самим пунктом. Например, Москва находится восточнее меридиана 30°. Дуга параллели между меридианом 30° и Москвой составляет 8°. Это значит, что географическая долгота Москвы 38°. Так как город расположен к востоку от нулевого меридиана, его долгота восточная — 38° в. д.
Определение расстояний по градусной сетке. С помощью градусной сетки на географической карте можно определять расстояния. Все меридианы имеют одинаковую длину. Поэтому длины дуг меридианов величиной 1° равны примерно 111 км. А вот длины дуг величиной 1° для разных параллелей неодинаковы — они уменьшаются по направлению от экватора к полюсам. Поэтому для расчётов расстояний используют таблицу значений длин дуг 1° параллелей для разных широт.
Широта, ° | 0 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 |
Длина 1°, км | 111,4 | 109,6 | 104,6 | 96,4 | 85,4 | 71,6 | 55,8 | 38,2 | 19,4 |
ВОПРОСЫ И ЗАДАНИЯ
1. Какие линии составляют градусную сетку? Для чего она служит?
Какие линии составляют градусную сетку? Для чего она служит?
2.Что такое географическая широта; географическая долгота?
3.По рисункам 54 и 55 определите географические координаты Владивостока и Лондона.
4.Определите по карте:
— какие горы протягиваются в Евразии вдоль параллели 30° с. ш.; вдоль меридиана 60° в. д.;
— какие объекты имеют географические координаты 78° с. ш. и 104° в. д.; 35° ю. ш. и 20° в. д.; 66° с. ш. и 170° з. д.; 52° с. ш. и 0° д.; 5° с. ш. и 10° в. д. Нанесите эти объекты на контурную карту;
— географические координаты Лондона, Нью-Йорка, Рио-де-Жанейро.
5.С помощью градусной сетки по карте полушарий определите:
— расстояние (в градусах и километрах) от экватора до места впадения реки Нил в Средиземное море;
— ширину Южной Америки (в градусах и километрах) по параллели 20° ю. ш.
Измерение расстояний в мировом пространстве
У каждого, кто начинает знакомиться с астрономией и узнает, что до Луны 380 тыс. , а до Солнца 150 млн. км, что звездные расстояния измеряются вместо километров сотнями, тысячами и миллионами «световых лет» и «парсеков», возникает вполне естественное и законное сомнение: «А как же измерили эти расстояния, эти миллионы и миллиарды километров? Ведь до Луны, а тем более до Солнца и звезд добраться нельзя, следовательно, нельзя применить и обычные способы измерения расстояний».
, а до Солнца 150 млн. км, что звездные расстояния измеряются вместо километров сотнями, тысячами и миллионами «световых лет» и «парсеков», возникает вполне естественное и законное сомнение: «А как же измерили эти расстояния, эти миллионы и миллиарды километров? Ведь до Луны, а тем более до Солнца и звезд добраться нельзя, следовательно, нельзя применить и обычные способы измерения расстояний».
Наука и жизнь // Иллюстрации
Рис. 1. Измерение расстояния до недоступного предмета.
Рис. 2. Измерение расстояния до Луны (относительное расстояние Луны и звезды Е сильно искажено).
Наука и жизнь // Иллюстрации
Рис. 3. Прохождение Венеры по диску Солнца (относительные размеры Солнца, Земли и Венеры не в масштабе).
Рис. 4. Противостояние Марса.
Рис. 5. Расположение орбит Марса, Эроса и Земли.
Рис. 6.
Наука и жизнь // Иллюстрации
Наука и жизнь // Иллюстрации
‹
›
Открыть в полном размере
Цель этой статьи — изложить вкратце способы, которыми астрономы измеряют расстояния до тел солнечной системы — Луны и Солнца.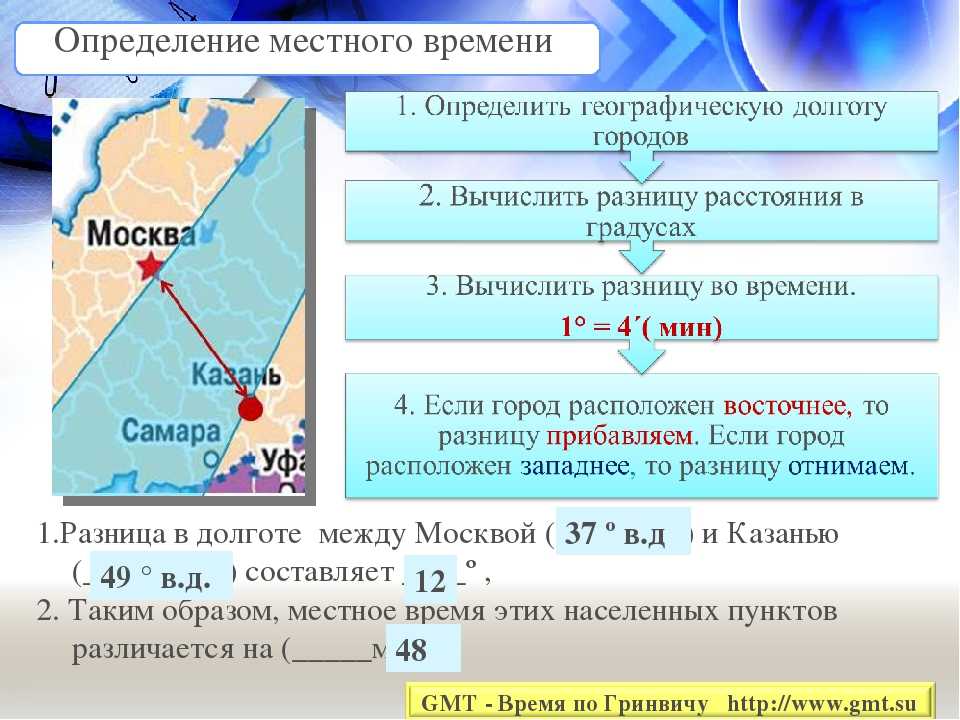 Определению расстояний более отдаленных объектов — звезд и туманностей — мы посвятим другую статью в с дном из ближайших номеров нашего журнала.
Определению расстояний более отдаленных объектов — звезд и туманностей — мы посвятим другую статью в с дном из ближайших номеров нашего журнала.
Измерение расстояния до Луны
Способы, применяемые астрономами для определения расстояния до близких к нам небесных тел, в принципе те же самые, которые применяют геодезисты при съемочных работах, землемеры, саперы, артиллеристы и т. д.
Как измерить расстояние до предмета, подойти к которому нельзя, например, до дерева на противоположной стороне реки (рис. 1)?
Топограф или землемер поступит просто. Он отложит на «своем» берегу линию АВ и измерит ее длину. Затем, став на один конец линии в точку А, измерит угол CAB — между направлением своей линии и направлением на предмет С. Перейдя в точку В он измерит угол СВА. А дальше можно поступить двумя способами: можно отложить на бумаге линию АВ в масштабе и построить на ее концах углы CAB и СВА, пересечение сторон которых и дает на плане точку С. Расстояние ее от точек А и В (да и от любой другой точки, отмеченной на плане) представит соответствующее действительное расстояние в том же самом масштабе, в котором изображена линия АВ. Или же можно по формулам тригонометрии, зная одну сторону треугольника и два его угла, вычислить все другие его линии, в том числе и высоту СН — расстояние точки С — далекого дерева до проведенной землемером линии АВ.
Расстояние ее от точек А и В (да и от любой другой точки, отмеченной на плане) представит соответствующее действительное расстояние в том же самом масштабе, в котором изображена линия АВ. Или же можно по формулам тригонометрии, зная одну сторону треугольника и два его угла, вычислить все другие его линии, в том числе и высоту СН — расстояние точки С — далекого дерева до проведенной землемером линии АВ.
Точно так же поступили и астрономы, определяя расстояние до Луны. Если в один и тот же момент два наблюдателя сфотографируют небо с Луной из двух далеких друг от друга мест А и В (рис. 2) и затем сравнят свои снимки, они увидят, что положение Луны относительно звезд несколько различно. Например, звезда Е на снимке наблюдателя А будет видна к северу от Луны, а у наблюдателя В — к югу.
Измеряя снимки или, что проще, определяя положение Луны на небе в двух местах с помощью специальных телескопов, снабженных угломерными приспособлениями, можно по видимому смещению Луны найти и ее расстояние до Земли.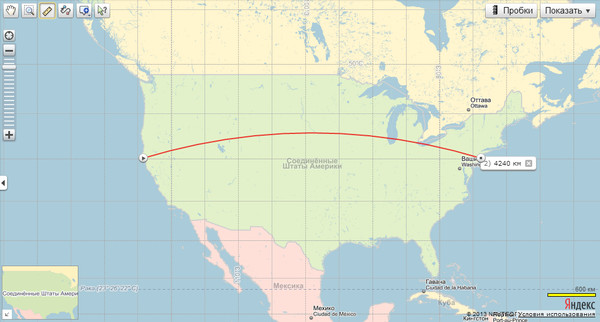 Вспомним одну простую теорему из геометрии — сумма углов в четырехугольнике равна 360° — и применим ее к Земле и Луне.
Вспомним одну простую теорему из геометрии — сумма углов в четырехугольнике равна 360° — и применим ее к Земле и Луне.
Измерения дадут величину углов z1 и z2 — углов между вертикальным направлением в обоих местах и направлением на Луну. Предположим, для простоты, что места А и В лежат на одном меридиане, т. е. на круге, проходящем через оба полюса Земли. ЕЕ — земной экватор и утлы φ 1 и φ2 —географические широты обоих мест.
Применяя теорему к четырехугольнику OALB, где О — центр Земли, найдем, что
[(180° — z1)+φ 1 + φ 12+ (180°—z2)[+] p]= 360°
или
р = (z1+ z2) — (φ1+ φ2)
По известным углам найдем угол р, под которым из центра Луны видна линия АВ. Длина линии АВ известна, так как известен радиус Земли и положение мест наблюдения А и В. По длине этой линии и углу р, так же как и в случае недоступного предмета, можно вычислить расстояние до Луны.
Угол, под которым из центра Луны или другого небесного тела видна линия, длиной равная радиусу Земли, называется параллаксом этого небесного светила. Измерив угол р для любой линии АВ, можно вычислить и параллакс Луны.
Такие измерения были сделаны еще древними греками. Современные точные намерения дают для параллакса Луны на ее среднем расстоянии от Земли величину немного меньше градуса — 57′ 2″,7, т. е. Земля видна с Луны как диск диаметром почти в 2° (в 4 раза больше диаметра видимого нами диска Луны).
Отсюда следует между прочим тесьма интересный вывод: жители Луны (если бы они были там) с большим правом смогли бы сказать, что Земля служит для освещения Луны, чем мы говорим обратное. В самом деле: диск Земли, видимый с Луны, по площади в 14 раз больше видимого нами диска Луны; а так как каждый участок поверхности диска Земли отражает в 6 раз больше света (из-за наличия атмосферы), чем такой же участок диска Луны, то Земля посылает на Луну в 80 раз больше света, чем Луна на Землю (при одинаковых фазах).
По параллаксу Луны сейчас же находим, что расстояние до нее в 60,267 раз больше радиуса Земли или равно 384 400 км.
Однако — это среднее расстояние: путь Луны не точный круг, и Луна, обращаясь вокруг Земли, то подходит к ней на 363000 км, то удаляется на 405 000 км.
Так решается первая, самая простая задача — измерение расстояния до самого близкого к нам небесного тела. Это сравнительно не трудно, потому что видимое смещение Луны велико, и его можно было измерить с помощью даже тех примитивных приборов, которыми пользовались древние астрономы.
Чему равно расстояние до Солнца
Казалось бы, можно применить тот же самый способ и для измерения расстояния: до Солнца — произвести одновременные наблюдения в двух местах, вычислить углы четырехугольников и треугольников, и задача решена. На деле, однако, обнаружилось весьма много трудностей.
Уже древние греки установили, что Солнце во много раз дальше Луны, но во сколько именно — установить не смогли.
Древнегреческий астроном Аристарх нашел, что Солнце в 20 раз дальше Луны; это измерение было неверно. В 1650—1675 гг. голландские и французские астрономы показали, что Солнце дальше Луны примерно в 400 раз. Стало понятным, почему не удавались попытки обнаружить видимое смещение Солнца, как это удалось сделать для Луны. Ведь параллакс Солнца в 400 раз меньше параллакса Луны, всего около 1/400 градуса, или 9 сек. дуги. А это значит, что даже при наблюдении с двух мест Земли, лежащих на противоположных концах диаметра Земли, например с северного и южного полюсов, видимое смещение Солнца было бы равно видимой толщине проволоки в 0,1 мм (человеческий волос) при рассматривании ее с расстояния в 1,5 м. Величина ничтожная, и заметить ее трудно, хотя и возможно с помощью точного угломерного прибора.
Но возникают большие добавочные трудности. Луну наблюдают ночью и ее положение сравнивают с положениями соседних звезд. Днем звезд не видно, и сравнивать положение Солнца не с чем, приходится целиком полагаться на разделенные круги самого прибора. Прибор нагревается лучами Солнца, различные части его деформируются, вызывая появление новых ошибок. Да и сам воздух, нагретый лучами Солнца, неспокоен, край Солнца кажется волнующимся, дрожащим, по небу как бы бегут волны. Погрешности наблюдений будут больше той величины, которую необходимо измерить. От самого простого метода пришлось отказаться и пойти обходными путями.
Прибор нагревается лучами Солнца, различные части его деформируются, вызывая появление новых ошибок. Да и сам воздух, нагретый лучами Солнца, неспокоен, край Солнца кажется волнующимся, дрожащим, по небу как бы бегут волны. Погрешности наблюдений будут больше той величины, которую необходимо измерить. От самого простого метода пришлось отказаться и пойти обходными путями.
Наблюдения видимых движений планет производились еще в глубокой древности. Из сравнения этих наблюдений с современными удалось с очень большой точностью определить время обращения планет вокруг Солнца. Так например, мы знаем что Марс совершает свой оборот в 1,8808 земных года. Но третий закон Кеплера говорит: «Квадраты времен обращения планет относятся, как кубы их средних расстояний от Солнца». Отсюда, принимая за единицу среднее расстояние Земли от Солнца, можно вычислить, что среднее расстояние Марса равно 1,5237. Таким путем можно построить точный «план» солнечной системы, нанести орбиты планет, Земли, комет, но у плана будет не хватать «мелочи» — масштаба. Мы сможем уверенно сказать, что Венера в 1,38 раза ближе к Солнцу, чем Земля, а Марс в 1,52 раз дальше, но ничего не будем знать о том, сколько же километров от Венеры или Земли до Солнца. Достаточно, однако, найти хотя бы одно из расстояний в километрах: мы получим в свои руки масштаб и, пользуясь им, сможем измерить любое расстояние на плане.
Мы сможем уверенно сказать, что Венера в 1,38 раза ближе к Солнцу, чем Земля, а Марс в 1,52 раз дальше, но ничего не будем знать о том, сколько же километров от Венеры или Земли до Солнца. Достаточно, однако, найти хотя бы одно из расстояний в километрах: мы получим в свои руки масштаб и, пользуясь им, сможем измерить любое расстояние на плане.
Именно этот способ был применен для измерения расстояния от Солнца до Земли. Меркурий и Венера находятся ближе к Солнцу, чем Земля. Может оказаться, что когда Земля и Венера будут находиться по одну сторону от Солнца, — центры Солнца и обеих планет окажутся на одной «прямой линии (рис. 3). Венера будет видна с Земли на диске Солнца. Расстояние от Земли до Венеры будет почти в 4 раза меньше расстояния до Солнца, а параллакс ее почти в 4 раза больше параллакса Солнца. Кроме того, нужно будет определить положение Венеры относительно центра Солнца, что можно сделать гораздо точнее, чем определение видимого положения Солнца (ошибки, присущие инструменту, влияют значительно меньше при определении относительного положения двух небесных тел).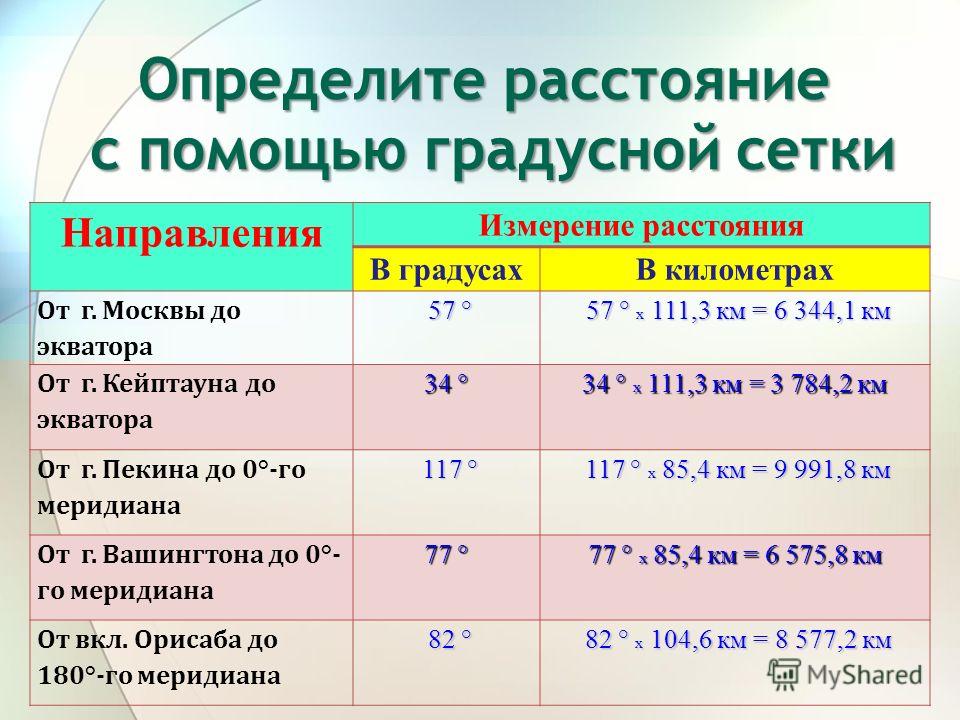
Если бы движение Земли и Венеры происходило в одной и той же плоскости, то «прохождения Венеры по диску Солнца» наблюдались бы каждый раз, когда Венера, движущаяся быстрее Земли, обгоняет ее, т. е. примерно раз в 1 год и 7 мес. Но плоскости путей Земли и Венеры наклонены друг к другу. Обгоняя Землю, Венера проходит выше или ниже Солнца и не может быть наблюдаема, так как она повернута к Земле темной, не освещенной Солнцем стороной. Мы увидим ее на диске Солнца лишь в том случае, если и «обгон» будет происходить вблизи линии пересечения плоскостей орбит обеих планет.
Такое «счастливое совпадение» случается не часто. После одного прохождения второе следует через 8 лет, но зато следующее — лишь через 105—120 лет. Впервые явление наблюдали в 1639 г. Следующие прохождения — 1761, 1769, 1874 и 1882 гг. наблюдались уже весьма тщательно для определения точного расстояния до Солнца. Для наблюдения последних двух прохождений было снаряжено большое число специальных экспедиций. Наблюдатели в далеко расположенных пунктах с наибольшей доступной точностью наблюдали моменты начала и конца явления, а также положение Венеры на диске Солнца. При наблюдениях последних прохождений применялось уже фотографирование Солнца. Видимый путь Венеры по диску Солнца будет несколько смещен у обоих наблюдателей (рис. 3). Из величины смещения можно вычислить расстояние от Земли до Венеры, т. е. найти тот ключ, масштаб, которого недоставало в построенном плане солнечной системы. Наблюдений прохождений Венеры дали для параллакса Солнца величину 8″,86 и для расстояния Солнца — 148 000 000 км.
Наблюдатели в далеко расположенных пунктах с наибольшей доступной точностью наблюдали моменты начала и конца явления, а также положение Венеры на диске Солнца. При наблюдениях последних прохождений применялось уже фотографирование Солнца. Видимый путь Венеры по диску Солнца будет несколько смещен у обоих наблюдателей (рис. 3). Из величины смещения можно вычислить расстояние от Земли до Венеры, т. е. найти тот ключ, масштаб, которого недоставало в построенном плане солнечной системы. Наблюдений прохождений Венеры дали для параллакса Солнца величину 8″,86 и для расстояния Солнца — 148 000 000 км.
Два ближайших прохождения Венеры по диску Солнца будут наблюдаться 8 июня 2004 г. и 6 июня 2012 г.
Могут наблюдаться и прохождения по диску Солнца ближайшей к Солнцу планеты — Меркурия. Они бывают значительно чаще, чем прохождения Венеры, но представляют несравненно меньше интереса для определения расстояния до Солнца: в момент прохождения расстояние от Земли до Меркурия составляет около 90 млн. км, и параллакс его лишь в 1,5 раза больше параллакса Солнца.
км, и параллакс его лишь в 1,5 раза больше параллакса Солнца.
Другое удобное расположение планет бывает тогда, когда Земля, двигаясь быстрее Марса, перегоняет его (рис. 4). В это время Марс виден на ночном небе в противоположном от Солнца направлении, почему такие положения его и называются противостояниями. Расстояние между Землей и Марсом уменьшается в среднем до 78 млн. км. Однако орбита Марса сильно отлична от круга, и если сближение Марса и Земли происходит в августе — сентябре, расстояние до Марса может быть всего 56 млн. км. Марс виден всю ночь, и его положение можно очень точно определить, пользуясь как опорными точками близкими звездами.
Наблюдения из двух пунктов дадут параллакс Марса, а отсюда можно вычислить его расстояние и по нему — масштаб к плану солнечной системы. Приближения Марса и Земли — противостояния Марса — повторяются приблизительно через 2 года и 2 мес., а так называемые «великие противостояния», когда Марс ближе всего к Земле, — раз в 15 —17 лет. Последнее «великое противостояние» было 24 августа 1924 г., а следующее будет 23 июля 1939 г. Каждое противостояние используется не только для определения расстояния, но и для физических наблюдений самого Марса.
Последнее «великое противостояние» было 24 августа 1924 г., а следующее будет 23 июля 1939 г. Каждое противостояние используется не только для определения расстояния, но и для физических наблюдений самого Марса.
Еще ближе к Земле может подойти Эрос, одна из семейства малых планет, орбиты большинства которых лежат между орбитам Марса и Юпитера. Орбита Эроса очень сильно отлична от круга, и значительная часть ее лежит даже внутри орбиты Марса (рис. 5). В некоторых случаях расстояние между Землей и Эросом может уменьшаться до 22 млн. км, т. е. до 1/7 расстояния Солнца, довольно близко Эрос подходил к Земле в 1900—1901 гг. (на 48 млн. км) и в 1930— 1931 гг. (на 26 млн. км). Эрос наблюдался в это время, как звездочка, положение которой среди других звезд может быть определено весьма точно.
Нужно заметить, что для определения параллакса по наблюдениям Эроса не нужно обязательно производить наблюдения из двух далеких пунктов. Вращение Земли вокруг оси уносит с собой наблюдателя и, если он находится на экваторе, за 12 час. вращение Земли перенесет его на расстояние, равное диаметру Земли, или 12,7 тыс. км. Наблюдатель, расположенный к северу или к югу от экватора, переместится меньше. И если снимки Эроса произведены в начале и в конце ночи, — они равносильны снимкам, сделанным на большом расстоянии друг от друга. Нужно, конечно, принять во внимание движение Земли и Эроса по орбитам за время между снимками.
вращение Земли перенесет его на расстояние, равное диаметру Земли, или 12,7 тыс. км. Наблюдатель, расположенный к северу или к югу от экватора, переместится меньше. И если снимки Эроса произведены в начале и в конце ночи, — они равносильны снимкам, сделанным на большом расстоянии друг от друга. Нужно, конечно, принять во внимание движение Земли и Эроса по орбитам за время между снимками.
Существуют ещё другие способы измерения расстояния до Солнца, но они не являются основными, и рассматривать их мы не имеем возможности. Между прочим такой же метод использовался древними и для определения параллакса Луны.
Сопоставление всех наиболее точных определений дает для параллакса Солнца величину 8″,803 с возможной ошибкой в 0″,001, а отсюда — среднее расстояние Земли равно 149 450 000 км с возможной ошибкой в 17 000 км.
Среднее расстояние Солнца—Земля является основным для выражения других расстояний в солнечной системе и названо «астрономической единицей». Но действительное расстояние до Солнца может отличаться от среднего, так как путь Земли около Солнца — не круг, а эллипс. В июле расстояние до Солнца на 2,5 млн. км больше среднего, а в январе на столько же меньше.
В июле расстояние до Солнца на 2,5 млн. км больше среднего, а в январе на столько же меньше.
Астрономическая единица есть та мера, которой мы измеряем «не только все расстояния до тел солнечной системы, но и расстояния самых далеких звезд, туманностей и звездных скоплений. Словом, это та мера, при помощи которой мы определяем масштаб строения вселенной. Поэтому на определения ее потрачено много усилий, и известна она современной науке с большой точностью.
Может показаться, что указанная выше ошибка в 17 000 км велика; но не надо забывать, что эта ошибка составляет лишь немногим больше 0,0001 всей астрономической единицы. Представим себе, что мы измерили длину комнаты в 9 м и при этом измерении ошиблись всего лишь на 1 мм. По сравнению с длиной комнаты эта ошибка соответствует точности, с которой известно среднее расстояние Земли от Солнца. Но если попробовать на самом деле измерить длину в 9 м с ошибкой в 1 мм, — это окажется совсем не так просто: потребуется большое внимание и хорошие измерительные инструменты, чтобы обеспечить такую точность при обыкновенном измерении по гладкому полу, во всех точках доступному измерителю. Тем более нужно отдать должное точности, с которой произведено измерение через межпланетное пространство расстояния до Солнца, к которому ни один человек ее приближался ближе чем на 147 млн. км, — расстояние, которое пушечное ядро сможет пролететь, двигаясь со скоростью 1000 м/сек, только в 4,5 года.
Тем более нужно отдать должное точности, с которой произведено измерение через межпланетное пространство расстояния до Солнца, к которому ни один человек ее приближался ближе чем на 147 млн. км, — расстояние, которое пушечное ядро сможет пролететь, двигаясь со скоростью 1000 м/сек, только в 4,5 года.
Морские единицы физических величин
Международная система единиц измерения в судоходстве отличается от единиц измерения, принятых в нашей повседневной жизни и соседствует с англосаксонскими основными единицами. Это связано с сохранившейся до нашего времени важной ролью англоязычных стран в судостроении и судоходстве.
Безусловно, в эпоху интернета не представляет особого труда перевести одни единицы в другие, воспользовавшись одним из множества приложений. Но как быть в открытом море, где по различным причинам интернет может отсутствовать?
Знать морские единицы измерения и свободно переводить их в общепринятые величины должен уметь каждый яхтсмен!
Единицы длинны
Морская миля — единица длины при измерении расстояний на море. Она равна длине одной минуты дуги меридиана (или 1/60 градуса, так как в градусе 60 минут).
Она равна длине одной минуты дуги меридиана (или 1/60 градуса, так как в градусе 60 минут).
Таким образом, передвижение на одну морскую милю вдоль меридиана примерно соответствует изменению географических координат на одну минуту широты.
Сокращенное обозначение морской мили, которое можно встретить на навигационных приборах nm
1 морская миля = 1852,3 м = 1,852 км
1 км = 0,54 морские мили
Кроме морской мили, для измерения расстояния на море приняты также следующие единицы длины:
1 Кабельтов = 0,1 морская миля = 185,2 м
Длина лодок обычно измеряется в футах. Как правило, в названии модели яхты содержится число соответствующее ее длине в футах, что позволяет сразу иметь представление о размерах судна.
Что же такое фут?
Фут (от англ. foot — ступня) — единица измерения длины в английской системе мер.
Первоначальный британский фут — это не что иное, как сандалия древнеримского легионера.
Для Англии этот «сандальный» фут стал античным наследием Рима. Фут продолжал использоваться по всей Европе в течение большей части последних двух тысяч лет, хотя национальные и региональные различия были обычным явлением. В зависимости от того, где (и когда) термин фут был использован, он может означать длину от 273 мм до 357 мм.
Таблица конвертации футов в метры
В 1959 году международное соглашение о ярдах и фунтах (между Соединенными Штатами и странами Содружества Наций), определило фут как 0,3048 метра (304,8 мм).
1 фут = 0.3048 м
1 метр = 3,28 фута
Сокращенное обозначение фута – ft
В свою очередь фут состоит из 12 дюймов. Дюйм имеет тоже свою историю, и в давние времена дюйм считали равным ширине большого пальца (по-русски дюйм – от голландского слова duim, что при дословном переводе обозначает – большой палец).
Международное обозначение дюйма inch, in или ″ — двойной штрих
1 дюйм = 1/12 фута =2,54 см
Скорость судна
Скорость морского судна измеряют узлами, т. е. количеством морских миль, которое оно проходит за 1 ч. Говорят, например, что судно имеет скорость 12 узлов, т. е. оно проходит 12 морских миль в час.
е. количеством морских миль, которое оно проходит за 1 ч. Говорят, например, что судно имеет скорость 12 узлов, т. е. оно проходит 12 морских миль в час.
Термин «узел» появился в эпоху парусного мореплавания, когда скорость хода судна измеряли с помощью, так называемого секторного лага — деревянного щитка секторообразной формы, выпускаемого с кормы судна в воду на лаглине (плетеном тросике). Такой сектор удерживался отростками лаглиня в трех точках, благодаря чему сохранял в воде перпендикулярное положение к направлению хода судна. Так как сектор тормозится водой, то лаглинь вытравливался приблизительно со скоростью хода судна.
Если лаглинь был с помощью узелков разбит на участки по 50,7 фута, то есть равные 1\120 мили (6080\50,7=120), тогда при скорости хода в 1 узел лаглинь за 1 минуту или за 1\60 часа вытравится на 1\60 мили (2 узелка), а за 0,5 минуты — на 1 узелок. Если же за 0,5 минуты вытравливалось, например, 9 узелков, то считалось, что судно идет со скоростью 9 узлов.
1 узел = 1 морская миля/час = 1,852 км/ч
Международное обозначение узла, которое можно встретить на навигационных приборах kts
Таблица конвертации узлов в м/с и км/ч для типичных скоростей парусной яхты
Формулы для перевода узлов в км/ч и м/с:
V км/ч = 1,852 * V узлов
V м/сек = 0,5145 * V узлов
V узлов = 0,5400 * V км/ч
V узлов = 1,943 * V м/сек
Грубо говоря, значение скорости судна в узлах в 2 раза меньше значения скорости судна в м/с
Скорость и сила ветра
Так же как и скорость судна, скорость ветра измеряется в узлах. Кроме того силу ветра измеряют в баллах по шкале Бофорта.
Шкала Бофорта — двенадцатибалльная шкала, принятая Всемирной метеорологической организацией для приближённой оценки скорости ветра по его воздействию на наземные предметы или по волнению в открытом море. Средняя скорость ветра указывается на стандартной высоте 10 метров над открытой ровной поверхностью.
Средняя скорость ветра указывается на стандартной высоте 10 метров над открытой ровной поверхностью.
Шкала разработана ирландским гидрографом Фрэнсисом Бофортом в 1805 году.
Более подробную таблицу с детальным описанием состояния моря и суши при различной силе ветра можно найти тут.
Направления и географические координаты
Все мы знаем, что положение точки на земной поверхности определяют географические координаты.
Координаты (широта от −90° до +90°, долгота от −180° до +180°) могут записываться:
— в ° градусах в виде десятичной дроби (десятичные градусы, современный вариант) – например, N55,755831°, E37,617673°
— в ° градусах и ′ минутах с десятичной дробью – например, 55°45.35′N, 37°37.06′E
— в ° градусах, ′ минутах и ″ секундах с десятичной дробью (исторически сложившаяся форма записи) – например, 55°45′20.9916″N, 37°37′3.6228″E
На картах поисковых систем по умолчанию показываются координаты в градусах с десятичной дробью со знаком «−» для отрицательной долготы.
В то же время часто используется и исконный способ записи с градусами, минутами и секундами. Например, при прокладке маршрута на навигационной карте обычно координаты записывают в формате «градусы, минуты, секунды»
При необходимости пересчитать форматы можно, конечно, использовать специализированные сервисы.
Но иногда бывает, что необходимо пересчитать форматы самостоятельно.
Напомним, что 1° (градус) = 60′ (минут), 1′ (минута) = 60″ (секунд)
Чтобы перейти из формата «градусы, минуты, секунды и доли секунд» в «десятичные градусы», нужно воспользоваться формулой:
Десятичные градусы = Град + Мин/60 + Сек/3600
Например, переведем 55°45′20.9916″N в десятичные градусы
55°45.35′N = 55 + 45/60 + 20,9916/60 = 55 + 0,75 + 0,005831 = 55.755831 °N
Чтобы перейти из формата «десятичные градусы» dd.ddddd в «градусы, минуты, секунды и доли секунд» dd mm ss, нужно воспользоваться формулой:
DD = TRUNC(DDD)
MM = TRUNC((DDD − DD) * 60)
SS = ((DDD − DD) * 60 − MM) * 60
где DDD — координаты в формате DD. DDDD, DD — градусы, MM (MM.MMMM) — минуты, SS — секунды
DDDD, DD — градусы, MM (MM.MMMM) — минуты, SS — секунды
Функция TRUNC в данном случае возвращает целое число
Например, переведем 55,755831°N в формат «градусы, минуты, секунды и доли секунд»
1) определим градусы: DD = целое число от 55,755831 = 55°
2) определим минуты: MM = целое число от (55,755831 – 55) * 60 = целое число от 45,34986 = 45′
3) определим секунды и доли секунд: SS = ((55,7558 – 55) * 60 – 45) * 60 = 20,9916″
Получается 55,755831°N = 55°45′20.9916″N
В тех случаях, когда не требуется особая точность в обозначении направления, применяют румбы.
Например, для обозначения направления ветра – «…NE 7 баллов…», течения «…W течение…» или приблизительного направления на какой-то географический район – «…к SW-ту от мыса Лизард…» и т.д.
Румбы сохранились со старых времен, когда не только конструкция магнитных компасов была не совершенна, но и точность удержания корабля на курсе измерялась десятком градусов, в виду несовершенства рулевого устройства. По мере совершенствования точности компасов и рулевых устройств, требовалась и более точная система отсчета, поэтому румбы разделили на части. С появлением гирокомпасов, электрических и гидравлических рулевых устройств, появилась возможность вести отсчет и удерживать судно на курсе с точностью до долей градуса. С этого времени румбы утратили практическое применение для целей курсоуказания, однако широко используются для общего обозначения направлений на море.
По мере совершенствования точности компасов и рулевых устройств, требовалась и более точная система отсчета, поэтому румбы разделили на части. С появлением гирокомпасов, электрических и гидравлических рулевых устройств, появилась возможность вести отсчет и удерживать судно на курсе с точностью до долей градуса. С этого времени румбы утратили практическое применение для целей курсоуказания, однако широко используются для общего обозначения направлений на море.
Итак, Румб (от греч. — юла, волчок, круговое движение) — в морской терминологии 1/32 полной окружности, а также одно из делений картушки компаса (расчерченной на 32 части) и соответственно одно из направлений относительно севера.
Существуют четыре основных румба:
• North — Север
• East — Восток
• South — Юг
• West — Запад
Четыре румба, производных от основных:
• North-West — Северо-запад
• North-East — Северо-восток
• South-East — Юго-восток
• South-West — Юго-запад
Обозначения румбов, отстоящих от основных на 11,25 градусов (1/32 полной окружности), получаются из обозначений одного из восьми выше перечисленных румбов, с добавлением после них слова «тень» или буквы «b» и названия основного направления, к которому отклоняется румб (например, NbE – румб, отклоненный от севера на 11,25 градусов к востоку).
Обозначения румбов, отстоящих от основных на 22,5 градуса (1/16 полной окружности), получаются из обозначений производных от основных румбов, с добавлением перед ними названия основного направления, к которому отклоняется румб (например, NNE – румб, отклоненный от севера на 22,5 градусов к востоку).
python — Преобразование километров (км) в десятичные градусы
Возможно, это не прямое решение, а скорее ссылка. Раньше я пытался использовать формулу гаверсинуса, но ее использование для вычисления множества ближайших n соседей становилось невыносимо длинным при использовании для тысяч точек.
Итак, я создал хэш-класс (или сопоставление?), который можно было бы поместить в двоичное дерево, чтобы обеспечить быстрый поиск. Он работает не с расстояниями, а с углами (широта, долгота).
Функция поиска работает, находя ближайшую точку в дереве, а затем проходя обратно вверх по дереву, пока не будет найдено n узлов.
geocode. py:
py:
единиц = [(31-q, 180,0/(2 ** q)) для q в диапазоне (32)]
def битовая_сумма (биты):
возвращаемая сумма([2**бит за бит в битах])
класс gpsash (объект):
def __init__(self, longitude = None, latitude = None, **kwargs):
если(kwargs):
if(kwargs.has_key("долгота") и kwargs.has_key("широта")):
self.longitude = геохеш (градусы = kwargs ["градусы"])
self.latitude = геохэш (градусы = kwargs ["хэш"])
еще:
если (долгота == Нет или широта == Нет):
self.longitude = геохэш (градусы = 0)
self.latitude = геохэш (градусы = 0)
еще:
self.longitude = геохэш (градусы = долгота)
self.latitude = геохэш (градусы = широта)
long_hash = self.longitude.bin_hash
lat_hash = self.широта.bin_hash
хэш_стр = ""
если (длина (long_hash) == длина (lat_hash)):
для i в диапазоне (len (long_hash)):
hash_str += (long_hash[i]+lat_hash[i])
self. other._hash) == 0)
еще:
вернуть ложь
деф кодировать(сам):
меньше = фильтр (лямбда (бит, угол): селф.градусы >= угол, единицы)
в сочетании = уменьшить (лямбда (биты, углы), (бит, угол): (биты + [бит], углы + угол) если ((углы + угол) <= само.градусы) еще (биты, углы), меньше, ( [], 0))
вернуть bit_sum (объединенный [0])
декодировать (сам):
меньше = фильтр (лямбда (бит, угол): self._hash> = (2 ** бит), единицы)
в сочетании = уменьшить (лямбда (биты, углы), (бит, угол): (биты + [бит], углы + угол) если ((битовая_сумма (биты + [бит])) <= self._hash) еще (биты, углы) , меньшее, ([], 0))
комбинированный возврат[1]
@имущество
деф хеш(я):
self._hash = self.encode()
вернуть "%08x" % self._hash
@имущество
определение inv_hash (я):
self._inv_hash = self.decode()
вернуть self._inv_hash
@имущество
определение bin_hash (я):
self._bin_hash = bin(self._hash)[2:].zfill(32)
вернуть self.
other._hash) == 0)
еще:
вернуть ложь
деф кодировать(сам):
меньше = фильтр (лямбда (бит, угол): селф.градусы >= угол, единицы)
в сочетании = уменьшить (лямбда (биты, углы), (бит, угол): (биты + [бит], углы + угол) если ((углы + угол) <= само.градусы) еще (биты, углы), меньше, ( [], 0))
вернуть bit_sum (объединенный [0])
декодировать (сам):
меньше = фильтр (лямбда (бит, угол): self._hash> = (2 ** бит), единицы)
в сочетании = уменьшить (лямбда (биты, углы), (бит, угол): (биты + [бит], углы + угол) если ((битовая_сумма (биты + [бит])) <= self._hash) еще (биты, углы) , меньшее, ([], 0))
комбинированный возврат[1]
@имущество
деф хеш(я):
self._hash = self.encode()
вернуть "%08x" % self._hash
@имущество
определение inv_hash (я):
self._inv_hash = self.decode()
вернуть self._inv_hash
@имущество
определение bin_hash (я):
self._bin_hash = bin(self._hash)[2:].zfill(32)
вернуть self. _bin_hash
класс gdict(объект):
'''
Базовый географический словарь
Критические компоненты взяты из Python26\Lib\UserDict.py
'''
__slots__ = ["родительский", "левый", "правый", "хэш_тип"]
hash_type = Нет
def __init__(я, ihash=Нет, iparent=Нет):
def set_helper (iparent, cur_hex, hex_list):
ret_bin_tree = self.__class__(Нет, родитель)
если (шестнадцатеричный_список):
ret_bin_tree.set_child (cur_hex, set_helper (ret_bin_tree, hex_list [0], hex_list [1:]))
вернуть ret_bin_tree
Элиф (cur_hex):
ret_bin_tree.set_child (cur_hex, ihash)
вернуть ret_bin_tree
сам.родитель = я
self.left = Нет
self.right = Нет
если (родитель! = Нет):
сам.родитель = родитель
если (экземпляр (ihash, self.hash_type)):
список = список (ihash.bin_hash)
если (длина (список) > 1):
ret_bin_tree = set_helper(self, ilist[1], ilist[2:])
если (ret_bin_tree):
self.
_bin_hash
класс gdict(объект):
'''
Базовый географический словарь
Критические компоненты взяты из Python26\Lib\UserDict.py
'''
__slots__ = ["родительский", "левый", "правый", "хэш_тип"]
hash_type = Нет
def __init__(я, ihash=Нет, iparent=Нет):
def set_helper (iparent, cur_hex, hex_list):
ret_bin_tree = self.__class__(Нет, родитель)
если (шестнадцатеричный_список):
ret_bin_tree.set_child (cur_hex, set_helper (ret_bin_tree, hex_list [0], hex_list [1:]))
вернуть ret_bin_tree
Элиф (cur_hex):
ret_bin_tree.set_child (cur_hex, ihash)
вернуть ret_bin_tree
сам.родитель = я
self.left = Нет
self.right = Нет
если (родитель! = Нет):
сам.родитель = родитель
если (экземпляр (ihash, self.hash_type)):
список = список (ihash.bin_hash)
если (длина (список) > 1):
ret_bin_tree = set_helper(self, ilist[1], ilist[2:])
если (ret_bin_tree):
self. set_child (список [0], ret_bin_tree)
def set_child (я, istr, ichild):
если(истр == "0"):
self.left = ребенок
Элиф (истр == "1"):
self.right = ребенок
def get_child (я, истр):
если(истр == "0"):
вернуть себя.слева
Элиф (истр == "1"):
вернуть себя.право
еще:
возвращаться ""
защита __repr__(сам):
def repr_print_helper (ibin_tree, fmt_str = "", depth = 1):
если (не экземпляр (ibin_tree, self.__class__)):
fmt_str += "\n"
fmt_str += ("%%%ds" % (глубина)) % ""
fmt_str += ibin_tree.__repr__()
еще:
if((ibin_tree.left != Нет и ibin_tree.right == Нет) или (ibin_tree.left == Нет и ibin_tree.right != Нет)):
если(ibin_tree.left != Нет):
fmt_str += "0"
fmt_str = repr_print_helper (ibin_tree.left, fmt_str, глубина + 1)
Элиф (ibin_tree.
set_child (список [0], ret_bin_tree)
def set_child (я, istr, ichild):
если(истр == "0"):
self.left = ребенок
Элиф (истр == "1"):
self.right = ребенок
def get_child (я, истр):
если(истр == "0"):
вернуть себя.слева
Элиф (истр == "1"):
вернуть себя.право
еще:
возвращаться ""
защита __repr__(сам):
def repr_print_helper (ibin_tree, fmt_str = "", depth = 1):
если (не экземпляр (ibin_tree, self.__class__)):
fmt_str += "\n"
fmt_str += ("%%%ds" % (глубина)) % ""
fmt_str += ibin_tree.__repr__()
еще:
if((ibin_tree.left != Нет и ibin_tree.right == Нет) или (ibin_tree.left == Нет и ibin_tree.right != Нет)):
если(ibin_tree.left != Нет):
fmt_str += "0"
fmt_str = repr_print_helper (ibin_tree.left, fmt_str, глубина + 1)
Элиф (ibin_tree. right! = Нет):
fmt_str += "1"
fmt_str = repr_print_helper (ibin_tree.right, fmt_str, глубина + 1)
еще:
если(ibin_tree.left != Нет):
fmt_str += "\n"
fmt_str += ("%%%ds" % (глубина - 1)) % ""
fmt_str += "0"
fmt_str = repr_print_helper (ibin_tree.left, fmt_str, глубина + 1)
если(ibin_tree.right != Нет):
fmt_str += "\n"
fmt_str += ("%%%ds" % (глубина - 1)) % ""
fmt_str += "1"
fmt_str = repr_print_helper (ibin_tree.right, fmt_str, глубина + 1)
вернуть fmt_str
вернуть repr_print_helper(я)
def find(self, ihash, itarget = 1):
классная квартира(список):
проходить
def find_helper_base (iparent, ibin_tree, ihash):
ret_find = Нет
если (экземпляр (ibin_tree, self.
right! = Нет):
fmt_str += "1"
fmt_str = repr_print_helper (ibin_tree.right, fmt_str, глубина + 1)
еще:
если(ibin_tree.left != Нет):
fmt_str += "\n"
fmt_str += ("%%%ds" % (глубина - 1)) % ""
fmt_str += "0"
fmt_str = repr_print_helper (ibin_tree.left, fmt_str, глубина + 1)
если(ibin_tree.right != Нет):
fmt_str += "\n"
fmt_str += ("%%%ds" % (глубина - 1)) % ""
fmt_str += "1"
fmt_str = repr_print_helper (ibin_tree.right, fmt_str, глубина + 1)
вернуть fmt_str
вернуть repr_print_helper(я)
def find(self, ihash, itarget = 1):
классная квартира(список):
проходить
def find_helper_base (iparent, ibin_tree, ihash):
ret_find = Нет
если (экземпляр (ibin_tree, self. hash_type)):
ret_find = родитель
Элиф (длина (ihash) > 0):
если (ibin_tree.get_child (ihash [0])):
ret_find = find_helper_base(ibin_tree, ibin_tree.get_child(ihash[0]), ihash[1:])
еще:
ret_find = ibin_tree
вернуть ret_find
def up_find (iflat, iparent, ibin_tree, ibias = "0"):
if((ibin_tree != iparent) и (len(iflat) < itarget)):
если (родитель.слева):
если (len (iflat) >= itarget):
возвращаться
если(iparent.left != ibin_tree):
down_find (iflat, iparent.left, ibias)
если (родитель.право):
если (len (iflat) >= itarget):
возвращаться
если(iparent.right != ibin_tree):
down_find(iflat, iparent.right, ibias)
up_find(iflat, ibin_tree.parent.parent, ibin_tree.
hash_type)):
ret_find = родитель
Элиф (длина (ihash) > 0):
если (ibin_tree.get_child (ihash [0])):
ret_find = find_helper_base(ibin_tree, ibin_tree.get_child(ihash[0]), ihash[1:])
еще:
ret_find = ibin_tree
вернуть ret_find
def up_find (iflat, iparent, ibin_tree, ibias = "0"):
if((ibin_tree != iparent) и (len(iflat) < itarget)):
если (родитель.слева):
если (len (iflat) >= itarget):
возвращаться
если(iparent.left != ibin_tree):
down_find (iflat, iparent.left, ibias)
если (родитель.право):
если (len (iflat) >= itarget):
возвращаться
если(iparent.right != ibin_tree):
down_find(iflat, iparent.right, ibias)
up_find(iflat, ibin_tree.parent.parent, ibin_tree. parent, ibias)
def down_find (iflat, ibin_tree, ibias = "0"):
если (len (iflat) >= itarget):
возвращаться
elif (экземпляр (ibin_tree, self.hash_type)):
iflat += [ibin_tree]
еще:
если (ибиас == "1"):
если(ibin_tree.left):
down_find(iflat, ibin_tree.left, ibias)
если(ibin_tree.right):
down_find(iflat, ibin_tree.right, ibias)
еще:
если(ibin_tree.right):
down_find(iflat, ibin_tree.right, ibias)
если(ibin_tree.left):
down_find(iflat, ibin_tree.left, ibias)
если (экземпляр (ihash, self.hash_type)):
плоский = плоский ()
хэш = ihash.bin_hash
base = find_helper_base(self, self.get_child(hasher[0]), hasher[1:])
если (база):
down_find (плоский, базовый)
смещение = более плоское [0].
parent, ibias)
def down_find (iflat, ibin_tree, ibias = "0"):
если (len (iflat) >= itarget):
возвращаться
elif (экземпляр (ibin_tree, self.hash_type)):
iflat += [ibin_tree]
еще:
если (ибиас == "1"):
если(ibin_tree.left):
down_find(iflat, ibin_tree.left, ibias)
если(ibin_tree.right):
down_find(iflat, ibin_tree.right, ibias)
еще:
если(ibin_tree.right):
down_find(iflat, ibin_tree.right, ibias)
если(ibin_tree.left):
down_find(iflat, ibin_tree.left, ibias)
если (экземпляр (ihash, self.hash_type)):
плоский = плоский ()
хэш = ihash.bin_hash
base = find_helper_base(self, self.get_child(hasher[0]), hasher[1:])
если (база):
down_find (плоский, базовый)
смещение = более плоское [0]. bin_hash[0]
up_find (плоский, базовый.родительский, базовый, смещение)
список возврата (плоский)
def слияние (я, from_bin_tree):
def merge_helper (to_bin_tree, from_bin_tree):
если (экземпляр (from_bin_tree, self.__class__)):
if(from_bin_tree.left != Нет):
если(to_bin_tree.left != Нет):
merge_helper(to_bin_tree.left, from_bin_tree.left)
еще:
from_bin_tree.left.parent = to_bin_tree
to_bin_tree.left = from_bin_tree.left
elif(from_bin_tree.right != Нет):
if(to_bin_tree.right != Нет):
merge_helper(to_bin_tree.right, from_bin_tree.right)
еще:
from_bin_tree.right.parent = to_bin_tree
to_bin_tree.right = from_bin_tree.right
merge_helper (я, from_bin_tree)
класс геодикт (gdict):
'''
Географический словарь
'''
hash_type = геохеш
def __init__(я, ihash=Нет, iparent=Нет):
gdict.
bin_hash[0]
up_find (плоский, базовый.родительский, базовый, смещение)
список возврата (плоский)
def слияние (я, from_bin_tree):
def merge_helper (to_bin_tree, from_bin_tree):
если (экземпляр (from_bin_tree, self.__class__)):
if(from_bin_tree.left != Нет):
если(to_bin_tree.left != Нет):
merge_helper(to_bin_tree.left, from_bin_tree.left)
еще:
from_bin_tree.left.parent = to_bin_tree
to_bin_tree.left = from_bin_tree.left
elif(from_bin_tree.right != Нет):
if(to_bin_tree.right != Нет):
merge_helper(to_bin_tree.right, from_bin_tree.right)
еще:
from_bin_tree.right.parent = to_bin_tree
to_bin_tree.right = from_bin_tree.right
merge_helper (я, from_bin_tree)
класс геодикт (gdict):
'''
Географический словарь
'''
hash_type = геохеш
def __init__(я, ihash=Нет, iparent=Нет):
gdict. __init__(я, ihash, iparent)
класс gpsdict(gdict):
'''
GPS-словарь
'''
hash_type = gpsash
def __init__(я, ihash=Нет, iparent=Нет):
gdict.__init__(я, ihash, iparent)
если(__name__ == "__main__"):
GPS = \
[
гпшаш(90, 90),
гпшаш(68, 24),
гпшаш(144, 60),
гпшаш(48, 91),
гпшаш(32, 105),
гпшаш(32, 150),
гпшаш(167, 20),
гпшаш(49, 116),
гпшаш(81, 82),
гпшаш(63, 79),
гпшаш(129, 76)
]
base_dict = gpsdict()
для cur_hash в GPS:
base_dict.merge (gpsdict (cur_hash))
print "Все места добавлены:"
распечатать base_dict
Распечатать ""
print "Попытка найти 3 ближайшие точки к:"
to_find = gpsash(60, 20)
напечатать to_find.__repr__()
найдено = base_dict.find (to_find, 3)
Распечатать ""
print "Обнаружено следующее:"
для x найдено:
распечатать x.__repr__()
__init__(я, ihash, iparent)
класс gpsdict(gdict):
'''
GPS-словарь
'''
hash_type = gpsash
def __init__(я, ihash=Нет, iparent=Нет):
gdict.__init__(я, ihash, iparent)
если(__name__ == "__main__"):
GPS = \
[
гпшаш(90, 90),
гпшаш(68, 24),
гпшаш(144, 60),
гпшаш(48, 91),
гпшаш(32, 105),
гпшаш(32, 150),
гпшаш(167, 20),
гпшаш(49, 116),
гпшаш(81, 82),
гпшаш(63, 79),
гпшаш(129, 76)
]
base_dict = gpsdict()
для cur_hash в GPS:
base_dict.merge (gpsdict (cur_hash))
print "Все места добавлены:"
распечатать base_dict
Распечатать ""
print "Попытка найти 3 ближайшие точки к:"
to_find = gpsash(60, 20)
напечатать to_find.__repr__()
найдено = base_dict.find (to_find, 3)
Распечатать ""
print "Обнаружено следующее:"
для x найдено:
распечатать x.__repr__()
Как перевести градусы в километры? – Reviews Wiki
com/embed/h5Uk8wFwy4Y» frameborder=»0″ allowfullscreen=»allowfullscreen» data-original-w=»720″ data-original-h=»520″>Аналогично, широта и долгота в метрах? На любой другой широте 1° долготы занимает: 111319,488*cos(широта) метров . Расстояние от Северного полюса до экватора около 10 000 км. Поскольку это охватывает 90 градусов широты, мы можем сделать вывод, что каждый градус широты составляет около 111,111 км или 111 111 метров.
Как перевести градусы в сантиметры?
- Как перевести градусы в сантиметры? …
- нельзя переводить градусы в см. …
- измерения, если они одного типа.
- На самом деле можно при определенных обстоятельствах. …
- измерение того, насколько колесо поворачивается от градусов до сантиметров, сейчас.
- ТО можно сделать.
- Просто найдите Окружность колеса * 360.
Сколько градусов составляет метр? Значение в десятичных градусах с точностью до 4 знаков после запятой соответствует 11,1 метрам (+/- 5,55 м) на экваторе. Значение в десятичных градусах с точностью до 5 знаков после запятой соответствует 1,11 метра на экваторе.
Значение в десятичных градусах с точностью до 5 знаков после запятой соответствует 1,11 метра на экваторе.
…
Точность.
| decimal places | degrees | distance |
|---|---|---|
| 0 | 1.0 | 111 km |
| 1 | 0.1 | 11.1 km |
| 2 | 0.01 | 1.11 km |
| 3 | 0,001 | 111 м |
• 24 мая 2011 г.
Во-вторых Сколько миль в градусе долготы? Расстояние между градусами долготы составляет около 60 морских миль на экваторе. Чем дальше на север или юг, тем меньше линии долготы сходятся к полюсам. Градусы широты всегда отстоят друг от друга на 60 морских миль. На экваторе сетка 1° долготы на 1° широты покрывает около 3600 квадратных миль.
Как перевести немецкие марки в метры?
com/embed/GlJ1PMIqkkE» frameborder=»0″ allowfullscreen=»allowfullscreen» data-original-w=»720″ data-original-h=»520″>то какое расстояние между двумя долготами? Самый широкий градус долготы находится на экваторе с расстоянием 69°.0,172 мили (111,321 км). Расстояние постепенно сокращается до нуля по мере того, как они встречаются на полюсах. На 40 градусах северной или южной долготы расстояние между градусами долготы составляет 53 мили (85 километров) .
Как считать градусы?
Каждый градус равен , разделенному на 60 равных частей, называемых минутами . Таким образом, семь с половиной градусов можно назвать 7 градусами и 30 минутами, записанными как 7° 30′. Каждая минута далее делится на 60 равных частей, называемых секундами, и, например, 2 градуса 5 минут 30 секунд записывается как 2° 5′ 30″.
Сколько дюймов в высоту составляет 30 градусов? Чтобы получить угол 30 градусов, вам нужно будет поднять изголовье кровати примерно на 41 дюйм … или вы можете спать на одной из наших клиньев для взрослых, которые поднимают верхнюю часть тела только до угла 30 градусов. У нас также есть клинья с малыми и большими степенями.
Какой угол равен 45 градусам?
Угол в 45 градусов составляет ровно половину угла в 90 градусов, образованного между двумя лучами. Это острый угол, и два угла, равные 45 градусам, образуют прямой угол градусов.0018 или угол 90 градусов. Мы знаем, что угол образуется, когда два луча встречаются в вершине.
Какое расстояние составляет 1 градус долготы? Один градус широты равен примерно 364 000 футов (69 миль), одна минута равна 6068 футам (1,15 мили), а одна секунда равна 101 футу. Один градус долготы равен 288 200 футов (54,6 мили) , одна минута равна 4800 футам (0,91 мили), а одна секунда равна 80 футам.
Как вы читаете широту и долготу?
com/embed/pAZUrlKk6CE» frameborder=»0″ allowfullscreen=»allowfullscreen» data-original-w=»720″ data-original-h=»520″>Сколько км составляет градус широты?
Приблизительные метрические эквиваленты градусов. На экваторе для долготы и широты в любом месте действительны следующие приближения: 1 = 111 км (или 60 морских миль)
Какое расстояние составляет 1 градус широты? Один градус широты равен приблизительно 364 000 футов (69 миль) , одна минута равна 6068 футам (1,15 мили), а одна секунда равна 101 футу. Один градус долготы равен 288 200 футам (54,6 мили), одна минута равна 4800 футам (0,91 миля), а одна секунда равна 80 футам.
Сколько градусов в миле? Каждый градус широты составляет примерно 69 миль (111 километров) друг от друга. Диапазон варьируется (из-за слегка эллипсоидной формы Земли) от 68,703 миль (110,567 км) на экваторе до 69,407 (111,699 км) на полюсах. Это удобно, потому что каждая минута (1/60 градуса) составляет примерно одну [морскую] милю.
Который находится на расстоянии 23,5 секунды от Земли?
Тропик Козерога расположен примерно на 23,5 градуса южной широты или на 23,5 градуса южнее экватора. Эта линия широты является южной границей области, именуемой тропиками. Эта линия отмечает самую дальнюю к югу точку, в которой солнце в полдень висит прямо вверх.
Как преобразовать DD в DMM? Чтобы преобразовать координаты широты и долготы в десятичных градусах в градусы с минутами и секундами или градусы с десятичными минутами, выполните следующие три шага:
- Возьмем целое число — это градусы.
- Умножьте десятичную часть на 60. Если вы хотите иметь десятичные минуты – вот они! …
- Умножьте остаток на 60.
Как перевести градусы в морские мили?
нм = град2нм( град , радиус ) преобразует расстояния из градусов в морские мили, измеренные по большому кругу на сфере с указанным радиусом.
Какое расстояние между двумя долготами и двумя широтами? По мере продвижения к полюсам расстояние между каждой линией долготы становится меньше, пока не сойдутся на Северном и Южном полюсах. Расстояние между долготами на экваторе такое же, как широта, примерно 69 миль . На 45 градусах северной или южной широты расстояние между ними составляет около 49 миль (79 км).
Расстояние между долготами на экваторе такое же, как широта, примерно 69 миль . На 45 градусах северной или южной широты расстояние между ними составляет около 49 миль (79 км).
Как рассчитать расстояние?
Чтобы определить расстояние, используйте формулу для расстояния d = st , или расстояние равно скорости, умноженной на время. Скорость и скорость похожи, поскольку они оба представляют некоторое расстояние в единицу времени, например мили в час или километры в час.
Как вычислить долготу? Земля делает один полный оборот (360º долготы) за один день. Следовательно, он поворачивается на один градус долготы за 1/360 дня, или каждые четыре минуты. Поэтому, чтобы рассчитать долготу, вам просто нужно определите разницу во времени между полуднем в вашем местоположении и полуднем в нулевом меридиане .
Что такое долгота в математике?
Воображаемые линии, идущие от полюса к полюсу . Они показывают положение восток-запад на Земле.
Быстрый перевод градусов Цельсия в градусы Фаренгейта для путешественников (плюс километры в мили!)
Эта статья может содержать ссылки на некоторых наших рекламных партнеров. Если вы нажмете на эти ссылки, мы можем получить компенсацию. Чтобы узнать больше о нашей политике в отношении рекламы, ознакомьтесь с нашим полным заявлением о раскрытии информации здесь.
Американские путешественники, это для вас! В этой статье объясняется, как быстро преобразовать градусы Цельсия в градусы Фаренгейта, когда вы путешествуете за границей. В качестве бонуса мы даже предложили несколько быстрых способов конвертации километров в мили. Наслаждаться!
Поднимите руку, если вы были в такой ситуации: вы в отпуске в другой стране . Вы просыпаетесь в своем отеле после спокойного сна и начинаете думать о том, как бы вы хотели провести свой день. Вы отправитесь на пляж, отправитесь в поход или посетите музей?
Если вы похожи на меня, ваш выбор может зависеть от погоды. Я имею в виду, что никто не хочет идти на пляж под дождем или гулять в жаркий день, верно? Итак, вы включаете телевизор или открываете приложение погоды на телефоне, чтобы узнать прогноз погоды, и… хммм… этого не может быть. Всего 27 градусов?!?
Я имею в виду, что никто не хочет идти на пляж под дождем или гулять в жаркий день, верно? Итак, вы включаете телевизор или открываете приложение погоды на телефоне, чтобы узнать прогноз погоды, и… хммм… этого не может быть. Всего 27 градусов?!?
Примерно в это время до вас, вероятно, доходит, что вы не имеете дело с морозами. Вместо этого вы имеете дело с этой надоедливой метрической системой.
Метрическая система
Почему, о, почему, о, почему кто-то когда-либо использовал чертову метрическую систему?
Что ж, согласно Википедии , метрическая система — это «международно принятая десятичная система измерения». Ключевая фраза здесь — «принято на международном уровне». Например, в основном в каждой стране мира используют его.
Но не мы! Здесь, в Америке, мы упрямы. Мы делаем все по-своему, и в этом сияющем городе на холме мы все еще питаем надежду, что старый способ измерения веса, расстояния и температуры возобладает!
К несчастью для американцев, эта битва была проиграна. Международное сообщество высказалось, и все они согласны с тем, что метрическая система — это правильный путь. Это также означает, что мы не синхронизированы с остальным миром, когда дело доходит до измерений.
Международное сообщество высказалось, и все они согласны с тем, что метрическая система — это правильный путь. Это также означает, что мы не синхронизированы с остальным миром, когда дело доходит до измерений.
В то время как мы по-прежнему мыслим в градусах Фаренгейта, футах, дюймах, фунтах и милях, люди, живущие в странах, которые используют метрическую систему, этого не делают. Вместо этого они используют градусы Цельсия, метры, сантиметры, килограммы и километры.
Это может показаться пустяком, но во время путешествия невозможность понять прогноз, ограничение скорости или расстояние до пункта назначения может довольно быстро надоесть. Не говоря уже о том, что это также может быть очень неловко, если это всплывет в разговоре с местными жителями. Я имею в виду, вы же не хотите быть в гостях у Дублина и не иметь возможности поддержать разговор, не так ли? В конце концов, погода — это универсальная тема для светской беседы.
К счастью, мы составили это удобное руководство по переводу градусов Цельсия в градусы Фаренгейта и километров в мили.
Быстрое и грязное преобразование градусов Цельсия в градусы Фаренгейта
Поверьте мне, когда наша семья путешествует по долине Луары во Франции, быть тупыми американцами, которые не могут измерить температуру, это отстой. К счастью, это больше не должны быть вы.
Если у вас нет под рукой телефона, калькулятора или компьютера, используйте эту быструю формулу для расчета перевода градусов Цельсия в градусы Фаренгейта:
Температура по Цельсию x 2 + 30 = приблизительная температура по Фаренгейту
Довольно просто, правда?
Например, если вы смотрите прогноз погоды, и он показывает 27 градусов по Цельсию, это 27 x 2 = 54 + 30 = 84. Итак, 27 градусов по Цельсию — это примерно 84 градуса по Фаренгейту. Другими словами, это довольно теплый день.
Имейте в виду, это только оценка. С повышением температуры формула становится менее точной. Но эй, вы не сообщаете о погоде; вы просто пытаетесь интерпретировать прогноз и не чувствовать себя идиотом. Так что для ваших целей эта формула вполне подойдет.
Так что для ваших целей эта формула вполне подойдет.
Цельсия в градусы Фаренгейта: реальная сделка
Если быть точным, фактическая формула преобразования градусов Цельсия в градусы Фаренгейта такова:
Температура по Цельсию x 1,8 + 32 = Температура по Фаренгейту к нашему примеру с 27 градусами Цельсия мы получаем:
27 x 1,8 = 48,6 + 32 = 81
Таким образом, 27 градусов Цельсия фактически равны 81 градусу Фаренгейта. Вы можете видеть, как это немного отличается от нашей оценки в 84 градуса, но это в общем случае.
Для справки в следующей таблице показан диапазон температур по Цельсию и их эквивалентов по Фаренгейту. Итак, в следующий раз, когда вы будете искать вещей, которые можно сделать в Лондоне , вы можете использовать эту удобную небольшую таблицу, чтобы решить, позволит ли это погода. Мы начали таблицу с -40 °C и дошли до 40 °C — будем надеяться, что вы не будете отдыхать при более экстремальных температурах, чем эти!
Таблица преобразования градусов Цельсия в градусы Фаренгейта (с округлением до целых градусов)
| Цельсия (°C) | Фаренгейта (°F) |
|---|---|
| -40 °C | -40 °F |
| -30 °C | -22 °F |
| -20°C | -4°F |
| -10 °C | 14 °F |
| -9°C | 16°F |
| -8°C | 18°F |
| -7°C | 19°F |
| -6 °C | 21 °F |
| -5°C | 23°F |
| -4°C | 25°F |
| -3 °C | 27 °F |
| -2 °C | 28 °F |
| -1°C | 30°F |
| 0 °С | 32 °F |
| 1°C | 34°F |
| 2 °C | 36 °F |
| 3 °C | 37 °F |
| 4 °С | 39 °F |
| 5°C | 41°F |
| 6°C | 43°F |
| 7°C | 45°F |
| 8°C | 46°F |
| 9°C | 48°F |
| 10°C | 50°F |
| 20 °C | 68 °F |
| 30 °C | 86 °F |
| 40 °C | 104 °F |
Километры в мили на лету
Теперь, когда вы понимаете преобразование градусов Цельсия в градусы Фаренгейта, давайте перейдем к преобразованию расстояния и скорости.
Точно так же, как преобразование температуры, непонимание скорости и расстояния может быть проблемой для американцев во время путешествия.
Позвольте мне сказать следующее: ограничение скорости на канадских автомагистралях определенно составляет , а не 100 миль в час (миль в час). 100 километров (км) в час — это совсем другое, и получается около 62 миль в час. Смешивание этого означает, что у вас, вероятно, будут проблемы с правоохранительными органами. Не знаю, как вы, а я не могу придумать более быстрого способа испортить отпуск, чем купить билет. (Дополнительные баллы, если вы поняли этот каламбур…)
Даже если вы не за рулем, полезно знать, сколько километров. Если кто-то говорит вам, что пункт назначения находится в 5 км, вы должны уметь придавать этому значение.
Вот несколько приемов для быстрого преобразования километров в мили:
5 миль = 8 км
Например, 50 миль = 80 км. Итак, если вы видите знак ограничения скорости, на котором написано 100 км в час, это означает около 60 миль в час.
Как нам получить эти числа? Если вы конвертируете километры в мили, вам нужно разделить километры на 8 и умножить на 5. Таким образом, 100/8 = примерно 12, умножить на 5 = 60.
Если вы переходите от миль к километрам, вам нужно разделить на 5 и умножить на 8. Это не точно, но достаточно близко.
Вот еще одна приблизительная оценка:
Км разделить на пять и затем умножить на 3 = приблизительное количество миль
Например, 75 км/5 = 15 x 3 = 45 миль
вы просто переворачиваете его. Разделите километраж на 3 и умножьте на 5, чтобы получить ответ.
Опять же, это не точно, но подходит для быстрой оценки.
Км в мили: реальная сделка
Если вы хотите придираться к этому, 1 км на самом деле равен 0,621 мили. Итак, чтобы перевести км в мили, вам просто нужно умножить его на 0,621. Теперь, если вы можете сделать это в уме на лету, вы намного лучше разбираетесь в математике, чем я!
С другой стороны, если вы не являетесь сверхчеловеком-математиком, вот таблица с (почти) точным преобразованием километров в мили, которую вы можете использовать для справки.
Преобразование км в мили (с округлением до одного десятичного знака)
| Километры | Мили |
|---|---|
| 1 | 0,6 |
| 5 | 3.1 |
| 10 | 6,2 |
| 15 | 9,3 |
| 20 | 12,4 |
| 25 | 15,5 |
| 30 | 18,6 |
| 35 | 21,7 |
| 40 | 24,9 |
| 45 | 28,0 |
| 50 | 31,1 |
| 55 | 34,2 |
| 60 | 37,2 |
| 65 | 40,4 |
| 70 | 43,5 |
| 75 | 46,6 |
| 80 | 49,7 |
| 85 | 52,8 |
| 90 | 55,9 |
| 95 | 59,0 |
| 100 | 62,1 |
| 105 | 65,2 |
| 110 | 68,4 |
| 115 | 71,5 |
| 120 | 74,6 |
Перевод метрических единиц для путешествий: последние мысли
Итак, у вас есть один быстрый способ конвертировать градусы Цельсия в градусы Фаренгейта и два простых способа конвертировать километры в мили.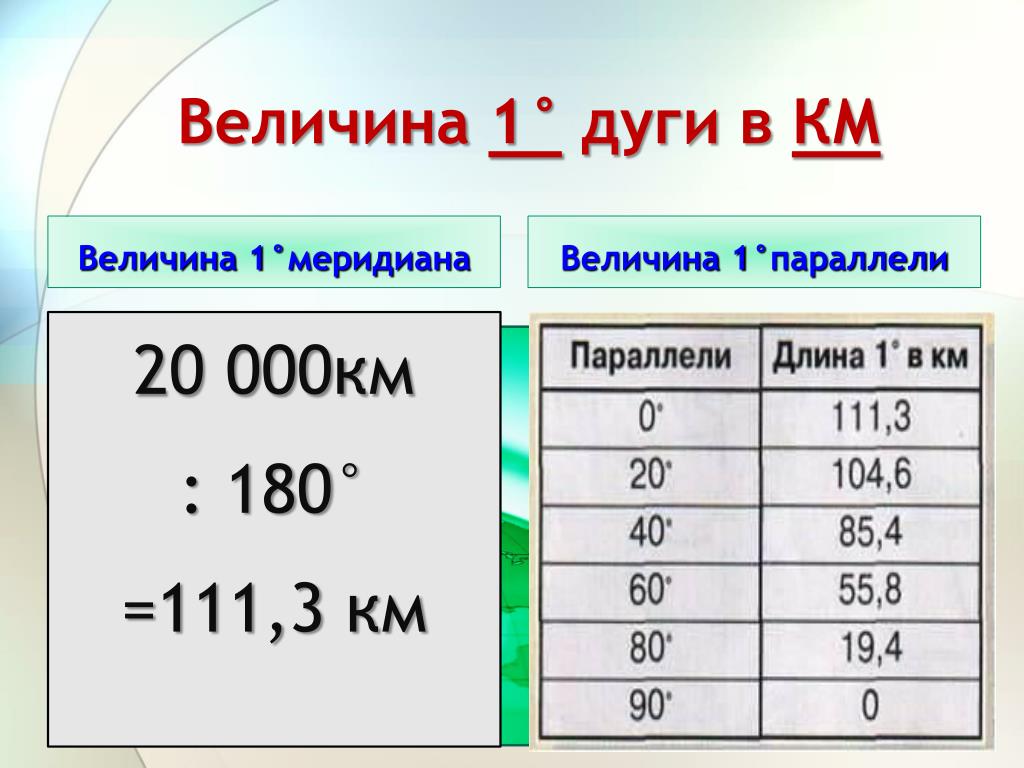 На всякий случай, если вам нужно быть более точным, у вас также есть настоящие формулы и соответствующие справочные таблицы.
На всякий случай, если вам нужно быть более точным, у вас также есть настоящие формулы и соответствующие справочные таблицы.
Самое главное, что в следующий раз, когда вы будете в Швейцарии (или в любой другой части мира), вам не нужно беспокоиться о том, чтобы быть тем невежественным американцем, который не может ориентироваться в проклятой метрической системе. Добро пожаловать 😉
У вас есть быстрый способ конвертировать градусы Цельсия в градусы Фаренгейта, который мы не рассмотрели? Дайте нам знать в комментариях ниже!
Преобразовать 360 морских миль в километры
Какова длина 360 морских миль? Как далеко 360 морских миль в километрах? Перевод 360 миль в км.
От АнгстремСантиметрыГаземыНогиФурлонгиДюймыКилометрыМетрМикроныМилиМиллиметрыНанометрыМорские милиПикометрыЯрды
До Ангстремы Сантиметры Морские сажени Ноги Фурлонги Дюймы Километры Метры Микроны Мили Миллиметры Нанометры Морские мили Пикометры Ярды 360 морских миль =
666,72 км
(точный результат)
Показать результат как NumberFraction (точное значение)
Морская миля — это единица длины, равная ровно 1852 метрам.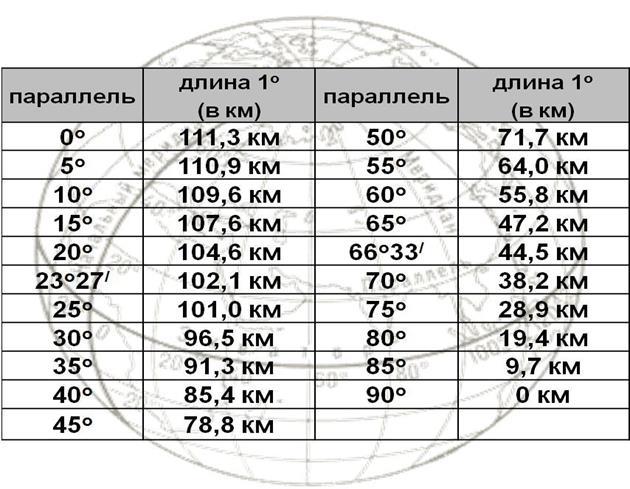 Первоначально он был основан на одной минуте (1/60) градуса широты.
Первоначально он был основан на одной минуте (1/60) градуса широты.
Километр или километр — это единица длины, равная 1000 метрам или примерно 0,621 мили. В большинстве стран мира это самая распространенная единица измерения расстояния между местами.
Перевод морских миль в километры
(некоторые результаты округлены)
| морских миль | км |
|---|---|
| 360,00 | 666,72 |
| 360,05 | 666,81 |
| 360,10 | 666,91 |
| 360,15 | 667,00 |
| 360,20 | 667,09 |
| 360,25 | 667,18 |
| 360,30 | 667,28 |
| 360,35 | 667,37 |
| 360,40 | 667,46 |
| 360,45 | 667,55 |
| 360,50 | 667,65 |
| 360,55 | 667,74 |
| 360,60 | 667,83 |
| 360,65 | 667,92 |
| 360,70 | 668,02 |
| 360,75 | 668,11 |
| 360,80 | 668,20 |
| 360,85 | 668,29 |
| 360,90 | 668,39 |
| 360,95 | 668,48 |
| 361,00 | 668,57 |
| 361,05 | 668,66 |
| 361,10 | 668,76 |
| 361,15 | 668,85 |
| 361,20 | 668,94 |
| нм | км |
|---|---|
| 361,25 | 669,04 |
| 361,30 | 669,13 |
| 361,35 | 669,22 |
| 361,40 | 669,31 |
| 361,45 | 669,41 |
| 361,50 | 669,50 |
| 361,55 | 669,59 |
| 361,60 | 669,68 |
| 361,65 | 669,78 |
| 361,70 | 669,87 |
| 361,75 | 669,96 |
| 361,80 | 670,05 |
| 361,85 | 670,15 |
| 361,90 | 670,24 |
| 361,95 | 670,33 |
| 362,00 | 670,42 |
| 362,05 | 670,52 |
| 362,10 | 670,61 |
362.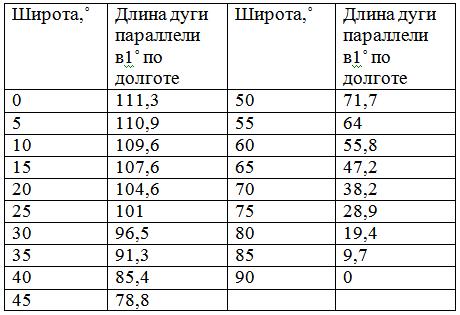 15 15 | 670,70 |
| 362,20 | 670,79 |
| 362,25 | 670,89 |
| 362,30 | 670,98 |
| 362,35 | 671,07 |
| 362,40 | 671,16 |
| 362,45 | 671.26 |
| нм | км |
|---|---|
| 362,50 | 671,35 |
| 362,55 | 671,44 |
| 362,60 | 671,54 |
| 362,65 | 671,63 |
| 362,70 | 671,72 |
| 362,75 | 671,81 |
| 362,80 | 671,91 |
| 362,85 | 672,00 |
| 362,90 | 672,09 |
| 362,95 | 672,18 |
| 363,00 | 672,28 |
| 363,05 | 672,37 |
| 363,10 | 672,46 |
| 363,15 | 672,55 |
| 363,20 | 672,65 |
| 363,25 | 672,74 |
| 363,30 | 672,83 |
| 363,35 | 672,92 |
| 363,40 | 673,02 |
| 363,45 | 673,11 |
| 363,50 | 673,20 |
| 363,55 | 673,29 |
| 363,60 | 673,39 |
| 363,65 | 673,48 |
| 363,70 | 673,57 |
| нм | км |
|---|---|
| 363,75 | 673,67 |
| 363,80 | 673,76 |
| 363,85 | 673,85 |
| 363,90 | 673,94 |
| 363,95 | 674,04 |
| 364,00 | 674,13 |
| 364,05 | 674,22 |
| 364,10 | 674,31 |
| 364,15 | 674,41 |
| 364,20 | 674,50 |
| 364,25 | 674,59 |
| 364,30 | 674,68 |
| 364,35 | 674,78 |
| 364,40 | 674,87 |
| 364,45 | 674,96 |
| 364,50 | 675,05 |
| 364,55 | 675,15 |
| 364,60 | 675,24 |
| 364,65 | 675,33 |
| 364,70 | 675,42 |
| 364,75 | 675,52 |
| 364,80 | 675,61 |
| 364,85 | 675,70 |
| 364,90 | 675,79 |
| 364,95 | 675,89 |
Перевести 112 километров в морские мили
Какова длина 112 километров? Что такое 112 километров в морских милях? Преобразование 112 км в нм.
От АнгстремСантиметрыГаземыНогиФурлонгиДюймыКилометрыМетрМикроныМилиМиллиметрыНанометрыМорские милиПикометрыЯрды
До Ангстремы Сантиметры Морские сажени Ноги Фурлонги Дюймы Километры Метры Микроны Мили Миллиметры Нанометры Морские мили Пикометры Ярды 112 километров =
60,475162 Морские мили
(округлено до 8 цифр)
Отобразить результат как NumberFraction (точное значение)
Километр или километр — это единица длины, равная 1000 метрам или примерно 0,621 мили. В большинстве стран мира это самая распространенная единица измерения расстояния между местами.
Морская миля — это единица длины, равная ровно 1852 метрам. Первоначально он был основан на одной минуте (1/60) градуса широты.
Перевод километров в морские мили
(некоторые результаты округлены)
| км | миль |
|---|---|
| 112.00 | 60,475 |
| 112,01 | 60,481 |
| 112,02 | 60,486 |
| 112,03 | 60,491 |
| 112,04 | 60,497 |
| 112,05 | 60,502 |
| 112,06 | 60,508 |
| 112,07 | 60,513 |
| 112,08 | 60,518 |
112.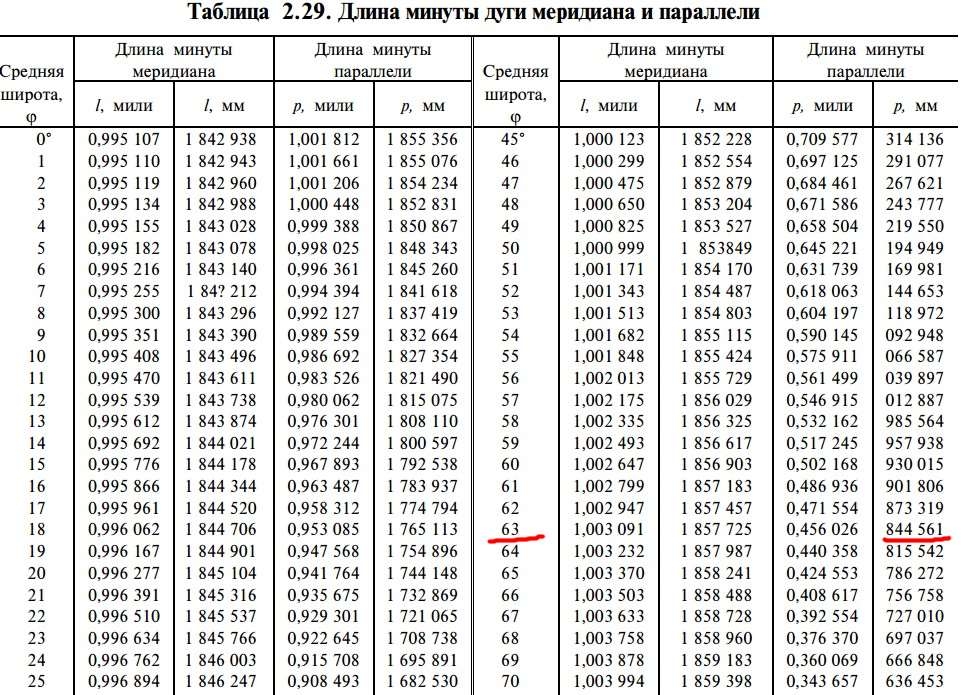 09 09 | 60,524 |
| 112,10 | 60,529 |
| 112,11 | 60,535 |
| 112,12 | 60,540 |
| 112,13 | 60,545 |
| 112,14 | 60,551 |
| 112,15 | 60,556 |
| 112,16 | 60,562 |
| 112,17 | 60,567 |
| 112.18 | 60,572 |
| 112,19 | 60,578 |
| 112,20 | 60,583 |
| 112,21 | 60,589 |
| 112,22 | 60,594 |
| 112,23 | 60,599 |
| 112,24 | 60.605 |
| км | миль |
|---|---|
| 112,25 | 60,610 |
| 112,26 | 60,616 |
| 112,27 | 60,621 |
| 112,28 | 60,626 |
| 112,29 | 60,632 |
| 112,30 | 60,637 |
| 112,31 | 60,643 |
| 112,32 | 60,648 |
| 112,33 | 60,653 |
| 112,34 | 60,659 |
| 112,35 | 60,664 |
| 112,36 | 60,670 |
| 112,37 | 60,675 |
| 112,38 | 60,680 |
| 112,39 | 60,686 |
| 112,40 | 60,691 |
| 112,41 | 60,697 |
| 112,42 | 60.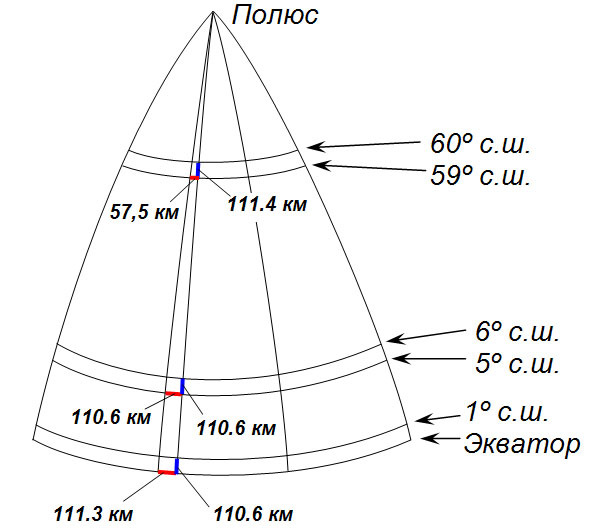 702 702 |
| 112,43 | 60,707 |
| 112,44 | 60,713 |
| 112,45 | 60,718 |
| 112,46 | 60,724 |
| 112,47 | 60,729 |
| 112,48 | 60,734 |
| 112,49 | 60.740 |
| км | миль |
|---|---|
| 112,50 | 60,745 |
| 112,51 | 60,751 |
| 112,52 | 60,756 |
| 112,53 | 60,761 |
| 112,54 | 60,767 |
| 112,55 | 60,772 |
| 112,56 | 60,778 |
| 112,57 | 60,783 |
| 112,58 | 60,788 |
| 112,59 | 60,794 |
| 112,60 | 60,799 |
| 112,61 | 60,805 |
| 112,62 | 60,810 |
| 112,63 | 60,815 |
| 112,64 | 60,821 |
| 112,65 | 60,826 |
| 112,66 | 60,832 |
| 112,67 | 60,837 |
| 112,68 | 60,842 |
| 112,69 | 60,848 |
| 112,70 | 60,853 |
| 112,71 | 60,859 |
| 112,72 | 60,864 |
| 112,73 | 60,869 |
| 112,74 | 60. 875 875 |
| км | миль |
|---|---|
| 112,75 | 60,880 |
| 112,76 | 60,886 |
| 112,77 | 60,891 |
| 112,78 | 60,896 |
| 112,79 | 60,902 |
| 112,80 | 60,907 |
| 112,81 | 60,913 |
| 112,82 | 60,918 |
| 112,83 | 60,923 |
| 112,84 | 60,929 |
| 112,85 | 60,934 |
| 112,86 | 60,940 |
| 112,87 | 60,945 |
| 112,88 | 60,950 |
| 112,89 | 60,956 |
| 112,90 | 60,961 |
| 112,91 | 60,967 |
| 112,92 | 60,972 |
| 112,93 | 60,977 |
| 112,94 | 60,983 |
| 112,95 | 60,988 |
| 112,96 | 60,994 |
| 112,97 | 60,999 |
| 112,98 | 61. 004 004 |
| 112,99 | 61.010 |
OpenStax College Physics Solution, глава 3, задача 21 (задачи и упражнения)
9\circ$.Вопрос от OpenStax находится под лицензией СС BY 4.0.
Окончательный ответ
а) Юг: $18,4 \textrm{ км}$, Запад $26,2 \textrm{ км}$
б) ЮЗ: $31,5 \textrm{ км}$, СЗ: $5,6 \textrm{ км}$
Примечание: в части B Шон ошибочно перевел единицы измерения на метры вместо километров. Все цифры правильные, но, пожалуйста, думайте о «км», когда видите «м».
Видеорешение
Зарегистрируйтесь для просмотра этого видеорешения!
Начать мою бесплатную неделю
Trustpilot
Рейтинг
ПлохоНе так уж плохоСреднеХорошоОчень хорошо
4 голоса со средней оценкой 3,3.
Скриншоты калькулятора
Стенограмма видео
Это ответы по физике в колледже с Шоном Дычко. Таким образом, вы пролетите 32,0 км в направлении 35,0 градусов к югу от запада. Итак, вот этот синий вектор, и вопрос задает нам вопрос: если бы вам нужно было добраться туда, сначала двигаясь на юг, а затем прямо на запад, как далеко вам нужно было бы идти на юг, а затем на запад. Так что это то же самое, что спросить нас, каковы компоненты этого вектора и направления y и x. Таким образом, южная часть вашей поездки, ваш первый этап вашей поездки, идущий прямо на юг, будет расстоянием, умноженным на синус 9.2077 тета , это 32,0 километра, умноженное на синус 35, что дает нам 18,4 километра к югу. Затем на запад вам нужно будет пройти д раз, потому что тета . Вам нужно будет пройти 32 километра, умноженное на 35, потому что эта сторона является смежной стороной этого прямоугольного треугольника. Вот почему мы используем косинус, чтобы найти их. Это 26,2 километра. Затем для части B говорится, что предположим, вы сначала прошли под углом 45 градусов к югу от запада, а затем пошли под углом 45 градусов к западу от севера, как далеко вам придется пройти на каждом этапе, чтобы достичь того же пункта назначения.
Таким образом, вы пролетите 32,0 км в направлении 35,0 градусов к югу от запада. Итак, вот этот синий вектор, и вопрос задает нам вопрос: если бы вам нужно было добраться туда, сначала двигаясь на юг, а затем прямо на запад, как далеко вам нужно было бы идти на юг, а затем на запад. Так что это то же самое, что спросить нас, каковы компоненты этого вектора и направления y и x. Таким образом, южная часть вашей поездки, ваш первый этап вашей поездки, идущий прямо на юг, будет расстоянием, умноженным на синус 9.2077 тета , это 32,0 километра, умноженное на синус 35, что дает нам 18,4 километра к югу. Затем на запад вам нужно будет пройти д раз, потому что тета . Вам нужно будет пройти 32 километра, умноженное на 35, потому что эта сторона является смежной стороной этого прямоугольного треугольника. Вот почему мы используем косинус, чтобы найти их. Это 26,2 километра. Затем для части B говорится, что предположим, вы сначала прошли под углом 45 градусов к югу от запада, а затем пошли под углом 45 градусов к западу от севера, как далеко вам придется пройти на каждом этапе, чтобы достичь того же пункта назначения. Так что это то же самое, что взять повернутую систему координат, а затем найти компоненты в этой новой системе координат. Итак, мы повернули эту систему координат на 45 градусов и сначала выясним, что такое 9.Компонент 2077 x в этой повернутой системе координат, которую я обозначил как d, индекс sw , или расстояние, или смещение, знаете, юго-западная составляющая. Тогда здесь у нас есть 45 градусов к западу от севера. Вот север, а там 45 градусов. Это западная составляющая севера здесь. Итак, сначала вам нужно идти на юго-запад на расстояние, равное общему расстоянию, умноженному на косинус тета-простое число и тета-простое число — это то немногое, что находится в этом новом прямоугольном треугольнике, который мы создали с помощью осей нашей повернутой системы координат. и вектор синим цветом. Итак, dsw является соседним катетом этого треугольника, поэтому мы используем косинус, чтобы найти его, и этот угол будет равен 10 градусам, потому что ось здесь для x простое число находится под углом 45 градусов по отношению к исходной оси x, а этот вектор находится в 35 градусов по отношению к этому, той же исходной оси X, которая оставляет 10 градусов, оставшихся для этого небольшого кусочка здесь, 45 минус 35 равно 10.
Так что это то же самое, что взять повернутую систему координат, а затем найти компоненты в этой новой системе координат. Итак, мы повернули эту систему координат на 45 градусов и сначала выясним, что такое 9.Компонент 2077 x в этой повернутой системе координат, которую я обозначил как d, индекс sw , или расстояние, или смещение, знаете, юго-западная составляющая. Тогда здесь у нас есть 45 градусов к западу от севера. Вот север, а там 45 градусов. Это западная составляющая севера здесь. Итак, сначала вам нужно идти на юго-запад на расстояние, равное общему расстоянию, умноженному на косинус тета-простое число и тета-простое число — это то немногое, что находится в этом новом прямоугольном треугольнике, который мы создали с помощью осей нашей повернутой системы координат. и вектор синим цветом. Итак, dsw является соседним катетом этого треугольника, поэтому мы используем косинус, чтобы найти его, и этот угол будет равен 10 градусам, потому что ось здесь для x простое число находится под углом 45 градусов по отношению к исходной оси x, а этот вектор находится в 35 градусов по отношению к этому, той же исходной оси X, которая оставляет 10 градусов, оставшихся для этого небольшого кусочка здесь, 45 минус 35 равно 10.


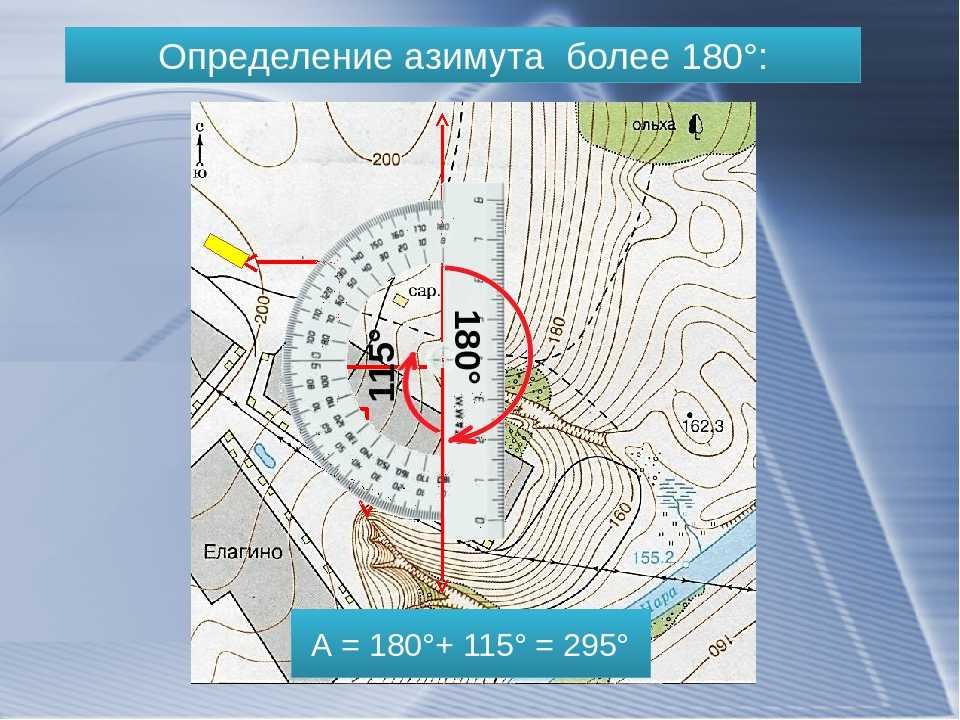 В северном полушарии конец тени от предмета показывает направление на север, в южном – на юг.
В северном полушарии конец тени от предмета показывает направление на север, в южном – на юг.
 ш.; острова Кермадек – в Тихом океане на 30° параллели к югу от экватора, их широта примерно 30° ю. ш.
ш.; острова Кермадек – в Тихом океане на 30° параллели к югу от экватора, их широта примерно 30° ю. ш.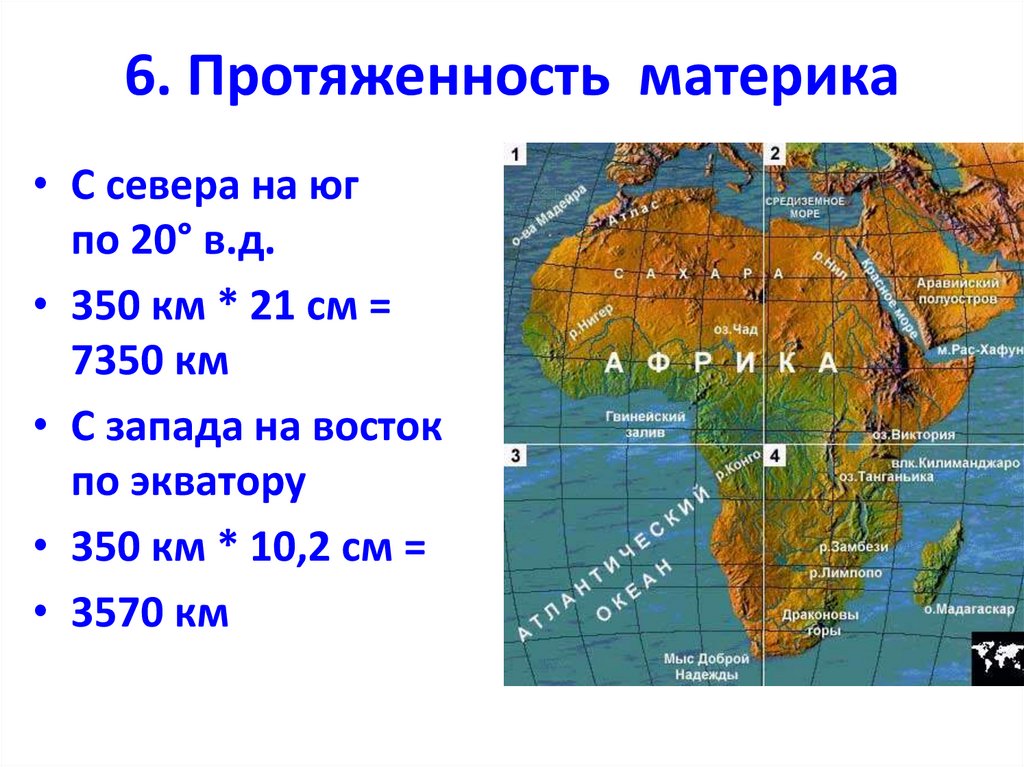 К востоку от нулевого меридиана до 180° отсчитывают восточную долготу (в. д.), к западу – западную (з. д.). На картах меридианы надписывают на экваторе или верхней и нижней рамках карты, а на глобусе – на экваторе. Меридианы, как и параллели, проводят через одинаковое число градусов. Например, Санкт-Петербург расположен на 30 меридиане к востоку от нулевого меридиана, его географическая долгота 30° в. д.; Мехико – на 100 меридиане к западу от нулевого меридиана, его долгота 100° з. д.
К востоку от нулевого меридиана до 180° отсчитывают восточную долготу (в. д.), к западу – западную (з. д.). На картах меридианы надписывают на экваторе или верхней и нижней рамках карты, а на глобусе – на экваторе. Меридианы, как и параллели, проводят через одинаковое число градусов. Например, Санкт-Петербург расположен на 30 меридиане к востоку от нулевого меридиана, его географическая долгота 30° в. д.; Мехико – на 100 меридиане к западу от нулевого меридиана, его долгота 100° з. д. Географические координаты записывают в целых градусах и минутах с указанием широты и долготы. При этом 1º = 60 мин (60′), а0,1° = 6′, 0,2°=12′ и т. д.
Географические координаты записывают в целых градусах и минутах с указанием широты и долготы. При этом 1º = 60 мин (60′), а0,1° = 6′, 0,2°=12′ и т. д.
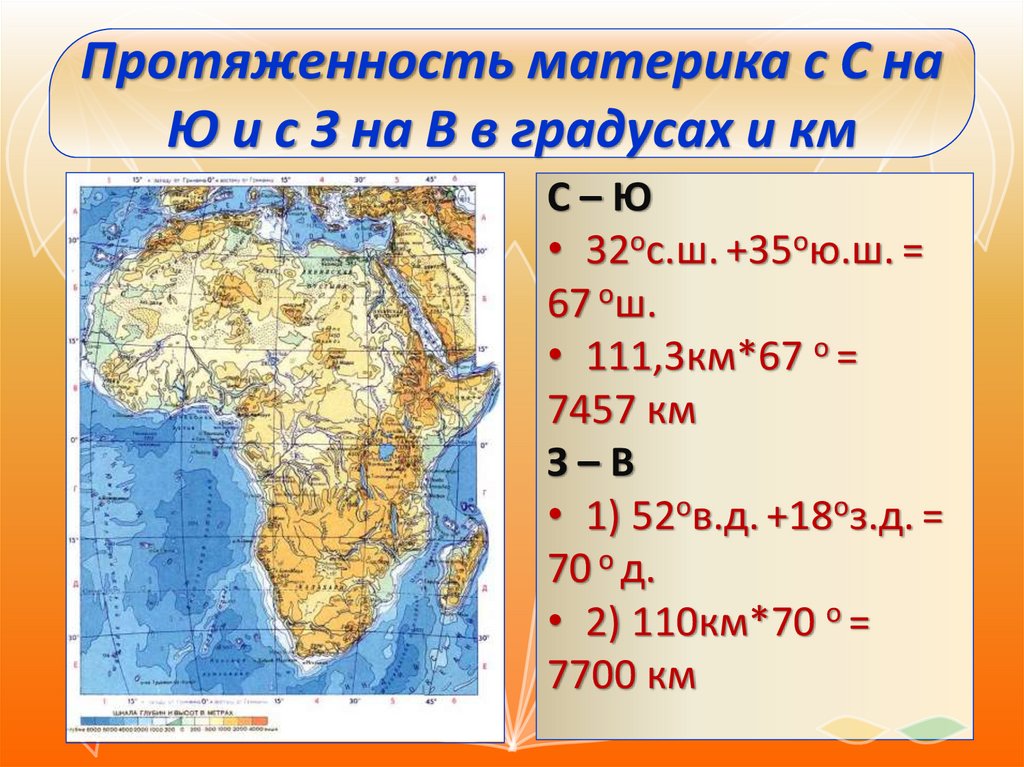 other._hash) == 0)
еще:
вернуть ложь
деф кодировать(сам):
меньше = фильтр (лямбда (бит, угол): селф.градусы >= угол, единицы)
в сочетании = уменьшить (лямбда (биты, углы), (бит, угол): (биты + [бит], углы + угол) если ((углы + угол) <= само.градусы) еще (биты, углы), меньше, ( [], 0))
вернуть bit_sum (объединенный [0])
декодировать (сам):
меньше = фильтр (лямбда (бит, угол): self._hash> = (2 ** бит), единицы)
в сочетании = уменьшить (лямбда (биты, углы), (бит, угол): (биты + [бит], углы + угол) если ((битовая_сумма (биты + [бит])) <= self._hash) еще (биты, углы) , меньшее, ([], 0))
комбинированный возврат[1]
@имущество
деф хеш(я):
self._hash = self.encode()
вернуть "%08x" % self._hash
@имущество
определение inv_hash (я):
self._inv_hash = self.decode()
вернуть self._inv_hash
@имущество
определение bin_hash (я):
self._bin_hash = bin(self._hash)[2:].zfill(32)
вернуть self.
other._hash) == 0)
еще:
вернуть ложь
деф кодировать(сам):
меньше = фильтр (лямбда (бит, угол): селф.градусы >= угол, единицы)
в сочетании = уменьшить (лямбда (биты, углы), (бит, угол): (биты + [бит], углы + угол) если ((углы + угол) <= само.градусы) еще (биты, углы), меньше, ( [], 0))
вернуть bit_sum (объединенный [0])
декодировать (сам):
меньше = фильтр (лямбда (бит, угол): self._hash> = (2 ** бит), единицы)
в сочетании = уменьшить (лямбда (биты, углы), (бит, угол): (биты + [бит], углы + угол) если ((битовая_сумма (биты + [бит])) <= self._hash) еще (биты, углы) , меньшее, ([], 0))
комбинированный возврат[1]
@имущество
деф хеш(я):
self._hash = self.encode()
вернуть "%08x" % self._hash
@имущество
определение inv_hash (я):
self._inv_hash = self.decode()
вернуть self._inv_hash
@имущество
определение bin_hash (я):
self._bin_hash = bin(self._hash)[2:].zfill(32)
вернуть self. _bin_hash
класс gdict(объект):
'''
Базовый географический словарь
Критические компоненты взяты из Python26\Lib\UserDict.py
'''
__slots__ = ["родительский", "левый", "правый", "хэш_тип"]
hash_type = Нет
def __init__(я, ihash=Нет, iparent=Нет):
def set_helper (iparent, cur_hex, hex_list):
ret_bin_tree = self.__class__(Нет, родитель)
если (шестнадцатеричный_список):
ret_bin_tree.set_child (cur_hex, set_helper (ret_bin_tree, hex_list [0], hex_list [1:]))
вернуть ret_bin_tree
Элиф (cur_hex):
ret_bin_tree.set_child (cur_hex, ihash)
вернуть ret_bin_tree
сам.родитель = я
self.left = Нет
self.right = Нет
если (родитель! = Нет):
сам.родитель = родитель
если (экземпляр (ihash, self.hash_type)):
список = список (ihash.bin_hash)
если (длина (список) > 1):
ret_bin_tree = set_helper(self, ilist[1], ilist[2:])
если (ret_bin_tree):
self.
_bin_hash
класс gdict(объект):
'''
Базовый географический словарь
Критические компоненты взяты из Python26\Lib\UserDict.py
'''
__slots__ = ["родительский", "левый", "правый", "хэш_тип"]
hash_type = Нет
def __init__(я, ihash=Нет, iparent=Нет):
def set_helper (iparent, cur_hex, hex_list):
ret_bin_tree = self.__class__(Нет, родитель)
если (шестнадцатеричный_список):
ret_bin_tree.set_child (cur_hex, set_helper (ret_bin_tree, hex_list [0], hex_list [1:]))
вернуть ret_bin_tree
Элиф (cur_hex):
ret_bin_tree.set_child (cur_hex, ihash)
вернуть ret_bin_tree
сам.родитель = я
self.left = Нет
self.right = Нет
если (родитель! = Нет):
сам.родитель = родитель
если (экземпляр (ihash, self.hash_type)):
список = список (ihash.bin_hash)
если (длина (список) > 1):
ret_bin_tree = set_helper(self, ilist[1], ilist[2:])
если (ret_bin_tree):
self. set_child (список [0], ret_bin_tree)
def set_child (я, istr, ichild):
если(истр == "0"):
self.left = ребенок
Элиф (истр == "1"):
self.right = ребенок
def get_child (я, истр):
если(истр == "0"):
вернуть себя.слева
Элиф (истр == "1"):
вернуть себя.право
еще:
возвращаться ""
защита __repr__(сам):
def repr_print_helper (ibin_tree, fmt_str = "", depth = 1):
если (не экземпляр (ibin_tree, self.__class__)):
fmt_str += "\n"
fmt_str += ("%%%ds" % (глубина)) % ""
fmt_str += ibin_tree.__repr__()
еще:
if((ibin_tree.left != Нет и ibin_tree.right == Нет) или (ibin_tree.left == Нет и ibin_tree.right != Нет)):
если(ibin_tree.left != Нет):
fmt_str += "0"
fmt_str = repr_print_helper (ibin_tree.left, fmt_str, глубина + 1)
Элиф (ibin_tree.
set_child (список [0], ret_bin_tree)
def set_child (я, istr, ichild):
если(истр == "0"):
self.left = ребенок
Элиф (истр == "1"):
self.right = ребенок
def get_child (я, истр):
если(истр == "0"):
вернуть себя.слева
Элиф (истр == "1"):
вернуть себя.право
еще:
возвращаться ""
защита __repr__(сам):
def repr_print_helper (ibin_tree, fmt_str = "", depth = 1):
если (не экземпляр (ibin_tree, self.__class__)):
fmt_str += "\n"
fmt_str += ("%%%ds" % (глубина)) % ""
fmt_str += ibin_tree.__repr__()
еще:
if((ibin_tree.left != Нет и ibin_tree.right == Нет) или (ibin_tree.left == Нет и ibin_tree.right != Нет)):
если(ibin_tree.left != Нет):
fmt_str += "0"
fmt_str = repr_print_helper (ibin_tree.left, fmt_str, глубина + 1)
Элиф (ibin_tree.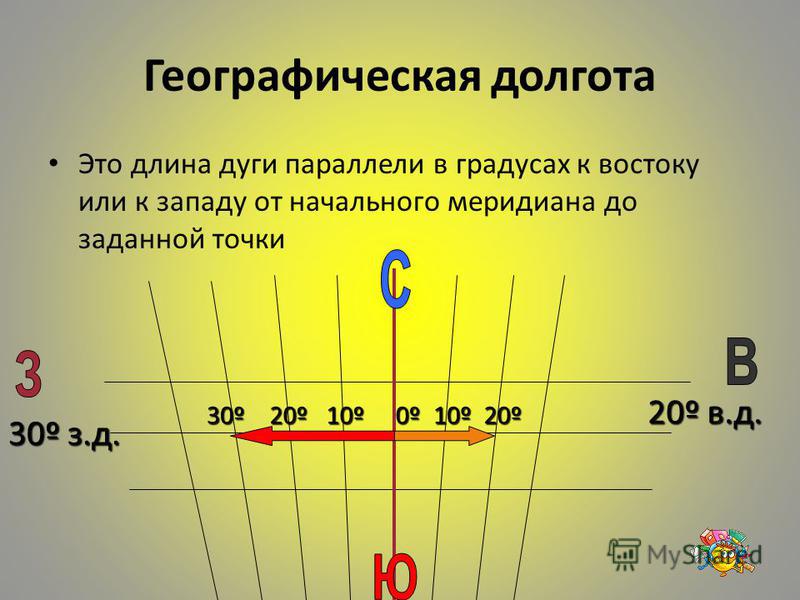 right! = Нет):
fmt_str += "1"
fmt_str = repr_print_helper (ibin_tree.right, fmt_str, глубина + 1)
еще:
если(ibin_tree.left != Нет):
fmt_str += "\n"
fmt_str += ("%%%ds" % (глубина - 1)) % ""
fmt_str += "0"
fmt_str = repr_print_helper (ibin_tree.left, fmt_str, глубина + 1)
если(ibin_tree.right != Нет):
fmt_str += "\n"
fmt_str += ("%%%ds" % (глубина - 1)) % ""
fmt_str += "1"
fmt_str = repr_print_helper (ibin_tree.right, fmt_str, глубина + 1)
вернуть fmt_str
вернуть repr_print_helper(я)
def find(self, ihash, itarget = 1):
классная квартира(список):
проходить
def find_helper_base (iparent, ibin_tree, ihash):
ret_find = Нет
если (экземпляр (ibin_tree, self.
right! = Нет):
fmt_str += "1"
fmt_str = repr_print_helper (ibin_tree.right, fmt_str, глубина + 1)
еще:
если(ibin_tree.left != Нет):
fmt_str += "\n"
fmt_str += ("%%%ds" % (глубина - 1)) % ""
fmt_str += "0"
fmt_str = repr_print_helper (ibin_tree.left, fmt_str, глубина + 1)
если(ibin_tree.right != Нет):
fmt_str += "\n"
fmt_str += ("%%%ds" % (глубина - 1)) % ""
fmt_str += "1"
fmt_str = repr_print_helper (ibin_tree.right, fmt_str, глубина + 1)
вернуть fmt_str
вернуть repr_print_helper(я)
def find(self, ihash, itarget = 1):
классная квартира(список):
проходить
def find_helper_base (iparent, ibin_tree, ihash):
ret_find = Нет
если (экземпляр (ibin_tree, self. hash_type)):
ret_find = родитель
Элиф (длина (ihash) > 0):
если (ibin_tree.get_child (ihash [0])):
ret_find = find_helper_base(ibin_tree, ibin_tree.get_child(ihash[0]), ihash[1:])
еще:
ret_find = ibin_tree
вернуть ret_find
def up_find (iflat, iparent, ibin_tree, ibias = "0"):
if((ibin_tree != iparent) и (len(iflat) < itarget)):
если (родитель.слева):
если (len (iflat) >= itarget):
возвращаться
если(iparent.left != ibin_tree):
down_find (iflat, iparent.left, ibias)
если (родитель.право):
если (len (iflat) >= itarget):
возвращаться
если(iparent.right != ibin_tree):
down_find(iflat, iparent.right, ibias)
up_find(iflat, ibin_tree.parent.parent, ibin_tree.
hash_type)):
ret_find = родитель
Элиф (длина (ihash) > 0):
если (ibin_tree.get_child (ihash [0])):
ret_find = find_helper_base(ibin_tree, ibin_tree.get_child(ihash[0]), ihash[1:])
еще:
ret_find = ibin_tree
вернуть ret_find
def up_find (iflat, iparent, ibin_tree, ibias = "0"):
if((ibin_tree != iparent) и (len(iflat) < itarget)):
если (родитель.слева):
если (len (iflat) >= itarget):
возвращаться
если(iparent.left != ibin_tree):
down_find (iflat, iparent.left, ibias)
если (родитель.право):
если (len (iflat) >= itarget):
возвращаться
если(iparent.right != ibin_tree):
down_find(iflat, iparent.right, ibias)
up_find(iflat, ibin_tree.parent.parent, ibin_tree. parent, ibias)
def down_find (iflat, ibin_tree, ibias = "0"):
если (len (iflat) >= itarget):
возвращаться
elif (экземпляр (ibin_tree, self.hash_type)):
iflat += [ibin_tree]
еще:
если (ибиас == "1"):
если(ibin_tree.left):
down_find(iflat, ibin_tree.left, ibias)
если(ibin_tree.right):
down_find(iflat, ibin_tree.right, ibias)
еще:
если(ibin_tree.right):
down_find(iflat, ibin_tree.right, ibias)
если(ibin_tree.left):
down_find(iflat, ibin_tree.left, ibias)
если (экземпляр (ihash, self.hash_type)):
плоский = плоский ()
хэш = ihash.bin_hash
base = find_helper_base(self, self.get_child(hasher[0]), hasher[1:])
если (база):
down_find (плоский, базовый)
смещение = более плоское [0].
parent, ibias)
def down_find (iflat, ibin_tree, ibias = "0"):
если (len (iflat) >= itarget):
возвращаться
elif (экземпляр (ibin_tree, self.hash_type)):
iflat += [ibin_tree]
еще:
если (ибиас == "1"):
если(ibin_tree.left):
down_find(iflat, ibin_tree.left, ibias)
если(ibin_tree.right):
down_find(iflat, ibin_tree.right, ibias)
еще:
если(ibin_tree.right):
down_find(iflat, ibin_tree.right, ibias)
если(ibin_tree.left):
down_find(iflat, ibin_tree.left, ibias)
если (экземпляр (ihash, self.hash_type)):
плоский = плоский ()
хэш = ihash.bin_hash
base = find_helper_base(self, self.get_child(hasher[0]), hasher[1:])
если (база):
down_find (плоский, базовый)
смещение = более плоское [0].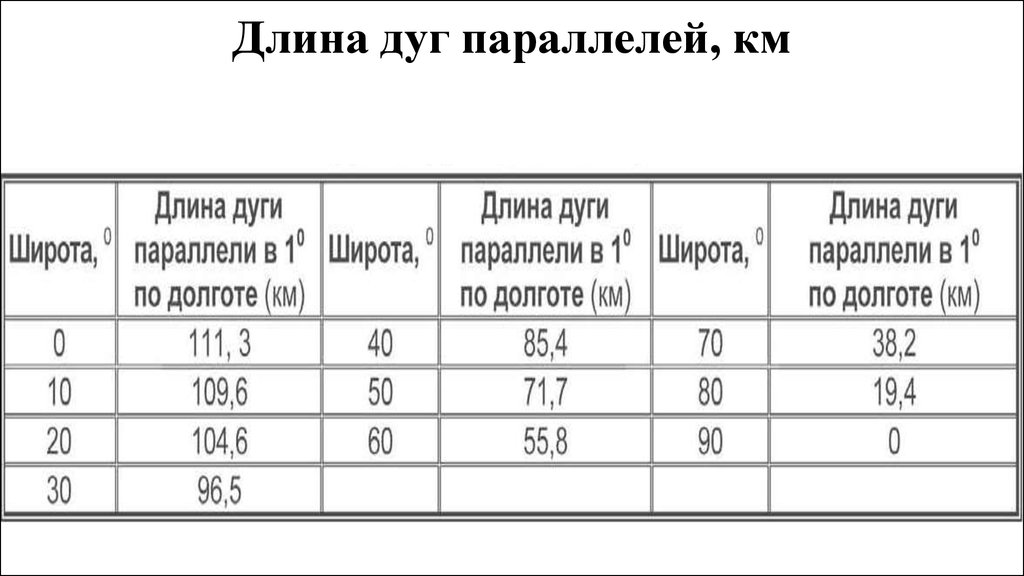 bin_hash[0]
up_find (плоский, базовый.родительский, базовый, смещение)
список возврата (плоский)
def слияние (я, from_bin_tree):
def merge_helper (to_bin_tree, from_bin_tree):
если (экземпляр (from_bin_tree, self.__class__)):
if(from_bin_tree.left != Нет):
если(to_bin_tree.left != Нет):
merge_helper(to_bin_tree.left, from_bin_tree.left)
еще:
from_bin_tree.left.parent = to_bin_tree
to_bin_tree.left = from_bin_tree.left
elif(from_bin_tree.right != Нет):
if(to_bin_tree.right != Нет):
merge_helper(to_bin_tree.right, from_bin_tree.right)
еще:
from_bin_tree.right.parent = to_bin_tree
to_bin_tree.right = from_bin_tree.right
merge_helper (я, from_bin_tree)
класс геодикт (gdict):
'''
Географический словарь
'''
hash_type = геохеш
def __init__(я, ihash=Нет, iparent=Нет):
gdict.
bin_hash[0]
up_find (плоский, базовый.родительский, базовый, смещение)
список возврата (плоский)
def слияние (я, from_bin_tree):
def merge_helper (to_bin_tree, from_bin_tree):
если (экземпляр (from_bin_tree, self.__class__)):
if(from_bin_tree.left != Нет):
если(to_bin_tree.left != Нет):
merge_helper(to_bin_tree.left, from_bin_tree.left)
еще:
from_bin_tree.left.parent = to_bin_tree
to_bin_tree.left = from_bin_tree.left
elif(from_bin_tree.right != Нет):
if(to_bin_tree.right != Нет):
merge_helper(to_bin_tree.right, from_bin_tree.right)
еще:
from_bin_tree.right.parent = to_bin_tree
to_bin_tree.right = from_bin_tree.right
merge_helper (я, from_bin_tree)
класс геодикт (gdict):
'''
Географический словарь
'''
hash_type = геохеш
def __init__(я, ihash=Нет, iparent=Нет):
gdict. __init__(я, ihash, iparent)
класс gpsdict(gdict):
'''
GPS-словарь
'''
hash_type = gpsash
def __init__(я, ihash=Нет, iparent=Нет):
gdict.__init__(я, ihash, iparent)
если(__name__ == "__main__"):
GPS = \
[
гпшаш(90, 90),
гпшаш(68, 24),
гпшаш(144, 60),
гпшаш(48, 91),
гпшаш(32, 105),
гпшаш(32, 150),
гпшаш(167, 20),
гпшаш(49, 116),
гпшаш(81, 82),
гпшаш(63, 79),
гпшаш(129, 76)
]
base_dict = gpsdict()
для cur_hash в GPS:
base_dict.merge (gpsdict (cur_hash))
print "Все места добавлены:"
распечатать base_dict
Распечатать ""
print "Попытка найти 3 ближайшие точки к:"
to_find = gpsash(60, 20)
напечатать to_find.__repr__()
найдено = base_dict.find (to_find, 3)
Распечатать ""
print "Обнаружено следующее:"
для x найдено:
распечатать x.__repr__()
__init__(я, ihash, iparent)
класс gpsdict(gdict):
'''
GPS-словарь
'''
hash_type = gpsash
def __init__(я, ihash=Нет, iparent=Нет):
gdict.__init__(я, ihash, iparent)
если(__name__ == "__main__"):
GPS = \
[
гпшаш(90, 90),
гпшаш(68, 24),
гпшаш(144, 60),
гпшаш(48, 91),
гпшаш(32, 105),
гпшаш(32, 150),
гпшаш(167, 20),
гпшаш(49, 116),
гпшаш(81, 82),
гпшаш(63, 79),
гпшаш(129, 76)
]
base_dict = gpsdict()
для cur_hash в GPS:
base_dict.merge (gpsdict (cur_hash))
print "Все места добавлены:"
распечатать base_dict
Распечатать ""
print "Попытка найти 3 ближайшие точки к:"
to_find = gpsash(60, 20)
напечатать to_find.__repr__()
найдено = base_dict.find (to_find, 3)
Распечатать ""
print "Обнаружено следующее:"
для x найдено:
распечатать x.__repr__()