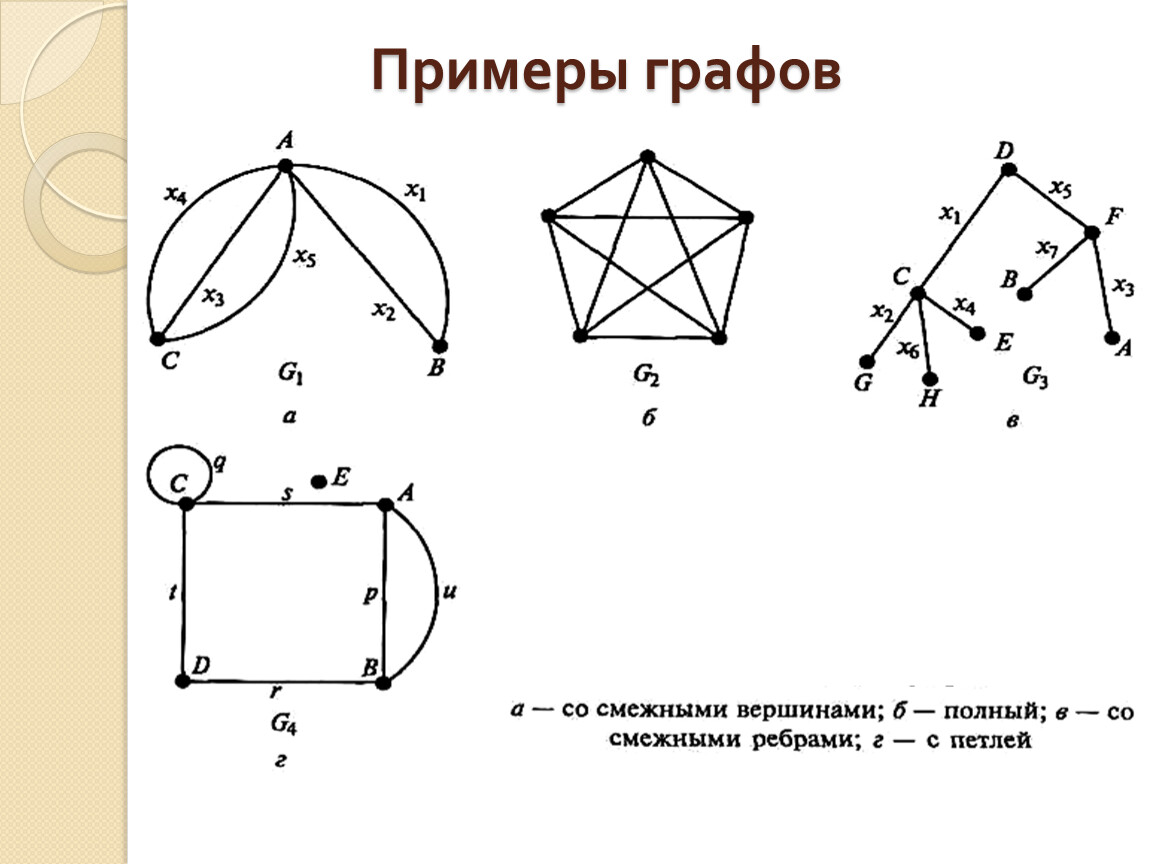
Граф (математика) | это… Что такое Граф (математика)?
У этого термина существуют и другие значения, см. Граф (значения).
Неориентированный граф с шестью вершинами и семью рёбрами
В математической теории графов и информатике граф — это совокупность непустого множества вершин и множества пар вершин (связей между вершинами).
Объекты представляются как вершины, или узлы графа, а связи — как дуги, или рёбра. Для разных областей применения виды графов могут различаться направленностью, ограничениями на количество связей и дополнительными данными о вершинах или рёбрах.
Многие структуры, представляющие практический интерес в математике и информатике, могут быть представлены графами. Например, строение Википедии можно смоделировать при помощи ориентированного графа (орграф), в котором вершины — это статьи, а дуги (ориентированные рёбра) — гиперссылки (см. Тематическая карта).
Содержание
|
Определения
Теория графов не обладает устоявшейся терминологией. В различных статьях под одними и теми же терминами понимаются разные вещи. Ниже приведены наиболее часто встречаемые определения.
Граф
Граф, или неориентированный граф — это упорядоченная пара , для которой выполнены следующие условия:
- — это непустое множество вершин, или узлов,
- — это множество пар (в случае неориентированного графа — неупорядоченных) вершин, называемых рёбрами.

(а значит и, , иначе оно было бы мультимножеством) обычно считаются конечными множествами. Многие хорошие результаты, полученные для конечных графов, неверны (или каким-либо образом отличаются) для бесконечных графов. Это происходит потому, что ряд соображений становится ложным в случае бесконечных множеств.
Вершины и рёбра графа называются также элементами графа, число вершин в графе — порядком, число рёбер — размером графа.
Вершины и называются концевыми вершинами (или просто концами) ребра . Ребро, в свою очередь, соединяет эти вершины. Две концевые вершины одного и того же ребра называются соседними.
Два ребра называются смежными, если они имеют общую концевую вершину.
Два ребра называются кратными, если множества их концевых вершин совпадают.
Ребро называется петлёй, если его концы совпадают, то есть .
Степенью вершины называют количество инцидентных ей рёбер (при этом петли считают дважды).
Вершина называется изолированной, если она не является концом ни для одного ребра; висячей (или листом), если она является концом ровно одного ребра.
Ориентированный граф
Основная статья: Ориентированный граф
Ориентированный граф (сокращённо орграф) — это упорядоченная пара , для которой выполнены следующие условия:
- — это непустое множество вершин или узлов,
- — это множество (упорядоченных) пар различных вершин, называемых дугами или ориентированными рёбрами.
Дуга — это упорядоченная пара вершин , где вершину называют началом, а — концом дуги. Можно сказать, что дуга ведёт от вершины к вершине .
Смешанный граф
Смешанный граф — это граф, в котором некоторые рёбра могут быть ориентированными, а некоторые — неориентированными. Записывается упорядоченной тройкой , где , и определены так же, как выше.
Ориентированный и неориентированный графы являются частными случаями смешанного.
Изоморфные графы
Граф называется изоморфным графу , если существует биекция из множества вершин графа в множество вершин графа , обладающая следующим свойством: если в графе есть ребро из вершины в вершину , то в графе должно быть ребро из вершины в вершину и наоборот — если в графе есть ребро из вершины в вершину , то в графе должно быть ребро из вершины в вершину . В случае ориентированного графа эта биекция также должна сохранять ориентацию ребра. В случае взвешенного графа биекция также должна сохранять вес ребра.
Прочие связанные определения
Путём (или цепью
) в графе называют конечную последовательность вершин, в которой каждая вершина (кроме последней) соединена со следующей в последовательности вершин ребром.Ориентированным путём в орграфе называют конечную последовательность вершин , для которой все пары являются (ориентированными) рёбрами.
Циклом называют путь, в котором первая и последняя вершины совпадают. При этом длиной пути (или цикла) называют число составляющих его рёбер. Заметим, что если вершины и являются концами некоторого ребра, то согласно данному определению, последовательность является циклом. Чтобы избежать таких «вырожденных» случаев, вводят следующие понятия.
Путь (или цикл) называют простым, если ребра в нём не повторяются; элементарным, если он простой и вершины в нём не повторяются. Несложно видеть, что:
- Всякий путь, соединяющий две вершины, содержит элементарный путь, соединяющий те же две вершины.
- Всякий простой неэлементарный путь содержит элементарный цикл.
- Всякий простой цикл, проходящий через некоторую вершину (или ребро), содержит элементарный (под-)цикл, проходящий через ту же вершину (или ребро).
- Петля — элементарный цикл.
Бинарное отношение на множестве вершин графа, заданное как «существует путь из в », является отношением эквивалентности и, следовательно, разбивает это множество на классы эквивалентности, называемые компонентами связности графа.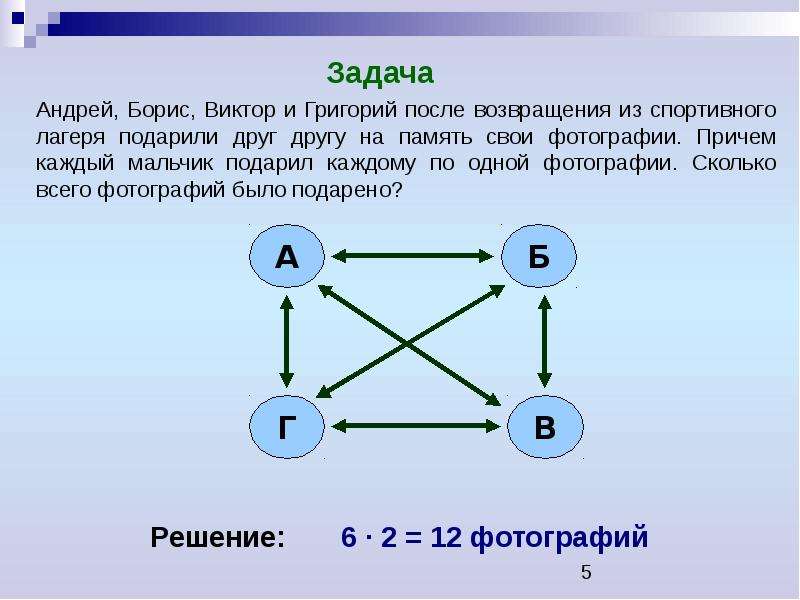 Если у графа ровно одна компонента связности, то граф связный. На компоненте связности можно ввести понятие расстояния между вершинами как минимальную длину пути, соединяющего эти вершины.
Если у графа ровно одна компонента связности, то граф связный. На компоненте связности можно ввести понятие расстояния между вершинами как минимальную длину пути, соединяющего эти вершины.
Всякий максимальный связный подграф графа G называется связной компонентой (или просто компонентой) графа . Слово «максимальный» означает максимальный относительно включения, то есть не содержащийся в связном подграфе с большим числом элементов
Ребро графа называется мостом, если его удаление увеличивает число компонент.
Дополнительные характеристики графов
Граф называется:
- связным, если для любых вершин , есть путь из в .
- сильно связным или ориентированно связным, если он ориентированный, и из любой вершины в любую другую имеется ориентированный путь.
- деревом, если он связный и не содержит простых циклов.
- полным, если любые его две (различные, если не допускаются петли) вершины соединены ребром.

- двудольным, если его вершины можно разбить на два непересекающихся подмножества и так, что всякое ребро соединяет вершину из с вершиной из .
- k-дольным, если его вершины можно разбить на непересекающихся подмножества , , …, так, что не будет рёбер, соединяющих вершины одного и того же подмножества.
- полным двудольным, если каждая вершина одного подмножества соединена ребром с каждой вершиной другого подмножества.
- планарным, если граф можно изобразить диаграммой на плоскости без пересечений рёбер.
- взвешенным, если каждому ребру графа поставлено в соответствие некоторое число, называемое весом ребра.
- хордальным, если граф не содержит индуцированных циклов с длиной больше трех.
Также бывает:
- k-раскрашиваемым
- k-хроматическим
Обобщение понятия графа
Простой граф является одномерным симплициальным комплексом.
Более абстрактно, граф можно задать как тройку , где и — некоторые множества (вершин и рёбер, соотв. ), а — функция инцидентности (или инцидентор), сопоставляющая каждому ребру (упорядоченную или неупорядоченную) пару вершин и из (его концов). Частными случаями этого понятия являются:
), а — функция инцидентности (или инцидентор), сопоставляющая каждому ребру (упорядоченную или неупорядоченную) пару вершин и из (его концов). Частными случаями этого понятия являются:
- ориентированные графы (орграфы) — когда всегда является упорядоченной парой вершин;
- неориентированные графы — когда всегда является неупорядоченной парой вершин;
- смешанные графы — в котором встречаются как ориентированные, так и неориентированные рёбра и петли;
- Эйлеровы графы — граф в котором существует циклический эйлеров путь (Эйлеров цикл).
- мультиграфы — графы с кратными рёбрами, имеющими своими концами одну и ту же пару вершин;
- псевдографы — это мультиграфы, допускающие наличие петель;
- простые графы — не имеющие петель и кратных рёбер.
Под данное выше определение не подходят некоторые другие обобщения:
- гиперграф — если ребро может соединять более двух вершин.
- ультраграф — если между элементами и существуют бинарные отношения инцидентности.

Способы представления графа в информатике
Матрица смежности
Основная статья: Матрица смежности
Таблица, где как столбцы, так и строки соответствуют вершинам графа. В каждой ячейке этой матрицы записывается число, определяющее наличие связи от вершины-строки к вершине-столбцу (либо наоборот).
Недостатком являются требования к памяти, прямо пропорциональные квадрату количества вершин.
- Двумерный массив;
- Матрица с пропусками;
- Неявное задание (при помощи функции).
Матрица инцидентности
Основная статья: Матрица инцидентности
Каждая строка соответствует определённой вершине графа, а столбцы соответствуют связям графа. В ячейку на пересечении -ой строки с -м столбцом матрицы записывается:
- 1
- в случае, если связь «выходит» из вершины ,
- −1,
- если связь «входит» в вершину,
- 0
- во всех остальных случаях (то есть если связь является петлёй или связь не инцидентна вершине)
Данный способ является самым ёмким (размер пропорционален ) для хранения, но облегчает нахождение циклов в графе.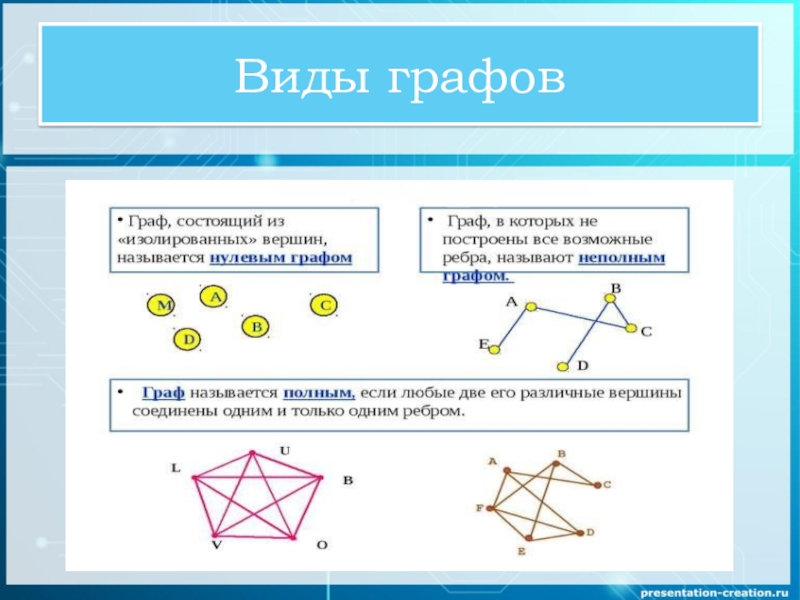
Список рёбер
Список рёбер — это тип представления графа, подразумевающий, что каждое ребро представляется двумя числами — номерами вершин этого ребра.
Языки описания и программы построения графов
Для описания графов в целях, пригодных для машинной обработки и одновременно удобном для человеческого восприятия используется несколько стандартизированных языков, среди которых:
- DOT (язык)
- GraphML
- Trivial Graph Format
- GML
- GXL
- XGMML
- DGML
Отметим специализированные коммерческие программы для построения графов:
- ILOG
- GoView
- Lassalle AddFlow
- LEDA (есть бесплатная редакция).
Из бесплатных можно отметить:
- Boost Graph Library.
Для визуализации графов можно использовать:
- Graphviz
- LION Graph Visualizer.
- Графоанализатор — русскоязычная программа, с простым пользовательским интерфейсом.
- Gephi — графическая оболочка для представления и изучения графов.

См. также
- Словарь терминов теории графов
- Визуализация графов
- Система графов
- Прямое произведение графов
- Теоремы теории графов
- Boost Graph — Библиотека для работы с графами на языке C++
Литература
- Оре О. Теория графов. М.: Наука, 1968. 336с. http://eqworld.ipmnet.ru/ru/library/books/Ore1965ru.djvu
- Ошемков А.А. Лекции по наглядной геометрии и топологии http://dfgm.math.msu.su/files/0ngit/oshemkov/00ngit.pdf
- Уилсон Р. Введение в теорию графов. Пер с англ. М.: Мир, 1977. 208с. http://eqworld.ipmnet.ru/ru/library/books/Uilson1977ru.djvu
- Харари Ф. Теория графов. М.: Мир, 1973. http://eqworld.ipmnet.ru/ru/library/books/Harari1973ru.djvu
- Кормен Т. М.и др. Часть VI. Алгоритмы для работы с графами // Алгоритмы: построение и анализ = INTRODUCTION TO ALGORITHMS. — 2-е изд. — М.: «Вильямс», 2006. — С. 1296. — ISBN 0-07-013151-1
- Салий В.
 Н. Богомолов А. М. Алгебраические основы теории дискретных систем. — М.: Физико-математическая литература, 1997. — ISBN 5-02-015033-9
Н. Богомолов А. М. Алгебраические основы теории дискретных систем. — М.: Физико-математическая литература, 1997. — ISBN 5-02-015033-9 - Емеличев В. А., Мельников О. И., Сарванов В. И., Тышкевич Р. И. Лекции по теории графов. М.: Наука, 1990. 384с. (Изд.2, испр. М.: УРСС, 2009. 392 с.)
- Кирсанов М. Н. Графы в Maple. М.: Физматлит, 2007. — 168 c. http://vuz.exponenta.ru/PDF/book/GrMaple.pdf http://eqworld.ipmnet.ru/ru/library/books/Kirsanov2007ru.pdf
Граф (математика) | это… Что такое Граф (математика)?
У этого термина существуют и другие значения, см. Граф (значения).
Неориентированный граф с шестью вершинами и семью рёбрами
В математической теории графов и информатике граф — это совокупность непустого множества вершин и множества пар вершин (связей между вершинами).
Объекты представляются как вершины, или узлы графа, а связи — как дуги, или рёбра. Для разных областей применения виды графов могут различаться направленностью, ограничениями на количество связей и дополнительными данными о вершинах или рёбрах.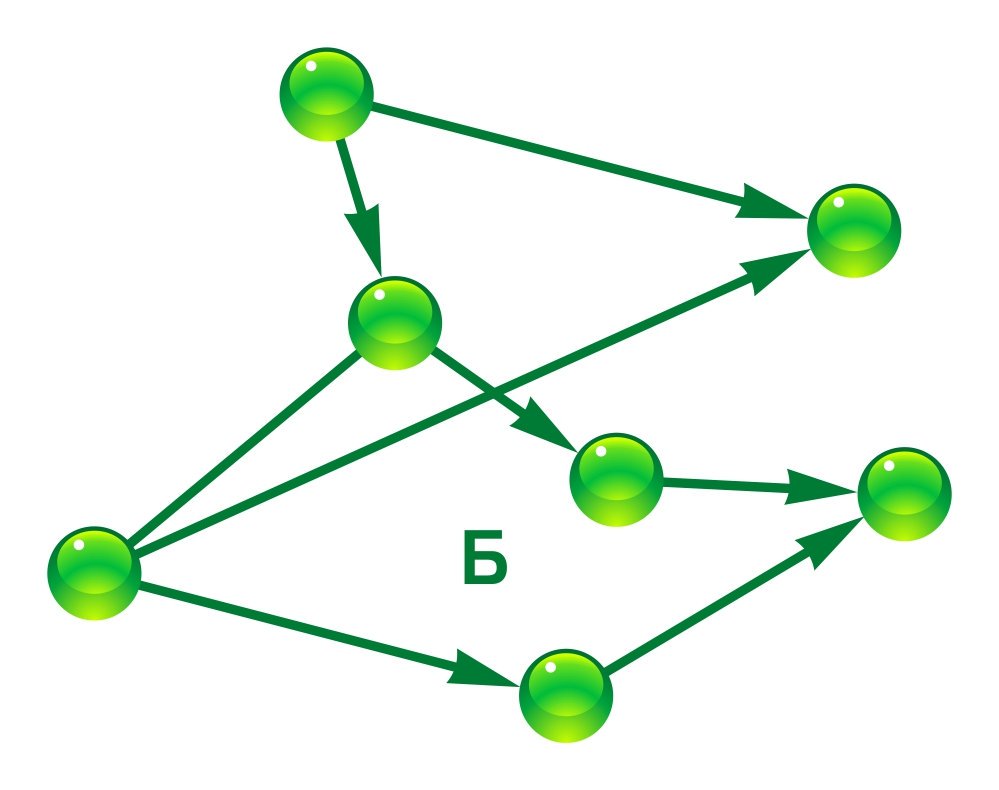
Многие структуры, представляющие практический интерес в математике и информатике, могут быть представлены графами. Например, строение Википедии можно смоделировать при помощи ориентированного графа (орграф), в котором вершины — это статьи, а дуги (ориентированные рёбра) — гиперссылки (см. Тематическая карта).
Содержание
|
Определения
Теория графов не обладает устоявшейся терминологией. В различных статьях под одними и теми же терминами понимаются разные вещи. Ниже приведены наиболее часто встречаемые определения.
Ниже приведены наиболее часто встречаемые определения.
Граф
Граф, или неориентированный граф — это упорядоченная пара , для которой выполнены следующие условия:
- — это непустое множество вершин, или узлов,
- — это множество пар (в случае неориентированного графа — неупорядоченных) вершин, называемых рёбрами.
(а значит и, , иначе оно было бы мультимножеством) обычно считаются конечными множествами. Многие хорошие результаты, полученные для конечных графов, неверны (или каким-либо образом отличаются) для бесконечных графов. Это происходит потому, что ряд соображений становится ложным в случае бесконечных множеств.
Вершины и рёбра графа называются также элементами графа, число вершин в графе — порядком, число рёбер — размером графа.
Вершины и называются концевыми вершинами (или просто концами) ребра . Ребро, в свою очередь, соединяет эти вершины.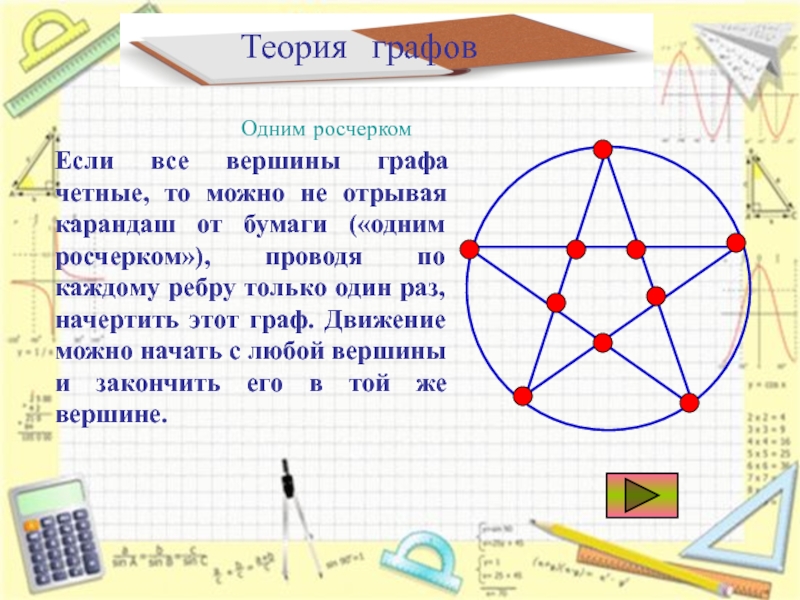 Две концевые вершины одного и того же ребра называются соседними.
Две концевые вершины одного и того же ребра называются соседними.
Два ребра называются смежными, если они имеют общую концевую вершину.
Два ребра называются кратными, если множества их концевых вершин совпадают.
Ребро называется петлёй, если его концы совпадают, то есть .
Степенью вершины называют количество инцидентных ей рёбер (при этом петли считают дважды).
Вершина называется изолированной, если она не является концом ни для одного ребра; висячей (или листом), если она является концом ровно одного ребра.
Ориентированный граф
Основная статья: Ориентированный граф
Ориентированный граф (сокращённо орграф) — это упорядоченная пара , для которой выполнены следующие условия:
- — это непустое множество вершин или узлов,
- — это множество (упорядоченных) пар различных вершин, называемых дугами или ориентированными рёбрами.

Дуга — это упорядоченная пара вершин , где вершину называют началом, а — концом дуги. Можно сказать, что дуга ведёт от вершины к вершине .
Смешанный граф
Смешанный граф — это граф, в котором некоторые рёбра могут быть ориентированными, а некоторые — неориентированными. Записывается упорядоченной тройкой , где , и определены так же, как выше.
Ориентированный и неориентированный графы являются частными случаями смешанного.
Изоморфные графы
Граф называется изоморфным графу , если существует биекция из множества вершин графа в множество вершин графа , обладающая следующим свойством: если в графе есть ребро из вершины в вершину , то в графе должно быть ребро из вершины в вершину и наоборот — если в графе есть ребро из вершины в вершину , то в графе должно быть ребро из вершины в вершину . В случае ориентированного графа эта биекция также должна сохранять ориентацию ребра. В случае взвешенного графа биекция также должна сохранять вес ребра.
Прочие связанные определения
Путём (или цепью) в графе называют конечную последовательность вершин, в которой каждая вершина (кроме последней) соединена со следующей в последовательности вершин ребром.
Ориентированным путём в орграфе называют конечную последовательность вершин , для которой все пары являются (ориентированными) рёбрами.
Циклом называют путь, в котором первая и последняя вершины совпадают. При этом длиной пути (или цикла) называют число составляющих его рёбер. Заметим, что если вершины и являются концами некоторого ребра, то согласно данному определению, последовательность является циклом. Чтобы избежать таких «вырожденных» случаев, вводят следующие понятия.
Путь (или цикл) называют простым, если ребра в нём не повторяются; элементарным, если он простой и вершины в нём не повторяются. Несложно видеть, что:
- Всякий путь, соединяющий две вершины, содержит элементарный путь, соединяющий те же две вершины.

- Всякий простой неэлементарный путь содержит элементарный цикл.
- Всякий простой цикл, проходящий через некоторую вершину (или ребро), содержит элементарный (под-)цикл, проходящий через ту же вершину (или ребро).
- Петля — элементарный цикл.
Бинарное отношение на множестве вершин графа, заданное как «существует путь из в », является отношением эквивалентности и, следовательно, разбивает это множество на классы эквивалентности, называемые компонентами связности графа. Если у графа ровно одна компонента связности, то граф связный. На компоненте связности можно ввести понятие расстояния между вершинами как минимальную длину пути, соединяющего эти вершины.
Всякий максимальный связный подграф графа G называется связной компонентой (или просто компонентой) графа . Слово «максимальный» означает максимальный относительно включения, то есть не содержащийся в связном подграфе с большим числом элементов
Ребро графа называется мостом, если его удаление увеличивает число компонент.
Дополнительные характеристики графов
Граф называется:
- связным, если для любых вершин , есть путь из в .
- сильно связным или ориентированно связным, если он ориентированный, и из любой вершины в любую другую имеется ориентированный путь.
- деревом, если он связный и не содержит простых циклов.
- полным, если любые его две (различные, если не допускаются петли) вершины соединены ребром.
- двудольным, если его вершины можно разбить на два непересекающихся подмножества и так, что всякое ребро соединяет вершину из с вершиной из .
- k-дольным, если его вершины можно разбить на непересекающихся подмножества , , …, так, что не будет рёбер, соединяющих вершины одного и того же подмножества.
- полным двудольным, если каждая вершина одного подмножества соединена ребром с каждой вершиной другого подмножества.
- планарным, если граф можно изобразить диаграммой на плоскости без пересечений рёбер.

- взвешенным, если каждому ребру графа поставлено в соответствие некоторое число, называемое весом ребра.
- хордальным, если граф не содержит индуцированных циклов с длиной больше трех.
Также бывает:
- k-раскрашиваемым
- k-хроматическим
Обобщение понятия графа
Простой граф является одномерным симплициальным комплексом.
Более абстрактно, граф можно задать как тройку , где и — некоторые множества (вершин и рёбер, соотв.), а — функция инцидентности (или инцидентор), сопоставляющая каждому ребру (упорядоченную или неупорядоченную) пару вершин и из (его концов). Частными случаями этого понятия являются:
- ориентированные графы (орграфы) — когда всегда является упорядоченной парой вершин;
- неориентированные графы — когда всегда является неупорядоченной парой вершин;
- смешанные графы — в котором встречаются как ориентированные, так и неориентированные рёбра и петли;
- Эйлеровы графы — граф в котором существует циклический эйлеров путь (Эйлеров цикл).

- мультиграфы — графы с кратными рёбрами, имеющими своими концами одну и ту же пару вершин;
- псевдографы — это мультиграфы, допускающие наличие петель;
- простые графы — не имеющие петель и кратных рёбер.
Под данное выше определение не подходят некоторые другие обобщения:
- гиперграф — если ребро может соединять более двух вершин.
- ультраграф — если между элементами и существуют бинарные отношения инцидентности.
Способы представления графа в информатике
Матрица смежности
Основная статья: Матрица смежности
Таблица, где как столбцы, так и строки соответствуют вершинам графа. В каждой ячейке этой матрицы записывается число, определяющее наличие связи от вершины-строки к вершине-столбцу (либо наоборот).
Недостатком являются требования к памяти, прямо пропорциональные квадрату количества вершин.
- Двумерный массив;
- Матрица с пропусками;
- Неявное задание (при помощи функции).

Матрица инцидентности
Основная статья: Матрица инцидентности
Каждая строка соответствует определённой вершине графа, а столбцы соответствуют связям графа. В ячейку на пересечении -ой строки с -м столбцом матрицы записывается:
- 1
- в случае, если связь «выходит» из вершины ,
- −1,
- если связь «входит» в вершину,
- 0
- во всех остальных случаях (то есть если связь является петлёй или связь не инцидентна вершине)
Данный способ является самым ёмким (размер пропорционален ) для хранения, но облегчает нахождение циклов в графе.
Список рёбер
Список рёбер — это тип представления графа, подразумевающий, что каждое ребро представляется двумя числами — номерами вершин этого ребра.
Языки описания и программы построения графов
Для описания графов в целях, пригодных для машинной обработки и одновременно удобном для человеческого восприятия используется несколько стандартизированных языков, среди которых:
- DOT (язык)
- GraphML
- Trivial Graph Format
- GML
- GXL
- XGMML
- DGML
Отметим специализированные коммерческие программы для построения графов:
- ILOG
- GoView
- Lassalle AddFlow
- LEDA (есть бесплатная редакция).

Из бесплатных можно отметить:
- Boost Graph Library.
Для визуализации графов можно использовать:
- Graphviz
- LION Graph Visualizer.
- Графоанализатор — русскоязычная программа, с простым пользовательским интерфейсом.
- Gephi — графическая оболочка для представления и изучения графов.
См. также
- Словарь терминов теории графов
- Визуализация графов
- Система графов
- Прямое произведение графов
- Теоремы теории графов
- Boost Graph — Библиотека для работы с графами на языке C++
Литература
- Оре О. Теория графов. М.: Наука, 1968. 336с. http://eqworld.ipmnet.ru/ru/library/books/Ore1965ru.djvu
- Ошемков А.А. Лекции по наглядной геометрии и топологии http://dfgm.math.msu.su/files/0ngit/oshemkov/00ngit.pdf
- Уилсон Р. Введение в теорию графов. Пер с англ. М.: Мир, 1977. 208с. http://eqworld.ipmnet.ru/ru/library/books/Uilson1977ru.
 djvu
djvu - Харари Ф. Теория графов. М.: Мир, 1973. http://eqworld.ipmnet.ru/ru/library/books/Harari1973ru.djvu
- Кормен Т. М.и др. Часть VI. Алгоритмы для работы с графами // Алгоритмы: построение и анализ = INTRODUCTION TO ALGORITHMS. — 2-е изд. — М.: «Вильямс», 2006. — С. 1296. — ISBN 0-07-013151-1
- Салий В. Н. Богомолов А. М. Алгебраические основы теории дискретных систем. — М.: Физико-математическая литература, 1997. — ISBN 5-02-015033-9
- Емеличев В. А., Мельников О. И., Сарванов В. И., Тышкевич Р. И. Лекции по теории графов. М.: Наука, 1990. 384с. (Изд.2, испр. М.: УРСС, 2009. 392 с.)
- Кирсанов М. Н. Графы в Maple. М.: Физматлит, 2007. — 168 c. http://vuz.exponenta.ru/PDF/book/GrMaple.pdf http://eqworld.ipmnet.ru/ru/library/books/Kirsanov2007ru.pdf
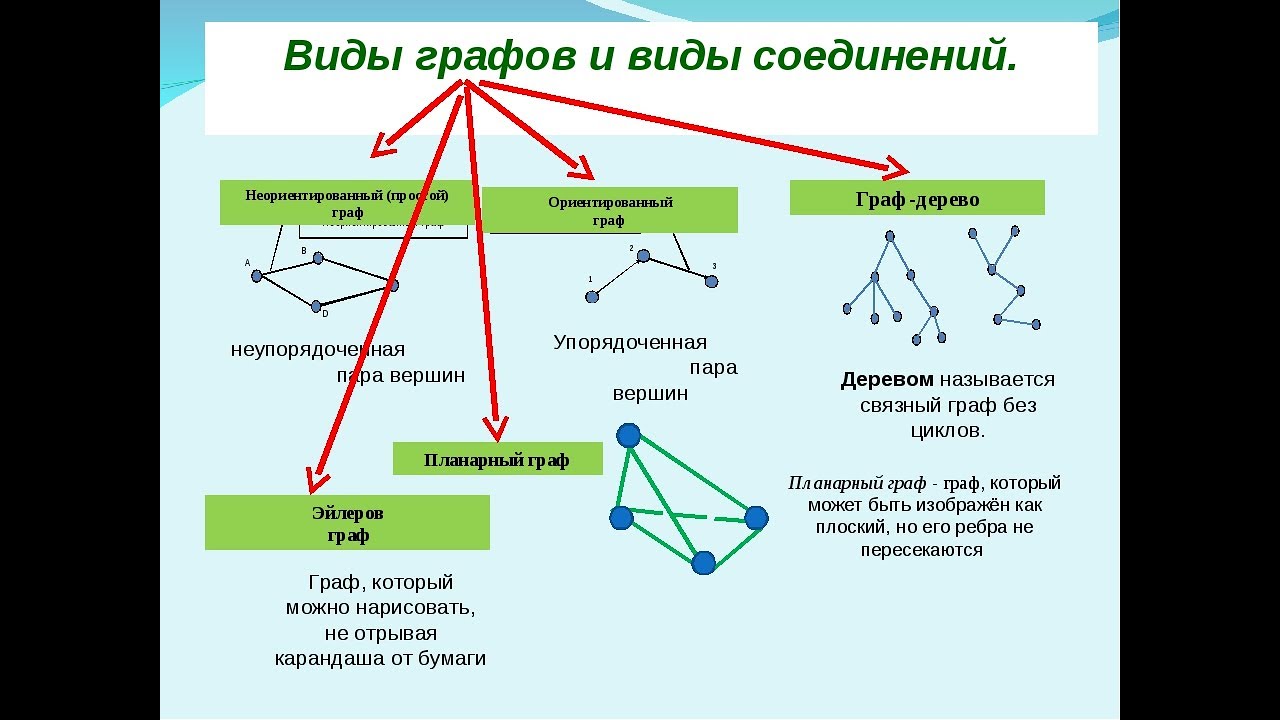
Математика | Основы теории графов — набор 1
Граф — это структура данных, которая определяется двумя компонентами:
- узел или вершина.

- Ребро E или упорядоченная пара — это соединение между двумя узлами u,v , которое идентифицируется уникальной парой (u,v). Пара (u,v) упорядочена, потому что (u,v) не совпадает с (v,u) в случае ориентированного графа. Ребро может иметь вес или установлено равным единице в случае невзвешенного графа.
Рассмотрим приведенный ниже график. Чтобы узнать о «графическом представлении», нажмите здесь
Приложения: График — это структура данных, которая широко используется в нашей реальной жизни.
- Социальная сеть: Каждый пользователь представлен в виде узла, а все его действия, предложения и список друзей представлены в виде ребра между узлами.
- Карты Google: Различные местоположения представлены в виде вершин или узлов, а дороги представлены в виде ребер, а теория графов используется для поиска кратчайшего пути между двумя узлами.
- Рекомендации для веб-сайтов электронной коммерции: Раздел «Рекомендации для вас» на различных веб-сайтах электронной коммерции использует теорию графов, чтобы рекомендовать элементы аналогичного типа по выбору пользователя.

- Теория графов также используется для изучения молекул в химии и физике.
Подробнее о графах: Характеристики графов:
- Смежный узел: Узел ‘v’ называется смежным узлом узла ‘u’ тогда и только тогда, когда существует ребро между «у» и «в».
- Степень узла: В неориентированном графе число вершин, инцидентных узлу, является степенью узла. В случае ориентированного графа Inстепень узла представляет собой количество ребер , прибывающих в узел. Степень исхода узла — это число исходящих ребер к узлу.
Примечание: 1 петля считается дважды
2 сумма степеней всех вершин в графе G четна.
- Путь: Путь длины «n» от узла «u» до узла «v» определяется как последовательность из n+1 узлов.
P(u,v)=(v0,v1,v2,v3……. vn)
vn)
- Путь является простым, если все узлы различны, исключение – источник и пункт назначения одинаковы.
- Изолированный узел: Узел со степенью 0 известен как изолированный узел. Изолированный узел можно найти с помощью поиска в ширину (BFS). Находит свое применение в Сеть LAN при определении того, подключена ли система или нет.
Типы графов:
- Ориентированный граф: Граф, в котором направление ребра определено к определенному узлу, является ориентированным графом.
- Направленный ациклический граф: Это ориентированный граф без цикла. Для вершины «v» в DAG нет направленного ребра, начинающегося и заканчивающегося вершиной «v». а) Применение: критический анализ игры, оценка дерева выражений, оценка игры.
- Дерево: Дерево — это просто ограниченная форма графа. То есть это группа DAG с ограничением, согласно которому дочерний элемент может иметь только одного родителя.

- Неориентированный граф: Граф, в котором направление ребра не определено. Таким образом, если ребро существует между узлами ‘u’ и ‘v’, то существует путь от узла ‘u’ к ‘ v’ и наоборот.
- Связный граф: Граф является связным, если между каждой парой вершин имеется путей. В связном графе нет недостижимых узлов.
- Полный граф: Граф, в котором каждая пара вершин графа соединена ребром. Другими словами, каждый узел «u» смежный с каждым другим узлом «v» в графе «G». Полный граф будет иметь n(n-1)/2 ребер. Доказательство см. ниже.
- Двусвязный граф: Связный граф, который нельзя разбить на какие-либо дополнительные части путем удаления какой-либо вершины. Это граф без точки сочленения.
Доказательство для полного графа:
- Рассмотрим полный граф с n узлами. Каждый узел соединен с другими n-1 узлами.
 Таким образом, получается n * (n-1) ребер. Но при этом каждое ребро считается дважды, потому что это неориентированный граф, поэтому разделите его на 2.
Таким образом, получается n * (n-1) ребер. Но при этом каждое ребро считается дважды, потому что это неориентированный граф, поэтому разделите его на 2. - Таким образом, получится n(n-1)/2.
Рассмотрим данный граф, //опускаем повторяющиеся ребра Ребра на узле A = (A,B),(A,C),(A,E),(A,C). Ребра на узле B = (B,C),(B,D),(B,E). Ребра в узле C = (C,D),(C,E). Ребра на узле D = (D,E). Ребра в узле E = EMPTY.https://en.wikipedia.org/wiki/Graph_theory Всего ребер = 4+3+2+1+0=10 ребер. Количество узлов = 5. Таким образом, n(n-1)/2=10 ребер. Так доказано. Читать следующий набор – Основы теории графов
Еще несколько графов:
1. Регулярный граф: Граф, в котором каждая вершина x имеет одинаковую/равную степень. k-регулярный граф означает, что каждая вершина имеет степень k.
Каждый полный граф K n будет иметь (n-1)-регулярный граф, что означает степень n-1.
Регулярные графы
2. Двудольный граф: Это граф G, в котором множество вершин можно разделить на два подмножества U и V так, что каждое ребро G имеет один конец в U, а другой конец в V.
Двудольный граф: Это граф G, в котором множество вершин можно разделить на два подмножества U и V так, что каждое ребро G имеет один конец в U, а другой конец в V.
Двудольный граф
3. Полный двудольный граф: это простой граф с множеством вершин, разделенным на два подмножества: и W={w 1 ,w 2 ,………..w n }
i. Существует ребро от каждого v i до каждого w j .
ii. селп-петли нет.
Полный двудольный граф
4. Граф циклов : Граф из n вершин (n≥3) . v 1 ,v 2 ,………………..v n с ребрами (v 1 ,v 2 ),(v 2 ,v 3 ),…… …..,(v n-1 ,v n ),(v n ,v 1 ).
Циклический график
Нежное введение в теорию графов | Вайдехи Джоши | basecs
Опубликовано в
·
11 мин чтения
·
20 марта 2017 г.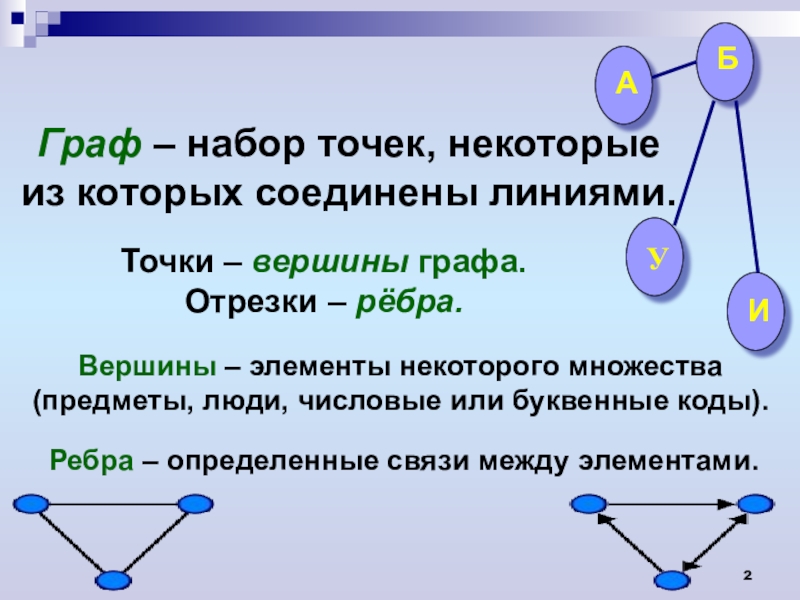
Так много всего в мире никогда бы не появилось, если бы не проблема, требующая решения. Эта истина применима ко всему, но мальчик, это очевидно в мире информатики.
Кому-то нужен был способ отслеживать порядок вещей, поэтому они экспериментировали и создавали различные структуры данных, пока не нашли ту, которая лучше всего подходит для конкретной проблемы, которую они пытались решить. Кому-то еще нужен был хороший способ хранения данных, поэтому они экспериментировали с различными системами счисления, пока не нашли ту, которая лучше всего подходит для той информации, которую они хотели содержать. Людям нужен был хороший способ маркировки и обработки задач, поэтому они нашли способ опираться на имеющиеся у них инструменты и создали способ жонглировать всеми задачами, которые должна была делать одна система, в любой момент времени.
Конечно, информатика — это не единственная область инноваций и развития того, что было до нее, но я действительно думаю, что она уникальна в одном отношении: инновации информатики опираются на ее собственные абстракции и строятся на них.
Я много говорил об абстракциях в этой серии, потому что, в конечном счете, эта серия о и состоит в том, чтобы находить радость в абстракциях, лежащих в основе вещей, которыми мы все пользуемся каждый божий день. И, что бы там ни было, когда я говорю «нас», я лишь частично говорю о нас как программистов, производителей технологий — я также имею в виду нас как пользователей, потребителей технологий.
Итак, о какой удивительной абстракции мы узнаем дальше? Что ж, теперь, когда мы являемся экспертами в древовидных структурах данных, кажется правильным понять, откуда взялись деревья. Деревья на самом деле являются подмножеством того, о чем вы, возможно, уже слышали: графов . Но чтобы по-настоящему узнать, почему мы используем графики и что они из себя представляют, нам нужно углубиться в самые корни того, что происходит из дискретной математики: теория графов .
Если это ваше первое знакомство с дискретной математикой, не бойтесь — это и мое! Давайте решать эту проблему вместе — и постарайтесь не потерять рассудок в процессе.
Когда мы впервые начали изучать нелинейные структуры, мы узнали об их самой фундаментальной характеристике: их данные не следуют порядку — по крайней мере, не очевидному числовому порядку, как мы видим в массивах или связанных списках. Как мы узнали, деревья начинаются с корневого узла и могут соединяться с другими узлами, что означает, что они могут содержать поддеревья внутри себя. Деревья определяются определенным набором правил: один корневой узел может соединяться или не соединяться с другими, но в конечном итоге все они происходят из одного определенного места. У некоторых деревьев даже более конкретных правил, таких как бинарные деревья поиска, которые могут иметь только две ссылки на два узла в любой момент времени.
Но что, если мы сделаем что-нибудь безумное и просто… выбросим эти правила в окно? Что ж, как оказалось, мы вполне можем это сделать! Просто мы больше не будем иметь дело с деревьями — мы будем иметь дело с чем-то, что называется графом .
Деревья — это не что иное, как ограниченные типы графов, но с гораздо большим количеством правил, которым нужно следовать. Дерево всегда будет графом, но не все графы будут деревьями.
Итак, что отличает дерево от большого зонтика графов?
Ну, во-первых, дерево может течь только в одном направлении, от корневого узла либо к листовым узлам, либо к дочерним узлам. Дерево также может иметь только односторонние соединения — у дочернего узла может быть только один родитель, а в дереве не может быть петель или циклических связей.
Древовидные структуры данных по сравнению со структурами данных графа С графами все эти ограничения исчезают. Графы не имеют понятия «корневой» узел. А зачем им? На самом деле узлы могут быть связаны любым возможным способом. Один узел может быть подключен к пяти другим! У графиков также нет понятия «однонаправленного» потока — вместо этого они могут иметь направление или вообще не иметь направления. Или, чтобы еще больше усложнить ситуацию, у них могут быть некоторые ссылки, которые имеют направление, а другие — нет! Но мы не будем вдаваться в это сегодня.
Давайте начнем с простых вещей.
Итак, мы знаем, что графики в значительной степени нарушают все известные нам правила. Однако есть одна характеристика, которой должен обладать каждый граф : каждый граф всегда должен иметь, по крайней мере, один-единственный узел. Точно так же, как деревьям нужен хотя бы один корневой узел, чтобы считаться «деревом», точно так же графу нужен хотя бы один узел, чтобы считаться «графом». Граф только с одним узлом обычно называют singleton graph , хотя на самом деле мы не будем иметь дело с ними.
Большинство графиков, с которыми мы будем иметь дело, немного сложнее. Но не беспокойтесь — сегодня мы не будем погружаться в сверхсложные графики . И поверьте мне, некоторые графики действительно сложны!
Вместо этого давайте рассмотрим два типа графов, которые довольно легко обнаружить и которые также довольно часто встречаются в задачах теории графов: ориентированные графы и неориентированные графы.
Как мы знаем, не существует реальных правил в отношении того, как один узел соединяется с другим узлом в графе. Края (иногда их называют ссылки ) могут соединять узлы в любым возможным способом .
Edges могут соединять узлы любым возможным способом!Различные типы ребер очень важны, когда дело доходит до распознавания и определения графов. На самом деле, это одно из самых больших и очевидных различий между одним графом и другим: типы ребер, которые у него есть. По большей части (кроме одного исключения, которое мы сегодня не будем рассматривать) графы могут иметь два типа ребер: ребро, имеющее направление или поток, и ребро, не имеющее направления или потока. Мы называем их направленный и ненаправленный края, с уважением.
В направленном ребре два узла соединены очень специфическим образом. В приведенном ниже примере узел A соединяется с узлом B; есть только один способ перемещения между этими двумя узлами — только одно направление , в котором мы можем двигаться.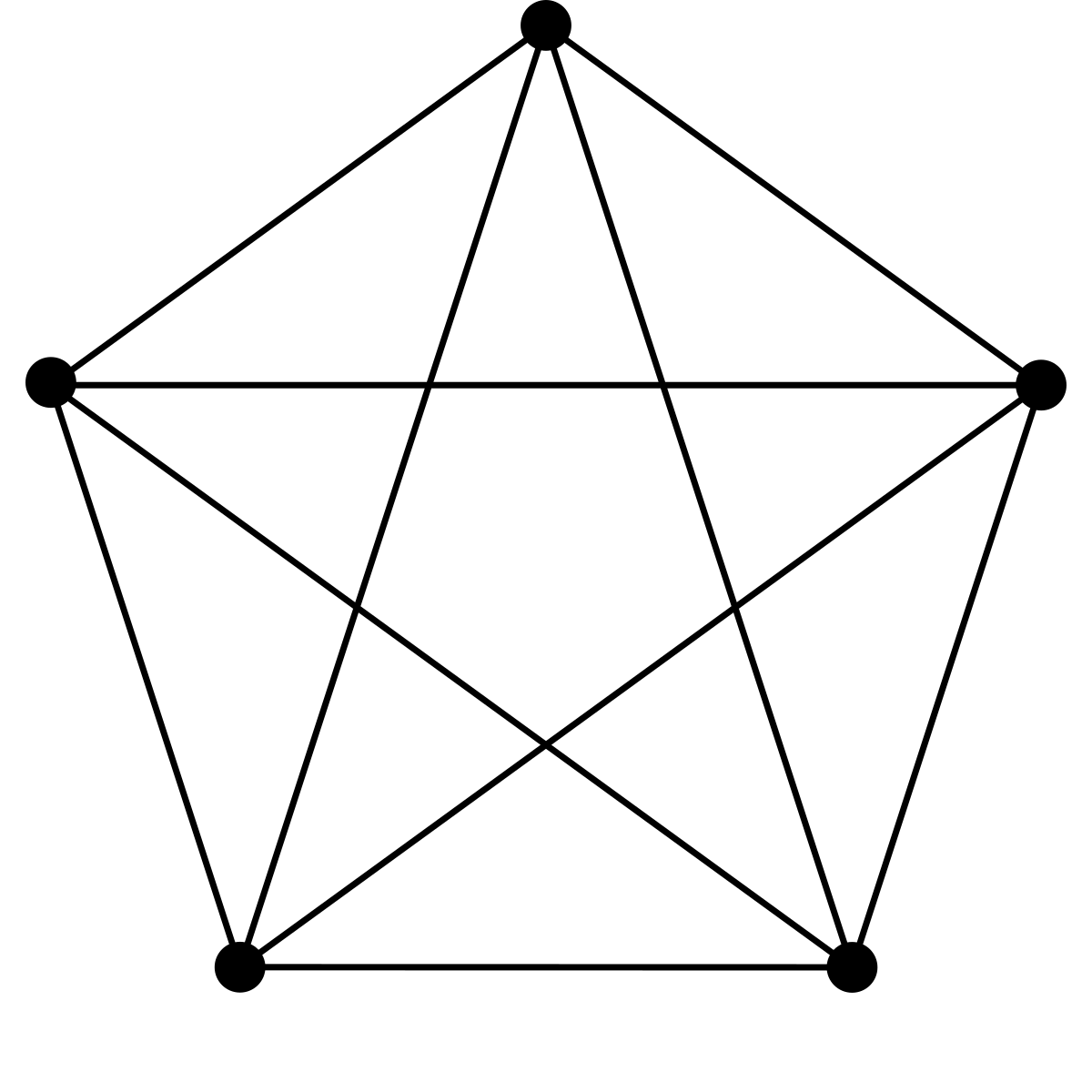 Довольно часто узел, с которого мы начинаем, называют источником , а узел, к которому мы направляемся , — пунктом назначения 9.0244 . В направленном ребре мы можем пройти только от источника к месту назначения и никогда наоборот.
Довольно часто узел, с которого мы начинаем, называют источником , а узел, к которому мы направляемся , — пунктом назначения 9.0244 . В направленном ребре мы можем пройти только от источника к месту назначения и никогда наоборот.
Однако с ненаправленными ребрами дело обстоит совсем по-другому. В ненаправленном ребре путь, по которому мы можем пройти, идет в обе стороны. Другими словами, путь между двумя узлами является двунаправленным , что означает исходный и конечный узлы не фиксированы .
Это различие на самом деле очень важно, потому что ребра в графе определяют, как называется граф. Если все ребра в графе направлены , граф называется ориентированным графом , также называемым орграфом . Если все ребра в графе неориентированные , то говорят, что граф — как вы уже догадались — неориентированный граф ! Поди разберись, да?
Ориентированные графы по сравнению с неориентированными графамиВсе это очень круто, но на данный момент я хочу знать две вещи — откуда взялись все эти графы происходит от , точно? И… какое нам дело?
Давайте разберемся.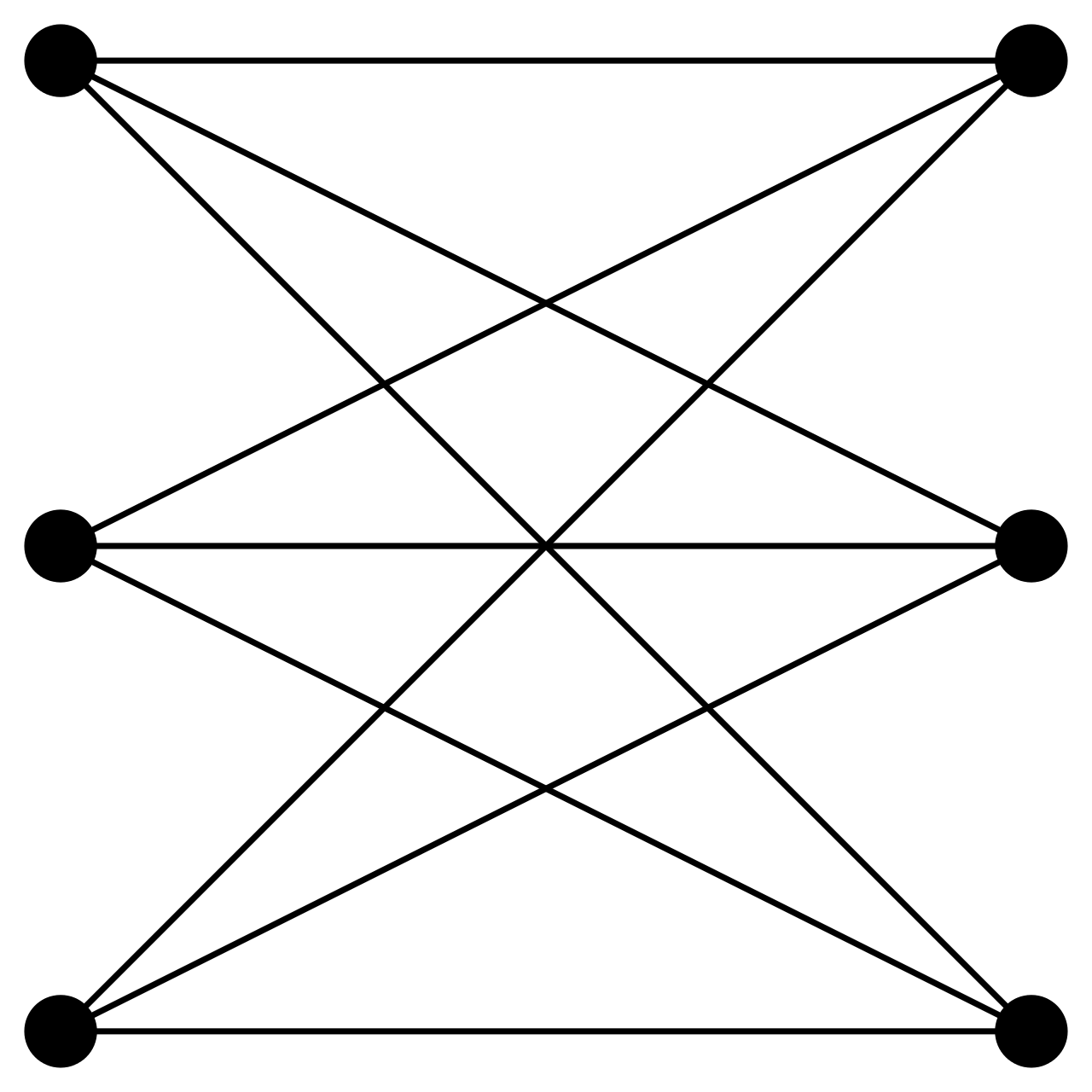
Информатика любит брать взаймы. В частности, он позаимствовал множество понятий из логики и математики. Как оказалось, это относится и к графикам.
Графовые структуры данных, известные нам как компьютерные науки, на самом деле происходят из математики и изучения графов, которые называются теорией графов .
В математике графы — это способ формального представления сети, которая, по сути, представляет собой просто набор взаимосвязанных объектов.
Как оказалось, когда ученые-компьютерщики применили теорию графов к коду (и в конечном итоге реализовали графы как структуры данных), они не сильно изменились. Таким образом, многие термины, которые мы используем для описания и реализации графов, являются точными терминами, которые мы найдем в математических справочниках по теории графов.
Например, в математических терминах мы описываем графы как упорядоченных пар . Помните школьную алгебру, когда мы узнали о (x, y) упорядоченных парных координатах? Аналогичная сделка здесь, с одним отличием: вместо x и y , части графа вместо этого: v , для вершин и e , для его ребер 9 0244 .
Формальное математическое определение графа таково: G = (V, E) . Вот и все! Действительно. Я обещаю.
Очень краткое введение в теорию графовНо подождите секунду — что, если наш граф имеет более одного узла и более одного ребра! На самом деле… будет всегда имеют несколько ребер, если у него более одного узла. Как же работает это определение?
Ну, это работает, потому что эта упорядоченная пара — (V, E) — на самом деле состоит из двух объектов : множества вершин и множества ребер.
Хорошо, теперь это имеет для меня больше смысла. Но было бы намного яснее, если бы у меня был пример и я действительно записал определение графа! Так что мы сделаем именно это. В приведенном ниже примере у нас есть неориентированный граф с 8 вершинами и 11 ребрами.
Формальное определение неориентированного графаТак что же здесь происходит?
Итак, мы выписали нашу заказанную пару (V, E) , но поскольку каждый из этих элементов является объектом, нам пришлось выписать и их.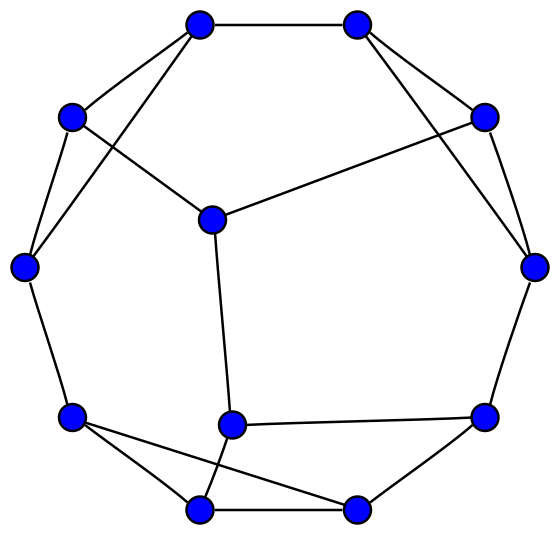 Мы определили V как неупорядоченных набора ссылок на наши 8 вершин. «Неупорядоченная» часть здесь действительно важна, потому что помните, в отличие от деревьев, не имеет иерархии узлов ! Это означает, что нам не нужно их упорядочивать, так как порядок здесь не имеет значения.
Мы определили V как неупорядоченных набора ссылок на наши 8 вершин. «Неупорядоченная» часть здесь действительно важна, потому что помните, в отличие от деревьев, не имеет иерархии узлов ! Это означает, что нам не нужно их упорядочивать, так как порядок здесь не имеет значения.
Мы также должны были определить E как объект, который содержит множество граничных объектов внутри себя. Заметьте еще раз, что наши краевые объекты также являются неупорядоченными . Почему это может быть? Ну и что это за график? Есть ли какое-то направление или течение? Существует ли фиксированное значение «происхождения» и «назначения»?
Нет, нет! Это неориентированный граф , что означает, что ребра являются двунаправленными, а исходный узел и узел назначения равны , а не 9.0244 исправлено. Итак, каждый из наших реберных объектов также представляет собой неупорядоченных пар .
Эта особенность, конечно, заставляет задуматься: а что, если бы это был -направленный -граф? Время для другого примера! Вот ориентированный граф с тремя вершинами и тремя ребрами:
Формальное определение ориентированного графа Способ, которым мы определяем вершины здесь, ничем не отличается, но давайте более внимательно рассмотрим определение нашего ребра. Наши реберные объекты в этом случае — это упорядоченных пары, потому что в этом случае направление действительно имеет значение! Поскольку мы можем путешествовать только от исходного узла к узлу назначения, наши ребра должен быть упорядочен , чтобы исходный узел был первым из двух узлов в каждом из наших определений ребра.
Наши реберные объекты в этом случае — это упорядоченных пары, потому что в этом случае направление действительно имеет значение! Поскольку мы можем путешествовать только от исходного узла к узлу назначения, наши ребра должен быть упорядочен , чтобы исходный узел был первым из двух узлов в каждом из наших определений ребра.
Круто, вот как мы определяем графики. Но… когда мы когда-нибудь на самом деле будем использовать графики ? Ну, вы, вероятно, использовали один из них сегодня. Возможно, вы еще этого не знаете! Время изменить это.
Графики окружают нас повсюду, просто мы не всегда видим их такими, какие они есть.
На самом деле, читая этот пост, вы прямо сейчас буквально на графике. Сеть представляет собой массивную графовую структуру! Когда мы щелкаем между веб-сайтами и перемещаемся между URL-адресами, мы на самом деле просто перемещаемся по графику. Иногда эти графы имеют узлы с ненаправленными ребрами — я могу переходить с одной веб-страницы на другую — и другие, которые являются направленными — я могу переходить только с веб-страницы А на веб-страницу Б и никогда наоборот.
Но есть еще лучший пример, прекрасно иллюстрирующий наше ежедневное взаимодействие с графами: социальные сети.
Facebook, огромная социальная сеть, представляет собой разновидность графа. И если мы больше подумаем об этом на самом деле, мы начнем лучше понимать , как мы можем определить , и какой именно тип графа. На Facebook, если я добавлю вас в друзья, вы должны принять мой запрос. Я не могу быть твоим другом в сети, если ты не будешь моим. Отношение между двумя пользователями (читай: узлы или вершины в терминах графа!) равно двунаправленному . Нет понятия «источник» и «пункт назначения» — вместо этого ты мой друг, а я твой.
Угадайте, какой тип графа реализован в Facebook?
Facebook как структура неориентированного графа Если вы угадали неориентированный граф , то вы правы! Отличная работа. Отношения двусторонние, поэтому, если бы мы определили сеть друзей Facebook как граф, все ее ребра оказались бы неупорядоченными парами, когда мы их записали.
Twitter, с другой стороны, работает совершенно иначе, чем Facebook. Я могу следовать за тобой, но ты можешь не следовать за мной в ответ. Показательный пример: я слежу за Бейонсе, но она определенно не следует за мной в ответ (к сожалению).
Twitter как структура ориентированного графаМы можем представить Twitter как направленный граф. Каждое ребро, которое мы создаем, представляет собой односторонних отношений . Когда вы подписываетесь на меня в Твиттере, вы создаете ребро на графике, где ваша учетная запись выступает в качестве исходного узла, а моя учетная запись — в качестве конечного узла.
Что произойдет, если я пойду за тобой? Могу ли я изменить край, который вы создали, когда следовали за мной? Он вдруг становится двунаправленным? Ну, нет, потому что я могу отписаться от тебя в любой момент. Когда я иду за тобой назад в Твиттере, я создаю второе ребро, где моя учетная запись является исходным узлом, а ваша — целевым.

 1 Граф
1 Граф

 Н. Богомолов А. М. Алгебраические основы теории дискретных систем. — М.: Физико-математическая литература, 1997. — ISBN 5-02-015033-9
Н. Богомолов А. М. Алгебраические основы теории дискретных систем. — М.: Физико-математическая литература, 1997. — ISBN 5-02-015033-9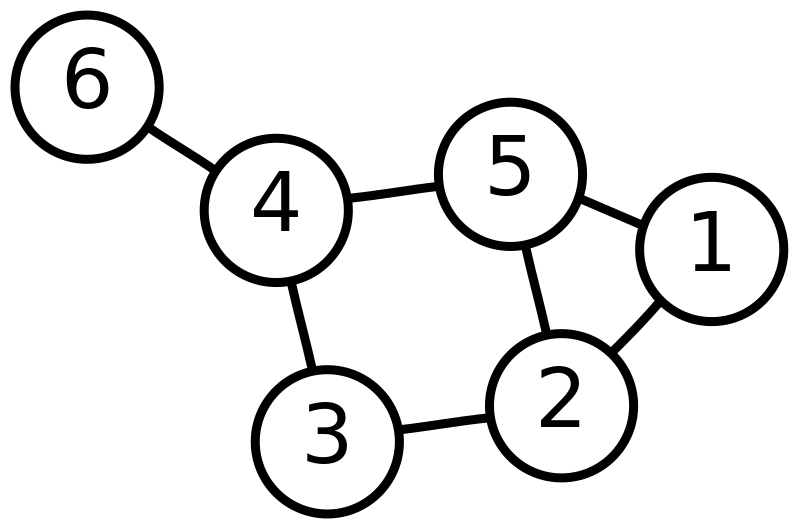



 djvu
djvu

 Таким образом, получается n * (n-1) ребер. Но при этом каждое ребро считается дважды, потому что это неориентированный граф, поэтому разделите его на 2.
Таким образом, получается n * (n-1) ребер. Но при этом каждое ребро считается дважды, потому что это неориентированный граф, поэтому разделите его на 2.