084. Графическое решение неравенств и систем неравенств
Неравенства с одной или двумя переменными и системы неравенств можно решить графически.
Рассмотрим графическое решение неравенства с одной переменной Для этого построим в одной системе координат графики функций и .
Решением неравенства будет множество значений переменной , при которых график функции находится выше графика функции , так как . Это показано на рисунке 6.17 (здесь решение: ) и на рисунке 6.18 (здесь решение: ).
Рассмотрим неравенство Известно, что решением неравенства с двумя переменными есть множество точек плоскости, координаты которых удовлетворяют этому неравенству. Рассмотрим на примерах решение некоторых неравенств с двумя переменными.
Пример 24. Решите графически неравенство .
Решение. Запишем неравенство в виде . Построим прямую .
Ответ. Координаты точек плоскости, которые лежат выше этой прямой, будут решением неравенства (на рис. 6.19 – это заштрихованная область).
6.19 – это заштрихованная область).
Пример 25. Решите неравенство
.
Решение. Запишем неравенство в виде . Построим параболу – это график функции .
Ответ. Решение неравенства – это множество точек плоскости, лежащих на параболе и выше нее (рис. 6.20).
Пример 26. Решите неравенство
.
Решение. Запишем неравенство в виде . Построим параболу .
Ответ. Решение неравенства – это множество точек плоскости, которые лежат в заштрихованной области (ниже построенной параболы) (рис. 6.21).
При решении систем неравенств с двумя переменными находят пересечение областей решений этих неравенств.
Пример 27. Решите графически систему неравенств
Решение. Решение первого неравенства – это множество точек плоскости, которые лежат вне окружности . Решение второго неравенства – это множество точек выше оси (верхняя полуплоскость). Решение третьего неравенства – это множество точек справа от оси (правая полуплоскость).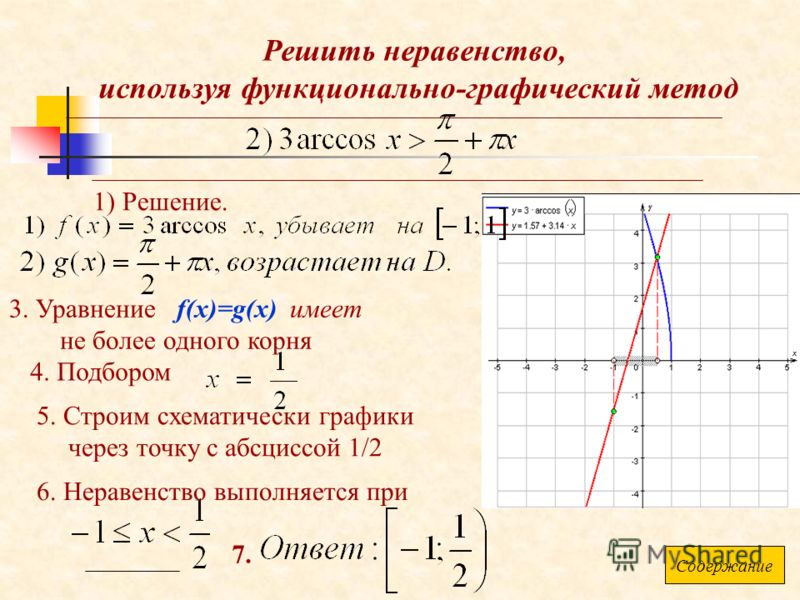
Решением исходной системы неравенств будет пересечение решений этих трех неравенств
Ответ. Решение системы неравенств – это множество точек, лежащих в заштрихованной области (рис. 6.22).
Пример 28. Решите систему неравенств
Решение. Решение первого неравенства– это множество точек плоскости, которые лежат выше прямой Решение второго неравенства – это множество точек плоскости внутри параболы . Решением исходной системы неравенств будет пересечение решений этих двух неравенств.
Найдем точки пересечения графиков функций и :
.
Ответ. Решение системы неравенств – это множество точек, лежащих в заштрихованной области (рис. 6.23).
Пример 29. Решите систему неравенств
Решение. Решение первого и второго неравенств – это множество точек первого координатного угла (рис. 6.24). Решением третьего неравенства является множество точек, лежащих выше ветви гиперболы при (рис.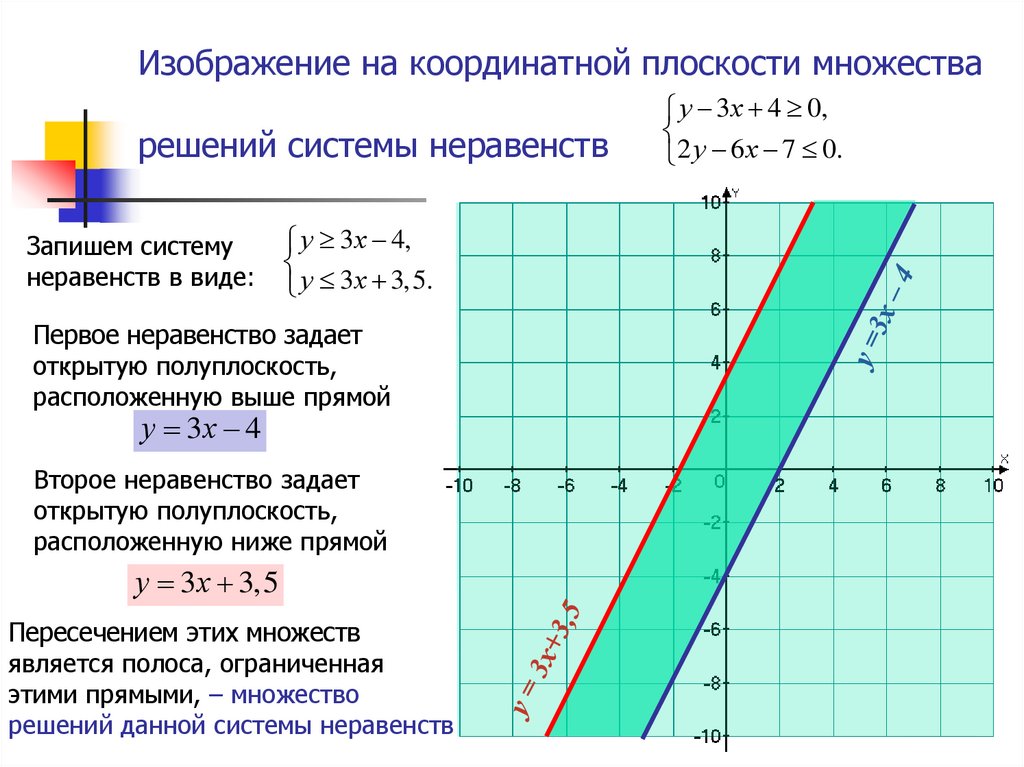
Решением четвертого неравенства является множество точек, лежащих ниже прямой (рис. 6.26).
Ответ. Решение системы – это множество точек, лежащих в первой координатной четверти ниже прямой и выше гиперболы (рис. 6.27).
| < Предыдущая | Следующая > |
|---|
Графическое решение системы линейных неравенств — Студопедия
Поделись
Для графического решения данной задачи необходимо уметь решать графически системы линейных неравенств с двумя переменными.
Решением линейного неравенства с двумя переменными называется множество пар значений переменных , которые удовлетворяют неравенству. Геометрически решением линейного неравенства является полуплоскость, границей которой является прямая .
Порядок действий:
1) записать уравнение и построить на плоскости граничную прямую;
2) выбрать искомую полуплоскость, координаты точек в которой удовлетворяют заданному неравенству.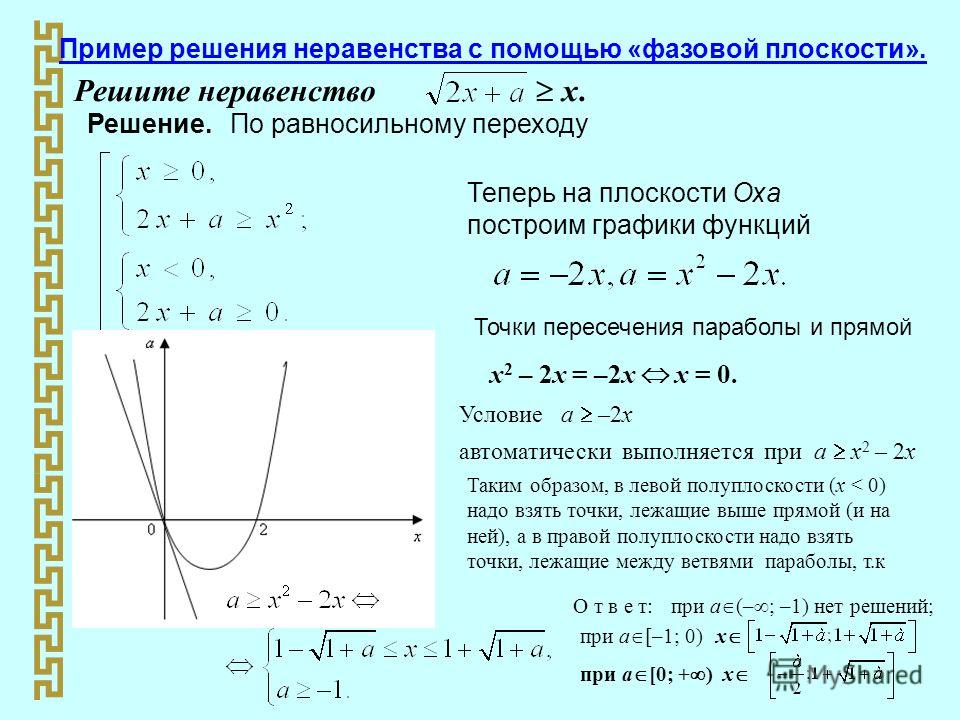 Для этого подставляют в неравенство координаты точки с известными координатами , не лежащей на граничной прямой. Если получится верное числовое неравенство, то искомая полуплоскость та, которая содержит точку (в противном случае берется другая полуплоскость). Плоскость выделяется штриховкой.
Для этого подставляют в неравенство координаты точки с известными координатами , не лежащей на граничной прямой. Если получится верное числовое неравенство, то искомая полуплоскость та, которая содержит точку (в противном случае берется другая полуплоскость). Плоскость выделяется штриховкой.
0
Отметим, что неравенство определяет правую координатную полуплоскость (от оси ), а неравенство – верхнюю координатную полуплоскость (от оси ).
Пример. Решить графически неравенство .
Запишем уравнение граничной прямой и построим её по двум точкам, например, и . Прямая делит плоскость на две полуплоскости.
0 2
–4
Координаты точки удовлетворяют неравенству ( – верно), значит, и координаты всех точек полуплоскости, содержащей точку , удовлетворяют неравенству. Решением неравенства будут координаты точек полуплоскости, расположенной справа от граничной прямой , включая точки на границе. Искомая полуплоскость на рисунке выделена.
Искомая полуплоскость на рисунке выделена.
Решением системы линейных неравенств называется множество пар значений переменных , которые удовлетворяют одновременно всем неравенствам. Геометрически решением системы линейных неравенств является область на плоскости, координаты точек которых лежат в пересечении
полуплоскостей.Решение системы неравенств называется допустимым, если его координаты неотрицательны , . Множество допустимых решений системы неравенств образует область, которая расположенав первой четверти координатной плоскости.
Пример. Построить область решений системы неравенств
Решениями неравенств является:
1) – полуплоскость, расположенная левее и ниже относительно прямой ( ) ;
2) – полуплоскость, расположенная в правой-нижней полуплоскости относительно прямой ( ) ;
3) – полуплоскость, расположенная правее прямой ( ) ;
4) – полуплоскость выше оси абсцисс, то есть прямой ( ) .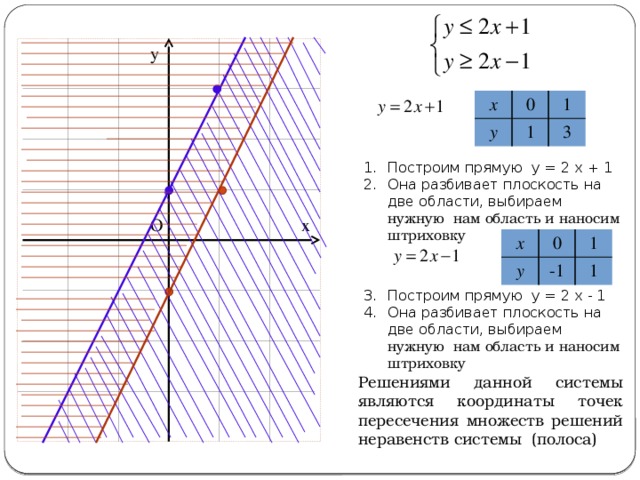
3
1 В
0
Область допустимых решений данной системы линейных неравенств – это множество точек, расположенных внутри и на границе четырехугольника , являющегося
Уровень 1. Решение систем линейных неравенств в графическом виде
Мать Марко просит его купить буррито и тако в ресторане рядом с их домом. Она дает ему 90 долларов и велит накормить 10 человек. Если буррито стоит 5 долларов каждое, а тако — 3 доллара, сколько каждого из них он может купить?
Показать решение expand_more
В этом упражнении есть ряд условий. Начнем с их осмысления. Давайте используем b для представления количества буррито, которое покупает Марко, и t для представления количества тако. Поскольку буррито стоят 5 долларов каждый, общая сумма, потраченная только на бурриоты, составляет 5 миллиардов долларов.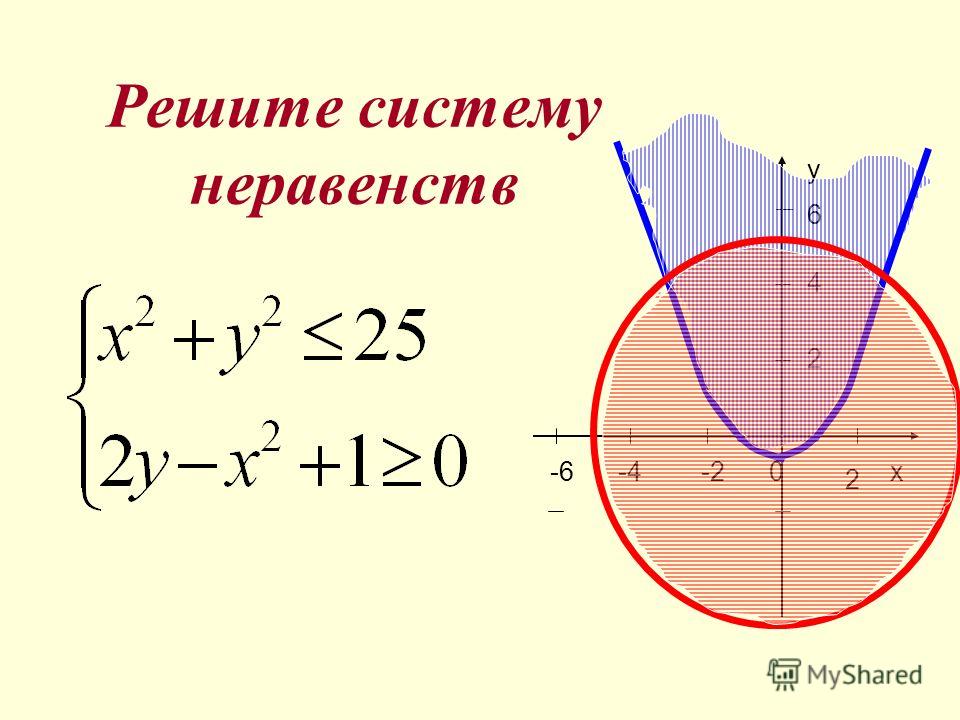 Точно так же, поскольку тако стоит 3 доллара, общая стоимость тако составляет 3 трлн. Таким образом, общая стоимость может быть выражена как
Точно так же, поскольку тако стоит 3 доллара, общая стоимость тако составляет 3 трлн. Таким образом, общая стоимость может быть выражена как
5б+3т.
Поскольку у Марко есть 90 долларов, он не может потратить больше этой суммы. Сумма должна быть меньше или равна 90. Это означает, что5b+3t≤90.
Мы также знаем, что Марко нужно купить достаточно еды, чтобы накормить 10 человек. Предполагая, что никто не хочет делиться тако или буррито, общее количество блюд должно быть не менее 10. Это дает
б+т≥10.
Поскольку оба эти неравенства должны выполняться, получаем следующее.
{5b+3t≤90b+t≥10
Решение этой системы дает все возможные комбинации буррито и тако, которые Марко может купить, покупая достаточно еды и не выходя за рамки своего бюджета. Чтобы решить систему, мы должны построить ее график. Сначала запишем неравенства, выделив b.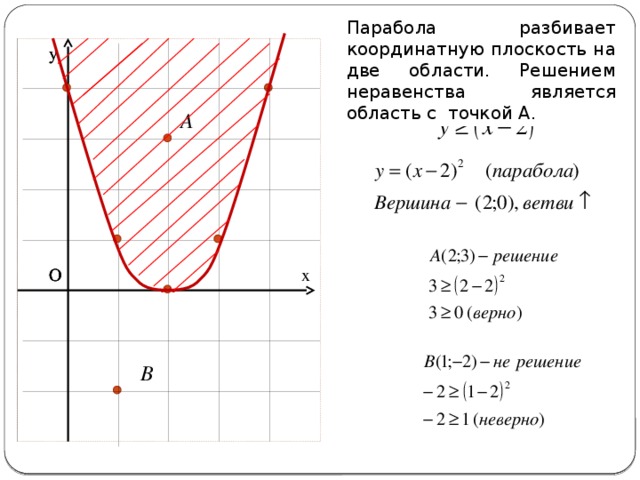
5b+3t≤90
Найти b
5b≤-3t+90
b≤-53t+590
b≤-0.6t+18
Первое неравенство можно выразить как b≤-0,6t+18. Запись второго неравенства в форме пересечения наклона может быть выполнена за один шаг. В частности, путем вычитания t с обеих сторон.
б+т≥10⇔б≥-т+10
Теперь система может быть выражена как
{b≤-0,6t+18b≥-t+10.
Мы обозначим каждое неравенство, показав его граничную линию и заштриховав соответствующую область.
Фиолетовая область представляет набор решений, удовлетворяющих обоим неравенствам. Поскольку Марко не может купить отрицательное количество буррито или тако, нас интересуют только положительные значения b и t.
Любая точка в этом регионе соответствует сочетанию буррито и тако стоимостью менее 9 долларов США.0 и кормит не менее 10 человек. Давайте посмотрим на уголки этого региона.
Отмеченные точки представляют минимальные и максимальные возможности.
- (10,0) и (0,10) означают, что Марко покупает 10 тако или 10 буррито. Тогда он накормит ровно 10 человек, и у него останутся деньги.
- (0,18) и (30,0) говорят, сколько каждого блюда может купить Марко, если он потратил все деньги и купил только тако или буррито. Таким образом, он может купить 18 буррито или 30 тако .
Поскольку мы не знаем, насколько голодны гости и каковы их предпочтения, Марко должен купить и буррито, и тако. Выберем точку в середине области.
Возможно, Марко купит 12 тако и 8 буррито. Таким образом, еды, вероятно, будет достаточно, и у него останутся деньги. Обратите внимание, что, несмотря на то, что десятичные числа являются частью набора решений, ответ следует давать целыми числами, если вы не можете купить часть тако или буррито.
Графически определите множество решений системы неравенств. 4x − y ≥ 8 8x − 2y
< −2 РЕШЕНИЕ. Определить графически множество решений системы неравенств.
Алгебра -> Системы координат и линейные уравнения -> РЕШЕНИЕ: Определить графически множество решений системы неравенств. 4x − у ≥ 8 8x − 2 года < −2 Войти
|


