Урок «Решение неравенств с модулем, содержащих параметр»
- Грачева Надежда Николаевна
Разделы: Математика
Тема: Решение неравенств с модулем, содержащих параметр.
Цели урока:
Обучающая — познакомить с методом решения неравенств с модулем, содержащих параметр.
Развивающая — развитие познавательной активности, логического мышления.
Воспитательная — воспитание организованности, внимания, математической наблюдательности.
ТСО: Проектор, компьютер. Дискета со приложениями №1,№2. Переносная доска.
Наглядность: таблица с формулами
Ход урока:
I. Актуализация знаний и проверка домашнего задания.
Вступительное слово учителя.
Задачи с параметром встречаются на ЕГЭ в группе «С» под номерами 3 и 5.
Так как среди вас есть те, кто претендует на высокий балл, то тема важна для изучения. Начнем с повторения ключевых задач по теме «Решение неравенств с модулем».
Назовите идею решения неравенств, записанных на доске и решите их:
| Ответы. | Ученик. |
Фёдоров С. Свиршевская М. Васильева А. Михеев А. |
На переносной доске работает Клинов А.
Решить неравенство:
Приходилось ли вам встречать и другие способы решения неравенств?
Ответ: графический. Приложение 1.
Рассмотрим, в чем заключается графический способ решения.
Решить неравенство :
Отмечаем точку пересечения графиков А.

Знак > понимаем так, что 1 график выше графика 2 и пишем ответ: X < 2
Приложение 1.
Повторим алгоритм решения линейных неравенств с параметром:
Клинов А. объясняет решение на переносной доске.
x(a+1)<a
если
если
если
II. Изучение новой темы:
Учитель: рассмотрим методы решения типовых примеров.
В числовых неравенствах заменив число на букву, получим неравенство с параметром.
Рассмотрим методы решения этих неравенств. Они аналогичны рассмотренным способам решения неравенств с модулем.
Т.к. знак модуля определён, т.е.
Решение зависит от выражения а+1
Учитель: решим следующее неравенство:
Ответ:
Если ;
Учитель: Решим 3 пример.
Какими способами можно решить неравенство, если бы вместо буквы а стояло число?
Ответ: возведение обеих частей неравенства в квадрат, методом «промежутков».
Те же способы применяются и для неравенства с параметром.
Методом «промежутков» пойдет решать Семенова Д.
Методом возведения в квадрат- Федоров С.
,
,
Проверили решения данного примера.
Каким еще способом можно решить данное неравенство?
Ответ: графический.
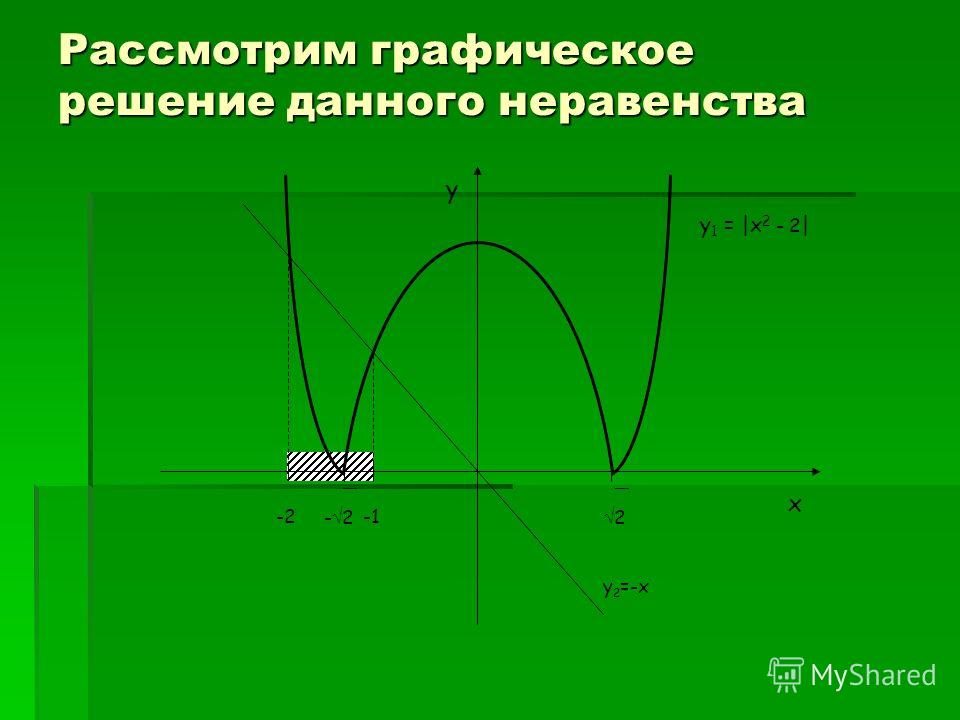
Показывается приложение 2.
1.Строим графики функций
Найдем те значения переменной Х, когда первый график лежит выше второго.
Приложение 2.
Возможны варианты, когда а < 5 и а > 5
Рассмотрев различные способы решения, сделаем вывод- какой метод наиболее рациональный? Какими методами можно решить неравенства с параметром?
Вывод:
Методы решения неравенств с модулем, содержащие параметр, аналогичны тем, что применяются при решении числовых неравенств с модулем: по определению модуля, возведение обеих частей в квадрат, метод интервалов, графический. Необходимо выбирать наиболее рациональный.
Необходимо выбирать наиболее рациональный.
Домашнее задание:
Подобрать и решить 3 уравнения с модулем, 3 неравенства с модулем и 3 неравенства с модулем, содержащие параметр. Можно придумать самим.
Рабочая программа «Решение уравнений и неравенств содержащих переменную под знаком модуля» | Рабочая программа по алгебре (9 класс):
Муниципальное бюджетное общеобразовательное учреждение
«Основная общеобразовательная школа №5 города Лесосибирска»
«Согласовано» Руководитель МО ________/ / Протокол № ______ от «__»___________2015г. | «Согласовано» Заместитель директора по УВР МБОУ «ООШ №5» ___________/ / «__»____________2015г. | Утверждаю Директор МБОУ «ООШ №5 » _____________/Попова Н.А./ Приказ № ___________ от «__»___________2015г. |
РАБОЧАЯ ПРОГРАММА КУРСА ПО ВЫБОРУ
«Решение уравнений и неравенств, содержащих переменную под знаком модуля».
Абакумова Зульфия Салиховна
педагог высшей категории
в 9 классе
Рассмотрено на заседании
методического совета
протокол № ____
от «__»_______2015г.
Пояснительная записка.
Данная программа ориентирована на учащихся 9 классов, которые в старшей ступени выберут профиль, связанный с математикой. Курс строится по программе повышенного уровня изучения предмета и помогает учащимся в подготовке к итоговой аттестации в новой форме.
Выбор темы обусловлен тем, что решение уравнений и неравенств, содержащих знак модуля, лишь вскользь затрагивается на уроках в неспециализированных классах, а программе упоминается на уровне определения модуля и решения простейших уравнений. Тем не менее, задания с модулем включены во второй части работ государственной итоговой аттестации в формате ОГЭ, где предъявляются более высокие требования к математической подготовке выпускников. Тема является благодатной с точки зрения освоения графических приёмов решения задач как равноправных с аналитическими методами, и обладает при этом хорошей наглядностью. Кроме того, данная тема развивает математическую культуру, логическое и альтернативное мышление – учащимся приходится столкнуться с задачами, для решения которых необходимо рассматривать несколько возможных вариантов. При решении уравнений и неравенств с модулем приходится рассматривать случаи, когда выражения, стоящие под знаком модуля неотрицательны и когда они отрицательны. Только после проработки всех возможных вариантов и их исследования, находится нужное решение.
Тем не менее, задания с модулем включены во второй части работ государственной итоговой аттестации в формате ОГЭ, где предъявляются более высокие требования к математической подготовке выпускников. Тема является благодатной с точки зрения освоения графических приёмов решения задач как равноправных с аналитическими методами, и обладает при этом хорошей наглядностью. Кроме того, данная тема развивает математическую культуру, логическое и альтернативное мышление – учащимся приходится столкнуться с задачами, для решения которых необходимо рассматривать несколько возможных вариантов. При решении уравнений и неравенств с модулем приходится рассматривать случаи, когда выражения, стоящие под знаком модуля неотрицательны и когда они отрицательны. Только после проработки всех возможных вариантов и их исследования, находится нужное решение.
Цели курса: — расширение представлений учащихся о методах решения уравнений и неравенств, содержащих модуль; расширение сферы математических знаний
Задачи курса:
- формировать и развивать у обучающихся оценки своего потенциала с точки зрения образовательной перспективы: готовность и способность осваивать математику на повышенном уровне;
- развить интеллектуальные и практические умения в области решения уравнений, неравенств, построения графиков, содержащих модуль;
- выработать умения самостоятельно приобретать и применять знания в различных ситуациях;
- развить творческие способности;
- совершенствовать коммутативные навыки, которые способствуют развитию умений работать в группе, аргументировать и отстаивать свою точку зрения и уметь слушать другого.

Содержание курса предполагает самостоятельную подготовку учащихся: работу с разными информационными источниками. В практическую часть включаются задания, предлагаемые при подготовке к сдаче ОГЭ и ЕГЭ.
Процесс обучения ориентирован на рациональное сочетание устных и письменных, практических ( составление справочной таблицы) видов работ .
В технологии проведения занятий присутствует этап самопроверки, который предоставляет учащимся возможность самим проверить, как ими усвоен изученный материал. Итоговой формой контроля может стать защита реферата или защита проекта по теме курса.
Требования к уровню подготовки учащихся.
Основными результатами освоения содержания курса являются умения:
- решать уравнения, содержащие один, два, три модуля;
- решать неравенства, содержащие модуль;
- строить графики функций, содержащих модуль;
- строить графики кусочной функции;
- решать графически простейшие линейные и квадратные уравнения, содержащие модуль и параметр.

- интерпретировать результаты своей деятельности;
Перечисленные умения формируются на основе знаний о модуле
(определения, свойств модуля), о влиянии модуля на расположение графиков функций на координатной плоскости, влиянии модуля при решении уравнений и неравенств.
Учебно – тематический план.
№ | Тема | Количество часов |
Вводное занятие. Понятие модуля. | 1 | |
Модуль действительного числа | 2 | |
Линейные уравнения, содержащие модуль. | 4 | |
Построение графиков линейных функций, содержащих знак модуля. | 2 | |
Графическое решение уравнений, содержащих переменную под знаком модуля. | 2 | |
Решение систем линейных уравнений, содержащих модуль. | 2 | |
Решение линейных уравнений с модулем и параметром | 4 | |
Квадратные уравнения, содержащие модуль | 4 | |
Построение графика квадратичной функции, содержащей знак модуля. | 2 | |
Графическое решение квадратных уравнений с модулем и параметром. | 4 | |
Решение неравенств с модулем | 4 | |
Защита проектов. | 2 | |
Итоговое занятие. | 1 | |
Итого | 34 |
Содержание курса.
- Вводное занятие.
 Понятие модуля.( 1 час)
Понятие модуля.( 1 час)
Актуальность курса, особенности организации занятий. Понятие модуля, его геометрический смысл.
- Модуль действительного числа.
Преобразование алгебраических
выражений, содержащих модуль рационального числс. (2).
- Линейные уравнения, содержащие модуль.(4)
Линейные уравнений, содержащих один, два , три модуля. Решение алгебраическим способом и методом интервалов.
4. Построение графиков линейных функций, содержащих знак модуля (2).
5. Понятие графика функций, содержащих модуль.
Виды графиков их свойства. Рациональные способы их построения.
6. Графическое решение уравнений, содержащих переменную под знаком модуля. (2)
Графическая интерпретация решения уравнений, содержащих переменную под знаком модуля ( количество корней, приближённые значения корней)
7. Решение систем линейных уравнений, содержащих модуль (2)
Системы линейных уравнений, содержащих модуль; способы их решения. Зависимость количества решений системы линейных уравнений от коэффициентов
Зависимость количества решений системы линейных уравнений от коэффициентов
.8. Решение линейных уравнений с модулем и параметром.
График линейной функции, зависимость расположения графика функции от коэффициентов. Общий вид уравнения прямой. Линейные уравнения, содержащие параметр. Взаимное расположение прямых на плоскости
9. Квадратные уравнения, содержащие модуль (4)
Квадратные уравнения с модулем. Решение алгебраическим способом и методом интервалов
10.Построение графиков квадратичной функций, содержащих знак модуля. (2)
Виды графиков .
11. Графическое решение квадратных уравнений с модулем и параметром.
Графический способ определения числа корней уравнения с модулем в зависимости от входящего в него параметра.
12. Решение неравенств с модулем (4)
Неравенства содержащие знак абсолютной величины (линейные и квадратн ые). Неравенства, содержащие под модулем линейный двучлен (неравенства вида ). Неравенства, содержащие под модулем квадратный трёхчлен.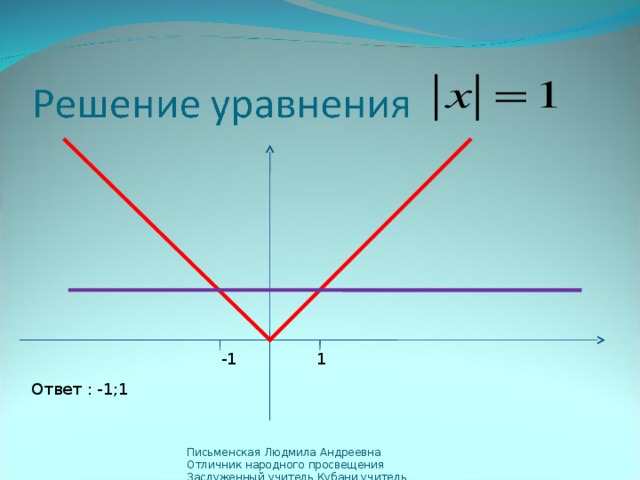
Способы их решения (алгебраический и геометрический)
Календарно – тематический план
№ | Тема | сроки |
Вводное занятие. Понятие модуля. | 3.09-8.09 | |
Линейные уравнения, содержащие модуль. | 10.09-15.09 | |
Модуль действительного числа | 17.09-22.09 | |
Модуль действительного числа | 24.09-29.09 | |
Линейные уравнения, содержащие модуль | 1. | |
Линейные уравнения, содержащие модуль. | 8.10-13.10 | |
Линейные уравнения, содержащие модуль. | 15.10- 20.10 | |
Построение графиков линейных функций, содержащих знак модуля. | 22.10-27.10 | |
Построение графиков линейных функций, содержащих знак модуля | 5.11-10.11 | |
Графическое решение уравнений, содержащих переменную под знаком модуля. | 12.11-17.11 | |
Графическое решение уравнений, содержащих переменную под знаком модуля. | 19.11-24.11 | |
Решение систем линейных уравнений, содержащих модуль. | 26.11-1.12 | |
Решение систем линейных уравнений, содержащих модуль. | 3.12-8.12 | |
Решение линейных уравнений с модулем и параметром | 10.12-15.12 | |
Решение линейных уравнений с модулем и параметром | 17. | |
Решение линейных уравнений с модулем и параметром | 24.12-29.12 | |
Решение линейных уравнений с модулем и параметром | 14.01- 19.01 | |
Квадратные уравнения, содержащие модуль | 21.01-16.01 | |
Квадратные уравнения, содержащие модуль | 28.01-2.02 | |
Квадратные уравнения, содержащие модуль | 4. | |
Квадратные уравнения, содержащие модуль | 11.02-16.02 | |
Построение графика квадратичной функции, содержащей знак модуля. | 18.02-23.02 | |
Построение графика квадратичной функции, содержащей знак модуля | 25.02-2.03 | |
Графическое решение квадратных уравнений с модулем и параметром. | 4.03-9.03 | |
Графическое решение квадратных уравнений с модулем и параметром | 11. | |
Графическое решение квадратных уравнений с модулем и параметром | 18.03-23.03 | |
Графическое решение квадратных уравнений с модулем и параметром | 1.04-6.04 | |
Решение неравенств с модулем | 8.04-13.04 | |
Решение неравенств с модулем | 15.04-20.04 | |
Решение неравенств с модулем | 22.04-27. | |
Решение неравенств с модулем | 29.05-4.05 | |
Защита проектов. | 6.05-11.05 | |
Защита проектов | 13.05-18.05 | |
Итоговое занятие | 20.05-25.05 |
Литература.
- Вавилов В.В. Задачи по математике. Уравнения и неравенства. Справочное пособие /Ред. В.В. Вавилов, И.И. Мельников, С.Н. Олехник,. М.: Наука, 1987.
- Галицкий М. Л. Сборник задач по алгебре.: Учеб. Пособие для 8-9 кл. с углубл.
 изучением математики / М. Л. Галицкий, А.М. Гольдман, Л.И. Звавич – 10-е изд. – М.: Просвещение, 2004.
изучением математики / М. Л. Галицкий, А.М. Гольдман, Л.И. Звавич – 10-е изд. – М.: Просвещение, 2004. - Дорофеев В.Г. и др. Оценка качества подготовки выпускников основной школы по математике. – М.: Дрофа, 2005.
- Кузнецова Г.М. и др. сборник заданий для проведения письменного экзамена по алгебре за курс основной школы. – М.: Дрофа, 2008.
- Макарычев Ю.Н. Изучение алгебры в 7 – 9 классах : кн. для учителя. — М.: Просвещение,2010
- Обязательный минимум содержания основного общего образования по математике(Приказ МО РФ от19.05.98. №1276).
- Приходько Л.А. Математика для поступающих в десятый лицейский класс: варианты конкурсных заданий: учебное пособие / Под общ. Ред. Райцина: — М.: Издательство «Экзамен».2006.
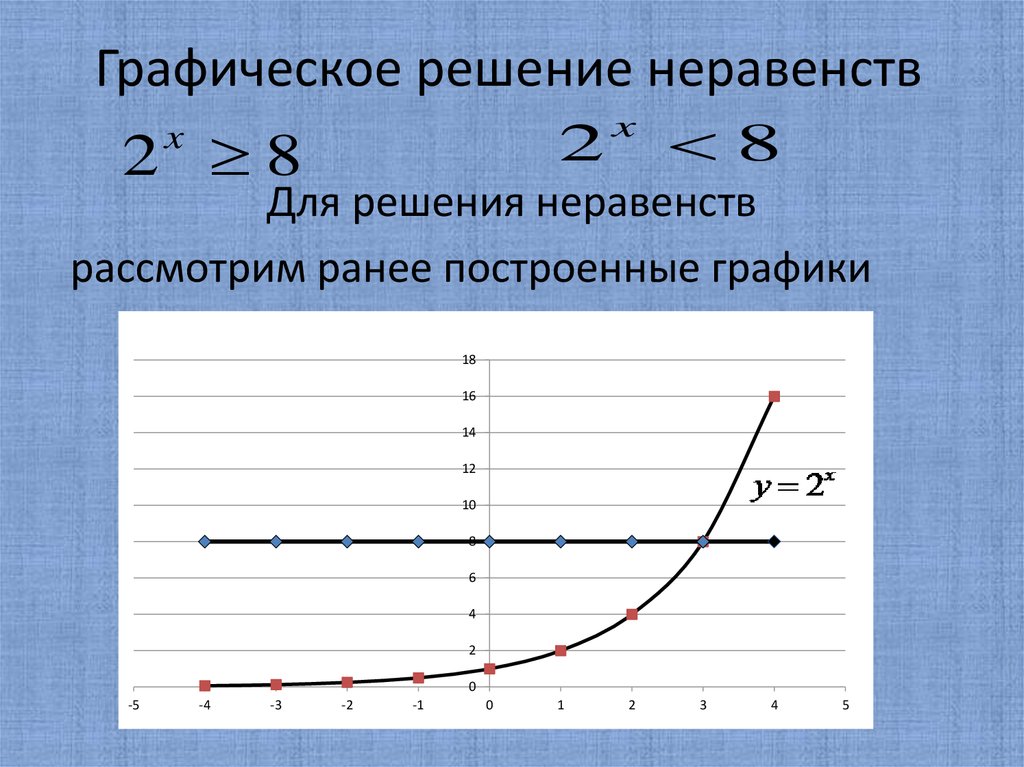
абсолютных значений неравенств. — Решение, График, Формула, Примеры
 Проще говоря, мы можем сказать, что абсолютное неравенство — это неравенство с символом абсолютного значения в нем. Ее можно решить, используя два метода: числовую прямую или формулы. Неравенство абсолютного значения представляет собой простое линейное выражение с одной переменной и имеет такие символы, как >, <, > , < .
Проще говоря, мы можем сказать, что абсолютное неравенство — это неравенство с символом абсолютного значения в нем. Ее можно решить, используя два метода: числовую прямую или формулы. Неравенство абсолютного значения представляет собой простое линейное выражение с одной переменной и имеет такие символы, как >, <, > , < .В этой статье мы познакомимся с понятием абсолютных неравенств и методами их решения. В основном мы сосредоточимся на линейных абсолютных неравенствах и обсудим, как отображать их в виде графиков с помощью различных решенных примеров для лучшего понимания концепции.
| 1. | Что такое абсолютное неравенство? |
| 2. | Решение абсолютных неравенств |
| 3. | Графики абсолютных неравенств |
| 4. | Формулы неравенств абсолютного значения |
| 5. | Часто задаваемые вопросы об абсолютных неравенствах |
Что такое абсолютное неравенство?
Абсолютное неравенство — это неравенство, включающее абсолютное алгебраическое выражение с переменными. Неравенства абсолютного значения представляют собой алгебраические выражения с функциями абсолютного значения и символами неравенства. То есть абсолютное неравенство может быть одной из следующих форм (или) может быть преобразовано в одну из следующих форм:
Неравенства абсолютного значения представляют собой алгебраические выражения с функциями абсолютного значения и символами неравенства. То есть абсолютное неравенство может быть одной из следующих форм (или) может быть преобразовано в одну из следующих форм:
- топор + b < с
- топор + б > с
- топор + б < в
- топор + б > в
Итак, абсолютные неравенства бывают двух типов. Они либо меньше или равны, либо больше или равны формам. Две разновидности неравенств таковы.
- один с < или ≤
- один с > или ≥
Решение абсолютных неравенств
В этом разделе мы научимся решать абсолютные неравенства. Вот процедура решения абсолютных неравенств с использованием числовой прямой. Процедура решения абсолютного неравенства показана шаг за шагом вместе с примером для лучшего понимания.
Пример : Решите абсолютное неравенство |x+2| < 4
Решение:
Шаг 1: Примите неравенство как уравнение и решите его.
Превратите знак неравенства «<" в нашем неравенстве в "=" и решите его.
⇒ |х + 2| = 4
Убрав знак абсолютного значения с левой стороны, мы получим знак + с другой стороны.
⇒ x + 2 = + 4
Это приводит к двум уравнениям, одно со знаком «+», другое со знаком «-».
⇒ x+2 = 4 и x+2 = -4
⇒ x = 2 и x = -6
Шаг 2: Представьте решения шага 1 на числовой прямой по порядку.
Здесь мы видим, что числовая линия разделена на 3 части/отрезка.
Шаг 3: Возьмите случайное число из каждого из этих интервалов и замените его данным неравенством. Определите, какое из этих чисел действительно удовлетворяет данному неравенству.
Интервал | Случайное число | Проверка заданного неравенства случайным числом |
|---|---|---|
| (-∞, -6) | -7 | |-7+2| < 4 ⇒ 5 < 4 ⇒ Это ложь |
| (-6, 2) | 0 | |0+2| < 4 ⇒ 2 < 4 ⇒ Верно |
| (2, ∞) | 3 | |3+2| < 4 ⇒ 5 < 4 ⇒ Это ложь |
Шаг 4: Решением данного неравенства является интервал(ы), который приводит к True в приведенной выше таблице
Следовательно, решением данного неравенства является (-6, 2) или (-6 < x < 2).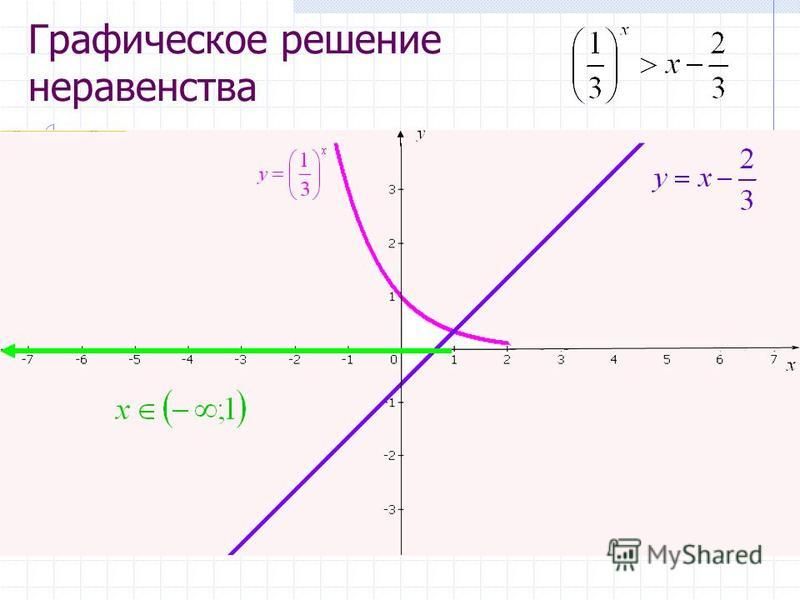 Эта процедура представлена в следующей блок-схеме.
Эта процедура представлена в следующей блок-схеме.
Примечание:
- Если проблема была |x+2| < 4, то решение было бы [-6, 2] (или) -6 < x < 2, т.е.
- Если |х + 2| < 4 ⇒ -6 < х < 2
- Если |x+2| ≤ 4 ⇒ -6 ≤ x ≤ 2
- Если проблема была |x+2| ≥ 4, то решение было бы (-∞, -6] U [2, ∞). то есть,
- Если |х + 2| > 4 ⇒ x ∈ (-∞, -6) U (2, ∞)
- Если |x+2| ≥ 4 ⇒ x ∈ (-∞, -6] U [2, ∞)
Графики абсолютных неравенств
Когда мы рисуем абсолютные неравенства, мы наносим решение неравенства на график. На изображении ниже показано, как построить график линейных абсолютных неравенств. При построении графика абсолютных значений неравенства мы должны помнить о следующих вещах.
- Используйте открытые точки на концах открытых интервалов (т.е. таких интервалов, как (a,b) ).
- Используйте закрытые/сплошные точки на концах закрытых интервалов (т.
 е. таких интервалов, как [a,b]).
е. таких интервалов, как [a,b]).
Формулы неравенств абсолютного значения
Итак, мы изучили процедуру решения абсолютных неравенств с использованием числовой прямой. Эта процедура работает для любого типа неравенства. На самом деле неравенства можно решать и с помощью формул. Чтобы применить формулы, во-первых, нам нужно выделить выражение абсолютного значения в левой части неравенства. Для решения неравенств по формулам нужно помнить 4 случая. Предположим, что а — положительное действительное число во всех случаях.
Случай 1. Когда неравенство имеет вид |x|
< а или |х| < а.В этом случае для решения неравенства используем следующие формулы: Если |x| < а ⇒ -а < х < а, и если | х | < а ⇒ -а < х < а.
Случай 2. Когда неравенство имеет вид |x| > а или |х|
> а. В этом случае для решения неравенства используем следующие формулы: Если |x| > a ⇒ x < -a или x > a, и если |x| > а, затем х < -а или х > а.
Случай 3. Когда неравенство имеет вид |x|
< -а или |х| < -aМы знаем, что абсолютное значение всегда дает положительное значение. Таким образом, |х| всегда положительный. Кроме того, -a отрицательно (поскольку мы предполагали, что «a» положительно). Таким образом, данные два неравенства означают, что «положительное число меньше (или меньше или равно) отрицательного числа», что никогда не бывает истинным. Таким образом, все такие неравенства имеют нет решения. Если |х| < -а или |х| ≤ -a ⇒ Нет решения.
Случай 4. Когда неравенство имеет вид |x| > -а или |х|
> -а. Мы знаем, что абсолютное значение всегда дает положительное значение. Таким образом, |х| всегда положительный. Кроме того, -a отрицательно (поскольку мы предполагали, что положительно). Таким образом, данные два неравенства означают, что «положительное число больше (или больше или равно) отрицательного числа», что всегда верно. Таким образом, решением всех таких неравенств является множество всех действительных чисел R.
Важные примечания к абсолютным неравенствам
- Если рядом с числом стоит скобка, это означает, что это число НЕ включено в решение.
- Если перед числом стоит квадратная скобка, это означает, что число включено в решение.
- Мы всегда используем круглые скобки при -∞ или ∞ независимо от заданного неравенства.
- Мы решаем использовать квадратные скобки (или) круглые скобки для числа в зависимости от того, есть ли в данном неравенстве «=».
Статьи по теме
- Домен и диапазон
- Линейные уравнения
- Стандартная форма линейных уравнений
Часто задаваемые вопросы об абсолютных неравенствах
Что такое абсолютные неравенства в алгебре?
Неравенства абсолютного значения — это алгебраические неравенства, которые включают алгебраические выражения с символами абсолютного значения и символами неравенства. Алгебраические выражения представлены символом абсолютного значения, а символ равенства заменяется символом больше или меньше. Представление абсолютного неравенства |ax + b | < в.
Алгебраические выражения представлены символом абсолютного значения, а символ равенства заменяется символом больше или меньше. Представление абсолютного неравенства |ax + b | < в.
Как решить абсолютное неравенство?
Абсолютное неравенство решается за последовательность шагов. Неравенство сначала рассматривается как равенство и решается относительно переменной ‘x’. Значения переменной представлены на числовой прямой. Теперь мы можем определить интервал на числовой прямой. Из каждого интервала взять случайное число и подставить в данное неравенство. Значение, которое удовлетворяет неравенству, и соответствующий интервал значения является решением неравенства абсолютного значения.
Какие символы используются в абсолютном неравенстве?
Символы, используемые в абсолютных неравенствах: больше (>), меньше (<), больше или равно ( > ) и меньше или равно ( < ).
Как построить график абсолютного неравенства?
График абсолютного неравенства строится, сначала рассматривая его как равенство. Готовится граф этого равенства, а затем из этого графа собираются определенные значения и подставляются в выражение неравенства. Значения, которые удовлетворяют неравенству, отображаются обратно на графике, и эта конкретная область графика представляет график неравенства абсолютного значения.
Готовится граф этого равенства, а затем из этого графа собираются определенные значения и подставляются в выражение неравенства. Значения, которые удовлетворяют неравенству, отображаются обратно на графике, и эта конкретная область графика представляет график неравенства абсолютного значения.
Где мы используем абсолютные неравенства?
Неравенства абсолютного значения используются в реальных жизненных ситуациях и при поиске решений в линейном программировании для поиска оптимального решения. Многие деловые ситуации требуют от нас поиска наилучшего решения, а не просто решения. Здесь мы можем использовать абсолютные неравенства для представления проблемной ситуации.
Когда вы переключаете знак в абсолютных значениях неравенства?
Мы меняем знак в абсолютном неравенстве, когда умножаем или делим обе части неравенства на отрицательное число. Это означает, что мы меняем знак «меньше» < на знак «больше» > и наоборот.
В чем разница между абсолютным неравенством и абсолютным равенством?
Абсолютное значение Неравенства состоят из абсолютных алгебраических выражений со знаками неравенства, такими как <, > ≤ или ≥.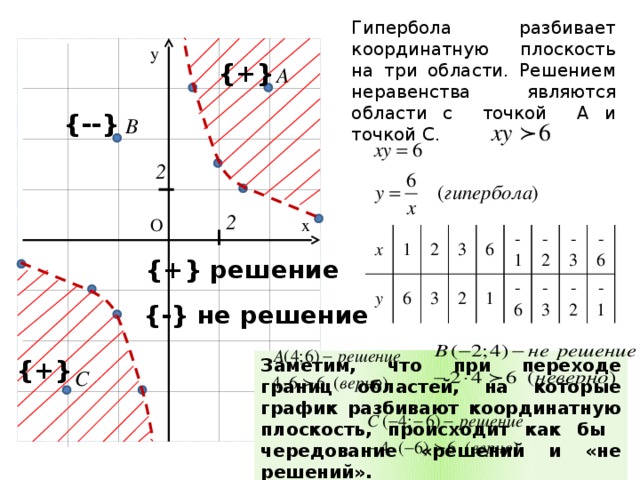 С другой стороны, абсолютные равенства значений состоят из абсолютных алгебраических выражений со знаком равенства =.
С другой стороны, абсолютные равенства значений состоят из абсолютных алгебраических выражений со знаком равенства =.
Линейные неравенства и абсолютные неравенства
Результаты обучения
- Используйте интервальную запись для выражения неравенств.
- Использовать свойства неравенств.
- Решение сложных неравенств.
- Решение абсолютных неравенств.
Нелегко попасть в список лучших университетов. Предположим, что студенты должны были нести нагрузку по курсу не менее 12 кредитных часов и поддерживать средний балл 3,5 или выше. Как можно математически выразить эти требования к спискам почета? В этом разделе мы рассмотрим различные способы выражения различных наборов чисел, неравенств и неравенств с абсолютными значениями.
Написание и обработка неравенств
Указание решения неравенства, такого как [latex]x\ge 4[/latex], может быть достигнуто несколькими способами.
Мы можем использовать числовую строку, как показано ниже. Синий луч начинается в точке [latex]x=4[/latex] и, как показано стрелкой, продолжается до бесконечности, что показывает, что набор решений включает все действительные числа, большие или равные 4.
Синий луч начинается в точке [latex]x=4[/latex] и, как показано стрелкой, продолжается до бесконечности, что показывает, что набор решений включает все действительные числа, большие или равные 4.
Мы можем использовать нотация построителя наборов : [latex]\{x|x\ge 4\}[/latex], что переводится как «все действительные числа x , так что x больше или равно 4». Обратите внимание, что фигурные скобки используются для обозначения набора.
Третий метод представляет собой интервальную нотацию , где наборы решений обозначаются скобками или квадратными скобками. Решения [латекс]x\ge 4[/латекс] представлены как [латекс]\влево[4,\infty \вправо)[/латекс]. Это, пожалуй, самый полезный метод, поскольку он применяется к понятиям, изучаемым позже в этом курсе, и к другим математическим курсам более высокого уровня.
Основная концепция, которую следует помнить, заключается в том, что круглые скобки представляют решения, большие или меньшие, чем число, а скобки представляют решения, которые больше или равны или меньше или равны числу.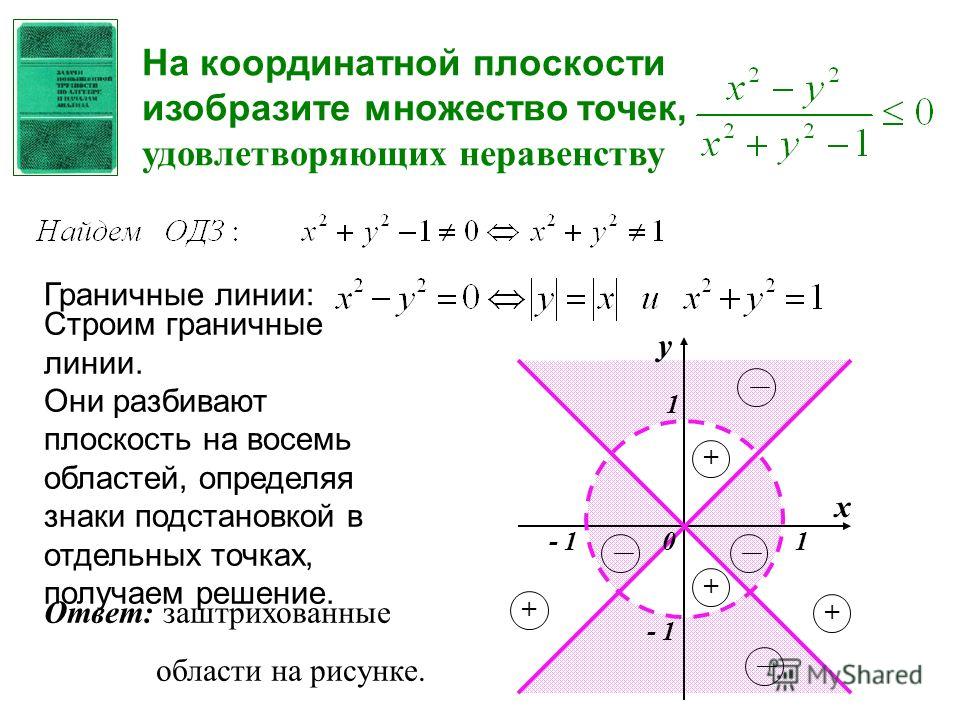 Используйте круглые скобки для обозначения бесконечности или отрицательной бесконечности, поскольку положительная и отрицательная бесконечность не являются числами в обычном смысле этого слова и, следовательно, не могут быть «приравнены». Несколько примеров интервал , или набор чисел, в который попадает решение, это [латекс]\влево[-2,6\вправо)[/латекс], или все числа между [латекс]-2[/латекс] и [латекс ]6[/латекс], включая [латекс]-2[/латекс], но не включая [латекс]6[/латекс]; [латекс]\влево(-1,0\вправо)[/латекс], все действительные числа между, но не включая [латекс]-1[/латекс] и [латекс]0[/латекс]; и [latex]\left(-\infty ,1\right][/latex], все действительные числа меньше и включая [latex]1[/latex]. В приведенной ниже таблице показаны возможные варианты.
Используйте круглые скобки для обозначения бесконечности или отрицательной бесконечности, поскольку положительная и отрицательная бесконечность не являются числами в обычном смысле этого слова и, следовательно, не могут быть «приравнены». Несколько примеров интервал , или набор чисел, в который попадает решение, это [латекс]\влево[-2,6\вправо)[/латекс], или все числа между [латекс]-2[/латекс] и [латекс ]6[/латекс], включая [латекс]-2[/латекс], но не включая [латекс]6[/латекс]; [латекс]\влево(-1,0\вправо)[/латекс], все действительные числа между, но не включая [латекс]-1[/латекс] и [латекс]0[/латекс]; и [latex]\left(-\infty ,1\right][/latex], все действительные числа меньше и включая [latex]1[/latex]. В приведенной ниже таблице показаны возможные варианты.
 «>
«>Пример: использование интервальной нотации для выражения всех действительных чисел, больших или равных числу
Используйте интервальную нотацию для обозначения всех действительных чисел, больших или равных [латекс]-2[/латекс].
Показать решение
Попробуйте
Используйте запись интервала для обозначения всех вещественных чисел между [латекс]-3[/латекс] и [латекс]5[/латекс] включительно.
Показать решение
Пример: использование записи интервалов для выражения всех действительных чисел, меньших или равных
a или больших или равных bЗапишите интервал, выражающий все действительные числа, меньшие или равные [латекс]-1[/ латекс] или больше или равно [латекс]1[/латекс].
Показать решение
Попробуйте
Выразите все действительные числа, меньшие [латекс]-2[/латекс] или большие или равные 3, в интервальной записи.
Показать решение
Использование свойств неравенств
Когда мы работаем с неравенствами, мы обычно можем обращаться с ними так же, как и с уравнениями, но не совсем так. Мы можем использовать свойство сложения и свойство умножения , чтобы решить их. Единственным исключением является то, что когда мы умножаем или делим на отрицательное число, мы должны перевернуть символ неравенства.
Мы можем использовать свойство сложения и свойство умножения , чтобы решить их. Единственным исключением является то, что когда мы умножаем или делим на отрицательное число, мы должны перевернуть символ неравенства.
Общее примечание: свойства неравенств
[латекс]\begin{array}{ll}\text{Свойство добавления}\hfill& \text{Если }a< b,\text{ then }a+c< b+ c.\hfill \\ \hfill & \hfill \\ \text{Свойство умножения}\hfill & \text{Если }a< b\text{ и }c> 0,\text{, то }ac< bc.\hfill \\ \hfill & \text{Если }a< b\text{ и }c< 0,\text{, то }ac> bc.\hfill \end{массив}[/latex]
Эти свойства также применимы к [латексу]a\le b[/латексу], [латексу]а>б[/латексу] и [латексу]а\геб[/латексу].
Пример: демонстрация свойства сложения
Проиллюстрируйте свойство сложения для неравенств, решая каждое из следующих действий:
- [латекс]х — 15<4[/латекс]
- [латекс]6\ge x — 1[/латекс]
- [латекс]x+7>9[/латекс]
Показать решение
Попробуйте
Решите [латекс]3x — 2<1[/латекс].
Показать решение
Пример: демонстрация свойства умножения
Проиллюстрируйте свойство умножения для неравенств, решая каждое из следующих действий:
- [латекс]3x<6[/латекс]
- [латекс]-2x — 1\ge 5[/латекс]
- [латекс]5-x>10[/латекс]
Показать решение
Попробуйте
Решите [латекс]4x+7\ge 2x — 3[/латекс].
Показать решение
Алгебраическое решение неравенств с одной переменной
Как показали примеры, мы можем выполнять одни и те же действия с обеими частями неравенства точно так же, как и с уравнениями; мы объединяем подобные термины и выполняем операции. Чтобы решить, мы изолируем переменную.
Пример: Алгебраическое решение неравенства
Решите неравенство: [latex]13 — 7x\ge 10x — 4[/latex].
Показать решение
Попробуйте
Решите неравенство и запишите ответ, используя интервальную запись: [латекс]-x+4<\frac{1}{2}x+1[/latex].
Показать решение
Пример. Решение неравенства с дробями
Решите следующее неравенство и запишите ответ в виде интервалов: [latex]-\frac{3}{4}x\ge -\frac{5}{8}+\frac {2}{3}x[/латекс].
Показать решение
Попробуйте
Решите неравенство и запишите ответ в интервальной записи: [латекс]-\frac{5}{6}x\le \frac{3}{4}+\frac{8}{3}x [/латекс].
Показать решение
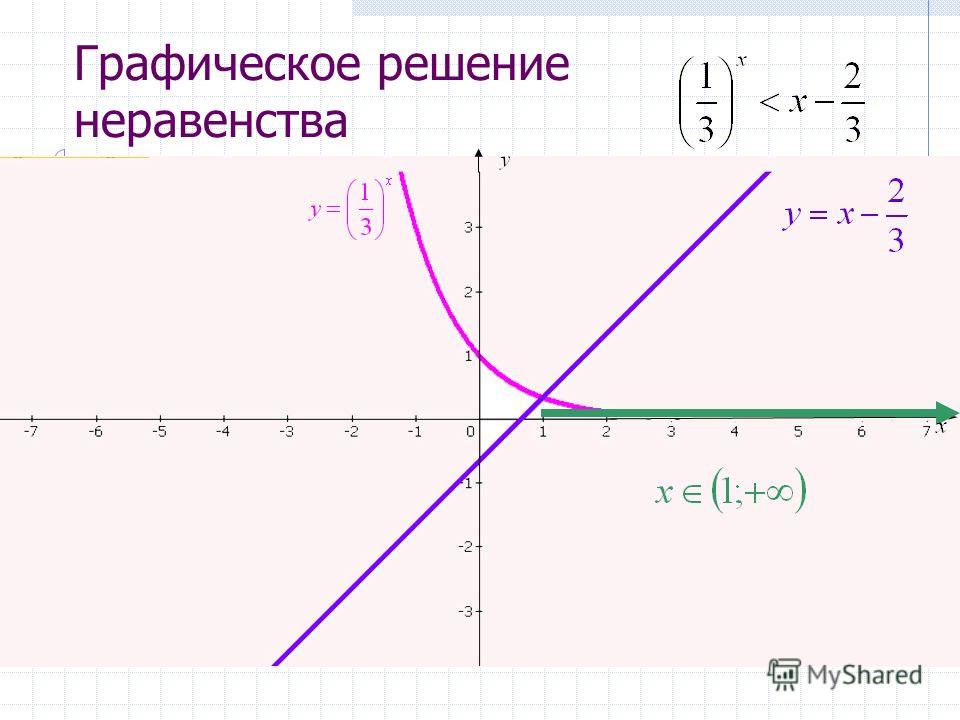
Составные и абсолютные неравенства
Составное неравенство включает два неравенства в одном выражении. Такой оператор, как [латекс]4 Решите составное неравенство: [латекс]3\le 2x+2<6[/латекс]. Показать решение Решите составное неравенство [латекс]4<2x - 8\le 10[/латекс]. Показать решение Решите составное неравенство с переменными во всех трех частях: [latex]3+x>7x — 2>5x — 10[/latex]. Показать решение Решите сложное неравенство: [латекс]3у<4 - 5у<5+3у[/латекс]. Показать решение Как известно, абсолютное значение величины — это положительное число или нуль. От начала координат точка, расположенная в [латекс]\влево(-x,0\вправо)[/латекс], имеет абсолютное значение [латекс]х[/латекс], поскольку она удалена на x единиц. Рассмотрим абсолютное значение как расстояние от одной точки до другой точки. Независимо от направления, положительного или отрицательного, расстояние между двумя точками представляется как положительное число или ноль. Ан абсолютное неравенство представляет собой уравнение формы [латекс]|А|<В,|А|\le B,|A|>B,\text{или }|A|\ge B[/латекс] , , где A , а иногда B , представляет собой алгебраическое выражение, зависящее от переменной x. Решить неравенство означает найти набор всех значений [latex]x[/latex] – , которые удовлетворяют задаче. Обычно этот набор будет интервалом или объединением двух интервалов и будет включать диапазон значений. Существует два основных подхода к решению абсолютных неравенств: графический и алгебраический. Преимущество графического подхода в том, что мы можем прочитать решение, интерпретируя графики двух уравнений. Преимущество алгебраического подхода в том, что решения являются точными, поскольку точные решения иногда трудно прочитать на графике. Предположим, мы хотим узнать все возможные доходы от инвестиций, если бы мы могли заработать некоторую сумму денег в пределах от 200 до 600 долларов. [latex]\begin{array}{c}-200\le x — 600\le 200\\ -200 +600\le x — 600+600\le 200+600\\ 400\le x\le 800\end{array}[/latex] Это означает, что наша прибыль составит от 400 до 800 долларов. Для решения абсолютных неравенств, как и в случае с абсолютными уравнениями, мы записываем два неравенства, а затем решаем их независимо друг от друга. Для алгебраического выражения X и [latex]k>0[/latex] абсолютное неравенство представляет собой неравенство вида: [latex]\begin {array}{l}|X|< k\text{ что эквивалентно }-k< X< k\hfill \text{ или }\ |X|> k\text{ что эквивалентно }X< -k \text{ или }X> k\hfill \end{array}[/latex] Эти утверждения также применимы к [latex]|X|\le k[/latex] и [latex]|X|\ge k[ /латекс]. Опишите все значения [latex]x[/latex] на расстоянии 4 от числа 5. Показать решение Опишите все x- значений на расстоянии 3 от числа 2. Показать решение Решить [латекс]|х — 1|\le 3[/латекс]. Показать решение Учитывая уравнение [latex]y=-\frac{1}{2}|4x — 5|+3[/latex], определите x -значения, для которых y -значения являются отрицательными. Показать решение Решите [латекс]-2|k — 4|\le -6[/латекс]. Показать решение Пример. Решение составного неравенства

Попробуйте
Пример. Решение составного неравенства с переменной во всех трех частях
Попробуйте
Решение абсолютных неравенств

 Мы можем решить алгебраически для множества x- значений, таких, что расстояние между [latex]x[/latex] и 600 меньше 200. Мы представляем расстояние между [latex]x[/latex] и 600 как [latex]|x — 600|[ /latex], и, следовательно, [латекс]|x — 600|\le 200[/latex] или
Мы можем решить алгебраически для множества x- значений, таких, что расстояние между [latex]x[/latex] и 600 меньше 200. Мы представляем расстояние между [latex]x[/latex] и 600 как [latex]|x — 600|[ /latex], и, следовательно, [латекс]|x — 600|\le 200[/latex] или Общее примечание: абсолютные неравенства

Пример: определение числа на заданном расстоянии
Попробуйте
Пример. Решение абсолютного неравенства
Пример: использование графического подхода для решения абсолютных неравенств
Попробуйте
Ключевые понятия
 Очень применимый в исчислении, это система скобок и квадратных скобок, которые указывают, какие числа включены в набор и включены ли конечные точки.
Очень применимый в исчислении, это система скобок и квадратных скобок, которые указывают, какие числа включены в набор и включены ли конечные точки.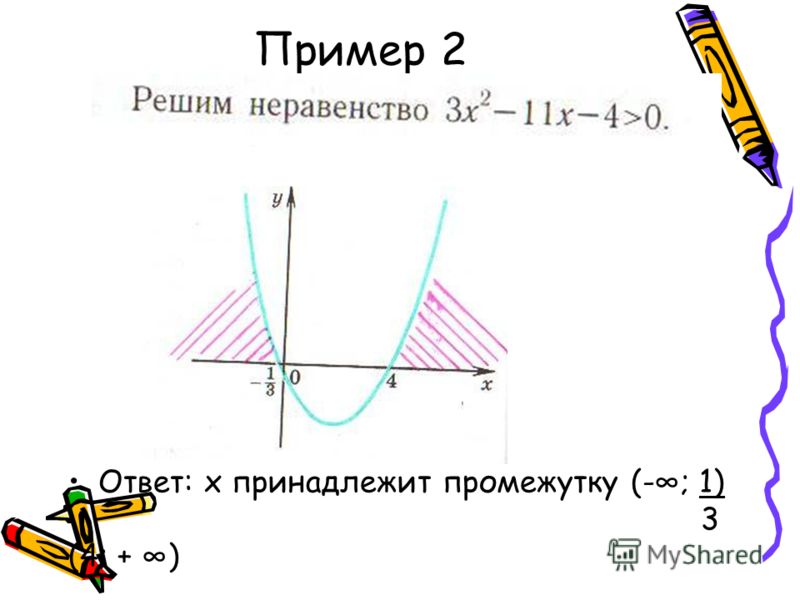





 Понятие модуля.( 1 час)
Понятие модуля.( 1 час) 10-6.10
10-6.10
 12-22.12
12-22.12 02-9.02
02-9.02 03-16.03
03-16.03 04
04 изучением математики / М. Л. Галицкий, А.М. Гольдман, Л.И. Звавич – 10-е изд. – М.: Просвещение, 2004.
изучением математики / М. Л. Галицкий, А.М. Гольдман, Л.И. Звавич – 10-е изд. – М.: Просвещение, 2004. е. таких интервалов, как [a,b]).
е. таких интервалов, как [a,b]).