Обратные тригонометрические функции
Определение обратных тригонометрических функций
Поскольку тригонометрические функции периодичны, то обратные к ним функции не однозначны. Так, уравнение y = sin x, при заданном , имеет бесконечно много корней. Действительно, в силу периодичности синуса, если x такой корень, то и x + 2πn (где n целое) тоже будет корнем уравнения. Таким образом, обратные тригонометрические функции многозначны. Чтобы с ними было проще работать, вводят понятие их главных значений. Рассмотрим, например, синус: y = sin x. Если ограничить аргумент x интервалом , то на нем функция y = sin x монотонно возрастает. Поэтому она имеет однозначную обратную функцию, которую называют арксинусом: x = arcsin y.
Если особо не оговорено, то под обратными тригонометрическими функциями имеют в виду их главные значения, которые определяются следующими определениями.
- Арксинус ( y = arcsin x )
- – это функция, обратная к синусу ( x = sin y ), имеющая область определения и множество значений .
- Арккосинус ( y = arccos x )
- – это функция, обратная к косинусу ( x = cos y ), имеющая область определения и множество значений .
- Арктангенс ( y = arctg x )
- – это функция, обратная к тангенсу ( x = tg y ), имеющая область определения и множество значений .
- Арккотангенс ( y = arcctg x )
- – это функция, обратная к котангенсу ( x = ctg y ), имеющая область определения и множество значений .
Графики обратных тригонометрических функций
Графики обратных тригонометрических функций получаются из графиков тригонометрических функций зеркальным отражением относительно прямой y = x. См. разделы Синус, косинус, Тангенс, котангенс.

y = arcsin x

y = arccos x

y = arctg x

y = arcctg x
Основные формулы
Здесь следует особо обратить внимание на интервалы, для которых справедливы формулы.
arcsin(sin x) = x при
sin(arcsin x) = x
arccos(cos x) = x при
cos(arccos x) = x
arctg(tg x) = x при
tg(arctg x) = x
arcctg(ctg x) = x при
ctg(arcctg x) = x
Формулы, связывающие обратные тригонометрические функции
См. также: Вывод формул обратных тригонометрических функцийФормулы суммы и разности
при или
при и
при и
при или
при и
при и
при
при
при
при
при
при
при
при
при
при
Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.
Автор: Олег Одинцов. Опубликовано:
Обратные тригонометрические функции, их свойства и графики. — Студопедия
Обратные тригонометрические функции (арксинус, арккосинус, арктангенс и арккотангенс) являются основным элементарным функциями. Часто из-за приставки «арк» обратные тригонометрические функции называют аркфункциями. Сейчас мы рассмотрим их графики и перечислим свойства.
Функция арксинус y = arcsin(x).
Изобразим график функции арксинус:
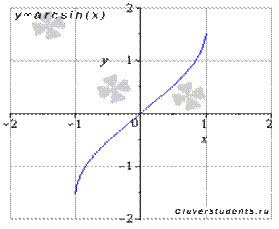
Свойства функции арксинус y = arcsin(x).
· Областью определения функции арксинус является интервал от минус единицы до единицы включительно: 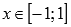 .
.
· Область значений функции y = arcsin(x): 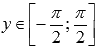 .
.
· Функция арксинус — нечетная, так как 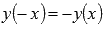
· Функция y = arcsin(x) возрастает на всей области определения, то есть, при 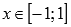 .
.
· Функция вогнутая при  , выпуклая при
, выпуклая при 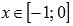 .
.
· Точка перегиба (0; 0), она же ноль функции.
· Асимптот нет.
Функция арккосинус y = arccos(x).
График функции арккосинус имеет вид:
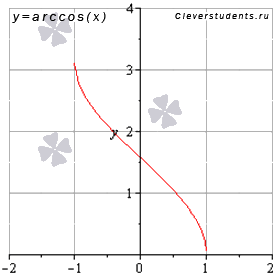
Свойства функции арккосинус y = arccos(x).
· Область определения функции арккосинус: 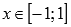
· Область значений функции y = arccos(x): 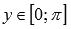 .
.
· Функция не является ни четной ни нечетной, то есть, она общего вида.
· Функция арккосинус убывает на всей области определения, то есть, при 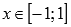 .
.
· Функция вогнутая при 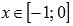 , выпуклая при
, выпуклая при  .
.
· Точка перегиба  .
.
· Асимптот нет.
Функция арктангенс y = arctg(x).
График функции арктангенс имеет вид:
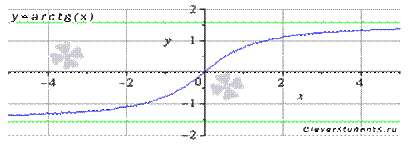
Свойства функции арктангенс y = arctg(x).
· Область определения функции y = arctg(x): 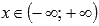 .
.
· Область значений функции арктангенс: 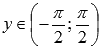 .
.
· Функция арктангенс — нечетная, так как 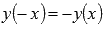 .
.
· Функция возрастает на всей области определения, то есть, при 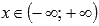 .
.
· Функция арктангенс вогнутая при 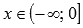 , выпуклая при
, выпуклая при  .
.
· Точка перегиба (0; 0), она же ноль функции.
· Горизонтальными асимптотами являются прямые  при
при 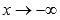 и
и 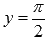 при
при 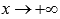 . На чертеже они показаны зеленым цветом.
. На чертеже они показаны зеленым цветом.
Функция арккотангенс y = arcctg(x).
Изобразим график функции арккотангенс:
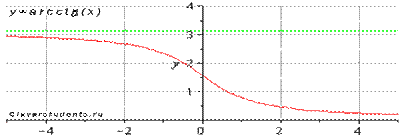
Свойства функции арккотангенс y = arcctg(x).
· Областью определения функции арккотангенс является все множество действительных чисел: 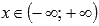
· Область значений функции y = arcctg(x): 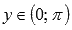 .
.
· Функция арккотангенс не является ни четной ни нечетной, то есть, она общего вида.
· Функция убывает на всей области определения, то есть, при 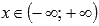 .
.
· Функция вогнутая при  , выпуклая при
, выпуклая при 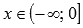 .
.
· Точка перегиба  .
.
· Горизонтальными асимптотами являются прямые 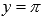 при
при 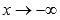
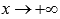 .
.| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(60) | |
| 4 | Найти точное значение | sin(30 град. ) | |
| 5 | Найти точное значение | ||
| 6 | Найти точное значение | tan(30 град. ) | |
| 7 | Найти точное значение | arcsin(-1) | |
| 8 | Найти точное значение | sin(pi/6) | |
| 9 | Найти точное значение | cos(pi/4) | |
| 10 | Найти точное значение | sin(45 град. ) | |
| 11 | Найти точное значение | sin(pi/3) | |
| 12 | Найти точное значение | arctan(-1) | |
| 13 | Найти точное значение | cos(45 град. ) | |
| 14 | Найти точное значение | cos(30 град. ) | |
| 15 | Найти точное значение | tan(60) | |
| 16 | Найти точное значение | csc(45 град. ) | |
| 17 | Найти точное значение | tan(60 град. ) | |
| 18 | Найти точное значение | sec(30 град. ) | |
| 19 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 20 | График | y=sin(x) | |
| 21 | Преобразовать из радианов в градусы | pi/6 | |
| 22 | Найти точное значение | cos(60 град. ) | |
| 23 | Найти точное значение | cos(150) | |
| 24 | Найти точное значение | tan(45) | |
| 25 | Найти точное значение | sin(30) | |
| 26 | Найти точное значение | sin(60) | |
| 27 | Найти точное значение | cos(pi/2) | |
| 28 | Найти точное значение | tan(45 град. ) | |
| 29 | График | y=sin(x) | |
| 30 | Найти точное значение | arctan(- квадратный корень 3) | |
| 31 | Найти точное значение | csc(60 град. ) | |
| 32 | Найти точное значение | sec(45 град. ) | |
| 33 | Найти точное значение | csc(30 град. ) | |
| 34 | Найти точное значение | sin(0) | |
| 35 | Найти точное значение | sin(120) | |
| 36 | Найти точное значение | cos(90) | |
| 37 | Преобразовать из радианов в градусы | pi/3 | |
| 38 | Найти точное значение | sin(45) | |
| 39 | Найти точное значение | tan(30) | |
| 40 | Преобразовать из градусов в радианы | 45 | |
| 41 | Найти точное значение | tan(60) | |
| 42 | Упростить | квадратный корень x^2 | |
| 43 | Найти точное значение | cos(45) | |
| 44 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 45 | Преобразовать из радианов в градусы | pi/6 | |
| 46 | Найти точное значение | cot(30 град. ) | |
| 47 | Найти точное значение | arccos(-1) | |
| 48 | Найти точное значение | arctan(0) | |
| 49 | График | y=cos(x) | |
| 50 | Найти точное значение | cot(60 град. ) | |
| 51 | Преобразовать из градусов в радианы | 30 | |
| 52 | Упростить | ( квадратный корень x+ квадратный корень 2)^2 | |
| 53 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 54 | Найти точное значение | sin((5pi)/3) | |
| 55 | Упростить | 1/( кубический корень от x^4) | |
| 56 | Найти точное значение | sin((3pi)/4) | |
| 57 | Найти точное значение | tan(pi/2) | |
| 58 | Найти угол А | tri{}{90}{}{}{}{} | |
| 59 | Найти точное значение | sin(300) | |
| 60 | Найти точное значение | cos(30) | |
| 61 | Найти точное значение | cos(60) | |
| 62 | Найти точное значение | cos(0) | |
| 63 | Найти точное значение | arctan( квадратный корень 3) | |
| 64 | Найти точное значение | cos(135) | |
| 65 | Найти точное значение | cos((5pi)/3) | |
| 66 | Найти точное значение | cos(210) | |
| 67 | Найти точное значение | sec(60 град. ) | |
| 68 | Найти точное значение | sin(300 град. ) | |
| 69 | Преобразовать из градусов в радианы | 135 | |
| 70 | Преобразовать из градусов в радианы | 150 | |
| 71 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 72 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 73 | Преобразовать из градусов в радианы | 89 град. | |
| 74 | Преобразовать из градусов в радианы | 60 | |
| 75 | Найти точное значение | sin(135 град. ) | |
| 76 | Найти точное значение | sin(150) | |
| 77 | Найти точное значение | sin(240 град. ) | |
| 78 | Найти точное значение | cot(45 град. ) | |
| 79 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 80 | Упростить | 1/( кубический корень от x^8) | |
| 81 | Найти точное значение | sin(225) | |
| 82 | Найти точное значение | sin(240) | |
| 83 | Найти точное значение | cos(150 град. ) | |
| 84 | Найти точное значение | tan(45) | |
| 85 | Вычислить | sin(30 град. ) | |
| 86 | Найти точное значение | sec(0) | |
| 87 | Упростить | arcsin(-( квадратный корень 2)/2) | |
| 88 | Найти точное значение | cos((5pi)/6) | |
| 89 | Найти точное значение | csc(30) | |
| 90 | Найти точное значение | arcsin(( квадратный корень 2)/2) | |
| 91 | Найти точное значение | tan((5pi)/3) | |
| 92 | Найти точное значение | tan(0) | |
| 93 | Вычислить | sin(60 град. ) | |
| 94 | Найти точное значение | arctan(-( квадратный корень 3)/3) | |
| 95 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 96 | Вычислить | arcsin(-1) | |
| 97 | Найти точное значение | sin((7pi)/4) | |
| 98 | Найти точное значение | arcsin(-1/2) | |
| 99 | Найти точное значение | sin((4pi)/3) | |
| 100 | Найти точное значение | csc(45) |
Пособие по теме Арксинус, арккосинус, арктангенс числа
ГОСУДАРСТВЕННОЕ АВТОНОМНОЕ ПРОФЕССИОНАЛЬНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ НОВОСИБИРСКОЙ ОБЛАСТИ «КУПИНСКИЙ МЕДИЦИНСКИЙ ТЕХНИКУМ»
МЕТОДИЧЕСКОЕ ПОСОБИЕ
Для самостоятельной работы студентов
По дисциплине: МАТЕМАТИКА: алгебра и начало математического анализа; геометрия
Тема: «АРКСИНУС, АРККОСИНУС, АРКТАНГЕНС ЧИСЛА»
Специальность: 34.02.01 Сестринское дело Курс: 1
(базовой подготовки)
Купино
2019
Рассмотрено на заседании предметной цикловой
Методической комиссии по общеобразовательным дисциплинам,
общему гуманитарному и социально-экономическому, математическому и
естественно-научному циклу
Протокол № _____ от «_____» _________20____г.
Автор – составитель: преподаватель математики высшей категории Тюменцева О.Н.
Купино
2019 г
Пояснительная записка к методическому пособию
Методическое пособие предназначено для повторения теоретических и практических знаний по теме.
Цель пособия – повторить понятия: тригонометрических функций, радианной меры углов, таблицы значений тригонометрических функций, формулы перевода градусов в радианы и наоборот, определения арксинуса, арккосинуса, арктангенса числа и подготовится к занятию по теме «Арксинус, арккосинус, арктангенс числа».
Данное пособие рекомендовано для студентов первого курса специальности 34.02.01 Сестринское дело. Пособие содержит определения, свойства и формулы по теме: Арксинус, арккосинус, арктангенс числа, тест для самоконтроля и ключи к тесту.
Пособие направлено на формирование навыков самостоятельной работы с учебным материалом, формирование навыков решения задач, формирование и развитие творческого потенциала, повышение интереса к дисциплине.
Арксинус, арккосинус, арктангенс числа
Арксинус
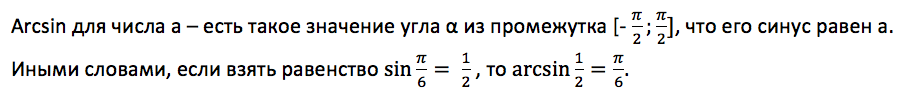
Чтобы больше понять о свойствах арксинуса, необходимо рассмотреть его функцию. График y = arcsin x имеет вид асимметричной кривой, проходящей через центр координат.
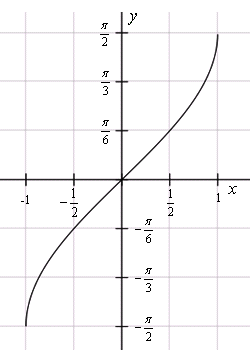
Свойства арксинуса:

Так как f(x) нечетная, то arcsin (- x) = — arcsin x.
Y = 0 при x = 0.
На всей своей протяженности график возрастает.
Если сопоставить графики sin и arcsin, у двух тригонометрических функций можно найти общие закономерности.

Арккосинус
Arccos числа а — это значение угла α, косинус которого равен а.
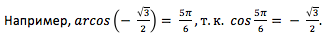
Кривая y = arcos x зеркально отображает график arcsin x, с той лишь разницей, что проходит через точку π/2 на оси OY.
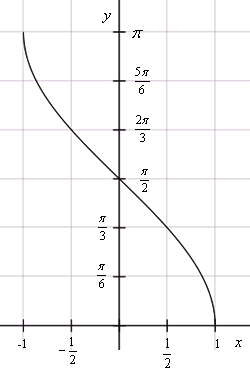
Рассмотрим функцию арккосинуса более подробно:
Функция определена на отрезке [-1; 1].
ОДЗ для arccos — [0, π].
График целиком расположен в I и II четвертях, а сама функция не является ни четной, ни нечетной.
Y = 0 при x = 1.
Кривая убывает на всей своей протяженности. Некоторые свойства арккосинуса совпадают с функцией косинуса.
Некоторые свойства арккосинуса совпадают с функцией косинуса.

Задание 1. Укажите функции изображенные на рисунке.

Ответ: рис. 1 – 4, рис.2 — 1.
Арктангенс
Arctg числа a – это такое значение угла α, что его тангенс равен а.
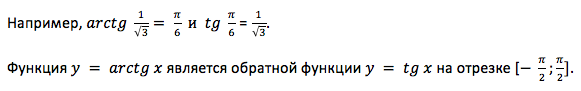
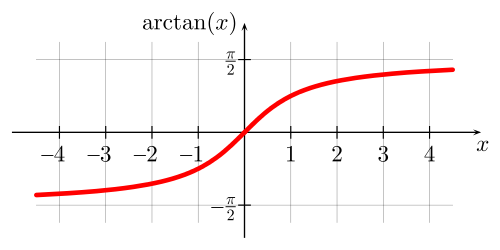
Если рассмотреть график арктангенса, можно выделить следующие свойства:
График бесконечен и определен на промежутке (- ∞; + ∞).
Арктангенс нечетная функция, следовательно, arctg (- x) = — arctg x.
Y = 0 при x = 0.
Кривая возрастает на всей области определения.

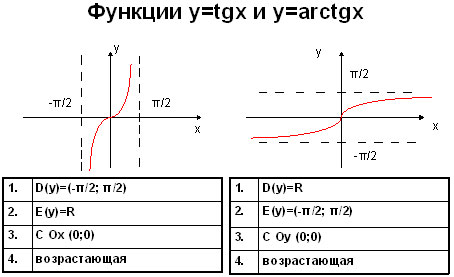
Приведем краткий сравнительный анализ tg x и arctg x в виде таблицы.
Арккотангенс
Arcctg числа a — принимает такое значение α из интервала (0; π), что его котангенс равен а.
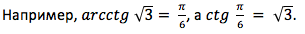


Свойства функции арккотангенса:
Интервал определения функции – бесконечность.
Область допустимых значений – промежуток (0; π).
F(x) не является ни четной, ни нечетной.
На всем своем протяжении график функции убывает.
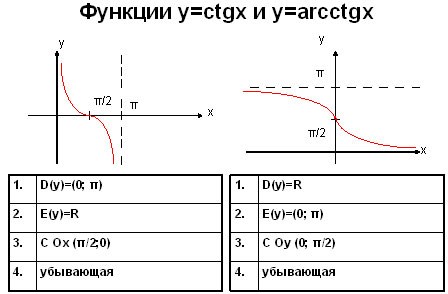
Сопоставить ctg x и arctg x очень просто, нужно лишь сделать два рисунка и описать поведение кривых.
Задание 2. Соотнести график и форму записи функции.

Если рассуждать логически, из графиков видно, что обе функции возрастающие. Следовательно, оба рисунка отображают некую функцию arctg. Из свойств арктангенса известно, что y=0 при x = 0,
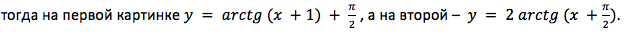
Ответ: рис. 1 – 1, рис. 2 – 4.
Пример 1. Вычислить значение 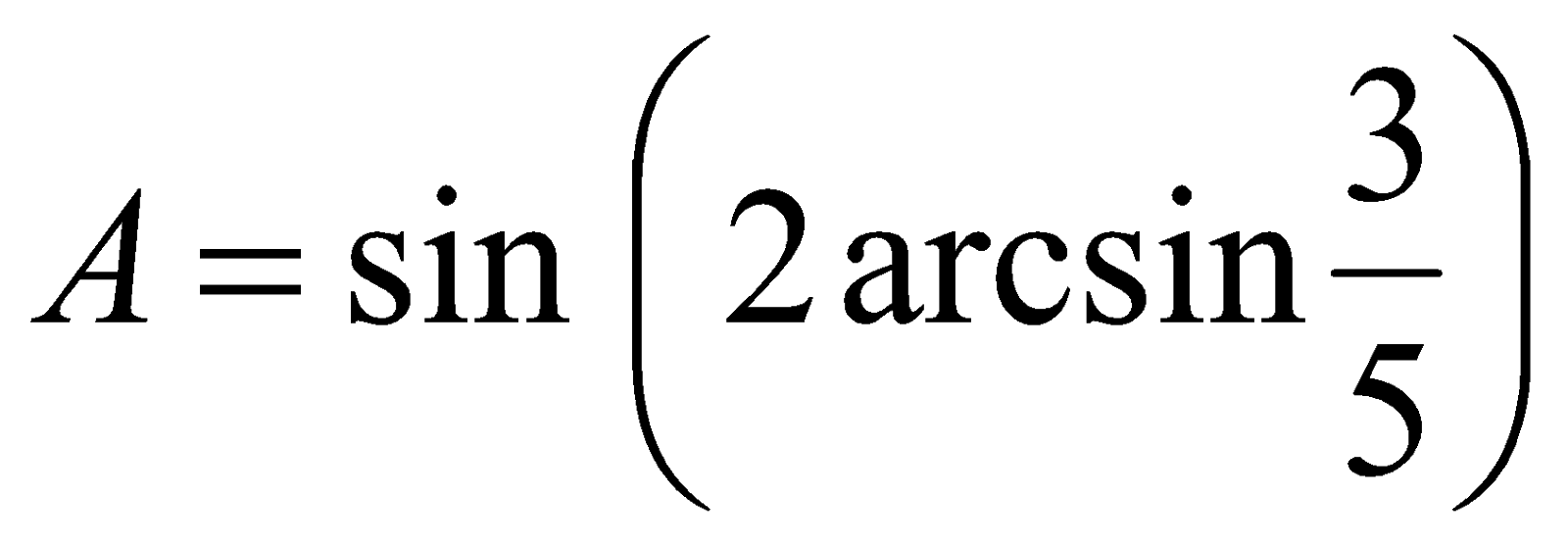 .
.
Решение. Если обозначить 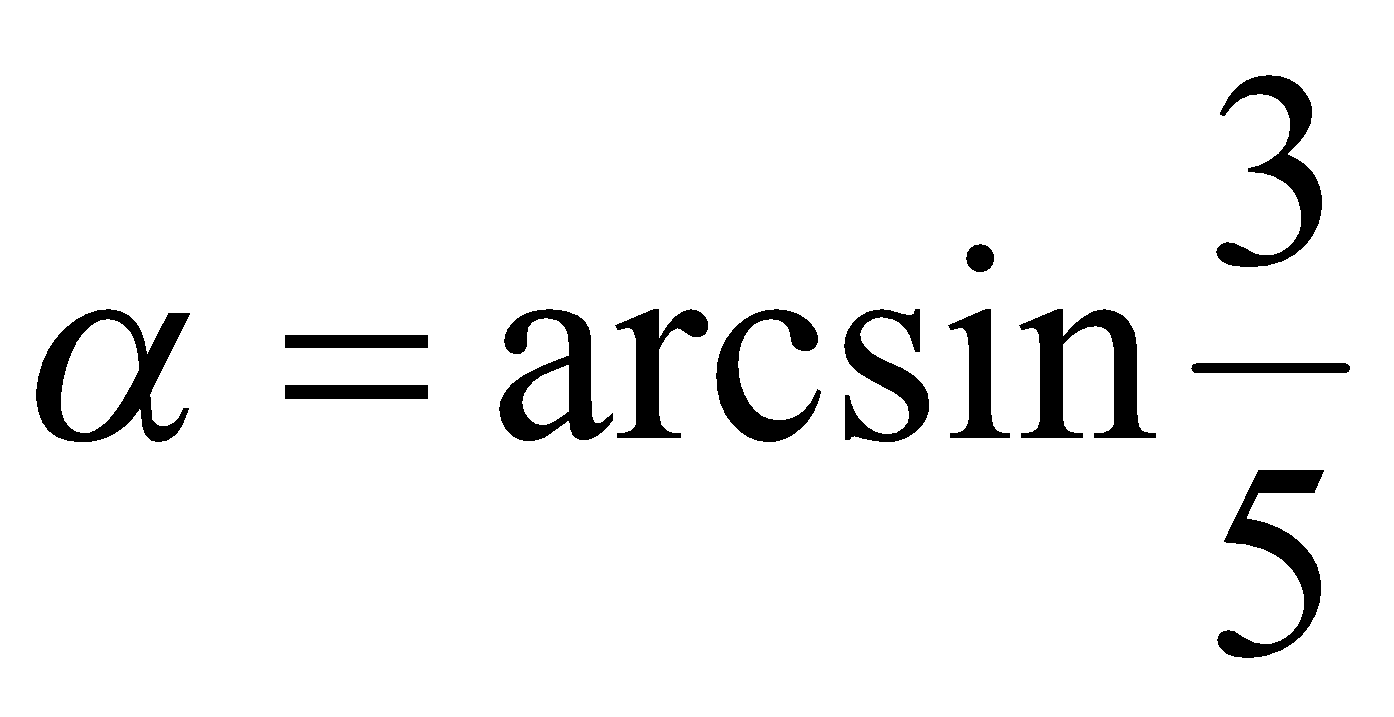 , то
, то 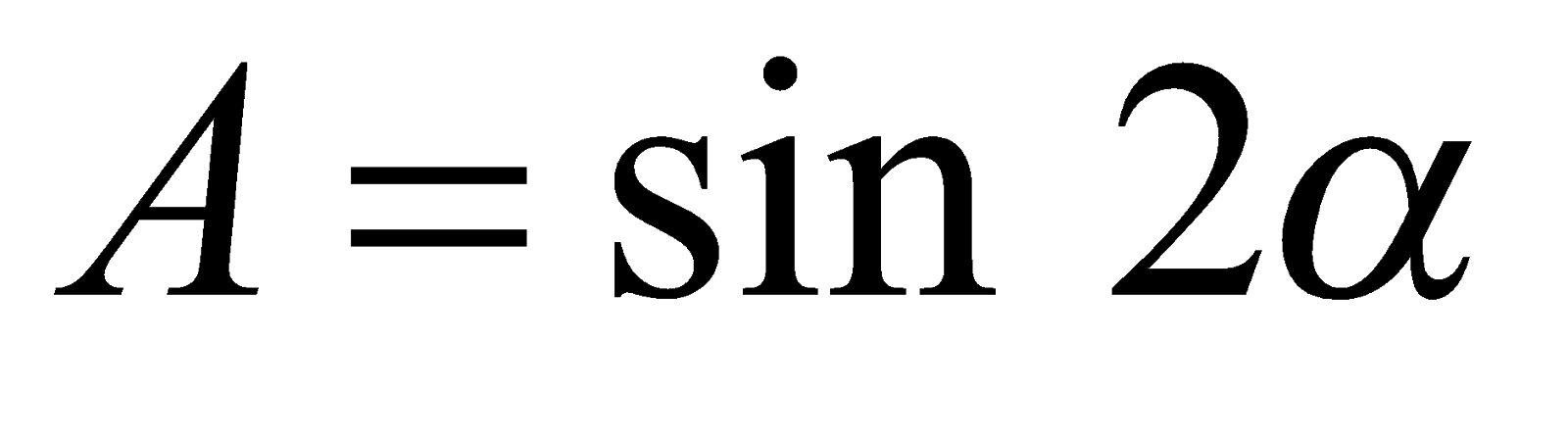 . Из определения функции
. Из определения функции 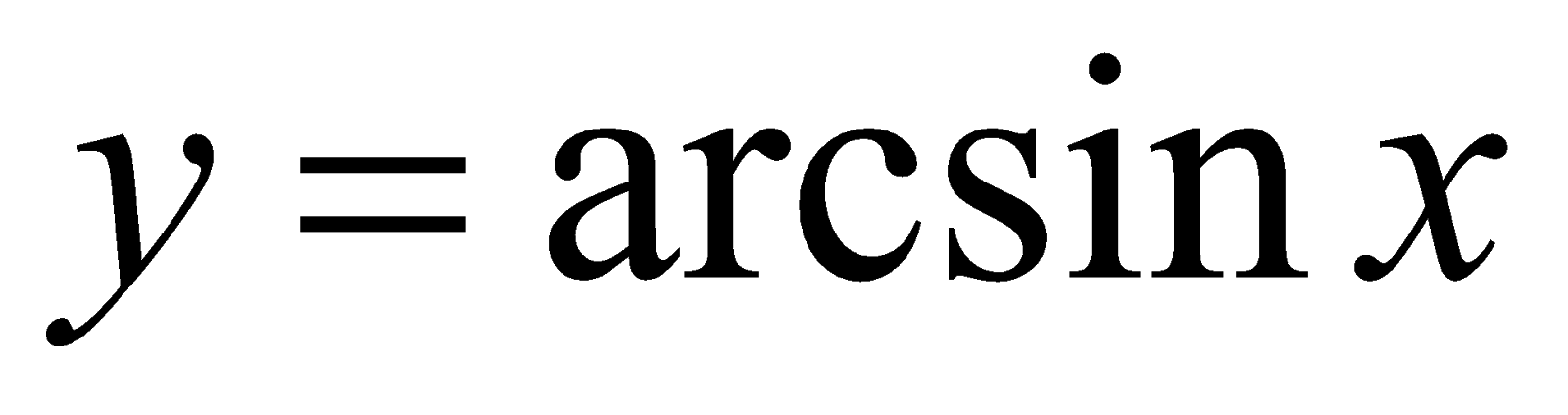 следует, что
следует, что 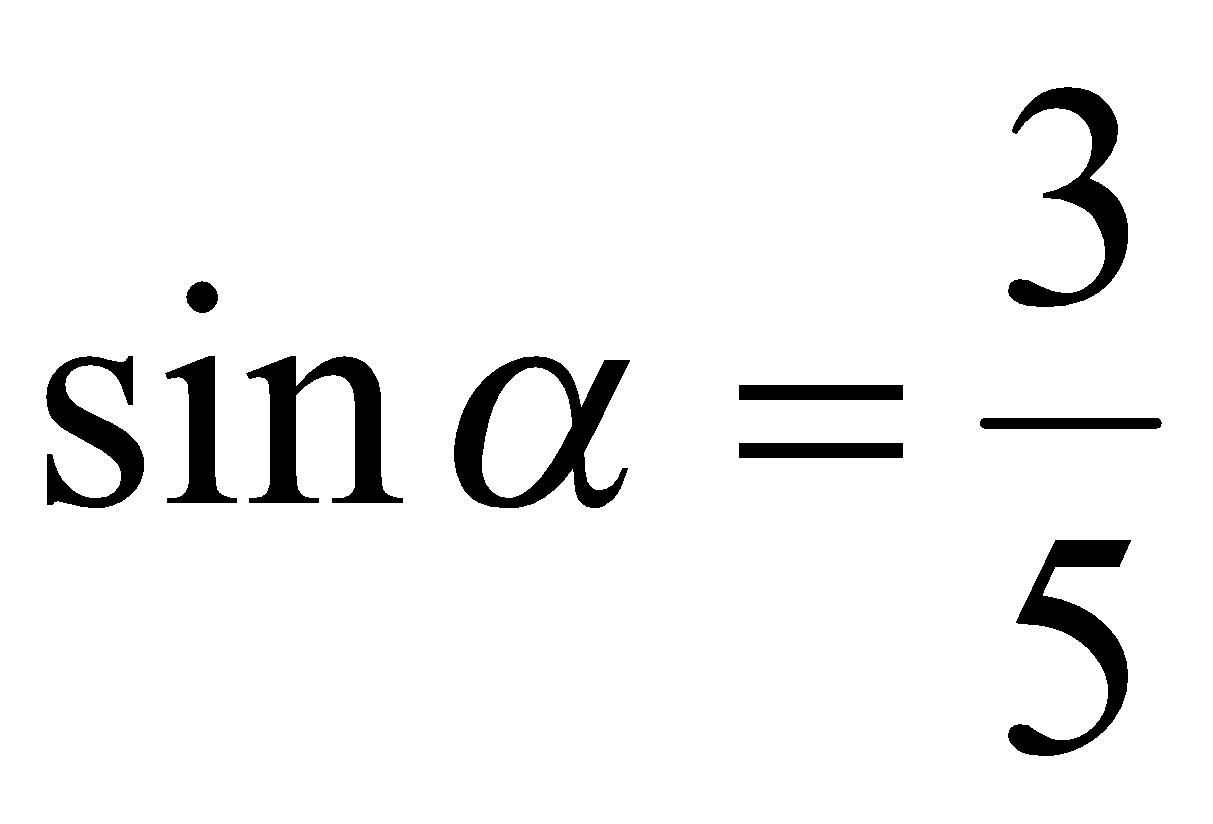 и
и 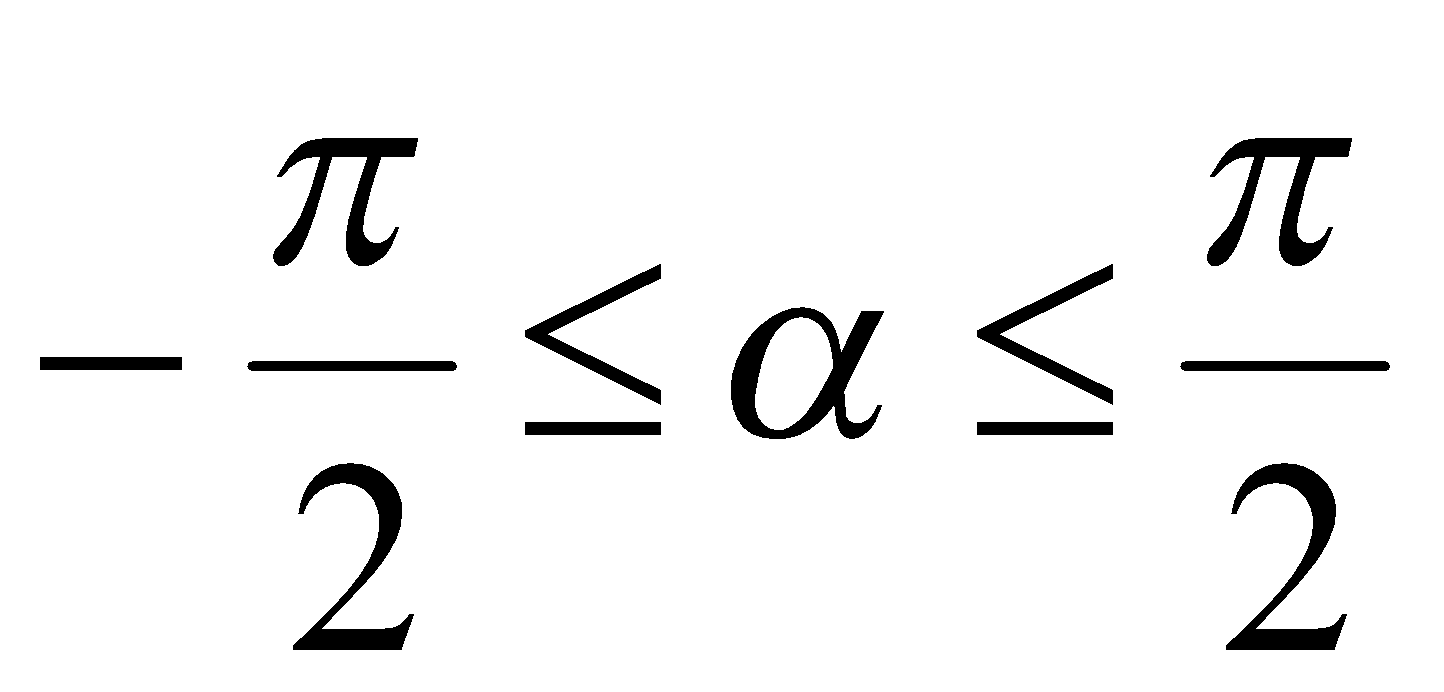 . Так как
. Так как 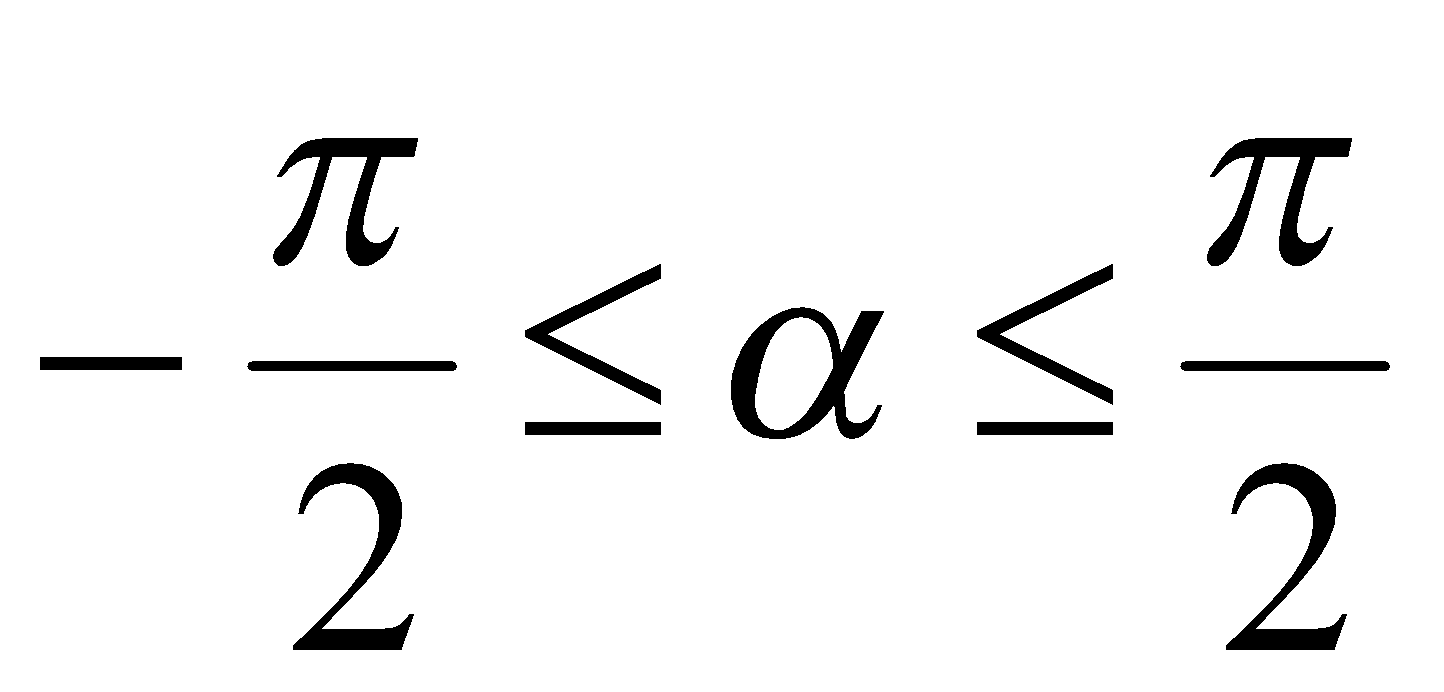 , то
, то 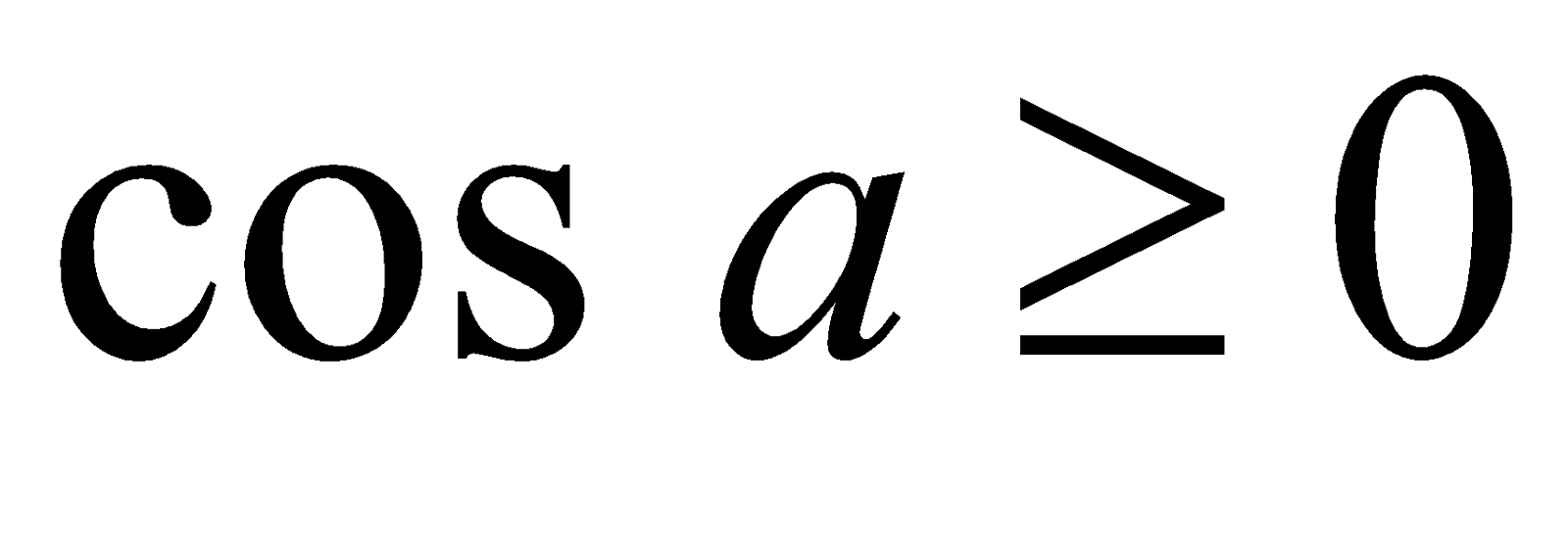 и
и 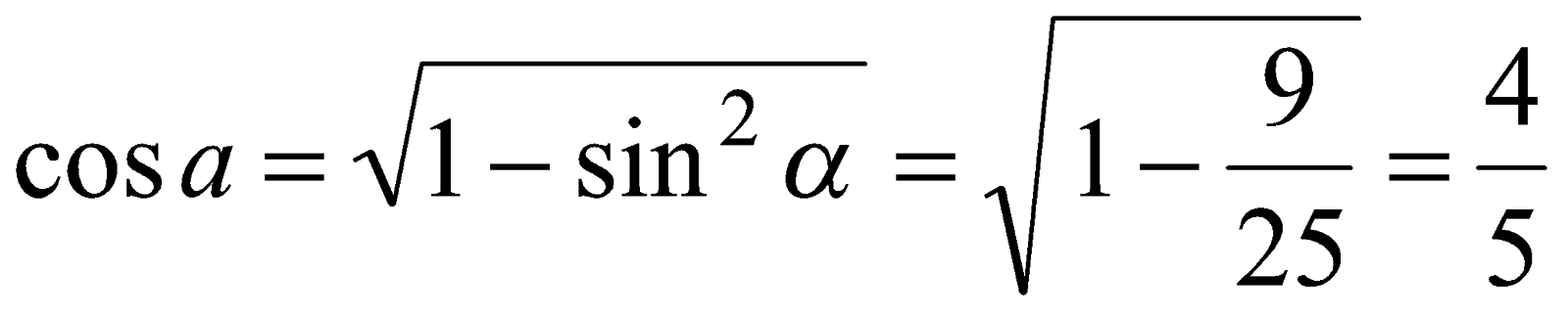 .
.
Однако  , поэтому
, поэтому 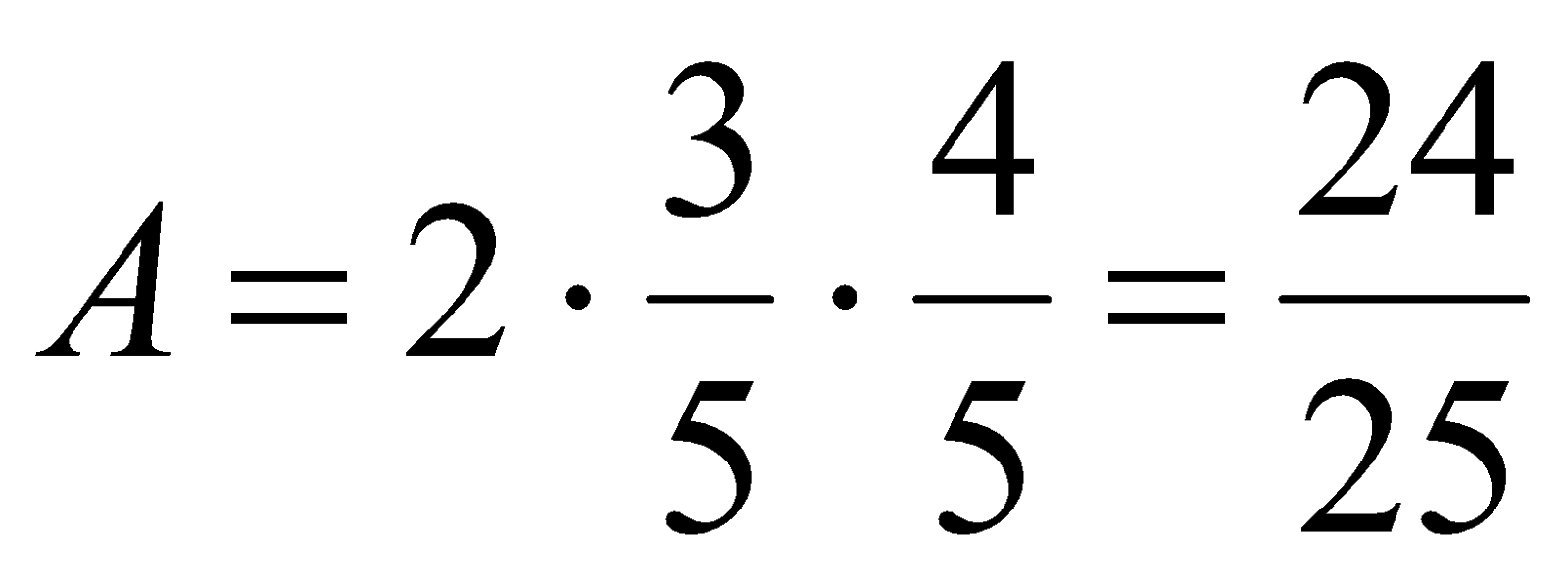 .
.
Ответ: 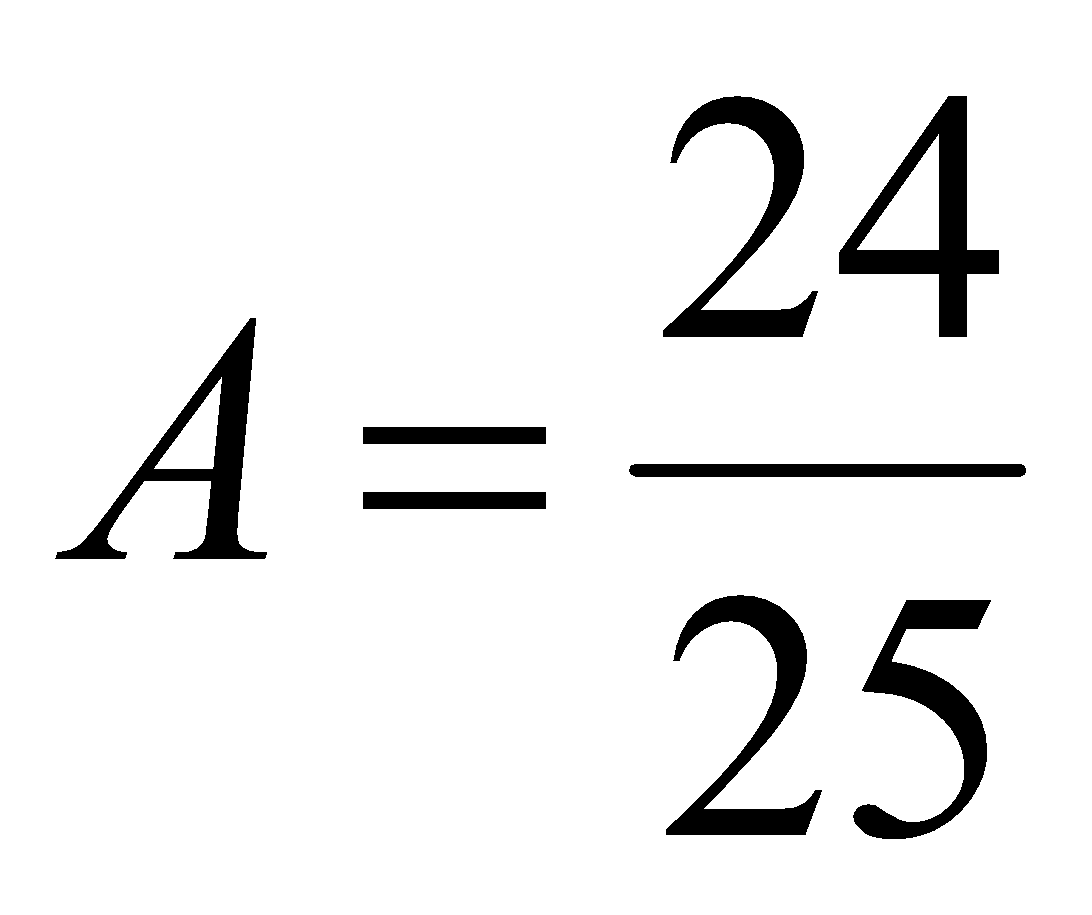 .
.
Пример 2. Вычислить значение 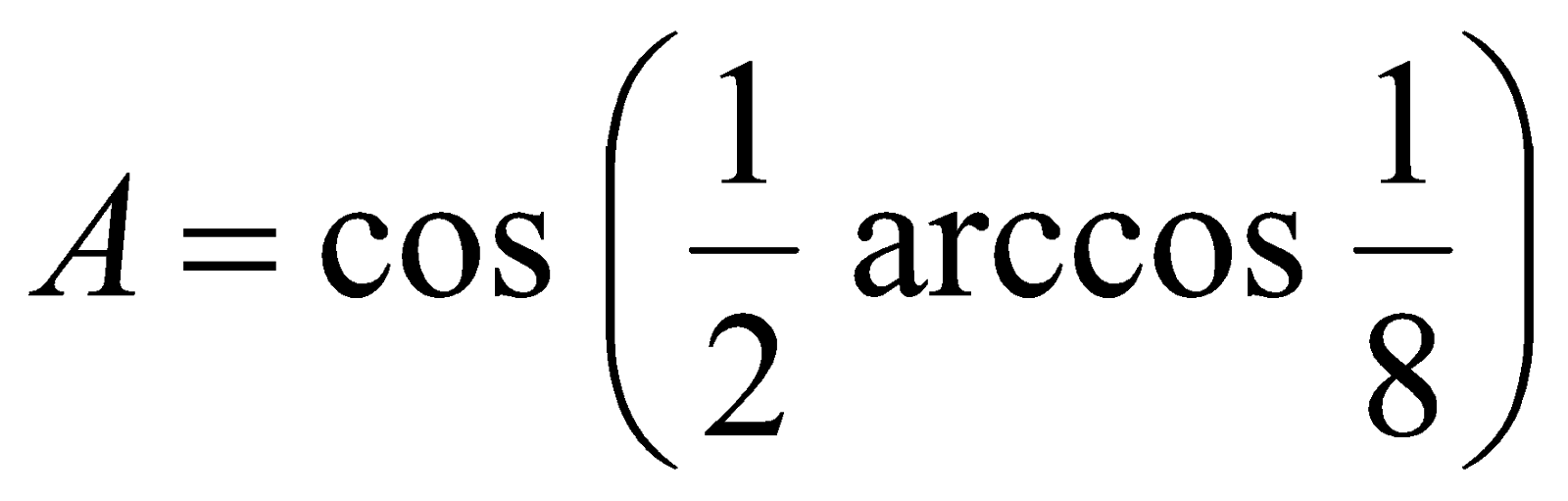 .
.
Решение. Если 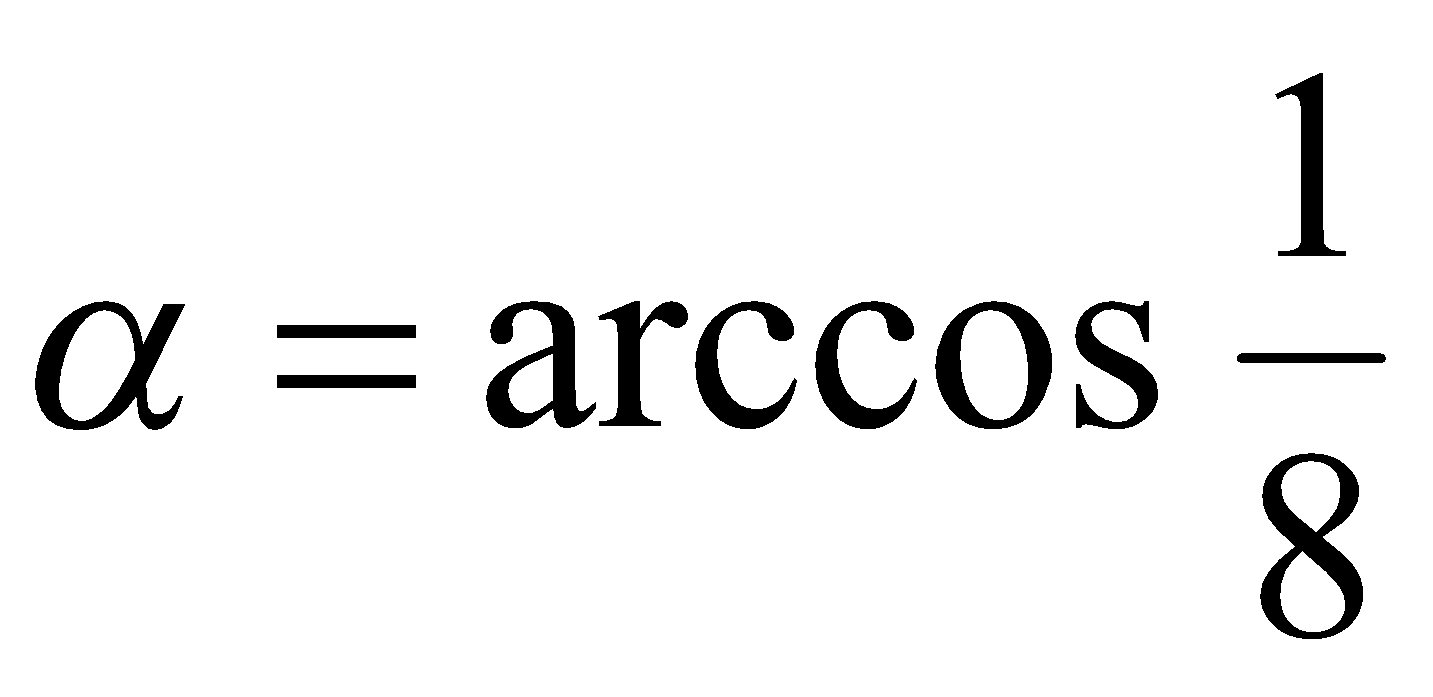 , то
, то 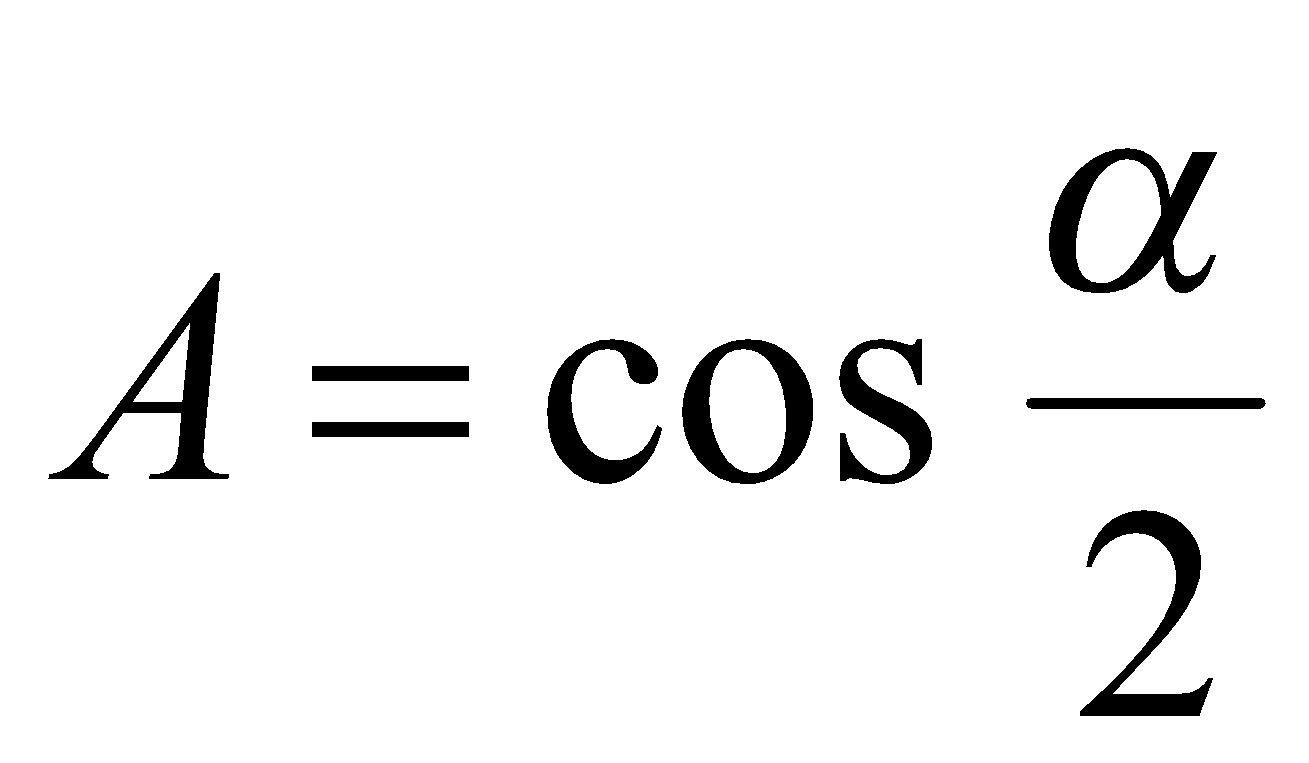 . Согласно определению функции
. Согласно определению функции 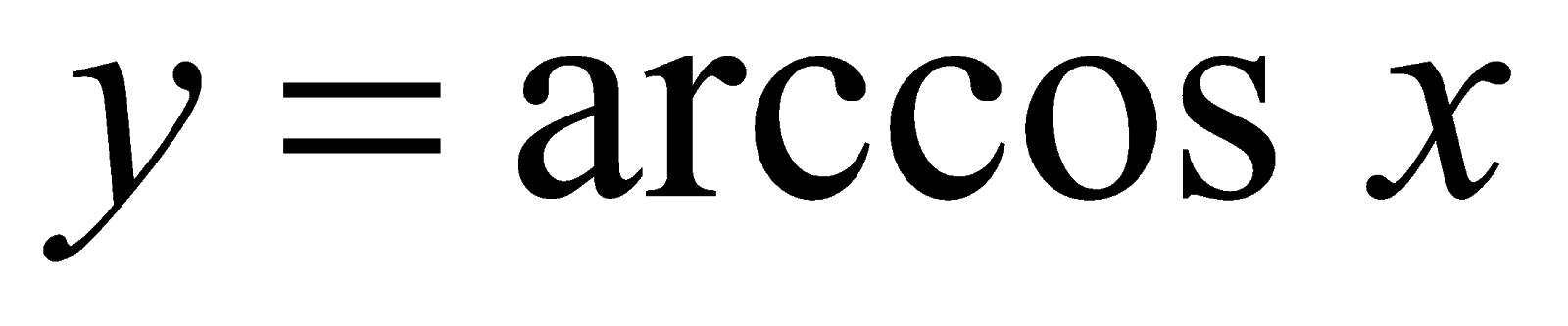 , имеем
, имеем 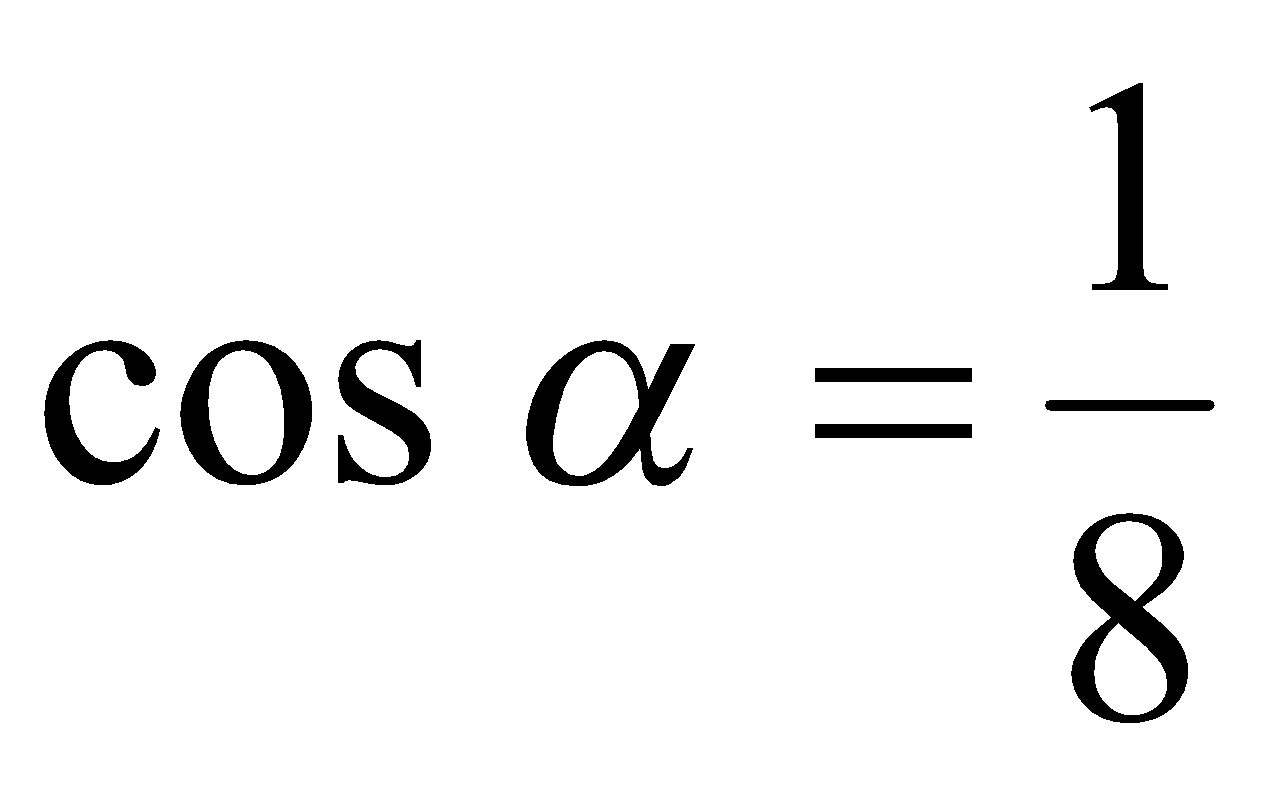 и
и  . Так как
. Так как  , то
, то 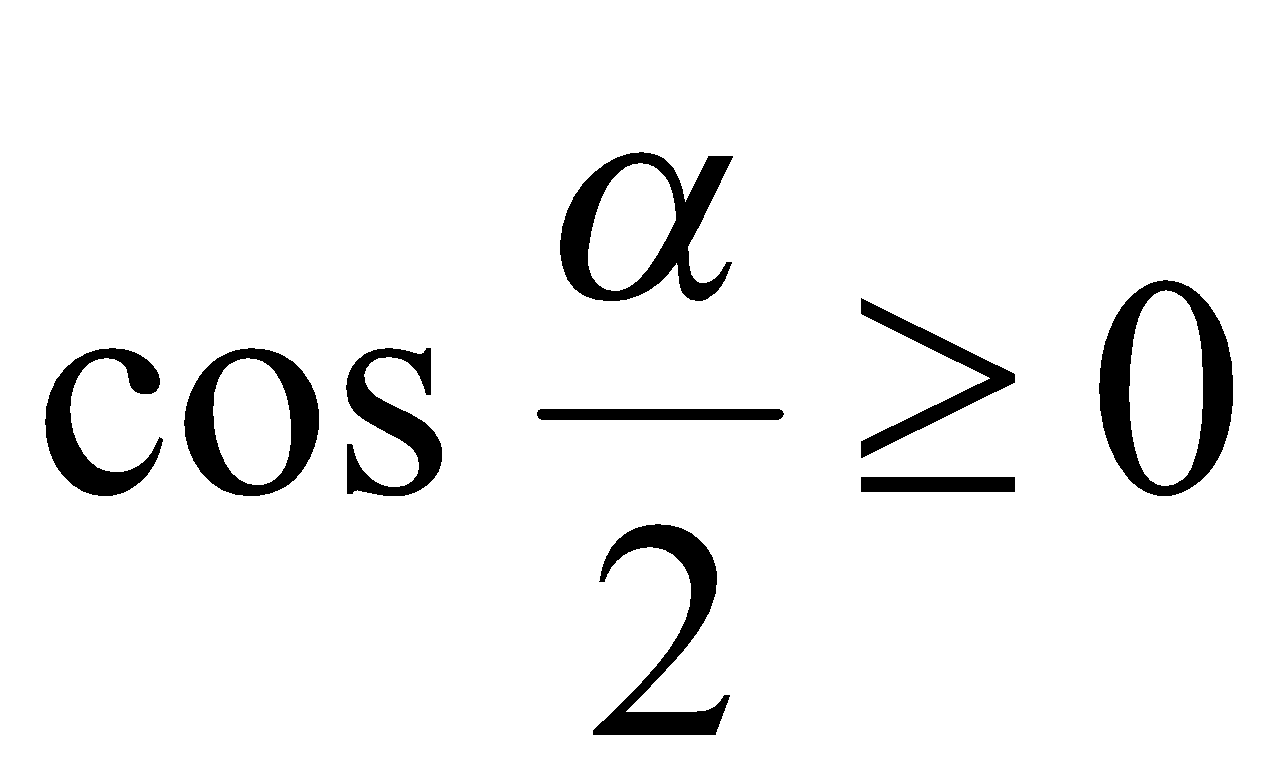 .
.
Поскольку 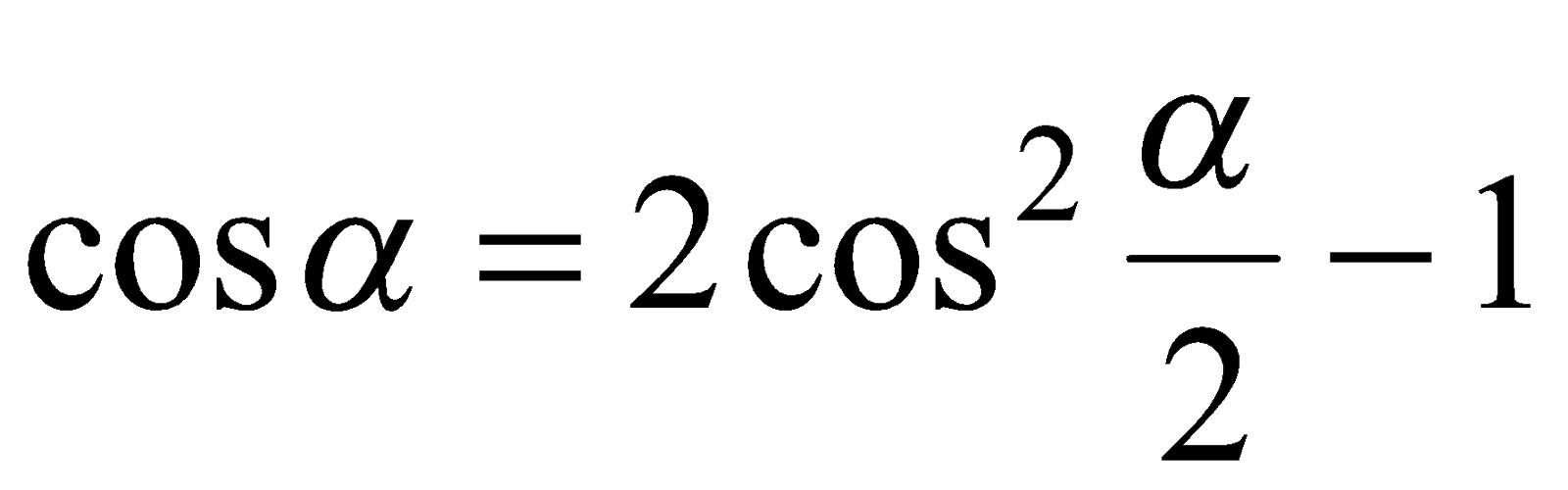 и
и 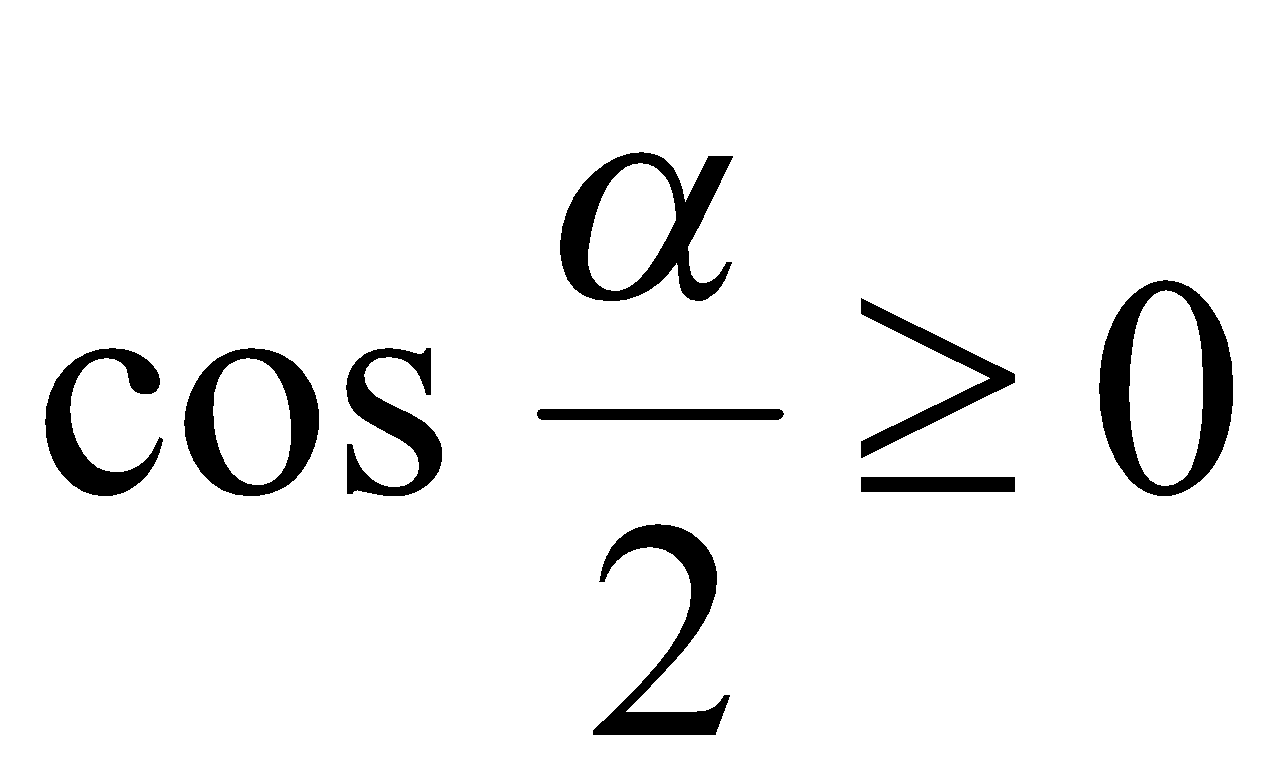 , то
, то  .
.
Ответ: 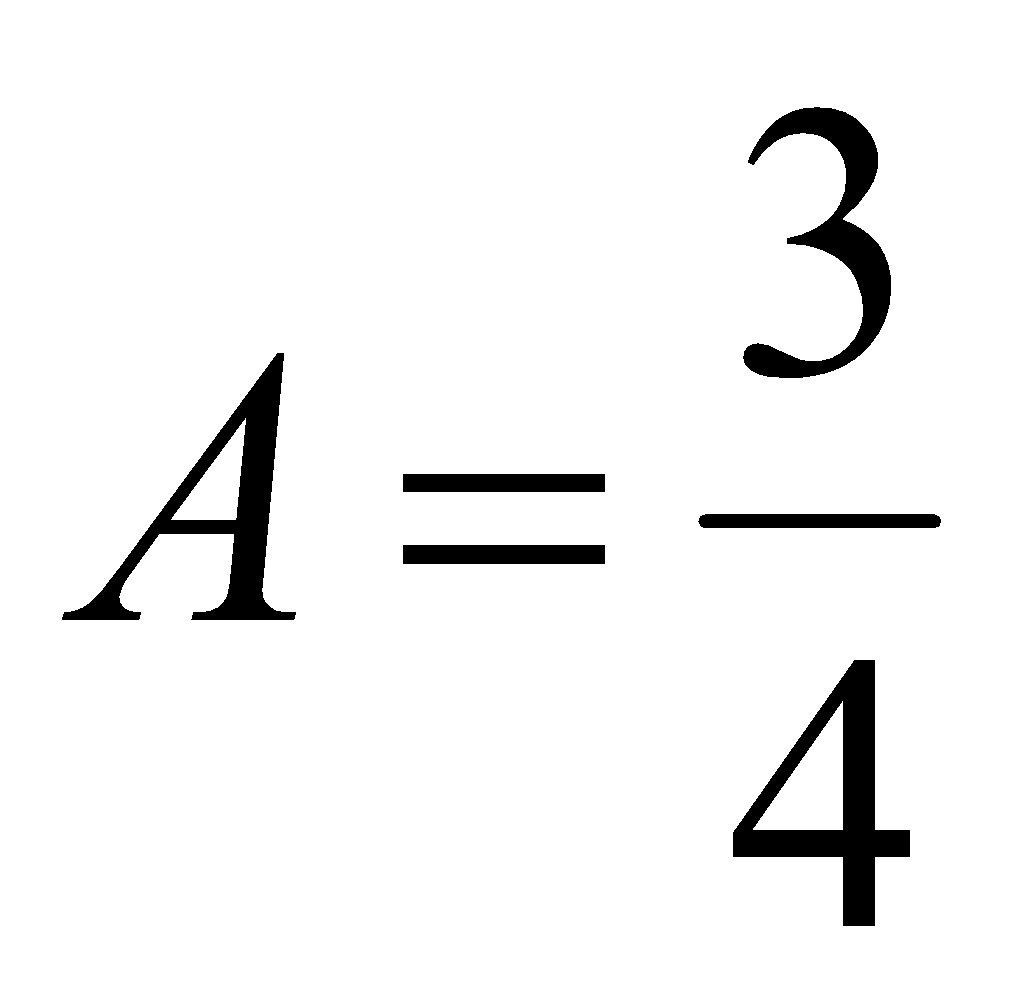 .
.
Пример 3. Вычислить значение 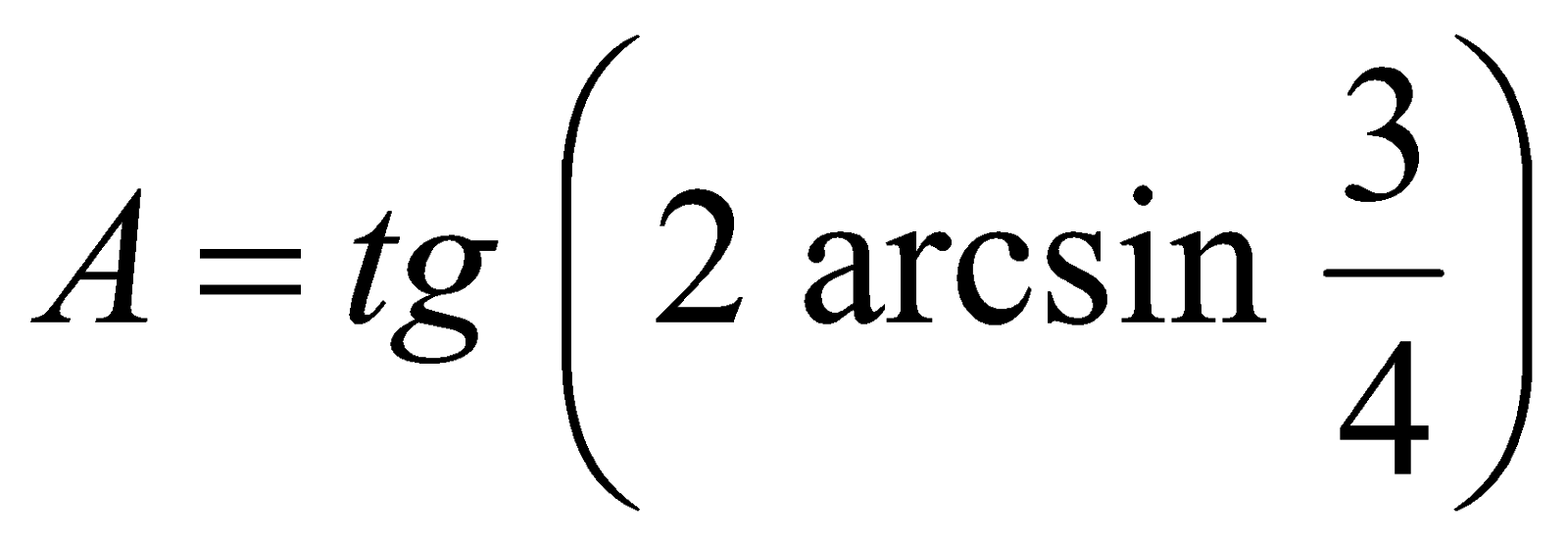 .
.
Решение. Пусть 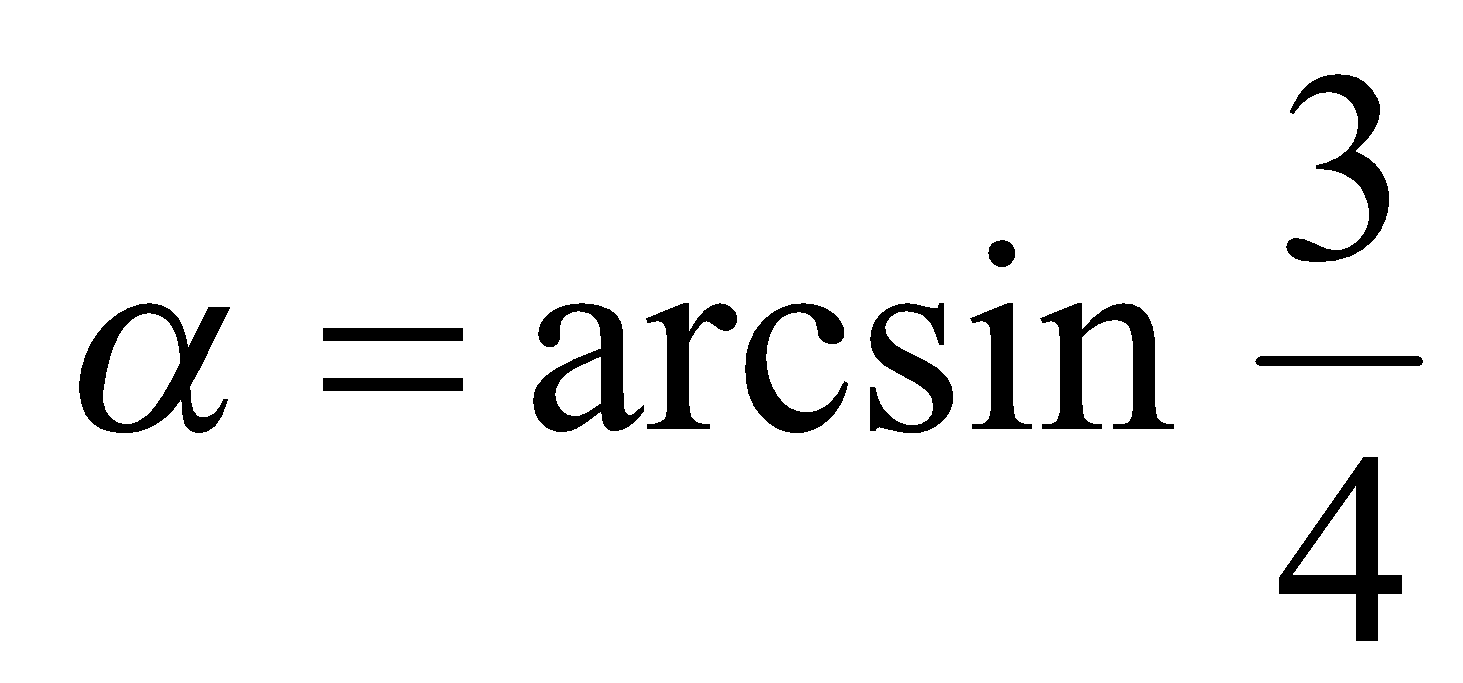 , тогда
, тогда 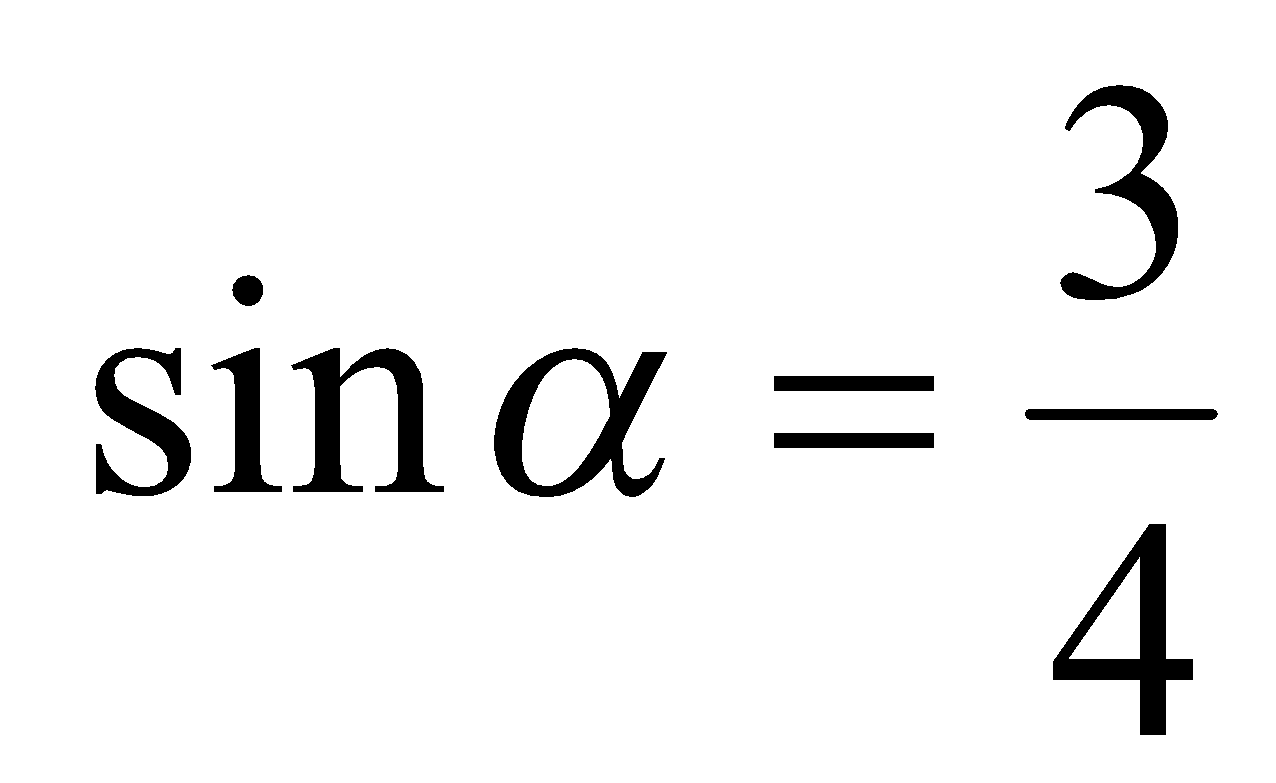 и
и 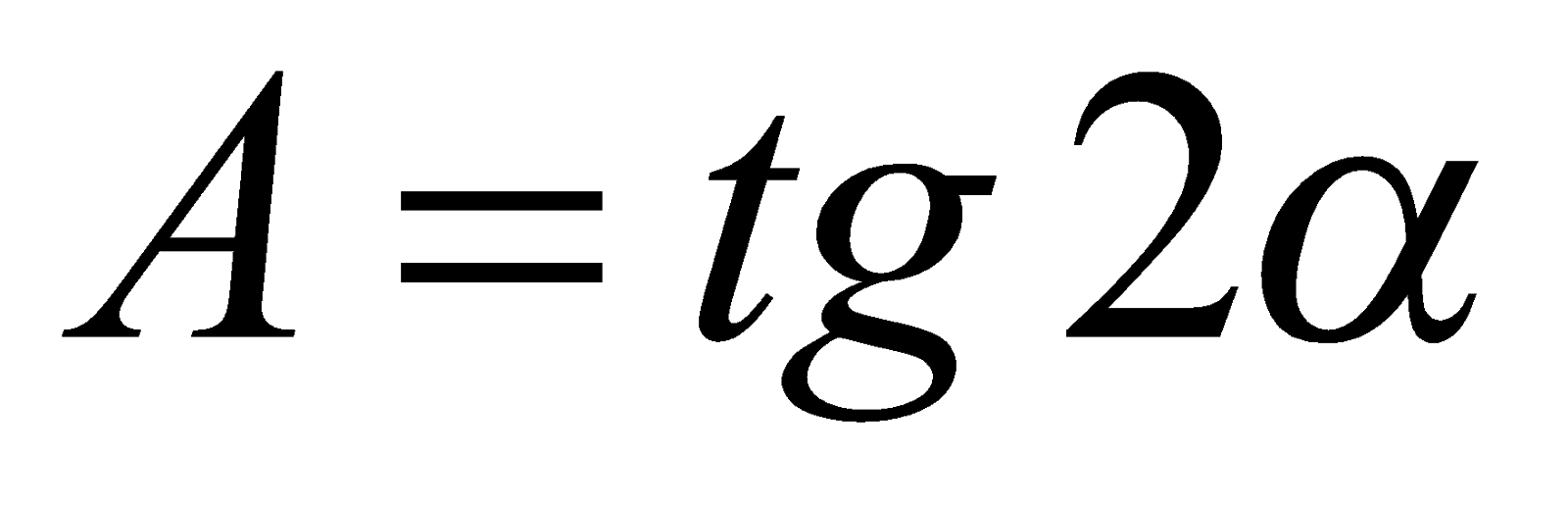 , где
, где 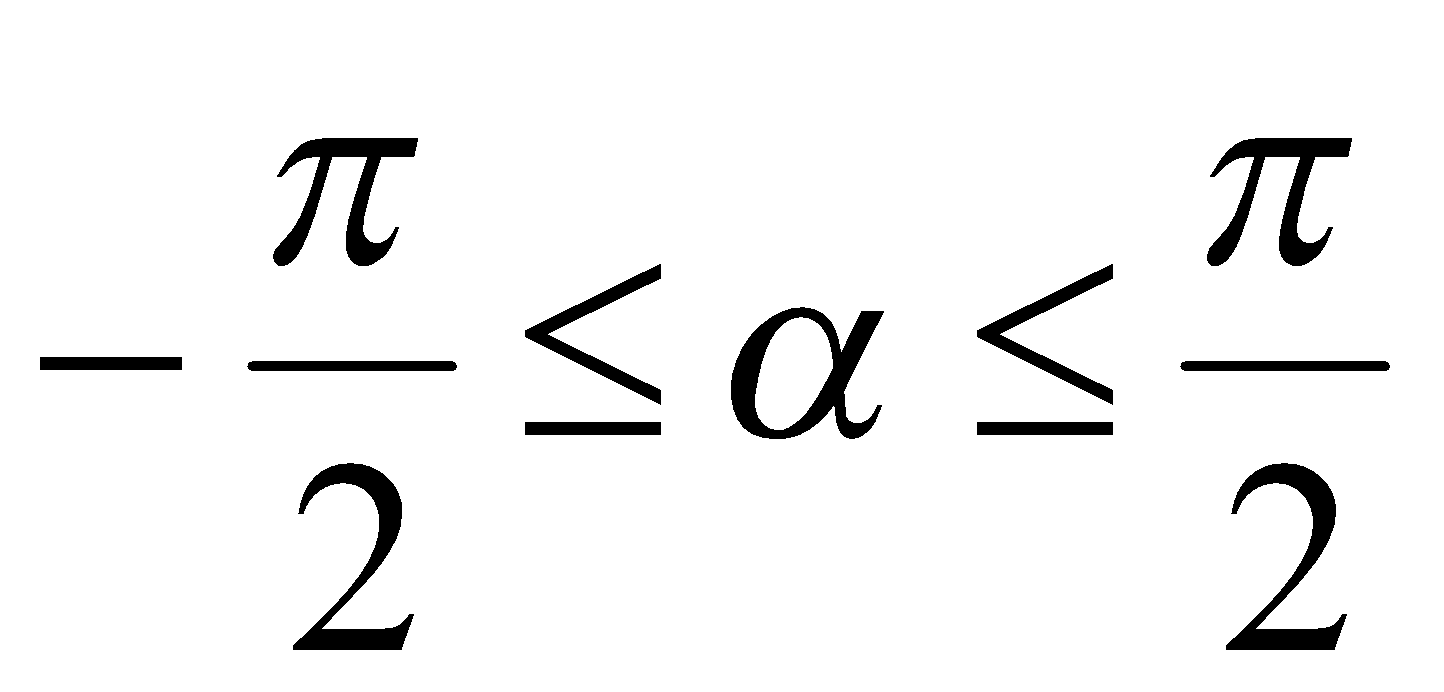 . В таком случае
. В таком случае 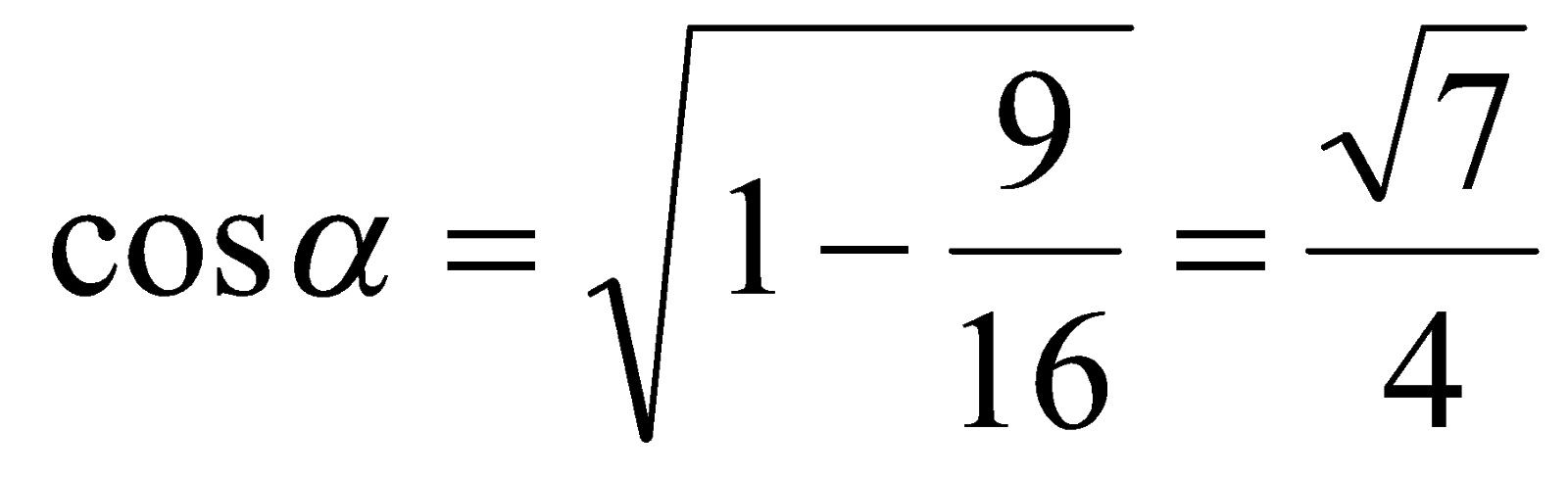 и
и 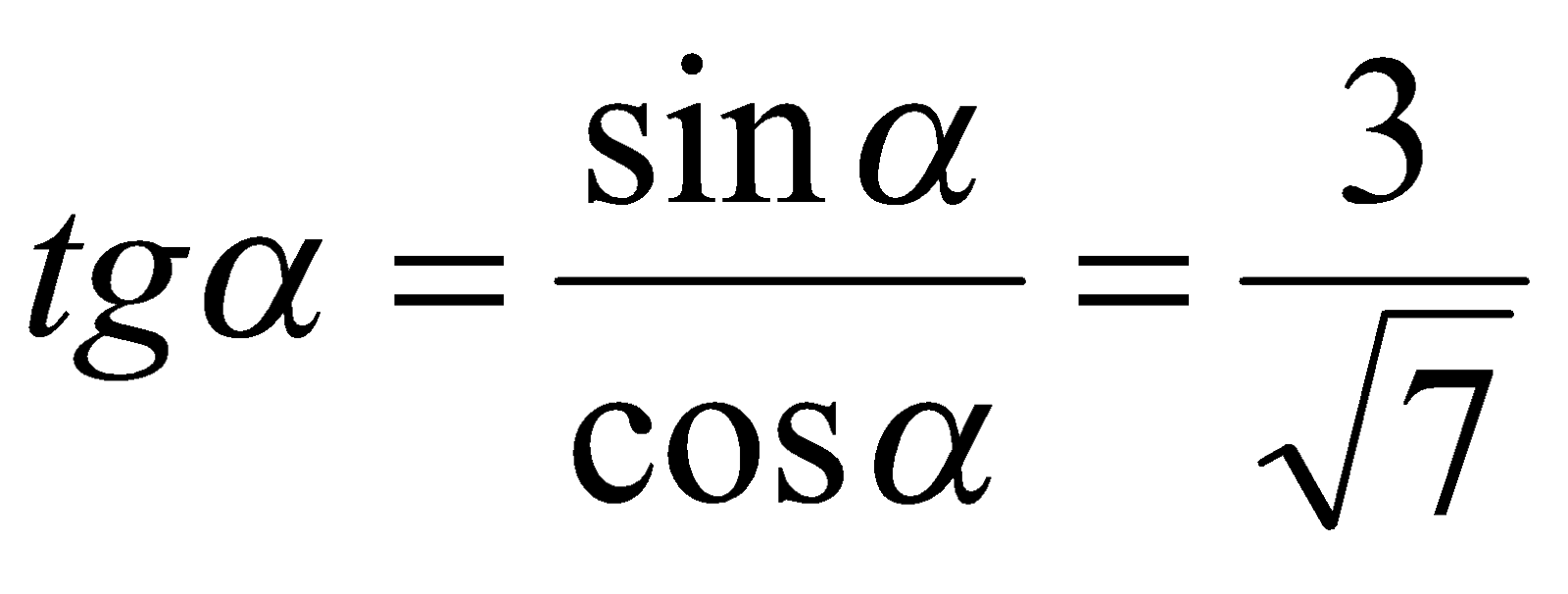 .
.
Поскольку 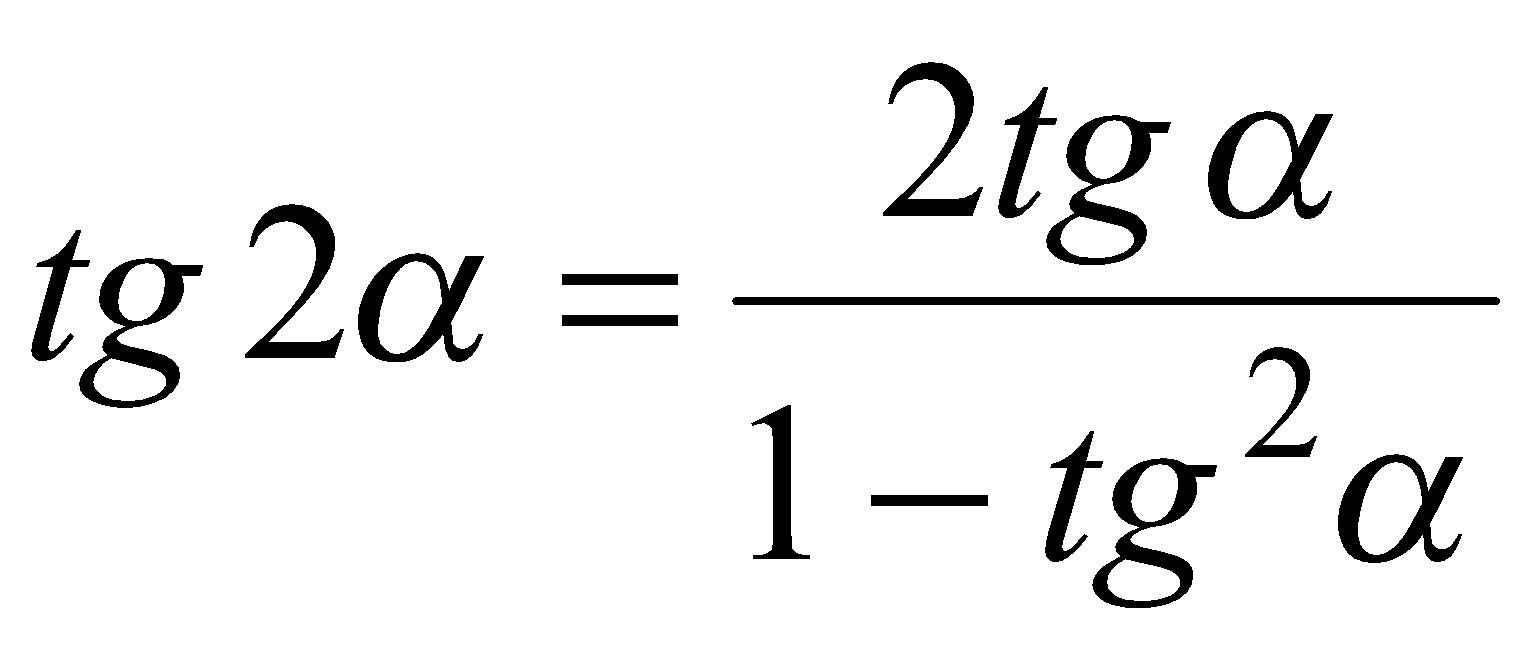 , то
, то 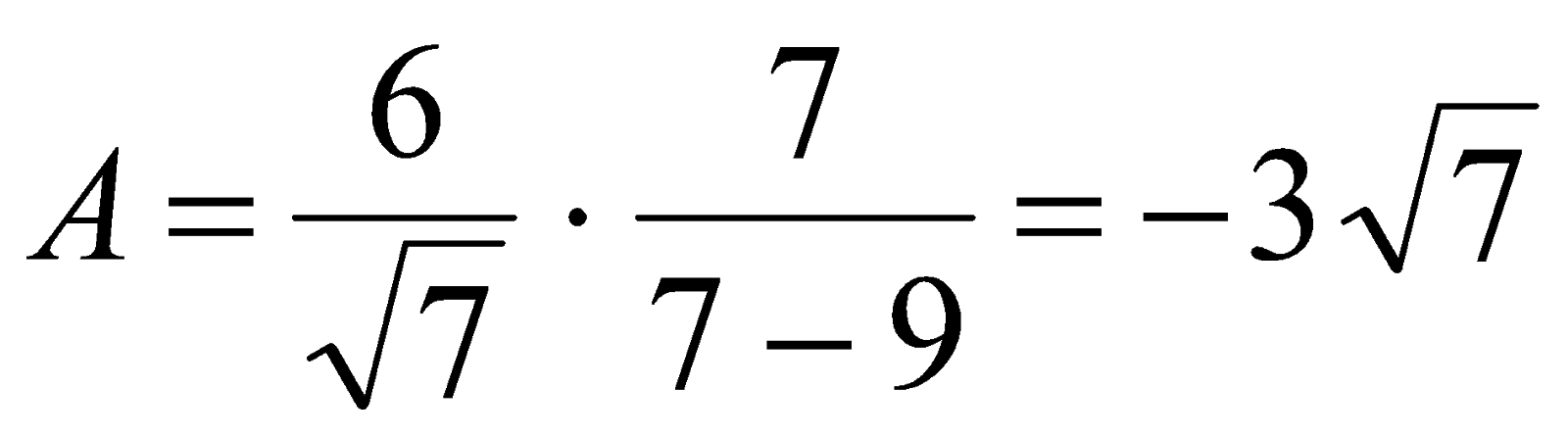 .
.
Ответ:  .
.
Пример 4. Вычислить значение 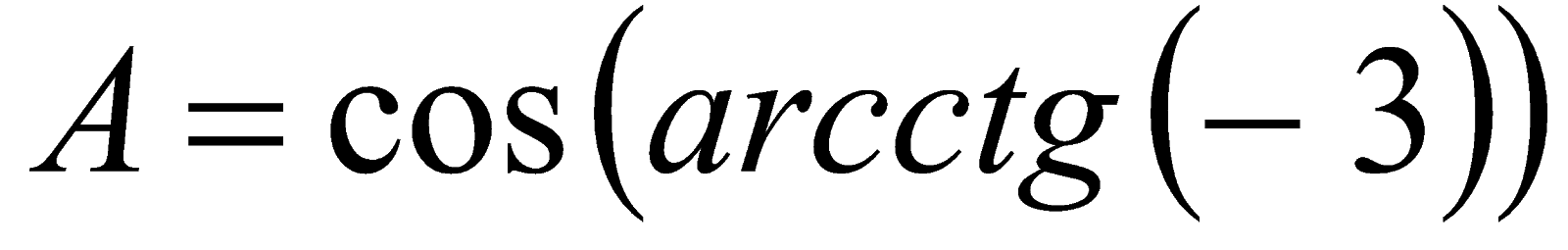 . Решение. Так как
. Решение. Так как 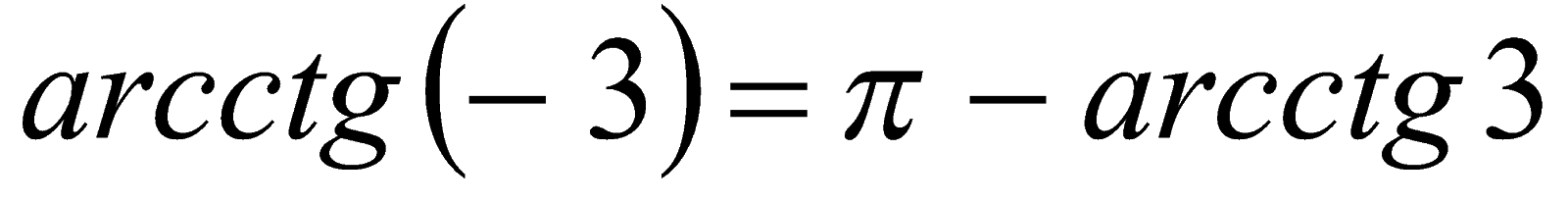 , то
, то 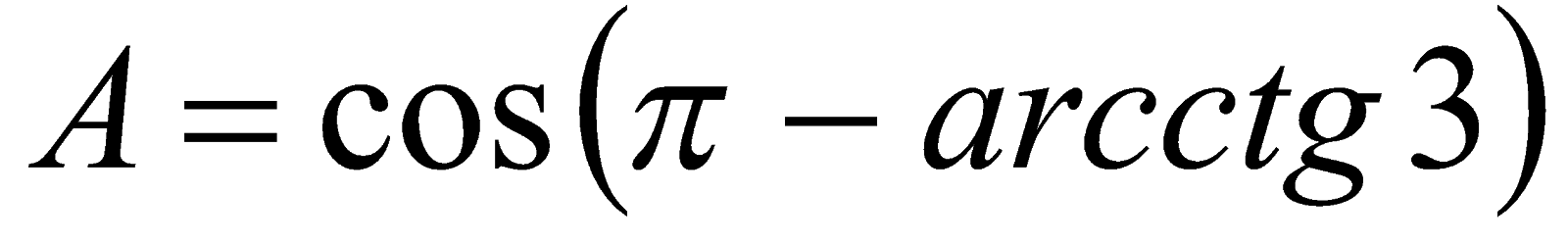 или
или 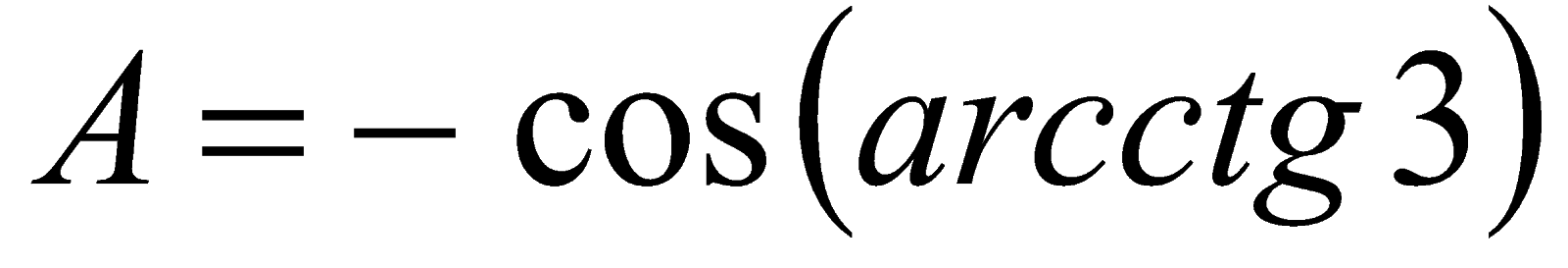 . Обозначим
. Обозначим  , тогда
, тогда  ,
, 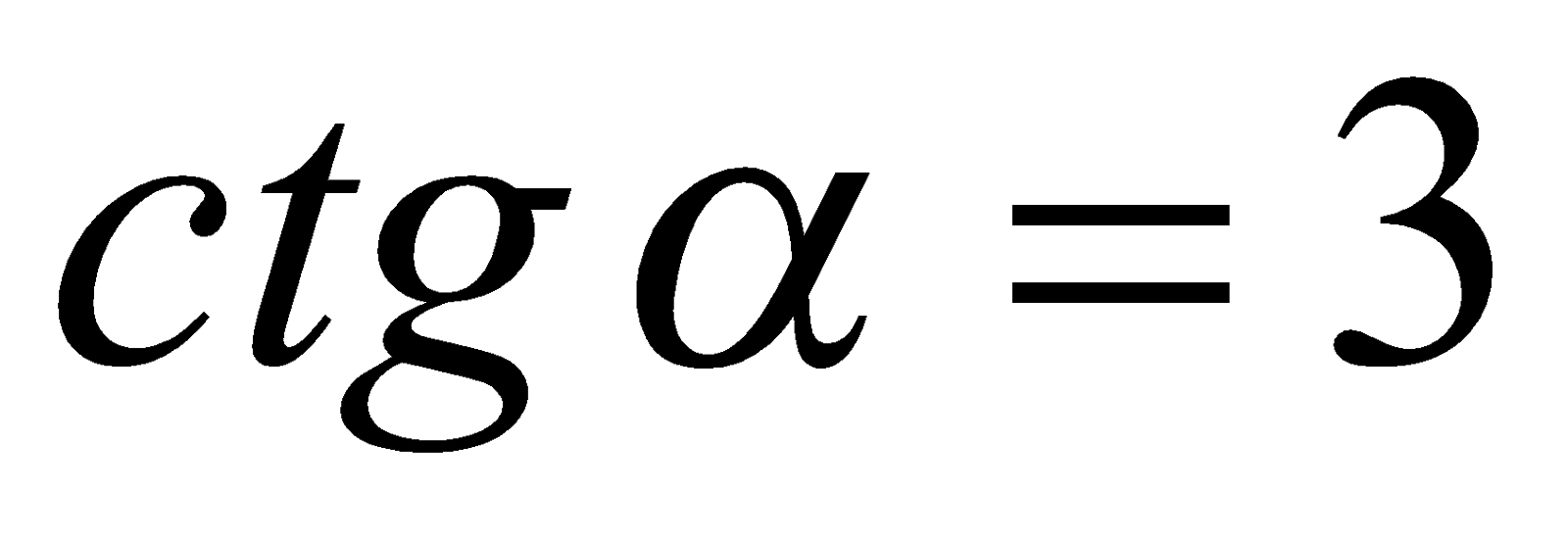
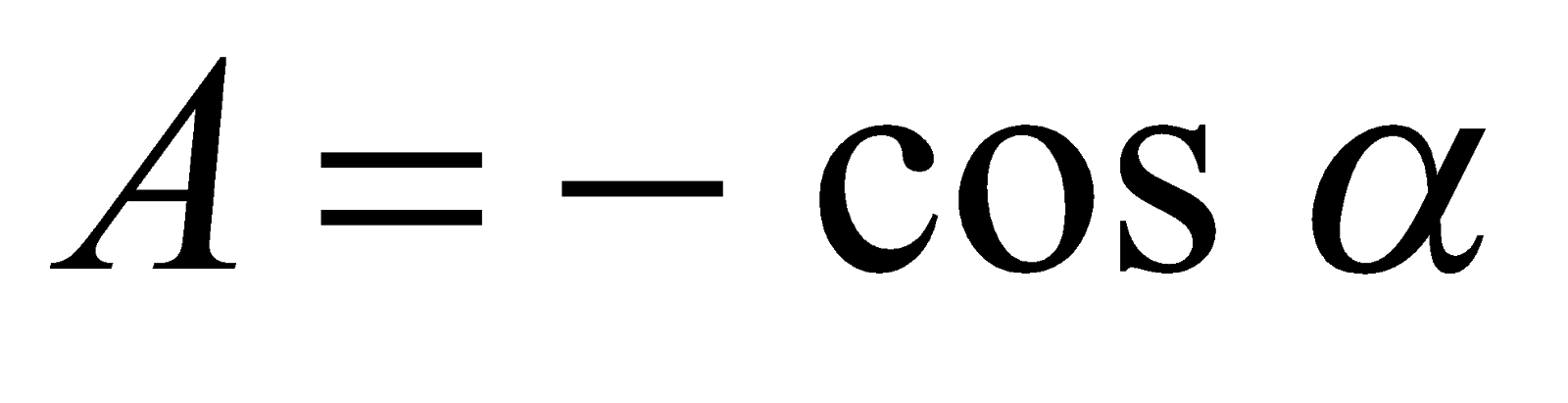 . Поскольку
. Поскольку 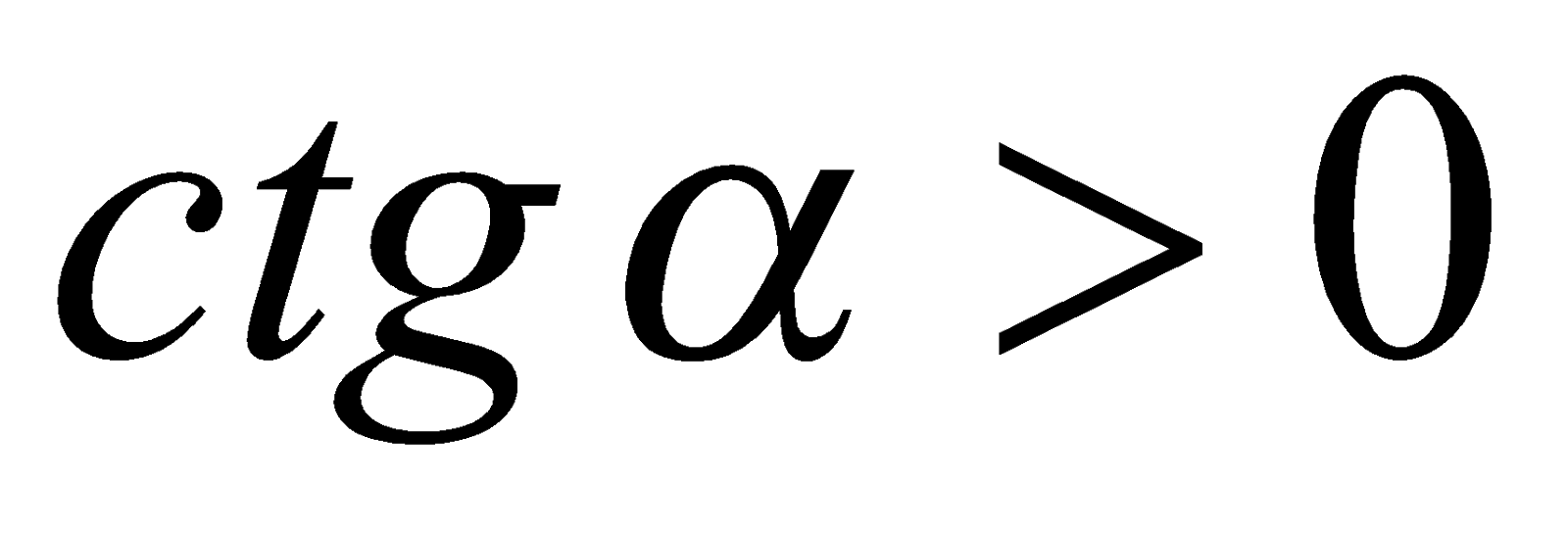 , то
, то 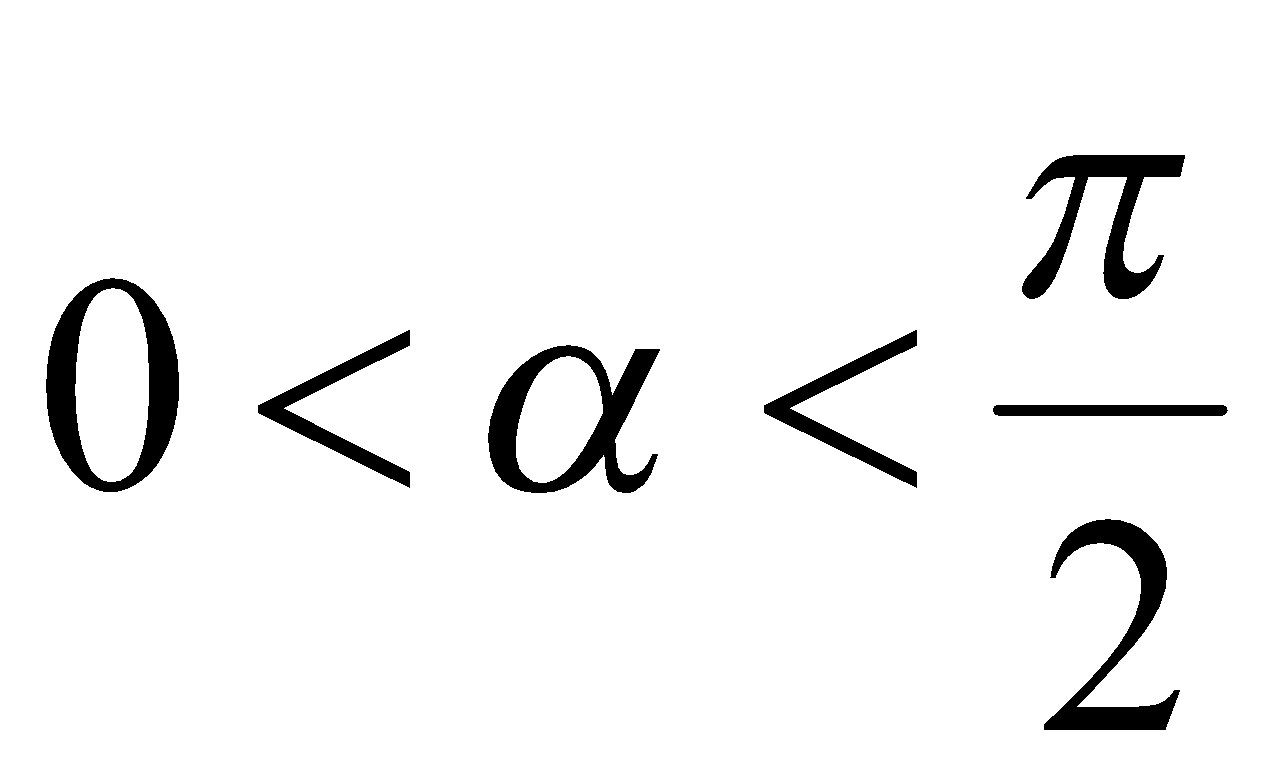 .
.
Если 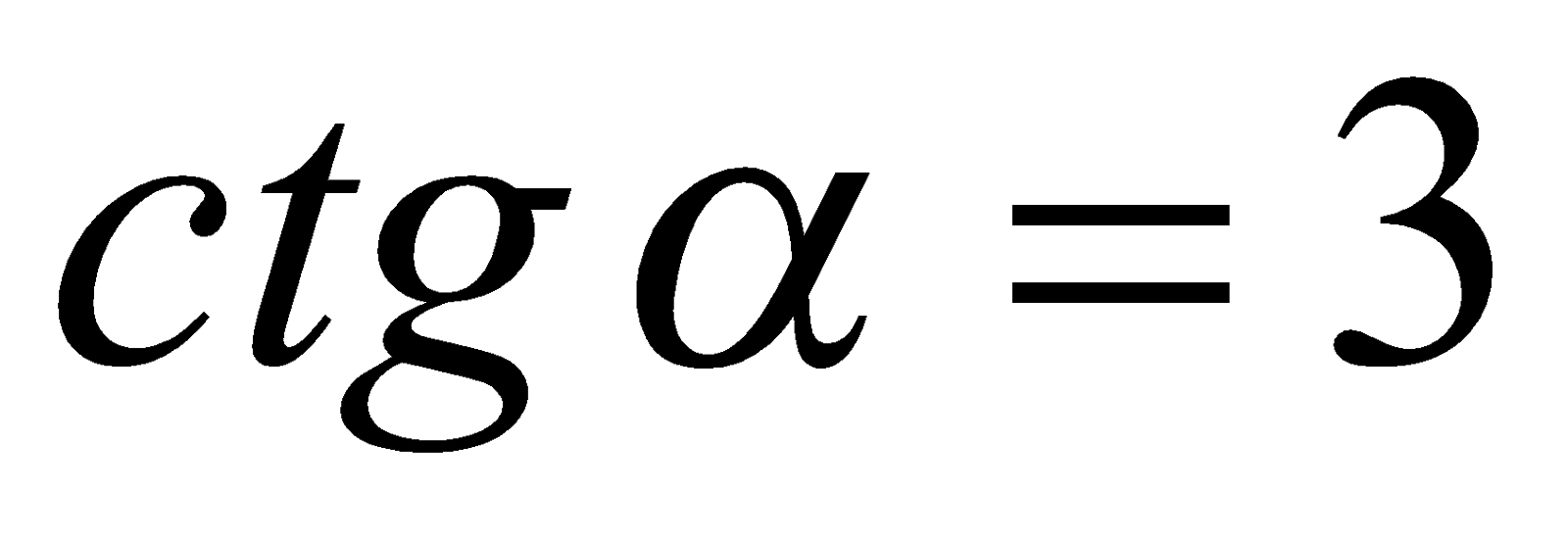 , то
, то 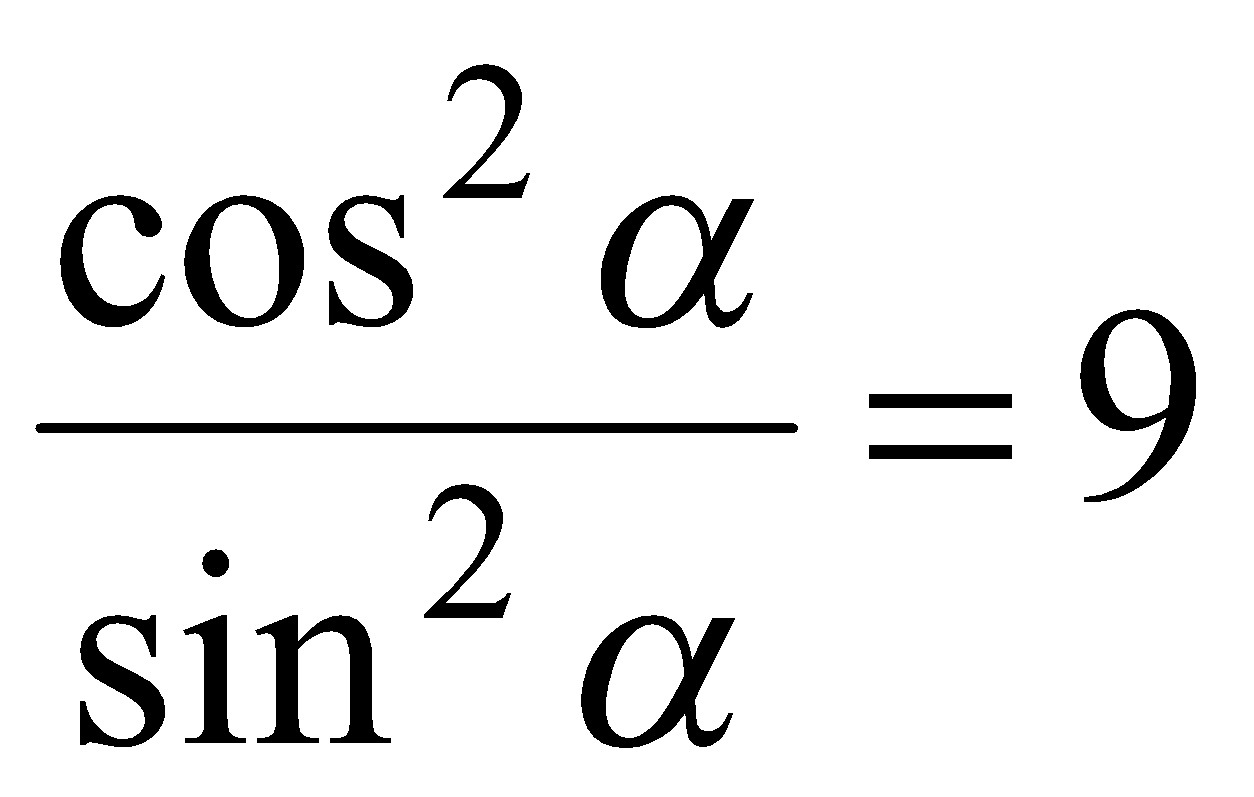 ,
, 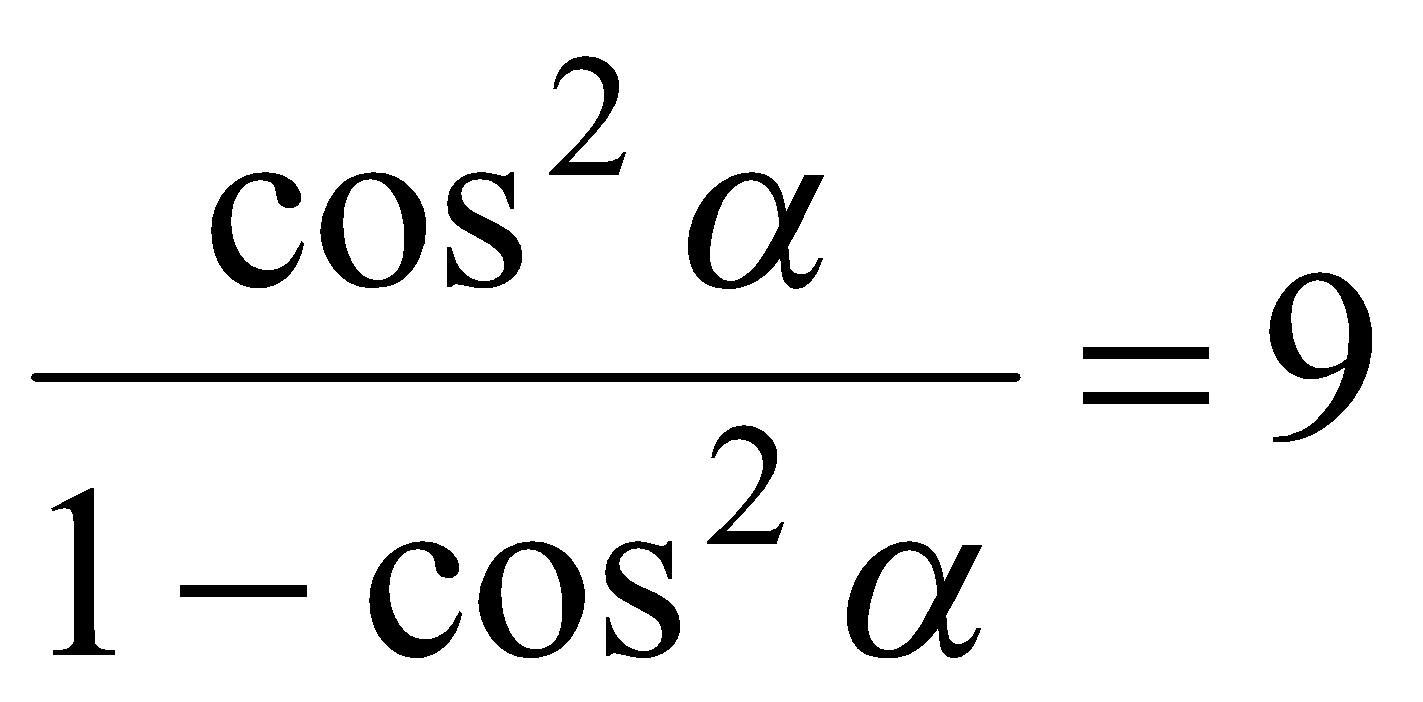 или
или 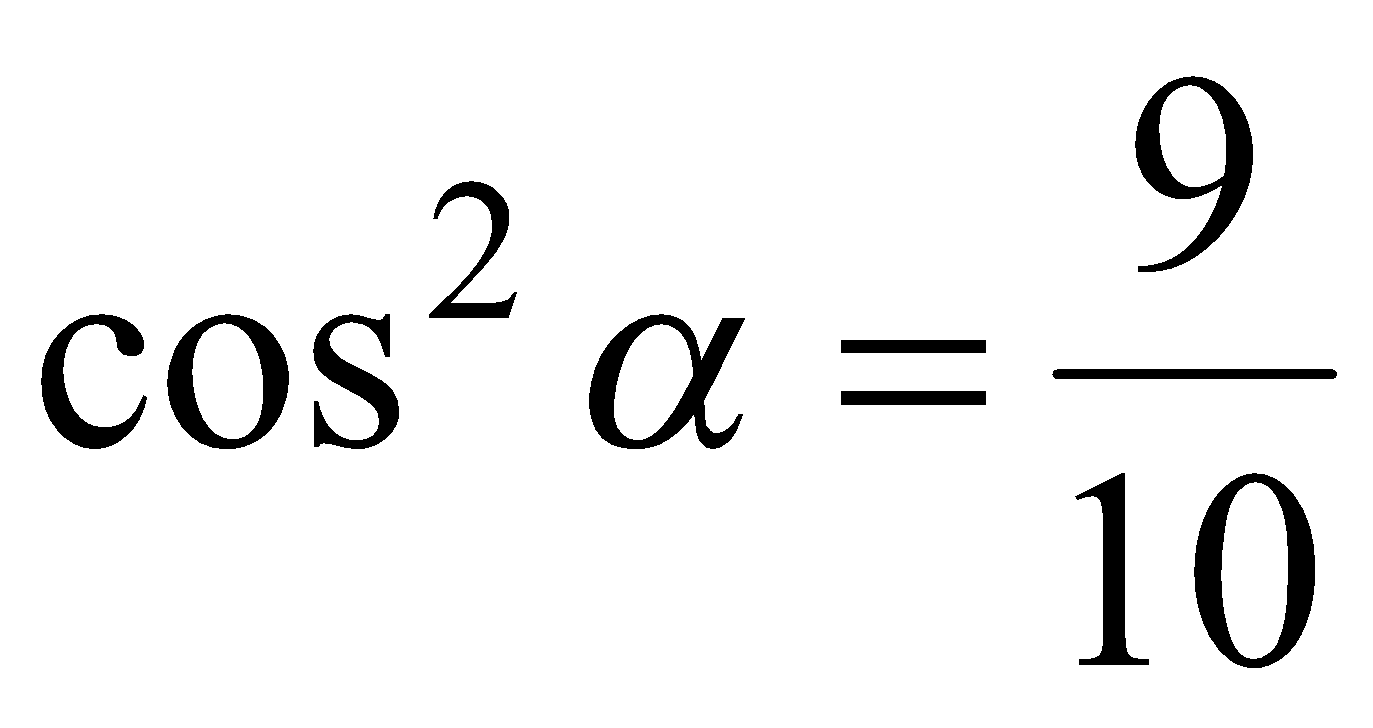 . Однако
. Однако 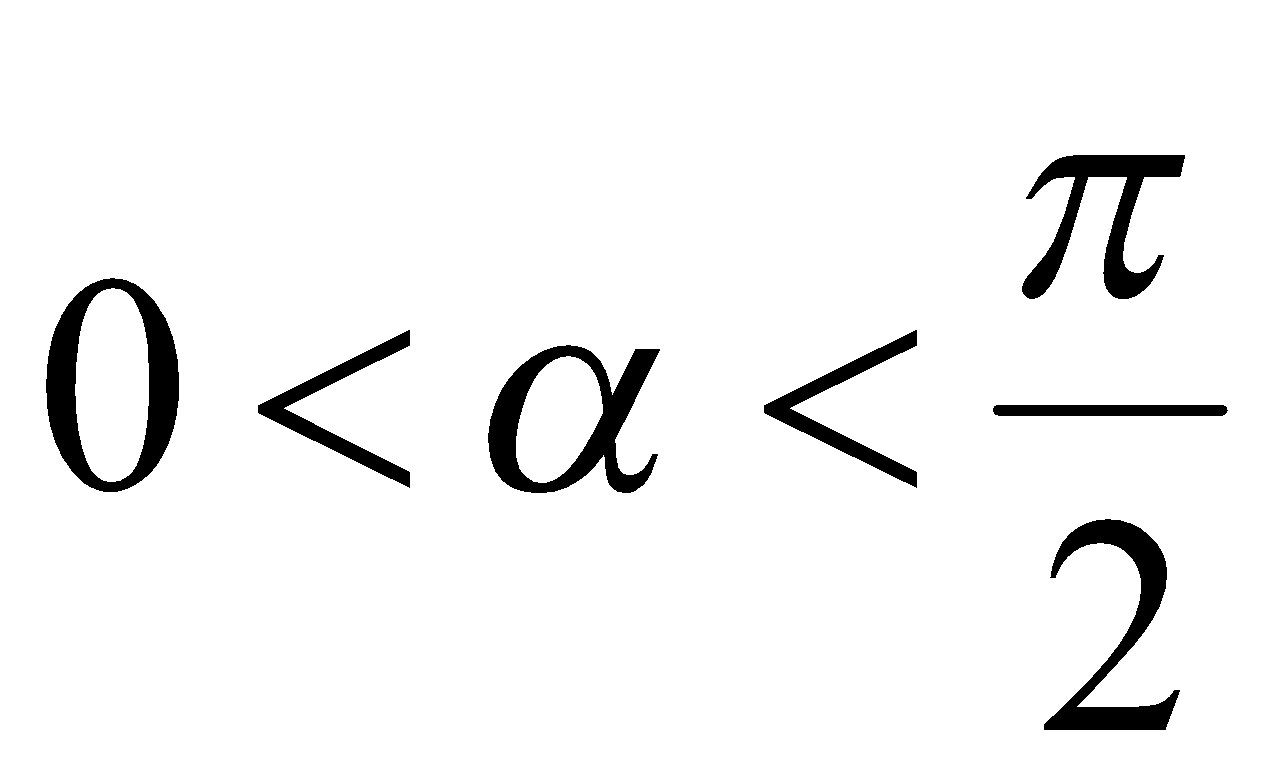 , поэтому
, поэтому  ,
, 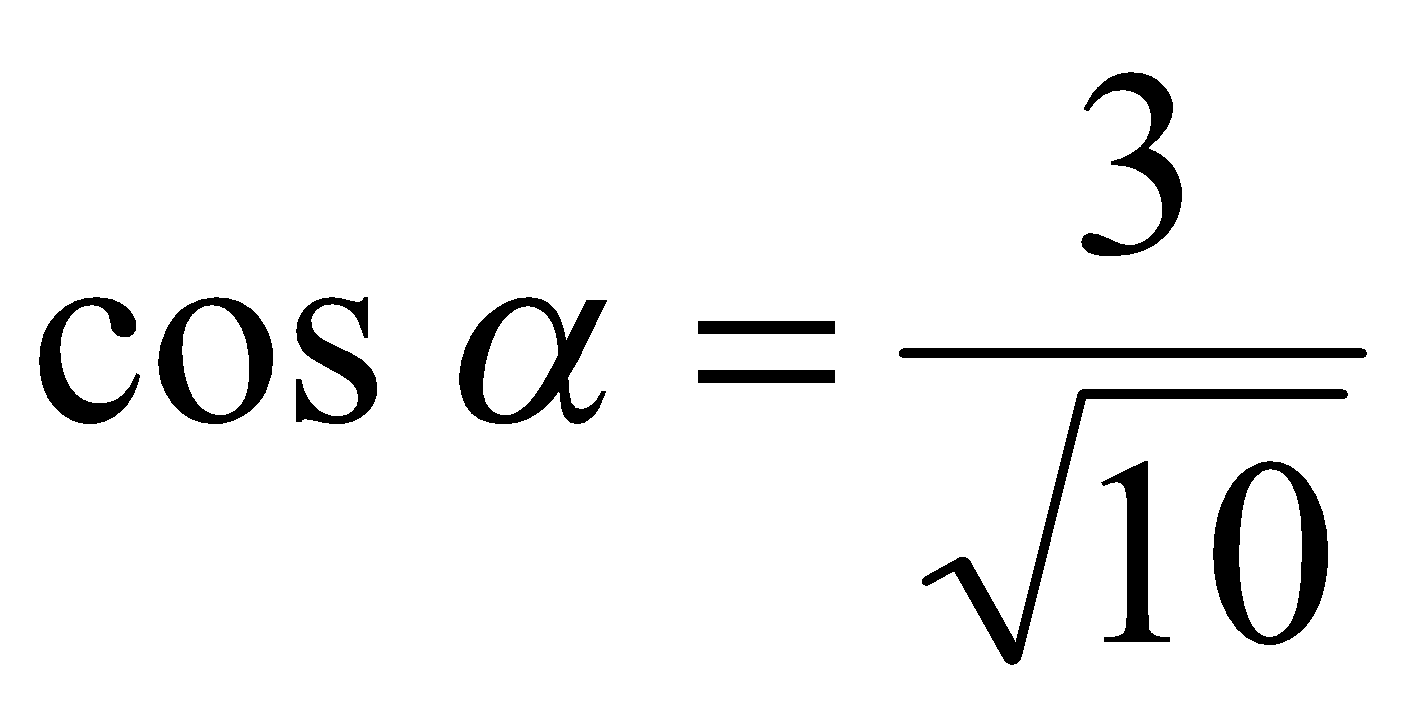 и
и 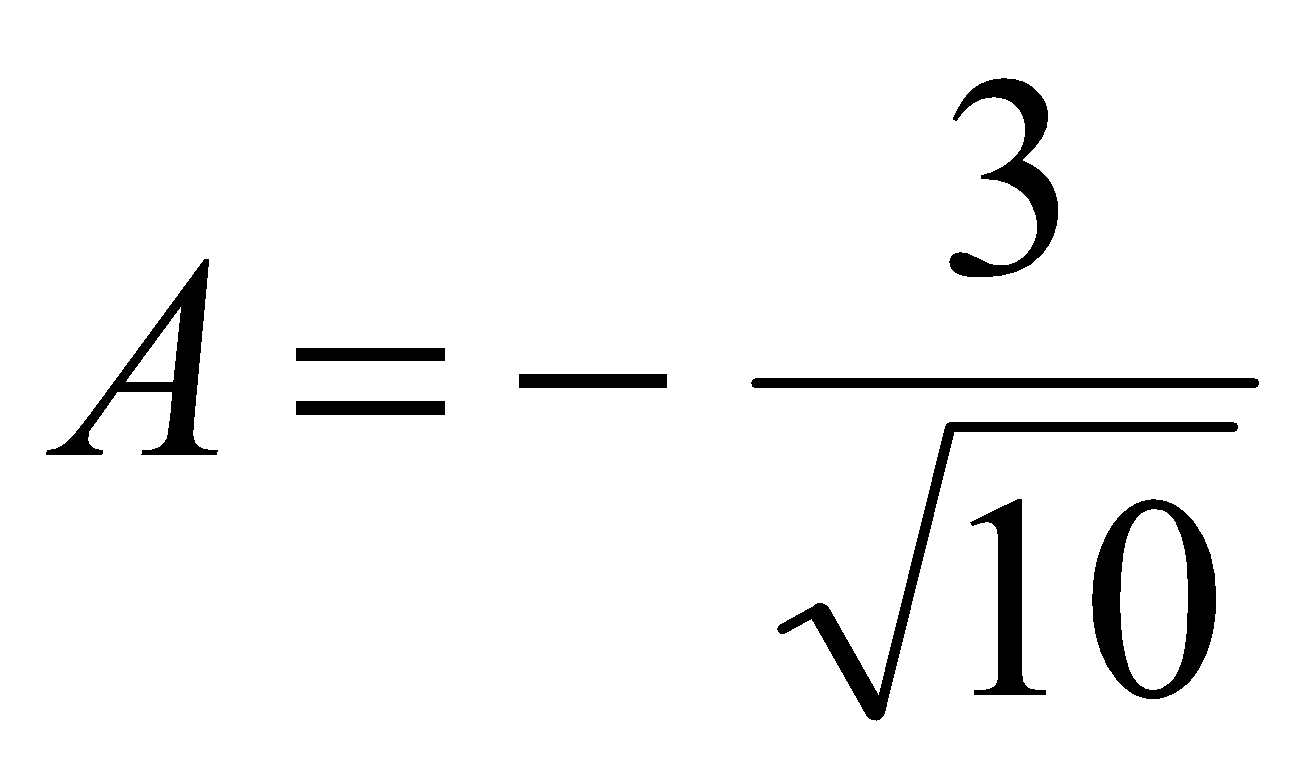 .
.
Ответ: 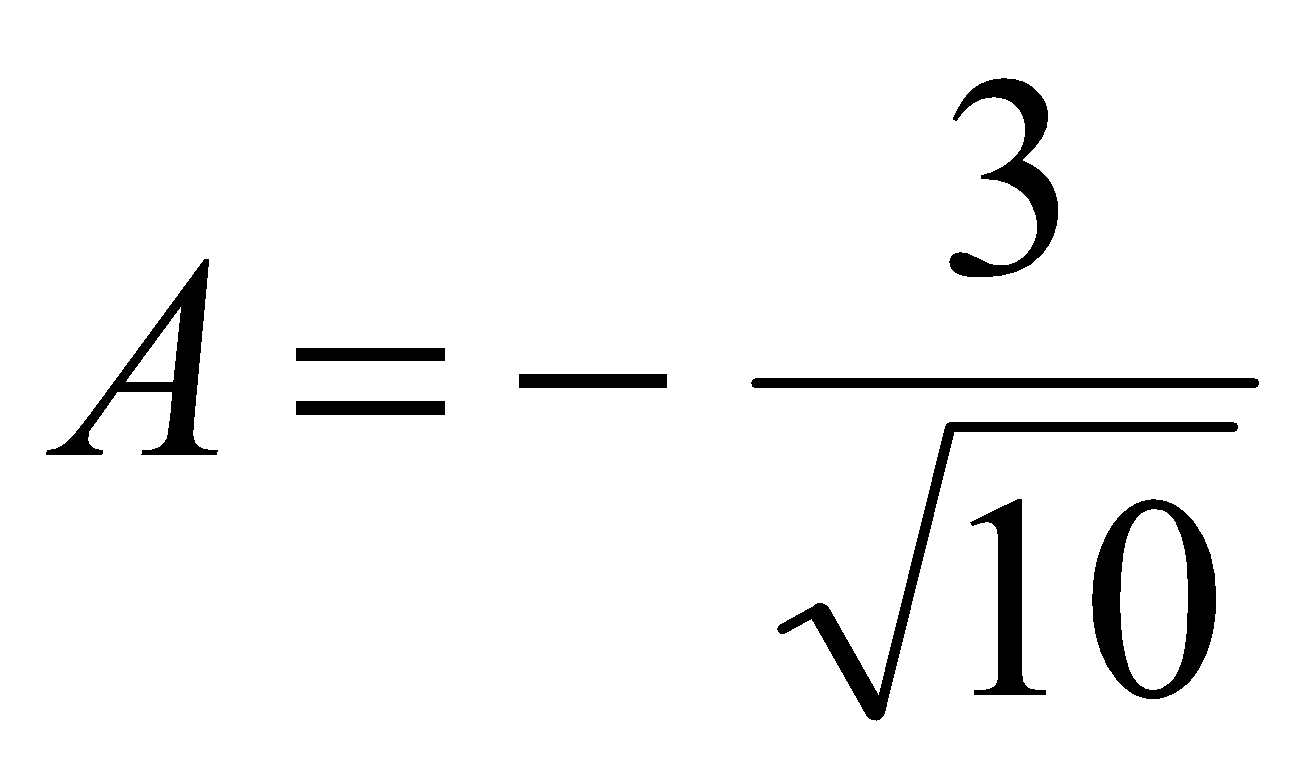 .
.
Пример 5. Вычислить значение  .
.
Решение. Если положить 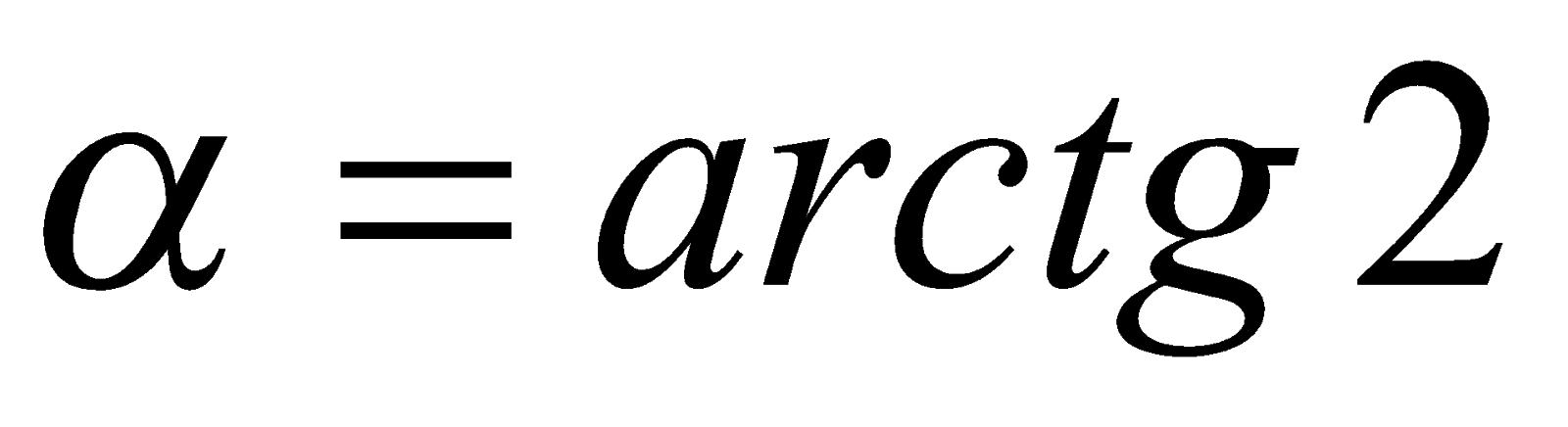 и
и  , то
, то 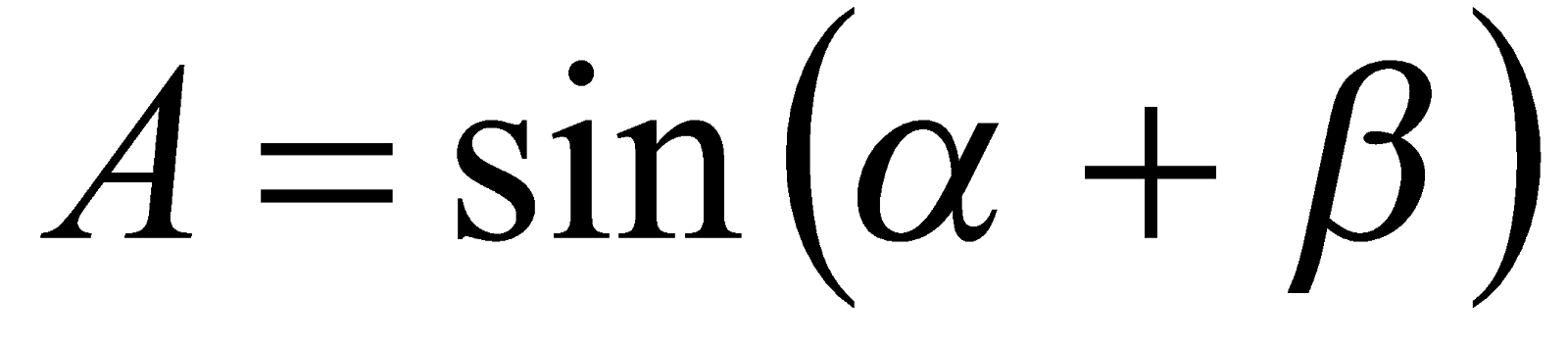 или
или
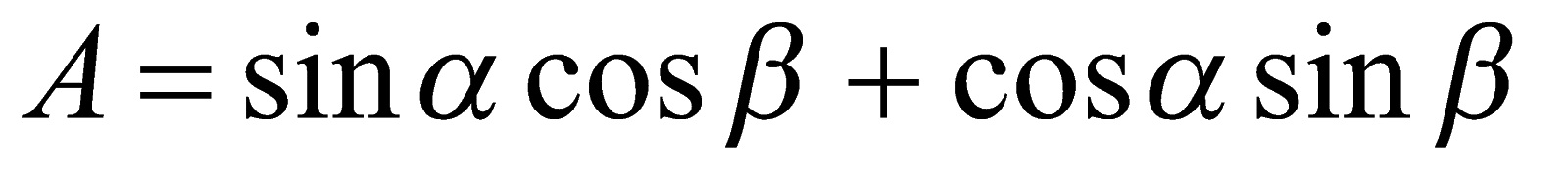 , (1)
, (1)
где из определения функции 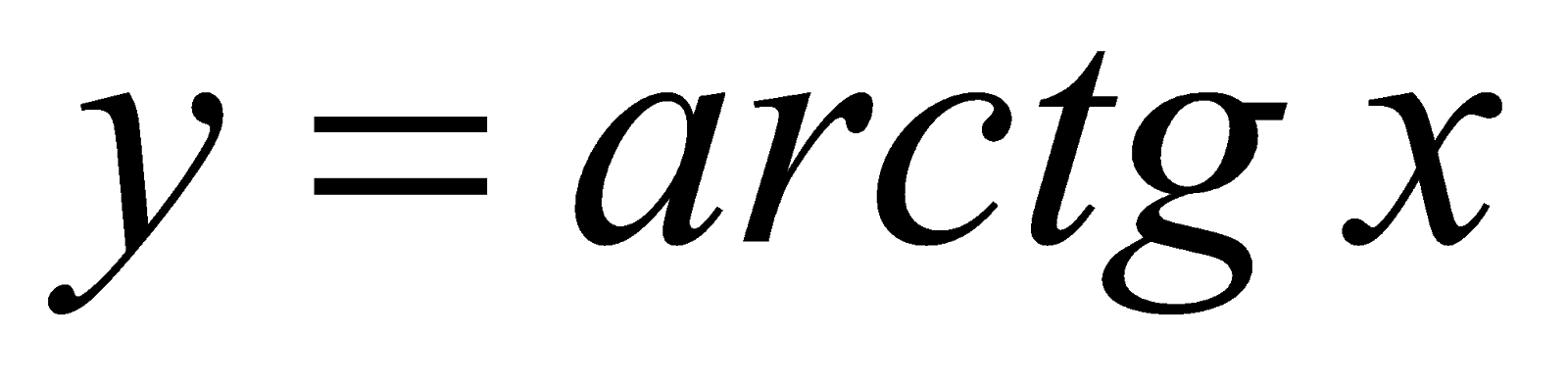 имеем
имеем 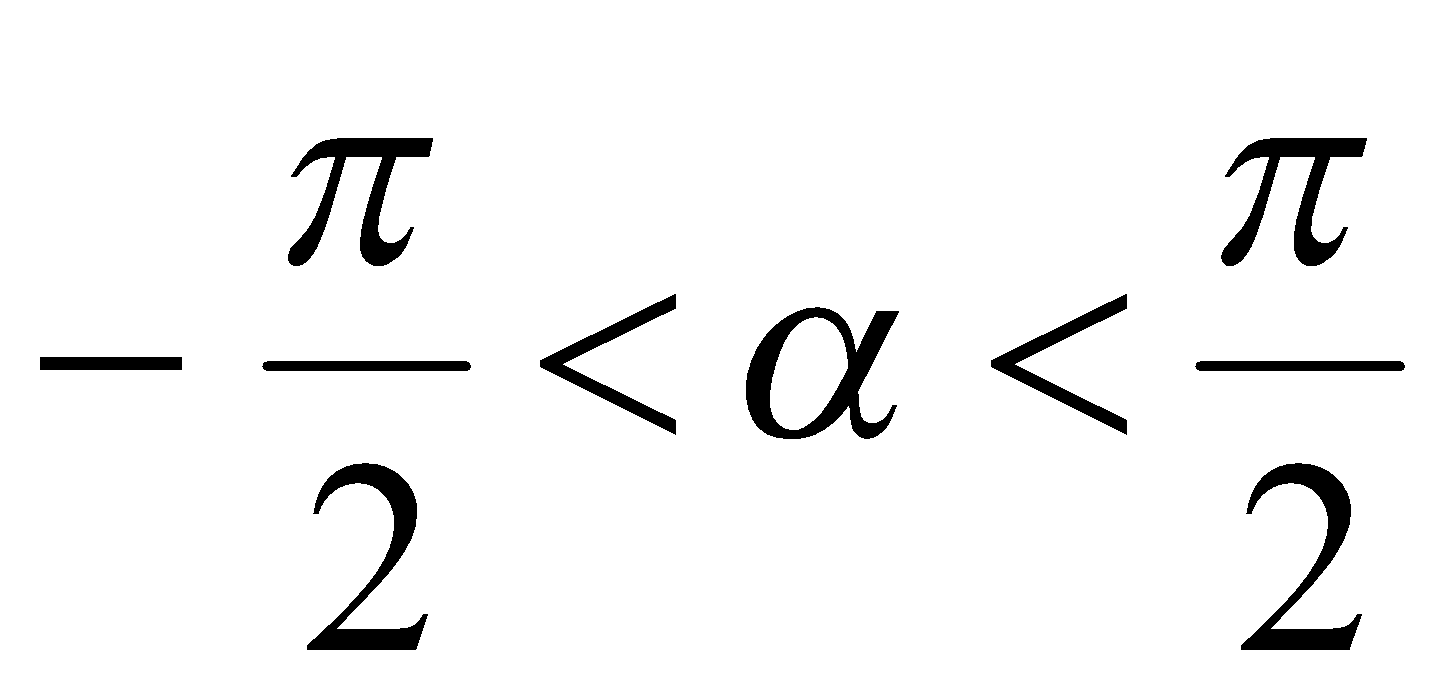 и
и 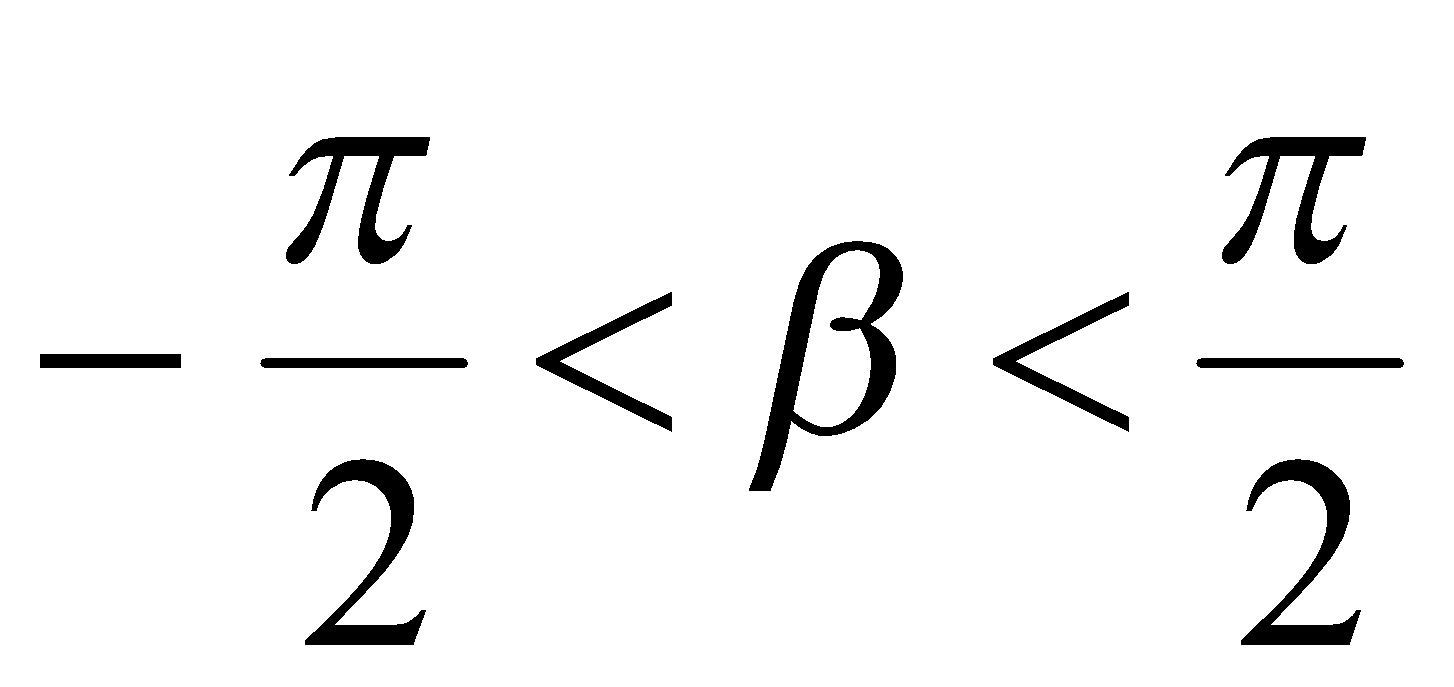 .
.
Однако 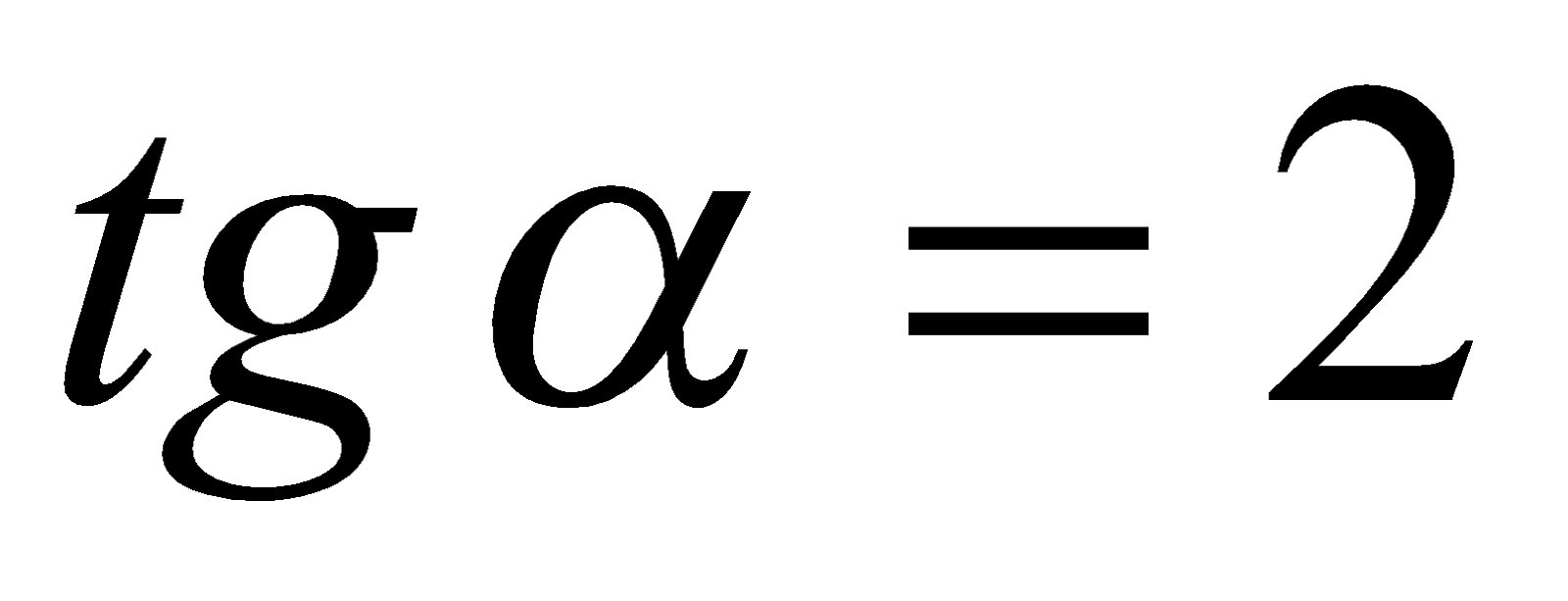 и
и  , поэтому
, поэтому 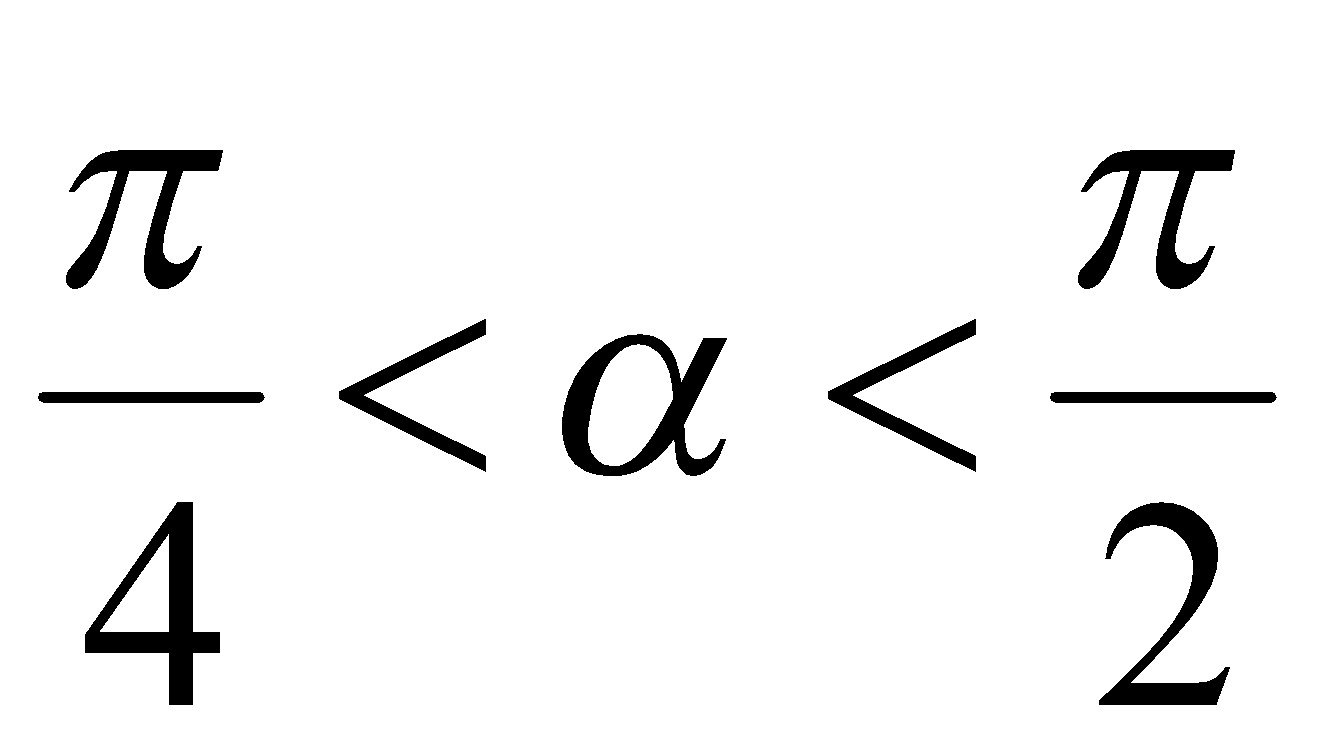 и
и 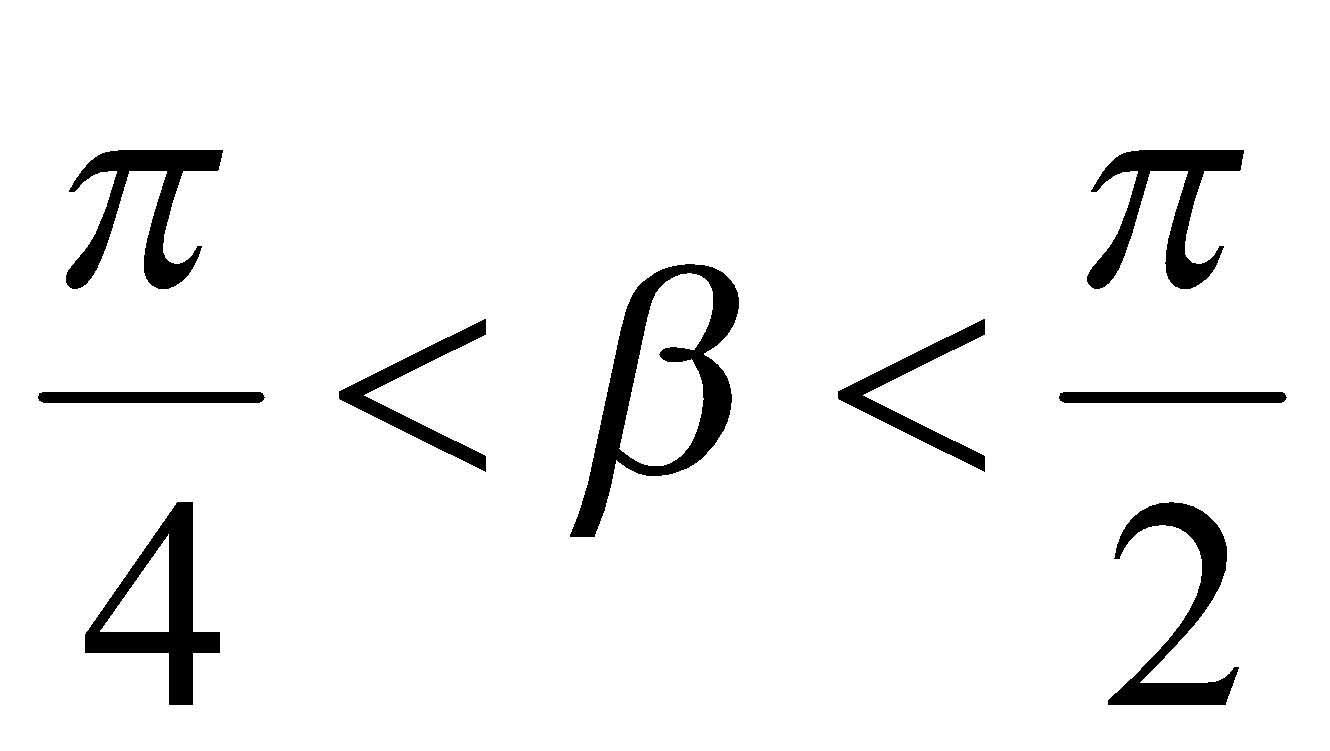 . В таком случае
. В таком случае 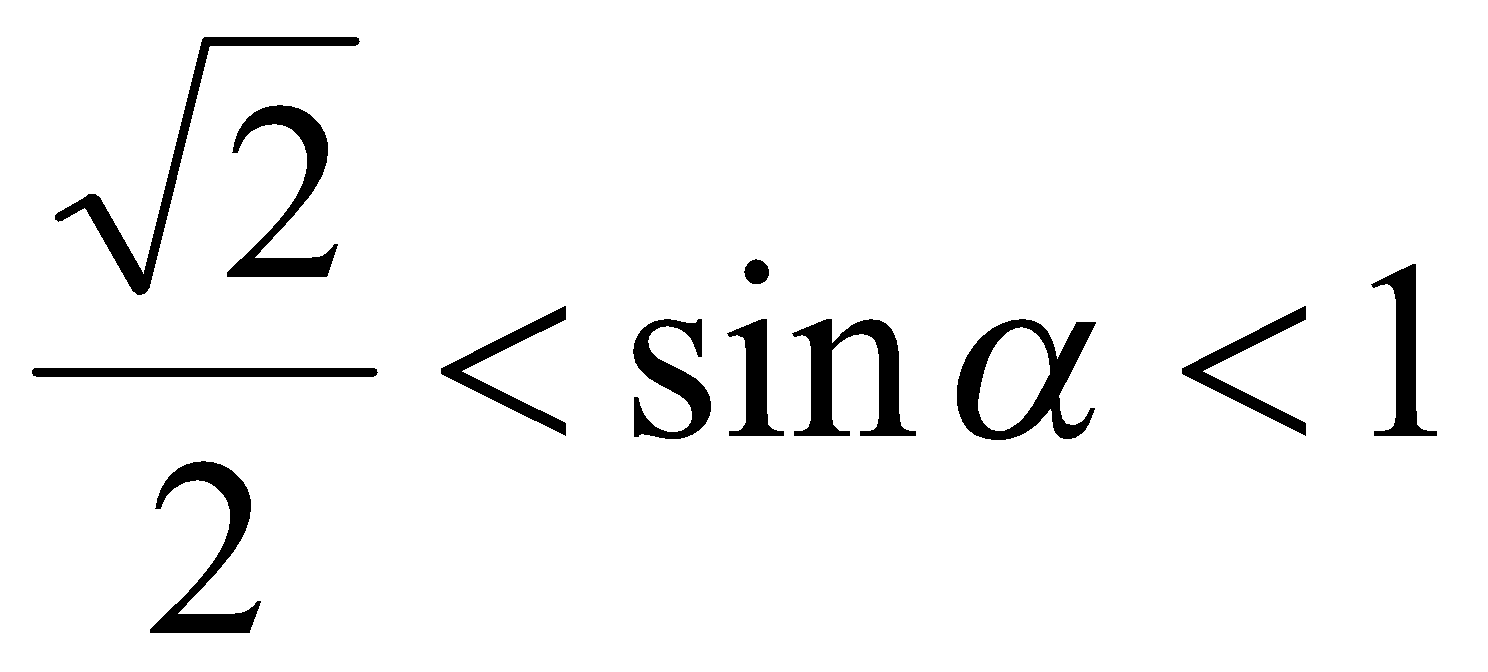 ,
, 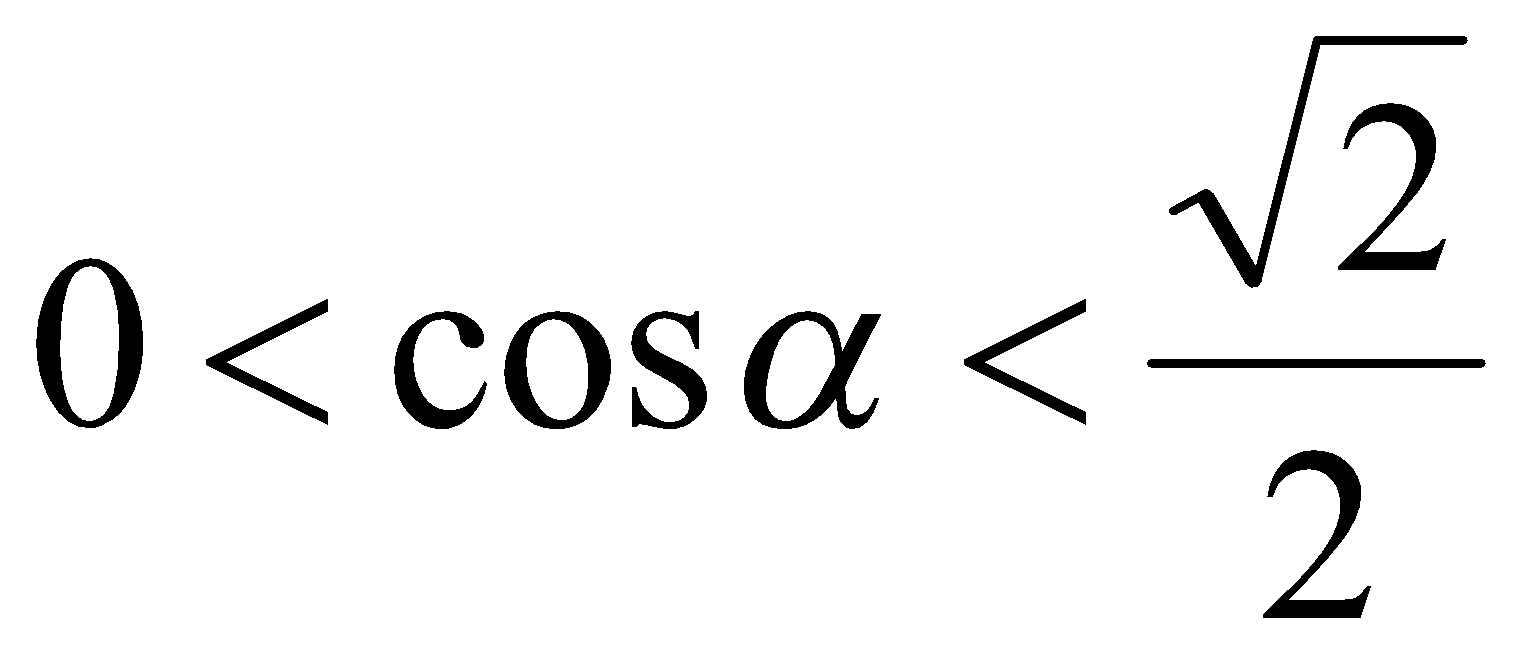 и
и 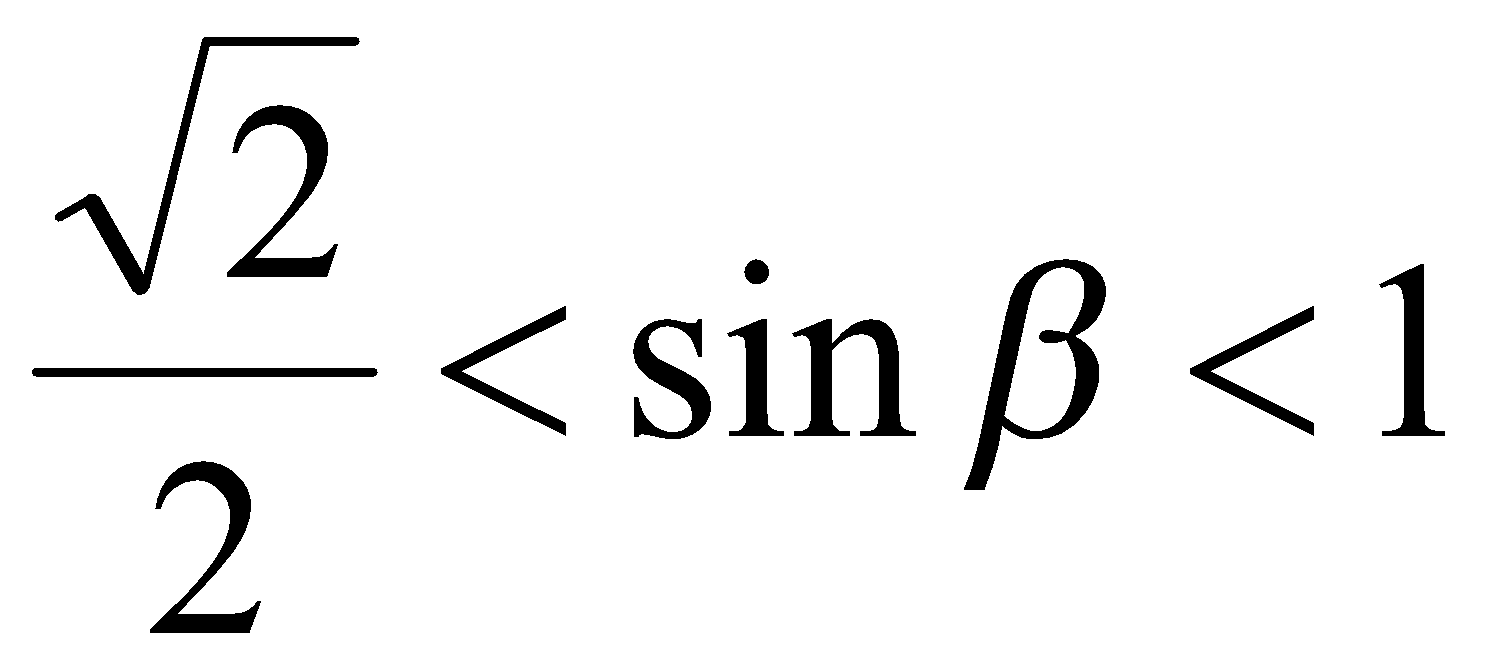 ,
,  .
.
Если 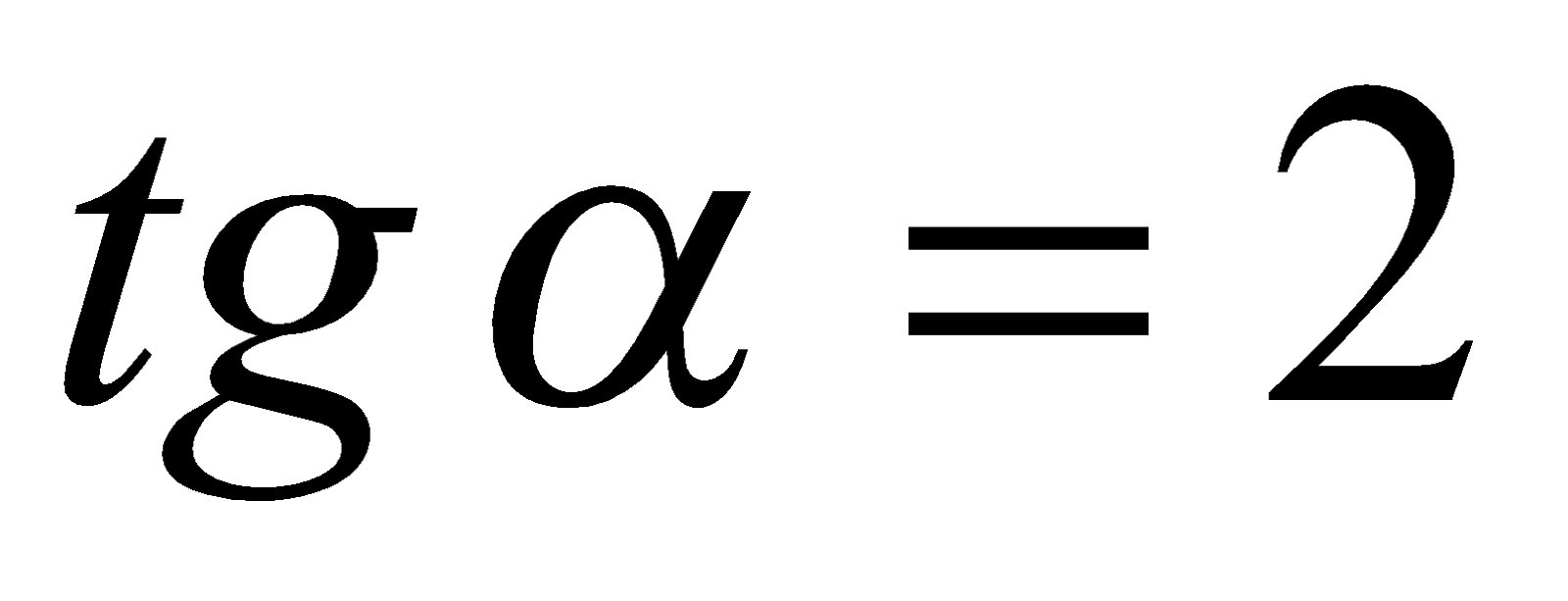 , то
, то 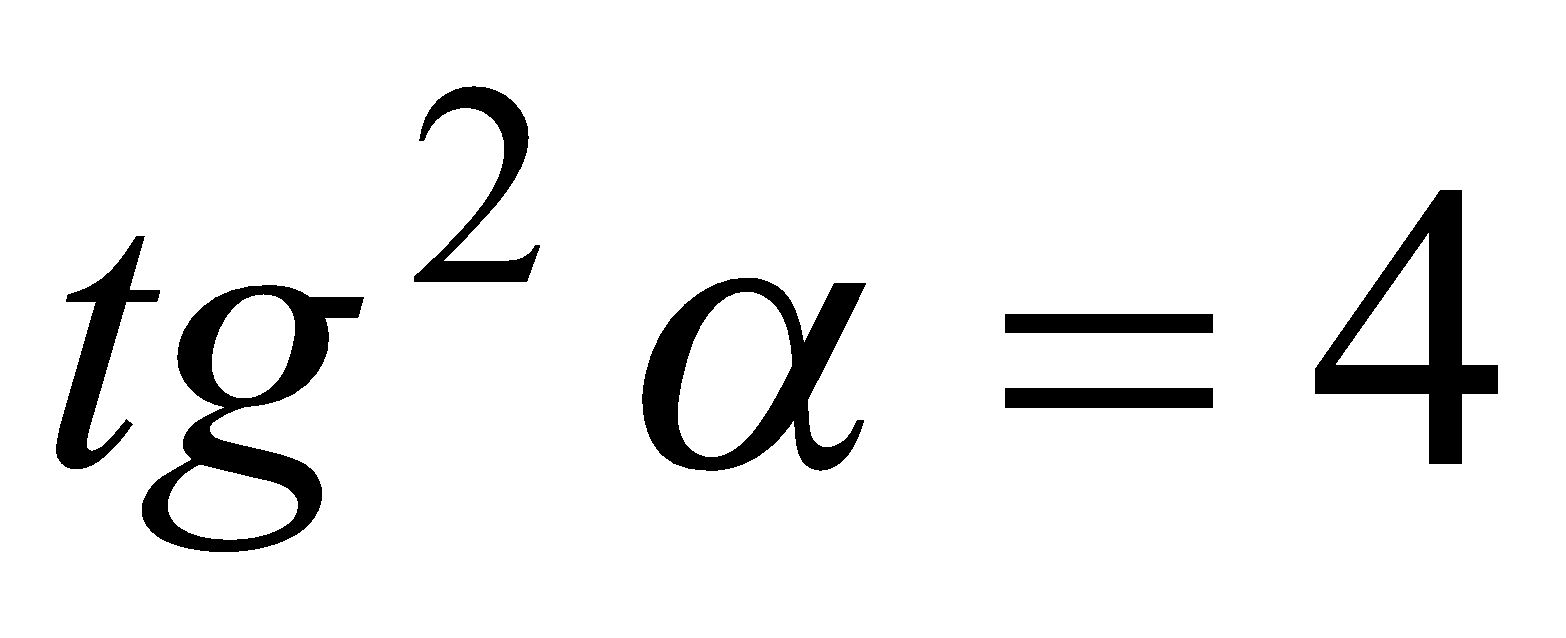 ,
, 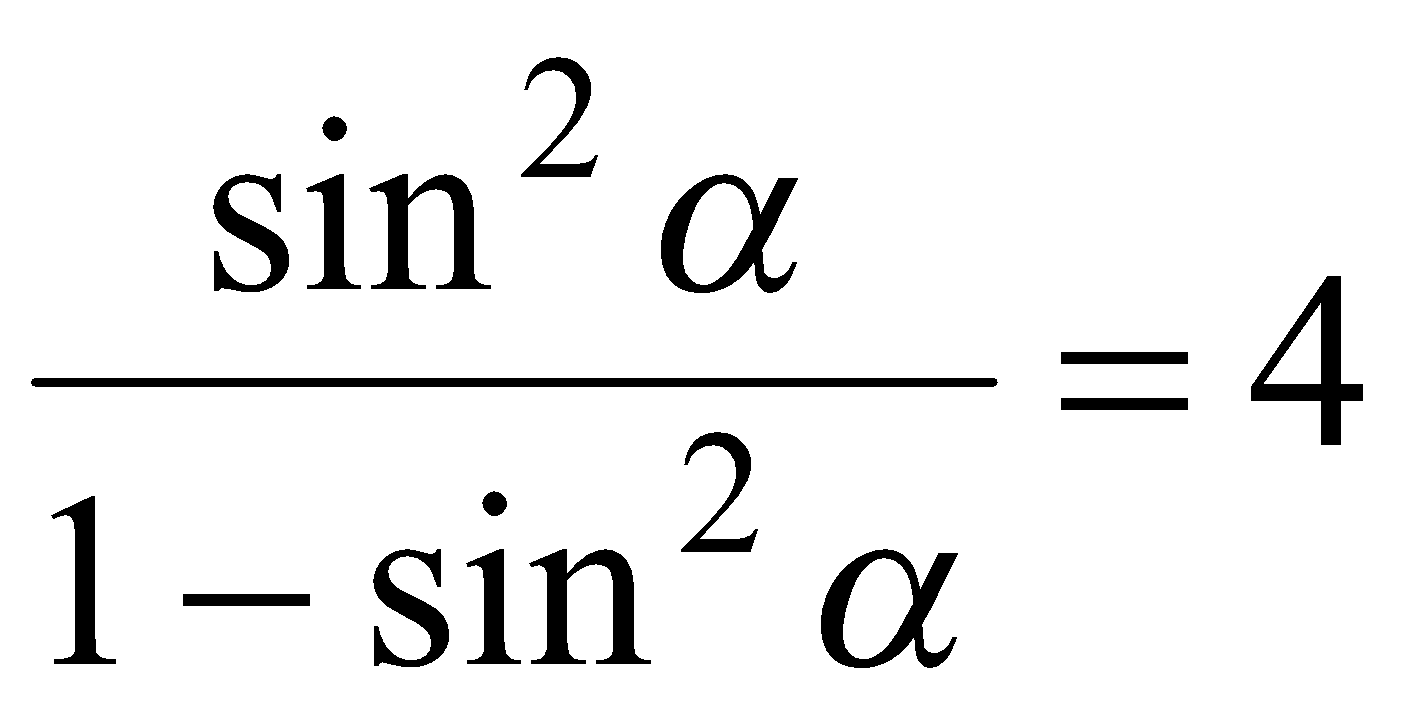 или
или 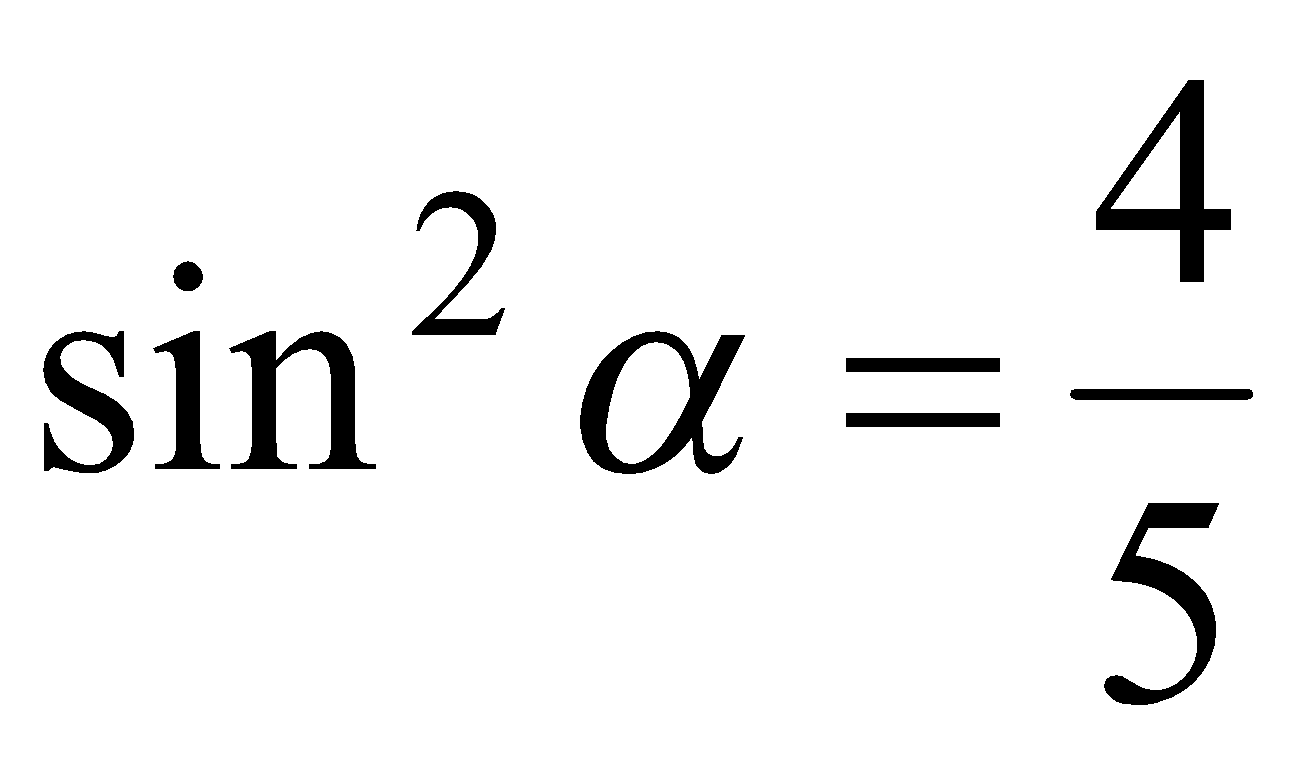 . Поскольку
. Поскольку  , то
, то  .
.
С учетом того, что 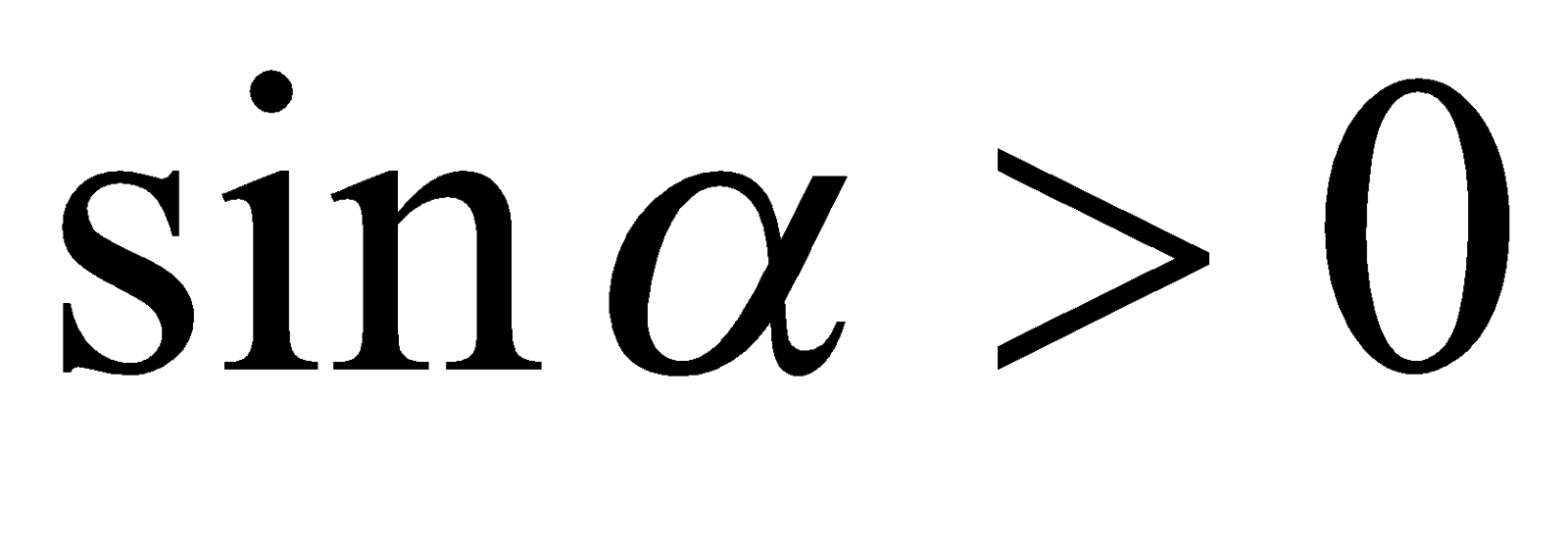 и
и  , имеем
, имеем 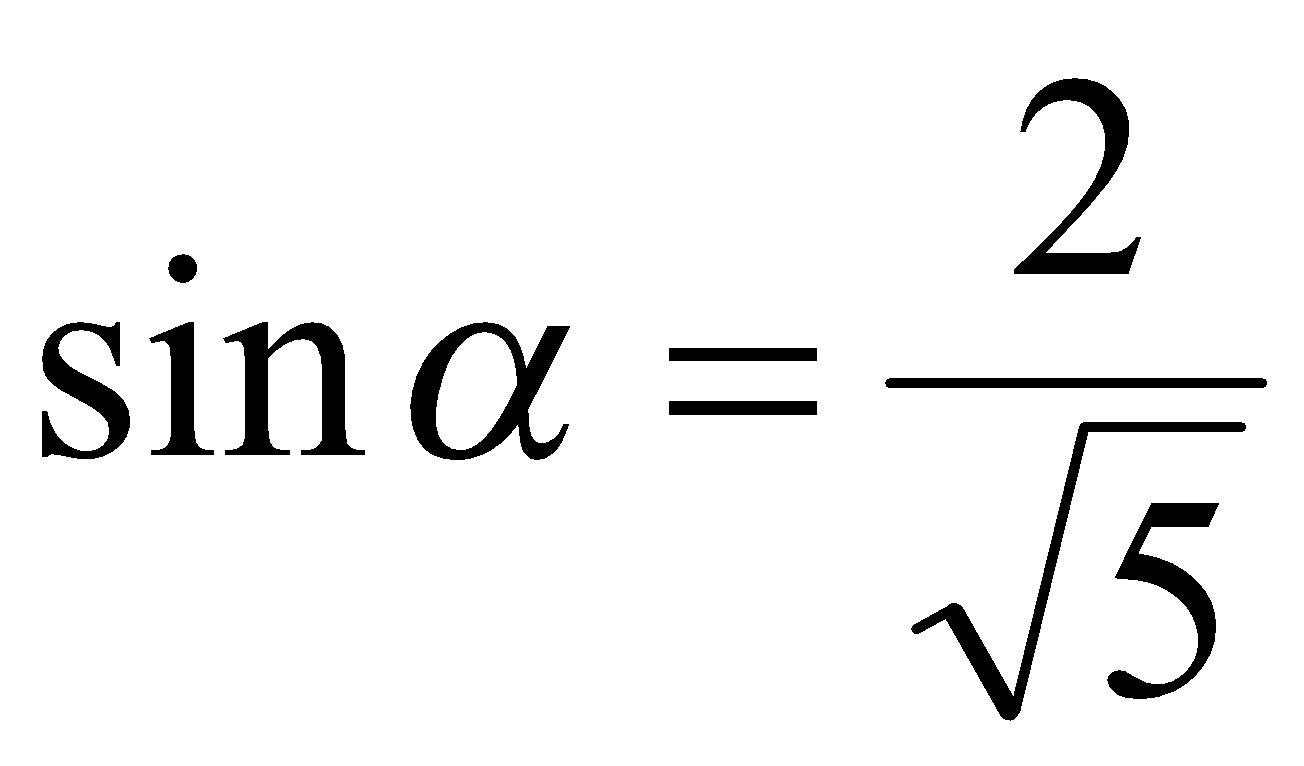 и
и 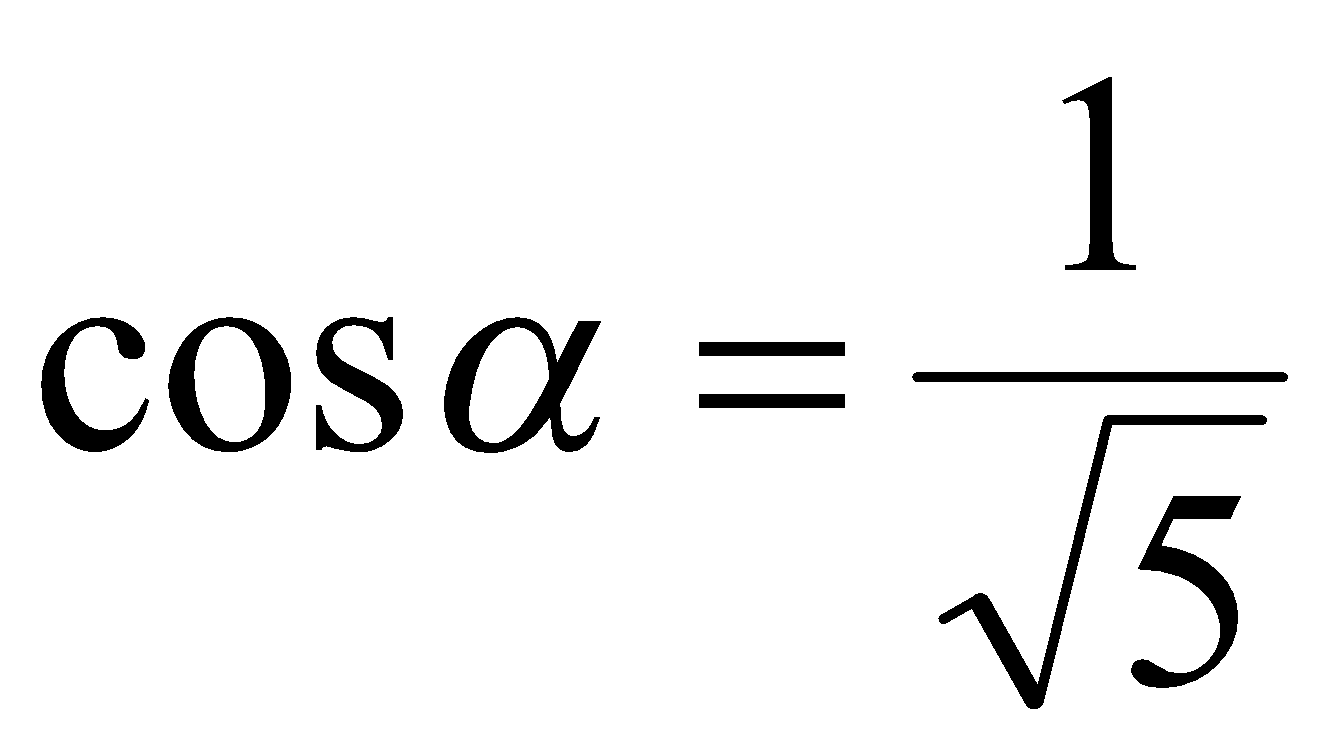 .
.
Если  , то повторяя рассуждения, приведенные выше, получаем
, то повторяя рассуждения, приведенные выше, получаем 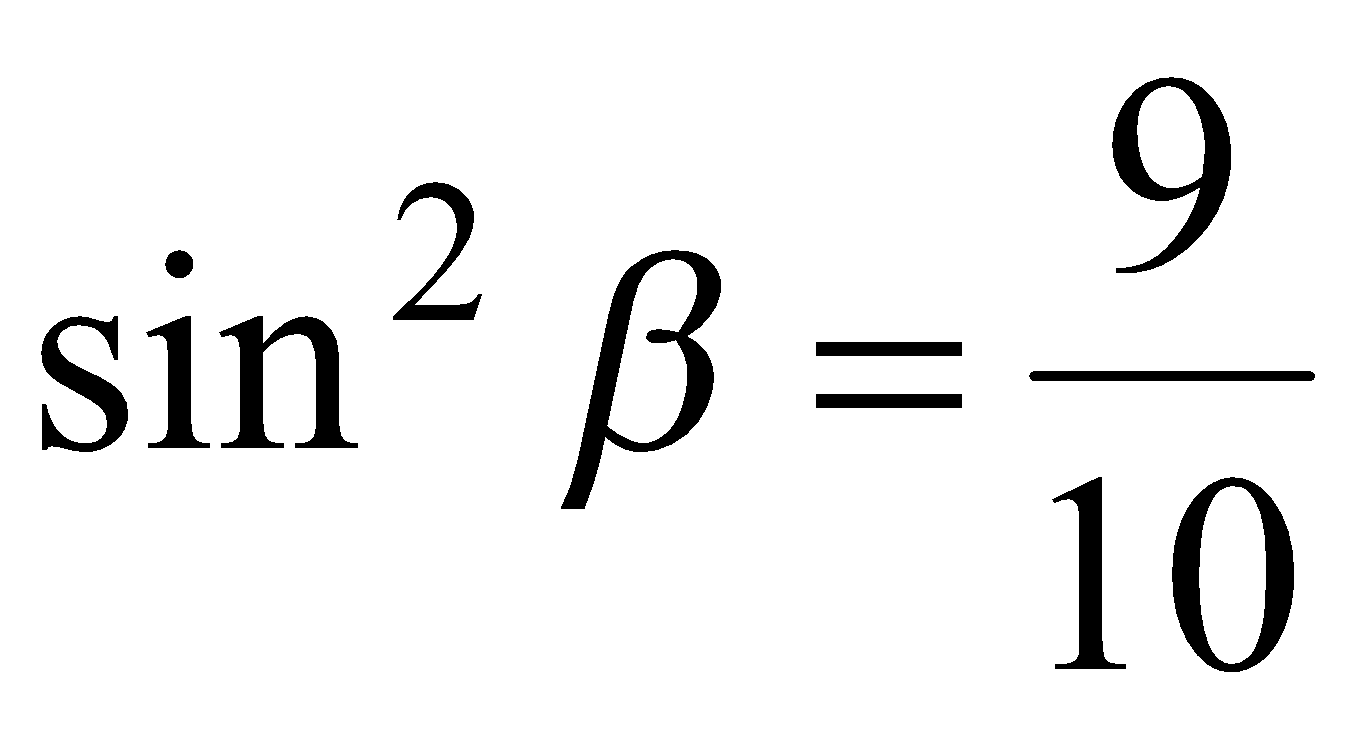 ,
, 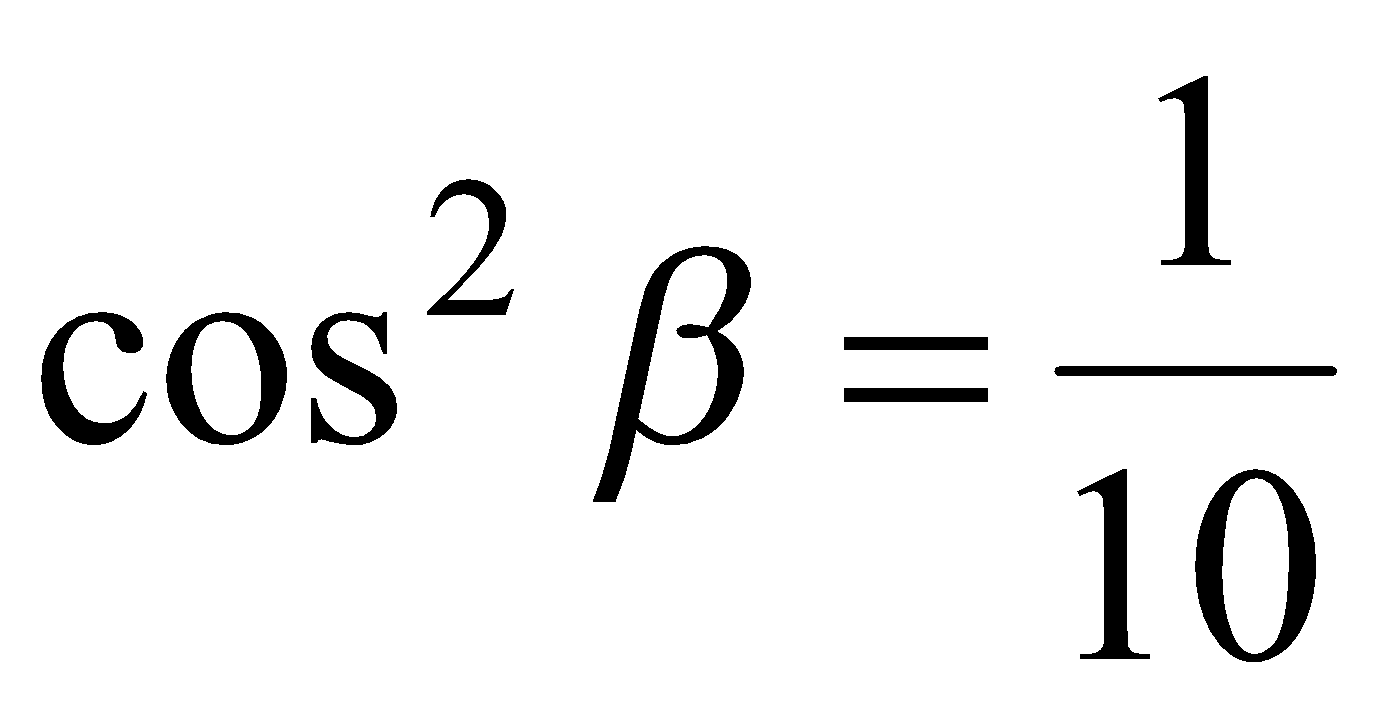 и
и 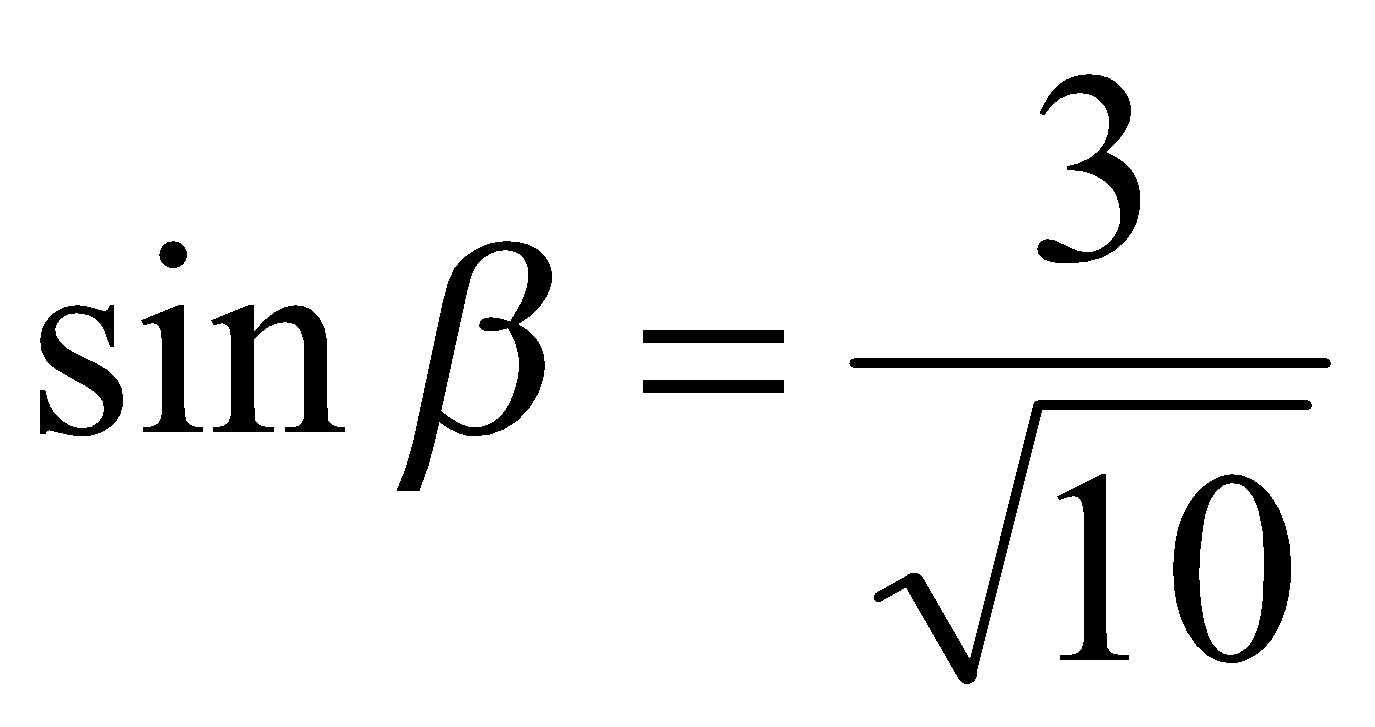 ,
, 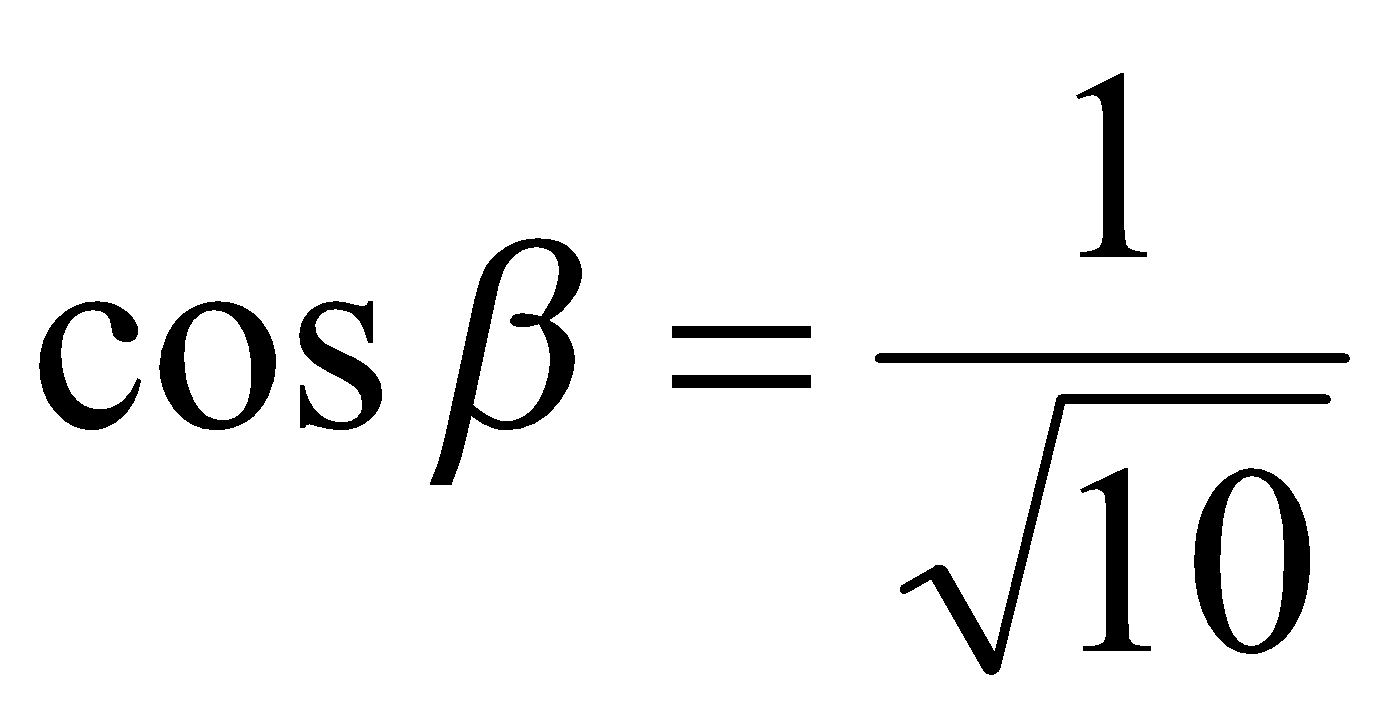 .
.
Подставляя значения 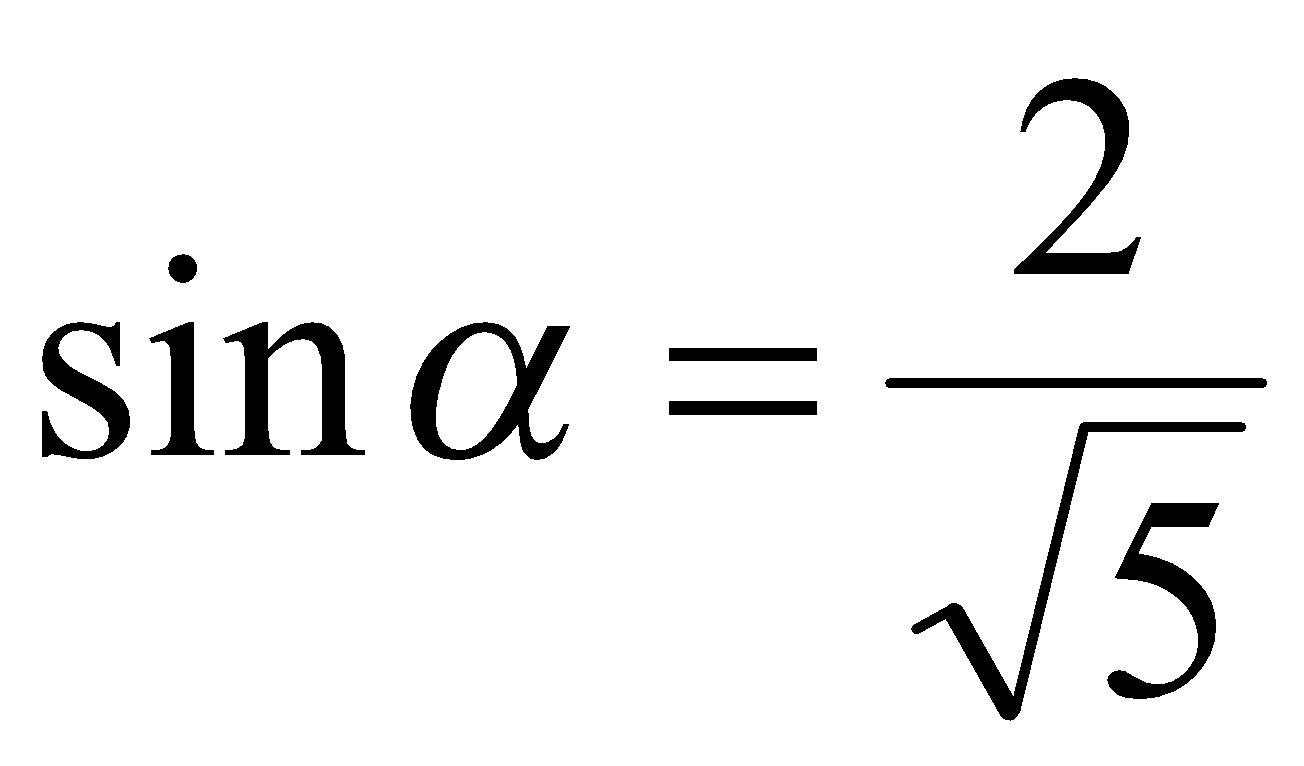 ,
, 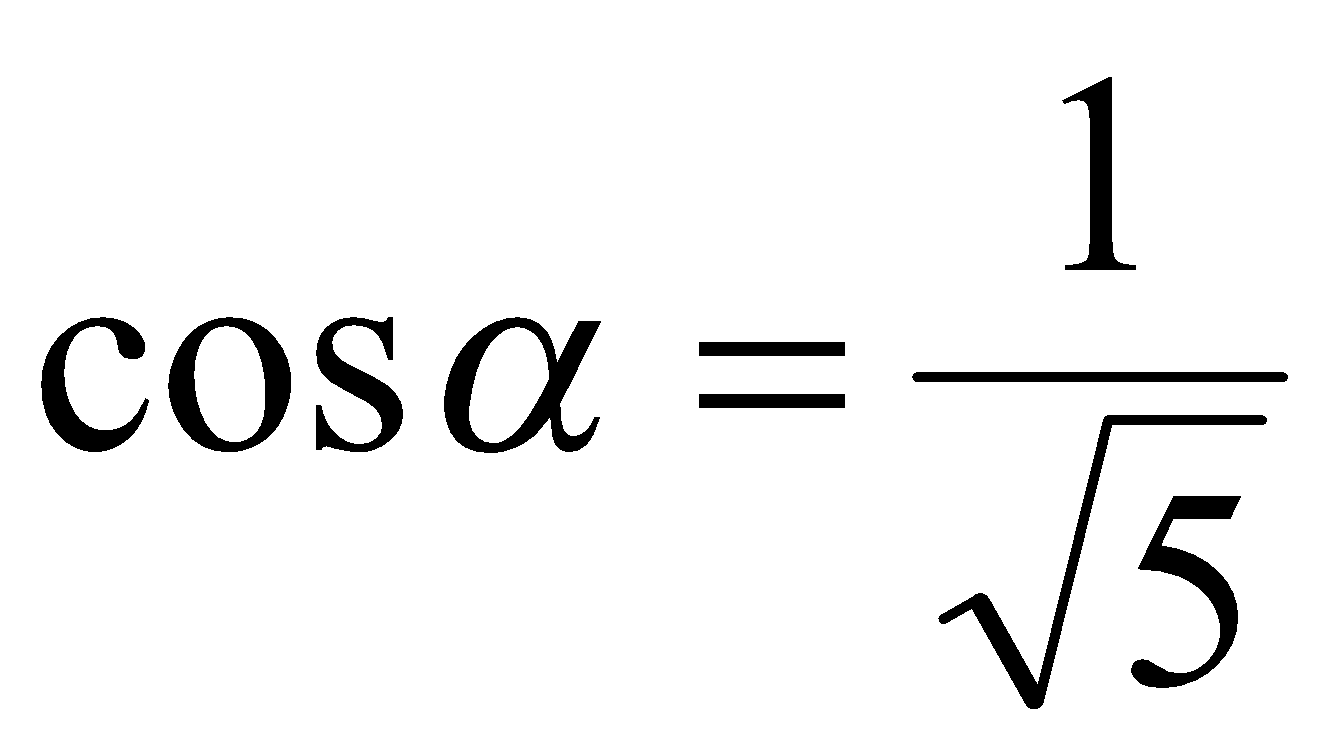 ,
, 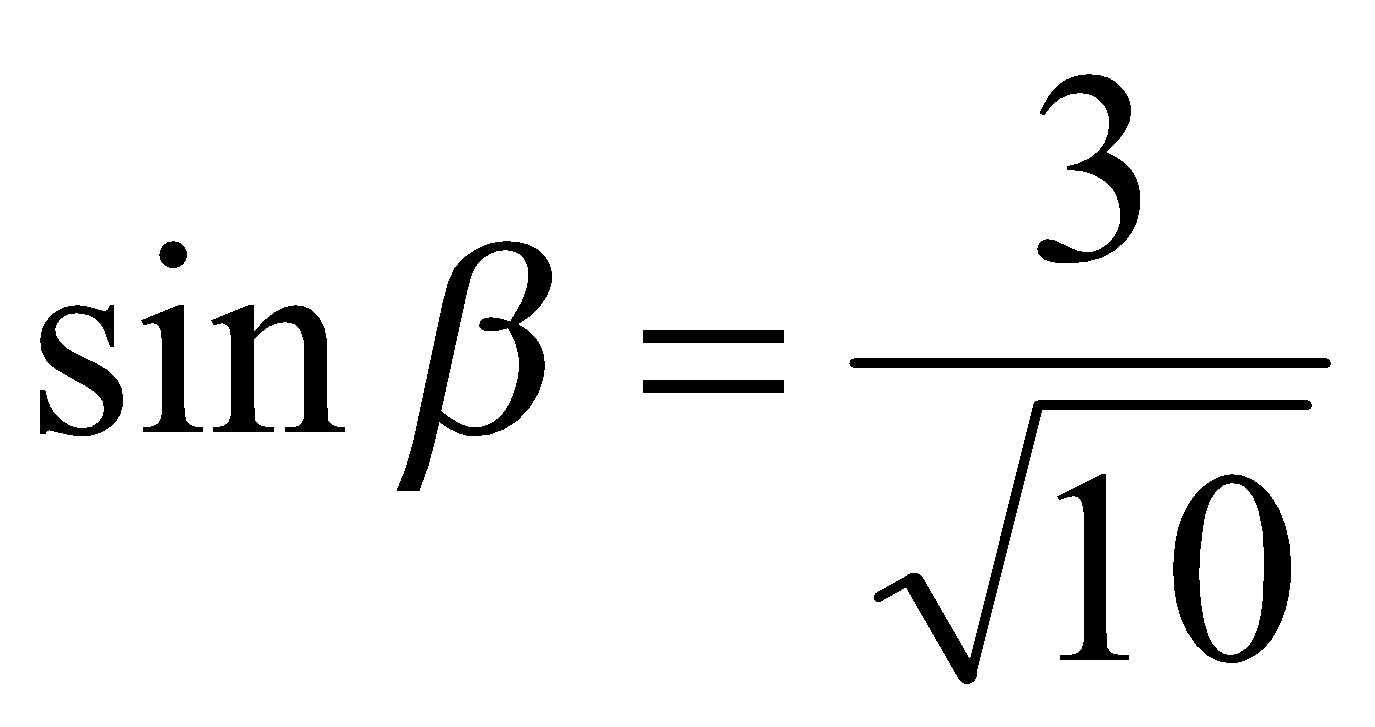 ,
, 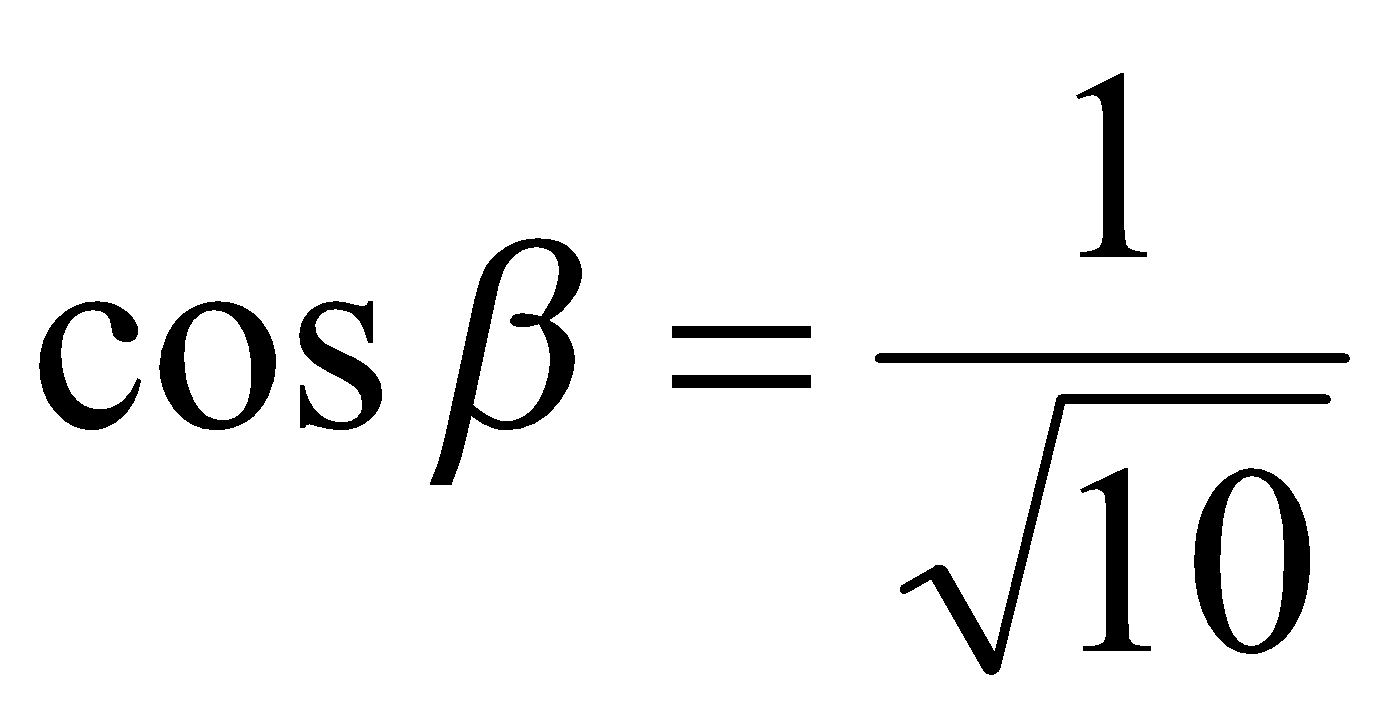 в выражение (1) получаем
в выражение (1) получаем 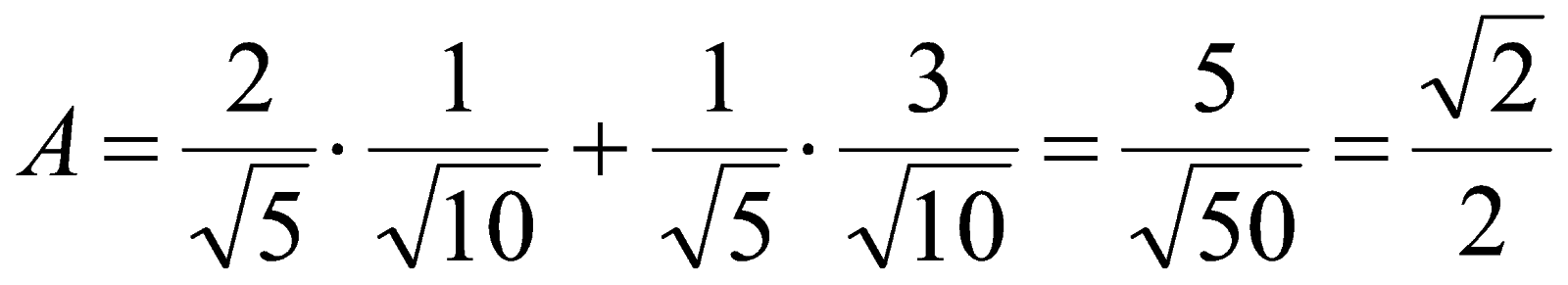 .
.
Ответ:  .
.
Примечание. Так как в примере 5 показано, что 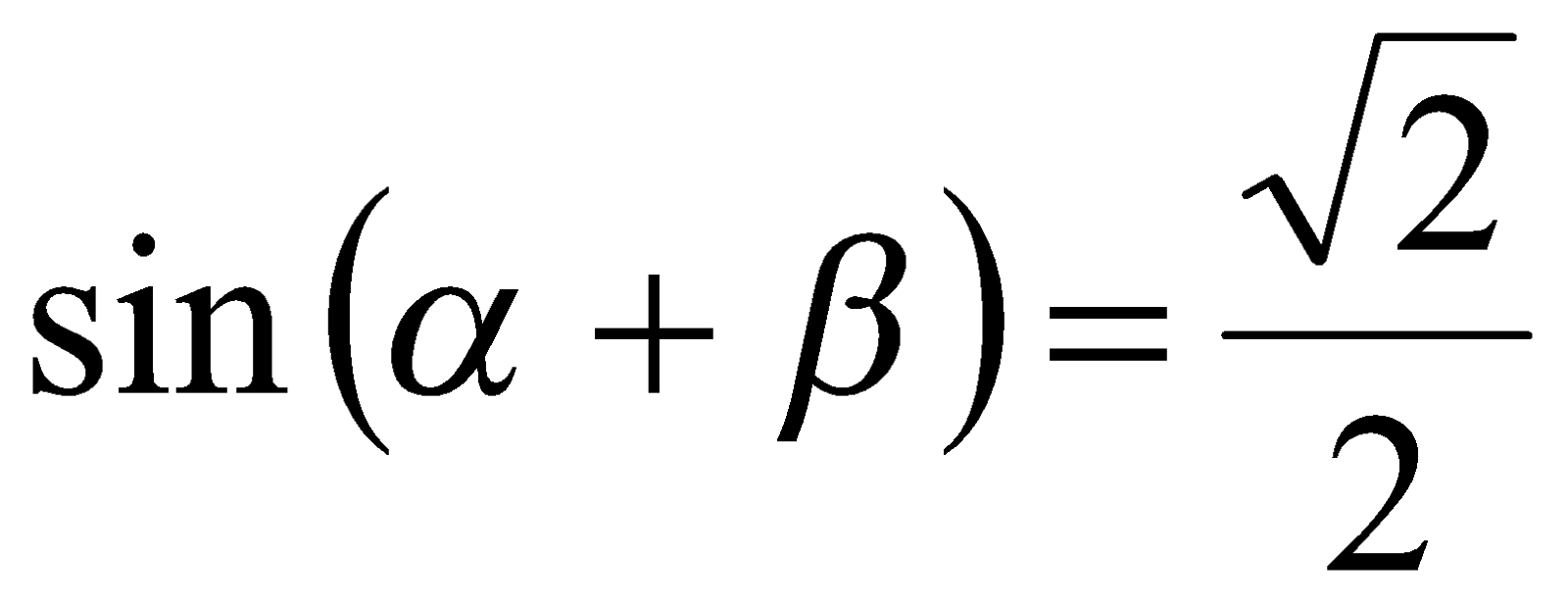 , где
, где 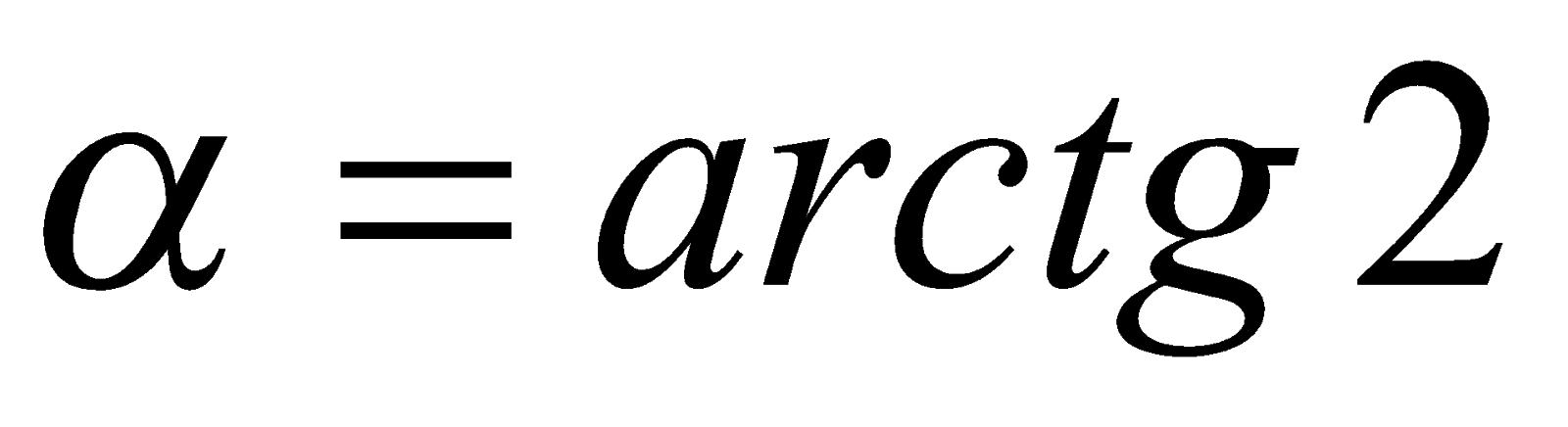 ,
,  и
и 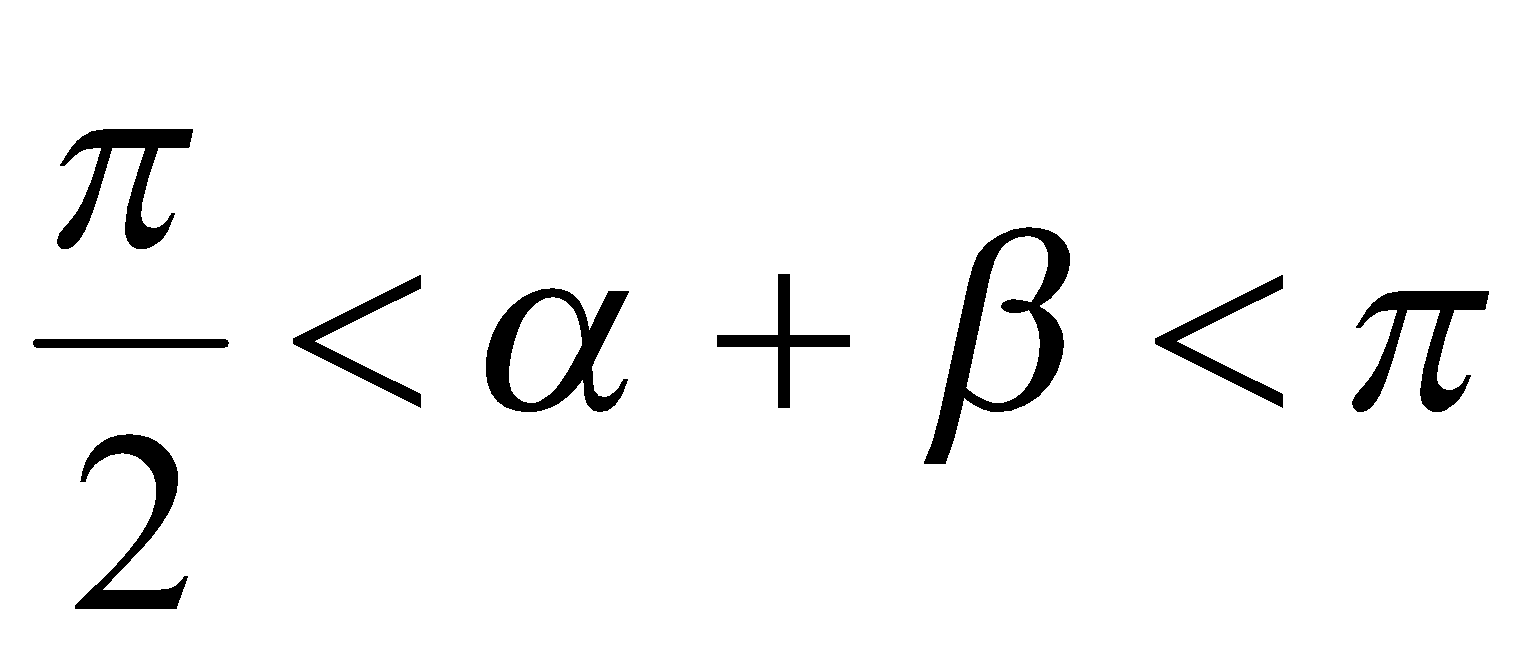 , то справедливо равенство
, то справедливо равенство
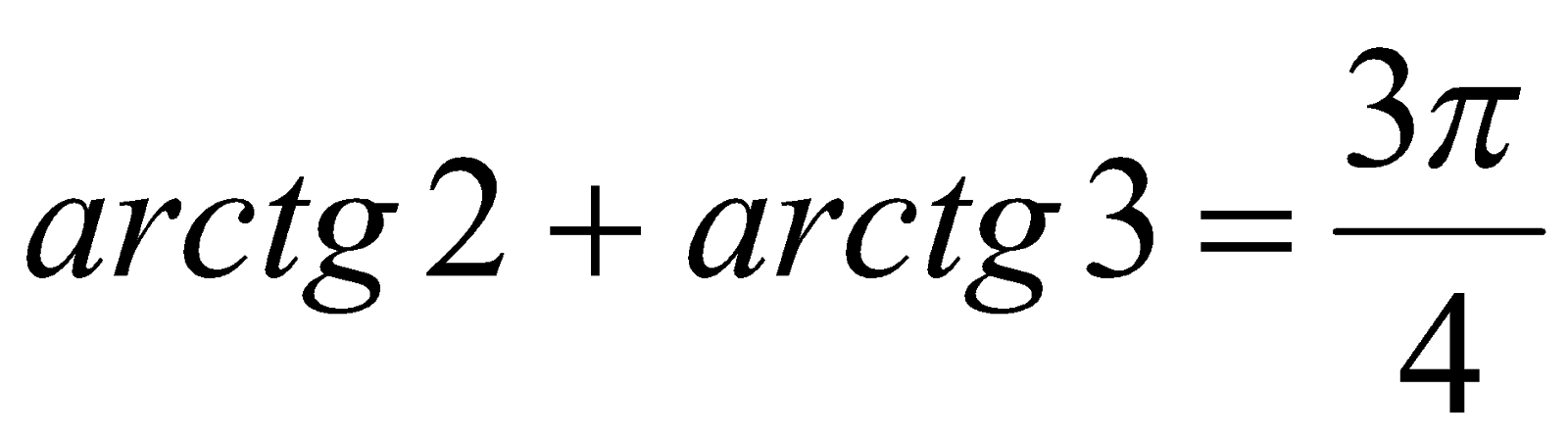 .
.
Отсюда также следует, что 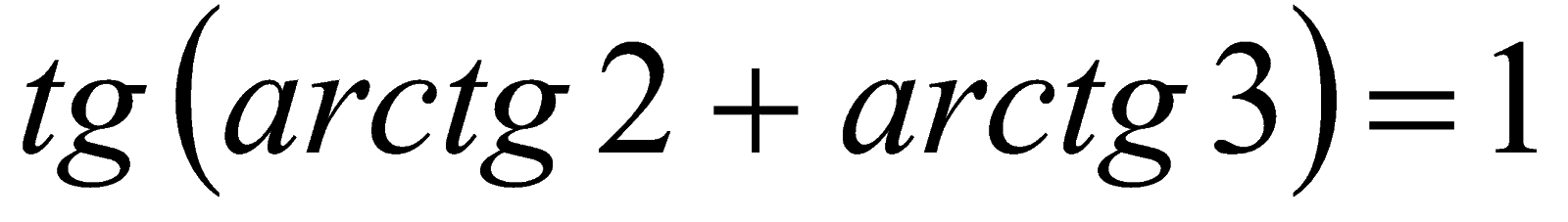 .
.
Пример 6. Вычислить значение 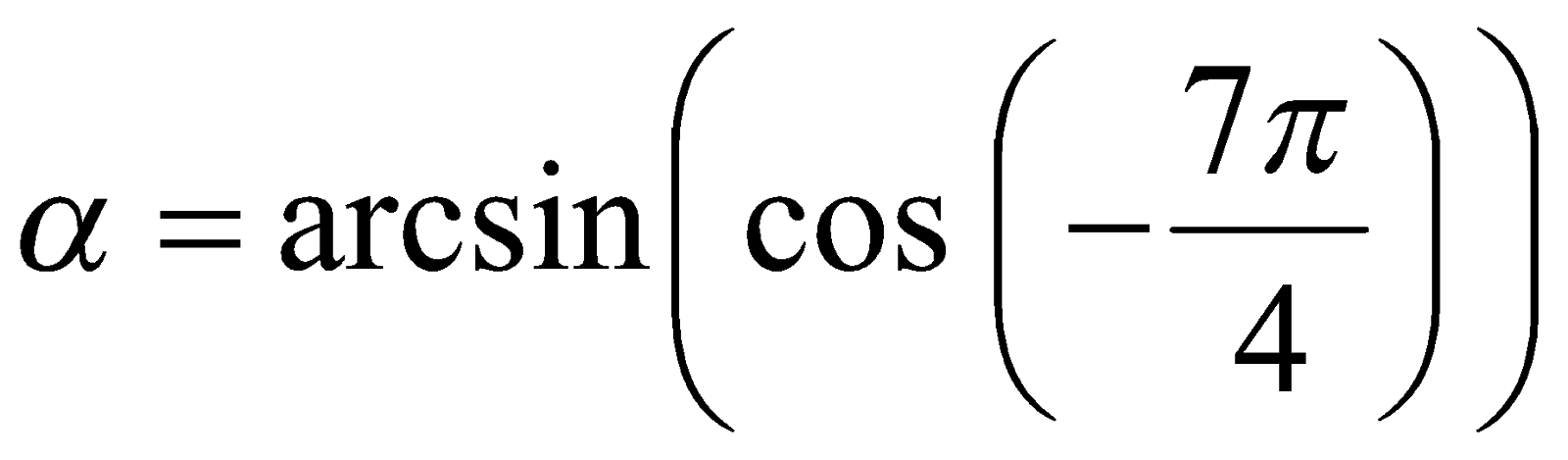 .
.
Решение. Из определения функции 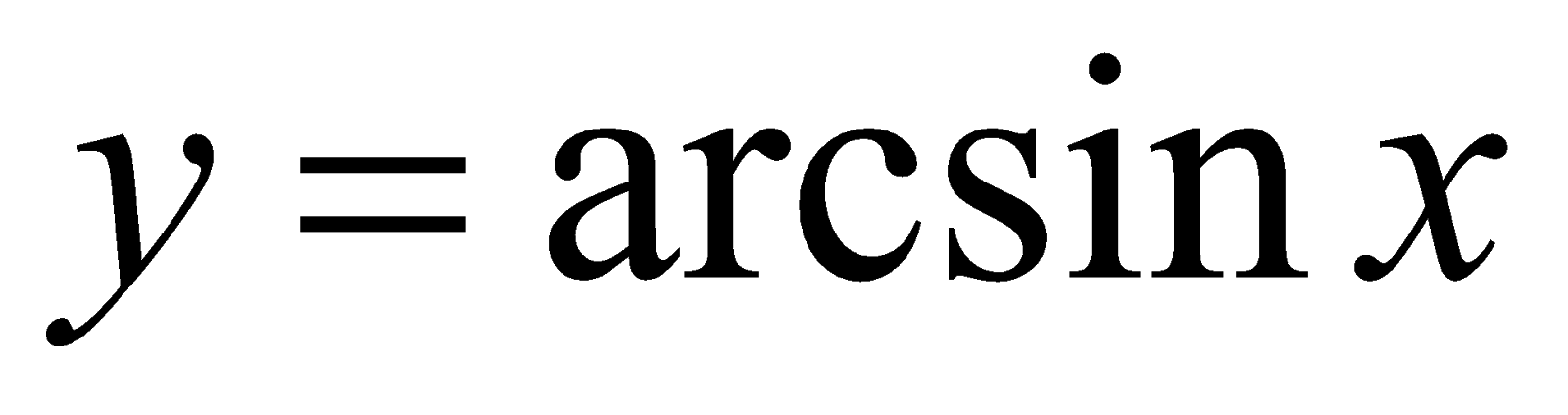 следует, что
следует, что 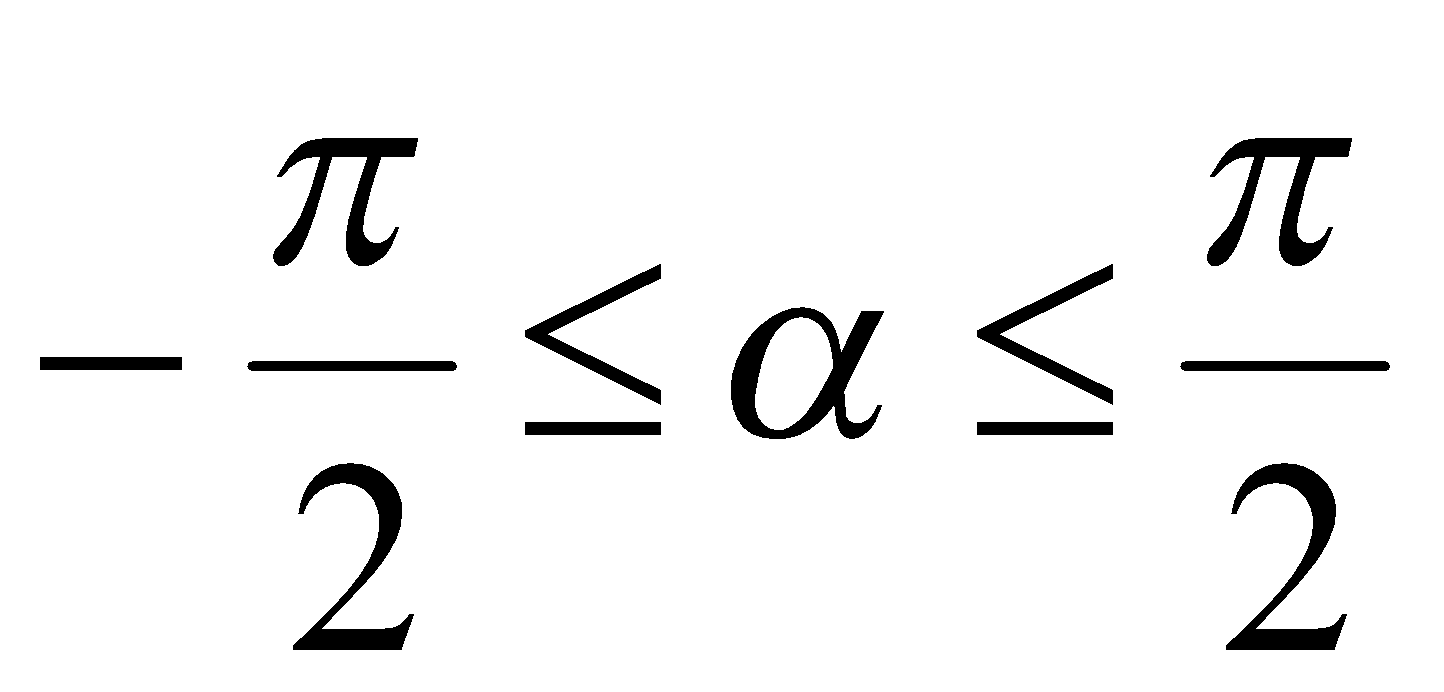 . Из условия примера получаем
. Из условия примера получаем 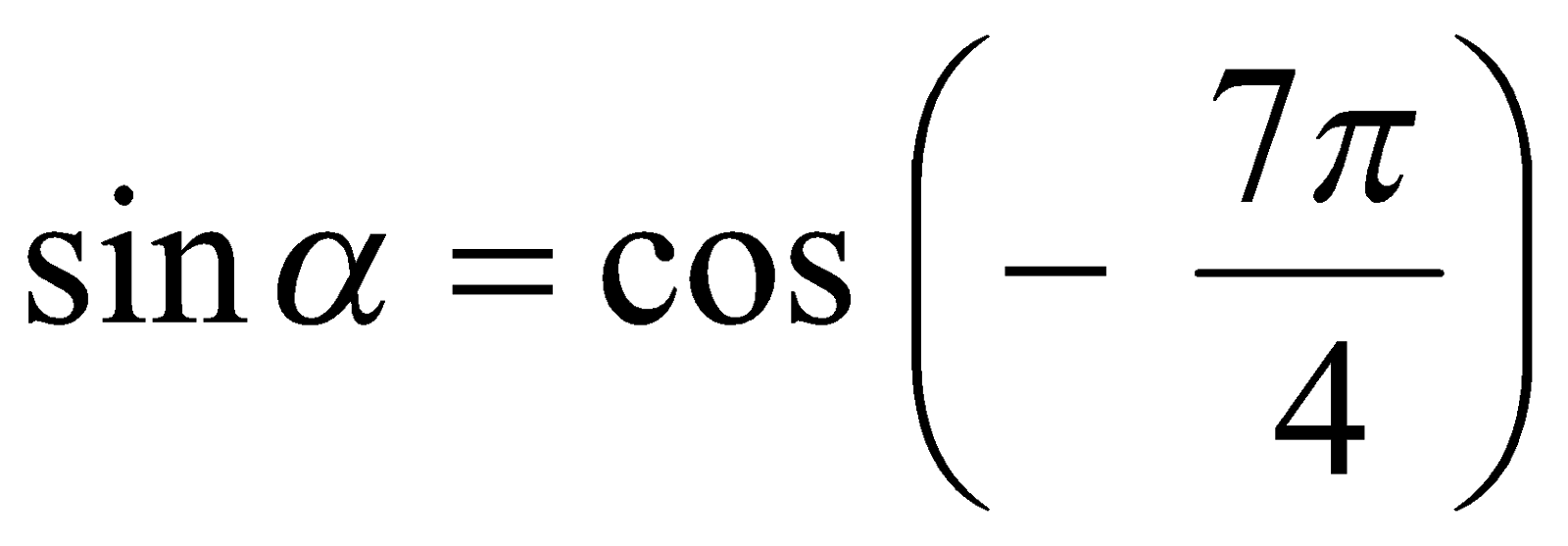 .
.
Так как 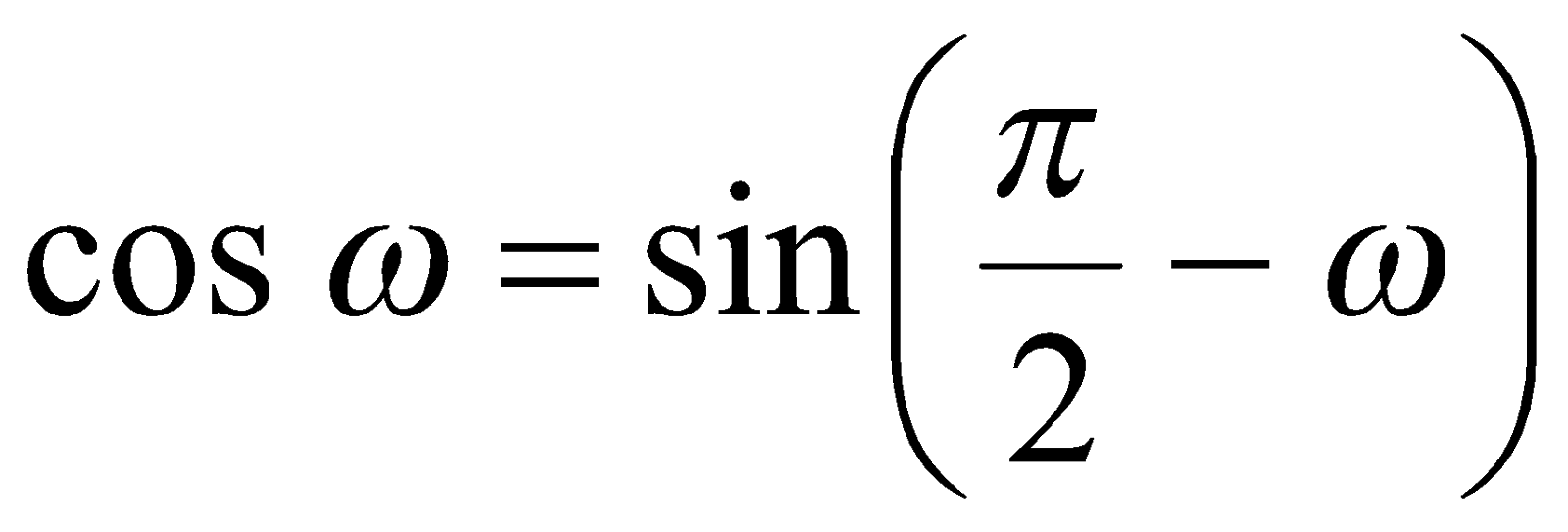 , то имеем уравнение
, то имеем уравнение 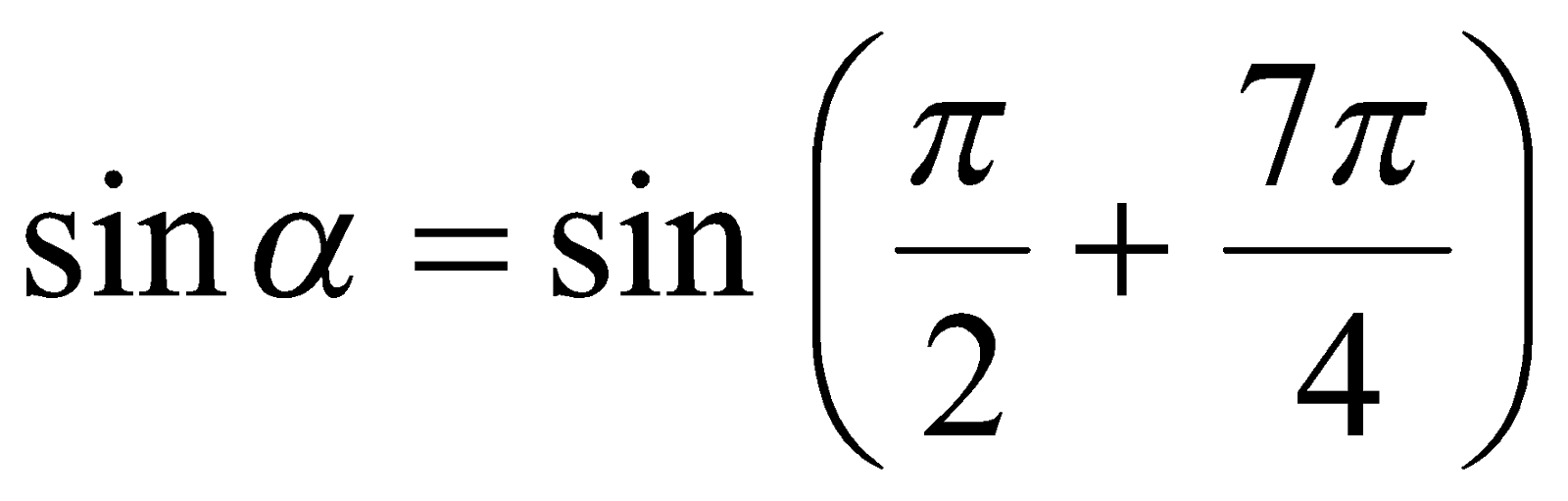 или
или 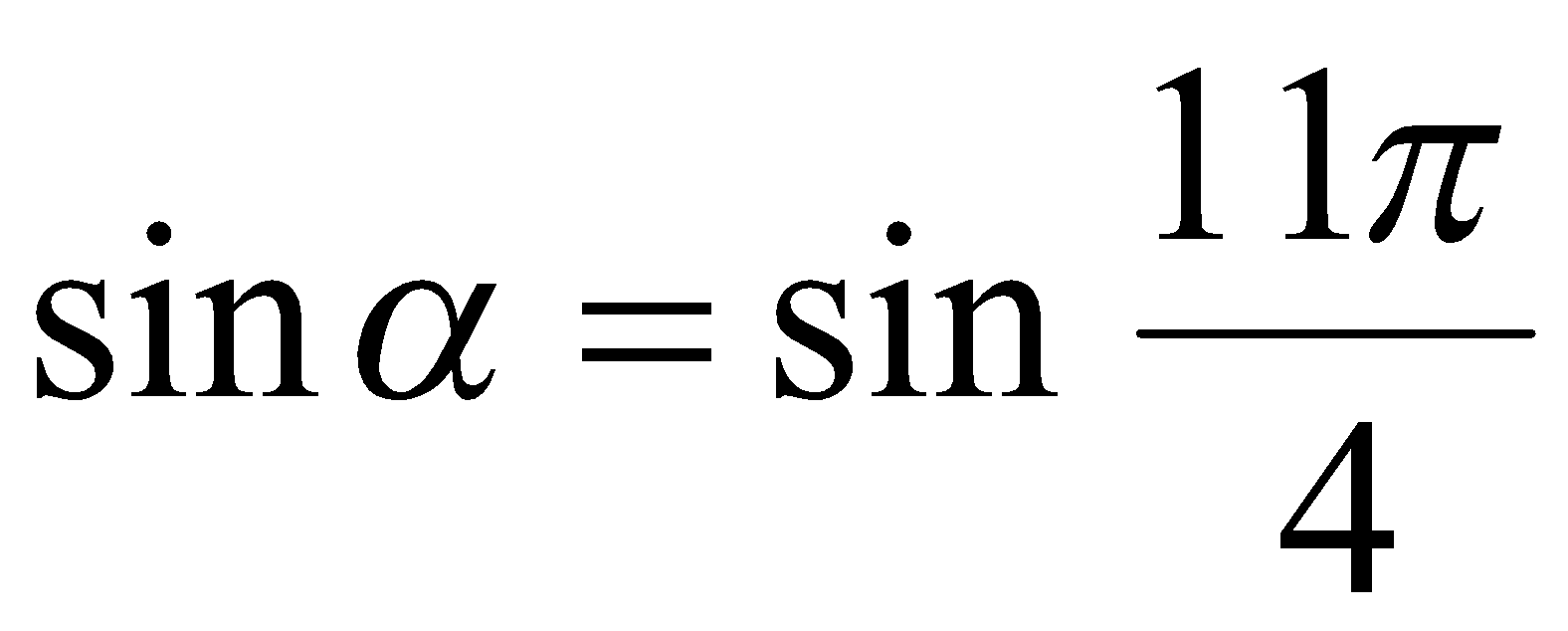 . Далее, принимая во внимание теорему 1, записываем две серии корней уравнения
. Далее, принимая во внимание теорему 1, записываем две серии корней уравнения 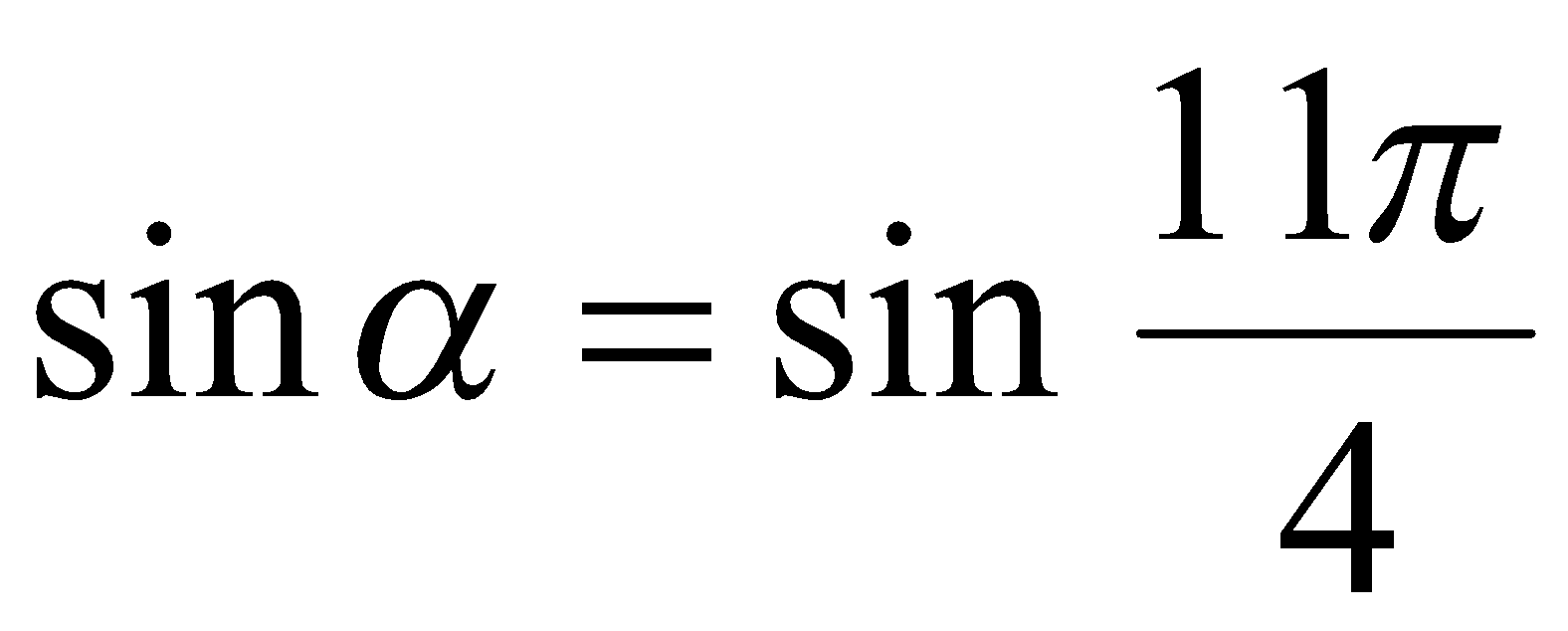 вида
вида
 и
и 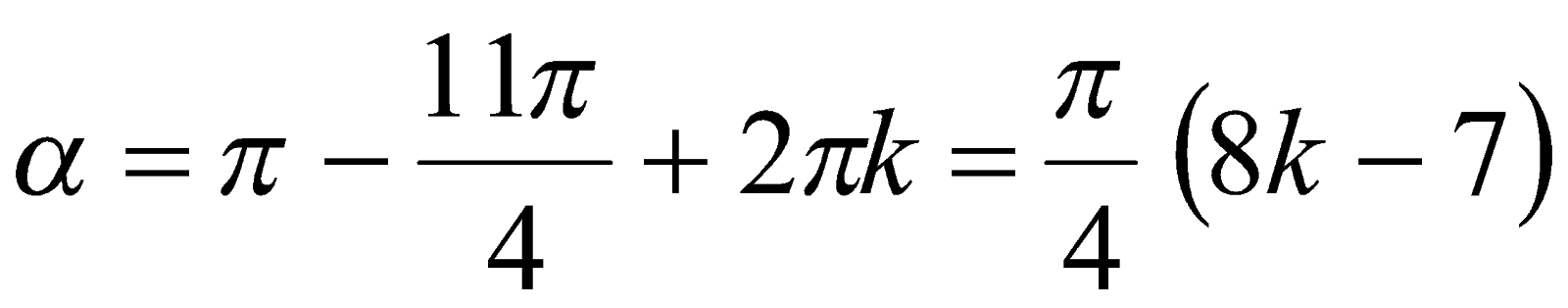 ,
,
где 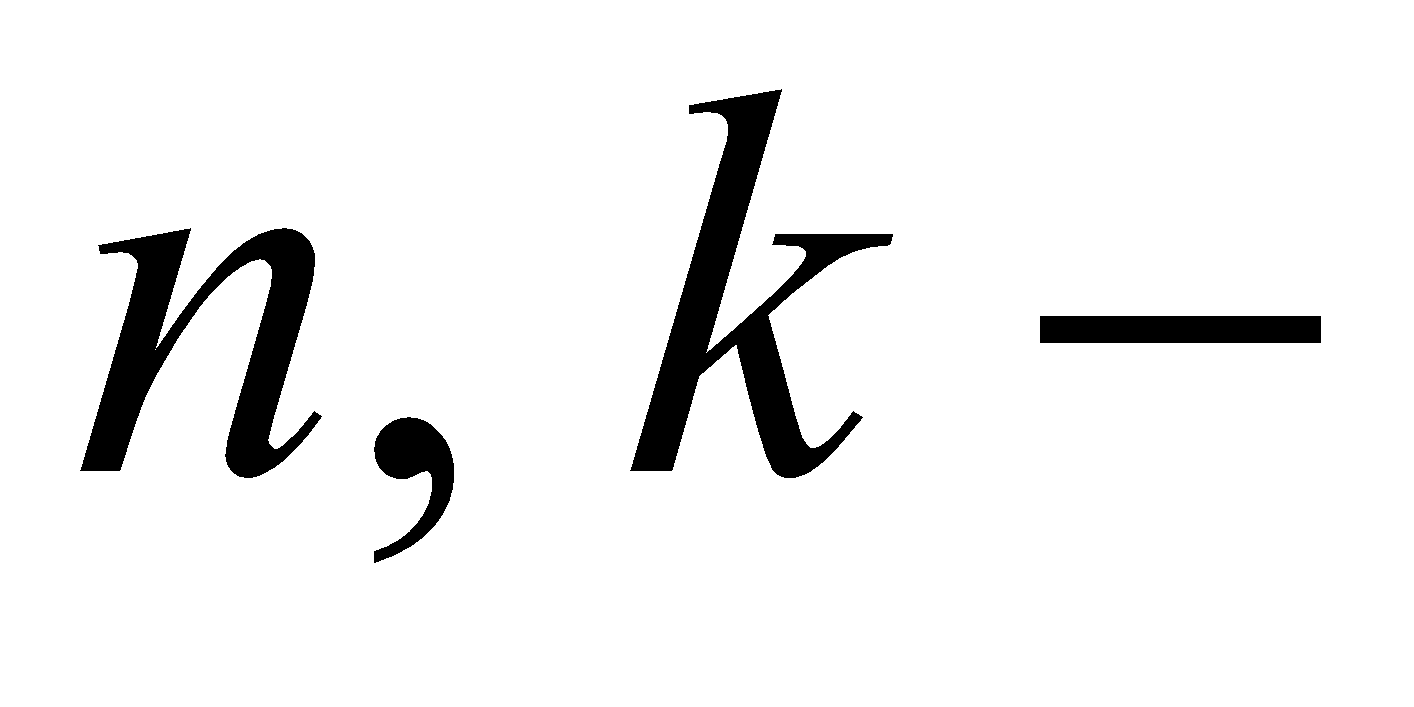 целые числа. Если положить
целые числа. Если положить 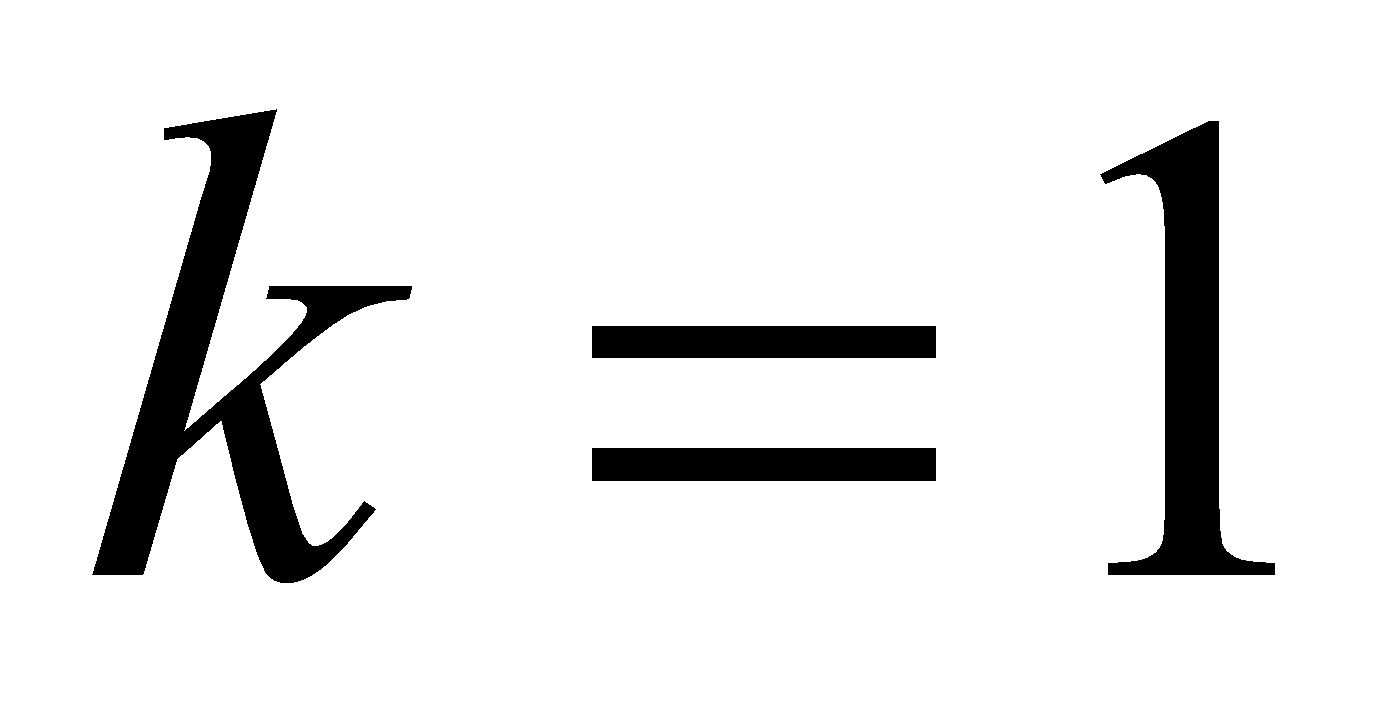 , то из второй серии корней вытекает единственное значение
, то из второй серии корней вытекает единственное значение  , которое удовлетворяет двойному неравенству
, которое удовлетворяет двойному неравенству 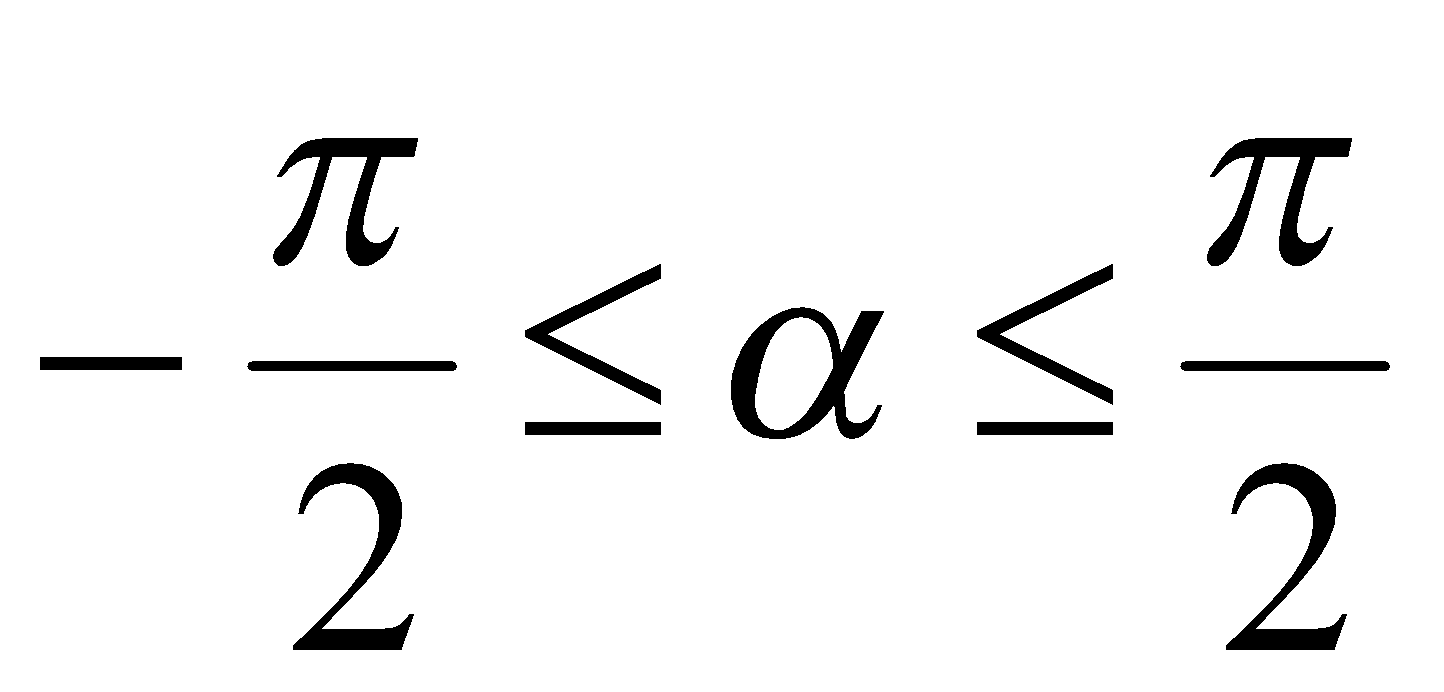 .
.
Ответ: 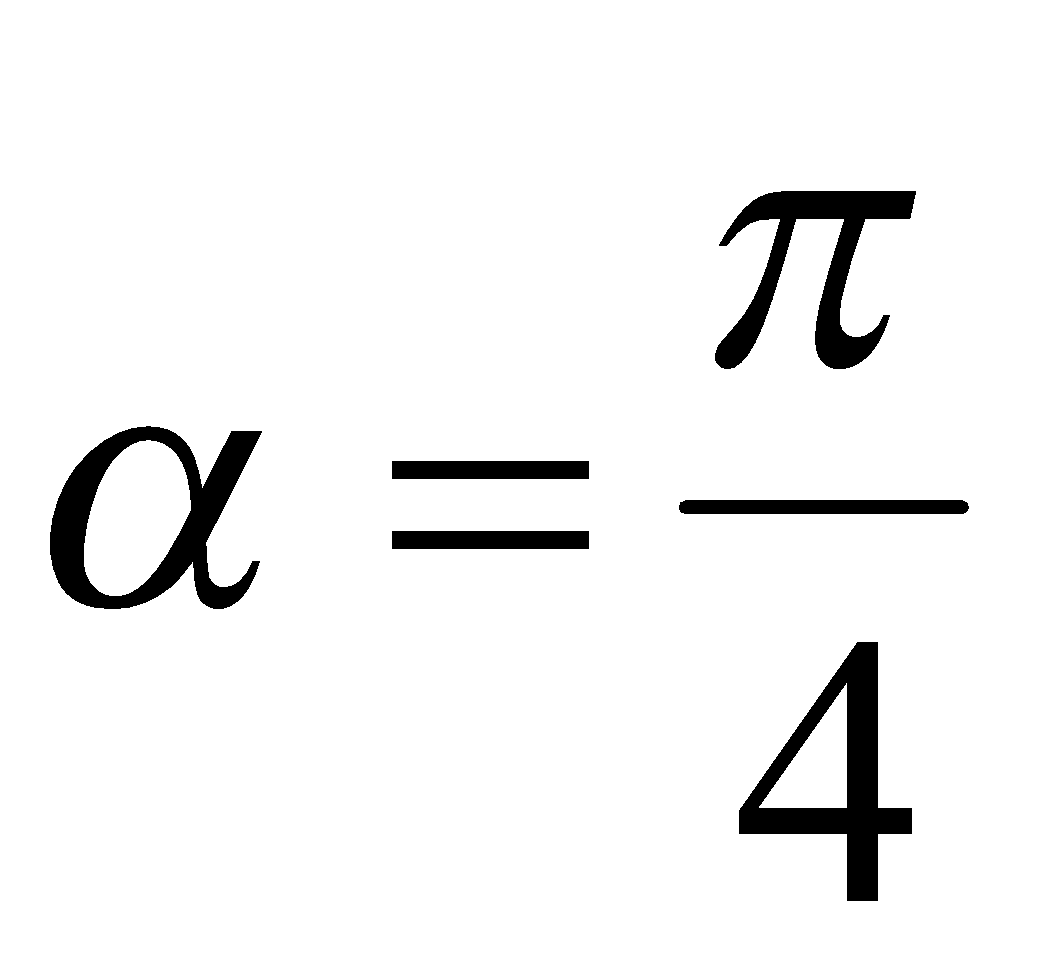 .
.
Пример 7. Вычислить значение 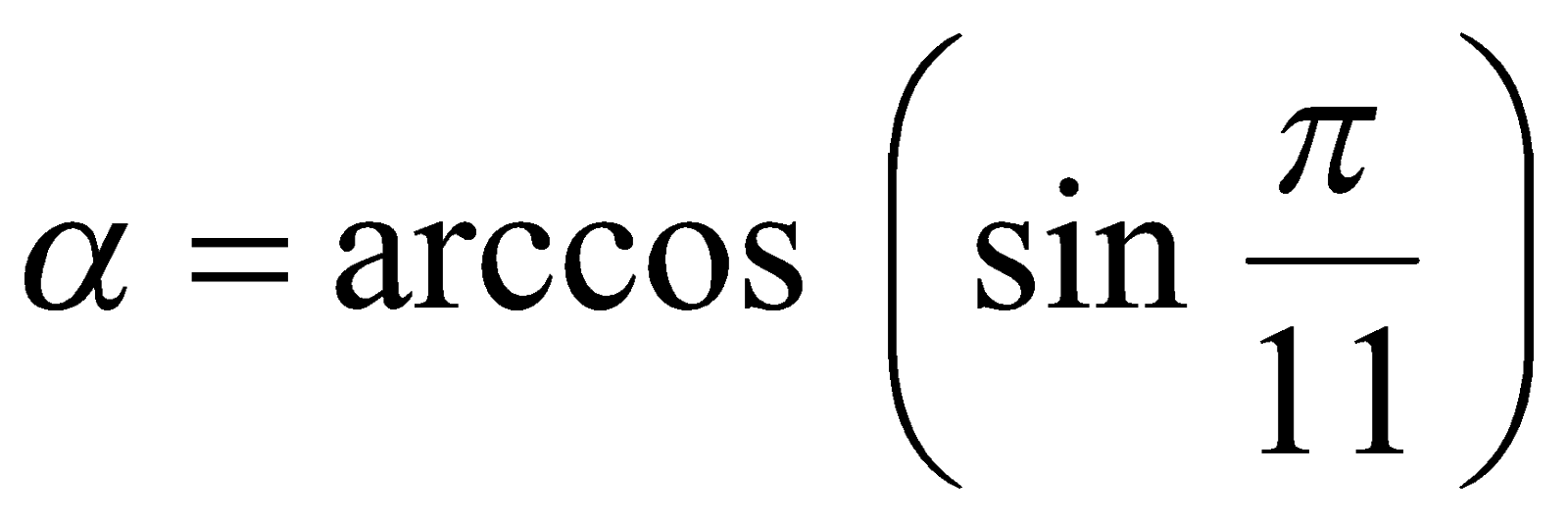 .
.
Решение. По определению функции 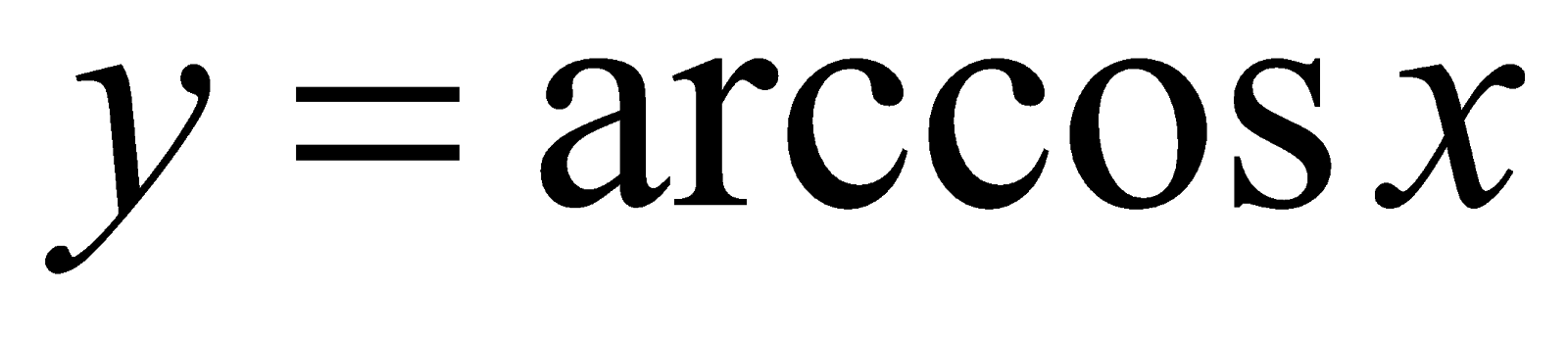 имеем
имеем  . Из условия следует, что
. Из условия следует, что 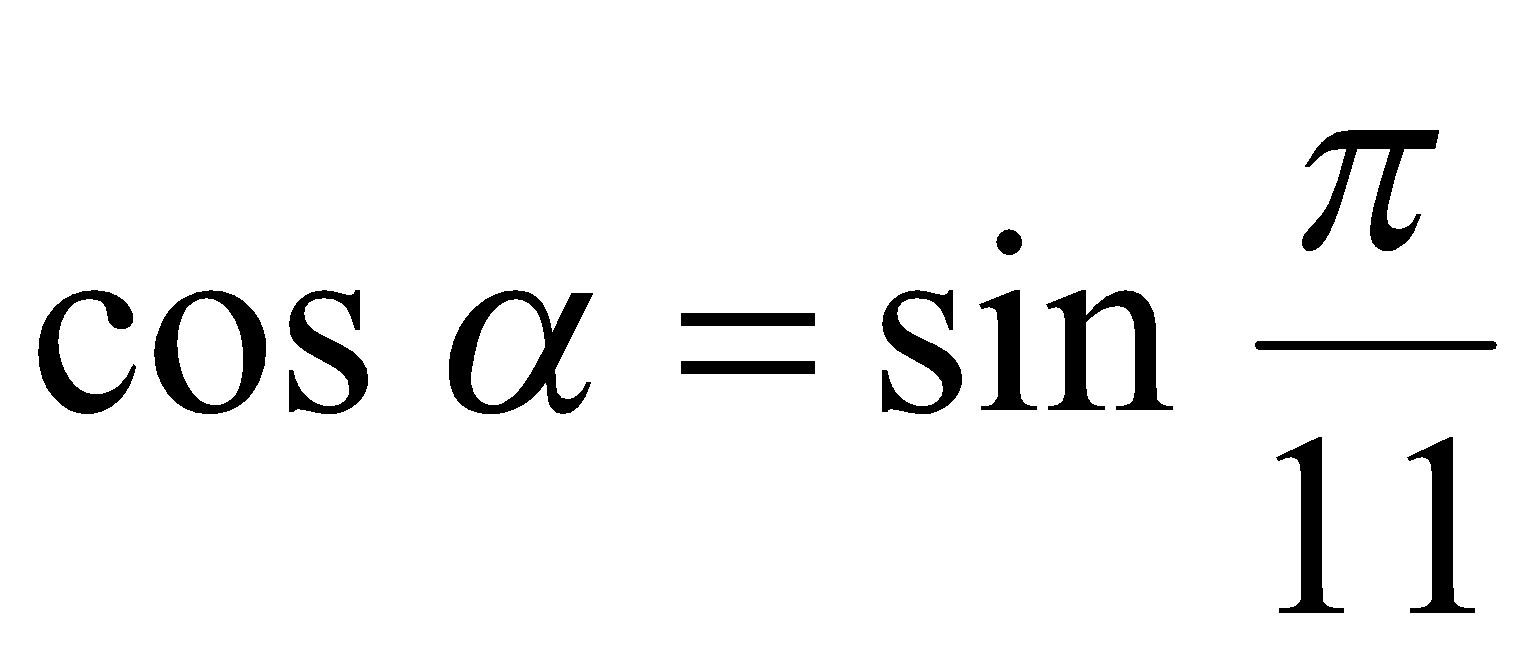 ,
, 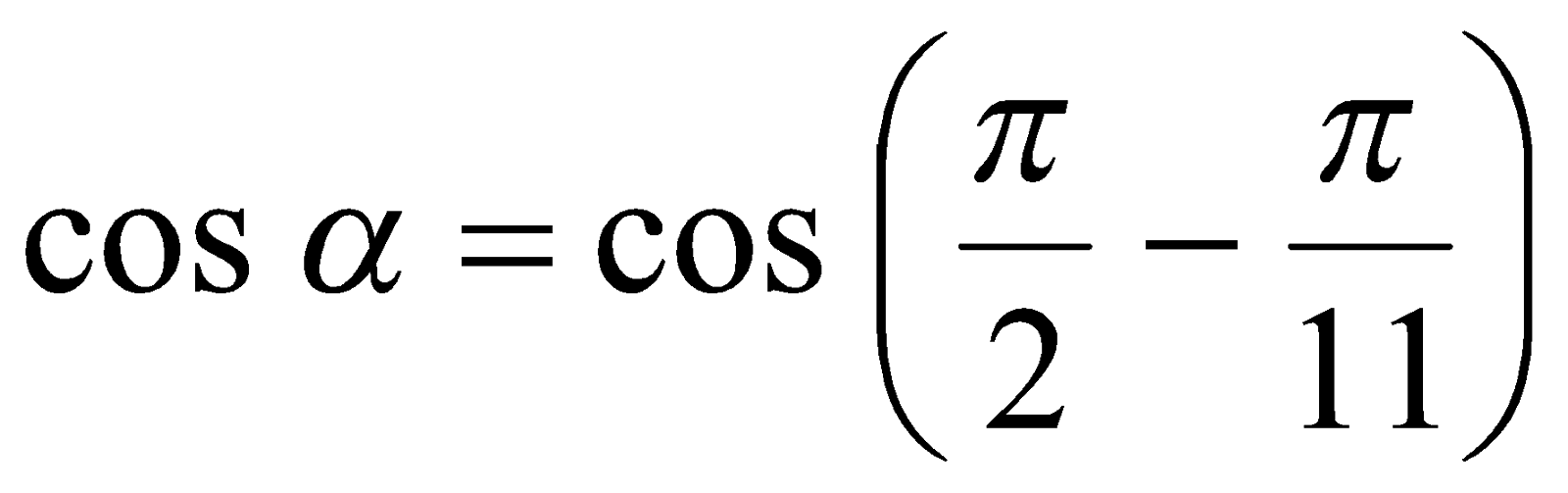 или
или
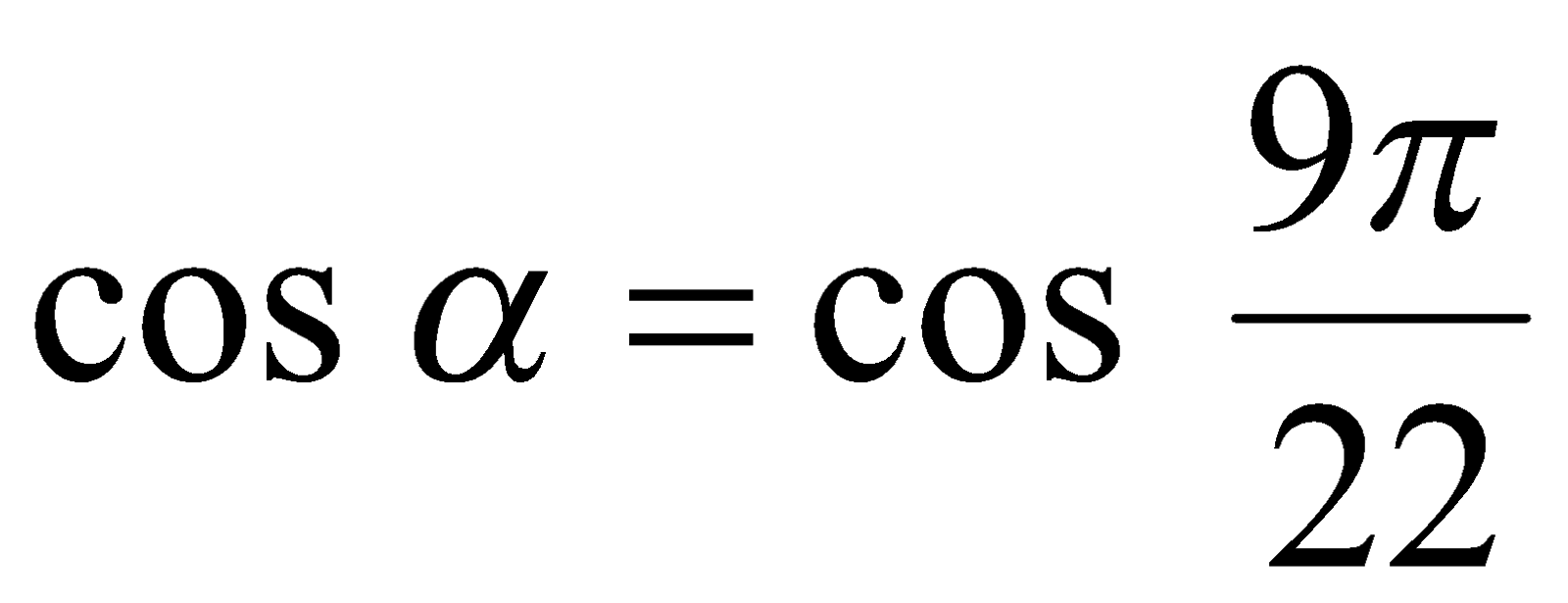 . (2)
. (2)
Согласно теореме 2, здесь имеем две серии корней уравнения (2):
 и
и 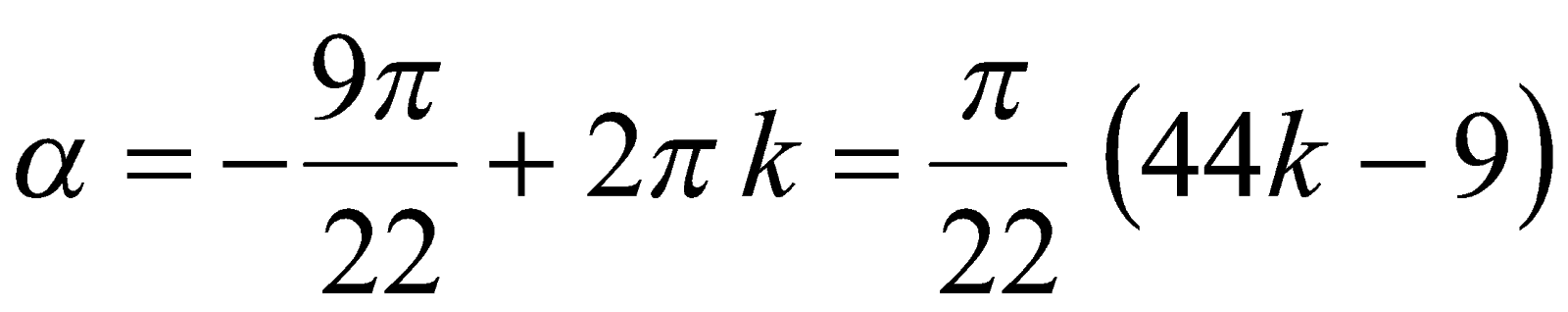 , где
, где 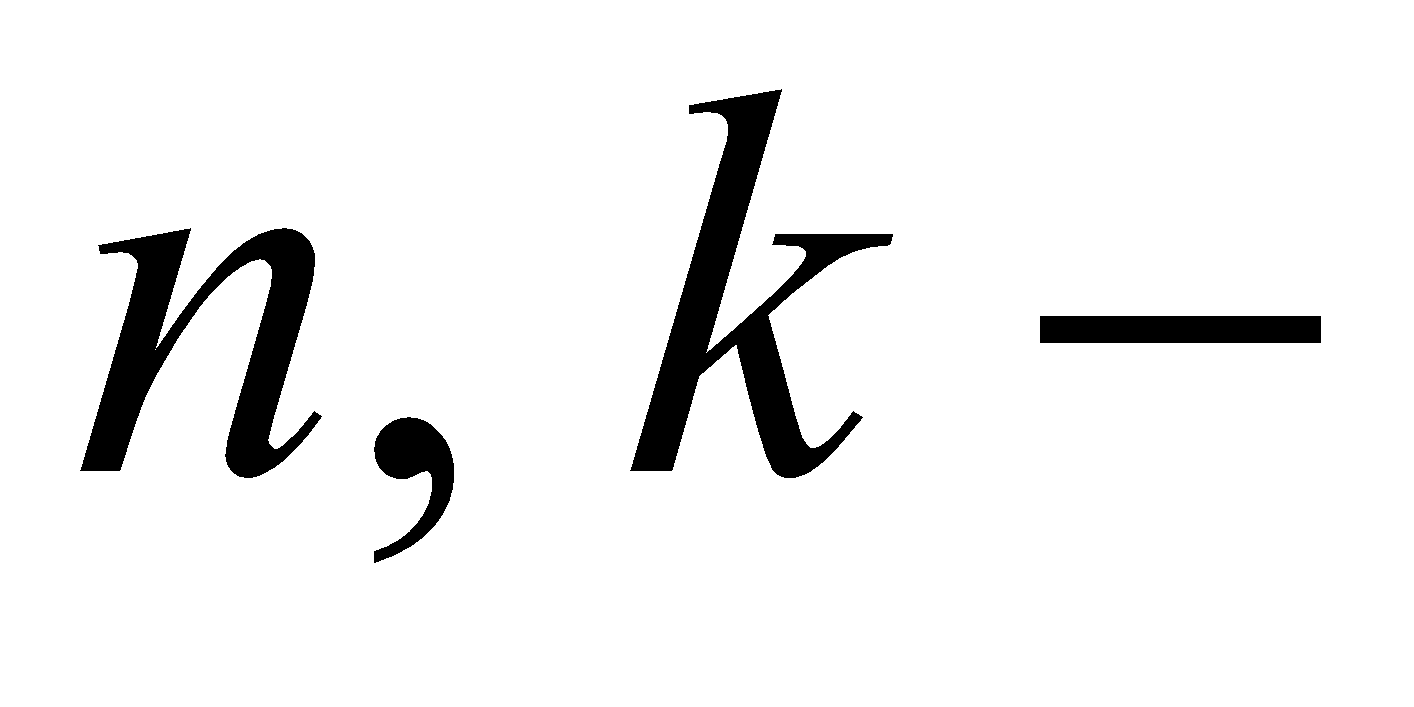 целые числа.
целые числа.
Так как  , то из первой серии корней при условии, что
, то из первой серии корней при условии, что 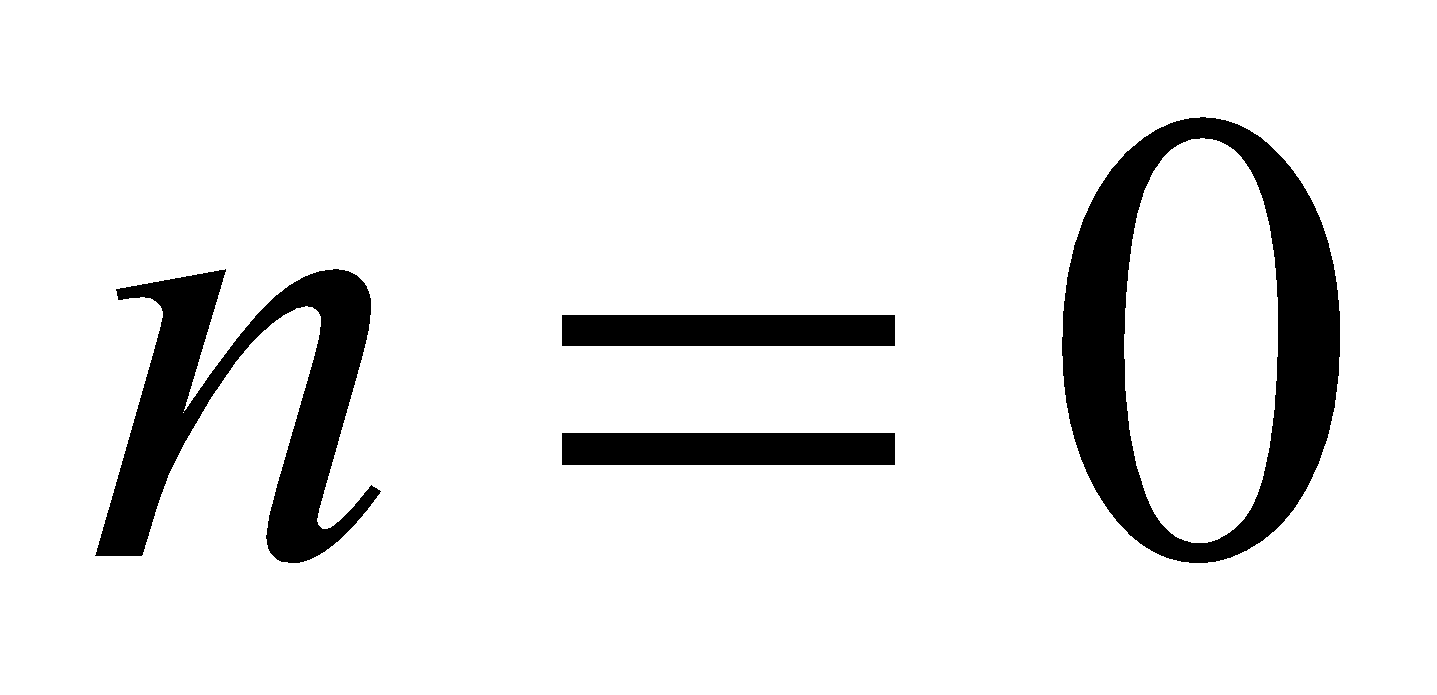 , получаем
, получаем 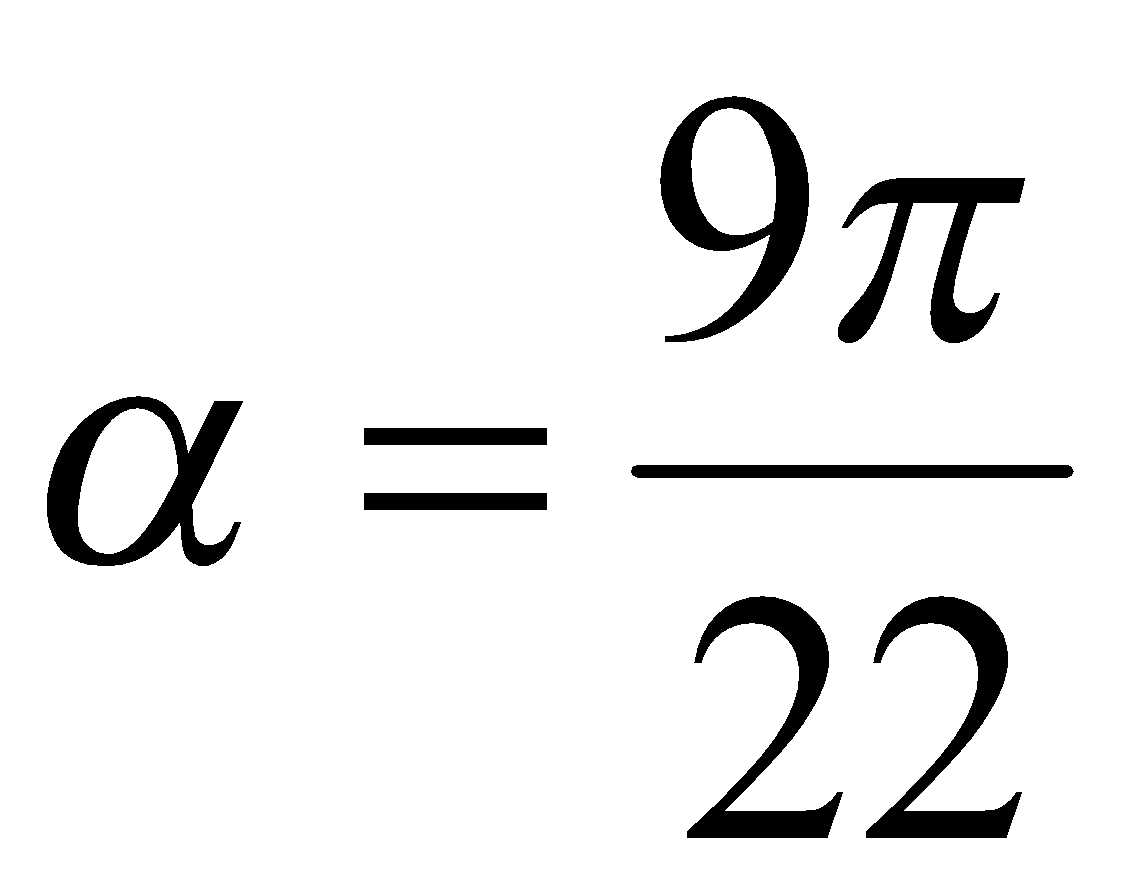 .
.
Ответ: 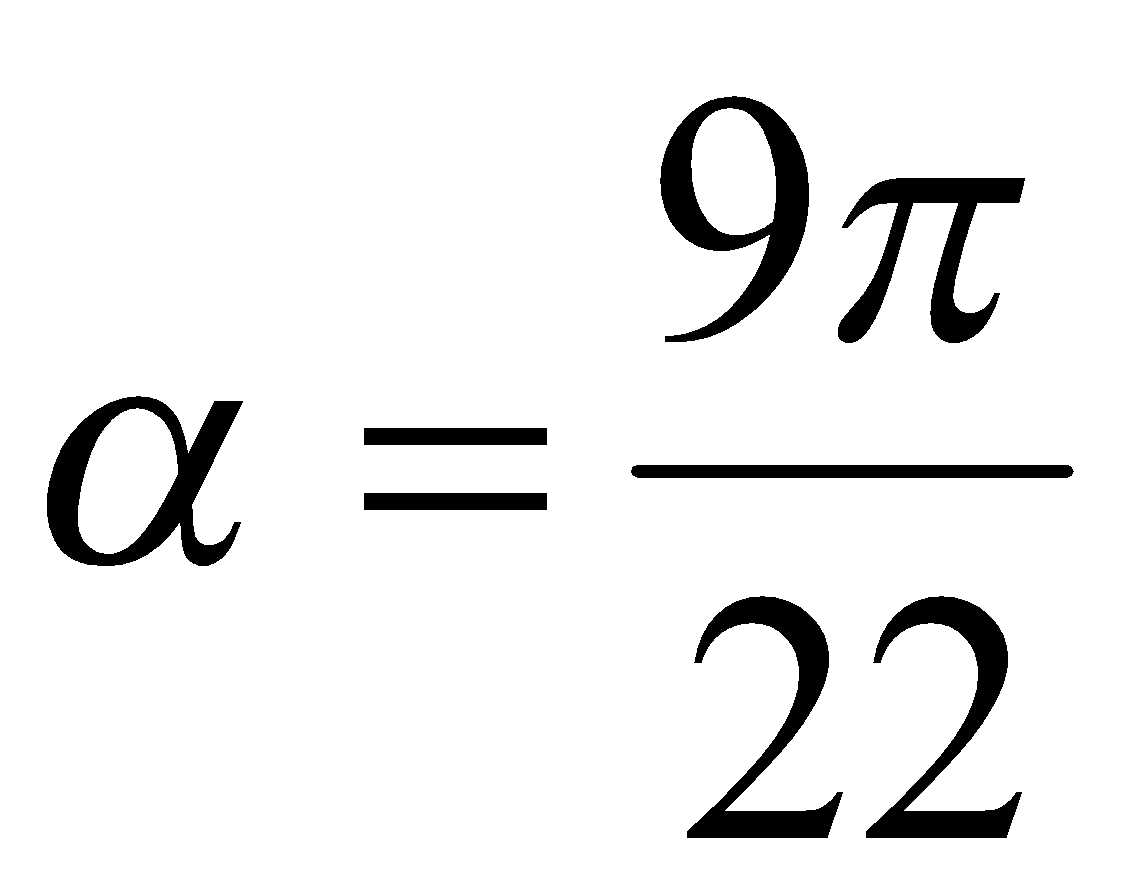 .
.
Тест по теме Арксинус, арккосинус, арктангенс числа
Найдите значение выражения:аrcsin (-

а)  ; б) —
; б) —  ; в)
; в) 
2. arcos (-1)
а)  ; б) —
; б) —  ; в) 0
; в) 0
arctg

а)  ; б) —
; б) —  ; в) 0
; в) 0
arctg (- 1) + arcsin 0
а) —  ; б)
; б)  ; в) 0
; в) 0
аrcsin (-
 ) + arcsin 0
) + arcsin 0
а)  ; б)
; б)  ; в)
; в)  г) нет верного ответа
г) нет верного ответа
sin (arcsin
 )
)
а)  ; б) —
; б) —  ; в) 0
; в) 0
sin (arcsin 0)
а) 0; б)  ; в) 1
; в) 1
Вариант 2
Найдите значение выражения:
аrcsin ( —
 )
)
а)  ; б)
; б)  ; в) —
; в) — 
arcos (-
 )
)
а) — ; б)
; б)  ; в)
; в) 
arctg

а)  ; б) —
; б) —  ; в) 1
; в) 1
arctg 1 + arcos 1
а)  ; б) 0; в)
; б) 0; в) 
аrcsin (-
 ) + arcos (-
) + arcos (- )
)
а)  ; б)
; б)  ; в) —
; в) — 
cos (arcos

а)  ; б) —
; б) —  ; в) 1
; в) 1
arcos (cos
 )
)
а)  ; б)
; б)  ; в) —
; в) — 
Ключ к тесту по теме Арксинус, арккосинус, арктангенс числа
п/пВариант
1
2
3
4
5
6
7
1
б
а
а
а
г
а
а
2
в
б
а
а
а
а
б
Критерии оценивания тестовых заданий
7 вопросов 5 (отлично) (7 ответов)
7 вопросов 4 (хорошо) (6 ответов)
7 вопросов 3 (удов) (5 ответов)
Литература
Алимов Ш.А. и др. Алгебра и начала анализа. 10 (11) кл. – М.: 2018
Башмаков М.И. Сборник задач: учеб. пособие (базовый уровень). 11 кл. – М.: 2012
Интернет-ресурсы
http://school-collection.edu.ru – Электронный учебник «Математика в
школе, XXI век».
http://fcior.edu.ru — информационные, тренировочные и контрольные материалы.
www.school-collection.edu.ru – Единая коллекции Цифровых образовательных ресурсов
| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(60) | |
| 4 | Найти точное значение | sin(30 град. ) | |
| 5 | Найти точное значение | sin(60 град. ) | |
| 6 | Найти точное значение | tan(30 град. ) | |
| 7 | Найти точное значение | arcsin(-1) | |
| 8 | Найти точное значение | sin(pi/6) | |
| 9 | Найти точное значение | cos(pi/4) | |
| 10 | Найти точное значение | sin(45 град. ) | |
| 11 | Найти точное значение | sin(pi/3) | |
| 12 | Найти точное значение | arctan(-1) | |
| 13 | Найти точное значение | cos(45 град. ) | |
| 14 | Найти точное значение | cos(30 град. ) | |
| 15 | Найти точное значение | tan(60) | |
| 16 | Найти точное значение | csc(45 град. ) | |
| 17 | Найти точное значение | tan(60 град. ) | |
| 18 | Найти точное значение | sec(30 град. ) | |
| 19 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 20 | График | y=sin(x) | |
| 21 | Преобразовать из радианов в градусы | pi/6 | |
| 22 | Найти точное значение | cos(60 град. ) | |
| 23 | Найти точное значение | cos(150) | |
| 24 | Найти точное значение | tan(45) | |
| 25 | Найти точное значение | sin(30) | |
| 26 | Найти точное значение | sin(60) | |
| 27 | Найти точное значение | cos(pi/2) | |
| 28 | Найти точное значение | tan(45 град. ) | |
| 29 | График | y=sin(x) | |
| 30 | Найти точное значение | arctan(- квадратный корень 3) | |
| 31 | Найти точное значение | csc(60 град. ) | |
| 32 | Найти точное значение | sec(45 град. ) | |
| 33 | Найти точное значение | csc(30 град. ) | |
| 34 | Найти точное значение | sin(0) | |
| 35 | Найти точное значение | sin(120) | |
| 36 | Найти точное значение | cos(90) | |
| 37 | Преобразовать из радианов в градусы | pi/3 | |
| 38 | Найти точное значение | sin(45) | |
| 39 | Найти точное значение | tan(30) | |
| 40 | Преобразовать из градусов в радианы | 45 | |
| 41 | Найти точное значение | tan(60) | |
| 42 | Упростить | квадратный корень x^2 | |
| 43 | Найти точное значение | cos(45) | |
| 44 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 45 | Преобразовать из радианов в градусы | pi/6 | |
| 46 | Найти точное значение | cot(30 град. ) | |
| 47 | Найти точное значение | arccos(-1) | |
| 48 | Найти точное значение | arctan(0) | |
| 49 | График | y=cos(x) | |
| 50 | Найти точное значение | cot(60 град. ) | |
| 51 | Преобразовать из градусов в радианы | 30 | |
| 52 | Упростить | ( квадратный корень x+ квадратный корень 2)^2 | |
| 53 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 54 | Найти точное значение | sin((5pi)/3) | |
| 55 | Упростить | 1/( кубический корень от x^4) | |
| 56 | Найти точное значение | sin((3pi)/4) | |
| 57 | Найти точное значение | tan(pi/2) | |
| 58 | Найти угол А | tri{}{90}{}{}{}{} | |
| 59 | Найти точное значение | sin(300) | |
| 60 | Найти точное значение | cos(30) | |
| 61 | Найти точное значение | cos(60) | |
| 62 | Найти точное значение | cos(0) | |
| 63 | Найти точное значение | arctan( квадратный корень 3) | |
| 64 | Найти точное значение | cos(135) | |
| 65 | Найти точное значение | cos((5pi)/3) | |
| 66 | Найти точное значение | cos(210) | |
| 67 | Найти точное значение | sec(60 град. ) | |
| 68 | Найти точное значение | sin(300 град. ) | |
| 69 | Преобразовать из градусов в радианы | 135 | |
| 70 | Преобразовать из градусов в радианы | 150 | |
| 71 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 72 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 73 | Преобразовать из градусов в радианы | 89 град. | |
| 74 | Преобразовать из градусов в радианы | 60 | |
| 75 | Найти точное значение | sin(135 град. ) | |
| 76 | Найти точное значение | sin(150) | |
| 77 | Найти точное значение | sin(240 град. ) | |
| 78 | Найти точное значение | cot(45 град. ) | |
| 79 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 80 | Упростить | 1/( кубический корень от x^8) | |
| 81 | Найти точное значение | sin(225) | |
| 82 | Найти точное значение | sin(240) | |
| 83 | Найти точное значение | cos(150 град. ) | |
| 84 | Найти точное значение | tan(45) | |
| 85 | Вычислить | sin(30 град. ) | |
| 86 | Найти точное значение | sec(0) | |
| 87 | Упростить | arcsin(-( квадратный корень 2)/2) | |
| 88 | Найти точное значение | cos((5pi)/6) | |
| 89 | Найти точное значение | csc(30) | |
| 90 | Найти точное значение | arcsin(( квадратный корень 2)/2) | |
| 91 | Найти точное значение | tan((5pi)/3) | |
| 92 | Найти точное значение | tan(0) | |
| 93 | Вычислить | sin(60 град. ) | |
| 94 | Найти точное значение | arctan(-( квадратный корень 3)/3) | |
| 95 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 96 | Вычислить | arcsin(-1) | |
| 97 | Найти точное значение | sin((7pi)/4) | |
| 98 | Найти точное значение | arcsin(-1/2) | |
| 99 | Найти точное значение | sin((4pi)/3) | |
| 100 | Найти точное значение | csc(45) |
Обратные тригонометрические функции, их свойства и графики.
Обратные тригонометрические функции (арксинус, арккосинус, арктангенс и арккотангенс) являются основным элементарным функциями. Часто из-за приставки «арк» обратные тригонометрические функции называют аркфункциями. Сейчас мы рассмотрим их графики и перечислим свойства.
Функция арксинус y = arcsin(x).
Изобразим график функции арксинус:

Свойства функции арксинус y = arcsin(x).
Областью определения функции арксинус является интервал от минус единицы до единицы включительно:
 .
.Область значений функции y = arcsin(x):
 .
.Функция арксинус — нечетная, так как
 .
.Функция y = arcsin(x) возрастает на всей области определения, то есть, при
 .
.Функция вогнутая при
 ,
выпуклая при
,
выпуклая при  .
.Точка перегиба (0; 0), она же ноль функции.
Асимптот нет.
Функция арккосинус y = arccos(x).
График функции арккосинус имеет вид:
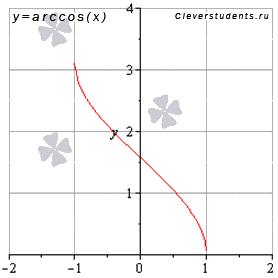
Свойства функции арккосинус y = arccos(x).
Область определения функции арккосинус:
 .
.Область значений функции y = arccos(x):
 .
.Функция не является ни четной ни нечетной, то есть, она общего вида.
Функция арккосинус убывает на всей области определения, то есть, при
 .
.Функция вогнутая при
 ,
выпуклая при
,
выпуклая при  .
.Точка перегиба
 .
.Асимптот нет.
Функция арктангенс y = arctg(x).
График функции арктангенс имеет вид:
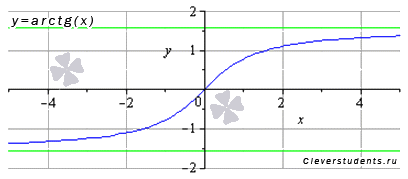
Свойства функции арктангенс y = arctg(x).
Функция арккотангенс y = arcctg(x).
Изобразим график функции арккотангенс:
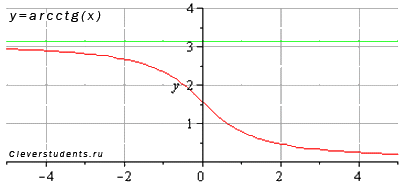
Свойства функции арккотангенс y = arcctg(x).
Функция тригонометрии arccos () — обратный косинус — математическое определение слова
Функция тригонометрии arccos () — обратный косинус — определение слова в математике — открытый справочник по математике Функция arccos является обратной функцией косинуса.
Возвращает угол, косинус которого является заданным числом.
Для каждой тригонометрической функции существует обратная функция, которая работает наоборот.Эти обратные функции имеют то же имя, но с дугой впереди. (На некоторых калькуляторах кнопка arccos может быть обозначена как acos, а иногда и cos -1 .) Итак, косинус, обратный cos, равен arccos и т. Д. Когда мы видим «arccos x», мы понимаем его как «угол, косинус которого равен x».
| cos30 = 0,866 | Означает: косинус 30 градусов равен 0,866 |
| arccos 0,866 = 30 | означает: угол, косинус которого равен 0,866, равен 30 градусам. |
См. Также Обратные функции — тригонометрия
Пример — использование arccos для поиска угла
На рисунке выше нажмите «сбросить».
Нам известны длины сторон, но нам нужно найти величину угла C.
Мы знаем, что поэтому нам нужно знать угол, косинус которого равен 0,866, или формально:
С помощью калькулятора находим arccos 0.866 равным 30 °.
Большие и отрицательные углы
Напомним, что мы можем применить триггерные функции на любой угол, включая большие и отрицательные углы.Но когда мы Рассмотрим обратную функцию, и мы столкнемся с проблемой, потому что существует бесконечное количество углов, которые имеют один и тот же косинус. Например, 45 ° и 360 + 45 ° будут иметь одинаковый косинус. Подробнее об этом см. Обратные тригонометрические функции.
Чтобы решить эту проблему, ассортимент обратных триггерных функций ограничены таким образом, чтобы обратные функции были взаимно однозначными, то есть для каждого входного значения был только один результат.
Диапазон и область действия arccos
Напомним, что область действия функции — это набор допустимых входных данных для нее.Диапазон — это набор возможных выходов.
Для y = arccos x:
По соглашению диапазон arccos ограничен от 0 до + 180 °. Итак, если вы используете калькулятор для решения, скажем, arccos 0,55, из бесконечного числа возможностей он вернет 56,63 °, тот, который находится в диапазоне функции.
Что попробовать
- На рисунке выше нажмите «сбросить» и «скрыть детали».
- Отрегулируйте треугольник до нового размера
- Используя функцию arccos, вычислите значение угла C из длин сторон
- Щелкните «Показать подробности», чтобы проверить ответ.
Другие темы по тригонометрии
Уголки
Тригонометрические функции
Решение задач тригонометрии
Исчисление
(C) Открытый справочник по математике, 2011 г.
Все права защищены.
Mathway | Решение задач тригонометрии
Mathway | Решение задач тригонометрииНовые сообщения
Пользователь набирает
Mathway требует javascript и современного браузера.
Этот веб-сайт использует файлы cookie, чтобы обеспечить вам максимальное удобство работы с ним.
Убедитесь, что ваш пароль состоит не менее чем из 8 символов и содержит каждое из следующих значений:
- номер
- письмо
- специальный символ: @ $ #!% *? &



 )
)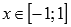 .
.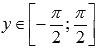 .
. .
.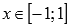 .
.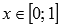 ,
выпуклая при
,
выпуклая при 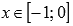 .
. .
.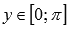 .
.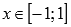 .
.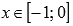 ,
выпуклая при
,
выпуклая при 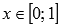 .
.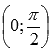 .
.