===графики обратных тригонометрических функций — презентация онлайн
Похожие презентации:
Обратные тригонометрические функции и их свойства. (10 класс)
Обратные тригонометрические функции и их свойства
Обратные тригонометрические функции и их свойства. 10 класс
Обратные тригонометрические функции
Обратные тригонометрические функции и их свойства. 10 класс
Обратные тригонометрические функции и их свойства
Обратные тригонометрические функции и их свойства
Обратные тригонометрические функции и их свойства
Обратные тригонометрические функции
Обратные тригонометрические функции. Свойства и графики
10 класс
Обратные тригонометрические функции
и их свойства
Содержание
• Функция y = arcsin x и ее свойства
• Функция y = arccos x и ее свойства
• Функция y = arctg x и ее свойства
• Функция y = arcctg x и ее свойства
Функция y=arcsinx и ее свойства
Если |а| ≤ 1, то arcsin а – это такое число
из отрезка [-π/2; π/2], синус которого
Если |а| ≤ 1, то
arcsin а = t
sin t = а,
-π/2 ≤ t ≤ π/2;
sin (arcsin a) = a
Функция y=arcsinx и ее график
у
π/2
y=arcsin x
y=sin x
х
-1
0
-π/2
1
π
Функция y=arcsinx и ее свойства
1. D(y) = [-1; 1].
2. E(y) = [-π/2; π/2].
3. arcsin (-x) = — arcsin x – функция
нечетная.
4. Функция возрастает на [-1; 1].
5. Функция непрерывна.
Функция y=arccosx и ее свойства
Если |а| ≤ 1, то arccos а – это такое число
из отрезка [0; π], косинус которого равен
а.
Если |а| ≤ 1, то
arccos а = t
cos t = а,
0 ≤ t ≤ π;
cos (arccos a) = a
arccos (-a) = π – arccos a, где -1 ≤ а ≤ 1
Функция y=arccosx и ее график
у
y=arccosx
π
π/2
Y=cos x
-1
π
0
1
х
Функция y=arccosx и ее свойства
1. D(y) = [-1; 1].
2. E(y) = [0; π].
3. Функция не является ни четной, ни
нечетной.
4. Функция убывает на [-1; 1].
5. Функция непрерывна.
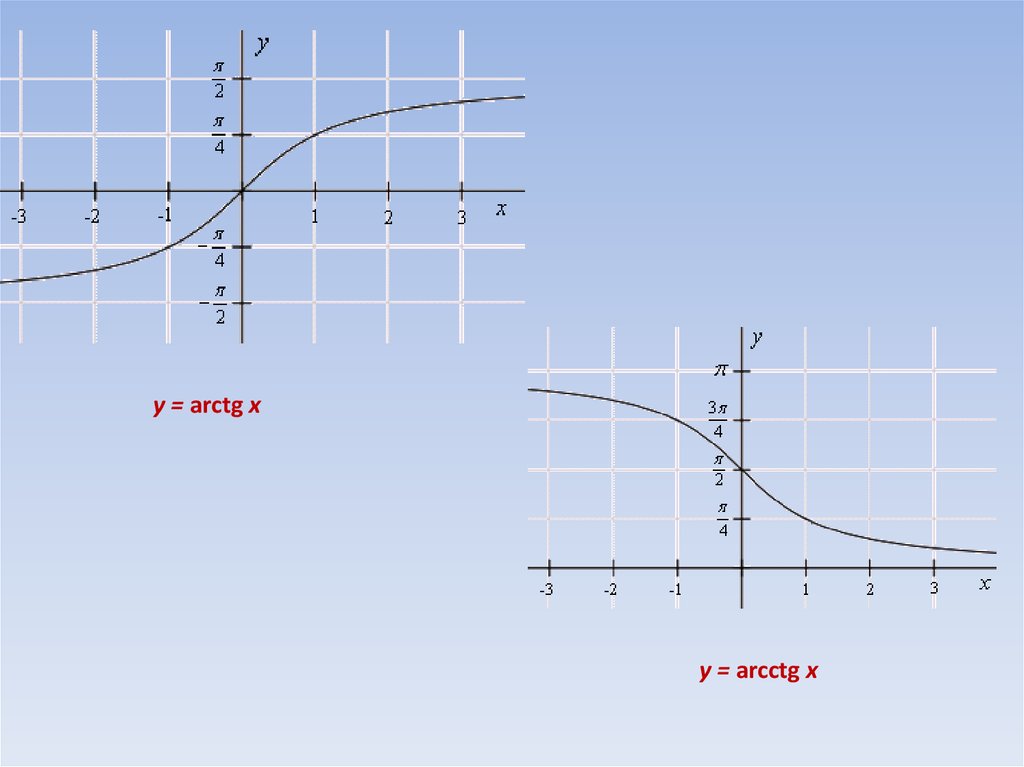
Функция y=arctgx и ее свойства
arctg а – это такое число из интервала (-π/2;
π/2), тангенс которого равен а.
arctg а = t
tg t = а,
-π/2 < t < π/2;
tg (arctg a) = a
Функция y=arctgx и ее график
у
π/2
y=arctg x
π/4
х
-1
0
-π/4
-π/2
y=tg x
1
π
Функция y=arctgx и ее свойства
1. D(y) = (- ; + ).
2. E(y) = (-π/2; π/2).
3. arctg (-x) = — arctg x – функция нечетная.
4. Функция возрастает на (- ; + ).
5. Функция непрерывна.
Функция y=arcctgx и ее свойства
arcсtg а – это такое число из интервала (0;
π), котангенс которого равен а.
arcсtg а = t
сtg t = а,
0 < t < π;
сtg (arcсtg a) = a
arcctg (-a) = π – arcctg a
Функция y=arcctgx и ее график
у
π
y=сtg x
π/2
-π
-π/2
0
π/2
π
х
Функция y=arcctgx и ее свойства
1. D(y) = (- ; + ).
2. E(y) = (0; π).
3. Функция не является ни четной, ни
нечетной.
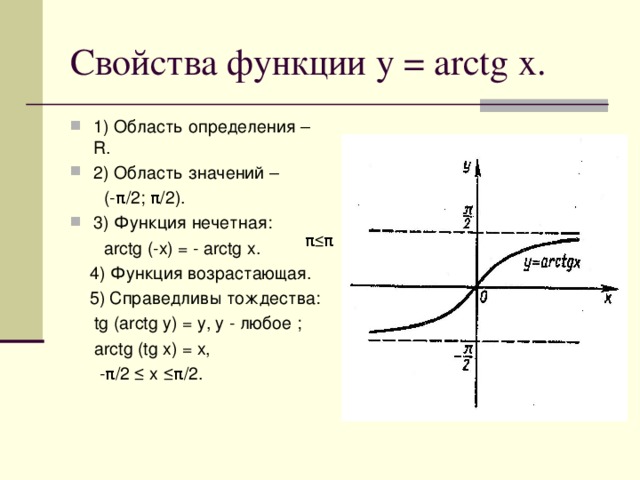
4. Функция убывает на (- ; + ).
5. Функция непрерывна.
English Русский Правила
график-функции / Вопрос про wolframalpha / Математика
|
Наверняка Вы все пользуетесь wolframalpha, поэтому вопрос решил задать здесь, так как не дружу с английским. При попытке построить там график функции arcctg(x), получается что-то незаурядное arcctg(x). Что он пытается мне построить? И как мне построить график нормального arcctg(x)? В связи с этим вытек вопрос по поводу $$\lim_{x \rightarrow — \propto } arcctg(x)$$ wolframalpha выдаёт ответ 0, когда на самом деле $$\pi$$ предел график-функции задан 8 Дек ’15 21:24  org/Person»>LonelyGamer171●4●38 94% принятых |
старыеновыеценные
|
Видимо у Вольфрама заложена функция арккотангенса по формуле $$ \text{arcctg}\;x=\text{arctg}\;\frac{1}{x} $$ То есть обращается не ветвь монотонности котангенса, а однозначный, но разрывный кусок функции, заданной на множестве $%\Big[-\frac{\pi}{2};0\Big)\cup\Big(0;\frac{\pi}{2}\Big]$%… Привычная функция арккотангенса может быть выражена формулой $$ \text{arcctg}\;x=\frac{\pi}{2}-\text{arctg}\;x $$ ссыль ссылка отвечен 8 Дек ’15 21:59  org/Person»>all_exist55.0k●3●13 |
Ваш ответ
Если вы не нашли ответ, задайте вопрос.
Здравствуйте
Математика — это совместно редактируемый форум вопросов и ответов для начинающих и опытных математиков, с особенным акцентом на компьютерные науки.
Присоединяйтесь!
регистрация »
отмечен:
график-функции
×196
предел
×175
задан 
8, 2015, 9:24 п.п.»>8 Дек ’15 21:24
показан
обновлен
8 Дек ’15 22:09
Связанные вопросы
Отслеживать вопрос
по почте:
Зарегистрировавшись, вы сможете подписаться на любые обновления
по RSS:
Ответы
Ответы и Комментарии
| 1 | Найти точное значение | грех(30) | |
| 2 | Найти точное значение | грех(45) | |
| 3 | Найти точное значение | грех(30 градусов) | |
| 4 | Найти точное значение | грех(60 градусов) | |
| 5 | Найти точное значение | загар (30 градусов) | |
| 6 | Найти точное значение | угловой синус(-1) | |
| 7 | Найти точное значение | грех(пи/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | грех(45 градусов) | |
| 10 | Найти точное значение | грех(пи/3) | |
| Найти точное значение | арктан(-1) | ||
| 12 | Найти точное значение | cos(45 градусов) | |
| 13 | Найти точное значение | cos(30 градусов) | |
| 14 | Найти точное значение | желтовато-коричневый(60) | |
| 15 | Найти точное значение | csc(45 градусов) | |
| 16 | Найти точное значение | загар (60 градусов) | |
| 17 | Найти точное значение | сек(30 градусов) | |
| 18 | Найти точное значение | cos(60 градусов) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | грех(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | загар (45 градусов) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 градусов) | |
| 25 | Найти точное значение | сек(45 градусов) | |
| 26 | Найти точное значение | csc(30 градусов) | |
| 27 | Найти точное значение | грех(0) | |
| 28 | Найти точное значение | грех(120) | |
| 29 | Найти точное значение | соз(90) | |
| 30 | Преобразовать из радианов в градусы | пи/3 | |
| 31 | Найти точное значение | желтовато-коричневый(30) | |
| 32 | 92|||
| 35 | Преобразовать из радианов в градусы | пи/6 | |
| 36 | Найти точное значение | детская кроватка(30 градусов) | |
| 37 | Найти точное значение | арккос(-1) | |
| 38 | Найти точное значение | арктан(0) | |
| 39 | Найти точное значение | детская кроватка(60 градусов) | |
| 40 | Преобразование градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2 шт. )/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | тан(пи/2) | |
| 45 | Найти точное значение | грех(300) | |
| 46 | Найти точное значение | соз(30) | |
| 47 | Найти точное значение | соз(60) | |
| 48 | Найти точное значение | соз(0) | |
| 49 | Найти точное значение | соз(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | сек(60 градусов) | |
| 53 | Найти точное значение | грех(300 градусов) | |
| 54 | Преобразование градусов в радианы | 135 | |
| 55 | Преобразование градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5 дюймов)/6 | |
| 57 | Преобразовать из радианов в градусы | (5 дюймов)/3 | |
| 58 | Преобразование градусов в радианы | 89 градусов | |
| 59 | Преобразование градусов в радианы | 60 | |
| 60 | Найти точное значение | грех(135 градусов) | |
| 61 | Найти точное значение | грех(150) | |
| 62 | Найти точное значение | грех(240 градусов) | |
| 63 | Найти точное значение | детская кроватка(45 градусов) | |
| 64 | Преобразовать из радианов в градусы | (5 дюймов)/4 | |
| 65 | Найти точное значение | грех(225) | |
| 66 | Найти точное значение | грех(240) | |
| 67 | Найти точное значение | cos(150 градусов) | |
| 68 | Найти точное значение | желтовато-коричневый(45) | |
| 69 | Оценить | грех(30 градусов) | |
| 70 | Найти точное значение | сек(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | КСК(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | загар((5pi)/3) | |
| 75 | Найти точное значение | желтовато-коричневый(0) | |
| 76 | Оценить | грех(60 градусов) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3 пи)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | угловой синус(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | КСК(45) | |
| 83 | Упростить | арктан(квадратный корень из 3) | |
| 84 | Найти точное значение | грех(135) | |
| 85 | Найти точное значение | грех(105) | |
| 86 | Найти точное значение | грех(150 градусов) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | загар((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | пи/4 | |
| 90 | Найти точное значение | грех(пи/2) | |
| 91 | Найти точное значение | сек(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | угловой синус(0) | |
| 95 | Найти точное значение | грех(120 градусов) | |
| 96 | Найти точное значение | желтовато-коричневый ((7pi)/6) | |
| 97 | Найти точное значение | соз(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразование градусов в радианы | 88 градусов |
тригонометрия — Решение $\arctan(x)+\arctan(2x)=\frac{\pi}{3}$.
Почему я получаю лишний рут?Задавать вопрос
спросил
Изменено 2 года, 9 месяцев назад
Просмотрено 404 раза
$\begingroup$
У меня есть это уравнение
$$\arctan(x)+\arctan(2x)=\frac{\pi}{3}$$ 92-4ac=9-(-4\cdot2\sqrt3\cdot\sqrt3)=33 \tag{9}$$ $$x_1= \frac{-3+\sqrt{33}}{4\sqrt3} \tag{10}$$ $$x_2= \frac{-3-\sqrt{33}}{4\sqrt3} \tag{11}$$
Надеюсь, это правильно (не уверен).
Но если это так, то я не понимаю, почему построение графика этой функции онлайн дает мне только один корень, который соответствует $x_1$.
Я также использовал сайт, позволяющий решать тригонометрические уравнения на лету, чтобы проверить мой ответ и там тот же результат: их ответ уникален и соответствует только моему $x_1$.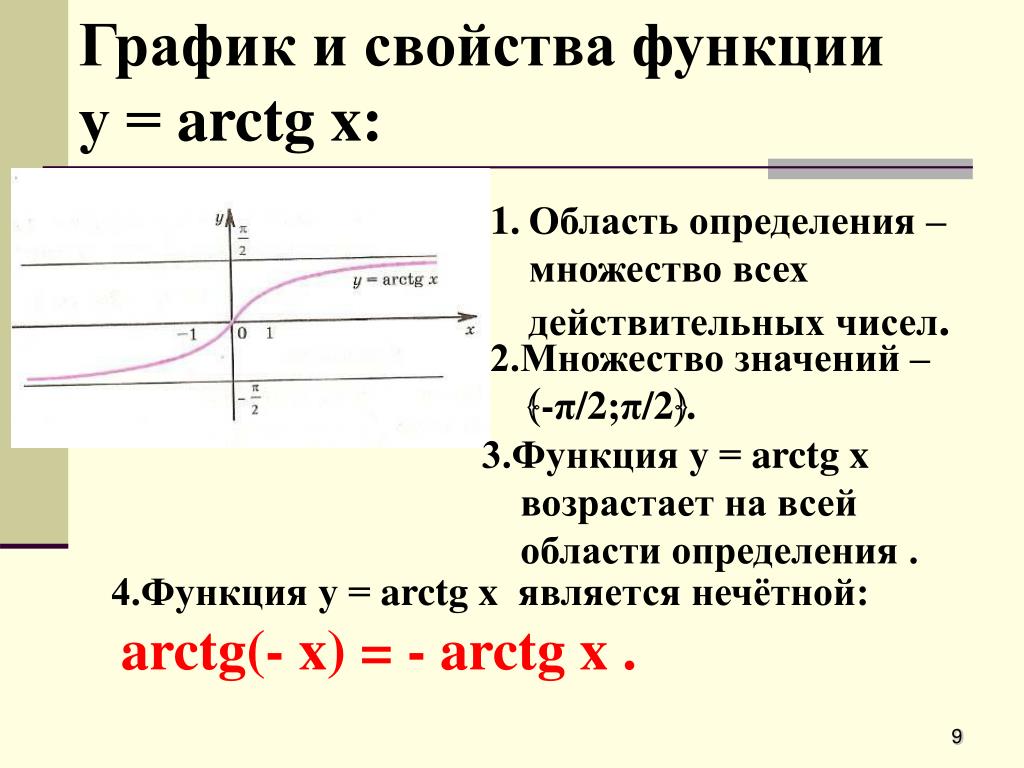
Может кто-нибудь объяснить мне это, пожалуйста?
Спасибо за помощь.
- тригонометрия
- корни
- графические функции
$\endgroup$
0
$\begingroup$
Это произошло потому, что не все шаги в вашем решении эквивалентны. Один конкретный шаг (я скажу вам, какой именно) является импликацией, но не эквивалентностью — и именно там мы можем получить посторонние решения; и, по-видимому, в этом случае мы это сделали. 92=x \подразумевается x=0,1,$$ и все же только $x=0$, но не $x=1$, является решением исходного уравнения.
Здесь произошло то же самое: если $a=b$, то $\tan(a)=\tan(b)$; но обратное не обязательно верно: из $\tan(a)=\tan(b)$ не следует $a=b$. Например, $\tan(0)=\tan(\pi)$ и еще $0\neq\pi$.
Вы эффективно решили уравнение $\tan(\mathrm{LHS})=\tan(\mathrm{RHS})$, и оно имеет два решения.
Но нет никакой гарантии, что любой из них удовлетворяет исходному уравнению. Вам нужно проверить каждое из них, подставив в исходное уравнение.
Альтернативой является определение некоторых ограничений на значения $x$, чтобы гарантировать обратимость этого шага. Иногда это лучшая идея. Но я не уверен, что здесь все достаточно просто; так что, возможно, подключение — это то, что вам нужно сделать.
$\endgroup$
6
$\begingroup$
Возьмите загар с обеих сторон уравнения. Задача триггера была разработана, чтобы превратиться в квадратичную: 9{-1}$, парабола) с осью x. На вашем графике отсутствует второй арктан.
Создавая более полный график с котерминальным добавлением $\pi$, мы получаем полный доступ к полям, включая все пересечения.
Корни равны $(x_1,x_2)\приблизительно (-1,26,+0,396)$ с учетом котерминальных углов, что полностью соответствует двум корням параболы.