График функции квадратного уравнения: Построение графика квадратичной функции — урок. Алгебра, 8 класс.

2 — 1/5, при условии, что это действительная квадратичная функция.

Как только вы введете правильное квадратичное выражение, вы можете нажать на кнопку «Вычислить», и на экране появится окно график функции будет сгенерирован, показывая этапы вычисления вершина параболы и Ось симметрии а также .

Квадратичные функции занимают главенствующее место в базовой алгебре, поскольку они часто используются в контексте решения задачи квадратные уравнения и прикладные проблемы.

По сути, они являются базовыми полиномы , которые обладают множеством интересных свойств.

Как построить график квадратичной формы?

Построить график квадратичной функции просто, в том смысле, что вы знаете, что ВСЕ квадратичные функции будут иметь форму параболы. Но все же парабол бесконечно много. Нам нужно знать немного больше, чтобы определить точную параболу, которая представляет данную квадратичную функцию.

Шаги для нахождения графика квадратичной функции

• Шаг 1: Четко определите заданную квадратичную функцию и при необходимости упростите ее
• Шаг 2: После упрощения определите функцию в виде f(x) = ax² + bx + c. Обратите внимание, что a не может быть нулем
• Шаг 3: Если a > 0, вы знаете, что график будет параболой, раскрывающейся вверх, тогда как если a
• Шаг 4: Ось симметрии находится в точке x* = -b/(2a), что указывает на «центр» параболы
• Шаг 5: Обратите внимание, что x* = -b/(2a) — координата x вершины параболы, а y* = f(x*) = a(x*)² + b(x*) + c — координата y вершины

Этого должно быть достаточно, чтобы иметь четкое представление о соответствующем квадратичном графике. Дальнейшим шагом будет построение некоторых точек на графике, выбирая различные точки на оси x и находя их соответствующее изображение через функцию, чтобы облегчить процесс нахождения функции график функции .

2 + bx + c = 0 \]

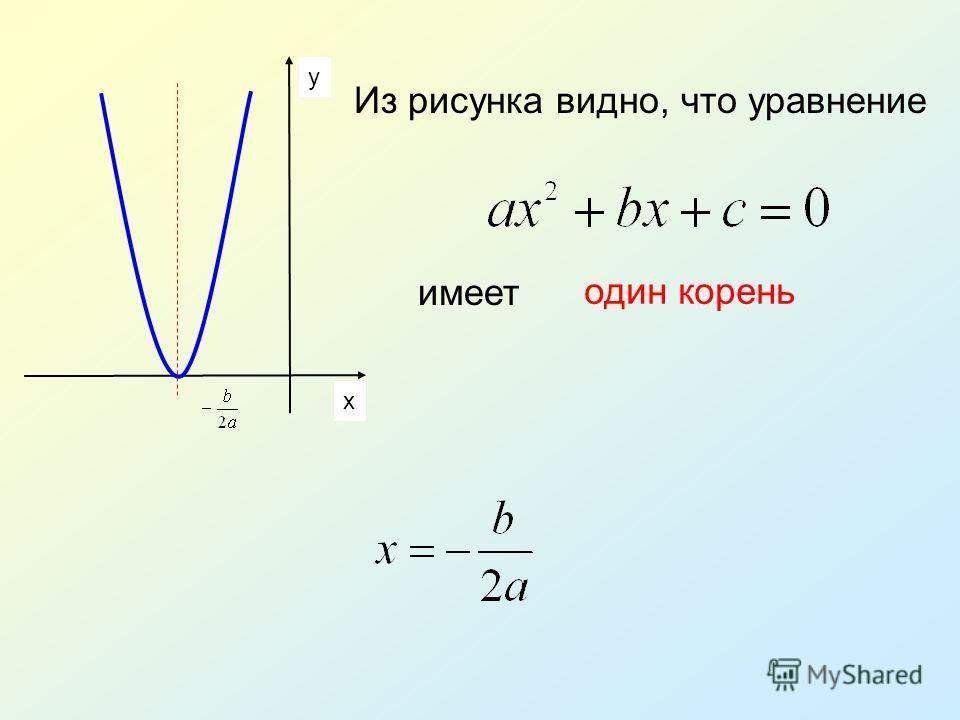
вы получите корни квадратного уравнения, а когда корни действительны, они представляют собой точки, в которых парабола пересекает ось x.

Особый случай имеет место, когда корни комплексные, в этом случае парабола не пересекает ось x.

Типы квадратичных графиков

Как мы уже говорили, ВСЕ одномерные квадратичные функции будут представлены параболами, но в зависимости от того, a > 0 или a

Другое различие типов парабол может быть для тех, которые «центрированы» (т.е вершина это происхождение), и те, которые не являются таковыми.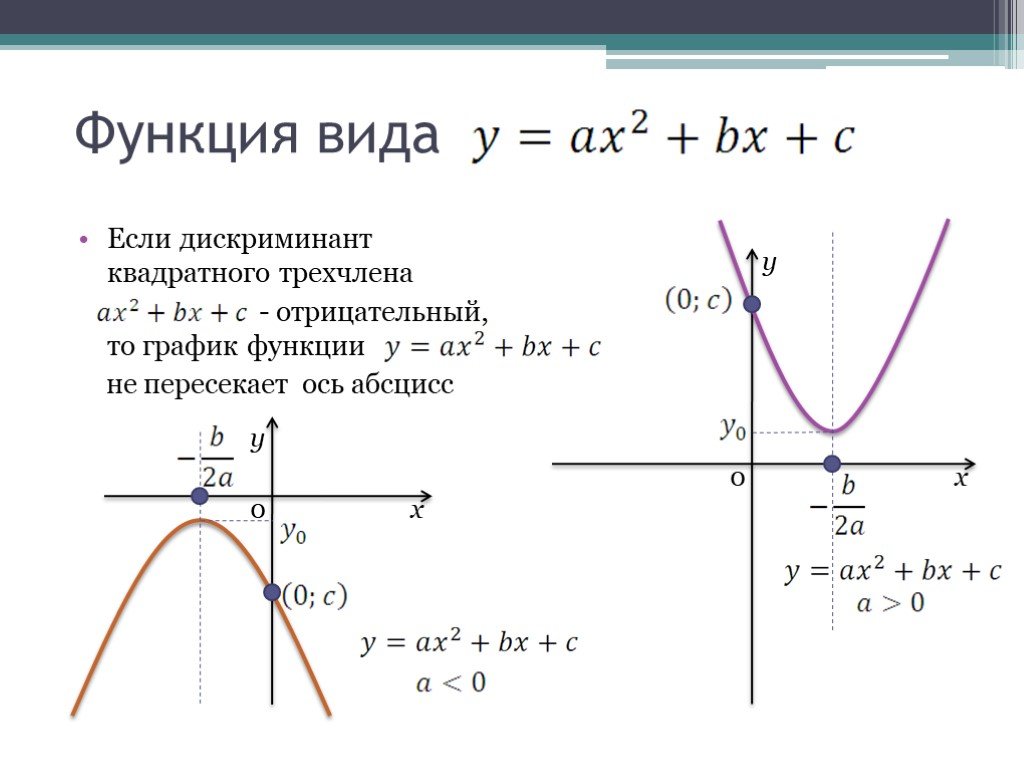 2+2x-3\), из чего следует, что соответствующие коэффициенты являются:

\[a = \frac{1}{3}\] \[b = 2\] \[c = -3\]

Подставляя известные значения \(a\) и \(b\) в формулу для x-координаты вершины, получаем:

\[x_V = \displaystyle -\frac{b}{2a} = \displaystyle -\frac{2}{2 \cdot \frac{1}{3}} = -3\]

Теперь нам нужно подставить значение \(x_V = \displaystyle -3\) в квадратичную функцию, чтобы получить:

\[y_V = f(x_V)\] \[ = \frac{1}{3}\cdot \left(-3\right)^2+2\cdot \left(-3\right)-3=\frac{1}{3}\cdot \left(-3\right)^2+2\cdot \left(-3\right)-3=9\cdot\frac{1}{3}-6-3=3-6-3=-6\]

Таким образом, координата x вершины равна \(x_V = \displaystyle -3\), а координата y вершины равна \(y_V = \displaystyle -6\).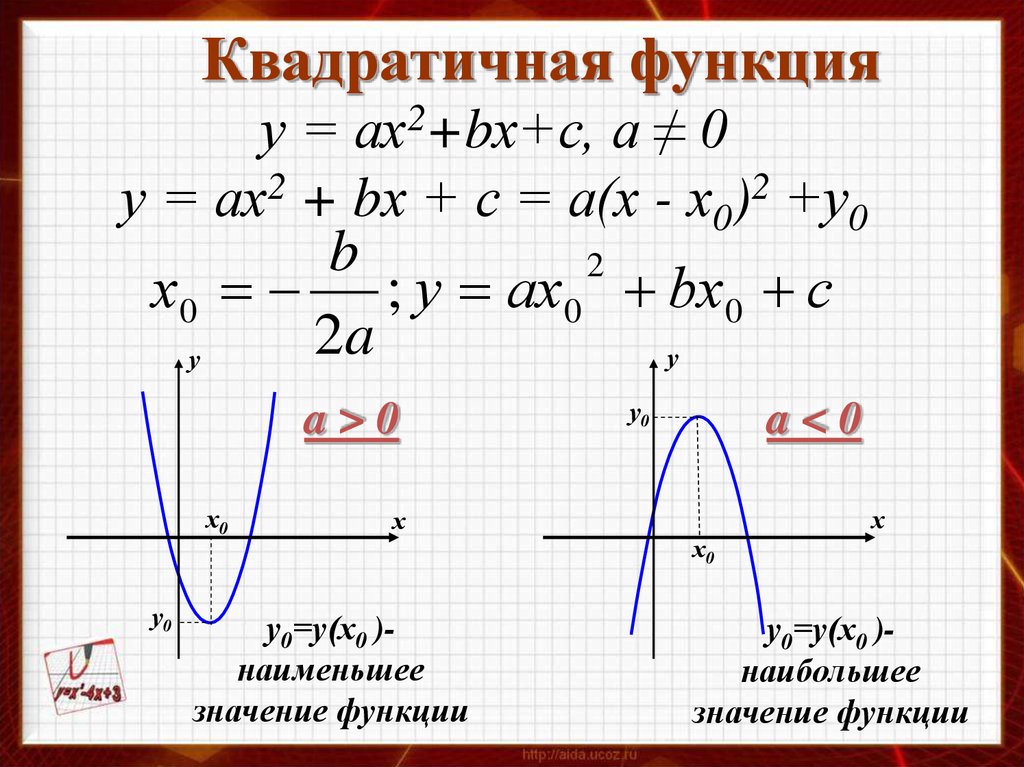 2+3x-2\), из чего следует, что соответствующие коэффициенты являются:

\[a = \frac{4}{3}\] \[b = 3\] \[c = -2\]

Подставляя известные значения \(a\) и \(b\) в формулу для x-координаты вершины, получаем:

\[x_V = \displaystyle -\frac{b}{2a} = \displaystyle -\frac{3}{2 \cdot \frac{4}{3}} = -\frac{9}{8}\]

Теперь нам нужно подставить значение \(x_V = \displaystyle -\frac{9}{8}\) в квадратичную функцию, чтобы получить:

\[y_V = f(x_V)\] \[ = \frac{4}{3}\cdot \left(-\frac{9}{8}\right)^2+3\cdot \left(-\frac{9}{8}\right)-2=\frac{4}{3}\cdot\frac{81}{64}+3\cdot \left(-\frac{9}{8}\right)-2=\frac{27}{16}-\frac{27}{8}-2=-\frac{59}{16}\]

Таким образом, координата x вершины равна \(x_V = \displaystyle -\frac{9}{8}\), а координата y вершины равна \(y_V = \displaystyle -\frac{59}{16}\). Это означает, что точка, обозначающая вершину, равна \( \displaystyle \left(-\frac{9}{8}, -\frac{59}{16}\right)\).

Графически получается следующее:

Больше квадратичных калькуляторов

Большинство всех приложений в базовой алгебре основаны на решении некоторого рода Квадратное уравнение , поэтому у него есть сильная педагогическая цель узнать об этом.

квадратичная формула является одним из самых печально известных учебных предметов в математике. Дело не в том, что кубические или квартовые уравнения не существуют, а в том, что квадратные уравнения это те, которые мы можем легко объяснить.

Функция у=ах², её график и свойства

Класс: 9.

Цели урока: закрепить умения раскладывать на множители квадратный трехчлен, применяя это разложение для сокращения дробей и упрощения выражений, повторить основные свойства функции.

Планируемые результаты: Знать и понимать функции y=ax², особенности графика. Уметь строить y=ax² в зависимости от параметра а.

Метапредметные:

• Коммуникативные: вступать в учебный диалог с учителем, участвовать в общей беседе.
• Познавательные: осознавать познавательную задачу, читать и слушать, извлекая необходимую информацию.
• Регулятивные: планировать необходимые действия, операции. Оценивать возникающие трудности, вносить коррективы в работу.

Личностные: осваивать новые виды деятельности.

Тип урока: комбинированный.

Оборудование: учебные принадлежности для урока математики, учебник

Основные понятия: трехчлен, многочлен, квадратное уравнение, корень, дискриминант, функция, область определения функции, область значения функции.

Ход урока

1. Организационный момент

Включение учащихся в учебную деятельность. Приветствие, проверка подготовленности к учебному занятию, организации рабочего места.

2. Актуализация знаний

Устная работа.

Дана функция: у = х².

1) Найдите значения функции в точках -1; 0; 1/9.

2) В каких точках значение функции равно 4; 1/25?

III. Объяснение нового материала

Квадратичной называют функцию вида:

Графиком квадратичной функции является парабола. Она состоит из двух ветвей и имеет вершину.

Ветви могут быть направлены вверх:

Ветви могут быть направлены вниз:

Квадратичная функция имеет свои свойства. Поговорим о них. В своей вершине квадратичная функция сменяет своё поведение с убывания на возрастание и с возрастания на убывание. Понятно, что областью определения в обоих случаях будет множество всех действительных чисел. Если говорим о нулях функции, то мы имеем ввиду те значения, при которых функция у=0. Когда находят нули функции по графику, то ищут точки пересечения графика с осью х. Если же находят нули функции по уравнению, то значение функции принимают равное 0. Тем самым получаем квадратное уравнение. Оно может иметь 2, 1 корень или не иметь корней. Соответственно, график может иметь 2 точки пересечения с осью х, 1 точку пересечения с осью х или не пересекать её. Понятно, что нулями квадратичной функции являются корни соответствующего квадратного уравнения. По графику удобно находить промежутки знакопостоянства и промежутки монотонности функции.

Рассмотреть свойства из учебника.

Пример: по графику квадратичной функции опишите её свойства.

На рисунке изображена парабола, ветви которой направлены вверх, значит a>0. Опишем её свойства.

Областью определения и областью значений являются:

Нулями функции являются:

y = 0 при x = -3 и x = 3

Промежутки знакопостоянства:

Промежутки монотонности:

Заметим, что описать свойства функции по её графику проще, чем по формуле. Поэтому очень важно уметь изображать график функции.

Рассмотрим частный случай квадратичной функции: y=ax²

Изобразим график этой функции схематично и обратим внимание на некоторые её свойства. Возможны два случая изображения графика.

Областью определения в обоих случаях является:

Область значений:

Функция такого вида обращается в ноль только при х=0, график будет пересекать ось х в одной точке. Первым свойством мы запишем, что если: х = 0, то y= 0.

Другими словами график такой функции всегда проходит через точку начала координат. Причём эта точка является вершиной параболы.

Если же , то график расположен выше или ниже оси Х.

Если взять противоположные значения аргумента, то видно, что им соответствуют одинаковые значения функции. Противоположным значениям аргумента соответствуют равные значения функции. Другими словами график функции симметричен относительно оси у.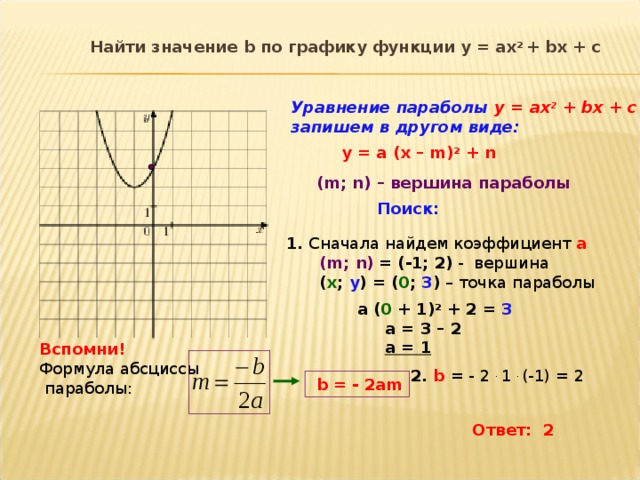

Пример.

В одной координатной плоскости изобразим графики функций: y = 2x² и y = -2x²

Получим два графика, они симметричны относительно оси х.

Рассмотрим пример: изобразим в одной координатной плоскости графики функции:

Изобразим графики этих функций:

График функции у=ах² можно получить из параболы у=х² растяжением от оси х в а раз, если а>0, и сжатием к оси х в 1/а раз к оси х, если 0<а<1.

IV. Формирование умений и навыков

Упражнения:

1. № 90, № 92, № 94.

V. Итоги урока

Вопросы учащимся:

— Как называется график функции у = ах²?

— Куда направлены ветви параболы, если а > 0 (а < 0)?

— Как может быть получен график функции у = 5х² из графика функции у = х²?
— Как может быть получен график функции у =1/7 · х² из графика функции у = х²?

— Как может быть получен график функции у = -4х² из графика функции

у = 4х²?

— Перечислите свойства функции у = ах² при а < 0.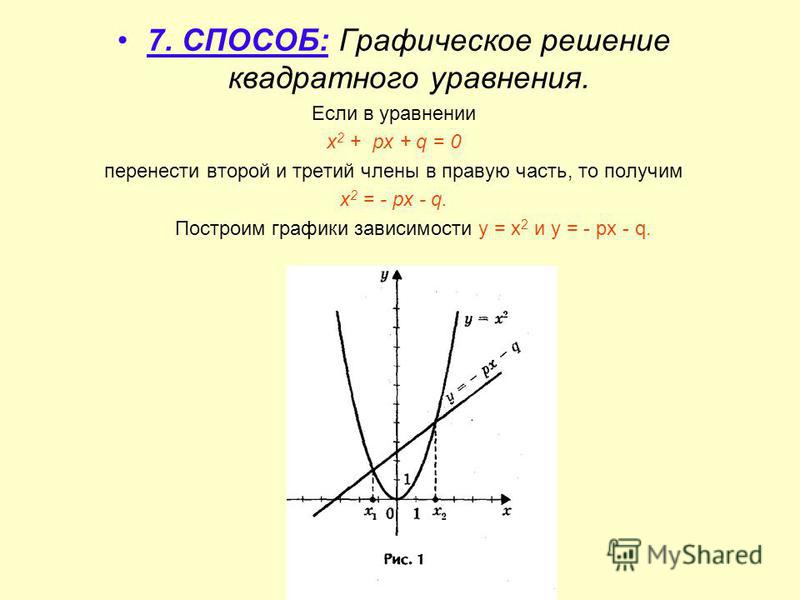

Домашнее задание: № 91, № 93, № 95.

Графики квадратных уравнений

Квадратное уравнение в стандартной форме
( a , b и c могут принимать любые значения, за исключением того, что a не может быть 0.)

Вот пример:

Графики

Вы можете нарисовать квадратное уравнение с помощью графического редактора функций, но чтобы действительно понять что происходит, вы можете построить график самостоятельно. Читай дальше!

Простейшее квадратное число

Простейшее квадратное уравнение:

f(x) = x ²

И его график тоже прост:

Это кривая f(x) = x ²
Это парабола.

Теперь давайте посмотрим, что происходит, когда мы вводим значение «а»:

f(x) = ах ²

• Большие значения и сжимают кривую внутрь
• Меньшие значения a расширить его наружу
• И отрицательные значения a переворачивают его вверх дном

 

Играй с этим Теперь самое время поиграть с «Quadratic Equation Explorer», чтобы вы могли увидеть, что делают различные значения и , b и c .

«Общий» Квадратичный

Перед построением графика мы переставляем уравнение, из этого:

f(x) = ах ² + Ьх + с

К этому:

f(x) = a(x-h) ² + k

Где:

• ч = -b/2а
• к = f( ч )

Другими словами, вычислите ч (= −b/2a), затем найдите

k путем вычисления всего уравнения для x=h

Но почему?

Самое замечательное в этой новой форме то, что h и k показывают нам самую нижнюю (или самую высокую) точку, называемую вершиной :

.

А также кривая симметрична (зеркальное отражение) относительно оси , которая проходит через x=h , что упрощает построение графика

 

Итак…

• h показывает нам, насколько далеко влево (или вправо) сместилась кривая от x=0
• k показывает, насколько вверх (или вниз) сместилась кривая от y=0

Давайте посмотрим пример того, как это сделать:

Пример: График f(x) = 2x

² − 12x + 16

Сначала запишем:

• a = 2,
• б = -12, и
• с = 16

Итак, что мы знаем?

• a положителен, поэтому это «восходящий» график («U»-образный)
• a равно 2, поэтому он немного «сжат» по сравнению с x ² график

Далее вычислим h:

h = −b/2a = −(−12)/(2×2) = 3

Далее мы можем вычислить k (используя h=3):

k = f( 3 ) = 2(3) ² − 12·3 + 16 = 18−36+16 = −2

Итак, теперь мы можем построить график (с реальным пониманием!):

Мы также знаем: вершина равна (3,−2), а ось равна x=3

От графика к уравнению

Что, если у нас есть график и мы хотим найти уравнение?

Пример: вы только что нанесли интересные данные, и они выглядят квадратичными:

Зная эти две точки, мы можем составить уравнение.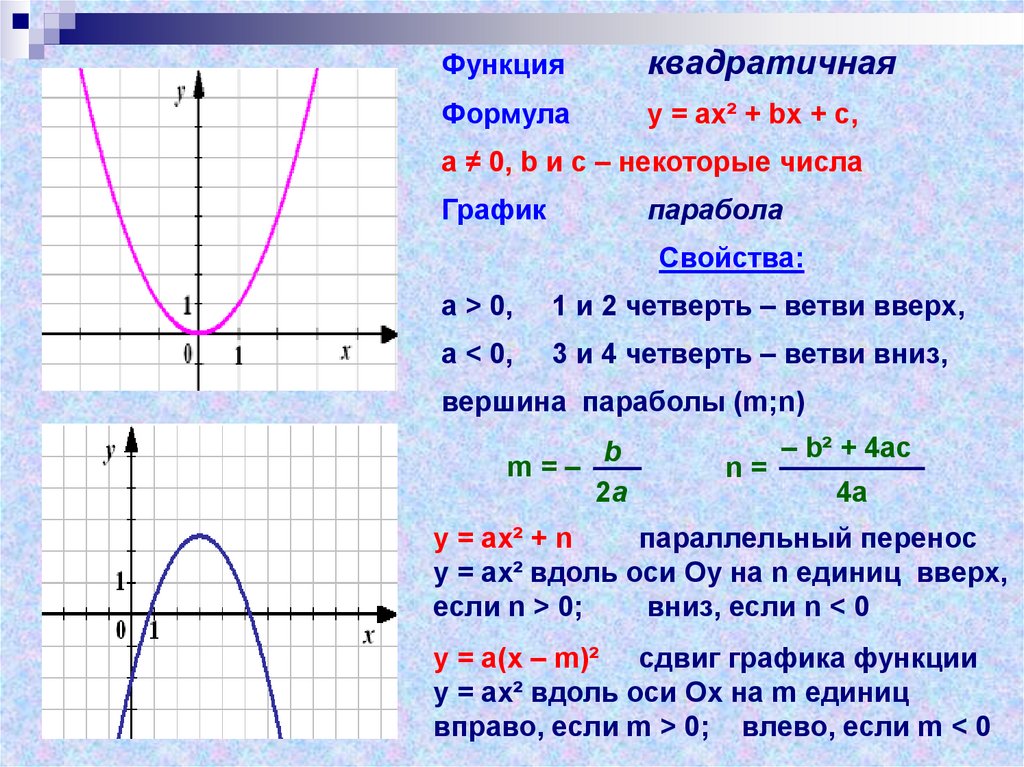

Во-первых, мы знаем h и k (в вершине):

(h, k) = (1, 1)

Итак, давайте подставим это в следующую форму уравнения:

f(x ) = a(x-h) ² + k

f(x) = a(x−1) ² + 1

Затем вычисляем «a»:

Нам известна точка (0, 1.5) итак: f(0) = 1,5

И a(x−1) ² + 1 при x=0 равно: f(0) = a(0−1) ² + 1

Они оба f(0) , поэтому приравняем их: a(0−1) ² + 1 = 1,5

Упростим: х) = 0,5(x−1) ² + 1

 

Примечание. Это может быть не правильное уравнение для данных, но это хорошая модель и лучшее, что мы можем придумать.

 

 

Учебник по алгебре для колледжей 34

Алгебра для колледжей 9Урок 34. Графики квадратичных функций Цели обучения

---

После завершения этого руководства вы сможете:

1. Найдите вершину квадратичной функции.
2. Определите, является ли вершина максимальной или минимальной точкой квадратичного функция.
3. График квадратичной функции.

Введение

---

В этом уроке мы рассмотрим графики квадратичных функций. График квадратичной функции называется параболой и имеет кривую форма. Одной из главных точек параболы является ее вершина. Это самая высокая или самая низкая точка на его графике. Вы можете думать как конец параболы. Я покажу вам, как найти вершина, а также ось симметрии, проходящая через эту точку. Я также освежу вашу память о том, как найти х — и у — перехваты. Если вам нужен обзор о том, что такое перехваты на графике, смело переходите к Tutorial 26: Уравнения линий.   При нахождении 90 112 x 90 115 -перехватов, вам придется решать квадратное уравнение. Если вы нужен обзор по решению квадратных уравнений, смело переходите к Tutorial 17: Квадратные уравнения.   Если вы учитесь в колледже по алгебре класс, работа с квадратичными функциями неизбежна, даже если это против твоя религия. Так что, я думаю, вам лучше начать.

 

 

Учебник

---

Квадратичная функция

Квадратичная функция — это функция, которую
можно записать в виде

где а , б , и с
константы и

Обратите внимание, что в квадратичной функции есть степень двойки на вашей независимой переменная, и это высшая степень.

Стандартная форма 
Квадратичная функция

Иногда квадратичная функция записывается в стандартной форме. Можно оставить его в таком виде при работе с вашей проблемой.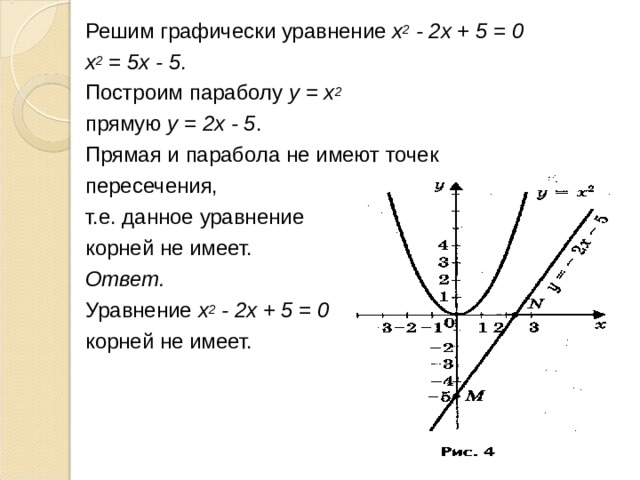 Я покажу вам, как построить параболу, используя любую форму.

График квадратичной функции

График квадратичной функции называется параболой . Это в основном изогнутая форма, открывающаяся вверх или вниз.

О чем нам говорят и ?

Если у вас есть квадратичная функция в любой форме, ИЛИ,

если a > 0, то парабола открывается вверх ,

если a < 0, то парабола открывается вниз .

Вершина

Вершина — самая низкая или самая высокая точка (в зависимости от направления) на графике квадратичной функции.

Нахождение вершины с помощью формы , :

Если ваша квадратичная функция имеет вид , , затем

вершина = .

В основном вы найдете x значение сначала вершину, а затем просто вставьте это значение в функцию, чтобы получить y или функциональное значение вершины.

Нахождение вершины с помощью формы :

Если ваша квадратичная функция имеет вид , затем

вершина = ( ч , к ).


Ось симметрии

Каждая парабола симметрична относительно вертикальной линии, называемой осью симметрии. Эта вертикальная линия проходит через вершину.

Думайте об этом как о зеркальном отражении этой вертикальной линии.

Следующие три графика иллюстрируют различные аспекты графика квадратичной функции или параболы.

Ниже приведен график функции :

Я хочу, чтобы вы обратили внимание на некоторые особенности этого график:

Прежде всего, посмотрите, как вершина является самая нижняя точка на графике. Он либо будет самым низким, либо наивысшая точка на графике квадратичной функции.

Во-вторых, посмотрите на ось симметрии . это не на самом деле часть самого графика, но важна тем, что парабола создает зеркальное изображение об этом. Обратите внимание, как он симметричен относительно оси симметрии. Также обратите внимание, как он проходит через вершину.

В-третьих, обратите внимание, как есть один y -intercept но нет x — перехват . квадратичный функция может не иметь ни одного, одного или двух x -перехватов.

Ниже приведен график функции :

Я хочу, чтобы вы обратили внимание на некоторые особенности этого график:

Прежде всего, посмотрите, как вершина является самая нижняя точка на графике. Он либо будет самым низким, либо наивысшая точка на графике квадратичной функции.

Во-вторых, посмотрите на ось симметрии . это не на самом деле часть самого графика, но важна тем, что парабола создает зеркальное изображение об этом. Обратите внимание, как он симметричен относительно оси симметрии. Также обратите внимание, как он проходит через вершину.

В-третьих, обратите внимание, как есть один у -intercept и один x — перехват . квадратичный функция может не иметь ни одного, одного или двух x -перехватов.

Ниже приведен график функции :

Я хочу, чтобы вы обратили внимание на некоторые вещи по этому поводу.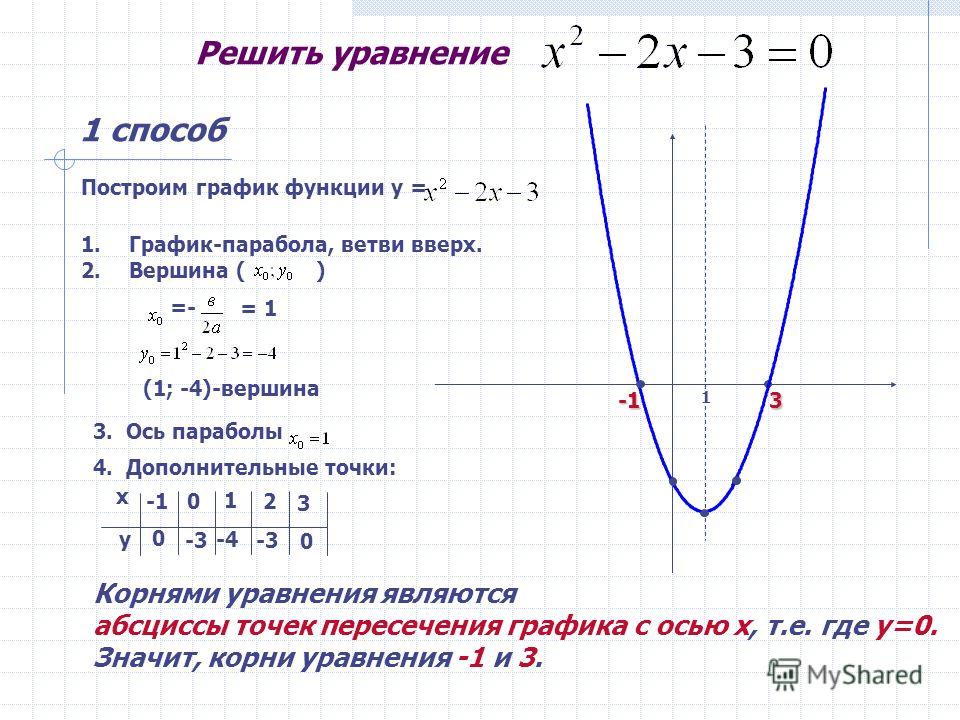 график:

Прежде всего, посмотрите, как вершина является наивысшая точка на графике. Он либо будет самым низким, либо наивысшая точка на графике квадратичной функции.

Во-вторых, посмотрите на ось симметрии . это не на самом деле часть самого графика, но важна тем, что парабола создает зеркальное изображение об этом. Обратите внимание, как он симметричен относительно оси симметрии. Также обратите внимание, как он проходит через вершину.

В-третьих, обратите внимание, как есть один y -intercept и два x -перехваты . квадратичный функция может не иметь, одну или две х -перехваты.

Пример 1 : Найдите координаты вершины .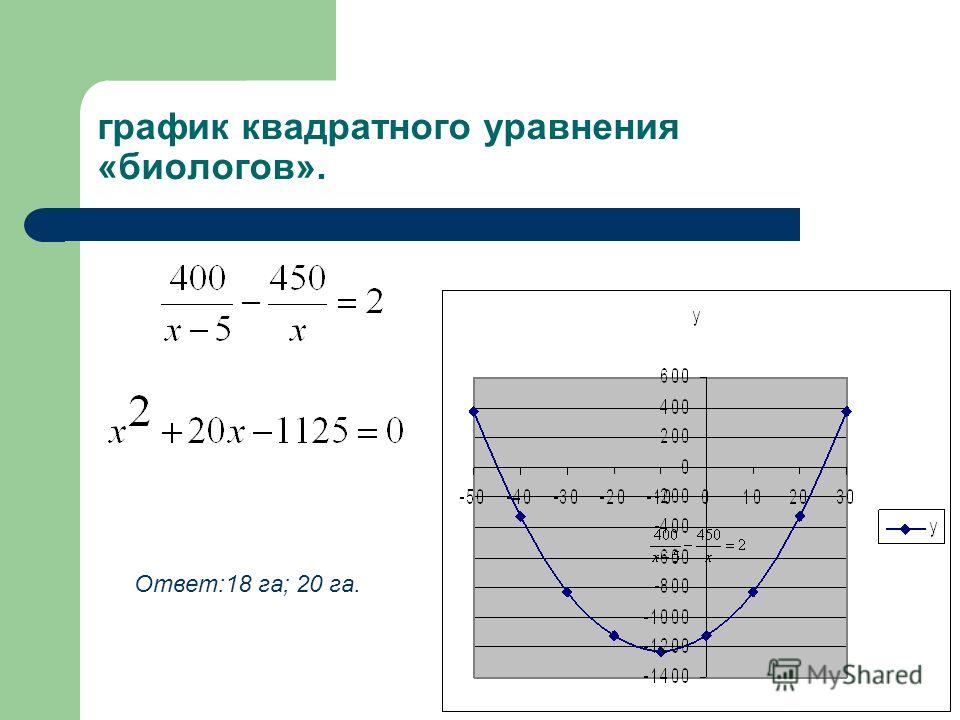 Без построения графика определите, является ли вершина максимальной или минимальной точкой квадратичной функции.

Вершина
Обратите внимание, как эта квадратичная функция записывается в стандартной форме. Это значит, что мы можем найти вершину, выровняв ее с общей стандартной формой и идентифицируйте ( h , k ).

*Стандартная форма четверки. функция

С ( ч , к ) является вершиной в стандартной форме, как вы думаете, что наша вершина для этого проблема?

Если вы сказали (1, -3), вы правы.

Будьте осторожны со своими знаками по этой проблеме.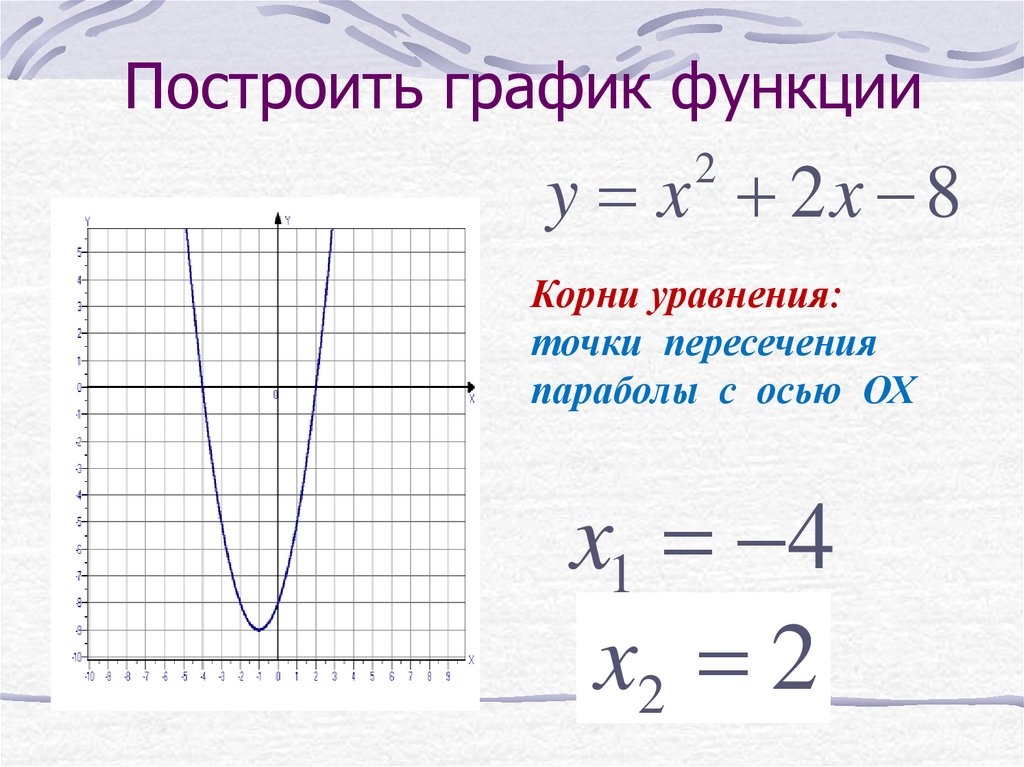 это реально заманчиво сказать, что вершина (1, 3). Однако внимательно посмотрите на стандартная форма. Обратите внимание, что знак перед h — минус, а перед k — плюс. Итак, ч — это число, которое мы вычитаем из х , что в нашем случае равно 1.  к это номер мы добавляем в конце, что в нашем случае мы добавляем минус 3.

Максимум или минимум?
Далее мы хотим определить, является ли вершина, мы нашли, (1, -3), является точкой максимума или минимума, без построения графика.

Если мы знаем, в каком направлении открывается кривая, то может помочь нам ответить на этот вопрос.

Так как a = 4 и 4 больше 0, эта парабола развернется .

Значит ли это, что вершина является максимальной или минимальной? точка?

Если вы сказали минимальный балл, вы правы.

Итак, наша вершина (1, -3) является точкой минимума.

Пример 2 : Найдите координаты вершины . Без построения графика определите, является ли вершина максимальной или минимальной точкой квадратичной функции.

Вершина
Обратите внимание, как эта квадратичная функция записывается в виде . Это означает, что мы можем найти вершину, используя формула .

*Укажите a , b , и с

*Подставить значения в вершинную форму. для а , б , и с

*Подставьте -5/4 дюйма для x , чтобы найти значение y вершины

Вершина будет .

Максимум или минимум?
Далее мы хотим определить, является ли вершина, мы нашли, , является максимальным или точка минимума, без построения графика.

Если мы знаем, в каком направлении открывается кривая, то может помочь нам ответить на этот вопрос.

Поскольку a = -2, и -2 меньше 0, эта парабола развернулась бы вниз .

Значит ли это, что вершина является максимальной или минимальной? точка?

Если вы сказали максимальный балл, вы правы.

Итак, наша вершина — это точка максимума.

График квадратичной функции

Шаг 1: Выполняется кривая графика вверх или вниз?

Шаг 2: Найдите вершина.

Шаг 3: Найдите точки пересечения.

Если вам нужен обзор перехватов, не стесняйтесь перейти к Tutorial 26: Уравнения линий .

Шаг 4: Постройте параболу.

Нанесите точки, найденные в шагах 2 и 3, и проведите кривую через их.

Пример 3 : Используйте вершину и точки пересечения, чтобы нарисовать график квадратичная функция. Найдите уравнение для оси симметрии этой функции.

Шаг 1: Выполняется кривая графика вверх или вниз?

Поскольку a = -1 и -1 < 0, то это выглядит как и , он будет изгибаться вниз.

Это дает нам хорошее представление о том, что мы идем в правильном направлении.

Шаг 2: Найдите вершина.

Как и в примере 1 выше, эта квадратичная функция записывается в стандартной форме. Это означает, что мы можем найти вершину, сопоставив ее с общей стандартной формой, и выявить ( ч , к ).

*Стандартная форма четверки. функция

С ( ч , к ) Вершина имеет стандартную форму, как вы думаете, что это за вершина?

Если вы сказали (-1, 4), вы правы.

Будьте осторожны со своими знаками по этой проблеме. Обратите внимание, как знак перед ч это минус, но один перед k положительный. Итак, ч число, которое мы вычитаем из x , что в нашем случае -1. k это число мы добавляем в конце, что в нашем случае мы добавляем 4.

Шаг 3: Найдите перехваты.

у -перехват
Напоминаем, что перехват y всегда где график пересекает ось y , что означает x = 0:

*Замените x на 0

Пересечение и равно (0, 3).

x — точка пересечения
Напоминаем, что перехват x всегда где график пересекает ось x , что означает y = 0:

*Замените y (или f(x)) с 0

*Решить квадратичный факторизацией

x -перехваты равны (-3, 0) и (1, 0).

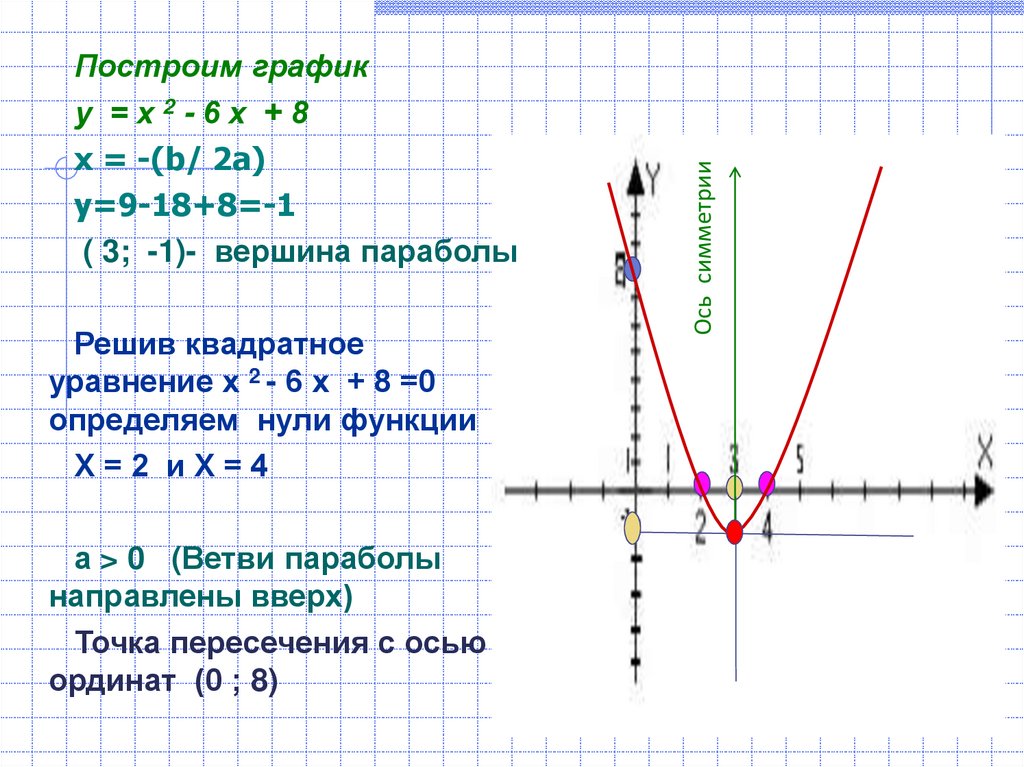
Шаг 4: График парабола.

Ось симметрии
Как показано на графике, ось симметрии равна x = -1.

Пример 4 : Используйте вершину и точки пересечения, чтобы нарисовать график квадратичная функция. Найдите уравнение для оси симметрии этой функции.

Шаг 1: Выполняется кривая графика вверх или вниз?

Так как a = 1 и 1 > 0, то это выглядит как это собирается изогнуться.

Это дает нам хорошее представление о том, что мы идем в правильном направлении.

Шаг 2: Найдите вершина.

Как и в примере 2 выше, эта квадратичная функция записывается в виде . Это означает, что мы можем найти вершину, используя формула .

*Укажите a , b , и с

*Подставить значения в вершинную форму. для а , б , и с

*Подставьте -1 к x , чтобы найти значение y вершины

Итак, вершина равна (-1, 1).

Шаг 3: Найдите перехваты.

у -перехват
Напоминаем, что перехват y всегда где график пересекает ось y , что означает x = 0:

*Замените x на 0

Пересечение и равно (0, 2).

x — точка пересечения
Напоминаем, что перехват x всегда где график пересекает ось x , что означает y = 0:

*Заменить г (или f(x)) с 0

Обратите внимание, что это не учитывается.   Попробуем решить с помощью квадратичная формула:

*Квадратичный формула

*Подставьте значения для a , b , и с

Обратите внимание, что мы получили отрицательное число под квадратным корнем.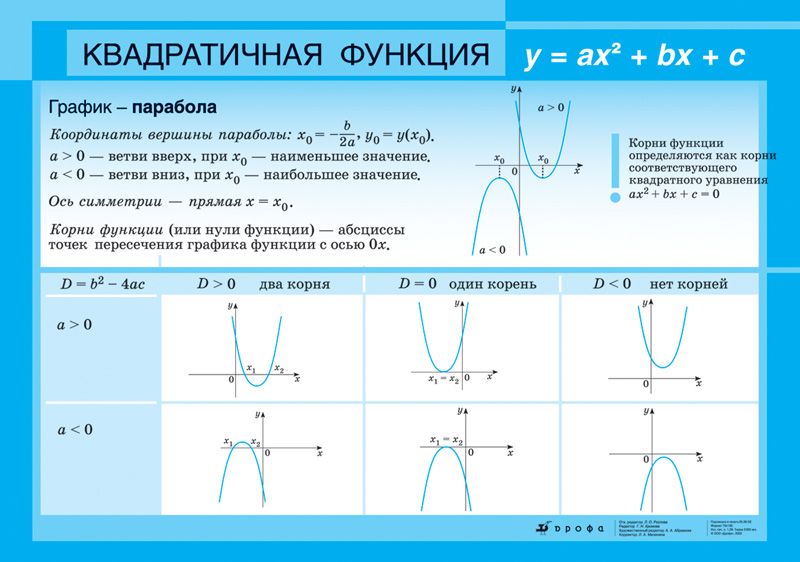 Это означает, что нет действительного числового решения. Это также означает, что НЕТ x -перехватов.

Шаг 4: График парабола.

Ось симметрии
Как показано на графике, ось симметрии равна x = -1.

Практические задачи

---

Это практические задачи, которые помогут вам перейти на следующий уровень. Это позволит вам проверить и понять, понимаете ли вы эти виды проблем. Математика работает так же, как и все в противном случае, если вы хотите добиться в этом успеха, вам нужно практиковаться. Даже лучшие спортсмены и музыканты получали помощь на этом пути и много практиковаться, практиковаться, практиковаться, чтобы преуспеть в своем виде спорта или игре на инструменте. На самом деле практики много не бывает.

Чтобы получить максимальную отдачу от этого, вы должны решить проблему на свой собственный, а затем проверьте свой ответ, нажав на ссылку для ответа/обсуждения для этой задачи . По ссылке вы найдете ответ а также любые шаги, которые привели к поиску этого ответа.

 

Практика Задачи 1а — 1б: Найти координаты вершины заданного квадратичная функция. Без построения графика определите, является ли вершина точка максимума или минимума квадратичной функции.

 

1а.
(ответ/обсуждение к 1а)

1б.
(ответ/обсуждение к 1б)

 

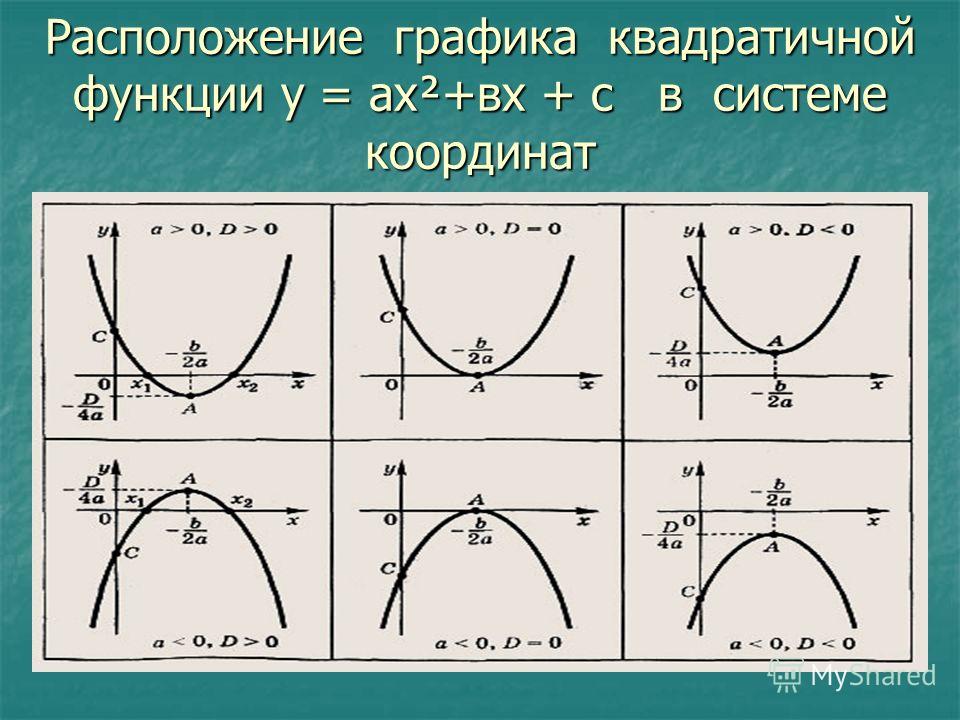
Практика Задачи 2a–2b: Используйте вершину и точки пересечения, чтобы нарисовать график заданной квадратичной функции.

No related posts.