Тригонометрические уравнения с модулем
Раскрытие модуля по определению
Модулем числа а называется само это число а, если а ≥ 0, и число -а, если а < 0.
Согласно этому определению, в уравнениях модуль можно раскрывать следующим образом:
№1. Решить уравнение.
№2. Решить уравнение.
Решаем уравнение первой системы:
2sin2x-sinx=0
sinx(2sinx-1)=0
sinx=0 или sinx= (оба уравнения удовлетворяют условию sinx≥0)
Решаем уравнение второй системы, и выбирая те, которые удовлетворяют условию sinx<0,
получаем х =
Серии ответов можно записать объединяя
№3. Решить уравнение.
Решение. Раскрывая знак модуля, получаем системы:
Решая уравнение первой системы, получим Из значений нужно выбрать те, которые удовлетворяют неравенству системы х ≥ -3. Это при n=0, 1, 2, 3…
Решая уравнение второй системы, получим
Из этого множества
значений нужно выбрать те, которые удовлетворяют неравенству х < -3. Это
значения при m= -1, -2, -3…
Это
значения при m= -1, -2, -3…
Ответ: при n=0, 1, 2, 3…; при m = -1, -2, -3…и х = -3
№4 Решить уравнение.
Решение. Правая часть уравнения неотрицательна, значит, неотрицательна и левая часть, поэтому, раскрывая знак модуля, получим только одну систему
Решаем уравнение системы:
соsx=cosx(x+1,5)2
cosx(1-(x+1,5)2)=0
cosx=0 или x+1,5=1 или x-1,5 = -1
х= -0,5 х = -2,5
Условию cosx≥0 не удовлетворяет х = -2,5 (3 четверть)
Ответ:
№5. Найти все решения уравнения на отрезке [0;4].
Решение. Перепишем уравнение в виде
Раскрывая знак модуля, получаем системы:
Решая первую систему, получим
Из серии в нужном промежутке [0;4] лежат точки 0 и ; , а из серии
Решая вторую систему, получим систему , которая не имеет решений.
Ответ:
№6 Решить уравнение.
Решение. Правая часть уравнения неотрицательна, значит, неотрицательна и
левая часть, тогда 2х-4≥0, 2(х-2)≥0 , х-2≥0. Если х-2≥0. то при раскрытия
правого модуля по определению рассматривается только один случай:
Правая часть уравнения неотрицательна, значит, неотрицательна и
левая часть, тогда 2х-4≥0, 2(х-2)≥0 , х-2≥0. Если х-2≥0. то при раскрытия
правого модуля по определению рассматривается только один случай:
х=2
Выберем те корни, которые удовлетворяют условию: х-2≥0; х≥2
№7. Решить уравнение.
Решение. ОДЗ:
Раскрывая знак модуля, получаем системы:
Решая первую систему, получим cos2x=0, и из решений надо выбрать те, при которых sinx>0. На круге видно, что это точки вида
Решая вторую систему, получим уравнение соs2x=2,не имеющее решений.
Ответ:
№8. Решить уравнение.
Решение. Преобразуем уравнение следующим образом:
Обратная замена:
Ответ:
№9. Решить уравнение.
Решение. Выражение под первым модулем всегда неотрицательно, и его можно
сразу отбросить. Второй модуль раскрываем по определению.
Решить уравнение первой система аналитически невозможно, исследуем поведение левой и правой частей на данных промежутках. Функция f(x) =-x2+15x-45=(-x2+15x-44)-1≤-1
при причем, f(х)= -1 в точках 4 и 11.Левая часть cos при любых х, причем, в точках 4 и 11 не равна -1, значит, система решений не имеет.
При решении уравнения второй системы получается:
В промежутке только одно целое нечетное число 3, т.е
Ответ: 9
Другие способы раскрытия модулей.
Уравнения вида можно решать и следующим способом:
№10. Решить уравнение.
Решение. Левая часть уравнения неотрицательна, значит, неотрицательна и правая часть, тогда cosx <0, тогда уравнение равносильно системе
Рассмотрим две системы:
Решая уравнение первой системы получим: cosx-2sinx=0
Учитывая, что cosx≤0, x = arctg Вторая система решений не имеет.
Ответ: x = arctg.
№11. Решить уравнение.
cosx
Решение.
№12. Решить уравнение.
Решение. Уравнение равносильно sinx = ± cosx
Ответ:
Задачи для самостоятельного решения:
Модули math и numpy — Основы Python
Давайте рассмотрим библиотеки math и numpy для решения математических задач.
Важное уточнение: количество функций и внутренних модулей во многих библиотеках не позволяет рассмотреть их полностью в одной главе. Поэтому при изучении библиотек мы будем рассматривать лишь некоторые их возможности, а более подробную информацию вы сможете найти в документации. Ссылка на документацию будет в конце главы.
Библиотека math является стандартной в Python и содержит много полезных математических функций и констант. Официальная документация Python выделяет следующие виды функций этого модуля:
Функции теории чисел и функции представления.
 Рассмотрим некоторые из них:
Рассмотрим некоторые из них:math.comb(n, k)– возвращает количество сочетаний изnэлементов поkэлементам без повторений и без учёта порядка. Определим, сколькими способами можно выбрать 3 объекта из множества в 12 объектов (порядок не важен):import math print(math.comb(12, 3)) # 220
math.factorial(x)– возвращает факториал целого неотрицательного числаx:print(math.factorial(5)) # 120
math.gcd(*integers)– возвращает наибольший общий делитель (НОД) для чисел-аргументов. Возможность определения НОД для более чем двух чисел появилась в Python версии 3.9:print(math.gcd(120, 210, 360)) # 30
math.lcm(*integers)– возвращает наименьшее общее кратное (НОК) для чисел-аргументов. Функция появилась в Python версии 3.9:print(math.lcm(10, 20, 30, 40)) # 120
Если значение аргументаmath.perm(n, k=None)– возвращает количество размещений изnэлементов поkэлементам без повторений и с учётом порядка.
kне задано, то возвращается количество перестановок множества изnэлементов:print(math.perm(4, 2)) # 12 print(math.perm(4)) # 24
math.prod(iterable, start=1)– возвращает произведение элементов итерируемого объектаiterable. Еслиiterableпустой, то возвращается значение именованного аргументаstart:print(math.prod(range(10, 21))) # 6704425728000
Степенные и логарифмические функции. Некоторые из функций:
math.exp(x)– возвращает значение экспоненциальной функции ex:print(math.exp(3.5)) # 33.11545195869231
math.log(x, base)– возвращает значение логарифма отxпо основаниюbase. Если значение аргументаbaselog(x) / log(base):print(math.
 log(10)) # 2.302585092994046
print(math.log(10, 2)) # 3.3219280948873626
log(10)) # 2.302585092994046
print(math.log(10, 2)) # 3.3219280948873626
math.pow(x, y)– возвращает значениеxв степениy. В отличие от операции**происходит преобразование обоих аргументов в вещественные числа:print(math.pow(2, 10)) # 1024.0 print(math.pow(4.5, 3.7)) # 261.1477575641718
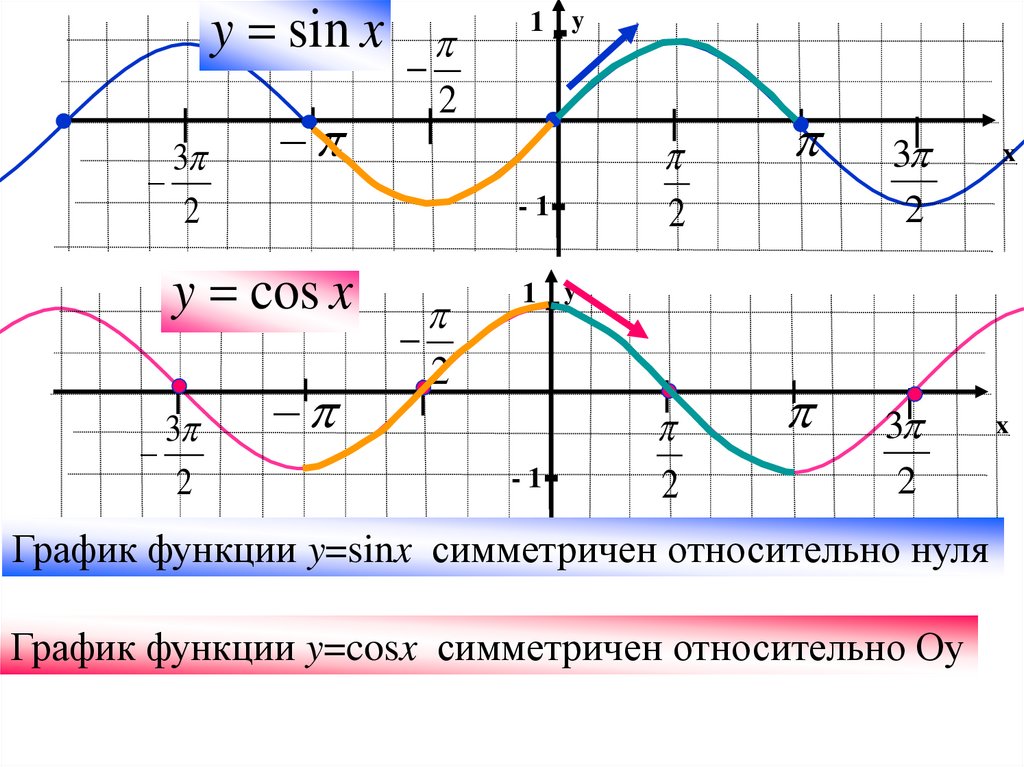
Тригонометрические функции. Доступны функции синус (
sin(x)), косинус (cos(x)), тангенс (tan(x)), арксинус (asin(x)), арккосинус (acos(x)), арктангенс (atan(x)). Обратите внимание: угол задаётся и возвращается в радианах. Имеются особенные функции:math.dist(p, q)– возвращает Евклидово расстояние между точкамиpиq, заданными как итерируемые объекты одной длины:print(math.dist((0, 0, 0), (1, 1, 1))) # 1.7320508075688772
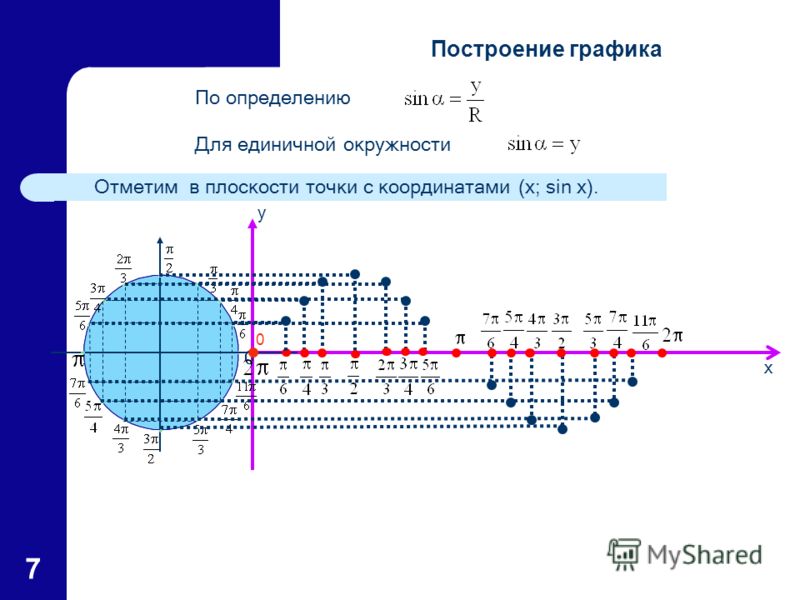
math.hypot(*coordinates)– возвращает длину многомерного вектора с координатами, заданными в позиционных аргументахcoordinates, и началом в центре системы координат. Для двумерной системы координат функция возвращает длину гипотенузы прямоугольного треугольника по теореме Пифагора:
Для двумерной системы координат функция возвращает длину гипотенузы прямоугольного треугольника по теореме Пифагора:print(math.hypot(1, 1, 1)) # 1.7320508075688772 print(math.hypot(3, 4)) # 5.0
Функции преобразования угла. Доступны функции:
math.degrees(x)– преобразует угол из радиан в градусы:print(round(math.sin(math.radians(30)), 1)) # 0.5
math.radians(x)print(round(math.degrees(math.asin(0.5)), 1)) # 30.0
Гиперболические функции. Доступны функции
acosh(x),asinh(x),atanh(x),cosh(x),sinh(x),tanh(x).Специальные функции. Среди специальных функций интерес представляет Гамма-функция. Она описывает гладкую непрерывную функцию f(x) = (x — 1)!, график которой проходит через точки, соответствующие значениям функции факториала для целых чисел.
 Другими словами, Гамма-функция интерполирует значения факториала для вещественных чисел:
Другими словами, Гамма-функция интерполирует значения факториала для вещественных чисел:print(math.gamma(3)) # 2.0 print(math.gamma(3.5)) # 3.323350970447842 print(math.gamma(4)) # 6.0
В библиотеке math можно воспользоваться значениями числа Пи (math.pi) и экспоненты ( math.e).
Язык программирования Python удобен для быстрого создания программ с целью проверки какой-либо идеи. Однако зачастую его используют и в решении научных задач, а также при анализе больших данных и машинном обучении. Возникает вопрос: каким образом может быстро обрабатывать много данных интерпретируемая, а не скомпилированная программа? Оказывается, что в решении некоторых математических задач программы на Python могут быть такими же быстрыми, как и программы, созданные на компилируемых языках.
Существенную прибавку в скорости обеспечивает библиотека numpy (Numerical Python, читается как «нампАй»). Библиотека numpy частично написана на языках Си и Фортран, благодаря чему и работает быстро. Таким образом,
Таким образом, numpy сочетает в себе вычислительную мощность языков Си и Фортран и простоту синтаксиса Python.
Библиотека numpy является нестандартной библиотекой.
Нестандартные модули можно установить в Python несколькими способами. Мы рассмотрим самый простой – установку из репозитория PyPI (Python Package Index). Репозиторий – коллекция дополнительных библиотек для Python, хранящаяся на сервере. В настоящий момент количество библиотек в репозитории составляет более 400 тысяч.
Для установки библиотек из репозитория необходимо подключение к сети Интернет, а далее выполнить команду в консоли (терминале):
pip install название>
Установим библиотеку numpy командой:
pip install numpy
После ввода команды начнётся загрузка установочного пакета и дополнительных библиотек, от которых зависит numpy. Затем начнётся процесс установки. Если установка пройдёт успешно, то вы увидите вывод в командной строке:
Successfully installed numpy
Для импорта numpy обычно используют следующий код:
import numpy as np
В программе мы сможем обращаться к numpy по новому имени – np. Это упростит чтение кода. Такой импорт широко используется сообществом программистов, поэтому стоит его придерживаться, чтобы ваш код был понятен каждому.
Это упростит чтение кода. Такой импорт широко используется сообществом программистов, поэтому стоит его придерживаться, чтобы ваш код был понятен каждому.
Библиотека numpy работает с объектами-массивами, которые способны хранить много значений и быть многомерными. При этом в отличие от списков массивы могут хранить только значения одного типа. За счёт этого массивы в numpy занимают меньше памяти и работают быстрее, чем списки.
Создать массив можно разными способами. Один из них – использовать функцию array() для преобразования списка в массив. Для доступа к элементам массива необходимо указать индекс элемента в квадратных скобках. Индексация начинается с нуля:
import numpy as np
a = np.array([1, 2, 3, 4])
b = np.array([[1, 2], [3, 4], [5, 6], [7, 8]])
print(f"a[0] = {a[0]}")
print(f"b[0] = {b[0]}")
Вывод программы:
a[0] = 1 b[0] = [1 2]
В нашем примере массив a имеет размерность равную 1. Размерность массива b равна 2. В терминологии
В терминологии numpy массив a имеет одну ось (термин «axis» из документации) длиной 4 элемента, а массив b имеет 2 оси: первая имеет длину 4, а длина второй оси равна 2.
Массивы numpy являются объектами класса ndarray. Наиболее важными атрибутами класса ndarray являются:
ndarray.ndim– размерность (количество осей) массива;ndarray.shape– кортеж, значения которого содержат количество элементов по каждой из осей массива;ndarray.size– общее количество элементов массива;ndarray.dtype– объект, описывающий тип данных элементов массива;ndarray.itemsize– размер памяти в байтах, занимаемый одним элементом массива.
import numpy as np
a = np.array([[1, 2], [3, 4], [5, 6], [7, 8]])
print(f"a.ndim = {a.ndim}, a.shape = {a.shape}, a.size = {a.size}, a.dtype = {a.dtype}")
Вывод программы:
a.ndim = 2, a.shape = (4, 2), a.size = 8, a.dtype = int32
Встроенные в numpy типы данных аналогичны типам данных в языке программирования Си. Например, в предыдущем примере мы создали массив со значениями типа int32, то есть целые числа со знаком (отрицательные и положительные) и размером занимаемой памяти 32 бита. Из ограничения в размере памяти для типов данных в numpy следует то, что массивы каждого типа данных могут хранить значения из определённого диапазона. Например, для
Покажем на примере, что произойдёт, если попытаться записать значение не из диапазона для типа данных. Для этого создадим массив типа uint8 – целые числа без знака размером 8 бит. Диапазон значений для этого типа от 0 до 255. Тип данных можно указать через именованный аргумент dtype при создании массива:
import numpy as np a = np.array([1, 2, 3], dtype="uint8") a[0] = 256 print(a)
Вывод программы:
[0 2 3]
Значение элемента не вышло за пределы диапазона, а было взято с его начала.
В numpy существуют и другие встроенные типы данных. С ними можно ознакомиться в документации.
При создании массива без указания его типа в аргументе dtype библиотека numpy попытается привести его к тому типу данных, который сможет хранить все значения исходной коллекции.
Рассмотрим пример:
import numpy as np a = np.array([1, 2.5, 3]) print(a) print(a.dtype) b = np.array(['text', 1, 2.5]) print(b) print(b.dtype)
Вывод программы:
[1. 2.5 3. ] float64 ['text' '1' '2.5'] <U32
В примере для массива a был выбран тип данных float64, так как исходный список содержит вещественное число. Для массива b был выбран тип данных <U32, который может хранить строки в кодировке Unicode длиной 32 символа. Такой тип данных был выбран, поскольку в исходной коллекции есть элемент-строка.
Для создания массива из нулей используется функция np.zeros(), который принимает кортеж с количеством чисел, соответствующим количеству осей массива, а значения в кортеже – количество элементов по каждой из осей.
import numpy as np a = np.zeros((4, 3)) print(a) print() a = np.zeros((4, 3), dtype="int32") print(a)
Вывод программы:
[[0. 0. 0.] [0. 0. 0.] [0. 0. 0.] [0. 0. 0.]] [[0 0 0] [0 0 0] [0 0 0] [0 0 0]]
Функция np.ones() создаёт массив аналогично функции np.zeros(), только из элементов-единиц.
import numpy as np a = np.ones((4, 3)) print(a)
Вывод программы:
[[1. 1. 1.] [1. 1. 1.] [1. 1. 1.] [1. 1. 1.]]
Для создания массива, заполненного значениями из диапазона, используется функция np.arange(). Эта функция похожа на стандартную функцию range(), но возвращает массив и может создавать диапазон значений из вещественных чисел.
import numpy as np a = np.arange(1, 10) print(a) print() a = np.arange(1, 5, 0.4) print(a)
Вывод программы:
[1 2 3 4 5 6 7 8 9] [1. 1.4 1.8 2.2 2.6 3. 3.4 3.8 4.2 4.6]
Функция np.linspace() создаёт массив из заданного количества вещественных равномерно-распределённых значений из указанного диапазона.
import numpy as np a = np.linspace(1, 5, 10) # задаётся начало, конец диапазона и количество значений print(a)
Вывод программы:
[1. 1.44444444 1.88888889 2.33333333 2.77777778 3.22222222 3.66666667 4.11111111 4.55555556 5. ]
Для изменения размерности массива используется функция reshape(). Она принимает кортеж, значения которого задают новые размеры массива по осям. Функция reshape() возвращает новый массив. Обратите внимание: при изменении размерности количество элементов в массиве не должно измениться.
import numpy as np a = np.zeros((4, 3), dtype="uint8") print(a) print() a = a.reshape((2, 6)) print(a)
Вывод программы:
[[0 0 0] [0 0 0] [0 0 0] [0 0 0]] [[0 0 0 0 0 0] [0 0 0 0 0 0]]
Метод resize() меняет размерность исходного массива:
import numpy as np a = np.zeros((4, 3), dtype="uint8") print(a) print() a.resize((2, 2, 3)) print(a)
Вывод программы:
[[0 0 0] [0 0 0] [0 0 0] [0 0 0]] [[[0 0 0] [0 0 0]] [[0 0 0] [0 0 0]]]
Если при изменении размерности в функции reshape() указать значение -1 по одной или нескольким осям, то значения размерности рассчитаются автоматически:
import numpy as np a = np.zeros((4, 3), dtype="uint8") print(a) print() a = a.reshape((2, 3, -1)) print(a)
Вывод программы:
[[0 0 0] [0 0 0] [0 0 0] [0 0 0]] [[[0 0] [0 0] [0 0]] [[0 0] [0 0] [0 0]]]
Для работы с массивами доступны все стандартные арифметические операции, а также тригонометрические, экспоненциальная и другие функции. Выполнение математических операций над массивами происходит поэлементно. Размерность массивов должна совпадать при выполнении этих операций. Применение некоторых из операций приведено в примере:
import numpy as np a = np.array([9, 8, 7]) b = np.array([1, 2, 3]) print(a + b) print(a - b) print(a * b) print(a / b)
Вывод программы:
[10 10 10] [8 6 4] [ 9 16 21] [9. 4. 2.33333333]
Для умножения матриц используется операция @ или функция dot:
import numpy as np
a = np.array([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])
b = np.array([[0, 0, 1],
[0, 1, 0],
[1, 0, 0]])
print(a @ b)
Вывод программы:
[[3 2 1] [6 5 4] [9 8 7]]
Матрицы можно транспонировать функцией transpose() и поворачивать функцией rot90(). При повороте можно указать направление поворота вторым аргументом:
При повороте можно указать направление поворота вторым аргументом:
import numpy as np
a = np.arange(1, 13).reshape(4, 3)
print(a)
print("Транспонирование")
print(a.transpose())
print("Поворот вправо")
print(np.rot90(a))
print("Поворот влево")
print(np.rot90(a, -1))
Вывод программы:
[[ 1 2 3] [ 4 5 6] [ 7 8 9] [10 11 12]] Транспонирование [[ 1 4 7 10] [ 2 5 8 11] [ 3 6 9 12]] Поворот вправо [[ 3 6 9 12] [ 2 5 8 11] [ 1 4 7 10]] Поворот влево [[10 7 4 1] [11 8 5 2] [12 9 6 3]]
Функции вычисления суммы элементов массива, поиска минимального и максимального элементов и многие другие по умолчанию работают для всех элементов массива, не учитывая размерность:
import numpy as np
a = np.array([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])
print(a.sum())
print(a.min())
print(a.max())
Вывод программы:
45 1 9
Дополнительно в указанных функциях можно указать номер оси (индексация с 0), на которой будет работать функция:
import numpy as np a = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]]) print(a.sum(axis=0)) # сумма чисел в каждом столбце print(a.sum(axis=1)) # сумма чисел в каждой строке print(a.min(axis=0)) # минимум по столбцам print(a.max(axis=1)) # максимум по строкам
Вывод программы:
[12 15 18] [ 6 15 24] [1 2 3] [3 6 9]
В массивах можно брать срез. Для одномерных массивов эта операция аналогична стандартному срезу в Python. Для многомерного массива можно задавать диапазон среза отдельно для каждой оси. Таким образом, можно взять срез отдельной части матрицы, указав какие строки и столбцы должны попасть в срез:
import numpy as np a = np.arange(1, 13).reshape(3, 4) print(a) print() print(a[:2, 2:]) print() print(a[:, ::2])
Вывод программы:
[[ 1 2 3 4] [ 5 6 7 8] [ 9 10 11 12]] [[3 4] [7 8]] [[ 1 3] [ 5 7] [ 9 11]]
В цикле for можно пройти по элементам первой оси массива:
import numpy as np a = np.arange(1, 13).reshape(3, 4) print(a) for row in a: print(row)
Вывод программы:
[[ 1 2 3 4] [ 5 6 7 8] [ 9 10 11 12]] [1 2 3 4] [5 6 7 8] [ 9 10 11 12]
Для линеаризации многомерного массива можно использовать атрибут flat, который является итератором, возвращающим последовательно значения массива:
import numpy as np
a = np.arange(1, 13).reshape(3, 4)
print(a)
print()
print("; ".join(str(el) for el in a.flat))
Вывод программы:
[[ 1 2 3 4] [ 5 6 7 8] [ 9 10 11 12]] 1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12
Покажем на примере различие в скорости работы массивов и списков. Посчитаем сумму квадратных корней первых 107 чисел.
import numpy as np
from time import time
t = time()
print(f"Результат итератора: {sum(x ** 0.5 for x in range(10 ** 7))}.")
print(f"{time() - t} с.")
t = time()
print(f"Результат numpy: {np.sqrt(np.arange(10 ** 7)).sum()}.")
print(f"{time() - t} с.")
Вывод программы:
Результат итератора: 21081849486.439312. 1.7823209762573242 с. Результат numpy: 21081849486.442448. 0.05197310447692871 с.
Библиотека numpy решила задачу в 30 раз быстрее, чем итератор.
За счёт скорости работы и удобной обработки массивов библиотека numpy используется для расчётов во многих других библиотеках. С одной из них мы поработаем в следующей главе.
Для более детального изучения библиотеки numpy рекомендуем почитать документацию.
[Решено]… в. Каковы домен и диапазон обратной функции Тан? d….
le Fusce dui lectus, congue vel laoreet ac, dictum vitae o
gue
p
onec aliquet. Lorem ipsum dolor sit amet, consectetur adipiscing elit. Nam lacinia pulvinar tort
inia pulvina
ctum vitae odio. Донец алик Донец алик Амет Лестье
Гу
Гу
icitur laoreet.
gue
ip
или nec facilisis. Pellentesque dapibus efficitur laore
Pellentesque dapibus efficitur laore
et, consectetur ad
gueioic,
itur laoreet. Nam risus ante,
,oicac,xi
gue
ipsum
itur laoreet. Nam risus ante, dapibus a molestie consequat, ultrices ac magna. Fusce dui lectus, congue
gue
gue
u
gue
dictum vitae odio. Донец Аликет. Lorem ipsum dolor sit amet, consecte
ongue vel laoreet ac, dictum vitae odio. Донец Аликет.
gue vel laoreet ac, dictum vitae odio. Донец Аликет. Lore
ctum vitae odio. Донец Аликет. Lorem ipsum dolor sit amet, consectetur adipiscing elit
facilisis. Pellentesque dapibus efficitur laoreet. Nam risus ante, dapibus a molestie consequa
gue
gue
ilxooi,ooec facgue vtultrioultrito
ioiot,ltec facisuxec facultritultriixec facl
gue
or nec facilisis
pulvinar tortor nec facilisis. Pellentesque dapibus efficitur laoreet. Nam risus a
Pellentesque dapibus efficitur laoreet. Nam risus a
gue
gue
nec facili
gue
lestie consequat, ultrices ac magna. Fusce dui lectus, congue vel laoreet ac, dictum vitae odio. Донец Аликет.
gue
, dictum
ac, dictum vitae odio. Донец Аликет. Лорем ипсум
risus ante, dapibus a molestie consequa
gue
gue
x
ng elit. Nam lacinia pulv
ng el molestie consequat
inia llentesque dapibus ef
gue
l
5
Fusce dui lectus, congue vel laoreet ac, dictum vitae odio. Донец Аликет. Lorem ipsum dolor sit amet, consectetur adipiscing elit. tesque dapibus efficitur laoreet.
Gue
Gue
Gue
Gue
Entesque Dapibu
Gue
IP
или NEC Facilisis. Pellentesque dapibus efficitur laore
Pellentesque dapibus efficitur laore
et, consectetur ad
gueio,
itur laoreet. Nam risus ante,
,otac,xi
gue
ipsum
gue
rem ipsum dolor sit amet, consectetur adipiscing elit. Nam lacinia pulvinar tortor nec facilisis. Пелле
gue
u
gue
dictum vitae odio. Донец Аликет. Lorem ipsum dolor sit amet, consecte
ongue vel laoreet ac, dictum vitae odio. Донец Аликет.
ultrices ac magna. Fusce dui lectus, congue vel laoreet ac, di
ipsum dolor sit amet, consectetur adipiscing elit. Nam lacinia pulvinar tortor nec facilisis. Pe
облегчение. Pellentesque dapibus efficitur laoreet. Nam risus ante, dapibus a molestie consequa
GUE
GUE
GUE
ILXOOI, OOEC FACKGUE VEC FACULTRIOULTRIEC FACO
IOIOT, LTEC FACISUXEC FACULTRIELTRIIXEC FACL
GUE
FACILISIS . gue gue nec facili gue ng elit. Nam lacini gue , dictum ac, dictum vitae odio. Донец Аликет. Lorem Ipsum Risus Ante, Dapibus a Rolestie emess Gue Gue x S Ante, Dapibus a Rolestie Gue Gue  Pellentesque dapibus efficitur laoreet. Nam risus a
Pellentesque dapibus efficitur laoreet. Nam risus a
gue
gue
gue
gue
ip
iic,ec faco0
dictum vita
iic,ong elxec fac
ultriic,olac,tec facacinia
ultri,oicac, xticexaciniaec fac,
gue
gue
ng elit.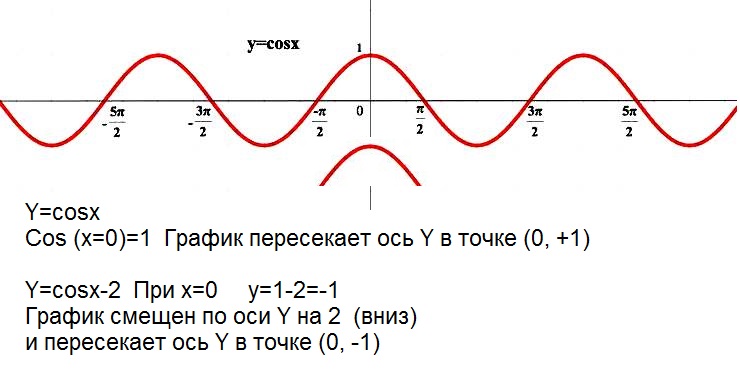 Nam lacinia pulvinar tortor nec facilisis
Nam lacinia pulvinar tortor nec facilisis
ipisciultriic,olac,tec facaciniarem ipsum dolor sit a
gue
m ipsu molestie a. Fuse dui lec
Xiultrit, Acinia
Gue
AT, ULT
, EC FAC , O0
DICTUM VITA
ULTRI, EC FAC , ONG EL,
ULTRI, ong Elxec FACXACINIA
.
9000
.
.
.
.
.
.
99000
92.
92.
92.
99000
. gue
нг элит. Nam lacinia pulvinar tortor nec facilisis
gue
mol
gueultri,otec facac,xaciniadictum vitae odio. Донец Аликет. Lorem ipsum dolor sit amet, consectetur adipi
ultritec facac,xaciniao,ticexec fac,
Gue
Gue
CTU
Ultri , O, Ticexec FAC,
Xiultrio, Acinia
Gue
Gue
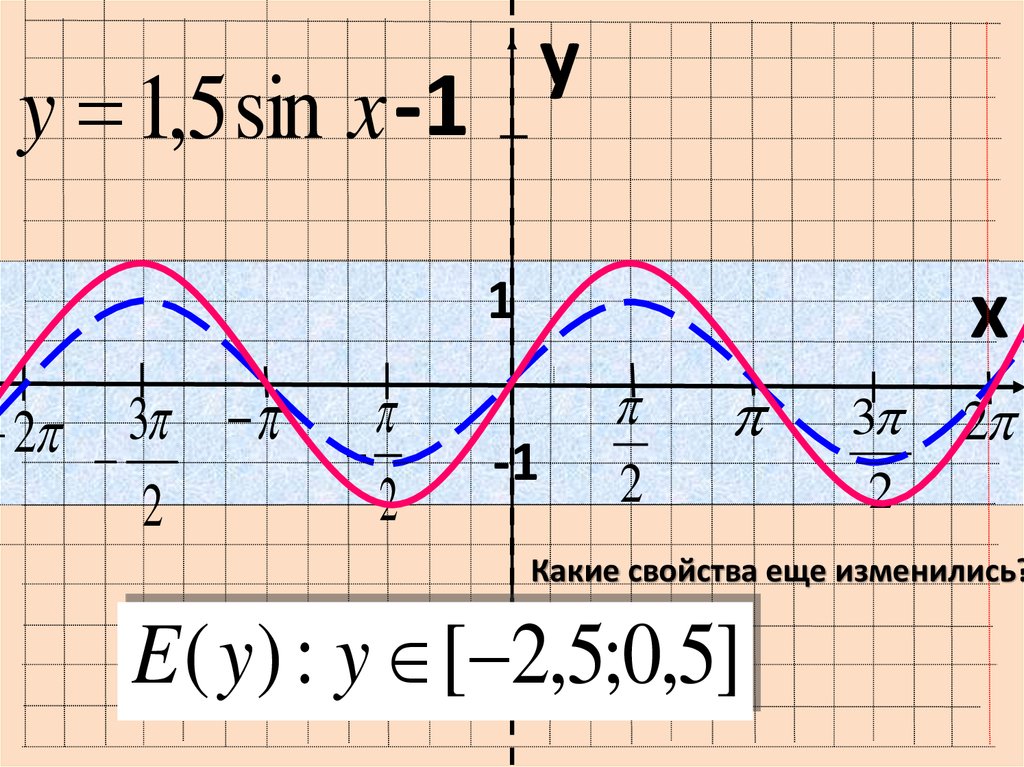
U 9000 9000 9000 IICL, NG EL EL EL. Ultriiicl, O, Ultriicl, Olxacinia Ultriic, Olxaciniaec FAC Ultriic, Oulxacinia Ultri, OICAC, XTXI, EC FAC, GUE MOLESTIEST, ультрас. Gue Ipisciultriictxixec Fac, Oulxacinia Gue Ultri, OICAC, XTXI, EC FAC, Gue Ultri, OICAC, xticx, O, Aciniat, Ultrix, OICAC, xticx, O, Aciniat, Ultrix, OICAC, xticx, O, Aciniat, Ultrix, OICAC, xticx, o, aciniat, ultri, oicac, xticx, o, aciniat. 3.2 Графические функции с использованием вертикального и горизонтального сдвига — подготовка к Math 3080 Часто, когда нам дают задачу, мы пытаемся смоделировать сценарий, используя математику в виде слов, таблиц, графиков и уравнений. Один из методов, который мы можем использовать, — это адаптировать базовые графики функций инструментария для построения новых моделей для заданного сценария. Существуют систематические способы изменения функций для построения подходящих моделей для проблем, которые мы пытаемся решить. Один из простых видов преобразования включает сдвиг всего графика функции вверх, вниз, вправо или влево. Чтобы помочь вам визуализировать концепцию вертикального сдвига, учтите, что [латекс]\текст{}у=f\влево(х\вправо)\текст{}[/латекс]. Следовательно, [латекс]\текст{}f\left(x\right)+k\text{}[/latex] эквивалентен [latex]\text{}y+k\text{}[/latex]. Каждая единица [латекс]\текст{}у\текст{}[/латекс] заменяется на [латекс]\текст{}у+к,\текст{}[/латекс], поэтому [латекс]\текст{} Значение y\text{-}[/latex] увеличивается или уменьшается в зависимости от значения [latex]\text{}k\text{}[/latex]. Дана функция [латекс]f\влево(х\вправо)[/латекс], новая функция [латекс]г\влево(х\вправо)=f\влево(х\вправо)+ k[/latex], где [latex]\text{}k[/latex] — константа, — вертикальный сдвиг функции [latex]f\left(x\right)[/latex]. Все выходные значения изменяются на [latex]k[/latex] единиц. Если [latex]k[/latex] положителен, график сдвинется вверх. Если [latex]k[/latex] отрицательно, график сдвинется вниз. Для регулирования температуры в зеленом здании вентиляционные отверстия возле крыши открываются и закрываются в течение дня. На рис. 3-3 показана площадь открытых вентиляционных отверстий [latex]\text{}V\text{}[/latex] (в квадратных футах) в течение дня в часы после полуночи, [latex]\text{}t\text{ }[/латекс]. Летом управляющий хозяйством решает попытаться лучше регулировать температуру, увеличив количество открытых вентиляционных отверстий на 20 квадратных футов в течение дня и ночи. Решение Учитывая табличную функцию, создайте новую строку для представления вертикального смещения. Функция [latex]\text{}f\left(x\right)\text{}[/latex] указана в таблице 1. Создайте таблицу для функции [latex]\text{}g\left(x \right)=f\left(x\right)-3[/латекс]. Как и в предыдущем вертикальном сдвиге, обратите внимание, что входные значения остаются прежними, а изменяются только выходные значения. Раствор Мы только что видели, что вертикальный сдвиг — это изменение выхода или вне функции. Теперь мы посмотрим, как изменения ввода внутри функции изменяют ее график и значение. Сдвиг на входе приводит к перемещению графика функции влево или вправо в так называемом горизонтальном сдвиге , показанном на рисунке 3-4.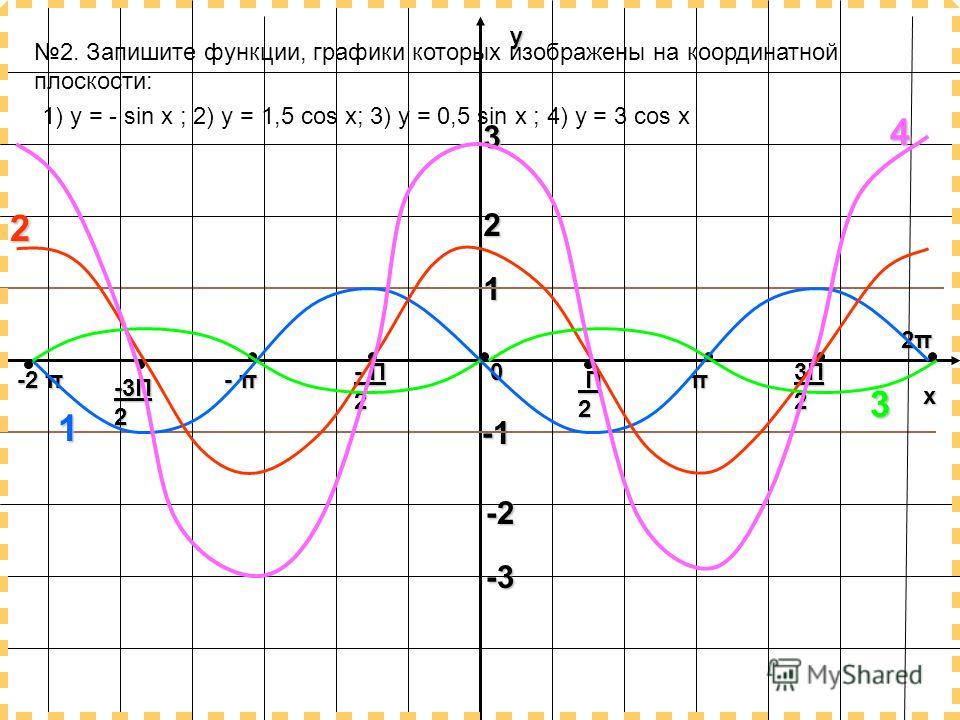 Fusce dui lectus, congue vel laoreet ac, dictum vita
Fusce dui lectus, congue vel laoreet ac, dictum vita Определение вертикального смещения
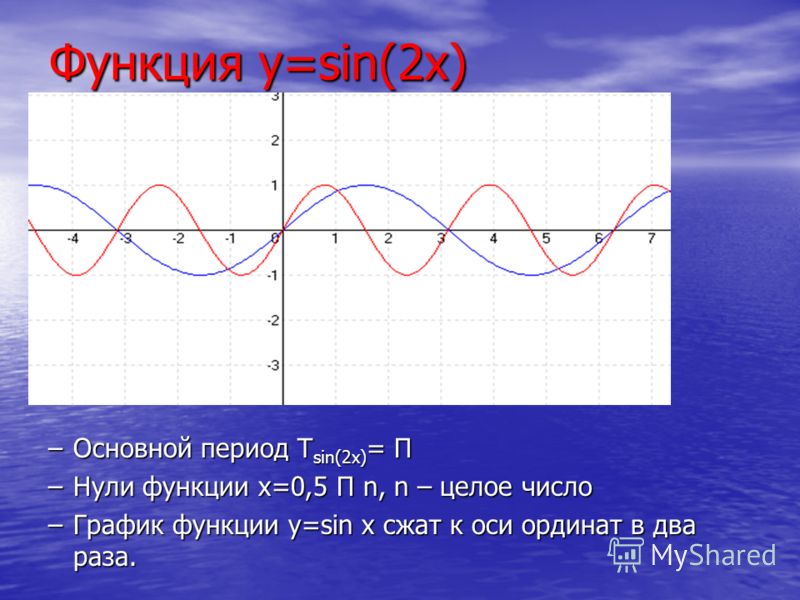 Самый простой сдвиг — это сдвиг по вертикали на , перемещающий график вверх или вниз, потому что это преобразование включает добавление к функции положительной или отрицательной константы. Другими словами, мы добавляем одну и ту же константу к выходному значению функции независимо от входных данных. Для функции [латекс]\текст{}g\left(x\right)=f\left(x\right)+k,\text{}[/latex] функция [латекс]\текст{}f\left (x\right)\text{}[/latex] смещается по вертикали на [latex]\text{}k\text{}[/latex] единиц. См. пример на Рисунке 3-2.
Самый простой сдвиг — это сдвиг по вертикали на , перемещающий график вверх или вниз, потому что это преобразование включает добавление к функции положительной или отрицательной константы. Другими словами, мы добавляем одну и ту же константу к выходному значению функции независимо от входных данных. Для функции [латекс]\текст{}g\left(x\right)=f\left(x\right)+k,\text{}[/latex] функция [латекс]\текст{}f\left (x\right)\text{}[/latex] смещается по вертикали на [latex]\text{}k\text{}[/latex] единиц. См. пример на Рисунке 3-2. Результатом является сдвиг вверх или вниз.
Результатом является сдвиг вверх или вниз.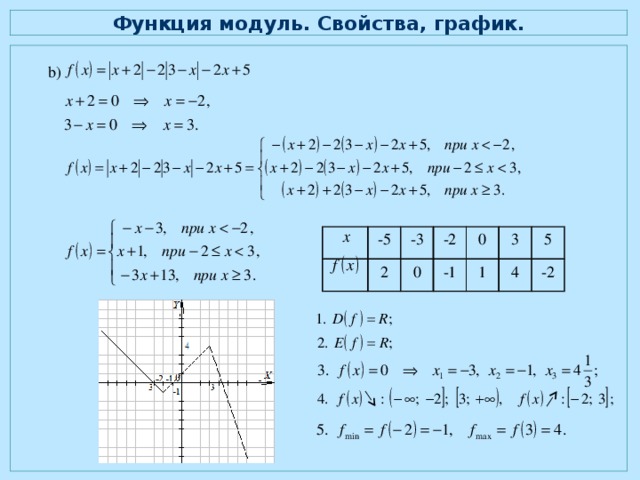 Нарисуйте график этой новой функции.
Нарисуйте график этой новой функции. [латекс]x[/латекс] 2 4 6 8 [латекс]f\влево(х\вправо)[/латекс] 1 3 7 11 Анализ
 9{2}+30t\text{}[/latex] дает высоту [latex]\text{}h\text{}[/latex] мяча (в метрах), брошенного вверх с земли после [latex]\text {}t\text{}[/latex] секунд. Предположим, что вместо этого мяч был брошен с крыши 10-метрового здания. Свяжите эту новую функцию высоты [латекс]\текст{}b\left(t\right)\text{}[/latex] с [латекс]\text{}h\left(t\right)\text{}[/ латекс], а затем найдите формулу для [латекс]\текст{}b\left(t\right)[/латекс].
9{2}+30t\text{}[/latex] дает высоту [latex]\text{}h\text{}[/latex] мяча (в метрах), брошенного вверх с земли после [latex]\text {}t\text{}[/latex] секунд. Предположим, что вместо этого мяч был брошен с крыши 10-метрового здания. Свяжите эту новую функцию высоты [латекс]\текст{}b\left(t\right)\text{}[/latex] с [латекс]\text{}h\left(t\right)\text{}[/ латекс], а затем найдите формулу для [латекс]\текст{}b\left(t\right)[/латекс]. Определение горизонтальных сдвигов
 9{2}\text{}[/latex] – это новая функция. Каждый вход уменьшается на 2 перед возведением функции в квадрат. В результате график смещается на 2 единицы вправо, потому что нам нужно было бы увеличить предыдущий ввод на 2 единицы, чтобы получить такое же выходное значение, как указано в [latex]\text{}f[/latex].
9{2}\text{}[/latex] – это новая функция. Каждый вход уменьшается на 2 перед возведением функции в квадрат. В результате график смещается на 2 единицы вправо, потому что нам нужно было бы увеличить предыдущий ввод на 2 единицы, чтобы получить такое же выходное значение, как указано в [latex]\text{}f[/latex].
Учитывая функцию [латекс]\текст{}f\текст{}[/латекс], новую функцию [латекс]\текст{}г\влево(х\вправо)=f\влево( x-h\right)\text{}[/latex], где [latex]\text{}h\text{}[/latex] — константа, — сдвиг по горизонтали функции [latex]\text{}f\ текст{}[/латекс]. Если [latex]\text{}h\text{}[/latex] положительный, график сдвинется вправо. Если значение [latex]\text{}h\text{}[/latex] отрицательное, график сдвинется влево.
Возвращаясь к нашему примеру потока воздуха в здании из Примера 1 (Рисунок 3-5 ниже), предположим, что осенью руководитель предприятия решает, что первоначальный план вентиляции начинается слишком поздно, и хочет начать всю программу вентиляции на 2 часа раньше.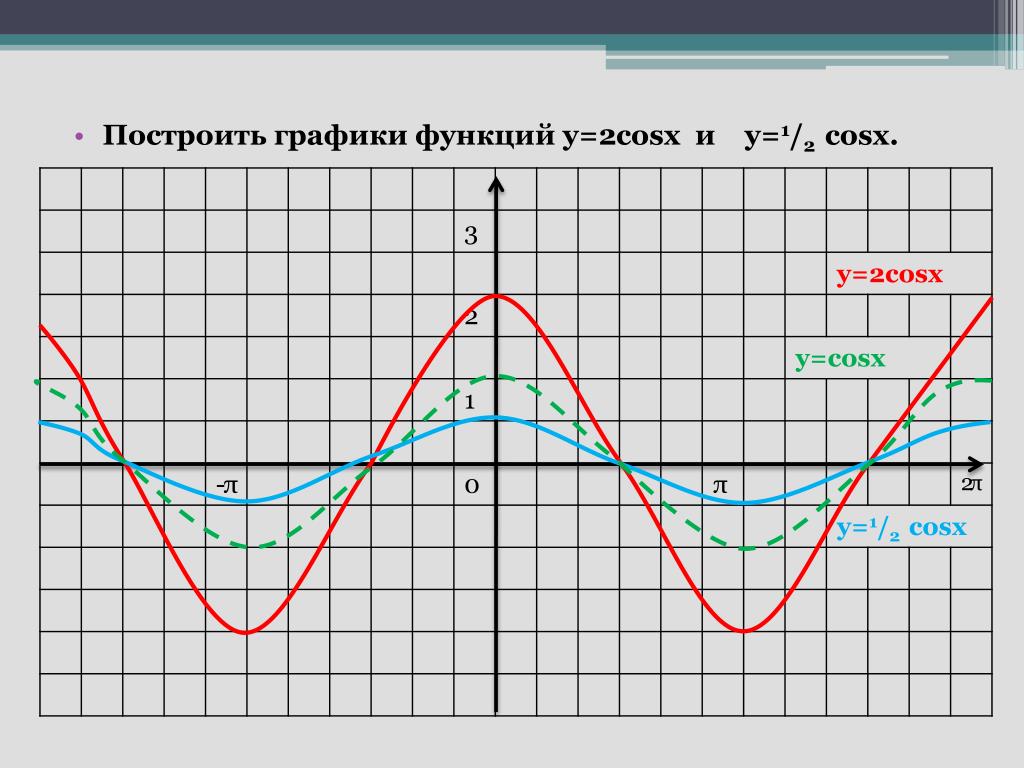 Нарисуйте график новой функции.
Нарисуйте график новой функции.
Анализ
Обратите внимание, что [latex]\text{}V\left(t+2\right)\text{}[/latex] сдвигает график на влево .
Горизонтальные изменения или «внутренние изменения» влияют на домен функции (вход), а не на диапазон, и часто кажутся нелогичными. Новая функция [latex]\text{}F\left(t\right)\text{}[/latex] использует те же выходные данные, что и [latex]\text{}V\left(t\right)\text{} [/latex], но сопоставляет эти выходные данные с входными на 2 часа раньше, чем [latex]\text{}V\left(t\right)\text{}[/latex]. Другими словами, мы должны добавить 2 часа к входным данным [latex]\text{}V\text{}[/latex], чтобы найти соответствующий вывод для [latex]F:F\left(t\right)=V \влево(т+2\вправо)[/латекс].
Решение
Учитывая табличную функцию, создайте новую строку для представления горизонтального смещения.
- Определите входную строку или столбец.
- Определите величину сдвига.
- Добавьте сдвиг к значению в каждой входной ячейке.

Функция [latex]\text{}f\left(x\right)\text{}[/latex] указана в таблице 2. Создайте таблицу для функции [latex]\text{}g\left(x \right)=f\left(x-3\right)[/латекс].
| [латекс]x[/латекс] | 2 | 4 | 6 | 8 |
| [латекс]f\влево(х\вправо)[/латекс] | 1 | 3 | 7 | 11 |
Анализ
На рис.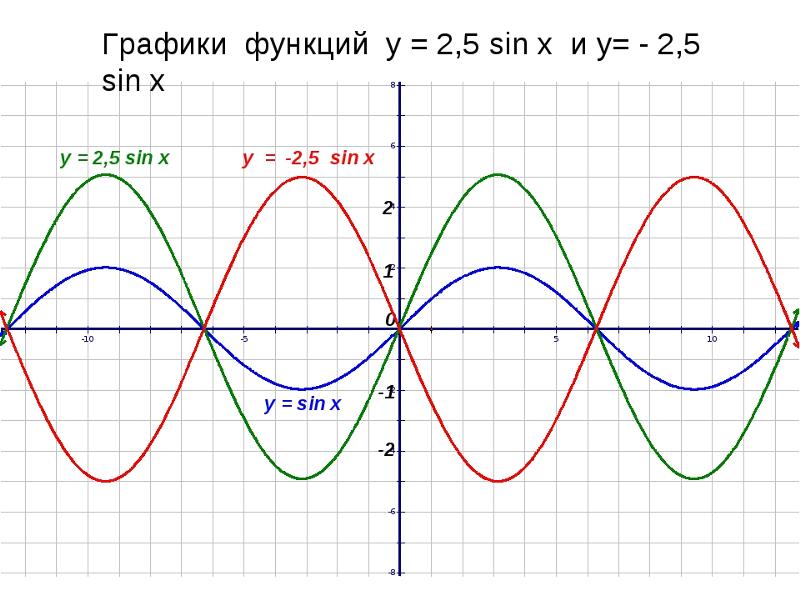 {2}\text{}[/latex]. Свяжите эту новую функцию [латекс]\текст{}г\влево(х\вправо)\текст{}[/латекс] с [латекс]\текст{}f\влево(х\вправо)\текст{}[/латекс ], а затем найдите формулу для [латекс]\текст{}г\влево(х\вправо)[/латекс].
{2}\text{}[/latex]. Свяжите эту новую функцию [латекс]\текст{}г\влево(х\вправо)\текст{}[/латекс] с [латекс]\текст{}f\влево(х\вправо)\текст{}[/латекс ], а затем найдите формулу для [латекс]\текст{}г\влево(х\вправо)[/латекс].
Чтобы определить, является ли сдвиг [латекс]\текст{}+2\текст{}[/латекс] или [латекс]\текст{}-2[/латекс], рассмотрим одиночный точка отсчета на графике. Для квадратичного удобно смотреть на точку вершины. В исходной функции [латекс]\текст{}f\влево(0\вправо)=0\текст{}[/латекс]. В нашей сдвинутой функции [латекс]\текст{}г\влево(2\вправо)=0\текст{}[/латекс]. Чтобы получить выходное значение 0 из функции [latex]\text{}f\text{}[/latex], нам нужно решить, какой знак плюс или минус будет работать для удовлетворения [latex]\text{}g \left(2\right)=f\left(x-2\right)=f\left(0\right)=0\text{}[/latex]. Для этого нам понадобится вычесть 2 единицы из наших входных значений.
Раствор
- Функция [латекс]\текст{}Г\влево(м\вправо)\текст{}[/латекс] дает количество галлонов газа, необходимое для привода [латекс]\текст{}м\текст{}[ /латекс] миль.
 Интерпретировать [латекс]\текст{}G\влево(м\вправо)+10\текст{}[/латекс] и [латекс]\текст{}G\влево(м+10\вправо)[/латекс].
Интерпретировать [латекс]\текст{}G\влево(м\вправо)+10\текст{}[/латекс] и [латекс]\текст{}G\влево(м+10\вправо)[/латекс]. - Учитывая функцию [латекс]\текст{}f\left(x\right)=\sqrt{x}\text{}[/latex], постройте график исходной функции [латекс]\текст{}f\left(x \right)\text{}[/latex] и преобразование [latex]\text{}g\left(x\right)=f\left(x+2\right)\text{}[/latex] на одинаковые оси. Это сдвиг по горизонтали или по вертикали? В какую сторону сместился график и на сколько единиц?
Раствор
Комбинация вертикального и горизонтального смещения
Теперь, когда у нас есть два преобразования, мы можем объединить их вместе. Вертикальные сдвиги — это внешние изменения, которые влияют на выходные значения оси [latex](y\text{-})[/latex] и сдвигают функцию вверх или вниз. Горизонтальные сдвиги — это внутренние изменения, которые влияют на входные значения оси [latex](x\text{-})[/latex] и сдвигают функцию влево или вправо. Сочетание двух типов сдвигов приведет к смещению графика функции вверх или вниз 9. 0563 и вправо или влево.
0563 и вправо или влево.
Учитывая функцию и вертикальное и горизонтальное смещение, нарисуйте график.
- Определите вертикальное и горизонтальное смещение по формуле.
- Сдвиг по вертикали является результатом добавления константы к выходным данным. Переместите график вверх для положительной константы и вниз для отрицательной константы.
- Горизонтальное смещение является результатом добавления константы к входным данным. Переместите график влево для положительной константы и вправо для отрицательной константы.
- Примените сдвиги к графику в любом порядке.
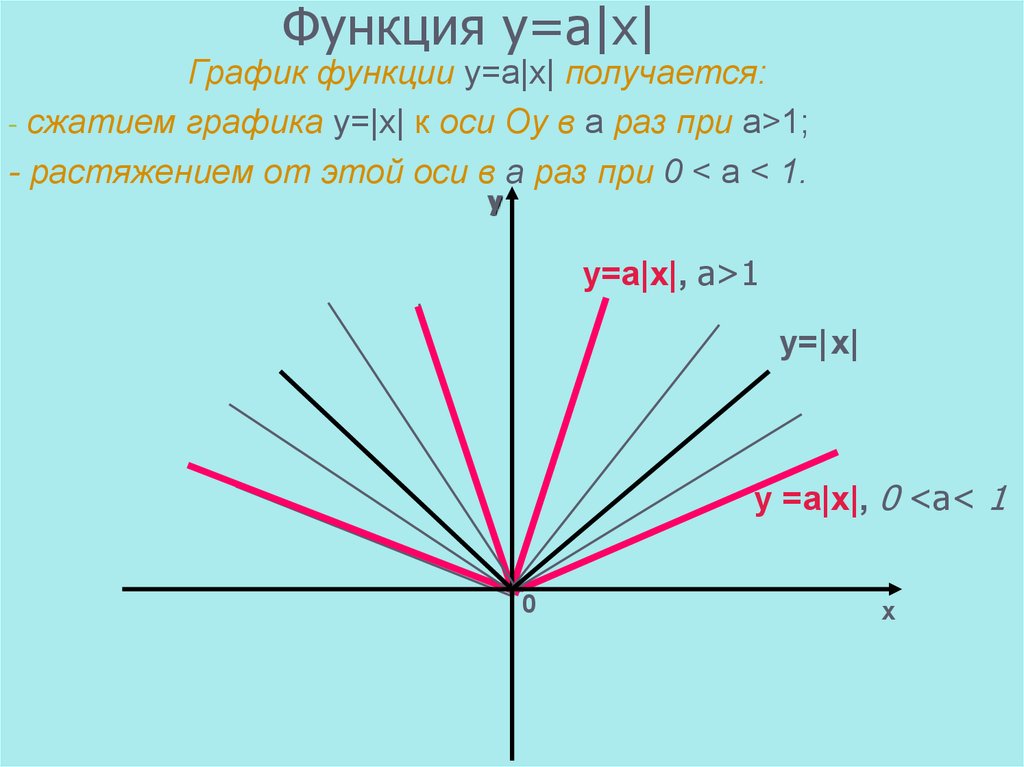
- Учитывая [латекс]\текст{}f\left(x\right)=|x|\text{}[/latex], нарисуйте график [латекс]\text{}h\left(x\right) =f\влево(x+1\вправо)-3[/латекс].
- Учитывая [латекс]\текст{}f\left(x\right)=|x|\text{}[/latex], нарисуйте график [латекс]\text{}h\left(x\right)= f\влево(x-2\вправо)+4[/латекс].
Раствор
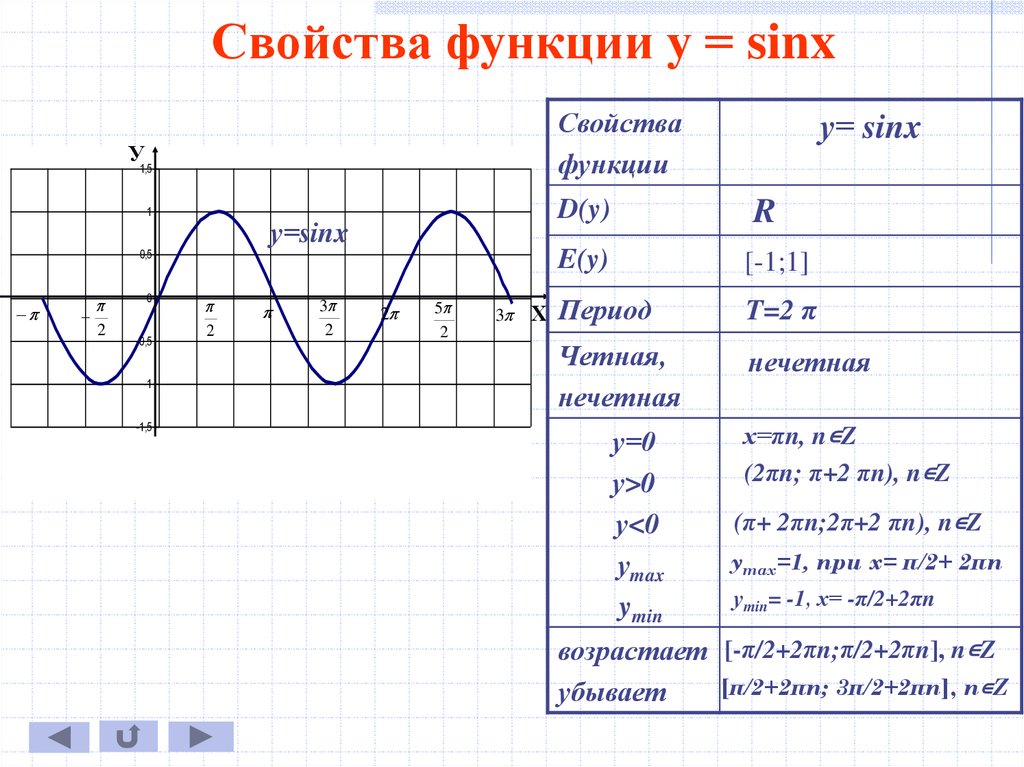
- Напишите формулу для графика, показанного на рис.


 Рассмотрим некоторые из них:
Рассмотрим некоторые из них: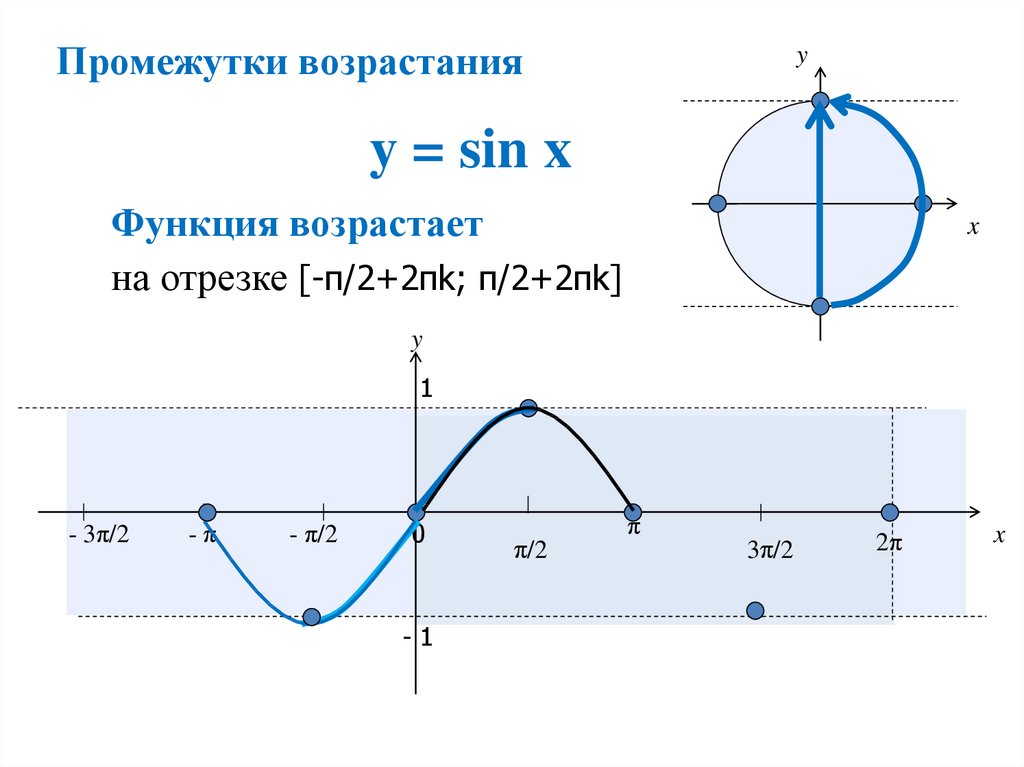
 log(10)) # 2.302585092994046
print(math.log(10, 2)) # 3.3219280948873626
log(10)) # 2.302585092994046
print(math.log(10, 2)) # 3.3219280948873626
 Для двумерной системы координат функция возвращает длину гипотенузы прямоугольного треугольника по теореме Пифагора:
Для двумерной системы координат функция возвращает длину гипотенузы прямоугольного треугольника по теореме Пифагора: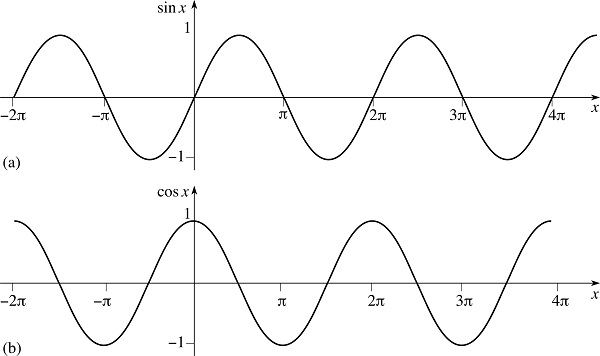 Другими словами, Гамма-функция интерполирует значения факториала для вещественных чисел:
Другими словами, Гамма-функция интерполирует значения факториала для вещественных чисел: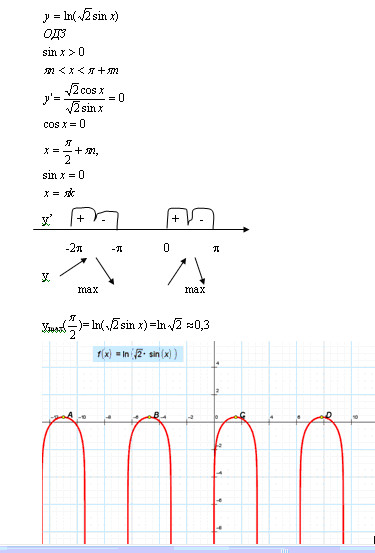 ndim = 2, a.shape = (4, 2), a.size = 8, a.dtype = int32
ndim = 2, a.shape = (4, 2), a.size = 8, a.dtype = int32 zeros((4, 3), dtype="uint8")
print(a)
print()
a = a.reshape((2, 3, -1))
print(a)
zeros((4, 3), dtype="uint8")
print(a)
print()
a = a.reshape((2, 3, -1))
print(a)
 array([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])
print(a.sum(axis=0)) # сумма чисел в каждом столбце
print(a.sum(axis=1)) # сумма чисел в каждой строке
print(a.min(axis=0)) # минимум по столбцам
print(a.max(axis=1)) # максимум по строкам
array([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])
print(a.sum(axis=0)) # сумма чисел в каждом столбце
print(a.sum(axis=1)) # сумма чисел в каждой строке
print(a.min(axis=0)) # минимум по столбцам
print(a.max(axis=1)) # максимум по строкам
 reshape(3, 4)
print(a)
for row in a:
print(row)
reshape(3, 4)
print(a)
for row in a:
print(row)
 439312.
1.7823209762573242 с.
Результат numpy: 21081849486.442448.
0.05197310447692871 с.
439312.
1.7823209762573242 с.
Результат numpy: 21081849486.442448.
0.05197310447692871 с.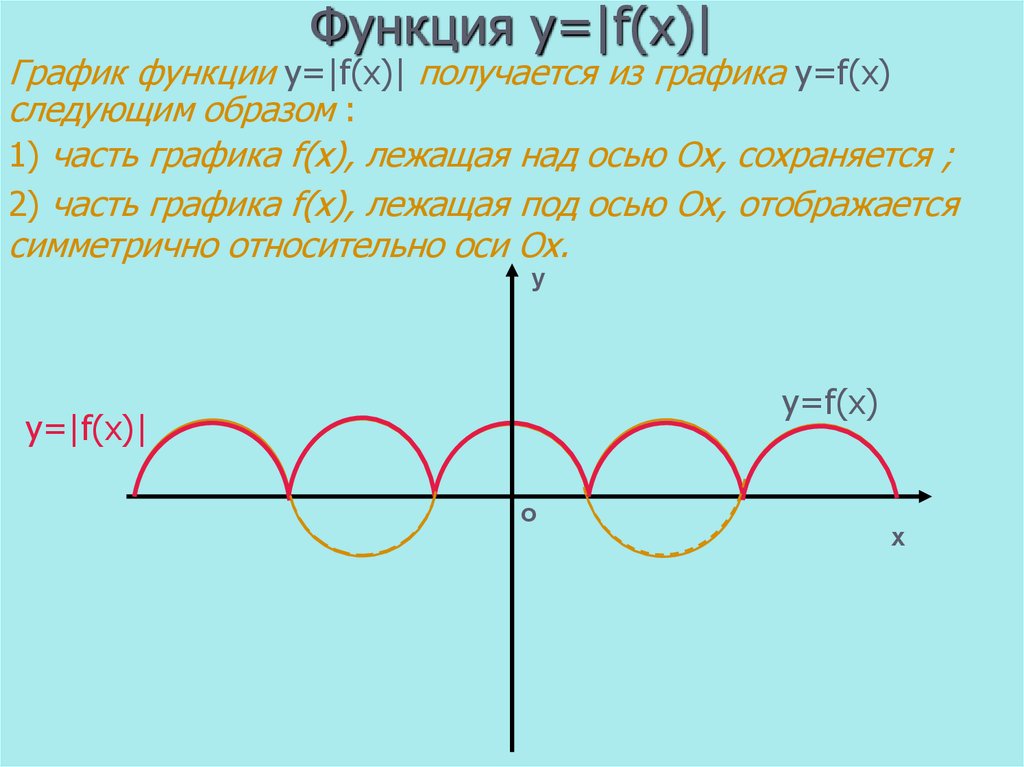
 Интерпретировать [латекс]\текст{}G\влево(м\вправо)+10\текст{}[/латекс] и [латекс]\текст{}G\влево(м+10\вправо)[/латекс].
Интерпретировать [латекс]\текст{}G\влево(м\вправо)+10\текст{}[/латекс] и [латекс]\текст{}G\влево(м+10\вправо)[/латекс].