График функции — математика и искусство
- Математический анализ
- Исторические заметки
- Пособия и таблицы
- График функции
Другие разделы > Математический анализ
График функции — один из способов ее представления. Представить ту или иную функцию можно по-разному, например словесным описанием. Из физики известно, что при равномерном движении пройденный путь прямо пропорционален времени, прошедшему с момента начала пути. Эта фраза описывает путь как линейную функцию времени.
В руках у электрика можно увидеть таблицу, где для проводов различных диаметров указаны предельно допустимые значения силы тока, на парте школьника-таблицы логарифмов и тригонометрических функций… Все это примеры табличного представления функций.
У каждого способа представления функции есть свои достоинства. Словесный наиболее прост и доходчив, если, конечно, функцию удается описать простыми фразами. Формулы часто используют потому, что с ними удобно проводить вычисления, их можно преобразовывать и анализировать, выясняя свойства функции.
Графический способ представления функции — самый наглядный. График функции — это линия, дающая цельное представление о характере изменения функции по мере изменения ее аргумента. Кардиограмму можно назвать графиком работы сердца.
Чтобы построить эскиз графика функции предварительно проводят ее исследование. Оно ведется поэтапно следующим путем.
Область определения
Область значений (легче находится после исследования монотонности), ограниченность сверху/снизу.
Нули (корни) функции — точки, где она обращается в ноль.
- Промежутки постоянства знаков, знаки в них.
Чётность/нечётность, периодичность.
Непрерывность
Если есть — точки разрыва, их типы; вертикальные асимптоты.
Первая производная, её нули (критические точки) или точки излома, если есть.
Экстремумы: максимумы и минимумы.
Промежутки монотонности
Вторая производная, её нули.
Точки перегиба, промежутки выпуклости.
Поведение на бесконечности, горизонтальные или наклонные асимптоты.
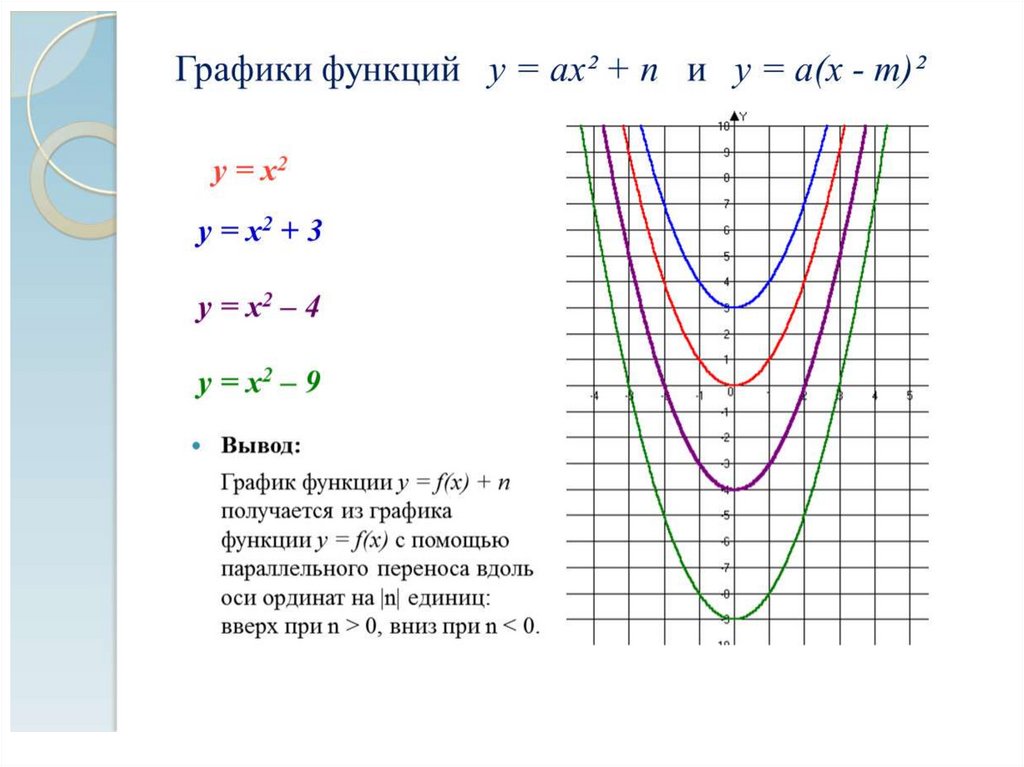
Преобразования графика функции
y = f(x — b), параллельный перенос графика вдоль оси абсцисс на | b | единиц вправо, если b > 0; влево, если b < 0.
y = f(x + b) влево, если b > 0; вправо, если b < 0.
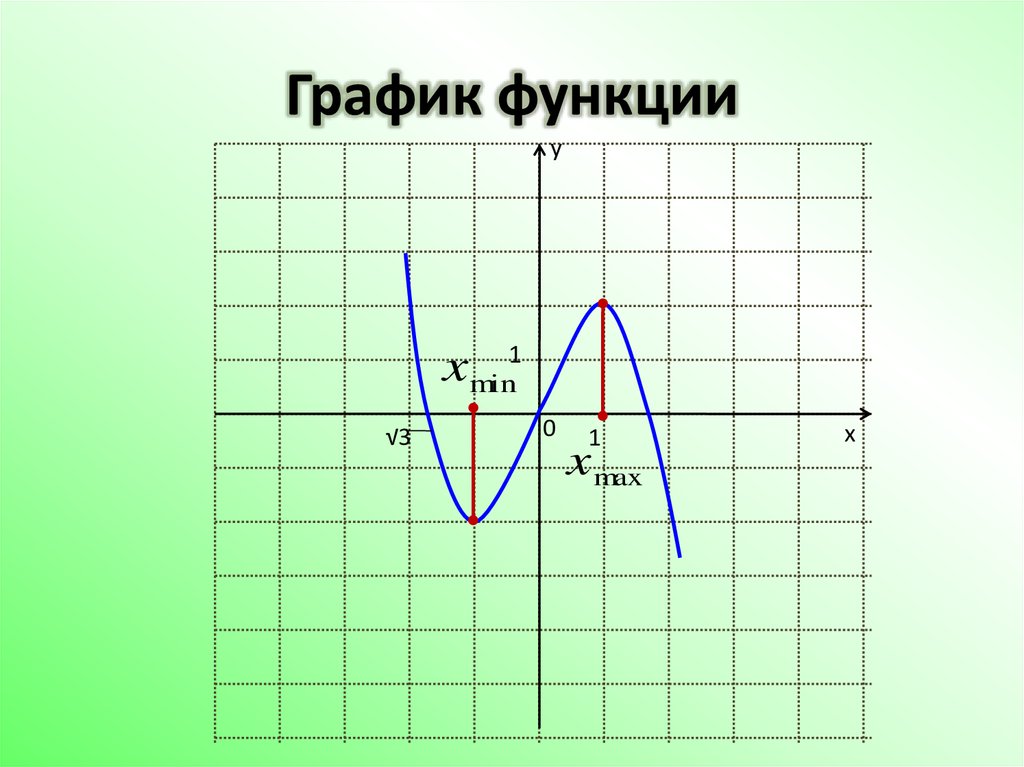
Отражение графика
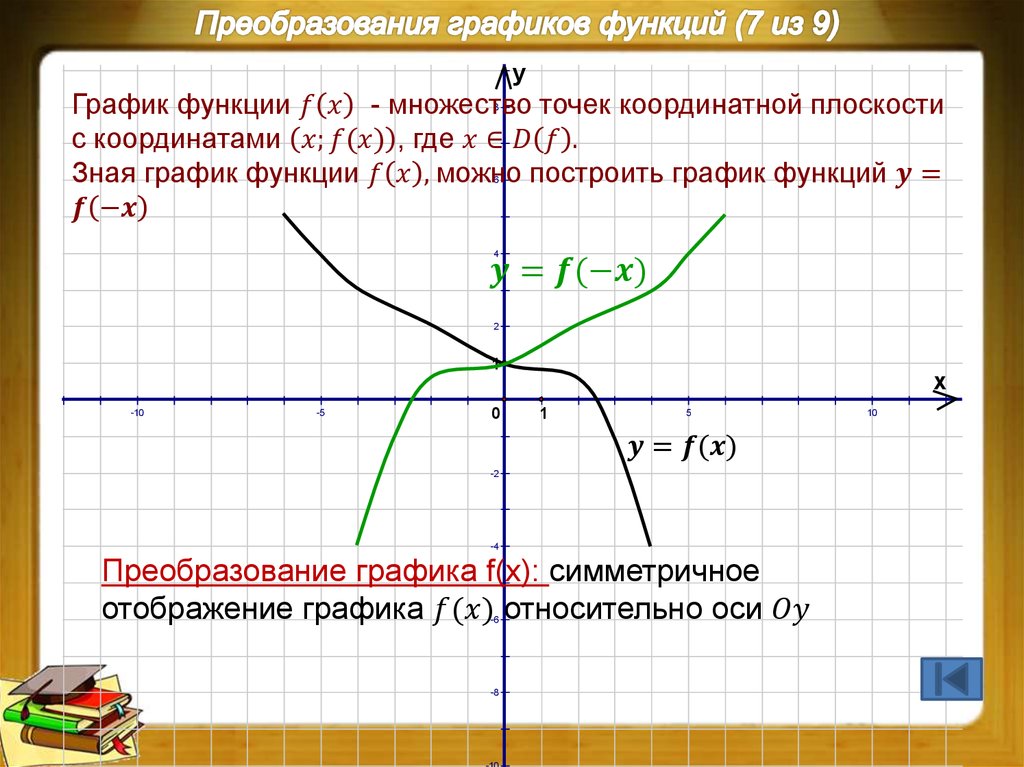
y = f( — x) симметричное отражение графика относительно оси ординат.
y = — f(x) симметричное отражение графика относительно оси абсцисс.
Сжатие и растяжение графика
y = f(kx)
y = kf(x)
Преобразования графика с модулем
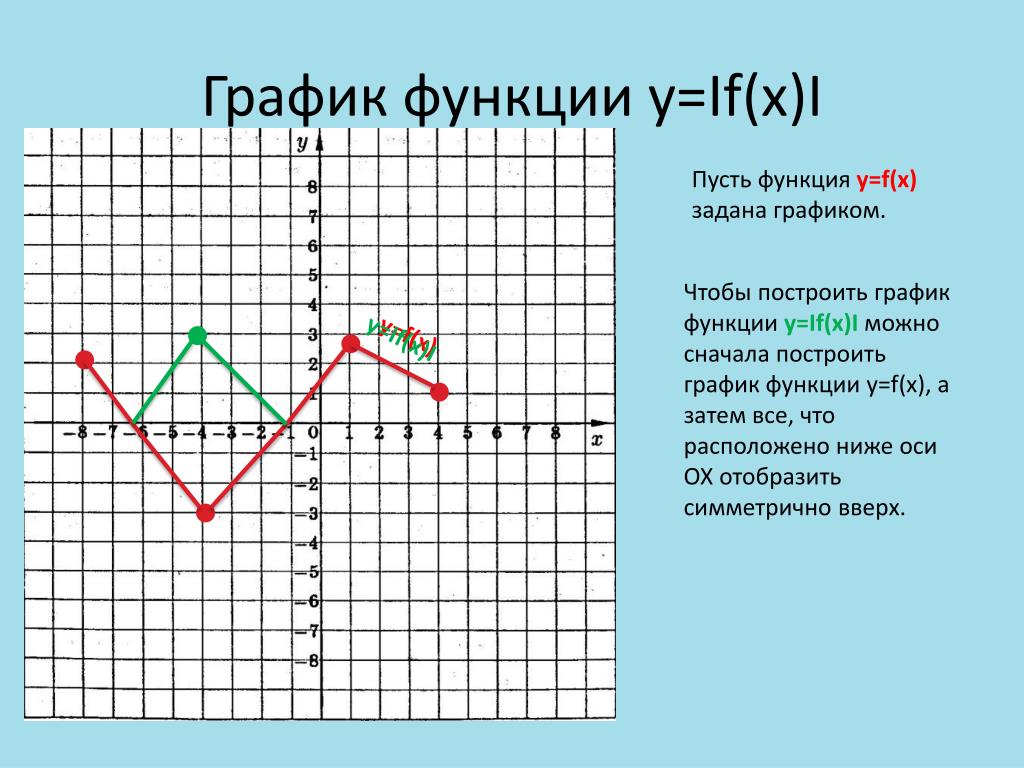
y = |f(x)|
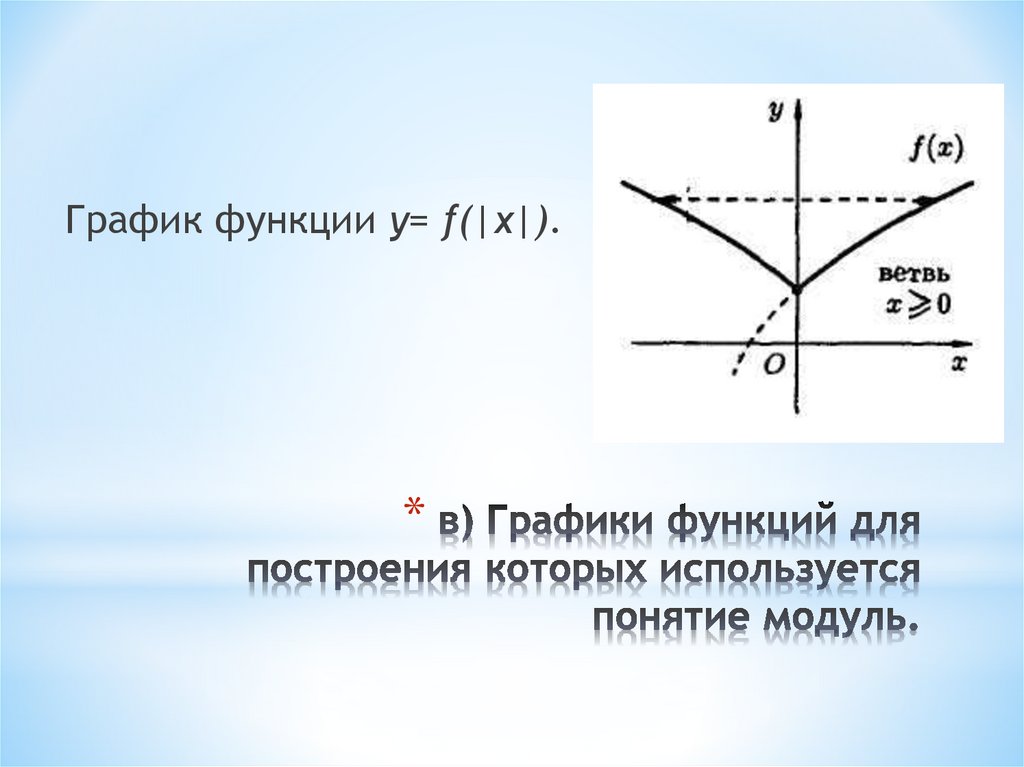
y = f(| x |)
Главная | Алгебра | Геометрия | Математика | Другие разделы | Искусство | Галерея | Биографии | Цитаты | К уроку рисования | Разное | Главная Карта Сайта
График функции — Энциклопедия по экономике
График функции Th = f(x) в рассматриваемых пределах изменения величины х представлен на рис. 21. [c.133] Так, если мы хотим проанализировать чувствительность (иу.э.с)опт к изменению стойкости элементов ленточного тормоза в условиях нашего примера, необходимо на основании выражений (ПО), (111), (121) и (123) построить графики функций [c.149]Рис. 4 дает возможность графически представить некоторые особенности производственной функции с двумя ресурсами производства.
На двумерном рисунке нельзя изобразить сам график функции У = F (K, L), так что приходится ограничиваться лишь анализом изоквант. Построение графика производственной функции было бы, однако, весьма желательным, поэтому прибегают к следующему приему, основанному на свойстве (2.5) производственной функции. Поскольку мы рассматриваем значения L > 0, то на основе (2.5) можно сделать преобразование соотношения У = = F (К, L), представив его в виде У = LF (K/L, 1) или Y/L = F (K/L, 1). Введем следующие обозначения у = = Y/L, k = K/L, f (k) = F (k, 1). Здесь у имеет смысл национального дохода на одного трудящегося, k — количество основных фондов на одного трудящегося (фондовооруженность), функция / (k) связывает эти два показателя и является одной из форм представления производственной функции. Зная функцию F (К, L), можно построить f (k),
[c.58] На рис. 3.3 изображены графики функций фактора фонда накопления для обычного и авансового аннуитетов.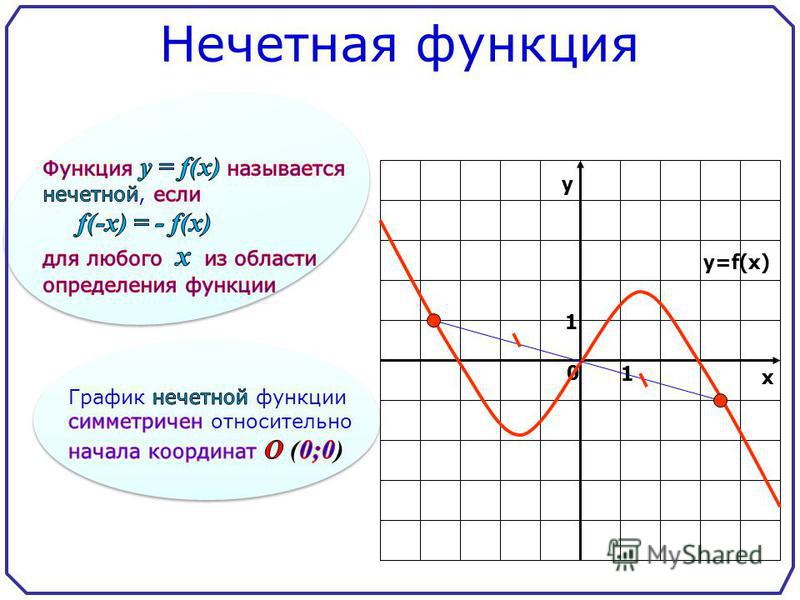
[c.315]
Графики функций А(у), АГ( ), h»(y), g(y) и h (y)/g(y) для функции затрат (2.7) при а = 0,5 приведены на рис. 2.12. [c.97]
График функции у(Г) для т г = 4 приведен на рис. 2.15. Изломы на графике соответствуют переходам к новым, до этого не использовавшимся, менее эффективным производственным способам. [c.103]
Проведем сначала графический анализ задачи. Построим графики функций у = stf(k) и y = ( i + t])k (см. рис. 4.1). Из рисунка следует, что имеются два решения (3.13). Это / = 0 и k = k. Точка f = 0 является решением уравнения (3.13) при любых значениях параметров л и т) и параметров производственной функции в силу того, что ф(0)=0. Ненулевая точка пересечения графиков у = s p(k) и у = (ц + т))А , вообще говоря, может существовать не всегда или быть не единственной. При сформулированных в предыдущем параграфе свойствах производственных функций и некоторых других естественных предположениях о народном хозяйстве точка k существует и единственна (доказательство см.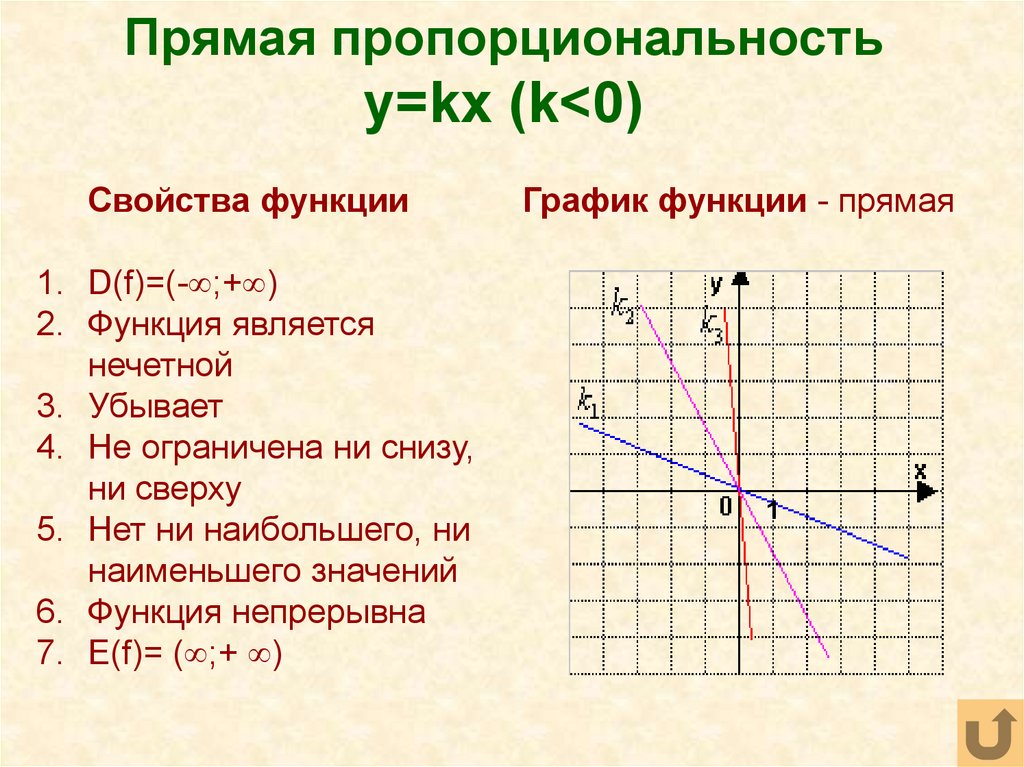
, например, в гл. 2 книги [34]).
[c.245]
В связи с этим график функции имеет начальную ординату 77,08 дол. Начальная ордината — это постоянный элемент формулы, который обеспечивает наилучшую линейную аппроксимацию поведения затрат внутри релевантной области. [c.234]
Для построения кривой спроса отложим на оси абсцисс точки, характеризующие количество товара, на которое предъявлен спрос, а на оси ординат — соответствующую им цену. Данная кривая есть график функции спроса от цены. [c.15]
Кофе, полученный смешиванием разных сортов, нельзя сравнить с аналогичными продуктами в других киосках. Наш кофе самый лучший, мы предлагаем вам не просто кофе, а допинг для переговоров на выставке . График функции спроса для кофе, продаваемого на выставке, мог бы иметь вид S-образной кривой, как на рис. 10. На ней есть ограниченная область крутого, не эластичного по отношению к цене спроса. В этой области возможно проведение индивидуальной политики цен. [c.61]
Рис. 10.3. Графики функций долевого участия собственных средств в их совокупно) стоимостной оценке с учетом принятых допущений |
| Рис. 10.4. Графики функций долевого участия собственных средств в их совокупней стоимостной оценке без учета принятых допущений |
| Рис. 10.13. График функции долевого участия собственных средств предприятия в их совокупной стоимостной оценке |
Сбор > i и ставка процента По мнению Дж. М. Кейнса, реальная процентная ставка не является основным детерминантом уровня сбережения и потребления населения. Вместо этого он утверждал, что уровень сбережения и потребления главным образом зависит от реального дохода.
[c.494]На рис. 19-3 приведен пример линейной функции сбережения. Угловой коэффициент функции сбережения (1 — Ь) является MPS, или 1 — МРС. Отметим, что b + + (1 — К) = 1, так что графики функций потребления и сбережения предполагают равенство МРС + MPS = 1. [c.501]
График совокупных расходов в закрытой экономике представляет собой сумму графиков ожидаемого потребления, инвестиций и государственных расходов. Отрезок, отсекаемый графиком на вертикальной оси, равен величине чистых совокупных автономных расходов потребителей, фирм и государства. Когда инвестиции, государственные расходы и чистые налоги являются автономными, угловой коэффициент графика совокупных расходов равен угловому коэффициенту графика функции потребления, или предельной склонности к потреблению, которая является дробным числом. [c.518]
Функцию потребления в кейнсианской модели экономики можно представить в виде с = с0 + ЬУ . Дайте определение и краткое объяснение каждого из двух компонентов ожидаемого потребления, заданных уравнением.
Постройте график функции потребления. Чему равен его угловой коэффициент Какое экономическое толкование можно дать этому коэффициенту [c.521]
При этом Р(х [c.118]
Показанный в предыдущем параграфе график функции предельной полезности (рис. 1.1, б) представляет собой линию с отрицательным наклоном, построенную в координатах MU, Q. Подобным же образом изображается обычно и линия индивидуального спроса, основное назначение которой состоит в том, чтобы выражать зависимость объема спроса конкретного индивидуума на определенное благо (QD) от уровня его цены (Р). [c.18]
| Рис. 6.2. Графики функций принадлежности. |
Последний факт может быть использован для определения того количества периодов, на которое мы в рамках мультипликативной модели можем получить относительно осмысленную оценку границ отклонений фактических значений от прогнозных.
[c.158]График функции приведен на рис. 5,6. [c.73]
Если для каждого свойства каждого вида продукции строить свой график функции, то сложность и большой объем работы сделают крайне затруднительным практическое применение метода. Следовательно, не должно быть чрезмерно большого множества кривых. [c.78]
Рассмотрим график функции Д у (Pj) (рис. 12). [c.117]
| Рисунок 9 — График функций желательности и ее приращения |
Любое решение в геологоразведочной отрасли связано с некоторым уровнем риска, определяющим величину показателя надежности. Эту величину можно планировать заранее, т. е. задавать допустимый уровень надежности или стратегию риска. Планирование
[c.215]Итак, в обоих потоках орел выпал четыре раза из десяти (аналогично, решка выпала в обоих потоках четыре раза из десяти), что дает вероятность 0,4. Обратите внимание, что если функция линейна, то есть изображается на графике прямой линией, то эта прямая проходит через точку, соответствующую коэффициенту корреляции 0,6 и вероятности 0,4. Если бы график функции отличался от прямой, то коэффициенту корреляции 0,6 соответствовало бы все, что угодно, кроме 0,4 (см. рис. 3.3). [c.146]
Зная, что многие поставщики данных не имеют в своих программах построения графиков функции постоянного масштаба, нами так разработано программное обеспечение, чтобы пользователи могли выбирать или полноэкранное масштабирование самых последних загруженных данных или постоянный масштаб от самого высокого максимума до самого низкого минимума всего ряда данных для инвесторов, испытывающих неудобство из-за необходимости конвертировать данные своих рядов данных.
[c.34]
| Рис. 5. График функции 1(а) в примере 1. |
График совокупных расходов в закрытой экономике без государственного сектора.
В экономике без государственного сектора совокупные ожидаемые реальные расходы равны сумме потребительских расходов домашних хозяйств и ожидаемых реальных инвестиционных расходов фирм. Следовательно, если мы сложим график автономных инвестиций с графиком функции потребления по вертикали, то получим график, отражающий уровни совокупных ожидаемых реальных расходов для любого данного уровня реального дохода. Это и есть график совокупных расюдов (с + / ).
[c.505]
Совок ипь лвтономные расходы и смещение графика совокупных расходов Что является причиной смещения графика совокупных расходов Чтобы ответить на этот вопрос, полезно рассмотреть уравнение, которым задан график совокупных расходов. Предположим, что величина автономных инвестиций равна /0. К тому же нужно помнить, что поскольку упрощенная модель экономики предполагает отсутствие государственного сектора (yd = у), то располагаемый доход равен доходу без налоговых вычетов. Поскольку график совокупных расходов строится путем сложения графиков функции потребления и автономных инвестиций, то уровень совокупных расходов будет равен [c.
510]
Предельная склонность к потреблению (marginal propensity to onsume, MP ) — дополнительное потребление вследствие роста дохода после уплаты налогов прирост потребительских расходов, деленный на соответствующий прирост располагаемого дохода угловой коэффициент графика функции потребления, когда по оси ординат откладываются значения располагаемого дохода. [c.519]
Предельная склонность к сбережению (marginal propensity to save, MPS) — дополнительно сберегаемые средства при увеличении располагаемого дохода отношение прироста сбережений к соответствующему приросту располагаемого дохода. Представляет собой угловой коэффициент графика функции сбережения, когда по оси ординат откладываются значения располагаемого дохода. [c.519]
Майклом Брэдли (Bradley) из университета Джорджа Вашингтона в 1989 г. Если ФРС нужно задать величину номинального национального дохода, то она будет изменять параметры инструментов своей политики, чтобы постоянно поддерживать номинальный доход на заданном уровне У.
Это означает, что она будет проводить политику с учетом обеспечения равенства Р X у = Y. Предположим, что целью ФРС является сохранение номинального национального дохода на заданном уровне Y = 4000 млрд. долл. тогда множество комбинаций уровень цен—национальный доход будет соответствовать этой цели. Примерами могут служить РО = 4, у0 = 1000, /, = 5, у = 800 и Р2 = 8, у2 = 500. Все эти и другие возможные комбинации уровня цен и реального дохода будут представлены на графике функции Рх у = Y (рис. 24-12). Этот график, как и график совокупного спроса в классической модели, описанный в главе 18, является гиперболой.
[c.664]
Теперь рассмотрим рис. 24-13, на котором представлена точка А — точка равновесия графиков совокупного спроса и совокупного предложения, в которой уровень цен РО = 4, а реальный уровень производства у( = 1000. К тому же естественный уровень производства (рис. 24-13) равен у = lOOO, что означает, что равновесный реальный объем производства при естественном уровне производства, описываемый графиком долгосрочного совокупного предложения (у к), достигается и точке А.
К тому же точка равновесия А принадлежит графику функции Р X у = Y (рис. 24-12). Следовательно, равновесный номинальный доход в точке А есть YQ = Рп х у( — 4 X X 1000, что равно номинальному доходу Y, выступающему в качестве промежуточной цели ФРС.
[c.665]
Протабулируем данную функцию на отрезке [-4,0 10,0] (расширять границы не имеет смысла, так как значения / (-4,0) и /(10,0) близки к предельным) с шагом 0,2. Кроме того, найдем приращение функции желательности на каждом шаге. По полученным значениям построим графики функции желательности и ее приращения (рисунок 9). [c.49]
Линейное программирование (планирование) — математический метод отыскания максимума или минимума линейной функции при наличии ограничений в виде линейных неравенств или уравнений. (Линейное здесь означает, что на графике функции изоб- [c.58]
график функции в nLab
Пропустить навигационные ссылки | Домашняя страница | Все страницы | Последние версии | Обсудить эту страницу |
Содержание- Идея
- Определение
- График функции
- График бинарного отношения
- Связь с теорией графов
- График многомерной связи
- Кограф функции
- Связь с теорией графов
- Обобщение
- Родственные понятия
Идея
График функции f:X→Yf : X \to Y есть подмножество, которое ff «вырезает» из декартова произведения X×YX \times Y.
{op} \times Y \stackrel {Home}{\к} \{0,1\}
\,.
Тогда χf\chi_f является характеристической функцией graph(f)graph(f) в том смысле, что диаграмма
graph(f)→*↓↓X×Y→χf{0,1} \множество{ график (f) &\to& {*} \\ \вниз && \вниз \\ X \times Y &\stackrel{\chi_f}{\to}& \{0,1\} }
— обратная диаграмма.
Другими словами, это означает, что в контексте теории категорий, обогащенной (-1)-категориями, график функции ff, рассматриваемой как обогащенный функтор, является категорией элементов соответствующего профунктора. Подробнее об этом на графике функтора.
Граф бинарного отношения
В более общем смысле можно сказать, что граф бинарного отношения от XX до YY является подмножеством X×YX \times Y; (a,b)(a,b) принадлежит графу тогда и только тогда, когда aa связано с bb. (Обратите внимание, что каждое подмножество X × YX \times Y определяет уникальное отношение; такое подмножество является графиком функции тогда и только тогда, когда отношение является одновременно функциональным и полным.
)
Обратите внимание, что с функцией f: X→Yf : X \to Y рассматривается как профунктор X×Y→(−1)CatX \times Y \to (-1)Cat, как описано выше, отношение R⊂X×YR \subset X \times Y соответствует вообще такой профунктор. Точнее имеем квадрат отката
R→*↓↓X×Y→χR{0,1} \множество{ Р &\к& {*} \\ \вниз && \вниз \\ X \times Y &\stackrel{\chi_R}{\to}& \{0,1\} }
где
R⊂X×YR \subset X \times Y — отношение RR, рассматриваемое как подмножество X×YX \times Y в традиционном смысле;
χR:X×Y→{0,1}\chi_R : X \times Y \to \{0,1\} — характеристическая функция этого подмножества.
Итак, в этом смысле обычное понятие отношения как подмножества действительно определяет 92. Аналогично отрезки от XX до XX соответствуют ориентированным псевдографам с множеством вершин XX.
Для случая отношения от XX к YY без X=YX = Y см. под графиком ниже.
Граф n-арного отношения
Граф отношения произвольной арности также является подмножеством произвольного декартова произведения; см.
теорию отношений для получения дополнительной информации об этом.
Кограф функции
Билл Ловер также рассматривал кограф функции, являющейся дуально фактормножеством несвязного объединения X⊎YX \upplus Y; aa отождествляется с bb, если f(a)=bf(a) = b (и могут последовать дополнительные отождествления). Однако может иметь больше смысла определить кограф как фактор-помножество (дискретного чу-множества) X⊎YX \upplus Y; мы объявляем a
Функция f:X→Yf : X \to Y определяет функтор f¯:I→Set\bar f : I \to Set из категории интервалов I=2={a→b}I = \mathbf{2 } = \{a \to b\} Установить, установив f¯(a)=X\bar f(a) = X, f¯(b)=Y\bar f(b) = Y и f¯(a →b)=f\bar f(a\to b) = f.
Тогда пусть cograph(f)cograph(f) будет соответствующей категорией элементов, заданной 2-протяжением
cograph(f)→*↓↓I→f¯Set \множество{ кограф(f) &\to& {*} \\ \вниз && \вниз \\ Я &\stackrel{\bar f}{\to}& Установить }
, который вычисляется путем строгого обратного вызова
cograph(f)→Set*↓↓I→f¯Set.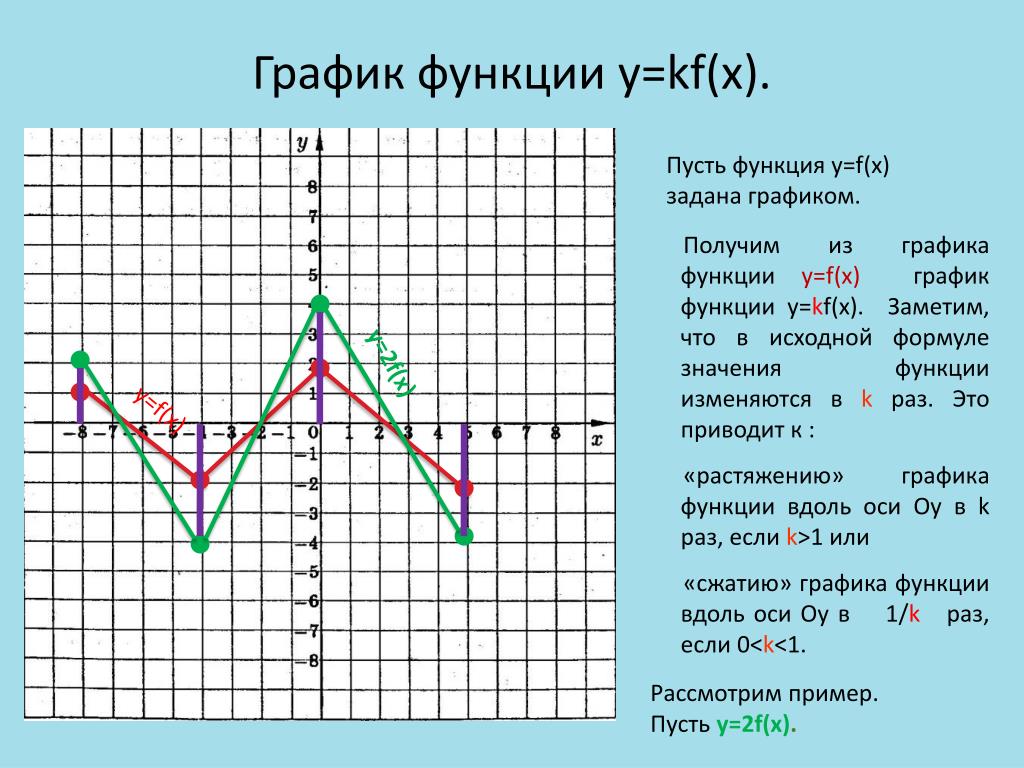
\множество{
кограф(f) &\to& Set_{*}
\\
\вниз && \вниз
\\
Я &\stackrel{\bar f}{\to}& Установить
}
\,.
Кографом ff в смысле Ловера называется множество компонент связности этой категории, т. е. π0(cograph(f))\pi_0(cograph(f)).
Связь с теорией графов
Понятие кографа функции может быть даже больше связано со смыслом графа в теории графов; хотя идентификация там не выполняется, кограф рисует картину, в которой любое отношение (или мультипромежуток) любой арности становится ориентированным графом (или ориентированным мультиграфом), множество вершин которого является несвязным объединением доменов отношения. Когда множество вершин таким образом разбивается на несвязное объединение, теоретики графов изучают это как многодольные графы ; в частности, ориентированные двудольные графы с множеством вершин, разбитым как X+YX+Y, точно соответствуют бинарным отношениям от XX до YY.
Обобщение
Понятие графа функции является частным случаем графа понятия функтора, полученного для функторов между 0-категориями.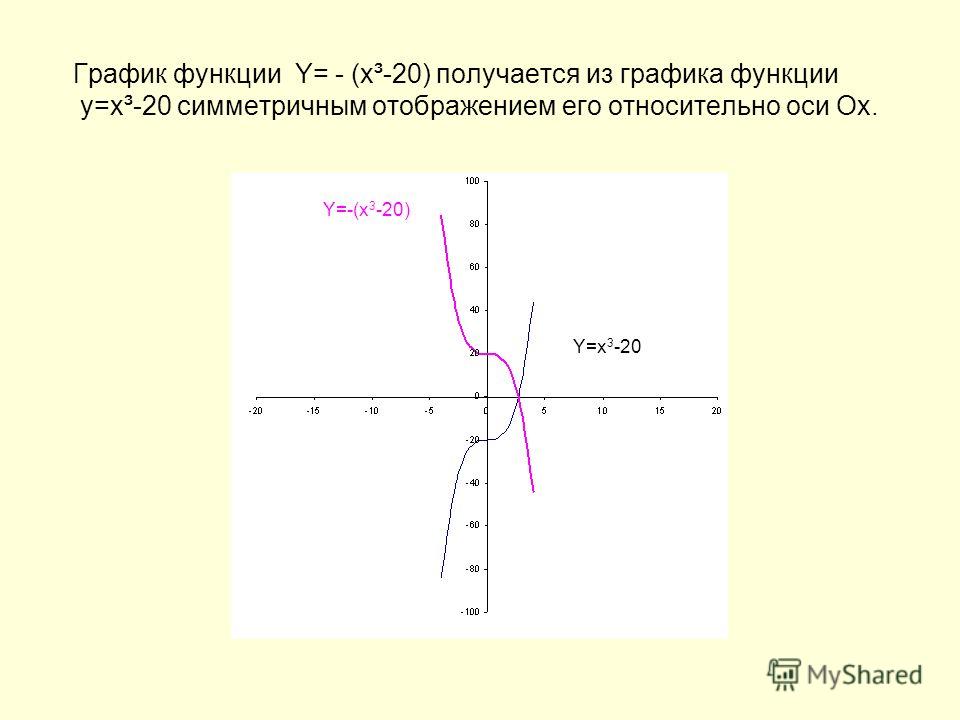
Соответственно, понятие кографа функции является частным случаем понятия кографа функтора.
- морфизм графов 91\;:\; f(x) = y\}$$
С другой стороны, вы можете задать вопрос о практической задаче: предположим, что вам дан график или вы рисуете график, нанося на него несколько точек. . Вы полагаете, что уловили общую суть графика, но как вы можете быть в этом уверены? Это глубокий вопрос, на который есть несколько хороших ответов.
Первая часть ответа заключается в том, что при чтении графиков мы делаем много неявных предположений. Эти предположения касаются функций, которые имеют смысл и которые мы реально ожидаем увидеть в определенных условиях. 92$ для всех значений $x$, за исключением небольшой области, где функция сильно колеблется. Если вы начертите эту функцию даже для большой области, вас могут обмануть, заставив поверить, что это простая квадратичная функция. Противник может внести произвольное количество отклонений, которые вы почти наверняка не заметите.
Но в практике мы часто рисуем что-то вроде результата реального физического процесса или идеализированную математическую модель, состоящую из простых функций. В этих случаях имеем веская причина предположить, что функция соответствует нашим ожиданиям и не является какой-либо неожиданной патологией. Кроме того, с другой точки зрения, мы часто имеем в виду цель, и в пределах допусков нашего приложения может быть достаточно , чтобы сказать, что функция является параболой, даже если это не совсем так. Так, например, если вы знаете, что ваша функция гладкая, и вы нанесли достаточное количество точек на график, вы можете просто соединить эти точки отрезками — ваш график может быть не совсем точным, но ошибка может быть в пределах допустимого для вашего графика. заявление.
Вторая часть ответа заключается в том, что в дополнение к предположениям о функциях, которые мы ожидаем увидеть в нашем текущем приложении, мы часто знаем много о самой построенной функции.
