Фрагмент урока по теме «Графики функций» 9 класс
| 12+ Свидетельство СМИ ЭЛ № ФС 77 — 70917 Лицензия на образовательную деятельность №0001058 | Пользовательское соглашение Контактная и правовая информация |
Педагогическое сообщество | Бесплатные всероссийские конкурсы | Бесплатные сертификаты | Нужна помощь? Инструкции для новых участников | Бесплатная онлайн-школа для 1-4 классов |
Всё для аттестацииПубликация в сборникеВебинарыЛэпбукиПрофтестыЗаказ рецензийНовости
Библиотека▪Публикации▪Статьи
Материал опубликовала
#9 класс #Алгебра #Методические разработки #Учитель-предметник #Первая категория #Школьное образование #Фрагмент урока #УМК любой
Устная работа
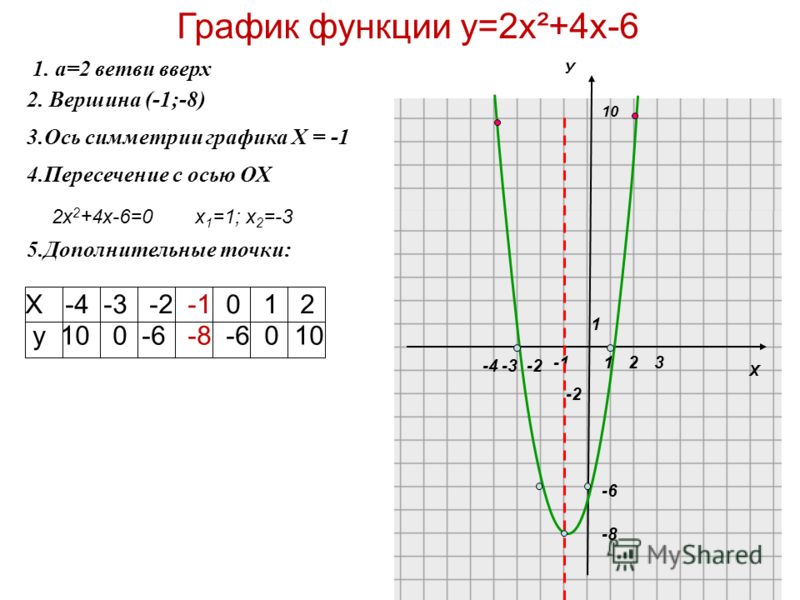
Тема: графики функций.
Для какой параболы нет соответствующего рисунка? 1 1 1 0 0 0 х х х у у у 1. у=х²+1 2. у=(х+1)² 3.у=(1-х)² 4. у=1-х²
2. На рисунке изображены графики функций вида y=kx+b. Установите соответствие между графиками и знаками коэффициентов k и b. а) k>0, b>0; 1. 2. 3. х у 0 х у 0 х у 0 б)k>0, b<0; в)k<0, b<0, г)k<0, b>0.
х у 0 у 0 у 0 х х 3. На рисунке изображены графики функций. Установите соответствие между графиками и формулами: 1. 2. 3. А) у=2х+2, Б) у=3х-4, В)у=х²-2, Г) у=2-х².
4. На рисунке изображен график функции у=-х²+4х-3. Решите неравенство: -х²+4х-3>0 у х 0 1 3 2 1 Ответ: (1;3)
5. Для решения какой системы уравнений выполнен рисунок? х²+у²=4 х+у=-2 х²+у=4 х+у=-2 х у 0 1 1 у=х²+4 у=-х-2 у=-х²+4 у=х-2 1 2 3 4
х
у
0
1
1
6. На рисунке изображены графики функций ух=6, х+у=1 и х=3.
Укажите систему уравнений, которая не имеет решений.
ху=6
х+у=1
х+у=1
х-3=0
ху=6
х-3=0
1
2
3
ху=6
х+у=1
Ответ:
На рисунке изображены графики функций ух=6, х+у=1 и х=3.
Укажите систему уравнений, которая не имеет решений.
ху=6
х+у=1
х+у=1
х-3=0
ху=6
х-3=0
1
2
3
ху=6
х+у=1
Ответ:
7. Пользуясь рисунком, укажите систему уравнений, решением которой является пара х=4, у=0. 7х+5у=-8 7х+5у=-8 х-2у=4 х-2у=4 х+у=4 х+у=4 х+у=4 х-2у=4 7х+5у=-8 1 2 3 х у 0 1 1 4 4 -4
8. На рисунке изображены графики функций у=х²-2х-3 и у=1-2х. Найдите решение системы уравнений: у=х²-2х-3 у=1-2х х у 3 1 0 2 -3 -2 5 Ответ: (2;-3), (-2;5).
9. Какая из прямых отсутствует на чертеже? у=2х+3 у=2х-3 у=-2х+3 у=-2х-3 х у 1 0 3 -3 у=2х+3 у=2х-3 у=-2х-3 Ответ: 3.
Практическая работа №4 | Учебно-методический материал по алгебре на тему:
ПРАКТИЧЕСКАЯ РАБОТА № 4
ОД. 10 Математика
10 Математика
Тема: Построение графиков функции.
Вид занятия: Практическое занятие
Цель занятия | учебная | Проверить знания и практические умения студентов при построении графиков функции, простейших преобразований графиков функции, нахождение обратных функций. |
воспитательная и развивающая | Обеспечить высокую творческую активность при выполнении практической работы. | |
Межпредметные связи | обеспечивающие | Математика (школьный курс) |
обеспечиваемые | Физика, техническая механика, экономика, курсовое и дипломное проектирование |
Обеспечение урока:
Использование ИКТ (информационно – коммуникационных технологий)
(мультимедийные презентации, проекционное оборудование, интерактивная доска, персональный компьютер, компьютерное тестирование)
Математика в Открытом колледже http://www. mathematics.ru
mathematics.ru
Наглядные пособия и раздаточный материал: методические указания для практической работы №4
Литература: Колмогоров А.Н. и др. Алгебра и начала анализа. 10 (11) кл. – М.: Просвещение, 2012
Цель работы:
Построение графиков функции, преобразование графиков функции, нахождение обратных функций.
Понятие об обратной функции
Мы уже сталкивались с задачей, когда по заданной функции f и заданному значению её аргумента необходимо было вычислить значение функции в этой точке. Но иногда приходится сталкиваться с обратной задачей: найти по известной функции f и её некоторому значению y значение аргумента, в котором функция принимает данное значение y.
Функция, которая, принимает каждое свое значение в единственной точке своей области определения, называется обратимой функцией.
Например, линейная функция будет являться обратимой функцией. А квадратичная функция или функция синус не будет являться обратимыми функциями. Так как одно и то же значение функция может принимать при различных аргументах.
Обратная функция
Положим, что f есть некоторая произвольная обратимая функция. Каждому числу из области её значений y0, соответствует лишь одно число из области определения x0, такое что f(x0) = y0.
Если теперь мы каждому значению х0 поставим в соответствие значение y0, то получим уже новую функцию. Например, для линейной функции f(x) = k * x + b функция g(x) = (x — b)/k будет являться обратной.
Если некоторая функция g в каждой точке х области значений обратимой функции f принимает значение у такое, что f(y) = x, то говорят, что функция g – есть обратная функция к f.
Если у нас будет задан график некоторой обратимой функции f, то для того чтобы построить график обратной функции, можно пользоваться следующим утверждением: график функции f и обратной к ней функции g будут симметричны относительно прямой, заданной уравнением y = x.
Если функция g является обратной к функции f, то функция g будет являться обратимой функцией. А функция f будет обратной к функции g. Обычно говорят, что две функции f и g взаимно обратные друг к другу.
Обычно говорят, что две функции f и g взаимно обратные друг к другу.
На следующем рисунке представлены графики функций f и g взаимно обратных друг к другу.
Выведем следующую теорему:
если функция f возрастает (или убывает) на некотором промежутке A, то она обратима.
Обратная к а функция g, определенная в области значений функции f, также является возрастающей (или соответственно убывающей) функцией.
Данная теорема называется теоремой об обратной функции.
Простейшие преобразования графиков функций
- y = f(x) + b – график функции получается из графика функции y = f(x) путем параллельного переноса этого графика на величину вдоль от ОУ. при этом, если b>0, то график функции f(x) + b располагается выше графика функции f(x), если b
- y = f (x + b) – график функции получается из графика функции y = f(x) с помощью параллельного переноса этого графика на величину b вдоль оси ОХ, при этом, если b>0, то сдвиг влево, а если b
- y = — f(x) – график симметричен графику y = f(x) относительно оси ОХ
Указанные преобразования не изменяют масштаба графика функции.
Рассмотрим преобразования графиков функций, которые изменяют масштаб графика
- y = аf(x) – график функции получается из графика функции y = f(x) с помощью растяжения или сжатия графика по оси ОУ пропорционально коэффициенту а, причем,
если a > 1, то все ординаты графика аf(x) увеличиваются в а раз, если a
- y = f(аx) – график функции получается из графика функции y = f(x) с помощью растяжения или сжатия вдоль оси ОХ пропорционально коэффициенту а, причем, если, а > 1, то график сжимается в а раз, если 0
- у = — для построения этого графика нужно построить график функции y = f(x) и отобразить относительно оси ОХ те части графика, которые расположены ниже этой оси.
у = у = х – 3; у =
ПРОСТЕЙШИЕ ФУНКЦИИ И ИХ ГРАФИКИ
- Постоянная функция
- Прямая пропорциональность
3.
Область определения:
Область изменения:
4.Квадратичная функция
Область определения:
Область изменения:
5. Обратная пропорциональная зависимость
Область определения:
Область изменения:
ВАРИАНТ – 1 1.Постройте график функции . Укажите координаты точек пересечения графика с осями координат. 2. Постройте графики функций и укажите координаты точек пересечения этих графиков. 3. Найдите функцию обратную данной и постройте графики данных функций в одной системе координат. 4. Параболу перенести параллельно самой себе вдоль оси ординат вниз на 4 единицы. Запишите новое уравнение параболы. 5. Найдите функцию обратную данной: 6. Постройте график функции . Какое значение принимает функция при х=1,5 | ВАРИАНТ – 2 1. 2. Постройте графики функций и укажите координаты точек пересечения этих графиков. 3. Найдите функцию обратную данной и постройте графики данных функций в одной системе координат. 4. Параболу перенести параллельно самой себе вдоль оси ординат вверх на 3,5 единицы. Запишите новое уравнение параболы. 5. Найдите функцию обратную данной: 6. Постройте график функции . Какое значение принимает функция при х=2,5 |
ВАРИАНТ – 3
ВАРИАНТ – 5
| ВАРИАНТ – 4
ВАРИАНТ – 6
.
|

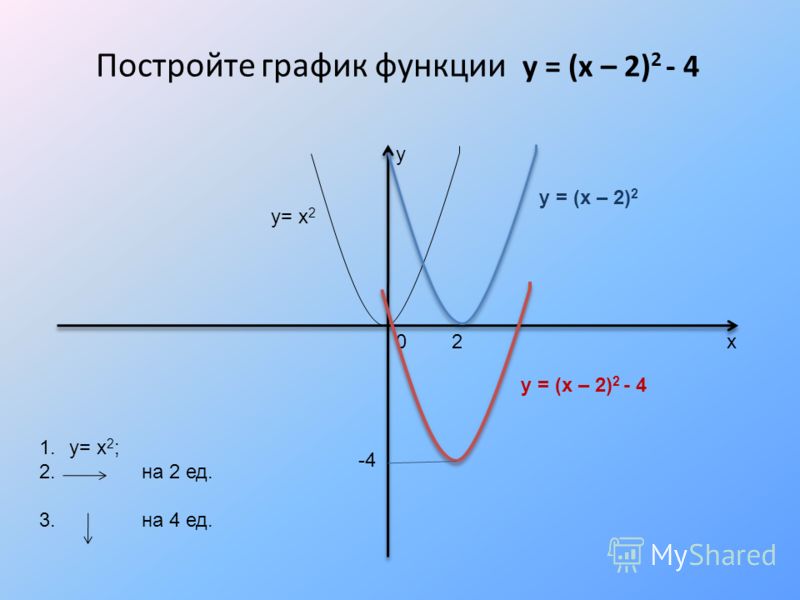 Постройте график функции . Укажите координаты точек пересечения графика с осями координат.
Постройте график функции . Укажите координаты точек пересечения графика с осями координат.
 Укажите координаты точек пересечения графика с осями координат.
Укажите координаты точек пересечения графика с осями координат.