График производной
Используй поиск, чтобы найти научные материалы и собрать список литературы
База статей справочника включает в себя статьи написанные экспертами Автор24, статьи из научных журналов и примеры студенческих работ из различных вузов страны
Содержание статьи
1. Свойства графика производной
Рассмотрим и сравним график функции и ее производной (рис.1)
Рисунок 1. График производной
- На интервалах возрастания производная положительна. Если производная в определённой точке из некоторого интервала имеет положительное значение, то график функции на этом интервале возрастает.
- На интервалах убывания производная отрицательна (со знаком минус). Если производная в определённой точке из некоторого интервала имеет отрицательное значение, то график функции на этом интервале убывает.
- Производная в точке х равна угловому коэффициенту касательной, проведённой к графику функции в этой же точке.
- В точках максимума-минимума функции производная равна нулю. Касательная к графику функции в этой точке параллельна оси ОХ.
Пример 1
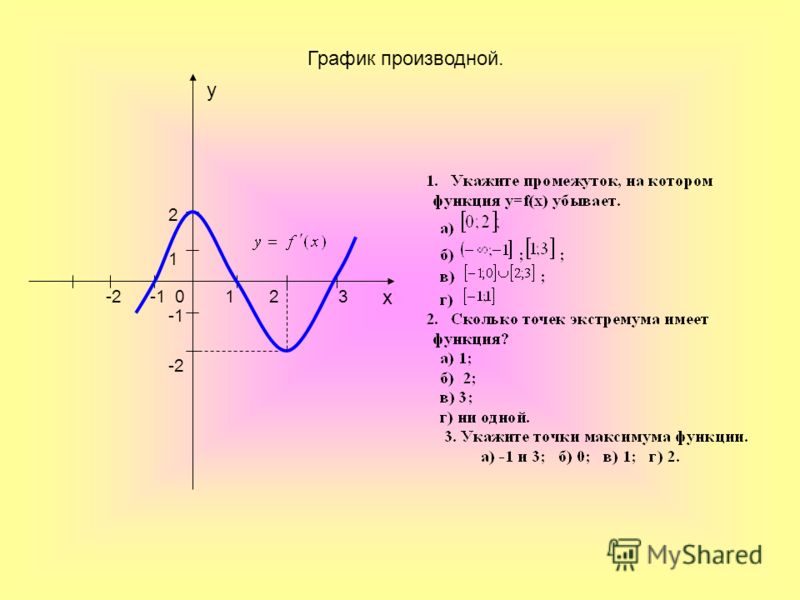
По графику (рис.2) производной определить, в какой точке на отрезке [-3; 5] функция максимальна.
Рисунок 2. График производной
Решение: На данном отрезке производная — отрицательна, а значит, функция убывает слева направо, и наибольшее значение находится с левой стороны в точке -3.
Пример 2
По графику (рис.3) производной определить количество точек максимума на отрезке [-11; 3].
Рисунок 3. График производной
Решение: Точки максимума соответствуют точкам смены знака производной с положительного на отрицательный. На данном промежутке функция два раза меняет знак с плюса на минус — в точке -10 и в точке -1. Значит количество точек максимума — две.
Пример 3
По графику (рис.3) производной определить количество точек минимума отрезке [-11; -1].
Решение: Точки минимума соответствуют точкам смены знака производной с отрицательного на положительный. На данном отрезке такой точкой является только -7. Значит, количество точек минимума на заданном отрезке — одна.
Пример 4
По графику (рис.3) производной определить количество точек экстремума.
Решение: Экстремумом являются точки как минимума, так и максимума. Найдем количество точек, в которых производная меняет знак:
- Точка -10 (максимум)
- Точка -7 (минимум)
- Точка -1 (максимум)
- Точка 2 (минимум)
Функция содержит 4 экстремума.
Пример 5
По графику (рис.4) производной определить количество целых точек на промежутке убывания.
Решение: Интервалам убывания соответствуют (-3,-1.5) и (4.5,6.5). Количество целых точек по прямой х: 2(на первом промежутке) и 2 (на втором промежутке).
Ответ: 4
Сообщество экспертов Автор24
Автор этой статьи
Дата последнего обновления статьи: 10.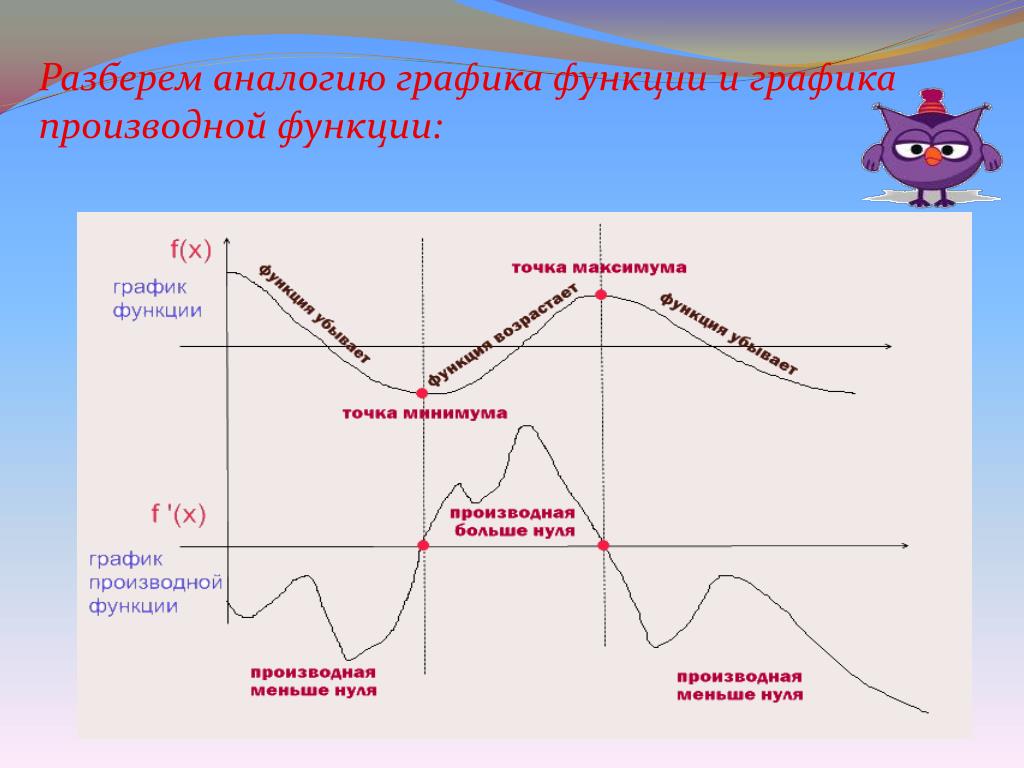
12.2021
Выполнение любых типов работ по математике
Решение задач по комбинаторике на заказ Решение задачи Коши онлайн Математика для заочников Контрольная работа на тему числовые неравенства и их свойства Контрольная работа на тему умножение и деление рациональных чисел Контрольная работа на тему действия с рациональными числами Дипломная работа на тему числа Курсовая работа на тему дифференциальные уравнения Контрольная работа на тему приближенные вычисления Решение задач с инвариантами
Подбор готовых материалов по теме
Дипломные работы Курсовые работы Выпускные квалификационные работы Рефераты Сочинения Доклады Эссе Отчеты по практике Решения задач Контрольные работы
Производная.
График производной функции — презентация онлайнПохожие презентации:
Исследование функции. Геометрический смысл производной
Производная и ЕГЭ. Геометрический смысл производной
Применение производной к исследованию функции и построению графика функции
Позиция 7 ЕГЭ 2016. Применение производной к исследованию функций по графику производной. Геометрический смысл производной
Производная функции в заданиях ЕГЭ. Факультативное занятие
Применение производной к исследованию функций
Производная. Геометрический смысл производной. Возрастание и убывание
В8. Решение заданий ЕГЭ
Производная. ЕГЭ, задание В9
Применение производной к исследованию функций. Готовимся к ЕГЭ. (Задание 7)
1. производная
• 1. На рисункеизображен
график производной
функции f(x) ,
определенной на
интервале (-9;8).
Найдите количество
точек, в которых
касательная к графику
функции
f(x) параллельна
прямой у=х-7 или
совпадает с ней.
(4)• 2. На рисунке изображен график производной
функции f(x) , определенной на интервале(-9;8)..
Найдите количество точек, в которых касательная к
графику функции f(x) параллельна прямой
у=-х+8 или совпадает с ней.( 2)
• 3. На рисунке изображен график производной
функции f(x), определенной на интервале
(-9;8).. В какой точке отрезка от -5 до -3
f(x) принимает наименьшее значение
• 4. На рисунке
изображен
график производной
функции f(x) ,
определенной на
интервале (-6;6). В
какой точке отрезка
от 3 до 5
f(x) принимает
наибольшее
значение.
• 5. На рисунке изображен график производной
функции f(x) , определенной на интервале
(-6;6). Найдите точку экстремума функции
f(x) на интервале (-4;5).
• 6. На рисунке изображен график функции f(x) ,
определенной на интервале (-5;5). Найдите
количество точек, в которых касательная к графику
функции параллельна прямой у=6.
• 7, На рисунке изображен график функции f(x) ,
определенной на интервале (-5;5).
количество целых точек, в которых производная
функции f(x) отрицательна.
• 8. На рисунке изображен график производной
функции f(x) , определенной на интервале
(-5;5). В какой точке отрезка от -4 до
-1 f(x) принимает наименьшее значение.
• 9. На рисунке изображен график производной
функции f(x) , определенной на интервале
(-5;5). Найдите количество точек экстремума
функции f(x) на отрезке от -4 до 4.
• 10. На рисунке изображен график функции
f(x) , определенной на интервале (-6;8).
Определите количество целых точек, в
которых производная функции положительна.
• 11. На рисунке изображен график функции f(x) ,
определенной на интервале (-5;5) . Определите
количество целых точек, в которых производная
функции f(x) отрицательна.
• 13. На рисунке изображен график функции
f(x) , определенной на интервале (-2;12).
Найдите сумму точек экстремума функции
f(x) .
• 14. На рисунке изображен график
производной функции f(x) , определенной на
интервале (-8;3).
В какой точке отрезка от -3до 2 f(x) принимает наибольшее значение.
• 15. На рисунке изображен график
производной функции f(x) , определенной на
интервале (-8;4). В какой точке отрезка от -7
до -3 f(x) принимает наименьшее значение.
• 16. На рисунке изображен график производной
функции f(x) , определенной на интервале (-7;14).
Найдите количество точек максимума функции
f(x) на отрезке от -6 до 9.
• 17. На рисунке изображен график
производной функции f(x) , определенной на
интервале (-18;6). Найдите количество точек
минимума функции f(x) на отрезке от -13 до 1.
• 18. На рисунке изображен график производной
функции f(x) , определенной на интервале(-11;11).
f(x) на отрезке от -10 до 10.
• 18. На рисунке изображен график производной
функции f(x) , определенной на интервале(-11;11).
Найдите количество точек экстремума функции
f(x) на отрезке от -10 до 10.
• 20.
На рисунке изображен график производнойфункции f(x) и, определенной на интервале (-5;7).
Найдите промежутки убывания функции f(x) . В
ответе укажите сумму целых точек, входящих в эти
промежутки.
• 21. На рисунке изображен график производной
функции f(x) , определенной на интервале (-11;3).
Найдите промежутки возрастания функции f(x) . В
ответе укажите длину наибольшего из них.
• 22. На рисунке изображен график производной
функции f(x) , определенной на интервале (-2;12).
Найдите промежутки убывания функции f(x) . В
ответе укажите длину наибольшего из них.
• 23. На рисунке изображен график производной
функции f(x) , определенной на интервале (-10;2).
Найдите количество точек, в которых касательная к
графику функции f(x) параллельна прямой
у=-2х-11 или совпадает с ней.
• 24. На рисунке изображен график
производной функции f(x) , определенной на
интервале (-4;8). Найдите точку экстремума
функции f(x) на отрезке от -2до 6.
• 25. На рисунке изображён график функции
f(x) и касательная к нему в точке с абсциссой
х0. Найдите значение производной функции
f(x) в точке х0.
• 26. На рисунке изображён график функции
f(x) и касательная к нему в точке с абсциссой
х0. Найдите значение производной функции
f(x) в точке х0.
• 27. На рисунке изображён график функции
f(x) и касательная к нему в точке с абсциссой
х0. Найдите значение производной функции
• 28. На рисунке изображён график функции
f(x) и касательная к нему в точке с абсциссой
х0. Найдите значение производной функции
f(x) в точке х0.
• 29. На рисунке изображен график функции f(x) .
Прямая, проходящая через начало координат,
касается графика этой функции в точке с абсциссой
8. Найдите значение производной в точке х=8.
• 30. На рисунке изображен график производной
функции f(x) . Найдите абсциссу точки, в которой
касательная к графику f(x) параллельна прямой
у=2х-2 или совпадает с ней.
• 31. На рисунке изображен график производной
функции f(x) . Найдите абсциссу точки, в которой
касательная к графику f(x) параллельна оси абсцисс
или совпадает с ней.
• 32. На рисунке изображен график функции
f(x) , определенной на интервале(-5;5).
Найдите количество точек, в которых
производная функции f(x) равна 0.
English Русский Правила
Как сравнить график функции и ее производной — Блог Magoosh
Захари, , 9 января 2017 г. , ОБНОВЛЕНО 17 марта 2019 г., в AP
Чтение графа производных является важной частью учебного плана AP Calculus. Типичные проблемы исчисления включают в себя заданную функцию или график функции и поиск информации о точках перегиба, наклоне, вогнутости или существовании производной.
Существует ли производная?
Во-первых, глядя на график, мы должны знать, существует ли вообще производная функции. Наш производный пост в блоге содержит немного больше информации об этом.
Три ситуации, когда производная не существует
Если на кривой есть разрыв, производная не существует.
Это каждый раз, когда на кривой есть разрыв, когда две части кривой не соединяются.
Типы разрывов:
Имеется устранимый разрыв. Представьте себе линейную функцию, такую как y = x + 3. Если бы мы добавили ограничение, при котором x не определено при x = 0, у нас был бы такой разрыв.
Существует бесконечный разрыв. Это происходит, когда у нас есть любое уравнение, в котором есть разрыв между двумя непрерывными участками кривой из-за того, что асимптоты достигают бесконечности. Например, пусть у = 3/(х-2). Обратите внимание, у нас есть две вертикальные асимптоты, которые не соединяются.
Наконец, у нас есть разрыв скачка. Это происходит с кусочными функциями, где два участка просто не соединяются.
Производная не существует там, где есть острый угол.
Это часто происходит с проблемами абсолютного значения.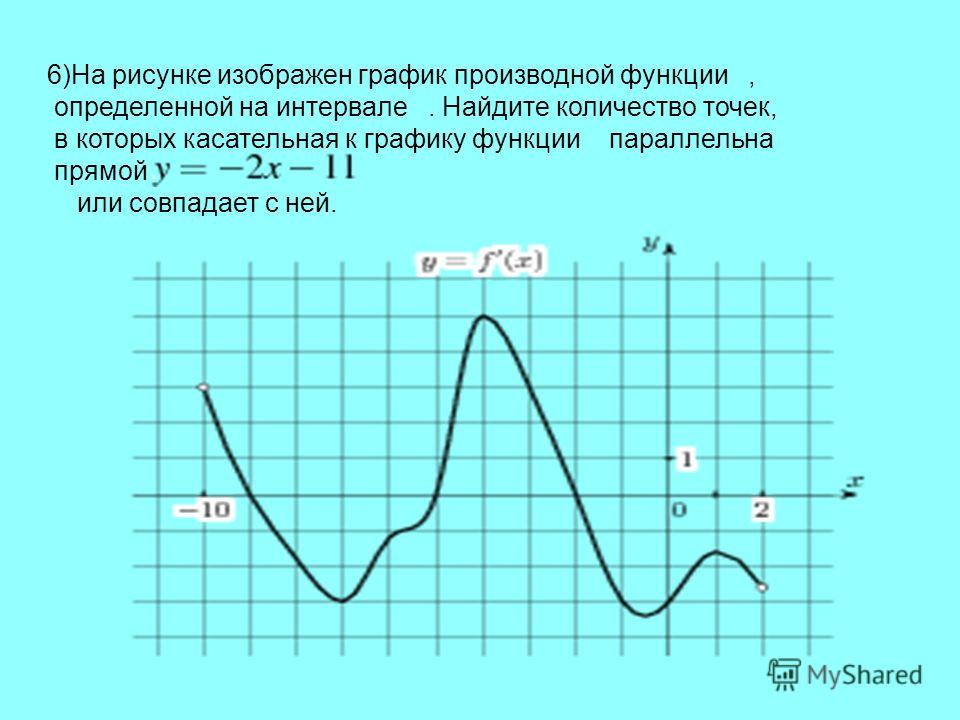
Посмотрим на график y = √x 2
При x = 0 производная отсутствует, потому что мы имеем резкий изгиб кривой.
Наконец, нигде нет производной, если есть вертикальный участок графика.
Если есть вертикальный участок графика, наклон не определен; следовательно, производная не существует.
Чтение графика производных.
Глядя на график, мы должны иметь возможность быстро увидеть наклон в любой точке и получить приблизительное представление о том, каким должен быть наклон. Это позволяет легко сопоставить график с его производной.
Глядя на первый график, сможете ли вы определить, какой из трех графиков ниже является графиком производной?
ф'(х):
и
б
с
Несколько ключей для получения правильного ответа. Сразу видно, что это какая-то тригонометрическая функция. Мы знаем, что наклон функции равен 0 в нескольких точках; следовательно, график производной должен в какой-то точке проходить через ось абсцисс.
Также, глядя на график, мы должны увидеть, что это происходит где-то между -2,5 и 0, а также между 0 и 2,5. Одного этого достаточно, чтобы убедиться, что последний график является правильным ответом.
График функции на основе производной и двойной производной.
Производная и двойная производная говорят нам несколько ключевых вещей о графике:
(Надлежащая практика точки доступа: как узнать, является ли она минимальной или максимальной?)
Ниже приведен график производной f(x).
Вот график функции. Можем ли мы увидеть, как они соответствуют?
Умение читать графики производной и знание того, какой должна быть общая форма исходной функции, является важной частью учебного плана AP Calculus. Убедитесь, что вы знаете, как определить точки перегиба, локальные минимумы и максимумы, а также где функция увеличивается или уменьшается.
Гарантированно улучшите свой результат SAT или ACT.
Начните свою 1-недельную бесплатную пробную версию Magoosh SAT Prep или 1-недельную бесплатную пробную версию Magoosh ACT Prep сегодня!Автор
Кстати, Magoosh может помочь вам подготовиться к экзаменам SAT и ACT. Нажмите сюда, чтобы узнать больше!
Расчет AP
← Предыдущий
Следующий →
Мы настоятельно рекомендуем учащимся помогать друг другу и отвечать на комментарии других учащихся, если это возможно!
Если вы являетесь студентом Premium Magoosh и хотели бы более персонализированного обслуживания от наших инструкторов, вы можете использовать вкладку «Справка» на панели инструментов Magoosh. Спасибо!
Производные и графики — Неформальное исчисление
35 Производные и графики
Как мы видели, одна из наиболее важных связей между функцией и ее производной заключается в том, что положительная производная означает, что величина увеличивается, а отрицательная производная означает, что величина уменьшается.
Возрастание и убывание
Наружная температура имеет положительную производную от 3:00 до 15:00 и отрицательную производную от 15:00 до 3:00. Нарисуйте график этого и обозначьте каждую часть графика как «возрастающую» или «убывающую».
При положительной производной с 3:00 до 15:00 это значение должно повышаться и обозначаться как «возрастающее». С 15:00 до 3:00 график идет вниз и помечен как «убывающий».
На границе между увеличением и уменьшением, в 3 часа дня, температура самая высокая. Это ключ к одному из самых полезных приложений исчисления: оптимизации! Оптимизация заключается в том, чтобы либо выяснить, когда количество максимально или максимально возможно, либо выяснить, когда количество минимизируется или как можно меньше. Часто это происходит на границе возрастания и убывания, то есть там, где функция переходит от положительной производной к отрицательной. Следовательно, одна из важнейших максим исчисления: оптимизация происходит, когда производная равна нулю! Мы вернемся к этому в следующем разделе.
А пока, используя представление о положительной, отрицательной или нулевой производной, мы можем нарисовать грубый набросок производной на основе графика функции. Рассмотрим пример.
Набросок производной
Нарисуйте производную следующей функции.
При наброске производной помните об этой идее: склоны становятся [латексными]y[/латексными] значениями . Во-первых, давайте отметим, где производная равна нулю:
Это места, которые на графике производной имеют нулевое значение [latex]y[/latex]-значения. Это означает, что это [latex]x[/latex]-перехваты!
Теперь отметим, где производная положительная, а где отрицательная.
Наконец, мы можем использовать это как грубое руководство для скетча, опять же помня, что наклон становится [латекс]y[/латекс]-значениями. Здесь производная выделена черным цветом, а исходная функция — серым.
Давайте посмотрим на другой пример.