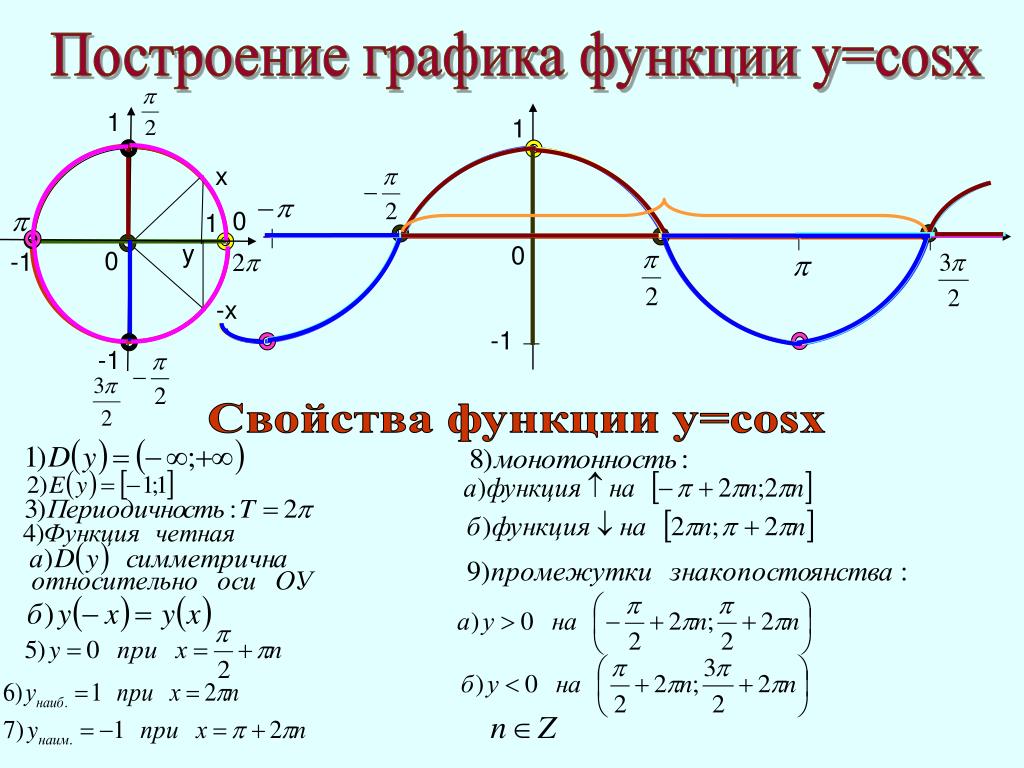
График синус: Свойства функции y = sinx и её график — урок. Алгебра, 10 класс.

График синуса — справочник для студентов и школьников

Синус-график имеет вид, как показано на рисунке 1. Кривая, определяющая синус-граф, называется синусоидальной.

Рис. 1

График функции \(\ y=\sin x \) пересекает ось \(\ \mathrm{Ox} \) в точках \(\ x=\pi n, n \in Z \) . Максимальные значения равны 1, функция принимает в точках \(\ x=\frac{\pi}{2}+2 \pi n, n \in Z \) и минимальные значения, равные (-1) на точек \(\ x=-\frac{\pi}{2}+2 \pi n, n \in Z \)

График функции возрастает при \(\ x \in\left(-\frac{\pi}{2}+2 \pi n, \frac{\pi}{2}+2 \pi n\right) \), \(\ n \in Z \) и уменьшается при \(\ x \in\left(\frac{\pi}{2}+2 \pi n, \frac{3 \pi}{2}+2 \pi n\right) \), \(\ n \in Z \)

Примеры решения проблем

ПРИМЕР 1

Задача

Построить график функции \(\ y=\sin 3 x-2 \)

Решение

Построим данный граф, используя элементарные преобразования графа функции \(\ y=\sin x \) . Во-первых, мы сжимаем график \(\ y=\sin x \) вдоль оси \(\ \bigcirc x \) три раза (уменьшая расстояние от каждой точки графика \(\ y=\sin x \) до оси ординат три раза), получаем график функции \(\ y=\sin 3 x \) (рис.

2)

Рис. 2

Затем, сдвинув график \(\ y=\sin 3 x \) на 2 единицы вниз, получим нужный граф \(\ y=\sin 3 x-2 \) (рис.3).

Рис. 3

ПРИМЕР 2

Задача

Построить график функций \(\ y=\frac{1}{2} \sin \left(x+\frac{\pi}{4}\right) \)

Решение

Построим данный граф, используя элементарные преобразования графа функции \(\ y=\sin x \) . Сначала сдвинем график \(\ y=\sin x \) в \(\ \frac{\pi}{4} \) влево, получим график \(\ y=\sin \left(x+\frac{\pi}{4}\right) \) (рис.4)

Рис. 4

Затем, дважды сжимая граф \(\ y=\sin \left(x+\frac{\pi}{4}\right) \) (уменьшая расстояние от каждой точки \(\ y=\sin \left(x+\frac{\pi}{4}\right) \) до оси абсцисс дважды), мы получаем желаемый график \(\ y=\frac{1}{2} \sin \left(x+\frac{\pi}{4}\right) \)(рис.5)

Рис. 5

Физика

166

Реклама и PR

31

Педагогика

80

Психология

72

Социология

7

Астрономия

9

Биология

30

Культурология

86

Экология

8

Право и юриспруденция

36

Политология

13

Экономика

49

Финансы

9

История

16

Философия

8

Информатика

20

Право

35

Информационные технологии

6

Экономическая теория

7

Менеджент

719

Математика

338

Химия

20

Микро- и макроэкономика

1

Медицина

5

Государственное и муниципальное управление

2

География

542

Информационная безопасность

2

Аудит

11

Безопасность жизнедеятельности

3

Архитектура и строительство

1

Банковское дело

1

Рынок ценных бумаг

6

Менеджмент организации

2

Маркетинг

238

Кредит

3

Инвестиции

2

Журналистика

1

Конфликтология

15

Этика

9

Формулы дифференцирования Синус двойного угла Синус 60 градусов Синус 45 градусов Синус 30 градусов

Узнать цену работы

Узнай цену

своей работы

Имя

Выбрать тип работыЧасть дипломаДипломнаяКурсоваяКонтрольнаяРешение задачРефератНаучно — исследовательскаяОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерскаяНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация в ВАКПубликация в ScopusДиплом MBAПовышение оригинальностиКопирайтингДругое

Принимаю  Политику  конфиденциальности

Подпишись на рассылку, чтобы не пропустить информацию об акциях

Построение с Matplotlib

Введение

Примеры

Простой сюжет в Matplotlib

Этот пример показывает , как создать простую синусоидальную кривую с использованием Matplotlib

 # Plotting tutorials in Python
# Launching a simple plot
import numpy as np
import matplotlib. pyplot as plt
# angle varying between 0 and 2*pi
x = np.linspace(0, 2.0*np.pi, 101)
y = np.sin(x)                        # sine function
plt.plot(x, y)
plt.show()
 

Добавление дополнительных функций к простому графику: метки оси, заголовок, метки оси, сетка и легенда

В этом примере мы берем график с синусоидой и добавляем к нему больше функций; а именно заголовок, метки оси, заголовок, метки оси, сетка и легенда.

 # Plotting tutorials in Python
# Enhancing a plot
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(0, 2.0*np.pi, 101)
y = np.sin(x)
# values for making ticks in x and y axis
xnumbers = np.linspace(0, 7, 15)
ynumbers = np.linspace(-1, 1, 11)
plt.plot(x, y, color='r', label='sin') # r - red colour
plt.xlabel("Angle in Radians")
plt.ylabel("Magnitude")
plt.title("Plot of some trigonometric functions")
plt.xticks(xnumbers)
plt.yticks(ynumbers)
plt.legend()
plt.grid()
plt.axis([0, 6.5, -1.1, 1.1]) # [xstart, xend, ystart, yend]
plt.show()
 

Создание нескольких графиков на одной фигуре путем наложения, аналогичного MATLAB

В этом примере кривая синуса и кривая косинуса изображены на одном рисунке путем наложения графиков друг на друга.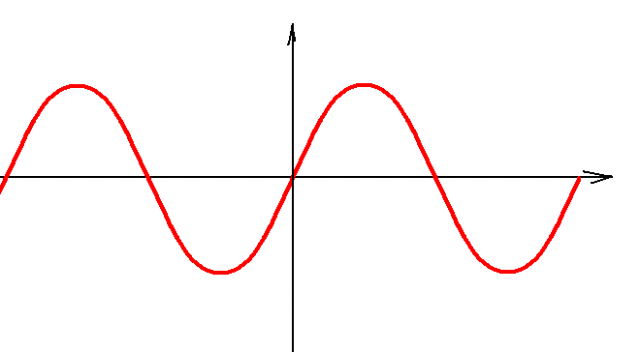

 # Plotting tutorials in Python
# Adding Multiple plots by superimposition
# Good for plots sharing similar x, y limits
# Using single plot command and legend
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(0, 2.0*np.pi, 101)
y = np.sin(x)
z = np.cos(x)
# values for making ticks in x and y axis
xnumbers = np.linspace(0, 7, 15)
ynumbers = np.linspace(-1, 1, 11)
plt.plot(x, y, 'r', x, z, 'g') # r, g - red, green colour
plt.xlabel("Angle in Radians")
plt.ylabel("Magnitude")
plt.title("Plot of some trigonometric functions")
plt.xticks(xnumbers)
plt.yticks(ynumbers)
plt.legend(['sine', 'cosine'])
plt.grid()
plt.axis([0, 6.5, -1.1, 1.1]) # [xstart, xend, ystart, yend]
plt.show()
 

Создание нескольких графиков на одном рисунке с использованием наложения графиков с отдельными командами графиков

Как и в предыдущем примере, здесь кривая синуса и косинуса строится на одном и том же рисунке с использованием отдельных команд построения. Это более Pythonic и может быть использовано для получения отдельных маркеров для каждого сюжета.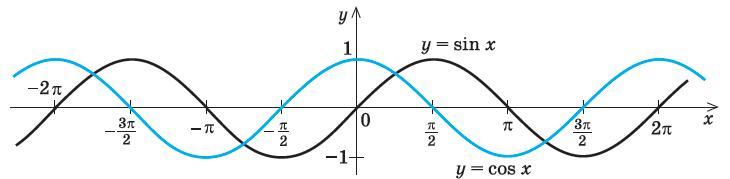

 # Plotting tutorials in Python
# Adding Multiple plots by superimposition
# Good for plots sharing similar x, y limits
# Using multiple plot commands
# Much better and preferred than previous
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(0, 2.0*np.pi, 101)
y = np.sin(x)
z = np.cos(x)
# values for making ticks in x and y axis
xnumbers = np.linspace(0, 7, 15)
ynumbers = np.linspace(-1, 1, 11)
plt.plot(x, y, color='r', label='sin') # r - red colour
plt.plot(x, z, color='g', label='cos') # g - green colour
plt.xlabel("Angle in Radians")
plt.ylabel("Magnitude")
plt.title("Plot of some trigonometric functions")
plt.xticks(xnumbers)
plt.yticks(ynumbers)
plt.legend()
plt.grid()
plt.axis([0, 6.5, -1.1, 1.1]) # [xstart, xend, ystart, yend]
plt.show()
 

Графики с общей осью X, но с другой осью Y: с использованием twinx ()

В этом примере мы построим синусоидальную и гиперболическую синусоидальные кривые на одном графике с общей осью X, имеющей разные оси Y.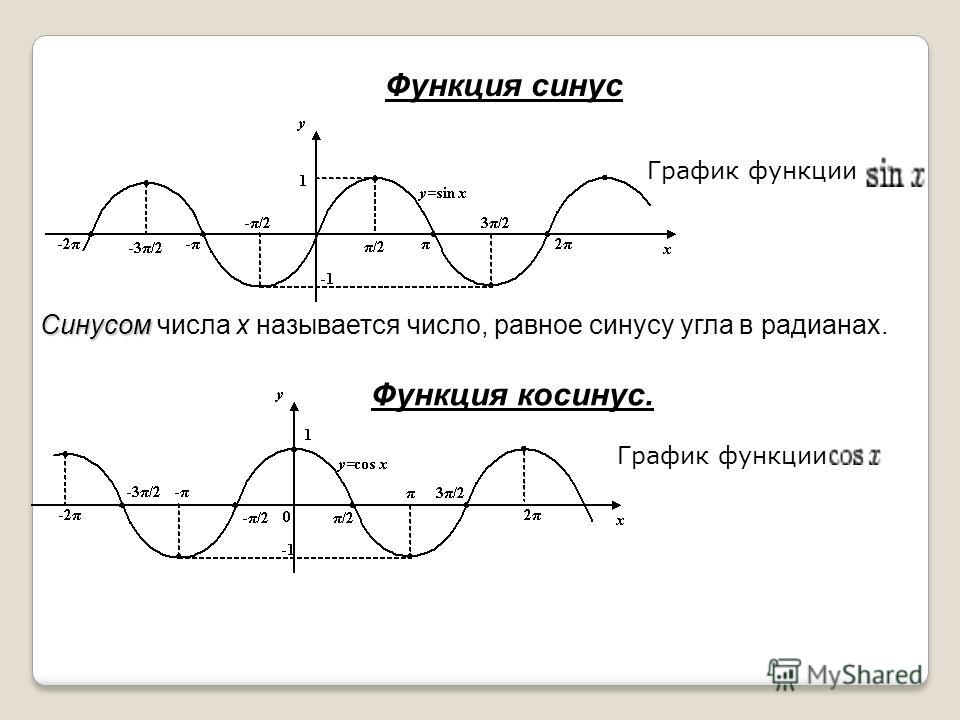 Это достигается за счет использования команды TwinX ().

# Plotting tutorials in Python
# Adding Multiple plots by twin x axis
# Good for plots having different y axis range
# Separate axes and figure objects
# replicate axes object and plot curves
# use axes to set attributes
# Note:
# Grid for second curve unsuccessful : let me know if you find it! :(
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(0, 2.0*np.pi, 101)
y = np.sin(x)
z = np.sinh(x)
# separate the figure object and axes object
# from the plotting object
fig, ax1 = plt.subplots()
# Duplicate the axes with a different y axis
# and the same x axis
ax2 = ax1.twinx() # ax2 and ax1 will have common x axis and different y axis
# plot the curves on axes 1, and 2, and get the curve handles
curve1, = ax1.plot(x, y, label="sin", color='r')
curve2, = ax2.plot(x, z, label="sinh", color='b')
# Make a curves list to access the parameters in the curves
curves = [curve1, curve2]
# add legend via axes 1 or axes 2 object.  
# one command is usually sufficient
# ax1.legend() # will not display the legend of ax2
# ax2.legend() # will not display the legend of ax1
ax1.legend(curves, [curve.get_label() for curve in curves])
# ax2.legend(curves, [curve.get_label() for curve in curves]) # also valid
# Global figure properties
plt.title("Plot of sine and hyperbolic sine")
plt.show()
 

Графики с общей осью Y и другой осью X с использованием twiny ()

В этом примере, график с кривыми , имеющими общую ось ординат , но разные оси х продемонстрирована с использованием метода twiny (). Кроме того, некоторые дополнительные функции, такие как заголовок, легенда, метки, сетки, метки осей и цвета, добавляются к графику.

# Plotting tutorials in Python
# Adding Multiple plots by twin y axis
# Good for plots having different x axis range
# Separate axes and figure objects
# replicate axes object and plot curves
# use axes to set attributes
import numpy as np
import matplotlib.pyplot as plt
y = np.  linspace(0, 2.0*np.pi, 101)
x1 = np.sin(y)
x2 = np.sinh(y)
# values for making ticks in x and y axis
ynumbers = np.linspace(0, 7, 15)
xnumbers1 = np.linspace(-1, 1, 11)
xnumbers2 = np.linspace(0, 300, 7)
# separate the figure object and axes object
# from the plotting object
fig, ax1 = plt.subplots()
# Duplicate the axes with a different x axis
# and the same y axis
ax2 = ax1.twiny() # ax2 and ax1 will have common y axis and different x axis
# plot the curves on axes 1, and 2, and get the axes handles
curve1, = ax1.plot(x1, y, label="sin", color='r')
curve2, = ax2.plot(x2, y, label="sinh", color='b')
# Make a curves list to access the parameters in the curves
curves = [curve1, curve2]
# add legend via axes 1 or axes 2 object.
# one command is usually sufficient
# ax1.legend() # will not display the legend of ax2
# ax2.legend() # will not display the legend of ax1
# ax1.legend(curves, [curve.get_label() for curve in curves])
ax2.legend(curves, [curve.get_label() for curve in curves]) # also valid
# x axis labels via the axes
ax1. set_xlabel("Magnitude", color=curve1.get_color())
ax2.set_xlabel("Magnitude", color=curve2.get_color())
# y axis label via the axes
ax1.set_ylabel("Angle/Value", color=curve1.get_color())
# ax2.set_ylabel("Magnitude", color=curve2.get_color()) # does not work
# ax2 has no property control over y axis
# y ticks - make them coloured as well
ax1.tick_params(axis='y', colors=curve1.get_color())
# ax2.tick_params(axis='y', colors=curve2.get_color()) # does not work
# ax2 has no property control over y axis
# x axis ticks via the axes
ax1.tick_params(axis='x', colors=curve1.get_color())
ax2.tick_params(axis='x', colors=curve2.get_color())
# set x ticks
ax1.set_xticks(xnumbers1)
ax2.set_xticks(xnumbers2)
# set y ticks
ax1.set_yticks(ynumbers)
# ax2.set_yticks(ynumbers) # also works
# Grids via axes 1 # use this if axes 1 is used to
# define the properties of common x axis
# ax1.grid(color=curve1.get_color())
# To make grids using axes 2
ax1.grid(color=curve2.get_color())
ax2.grid(color=curve2. get_color())
ax1.xaxis.grid(False)
# Global figure properties
plt.title("Plot of sine and hyperbolic sine")
plt.show()
 

Синтаксис

Параметры

Примечания

График синусоидальной функции — Тригонометрия

График синусоидальной функции — Тригонометрия — Открытый справочник по математике

Открытый справочник по математике

Главная Контакт О Тематический указатель

Когда синус угла строится относительно этой меры угла,
результат представляет собой классическую форму «синусоидальной кривой».

Попробуйте это Перетащите вершину треугольника и посмотреть, как функция синуса зависит от угла.

Чтобы построить график синусоидальной функции, мы отмечаем угол по горизонтальной оси x и для каждого угла откладываем синус этого угла по вертикальной оси y. В результате, как видно выше, получается гладкая кривая, меняющаяся от +1 до -1.

Кривые, которые следуют этой форме, называются «синусоидальными» по названию синусоидальной функции.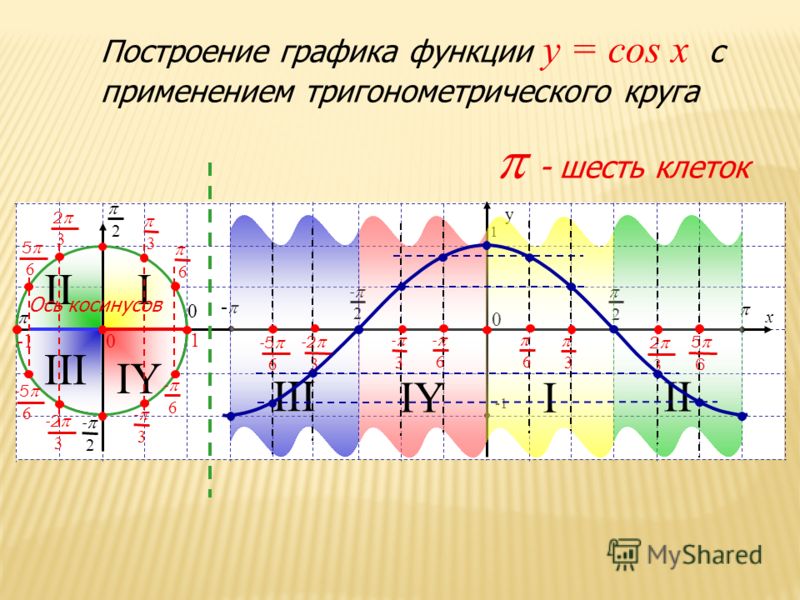 Эту форму также называют синусоидой, особенно когда она появляется в радио- и электронных схемах.

На диаграмме выше перетащите точку A по круговой траектории, чтобы изменить угол CAB. При этом точка на графике перемещается в соответствии с углом и его синусом. (Если вы установите флажок «прогрессивный режим», кривая будет рисоваться при перемещении точки A вместо отслеживания существующей кривой.)

Область определения синуса

Когда вы перетаскиваете точку A, обратите внимание, что после полного поворота вокруг точки B форма графика повторяется. Форма синусоиды одинакова для каждого полного поворота угла, поэтому функция называется «периодической». Период функции составляет 360° или 2π радиан. Вы можете вращать точку столько раз, сколько захотите. Это означает, что вы можете найти синус любого угла, независимо от того, насколько он велик. В математических терминах мы говорим, что «область определения» синуса — это набор всех действительных чисел.

Диапазон

Диапазон функции — это набор значений результата, которые она может произвести.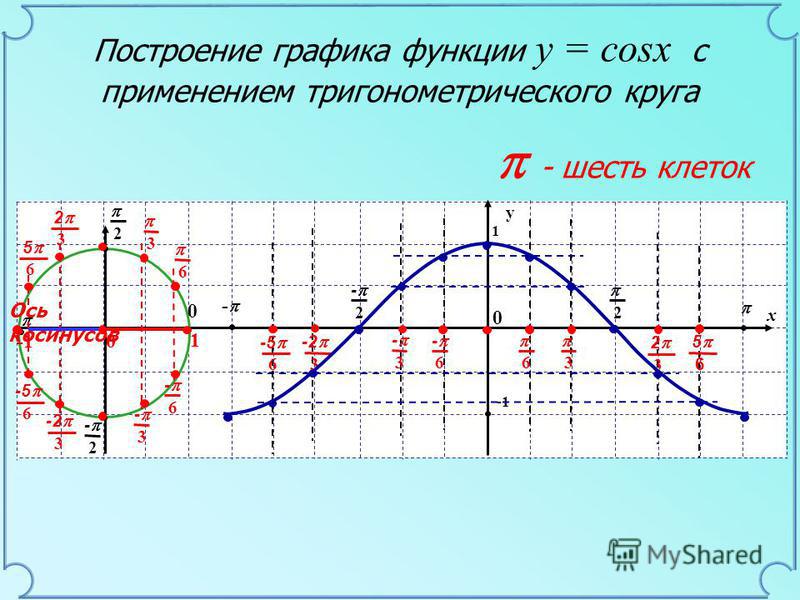 Функция синуса имеет диапазон от -1 до +1. Глядя на кривую синусоиды, вы можете видеть, что она никогда не выходит за пределы этого диапазона.

Функция обратного синуса

Что, если бы нас попросили найти арксинус числа, скажем, 0,5? Другими словами, у какого угла синус равен 0,5?

Если мы посмотрим на кривую выше, то увидим четыре угла, синус которых равен 0,5 (красные точки). На самом деле, поскольку график бесконечно продолжается в обоих направлениях, существует бесконечное количество углов, синус которых равен 0,5.

Так что же говорит калькулятор?

Если вы попросите калькулятор найти арксинус (sin ^-1 ) числа, он не сможет вернуть бесконечно длинный список углов, поэтому по соглашению он найдет только первый из них. Но помните, есть много других.

Другие темы по тригонометрии

Уголки

• Определение угла, свойства углов
• Стандартное положение на углу
• Начальная сторона угла
• Конечная сторона угла
• Четырехугольники
• Котерминальные уголки
• Базовый угол

Тригонометрические функции

• Знакомство с шестью триггерными функциями
• Функции больших и отрицательных углов
• Инверсные триггерные функции
• SOH CAH TOA Память


• Синусоидальная функция (sin) в прямоугольных треугольниках
• Функция обратного синуса (арксинус)
• График синусоидальной функции
• Синусоида


• Функция косинуса (cos) в прямоугольных треугольниках
• Функция арккосинуса (arccos)
• График функции косинуса


• Касательная функция (тангенс) в прямоугольных треугольниках
• Функция арктангенса (арктангенс)
• График функции касательной


• Функция котангенса cot (в прямоугольных треугольниках)
• Функция секанса сек (в прямоугольных треугольниках)
• Функция косеканса csc (в прямоугольных треугольниках)

Решение задач по тригонометрии

• Общий подход
• Определение наклонного расстояния вдоль склона или пандуса
• Определение угла уклона или пандуса

Исчисление

• Производные тригонометрических функций

(C) 2011 Copyright Math Open Reference.
Все права защищены

Sin Graph — Математика GCSE

Введение

Что такое график грехов?

Как построить график sin

Единичный круг

График функции синуса

Обратное значение sin(θ)

Сравнение графиков sin(θ) и cos(θ)

Как использовать синусоиды

Синусоидальный график

Распространенные заблуждения

Похожие уроки

Практикуйте вопросы по диаграмме грехов

График грехов Вопросы GCSE

Контрольный список обучения

Следующие уроки

Все еще застряли?

Индивидуальные занятия по математике, созданные для успеха KS4

Теперь доступны еженедельные онлайн-уроки повторения математики GCSE

Узнать больше

Введение

Что такое график грехов?

Как построить график sin

Единичный круг

График функции синуса

Обратное значение sin(θ)

Сравнение графиков sin(θ) и cos(θ)

Как использовать синусоиды

Синусоидальный график

Распространенные заблуждения

Похожие уроки

Практические вопросы по диаграмме синусов

График грехов Вопросы GCSE

Контрольный список обучения

Следующие уроки

Все еще застряли?

Здесь мы узнаем о синусоидальных графиках, в том числе о том, как распознавать график синусоидальной функции, рисовать синусоидальную кривую и обозначать важные значения, а также интерпретировать синусоидальный график.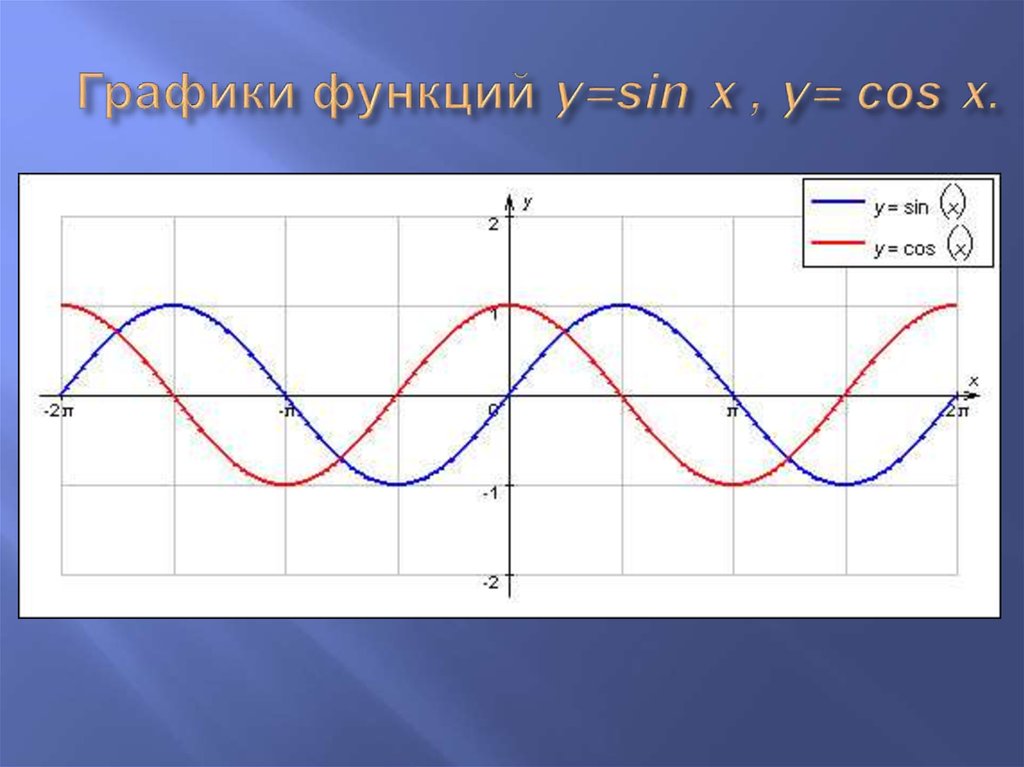

Существуют также рабочие листы с синусоидальными графиками, основанные на экзаменационных вопросах Edexcel, AQA и OCR, а также дополнительные рекомендации о том, что делать дальше, если вы все еще застряли.

Что такое граф грехов?

Диаграмма синуса — это визуальное представление функции синуса для заданного диапазона углов. 9o

Максимальное значение равно 1, а минимальное значение равно -1.

 В этом уроке мы рассмотрим график функции синуса только для углов в градусах, хотя его также можно представить в радианах.

Что такое sin graph?

Как построить график синусов

Помните, что \sin(\theta) — это отношение между противолежащей стороной и гипотенузой прямоугольного треугольника:

Давайте посмотрим на 3 треугольника, где мы использовали бы отношение синусов к вычислить размер угла \theta . Для каждого треугольника гипотенуза одинакова, но длина противоположной стороны и связанный с ней угол меняются.

Здесь мы видим, что поскольку \sin(\theta)=\frac{opp}{hyp} , с увеличением угла \theta увеличивается и длина стороны, противоположной углу. Итак, для каждого треугольника имеем:

• Треугольник 1: \sin(\theta)=\frac{2}{10}=0,2
• Треугольник 2: \sin(\theta)=\frac{6}{10} =0,6
• Треугольник 3: \sin(\theta)=\frac{9}{10}=0,9

Итак, что произойдет, если сторона, противоположная углу, будет равна 10?

\sin(\theta)=\frac{10}{10}=1 9о . Для любых больших или меньших углов нам нужно смотреть на единичный круг.

Объясните, как построить график синуса

Единичная окружность

Единичная окружность — это окружность радиусом 1 с центром в начале координат. Мы можем пометить значения, в которых окружность пересекает оси, потому что мы знаем, что радиус единичной окружности равен 1 единице.

Мы все еще можем построить треугольник внутри единичного круга с углом, начинающимся с положительной оси x.

Глядя на тригонометрические отношения синуса и косинуса, мы можем сказать, что:

• \sin(\theta)=\frac{a}{1} \; \текст{так} \; a=\sin(\theta)
• \cos(\theta)=\frac{b}{1} \; \текст{так} \; b=\cos(\theta)
• \tan(\theta)=\frac{a}{b} \; \текст{так} \; \tan(\theta)=\frac{\sin(\theta)}{\cos(\theta)}

Это означает, что ширина треугольника равна \cos(\theta), а высота треугольник равен \sin(\theta) . Таким образом, точка на единичной окружности является координатой ( \cos(\theta) , \; \sin(\theta) ): 9o , значение y отрицательно, поэтому \sin(\theta) равно отрицательному .

Визуализируя это с помощью осей координат, мы можем показать, когда \sin(\theta) является положительным и отрицательным:

Мы больше не ограничены диапазоном значений для \theta, поскольку мы можем продолжать поворачивать любой угол, положительное или отрицательное направление и получить значение для \sin(\theta) . Поэтому мы можем расширить нарисованный ранее график, чтобы представить этот новый набор значений на графике для углов между -360° и 360°.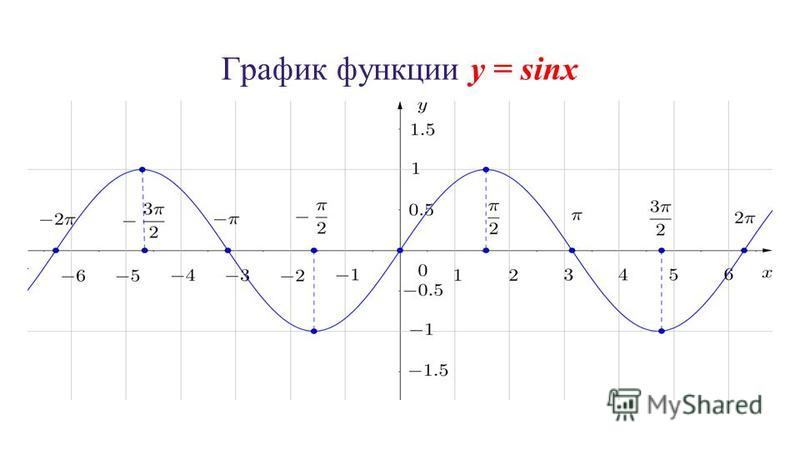 9о).

Функция \sin(\theta) может быть описана как волна, а именно синусоида, с амплитудой 1, поскольку функция ограничена значениями -1 и 1 . Таким образом, максимальное значение равно 1, а минимальное значение равно -1.

Синусоида может иметь разную амплитуду при преобразовании функции.

Пошаговое руководство: преобразований тригонометрических функций.

Вы должны уметь интерпретировать единичный круг, чтобы определить значение \theta. 9{-1}(\тета) .

Обозначения, используемые для обратных функций, не следует путать с обратной функцией . На уровне математики мы узнаем, что функция , обратная к \sin(\theta), называется косекансом или \cosec(\theta), где \cosec(\theta)=\frac{1}{\sin(\theta) )} .

Сравнение графиков sin(θ) и cos(θ)

Графики \sin\theta и \cos\theta очень похожи. На самом деле, если вы примените фазовый сдвиг к любому графику, вы получите график другой функции.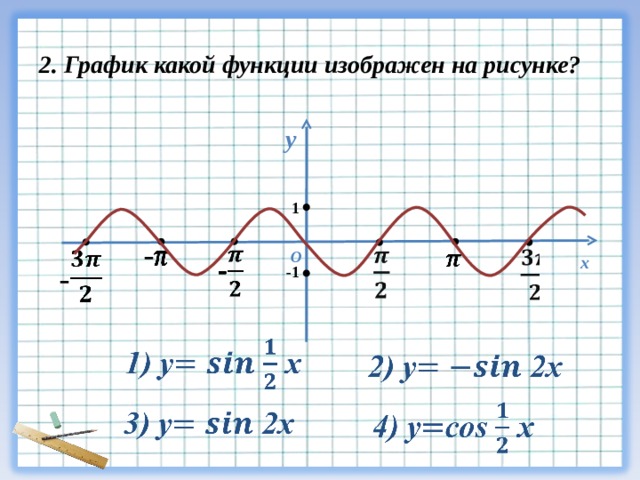

График функций y=\sin(\theta) (зеленым цветом) и y=\cos(\theta) (синим цветом):

Если мы переместим график \cos \theta вправо, вычитая 90 градусов от каждого угла (\cos(\theta+90)) мы получаем \sin(\theta) . Этот горизонтальный сдвиг может быть в любом направлении. Мы также можем выполнять вертикальное смещение, горизонтальное растяжение, вертикальное растяжение, вращение и многое другое!

Пошаговое руководство: преобразование тригонометрических графиков .

Как использовать графики синуса

Чтобы использовать графики синусоиды:

1. Проведите прямую линию от оси известного значения до кривой синусоиды.
2. Нарисуйте прямую перпендикулярную линию в точке пересечения с другой осью.
3. Считайте значение, где перпендикулярная линия пересекает другую ось.

Рабочий лист с синусоидальным графиком

Получите бесплатный рабочий лист с 20+ вопросами и ответами. Включает рассуждения и прикладные вопросы.

СКОРО

Икс 9o считывается с графика.

• Графики синуса и косинуса перепутаны

Графики синуса и косинуса очень похожи, и их легко спутать друг с другом. Совет, который следует помнить, заключается в том, что вы «синусируете вверх» от 0 для синусоидального графика, поэтому линия увеличивается, тогда как вы «косинусируете вниз» от 1, поэтому линия уменьшается для косинусного графика.

• Неправильно построены асимптоты для графика функции тангенса 9о и так далее.
  • Графики рисуются с помощью линейки

  Каждый тригонометрический график представляет собой кривую, поэтому единственный раз, когда вам требуется использовать линейку, — это начертить набор осей. Потренируйтесь рисовать каждую кривую от руки и отмечайте важные значения на каждой оси.

  • Значение, указанное вне диапазона

  При нахождении значения \theta с помощью тригонометрического графика необходимо убедиться, что значение \theta находится в пределах диапазона, указанного в вопросе. o .

   

   

  Если \sin(x)=0,7 , какое другое значение для \theta вернет то же значение \sin(\theta) ?

   

  (1 балл)

  Показать ответ

  180-x

  (1)

  2. (a) Напишите уравнение относительно \theta для величины угла CAB .

   

   

  (b) Используйте график y=\sin(\theta) для оценки значения \theta в треугольнике ABC . 9о

  (1)

  Учебный контрольный список

  Теперь вы научились:

  • распознавать, чертить и интерпретировать графики тригонометрических функций (с аргументами в градусах) y = sin \; x для углов любого размера.

  Все еще застряли?

  Подготовьте своих учеников KS4 к успешной сдаче выпускных экзаменов по математике с помощью программы Third Space Learning. Еженедельные онлайн-уроки повторения GCSE по математике, которые проводят опытные преподаватели математики.

  No related posts.