График sinx x: График y = f(x) = (sin(x))/x ((синус от (х)) делить на х) постройте график функции и изобразите его. Исследуйте данную функцию. [Есть ОТВЕТ!]

alexxlab / / Разное

Mathway | Популярные задачи

1Найти точное значениеsin(30)
2Найти точное значениеsin(45)
3Найти точное значениеsin(30 град. )
4Найти точное значениеsin(60 град. )
5Найти точное значениеtan(30 град. )
6Найти точное значениеarcsin(-1)
7Найти точное значениеsin(pi/6)
8
Найти точное значение		cos(pi/4)
9Найти точное значениеsin(45 град. )
10Найти точное значениеsin(pi/3)
11Найти точное значениеarctan(-1)
12Найти точное значениеcos(45 град. )
13Найти точное значениеcos(30 град. )
14Найти точное значениеtan(60)
15
Найти точное значение		csc(45 град. )
16Найти точное значениеtan(60 град. )
17Найти точное значениеsec(30 град. )
18Найти точное значениеcos(60 град. )
19Найти точное значениеcos(150)
20Найти точное значениеsin(60)
21Найти точное значениеcos(pi/2)
22Найти точное значениеtan(45 град. )
23Найти точное значениеarctan(- квадратный корень из 3)
24Найти точное значениеcsc(60 град. )
25Найти точное значениеsec(45 град. )
26Найти точное значениеcsc(30 град. )
27Найти точное значениеsin(0)
28Найти точное значениеsin(120)
29Найти точное значениеcos(90)
30Преобразовать из радианов в градусыpi/3
31Найти точное значениеtan(30)
32Преобразовать из градусов в радианы45
33Найти точное значениеcos(45)
34Упроститьsin(theta)^2+cos(theta)^2
35Преобразовать из радианов в градусыpi/6
36Найти точное значениеcot(30 град. )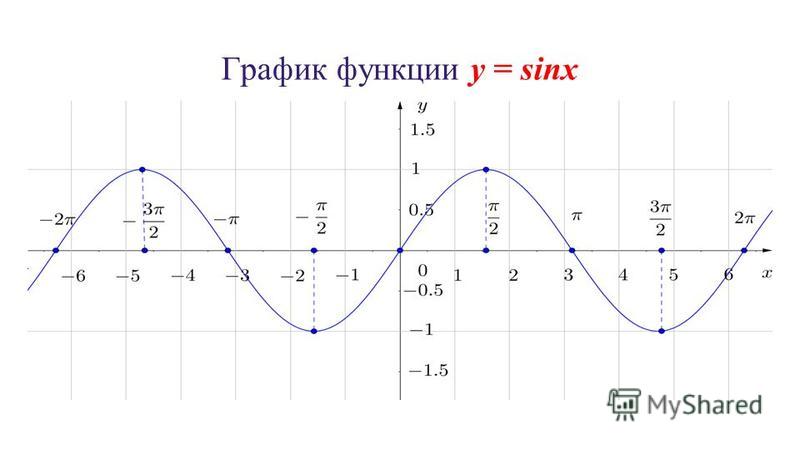
37Найти точное значениеarccos(-1)
38Найти точное значениеarctan(0)
39Найти точное значениеcot(60 град. )
40Преобразовать из градусов в радианы30
41Преобразовать из радианов в градусы(2pi)/3
42Найти точное значениеsin((5pi)/3)
43Найти точное значениеsin((3pi)/4)
44Найти точное значениеtan(pi/2)
45Найти точное значениеsin(300)
46Найти точное значениеcos(30)
47Найти точное значениеcos(60)
48Найти точное значениеcos(0)
49Найти точное значениеcos(135)
50Найти точное значениеcos((5pi)/3)
51Найти точное значениеcos(210)
52Найти точное значениеsec(60 град. )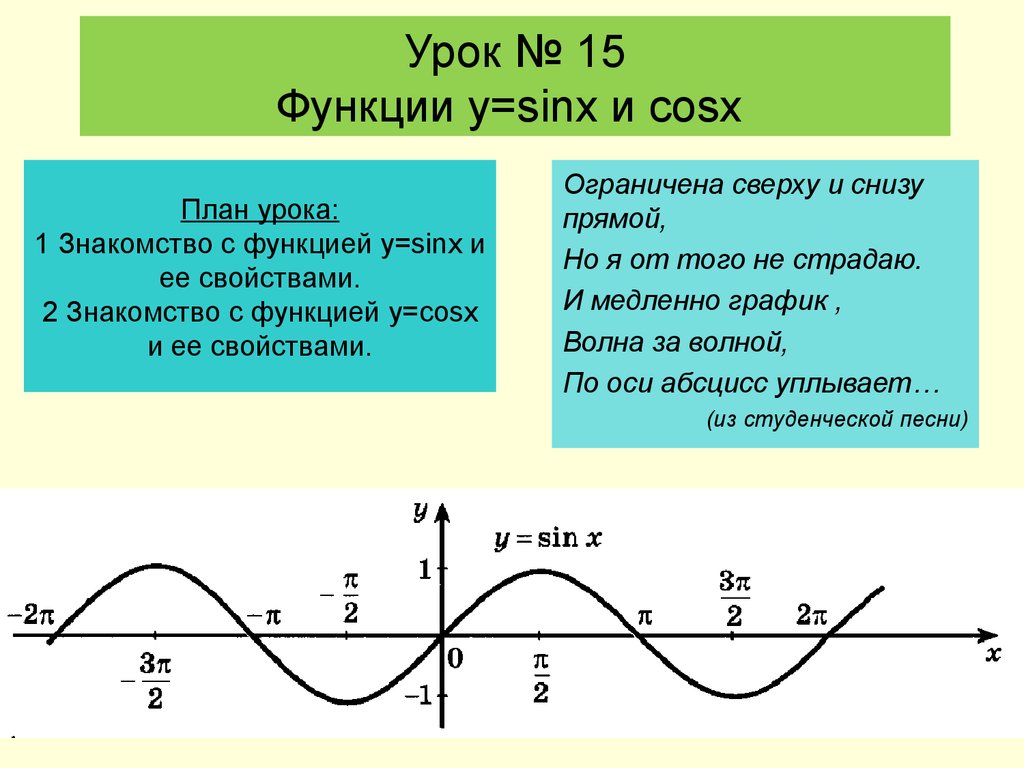
53Найти точное значениеsin(300 град. )
54Преобразовать из градусов в радианы135
55Преобразовать из градусов в радианы150
56Преобразовать из радианов в градусы(5pi)/6
57Преобразовать из радианов в градусы(5pi)/3
58Преобразовать из градусов в радианы89 град.
59Преобразовать из градусов в радианы60
60Найти точное значениеsin(135 град. )
61Найти точное значениеsin(150)
62Найти точное значениеsin(240 град. )
63Найти точное значениеcot(45 град. )
64Преобразовать из радианов в градусы(5pi)/4
65Найти точное значениеsin(225)
66Найти точное значениеsin(240)
67Найти точное значениеcos(150 град. )
68Найти точное значениеtan(45)
69Вычислитьsin(30 град. )
70Найти точное значениеsec(0)
71Найти точное значениеcos((5pi)/6)
72Найти точное значениеcsc(30)
73Найти точное значениеarcsin(( квадратный корень из 2)/2)
74 Найти точное значениеtan((5pi)/3)
75Найти точное значениеtan(0)
76Вычислитьsin(60 град. )
77Найти точное значениеarctan(-( квадратный корень из 3)/3)
78Преобразовать из радианов в градусы(3pi)/4
79Найти точное значениеsin((7pi)/4)
80Найти точное значениеarcsin(-1/2)
81Найти точное значениеsin((4pi)/3)
82Найти точное значениеcsc(45)
83Упроститьarctan( квадратный корень из 3)
84Найти точное значениеsin(135)
85Найти точное значениеsin(105)
86Найти точное значениеsin(150 град. )
87Найти точное значениеsin((2pi)/3)
88Найти точное значениеtan((2pi)/3)
89Преобразовать из радианов в градусыpi/4
90Найти точное значениеsin(pi/2)
91Найти точное значениеsec(45)
92Найти точное значениеcos((5pi)/4)
93Найти точное значениеcos((7pi)/6)
94		Найти точное значениеarcsin(0)
95Найти точное значениеsin(120 град. )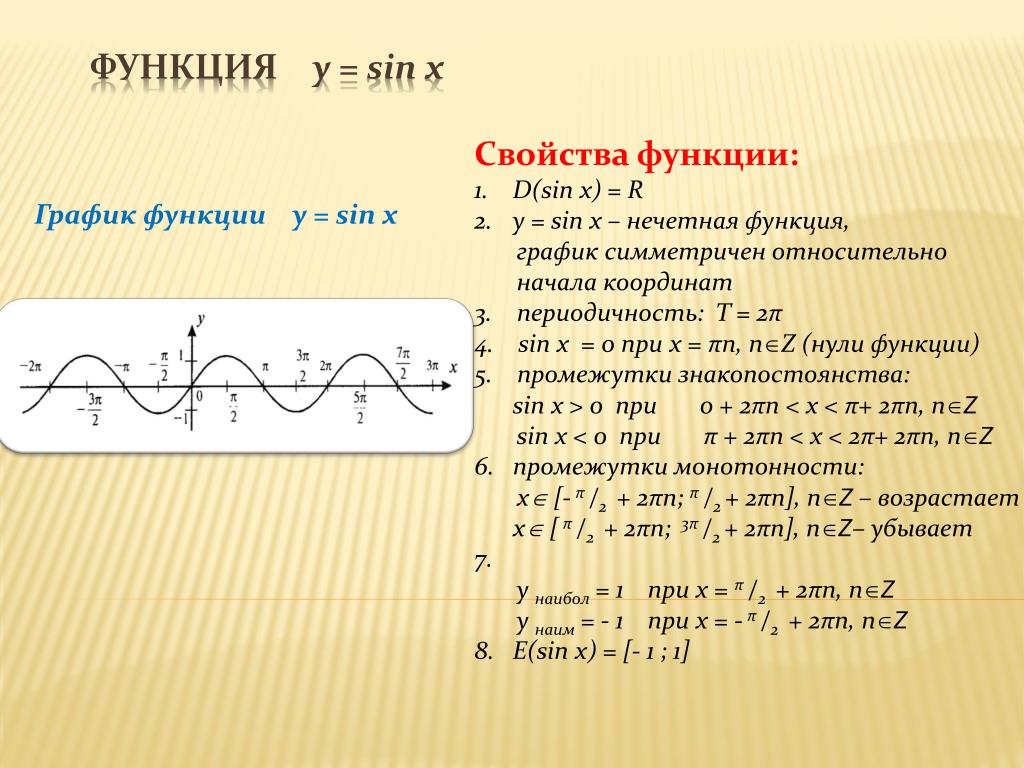
96Найти точное значениеtan((7pi)/6)
97Найти точное значениеcos(270)
98Найти точное значениеsin((7pi)/6)
99Найти точное значениеarcsin(-( квадратный корень из 2)/2)
100Преобразовать из градусов в радианы 88 град.

Как построить график функции в Excel – База знаний Timeweb Community

Виктор Бухтеев

26K

1 комментарий

Личный опыт #Программы #Microsoft

7 мин. 2, заменив номер ячейки.

  • Теперь достаточно зажать левую кнопку мыши на нижней точки готовой ячейки и растянуть таблицу, чтобы формула автоматически подставилась в остальные ячейки, и вы могли сразу ознакомиться с результатом.

  • Перейдите на вкладку вставки и выберите раздел с рекомендуемыми диаграммами.

  • В списке отыщите точечную диаграмму, которая подойдет для составления подходящего графика.

  • Вставьте ее в таблицу и ознакомьтесь с результатом. На следующем скриншоте вы видите параболу и значения X, при которых она получилась правильной (такую часто показывают в примерах на математике).

    • Всего 7 простых шагов потребовалось для достижения желаемого результата. Вы можете подставлять свои значения в таблицу и изменять их в любое время, следя за тем, как перестраивается график функций.

    Комьюнити теперь в Телеграм

    Подпишитесь и будьте в курсе последних IT-новостей

    Подписаться

    График функции y=sin(x)

    y=sin(x) – вторая функция, которую мы возьмем за пример.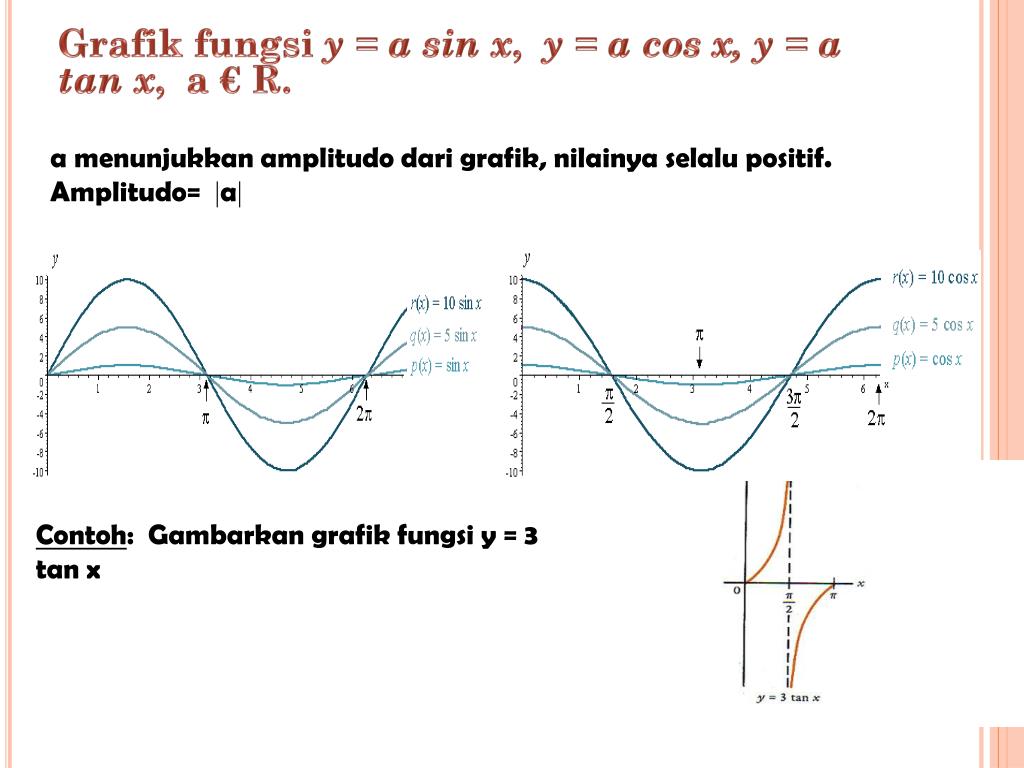 Может показаться, что ее составление осуществляется сложнее, хотя на самом деле это не так. Дело в том, что Excel сам посчитает значения, а вам останется только задать известные числа и вставить простой линейный график для вывода результатов на экран.

    1. Если вам будет проще, впишите в отдельную клетку функцию, укажите интервал и шаг. Так вы не запутаетесь при дальнейшем заполнении ячеек.

    2. Добавьте два столбца, в которые будут вписаны значения каждой оси. Это нужно не только для обозначения чисел, но и для их вычисления при помощи функций программы.

    3. Начните вписывать значения X с необходимым интервалом и шагом. Кстати, вы можете заполнить всего несколько полей, а затем растянуть клетки таким же образом, как было показано в предыдущем примере, чтобы они подставились автоматически до конца вашего интервала.

    4. Теперь более сложное, но не страшное действие – определение значения Y. Понятно, что он равняется синусу X, значит, нужно вписать функцию =SIN(A1), где вместо A1 используйте нужную ячейку, а затем растяните функцию на оставшийся интервал.

    5. На следующем скриншоте вы видите результат заполнения таблицы. Используйте округление для удаления лишних знаков после запятой.

    6. Вставьте обычную линейчатую диаграмму и ознакомьтесь с результатом.

    На примере этих двух функций уже можно понять, как работает построение графиков в Экселе. При использовании других функций просто учитывайте особенности заполнения ячеек и не забывайте о том, что вам не нужно ничего считать, поскольку Excel все сделает за вас после указания необходимой формулы.

    Личный опыт

    Наши постоянные авторы и читатели делятся лайфхаками, основанными на личном опыте. Полная свобода самовыражения.

    Рекомендуем

    график y = sin (x/3)

    график y = sin (x/3) | mathtestpreparation. com

    вернуться к математический вопрос и ответ

    График y = A sin Bx обладает свойством
    (1). амплитуда = |А|
    (2). период = 2pi/B
    Для y = sin(x/3),
    , поскольку A = 1, поэтому его амплитуда равна |1|
    , так как B = 1/3, поэтому его период = 2pi/B = 2pi &divide 1/3 = 2pi &times 3 = 6pi
    Таким образом, его амплитуда равна 1, а период равен 6pi
    Найти пять точек за один период
    один период равен 6pi, половина периода равна 3pi, четверть периода равна 3pi/2
    разделить пять точек поровну в периоде [0, 6pi]
    , поэтому пять точек по оси x:
    х 1 = 0
    х 2 = 3pi/2
    х 3 = 3pi
    x 4 = 3pi + 3pi/2 = 6pi/2 + 3pi/2 = 9pi/2
    x 5 = 9pi/2 + 3pi/2 = 12pi/2 = 6pi
    , поэтому пять точек в плоскости xy: (0, ?), (3pi/2, ?), (3pi, ?), (9pi/2, ?), (6pi, ?)
    Теперь найдите значения функции y = sin(x/3) в пяти точках
    , когда x = 0, y = sin(x/3) = sin[(1/3) × 0] = sin(0) = 0, поэтому точка равна (0, 0)
    , когда x = 3pi/2, y = sin(x/3) = sin[(1/3) &times 3pi/2] = sin(pi/2) = 1, поэтому точка равна (3pi/2, 1)
    , когда x = 3pi, y = sin(x/3) = sin[(1/3) &times 3pi] = sin(pi) = 0, поэтому точка равна (3pi, 0)
    , когда x = 9pi/2, y = sin(x/3) = sin[(1/3) &times 9pi/2] = sin(3pi/2) = -1, поэтому точка равна (9pi/2, -1)
    , когда x = 6pi, y = sin(x/3) = sin[(1/3) &times 6pi] = sin(2pi) = 0, поэтому точка равна (6pi, 0)
    Пять точек: (0, 0), (3pi/2, 1), (3pi, 0), (9pi/2, -1), (6pi, 0)
    Нарисуйте график y = sin(x/3) на основе пяти точек
    Значения функции синуса для специальных углов:
    грех(0) = 0
    sin(pi/2) = 1
    грех (пи) = 0
    sin(3pi/2) = -1
    sin(2pi) = 0
    Анализ графика:
    х = 0, у = 0.
    x = 3 pi — его полупериод, в этот момент его значение y равно 0.
    x = (3/2)pi — его четвертьпериод, в этот момент его значение y равно 1, что является максимальным.
    x = (9/2)pi — это его три четверти периода, в этот момент его значение y равно -1, что является минимальным.
    x = 6 pi является конечной точкой одного периода, в этой точке его значение y равно 0,
    Кривая y = sin (x/3) непрерывна,
    его второй период от x = 6 pi до x = 6 pi + 6 pi = 12 pi,
    его третий период от 12 пи до 12 пи + 6 пи = 18 пи,
    его четвертый период от 18 pi до 18 pi + 6 pi = 24 pi и так далее.

    Краткий обзор синусоидального графика


    Прежде всего, мы дадим вам несколько новых терминов. Надеюсь, вы принесли свою рукавицу ловца.

    Ваша базовая синусоидальная функция имеет следующую форму:

    Период триггерной функции представляет собой горизонтальную длину одного полного цикла. Например, приведенный выше график начинает повторять свою форму через 2π единиц на 9-й шкале.0126 x -ось, поэтому период равен 2π.

    В общем, для y = a sin( bx ) , период равен

    Средняя линия функции в значительной степени то, на что она похожа: горизонтальная линия, проходящая через «середину» нашей триггерной функции. Это будет прямо между максимальным и минимальным значениями графика. Поскольку это горизонтальная линия, она всегда будет выглядеть как y = (что-то).

    Для функций вида y = a sin( bx ), как и на графике выше, средняя линия всегда представляет собой ось x , также известную как линия y = 0. Посмотрим, что произойдет, когда эта линия скользит вокруг немного позже.

    Амплитуда триггерной функции — это ее «высота» или расстояние по вертикали между средней линией и максимальным или минимальным значением. По сути, это то, насколько высокими становятся «волны» функции. График выше имеет пики на y = 1 и y = -1, поэтому его амплитуда равна всего 1.

    В общем, для y = a sin( bx ) амплитуда равна | и |. Также важно отметить, что если a < 0, график переворачивается (инвертируется).

    Разговоры дешевы, так что теперь давайте посмотрим на них в действии.

    Пример задачи

    Как выглядит график y = sin x ?

    Амплитуда (максимальное значение) y = грех x равно |1| = 1. Период (время, необходимое для одного полного цикла) y = sin x равен 2π ⁄ 1 = 2π. Средняя линия y = sin x является осью x . Построим график у = sin х.

    Как и в случае с любым графиком, он помогает построить график значений x и y . Включите пять ключевых углов, используя период 2π, и пять ключевых точек, полученных из этих углов.

    График x против y дает нам:

    Пример задачи

    График y = 3 sin x.

    На этот раз наша амплитуда равна |3| = 3. Наш период по-прежнему 2π ⁄ 1 = 2π, а наша средняя линия по-прежнему y = 0.

    Давайте составим нашу таблицу.

    Применим период 2π к пяти ключевым углам и амплитуду 3 к пяти ключевым точкам.

    Расставьте точки.

    Пример задачи

    Укажите амплитуду и период y = 4 sin x. Затем постройте график функции.

    Из y = a sin( bx ) мы получаем амплитуду |4| = 4, а период 2π ⁄ 1 = 2π.

    Теперь нарисуйте это.

    Начните со стола.

    При построении этого графика мы просто будем следовать той же схеме, чтобы расширить график до 2π.

    No related posts.

    Добавить комментарий

    Ваш адрес email не будет опубликован. Обязательные поля помечены *